アインシュタインの特殊相対性理論(1905年)
アインシュタインの1905年論文「運動物体の電気力学について」をもとにして、特殊相対性理論を説明します。
準備としてBorn文献202.の第Ⅴ章をお読みに成ることを勧めます。私が長いあいだ相対性理論の“光速不変の原理”を納得できなかったのはここに書かれている事柄をあらかじめ学んでおかなかったからだと思っています。
相対性理論を理解するにはこの引用文の最後でBornが述べている認識(旧版の訳はこちら)に到達することが大切なのではないでしょうか。また、Sommerfeldの著書「光学」の§49に記されている説明も秀逸です。これも前記Bornの認識に通じるものですが、特殊相対性理論を理解する為の必須の認識事項です。
また、本稿を読まれた後にEinstein文献108.をお読みになることを勧めます。この本の前書きに述べられている様に、読み通すにはかなりの忍耐力と意志力が必要ですが読む価値のある本です。
前記Bornの文献に倣って、この稿では電磁気学を全てGauss単位系で論じます。
なぜなら
1.アインシュタインの源論文がGauss単位系で説明されているのでアインシュタイン論文と比較しやすい。
2.Gauss単位系では場に関する量が全て同じ次元となり電気と磁気の双対性が良く、方程式の対称性が良くなる。
3.アインシュタインが相対性理論を構築する際に拠り所としたローレンツ電子論の記述に最も適している。
4.電磁気学を真に理解するには静電単位・電磁単位・ガウス単位・MKSA有理化単位の全てに通じおくべき。
だからです。
単位系については別稿「電磁気学の単位系が難しい理由」をご覧下さい。
1.導入
アインシュタインは最初に“物理法則に対する相対性原理”と“光速度一定の原理”を掲げて、話を始めます。
(1)相対性原理
物理現象を観測するある座標系(K系とする)とそれに対して一定速度vで移動している座標系(k系orK’系とする)を考える。これらの座標系の様に、相手に対して互いに一定速度で動いている座標系を、“慣性系”という言う。
それら互いに慣性系の関係にある座標系の座標値を用いて表した各座標系に於ける力学の運動方程式(ニュートンの“運動の第二法則”や“運動の第三法則(作用反作用の法則))”は、全て同じ形で表されることが知られている。これはガリレオ・ニュートンの相対性原理として知られているものですが、その詳細は文献205.のp24~28をご覧下さい。
このように力学現象を表す法則が座標系の選び方によらず全て同じ形式で表されることを“自然法則の相対性原理”という。ただしここでは互いに一定速度で動いている座標系に対してのもので、互いに加速度運動をしている座標系間についてのものではない。互いに等速度で動いている座標系に付いての相対性なので“特殊”相対性原理と言うことにする。
この事は、力学的な現象をいくら詳しく調べてみても、自分たちが互いに等速度で動いている座標系の中のどの座標系に存在するのかを知ることができない事を意味する。つまり我々は絶対的な空間を直接認識する何らの手段(少なくとも力学的な手段の中には)を持っていないことになる。
アインシュタインは、その様に絶対的な空間を知ることができないという考え方に導かれて相対性理論を打ち立てた。そのとき大きな影響を受けたのがマッハの『力学』であったようです。アインシュタインはマッハの死去に際しての追悼文で、特に『力学』の第Ⅱ章§6と§7に述べられた考察を見ることを勧めている[Einstein,Phys.Zeits.,17,p102,1916年]。これらの節はマッハ『力学』の中でも特に有名なところなので別稿にて引用しておきます。この当たりはアインシュタインの自伝ノート[文献106.]もご覧下さい。
[補足説明]
ニュートンの力学方程式はガリレオ変換に対しては、“物理法則の相対性原理”を満たしますが、後で説明する真に正しいローレンツ変換に対しては満たしません。
またマックスウェルの電気力学方程式はガリレオ変換に対しては“物理法則の相対性原理”を満たしませんが、ローレンツ変換に対しては満たします。このことは後に証明される。
だから、アインシュタインの言う“物理法則の相対性原理”を満たす真に正しい力学方程式や電気力学方程式がどのような形になるのかは、最初はまったく解っていないことに注意して下さい。
アインシュタインは深い哲学的考察(ランダウ・リフシュツの文献302.§1も参照)からこの原理が成り立つべきだと確信していたのです。
この事に関してアインシュタイン自身は、後に1917年の文献108.第5章で次のように述べている。



(2)光速不変原理
このような絶対的な空間というのが、物理学者や天文学者に強く意識されるようになったのは、19世紀に発達した光学や電磁気学が深く関わっています。電磁波や(光が電磁波の一種で在ると言う認識が確立して以降の)光の波が何を伝わるのかが重要な研究対象になってきます。そのとき物理学者・天文学者はその電磁波を伝える空間こそが絶対的な空間であり、光はその空間に対して等速度で伝わると考えていました。
だから、多くの物理学者・天文学者は、光や電磁波の性質を調べればそれを伝える絶対的な空間(光・電磁波はその空間を占めるエーテルを一定速度で伝わる)が解るに違いないと考えていた。そして多くの実験・観測が行われた。
19世紀後半は、ニュートンの力学法則(運動方程式)とは別の、マクスウェルの電磁気学法則(電荷・電流と電場・磁場で記述される方程式系)が知られてきて、電磁気学的な現象はこの方程式系で正確に記述されるということが解ってきた。それはまさに、電磁場の波動である電波が発見され、光も電磁場の波動そのものであるという認識が確立した時代です。以下は文献205.第2章§2(p28~29)より引用。

これは、別稿「線形振動子・・」1.や、別稿「Maxwell・・」2.(3)3.や、本稿3.(2)1.[補足説明1]で示すように波動方程式の形にしてみて解ることです。




これらの結果は物理学者・天文学者を困惑させた。そのときアインシュタインは次のように考えた。
まず、(1)“物理法則は、互いに等速並進運動をしている全ての慣性系に対して同一の形式であるべきである。”とした。この第一の要請は前節で述べた、ガリレイ・ニュートンの相対性原理となんら変わるところが無いようにみえるが、彼はこの要請が力学的な現象ばかりではなく、電磁気現象や、その他全ての物理現象の法則に対しても成り立つべきだとした。
これは革新的な考え方で、彼がこの考え方に到達するに当たってマッハの『力学』は大きな影響を与えたようです。その様に相対性原理を全ての物理現象に広げれば、絶対静止という特別な空間を占めるエーテルなどは考える必要がなくなり、絶対空間(エーテル)の存在を仮定して作り上げようとしていた多くの物理理論が抱えていた困難や疑問を解決できるだろうと予想した。
この第一の要請を今後“アインシュタインの特殊相対性原理”と呼ぶことにする。特殊という言葉が付いているのは、この要請が互いに等速並進運動をする慣性系間のみに限られているからです。
さらにアインシュタインは第二の要請をします。それは、(2)“光は光源と観測者の相対速度に関係なく、全ての観測者に対して同一の値を持っている。”というものです。この要請はなかなか解りにくいものですが、どのような慣性系に静止している観測者にとっても光の速度は光源の速度に関係なく同じ速度で進むというものです。
これは、v/cの一次の精度において、あるいは二次の精度(マイケルソン・モーリーの実験)において繰り返された多くの光速度測定実験に於いて、観測者の移動速度に拠って光速度が変化する事を示す証拠が何も得られなかったという実験・観測結果をそのまま要請したものです。
今後これを“光速度不変の原理”と呼ぶことにしましょう。
[補足説明1]
“光速度不変の原理”を納得・理解するのは難しい。
確かに、最も素朴な形での光速度不変の原理はマックスウェルの電気力学方程式から受け継いでいます。その中に現れる不変定数cは、その電気力学方程式から導かれる波動方程式中の位相速度なのだから(3.(2)1.[補足説明1]を参照)。もしマックスウェルの電気力学方程式が前記の“物理法則の相対性原理”を満たしているのなら、“光速度不変の原理”は当然満たされていることになります。そのため、さらに光速度不変の原理を導入するのは二重の要請の様に見えます。
しかし、マックスウェルの電磁場方程式はガリレオ変換に対する相対性原理を満たしてはいません。そのため、当時の大多数の物理学者、天文学者は光速度が不変なのは、絶対的に静止した空間(エーテルはそこを満たしている)に対してのもので、それに対して慣性運動をしている任意の座標系に関して成り立つとは思っていなかったのです。だからこそエーテル空間を検出する多くの試みが繰り返された。
アインシュタインの言う“光速度不変の原理”とは任意の慣性系から見た光速度に対して成り立つものです。だから“光速度不変の原理”はマックスウェルの電気力学方程式を含めた任意の物理法則に関して成り立つ相対性原理とは独立の要請であることに注意して下さい。光の速度が不変であることは、マックスウェルの電気力学方程式が正しいかどうかなどとは次元の違うもっと根源的な原理なのです。
実際、ガリレオ変換に対して完全に相対性原理を満たしているニュートンの力学方程式は、ローレンツ変換に対してはv≪cの場合に近似的に相対性原理をみたしているに過ぎません。また、マックスウェルの電気力学方程式が相対性原理を完全に満たしているのかどうかは(ローレンツ変換がまだ発見されていない段階では)解らないことです。だから、“物理法則の相対性原理”が根源的な要請だったと同じように、“光速度不変の原理”もそれと独立な根源的な要請なのです。
アインシュタイン自身は後に1917年の文献108.第7章で次のように述べている。



さらに後の1952年に、文献108.の最終版に付け加えた附録5で次のように述べている。




前記の二つの原理は、別々に考えると真であるように見えるのですが、この二つの要請は互いに矛盾する結果を導きます。それは時間に関して考察してみれば解ります。以下は文献205.のp30~31より引用。



この例はアインシュタインが最初に取り上げたもので、相対性理論の導入として特に有名なものです。繰り返しになりますが、文献212.の佐藤先生の解説が解りやすいので引用しておきます。


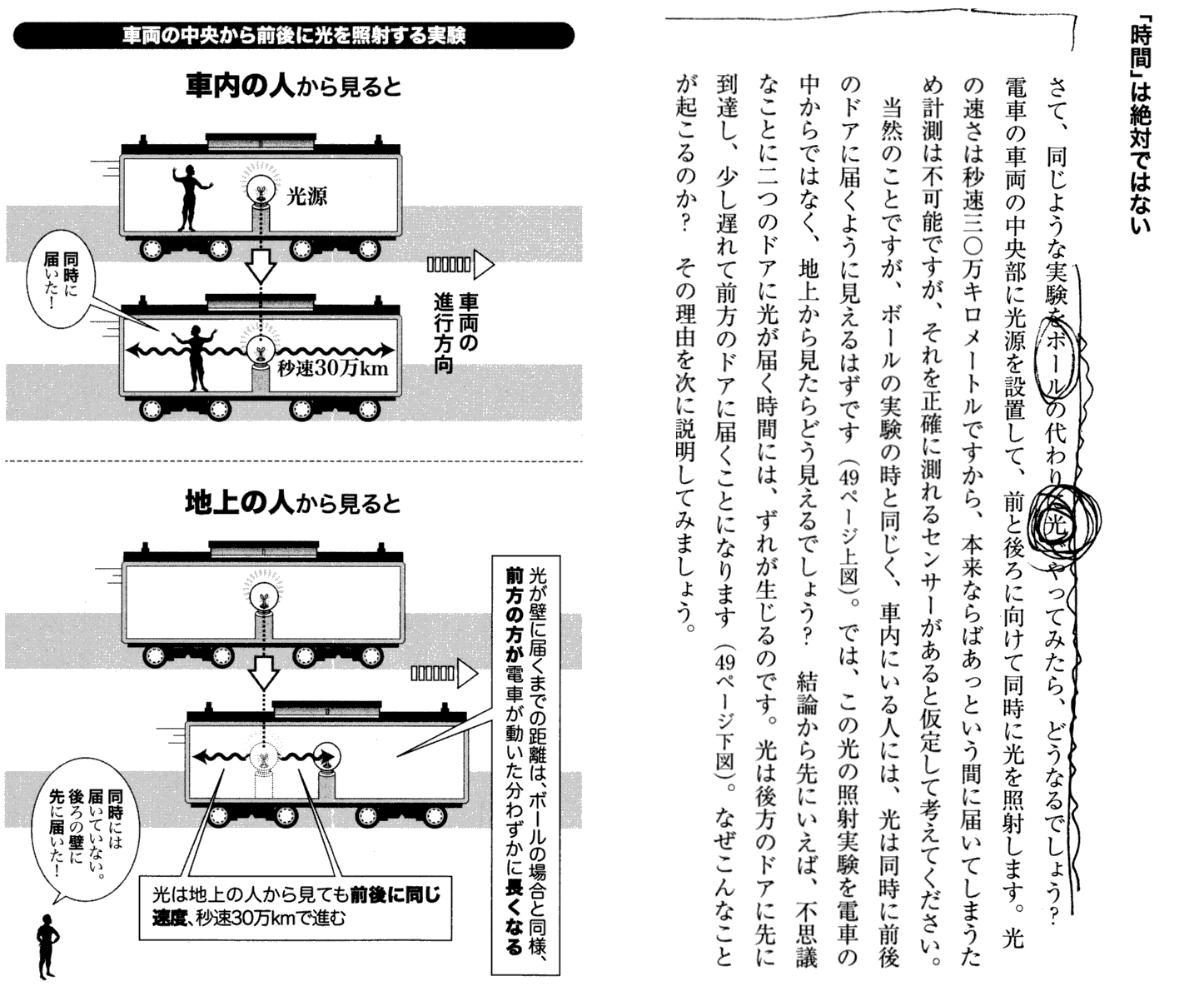

上記の説明は非常に解りにくい所です。この説明の中で、光の速度は光源の速度に関係しない事に特に注意して下さい。光源の速度に関係しないのなら車両の中の人に取って車両の両端に光が同時に到着するはずは無いと言われるかも知れませんが、光の場合は光源の速度に関係しないのに同時に到着するのです。ここは解りにくい所ですがやがてそのわけを説明しますから今はその様に思っておいて下さい。
最初のボールの例では二つのボールを打ち出す車内装置の速度にボールの速度は依存しています。そのように、ボールの速度がボールを打ち出す装置の速度(つまり車両の速度)に依存すれば、地上の人から見たボールの速度は車両の進行方向が速く、その逆方向が遅くなります。そのためボールは車両内の人から見ても、地上の人から見ても車両の前後の壁に同時に衝突します。
[補足説明2]
アインシュタインはここで説明した光速度が関係したときの矛盾に深く悩みます。そして一年近く悶々とした思考を続けます。この“同時性の矛盾”を解決する事こそが全ての鍵でした。
その時の事情を文献107の京都講演で語っています。その中の友人との議論(p82)をご覧下さい。ここは引用されることが多い有名な箇所です。
議論相手の友人はミケーレ・ベッソーで、1905年の論文でただ一人感謝を捧げている人です。このことからも時間の同時性に付いての考察がいかに重要だったかが読み取れます。
ついでに補足しますと、文献503の中(p24)でゼーリッヒの“マッハ『力学』を知ったのはいつか”という質問に答えて、ローマ大学からスイス連邦工科大学の機械工学部に移ってきていた同窓のミケーレ・アンジェロ・ベッソー(彼はアンシュタインより6歳年長)がこの革命的な著作の中に物理学の核心を感じとり、たぶん1897年にアインシュタインの注意をこの本に向けさせたと語ったことが紹介されています。
そのとき「この本は、基本概念および基礎法則に対する批判的態度のゆえに、のちに読んだ『熱学の諸原理』などよりもはるかに深く、はるかに永続的な影響をわたしに与えてくれた。」と語っている。
また話がベッソーのことに及んだとき、アインシュタインは「ヨーロッパ中に彼以上の共鳴板を見いだすことはできなかったであろう。」と賞賛した事を記している(p59)。
[補足説明3]
“光速度不変の原理”と“相対性原理”の二つが特殊相対性理論の中でどのような位置を占めるかを理解するのは難しい。すべてを学んだ後でないと解らないのですが、取りあえず以下の様に考えて下さい。
まず『ニュートンの運動方程式』はガリレオ変換に対して不変ですから、その意味において、“相対性原理”を満たした物理法則です。また、『Maxellの電磁場方程式』はローレンツ変換に対して不変ですから、その意味に於いて“相対性原理”を満たした物理法則です。だから物理法則は“相対性原理”を満たさねば成らないと言う意味に於いては両方の物理法則とも満たしてします。
問題はガリレオ変換が正しいのか、ローレンツ変換が正しいのかと言うことです。
正しいのはローレンツ変換ですが、このローレンツ変換は何から導かれるかと言いますと、“光速度不変の原理”から導かれます(ただし、このとき“相対性原理”を援用しています)。これから、時間の相対性、長さの相対性が導かれるのですから“光速度不変の原理”は特殊相対性理論に於いて最も根本的な原理です。
つまり“光速度不変の原理”は“相対性原理”が依って立つ変換法則を導くときに利用する原理です。
このローレンツ変換が導かれ確立したとき、“相対性原理”は元の『古典的なNewtonの運動方程式』はその原理を満たしていないことを明らかにします。そのため、ローレンツ変換を満たすように運動方程式を修正しなければならないのですが、その修正の仕方を教えてくれる指導原理が“相対性原理”です。その修正された正しい『相対論的な力学運動法則』を見つけるために“相対性原理”が働いて利用されている。
また、Maxwell方程式もそのままではローレンツ変換に対する“相対性原理”を満たしません。Maxwell方程式がローレンツ変換に対して不変であるべきであると言う“相対性原理”を満たすためには、アインシュタインが導いたように電磁場もローレンツ変換共変の変換則で変換されねばなりません。電磁場もその様に変換されねばならないと言うことを導く所に“相対性原理”が働いて利用されている。
“光速度不変の原理”は根本的な大原理で、それから導かれるローレンツ変換を様々な物理法則に適用して真に正しい物理法則を見つける所に“相対性原理”が働いている。これが特殊紙相対性理論に於いて“光速度不変の原理”と“相対性原理”が占める位置とその働きではないでしょうか。
だから、その二つの原理に対して、“相対論的な運動方程式”、“Maxwell方程式”、さらに電磁場中の荷電粒子に対する“ローレンツの力の法則”、等々・・・は物理法則(原理の一種)としては一段階低いレベルの法則・原理です。つまり、“相対論的な運動方程式、Maxwell方程式、ローレンツの力の法則、等々・・・”は、それぞれ限られた分野の限定的な現象に対してのみ有効な法則でしかありません。
もう少し補足しますと、“物理学における原理”というものは、それが原理であることが先験的に解るものでは無く、いろいろな自然現象を観察し考察する内にそれが原理ではないかと、少しずつ解ってきて、それがいつとはなく原理として確立していくようなものだと思います。
“光速度不変の原理”と“相対性原理”の関係も、それが互いに独立であるのか互いに依存しているのかが先験的に問題となる様なものでは無くて、互いに依存しており微妙にその役割・働き所も違うが確かに原理といって良い様なものであることが後から解る様なものでしょう。実際のところ、特殊相対性理論の元になるローレンツ変換は光速度不変の原理と相対性原理から導かれたものですから。
(3)同時の概念
時間の同時の概念は極めて解りにくい所なので、しつこい様ですが文献202.第Ⅵ章§1(p221~224)からBornの説明を引用しておきます。




ここは別稿「マイケルソン・モーリーの実験の特殊相対性理論による説明」1.[補足説明]をご覧下さい。








ここも何を言っているのか解りにくいと思います。2章以降で詳しく説明しますので、今はそんなものかと思っていて下さい。
(4)相対的同時の決定
前節で説明したように“絶対的な同時”の概念は意味を成さないのですが、“相対的な同時”は定義することができるし意味を持ちます。アインシュタインは以下のように“相対的な同時”を決めた。ここは文献205.第2章§3(p31~33)の引用です。





(5)長さと時間の相対性
次に、アインシュタインは、時間のみならず長さも相対的なものだと説明します。このとき重要なのは、長さの相対性は時間の相対性と深く関係していることです。
これは別稿「マイケルソン・モーリーの実験(1987年)」5.[補足説明3]で注意した、“ローレンツの収縮仮説が整合的に成り立つためには局所時が必要だった。”に関係する事柄です。
ここの所も解りにくいところですが、文献212.の佐藤先生の説明が秀逸ですので引用しておきます。佐藤先生は長さの相対性の説明に先立って時間の短縮の話から始められますが、ここに本質があります。

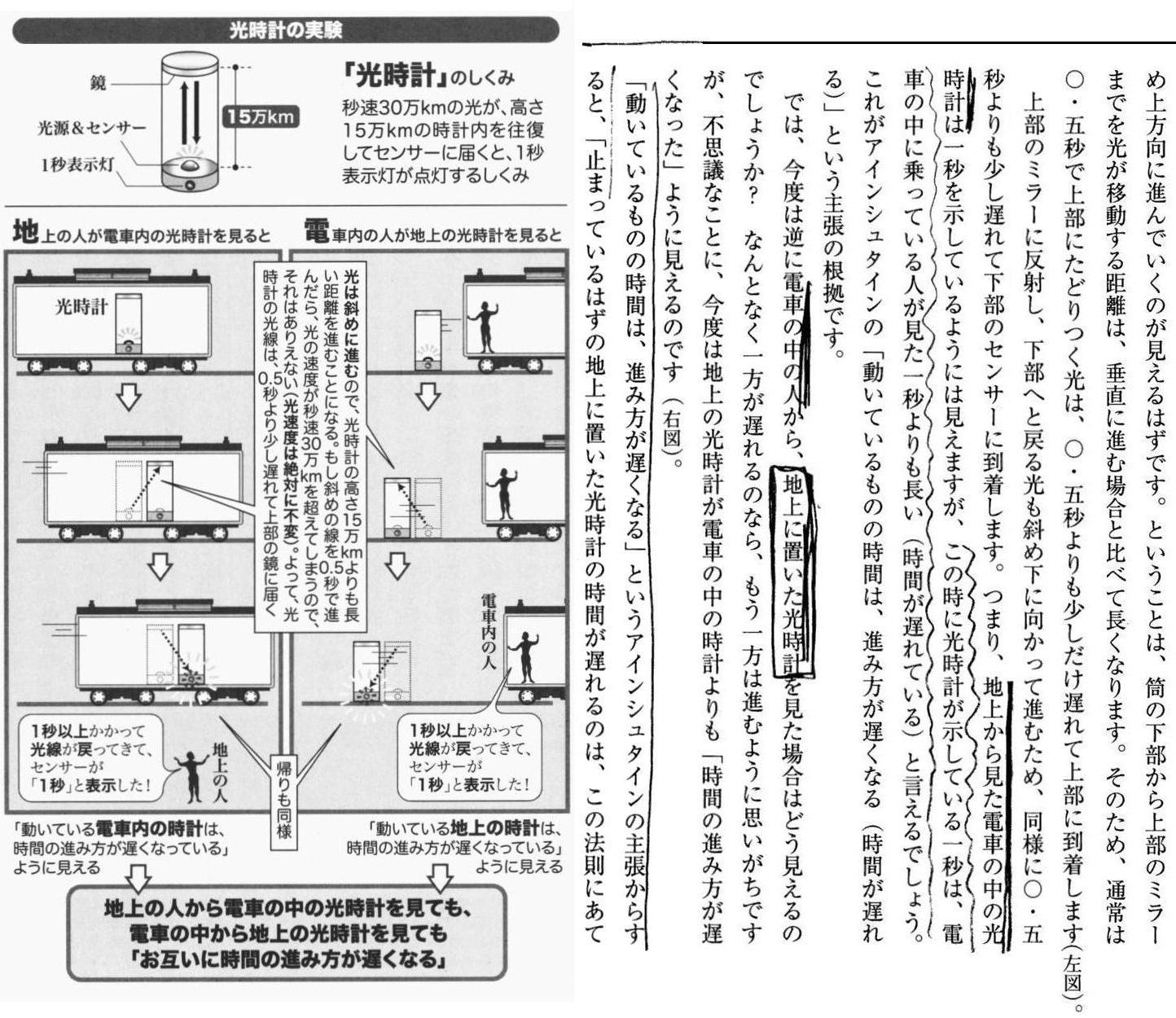
上図の“光時計”の話は良く取り上げられますが、この現象を正しく理解するのは、マイケルソン・モーレーの実験を正しく理解するのが難しいのと同様に、極めて難しいです。

上記の計算式はやがて導きますが、取りあえず“光時計”について文献208.の説明を引用しておきます。ただし、この説明を正しく理解するのは結構難しいです。本稿を読了後に、別稿の議論などを参考にされながら振り返られて下さい。




長さの縮みの計算式もやがで導きます。ここでは文献208.の説明を引用してもう少し補足しておきます。この説明文中の動いている物体の長さの測り方に注意して下さい。このようにして測らねばならないことに本質があります。
この例を検討されれば、動いている物体の長さが縮むのは時間の相対性に関係することがお解りになると思います。

[補足説明]
以上で導入は終わりですが、ランダウ・リフシュツの「場の古典論」§1.の導入部も秀逸ですので引用しておきます。最後にもう一度以下の事を強調したい。
相対性理論が出て来る前の状況というのは、様々な物理学分野(特に電磁気学や光が関係する現象)に於いて理論的に旨く説明できない実験・観測結果がつぎづぎと集積していた時代でした。そして、その矛盾を解決するための様々な模索が多くの人々に依って試みられていた。フレネルの随伴係数、収縮仮説、局所時間、電磁質量の速度依存性、様々な座標変換公式、・・・・等々。そのため相対性理論はやがて誰かによって発見されていたでしょう。
そんな状況下で、アインシュタインが偉大だったのは、非常に一般的な哲学原理に基づいて時間と空間のとらえ方を革命的に変え、それまでに存在していた矛盾の全てを一気に解決してしまったことです。
そして、それ以後の物理学者に“物理学は相対性理論の元でのみ辻褄の合う理論が構築できる”を確信させたことです。
この事についてホルトンは、文献510.の論文(p81)で、下記引用のウィーンの言葉を紹介している。
“・・・・鋭い感覚をもつ物理学者のW.Wienは、はじめは相対論に同意できぬことを公表していたが、1909年になってようやく納得した。それも、明快な証拠が実験によって得られたからではなく、審美的な理由だった。次のようなWienの言葉はEinsteinなら高く買うにちがいない。
『・・・しかしながら、なによりもこの理論の正しさを訴えているのは、その内的な首尾一貫性である。これによって、自己矛盾を含まず、物理現象の全体に適用できるような基礎をおくことが可能となった。もっともそのさい慣用の諸概念は変更を受けるのだが。・・・』(U¨ber Elektronen,2nd ed.,Leipzig,B.G.Teubner1909年、p32)
・・・・”
そのウィーンが1912年にはアインシュタインとローレンツをノーベル賞に推薦(Paisの文献502.p194~195参照)するのですから、かなり短い期間にこの理論の持つ威力が物理学者の間に浸透していったことが解る。
おそらく、このWienの認識が当時の有力な物理学者の平均的な状況であったのだろう。この当たりについてのインフェルトの説明。
さらに注意すべきは、Bornが文献202で、“一般にアインシュタインの名のみが相対性理論に結びつけられているのはアインシュタインの理論が発表以後も引き続いて発展を続けたためである。彼が1905年に発表した研究はいっそう基礎的な重力の新理論を含み、宇宙の構造の理論に新しい展望を開いた「一般相対性理論」への出発点に過ぎなかったのである。”と述べていることです。
確かに、この事を心に留めて「特殊相対性理論」を学ぶ必要があるのでしょう。実際、文献107.や文献502.などによると、アインシュタインは1907年頃にはすでに一般相対性理論の構築を模索し始めているようです。この当たりについてのインフェルトの説明。
2.相対論的運動学
ここから、いよいよEinsteinの1905年論文「運動物体の電気力学について」の説明に入ります。以下の訳文は文献103.より引用した。ただし、原論文では光速をVで表しているが、ここではcに変更されています。また、挿入されている[No.]を実線で四角に囲った注記は内山先生による。
最初に前書き、および§1、§2の部分を引用します。ここは、簡潔な文体で相対性理論の本質を的確かつ見事に表現しており、歴史に残る名文です。名文ですので佐藤文隆先生の訳文と解説もお読み下さい。
(1)原論文の前書き





[補足説明1]
上記の事柄は別稿「交流電気回路」1.(1)[補足説明]で注意を喚起したものです。
アインシュタインは下記の二つの場合を取り上げて説明している。
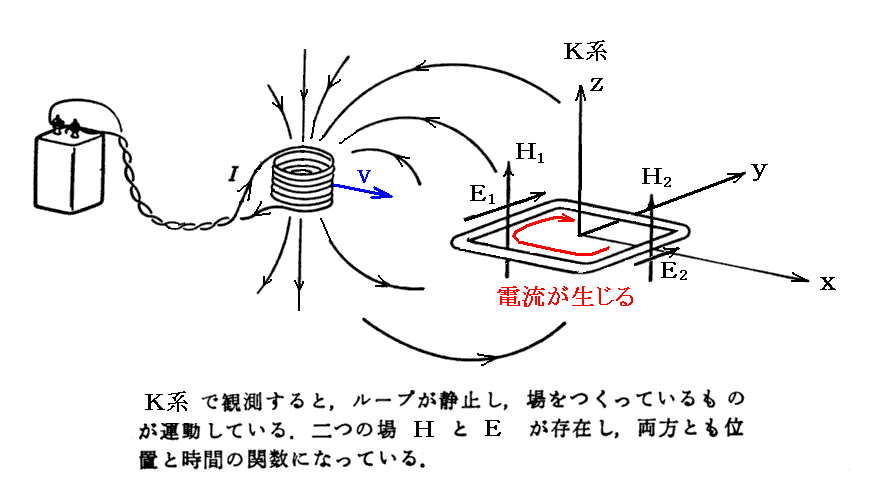
最初の例は、“ファラデーの電磁誘導の法則”で説明できる。導線の位置の磁場が時間的に変化するために、その導線部分に誘導電場が生じて、導線中の電荷はその電場によって動かされる。
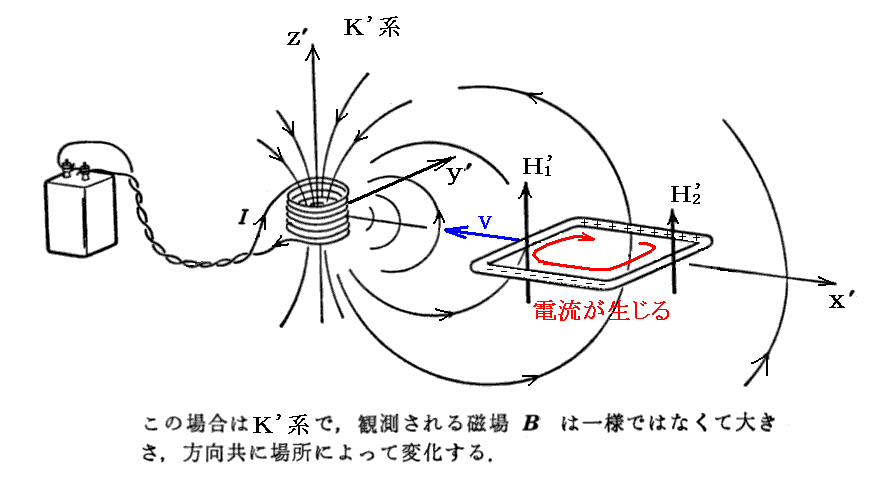
二番目の例は、時間的に変化しない磁場中を導線が動き、その導線中の電荷に対して“ローレンツの力の法則”F=q/c[v×H](磁場をHで表したGauss単位系表示)による力が働き、導線中の電荷が動かされる。
“ファラデーの電磁誘導の法則”と“ローレンツの力の法則”の関係については別稿「電磁気学の単位系が難しい理由」5.(4)まとめ で説明しましたように
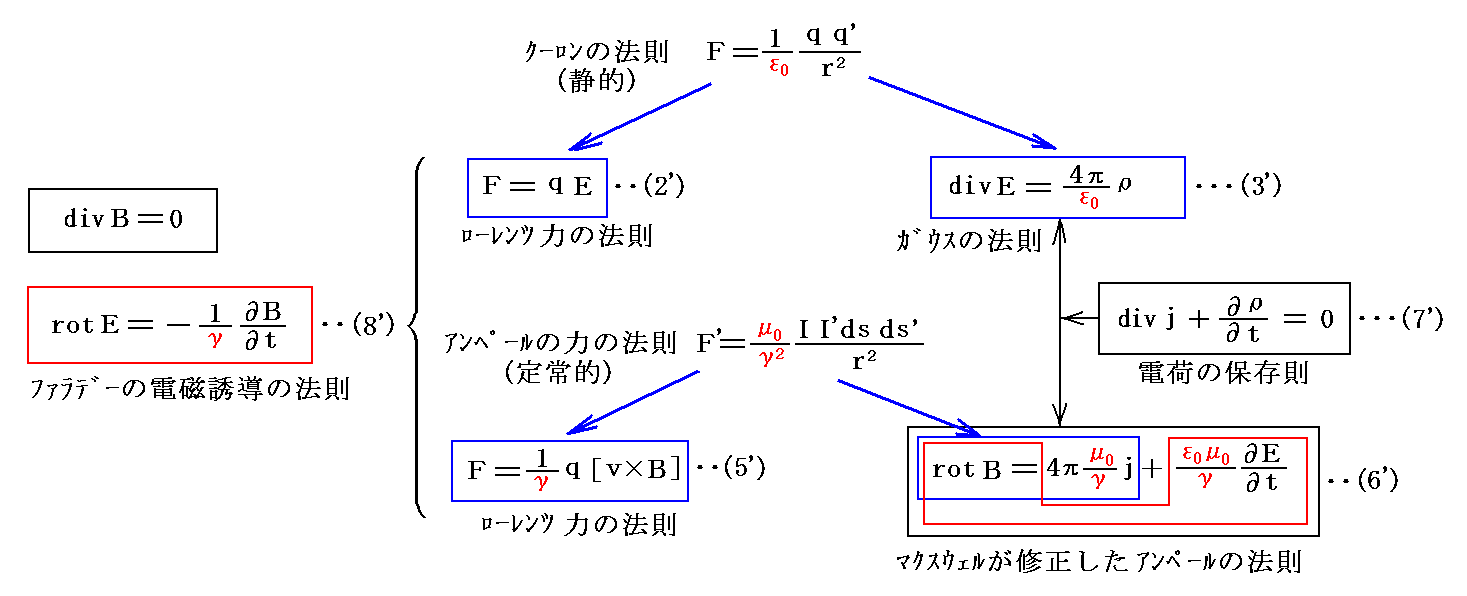
となる。
この稿で利用しているGauss単位系では、上記式でε0=μ0=1、γ=cとなります。またGauss単位系ではB=Hとなり、この稿では磁気的な場としては“磁束密度”Bではなくて“磁場”Hを採用していますので、B→μ0H→H(μ0=1) と置きかえることになります。つまり
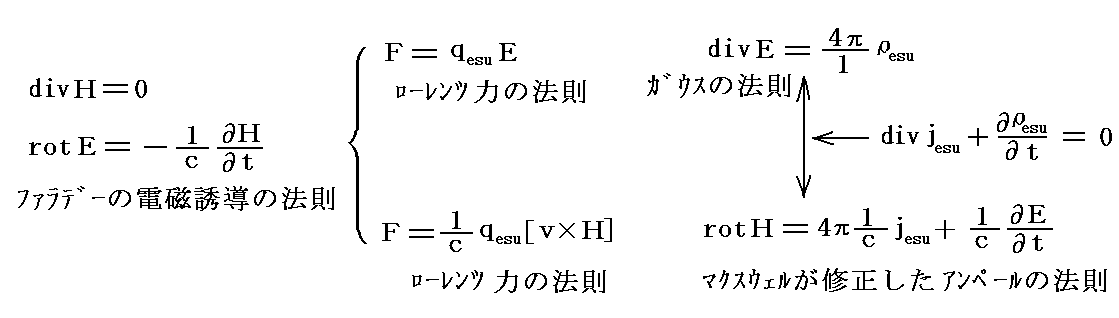
となる。
上で説明した二つの状況のどちらの導線中の電荷に対しても“ほぼ同じ効果が生じる”のですが、それを見る座標系によってMaxwell方程式系は全く異なった説明を与える。最初の例はファラデーの電磁誘導の法則、二番目の例はローレンツの力の法則に拠ることになる。
アインシュタインはこの事に深く悩みますが、後で説明するようにK系で見える電場E=(Ex,Ey,Ez)と磁場H=(Hx,Hy,Hz)は、それに対して速度vで動くK’系(アインシュタインはk系と言っている)から見ると以下の変換式にしたがった電場E’=(Ex’,Ey’,Ez’)と磁場H’=(Hx’,Hy’,Hz’)として観測される事を相対性理論によって導きます。
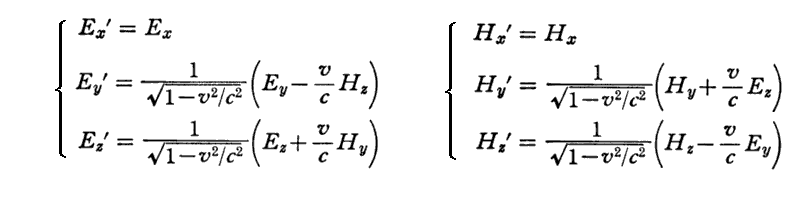
そのとき、K系でのMaxwell方程式を、後に説明する“ローレンツ変換”によってK’系での方程式に変換したとき、電場と磁場を上記の変換式にしたがって置き換えると、Maxwell方程式が全く同じ形になることに気付きます。
そうして、電磁場に対するMawell方程式が相対性原理を満たしていることを確かめて、上記の現象を全て辻褄が合う形で説明することができたのです。この事についての詳細は3.電気学(1)をご覧下さい。
[補足説明1-1](2019年10月30日追記)
誤解の無いように補足しておきます。前紀の2つの図の状況で回路を流れる電流値(つまりK系から見たときの電流値 j とK’系から見た時の電流値 j’)が完全に等しいわけではありません。K系とK’系に於ける電流( j と j’)は導線の帯電電荷密度(K系から見た場合のρとK’系から見た場合のρ’は少し異なります)と共にローレンツ変換によって互いに結びつけられます。だから互いに少し異なりますので“全く同じ効果が生じる”と言う言い方は語弊があります。“ほぼ同じ効果が生じる”と書くべきです。
ただし、K系とK’系との相対速度vがv≪cを満たす場合は、K系とK’系での電流値(j と j’)や帯電電荷密度(ρとρ’)の違いはほとんど有りません。その意味に於いて、両系で“全く同じ効果が生じる”と言っても良いということです。
この当たりの詳細については別稿「電磁場の相対性」5.[補足説明2]をご覧下さい。そこの試験電荷qが上記図中の回路内の伝導電子と解釈されて下さい。その伝導電子が図中の力を受けて動き出して電流となり、それが再び「電磁場の相対性」5.[補足説明2]に説明する変換式で互いに結びつけられると考ます。そこのローレンツ変換式をご覧になると解る様にv≪cでρ≒ρ’≒0と見なせる場合には j≒j’ となります。
[補足説明1-2](2019年11月10日追記)
上記2つの見方を特殊相対性理論を用いて正しく関係付けるのはかなり難しいです。そのことについては別稿「電磁場の相対性と特殊相対性理論」をご覧下さい。
[補足説明1-3](2020年3月2日追記)
前記の稿を更に解りやすくした別稿「電磁場の相対性と特殊相対性理論(補足説明)」を追加しました。
[補足説明2]
上記Gauss単位系の方程式系に具体的な数値を代入するときの注意事項を補足する。
ガウス単位系においては、電気的な量の定義は電荷に関するクーロンの法則による電気量 q の定義から出発する。そして、磁気的な量の定義としては今日では磁荷のクーロンの法則よりも、電流が生み出す電磁気力を磁気力の基本とする立場を取る。そのため磁気的な量も電気的な電流 I を定義することから出発する。それが電磁単位系の電流の定義である。
そのとき電流は電気量を時間微分したものだから、そのままでは電気量という物理量に対して二通りの定義が存在することになってしまう。そのことを避けるために電磁単位で測った電流密度値に光速を掛けてから速度で割って静電単位の電気密度の定義に一致させる。つまり
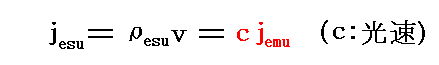
の関係式を設定する。
そのため、ガウス単位系に於いて磁気的な量を定義するとき、磁荷の磁気力ではなくて、電流が生み出す電磁気力を磁気力の基本とする立場をとれば、ガウス単位系における電流や電流密度は電気的な量であるにもかかわらず電磁単位系のそれらと同じ次元と数値を持つことになる。だから、MKSA有理化単位系からガウス単位系へ電流や電流密度の数値を変換するときの変換係数も電磁単位系の対応するものと同じになる。
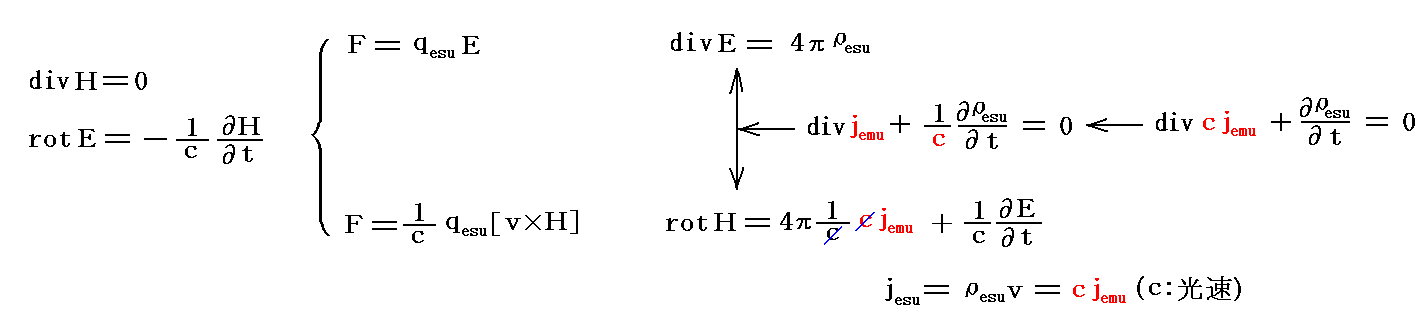
電磁単位の1単位の電気量は静電単位の1単位の電気量のc倍だから、測定数値としては電磁単位で測った値の方が1/c倍小さい。そのためc倍しておかなければいけない。この当たりはとても混乱するところですが、ガウス単位系で実際の数値を取り扱うときには注意しなければならない。
もちろんガウス単位系の電流単位も静電単位で定義した電気量に速度vを乗じたものであると定義すると、このような混乱は起こらないで前記の方程式系の表現がそのまま使える。今後はそちらの表現式を用いることにする。







(2)原論文§1


[補足説明1]
以後の議論でアインシュタインは“静止した系(K系)”とか、それに対して“速度vで動いている系(k系)”という言い方をしばしばします。しかし、本来どちらの系が静止していて、どちらの系が動いているのかを判定する方法は無いのです。
だからアインシュタインの上記の言い方は単に言い表し方を簡単化するために言っているだけであって、どちらが止まっていてどちらが運動しているかを定めているわけではないことに注意して下さい。読者が混乱せず理解しやすいように、そのように言っているだけです。
解るのは、k系はK系に対して速度ベクトルvで動いており、K系はk系に対して速度ベクトル-vで動いているという相対的な運動だけです。この相対的な運動ならば互いに判定して定めることは出来ます。
[補足説明2]
アインシュタインは様々な機会に“空間”という言葉について説明してます。例えば文献108.第1部3章で、『さしあたり“空間”というあいまいな言葉をまったくのけてしまおう。そういう言葉では、正直いって何一つ考えることができない。そのかわりに、“事実上剛体である基準体に対する運動”と置く。基準体(列車または地面)に対する位置はすでに前の章で詳しく定義してある。』
と述べています。
ここで述べている空間とは(剛体の)基準体そのもののことであり、前の2章で詳しく定義してある。解りやすく言えば、基準体に設置されている縦、横、上向きに互いに垂直になるように立てた物差しの棒そのものが空間だと言うことです。その物差しの棒で測られる縦横高さの量がその基準体で測られた空間の座標値だと言うことです。
だから今後、“地面に静止する観測者”や、地面に対して速度vで移動する“列車に静止している観測者”や、列車に乗っている観測者から“前方に投げ出されたボール”というような物体が議論されるのですが、地面に設置している(縦、横、上向きの)物差しの棒のセット、列車に設置してある同様な物差しの棒のセット、ボールそのものにくっついている物差し棒のセットで測られる座標値がそれぞれの空間ということです。
















(3)原論文§2



















[補足説明1]
アインシュタインは、ここではまだ時間の相対性、長さの相対性を述べるだけで、その証明やそれを表す式を具体的に与えてはいません。その理論式を求めるために必要なローレンツ変換式は次の§3で求められます。
[補足説明2]
アインシュタインは、§2節で有名な“光速不変の原理”を説明していますが、その定義文に“光速度は光源の移動速度に依らない”という但し書きと“光速度の測り方”の注意書きを付記しています。
なぜこれらを付け加える必要があったのか?その深遠な理由については、別稿「アインシュタインの公式E=mc2の証明」3.[補足説明3]とそれに続く説明を参照して下さい。
(4)原論文§3 ローレンツ変換
原論文第Ⅰ部§3は有名なローレン変換式を導いている所でこの論文の中心です。ただし、かなり難しい所なので繰り返し読まれることを勧めます。






上記の内山補注[9.]は長文なので別ページで引用。




[補足説明0]
上式の意味は解りにくいので補足する。
まず、ここでは(K系の時計で)時刻tにkの原点から発射された光がk座標系のある点に固定された鏡で反射されてk系の原点に帰る迄の現象を解析している。もちろんK系から見るとその原点は光が往復する間に速度vで動いている。その同一の現象をk系で見た場合とK系で見た場合を対比している。
k系の原点とk系の座標x’の点(鏡が固定されている点)を結ぶ棒がK系から見てK系のX軸に沿って正方向へ速度vで動いていると考えればよい。その時k系の時計でτ(0,0,0,t)にk系の原点を出発してk系の座標点x’へ進む光をK系で見ている。K系ではその光は当然光速度cで進みます。それに対してk系の上記の棒(K系の物差しで測って長さx’≡l’の棒)は速度vで右に動いているのですから、その棒に取って光は速度(c-v)で追いついてくるように見えるわけです。だからそのK系から見たその光がk系の原点から出発後にk系上の鏡(座標x’)に到達する時刻はK系の時計で
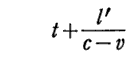
の時刻になる。
同様に考えると、x’に到着した後に、そこの鏡で反射してk系の原点に帰るまでの時間経過はK系の時計で
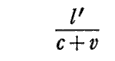
となります。
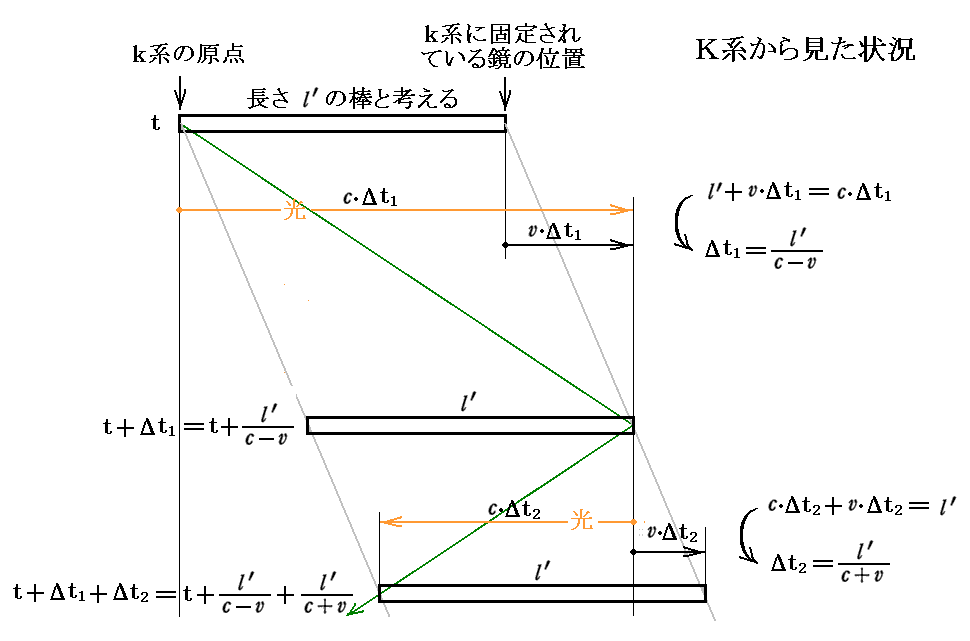
だからK系から見て動いているk系の座標に付着した0-x’=長さl’の棒の動きは式の中でちゃんと考慮されています。そのとき式中のτはK系から見て動いているk系に付着している時計の指し示している時刻であることを忘れないで下さい。それはK系に対して静止している時計が指し示す時刻tの関数となります。やがて解るように時計の存在する場所x’にも関係します。
さらに補足すると、式中のx’=l’はK系に静止している物差しで測ったk系における光の反射点とk系原点との間の距離です。実際、少し前の文節でアインシュタインが説明しているように

だったのですから。


[補足説明1]
上記の関係式については、1.(5)で佐藤先生が説明されている“光時計”、あるいは、そこで引用した文献208.の説明を参照されて下さい。これから、すぐ後で必要になる
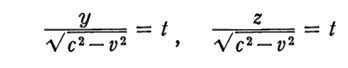
が導かれます。


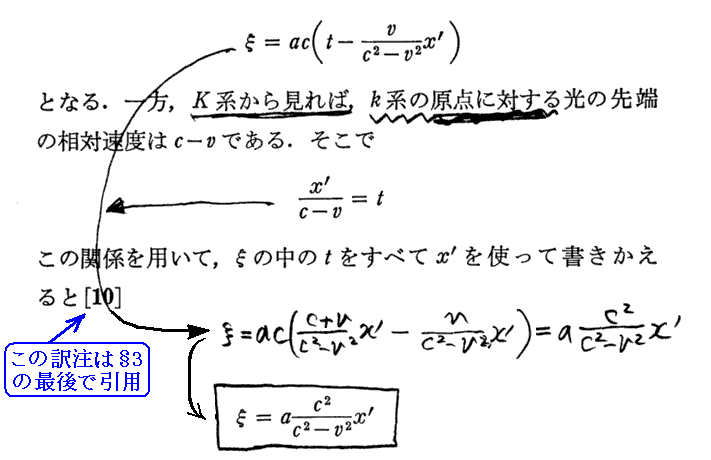
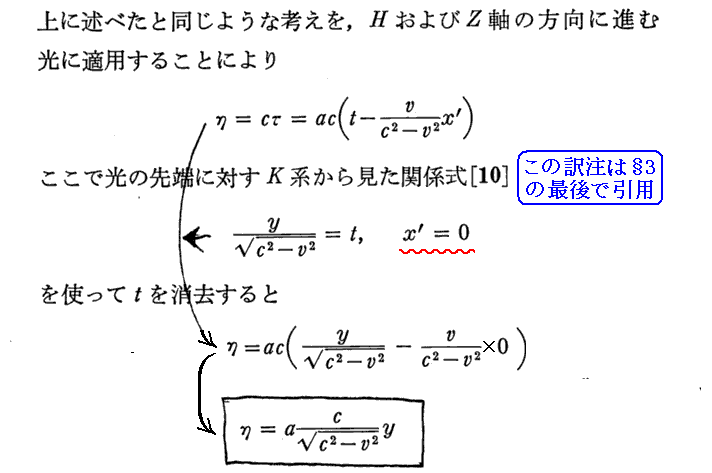
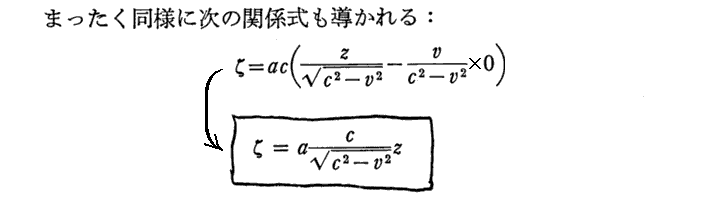
[補足説明2]
式変形を補足する。
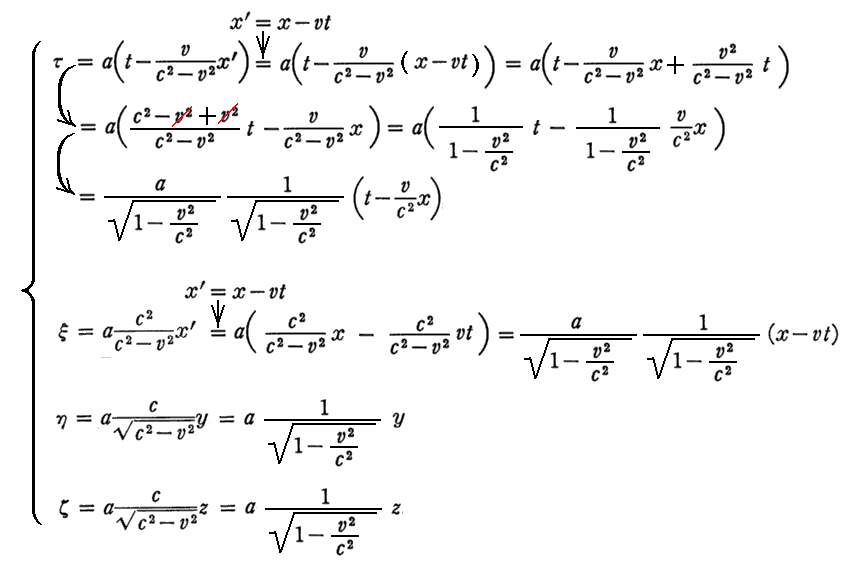




[補足説明3]
上記の“簡単な計算”は下記の通りです。
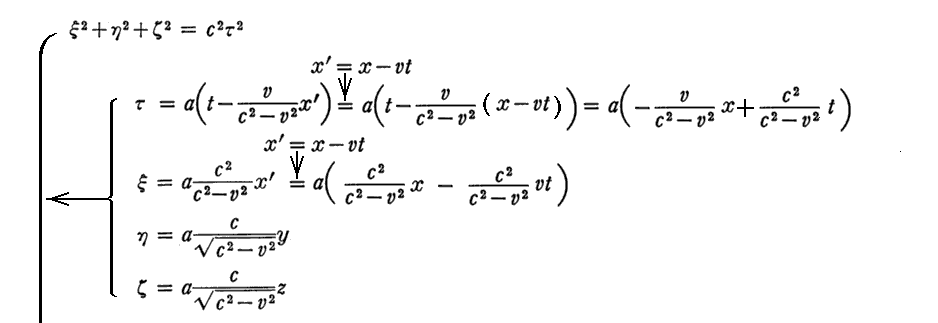
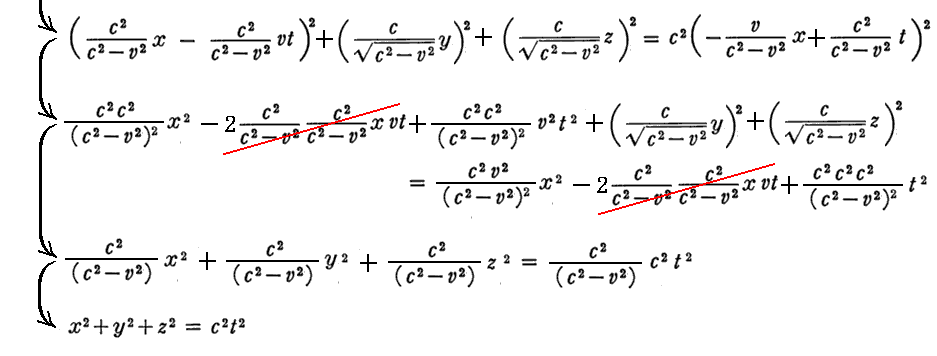
この関係式についてさらに補足します。
本論文は1913年にSommerfeldとBlumenthalが編集した相対論関係論文集に再掲載されるのですが、その版のこの箇所に、『(光速不変の原理から言える)K系で見た光の球面波とk系で見た光の球面波の同等性から(t,x,y,z)と(t’,x’,y’,z’)の間に成り立つローレンツ変換公式を簡単に導くことができる』という注記が追記されている。
この注記はSommerfeldからの依頼によりEinstein本人が付け加えたものと思われますが、Einsteinが1917年に出版した啓蒙書の附録の証明がその簡単な導出法です。
実際、今日の教科書の多くはこの“光速不変の原理”を前面に出して“ローレンツ変換公式”を導いています。文献211.の説明が解りやすい。また文献406.「力学」の説明も教訓的です。更に文献305.の説明も引用しておきます。
それぞれの導き方は微妙に異なりますが、どれも同じ結論になります。そのとき、いずれの証明に於いても途中で“相対性原理”を援用することは必要です。



[補足説明4]
上式導出の補足です。

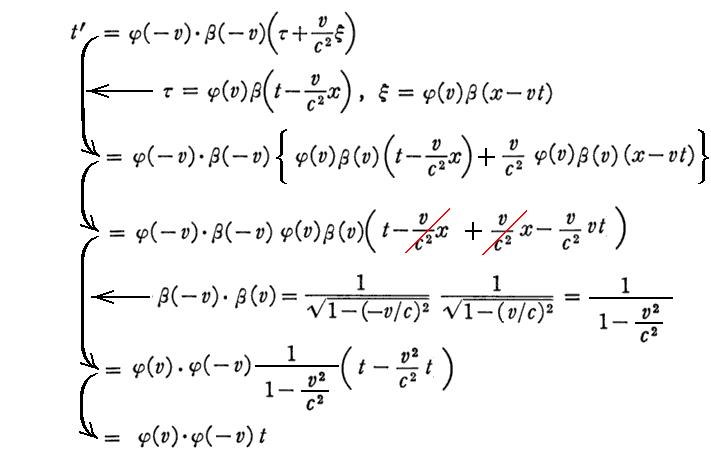
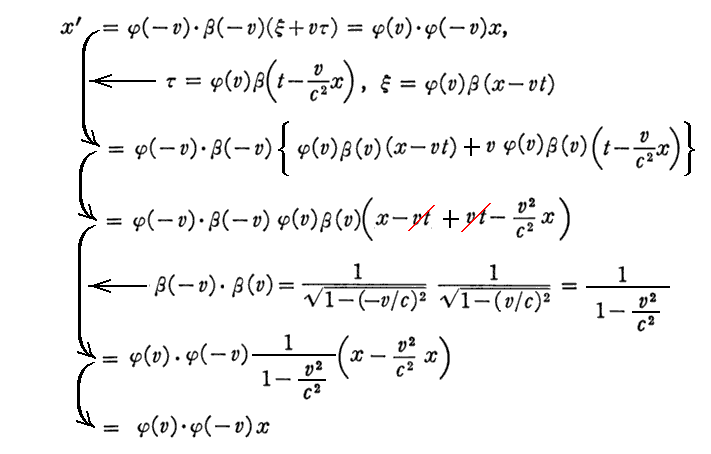
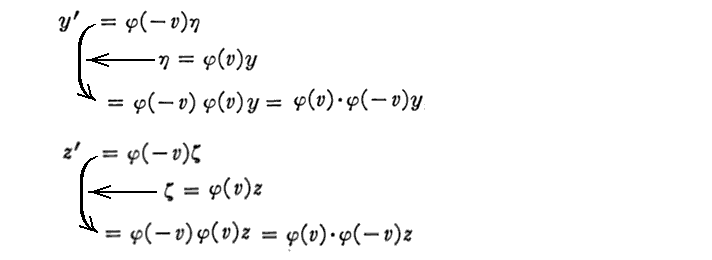


[補足説明5]
上記計算の補足です。
上端に対しては
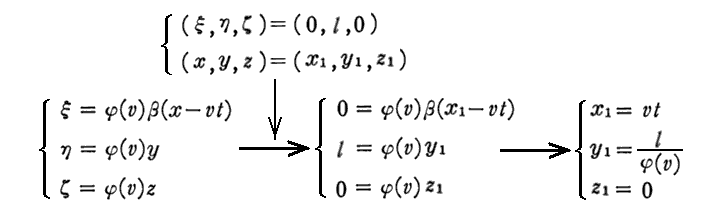
下端に対しては
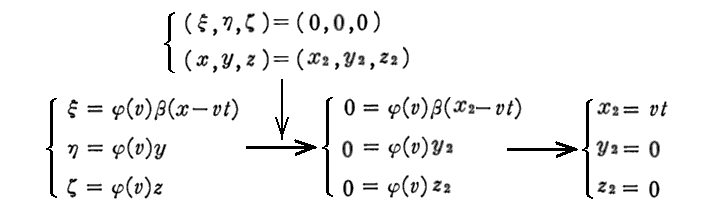
となる。



以上が原論文§3の“ローレンツ変換”の導き方ですが、微妙に解りにくいところがあります。これより見通しが良いかどうかは解りませんが、内山先生の補注[10]を別ページで引用しておきますので参照して下さい。
“ローレンツ変換”の意味については別稿「ローレンツ変換とは何か[Einsteinのローレンツ変換導出法(1905年)への補足]」で詳しく説明していますのでご覧下さい。
(5)矢野文献205.のローレンツ変換説明
アインシュタインは後(1918年)に文献108.の附録1「ローレンツ変換の簡単な導き方」でもっと解りやすい説明をしています。解説本の多くはこれを利用していますが、その中で文献205.第2章§4(p33~39)の矢野先生の説明が解りやすい。繰り返しになりますが、大事な所なので以下に引用しておきます。
原論文の(ξ,η,ζ,τ)が(x’,y’,z’,t’)に置き換えらていることに注意されてお読み下さい。


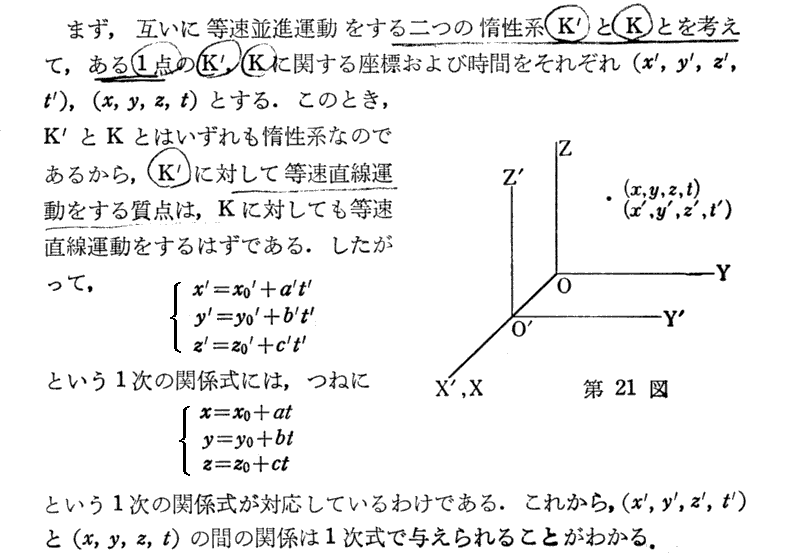



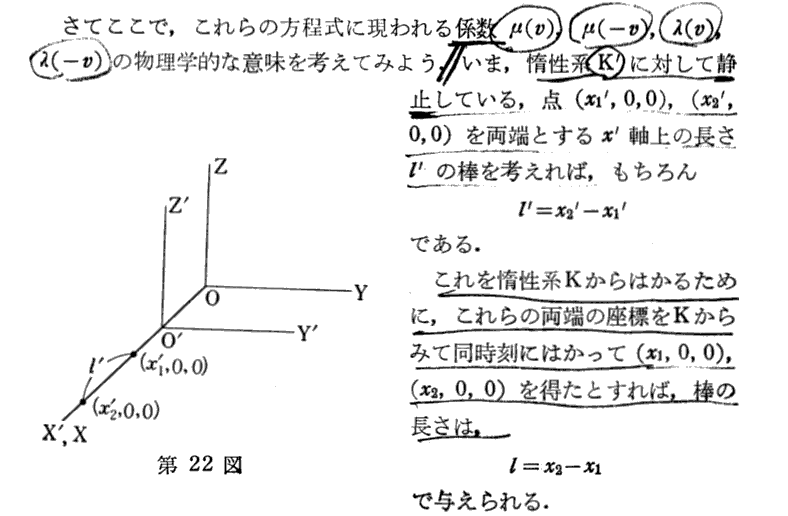


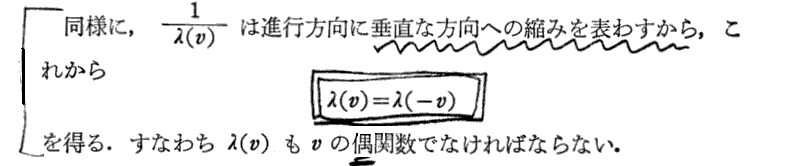
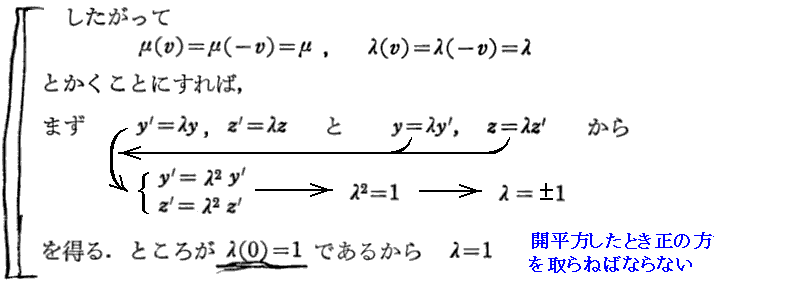
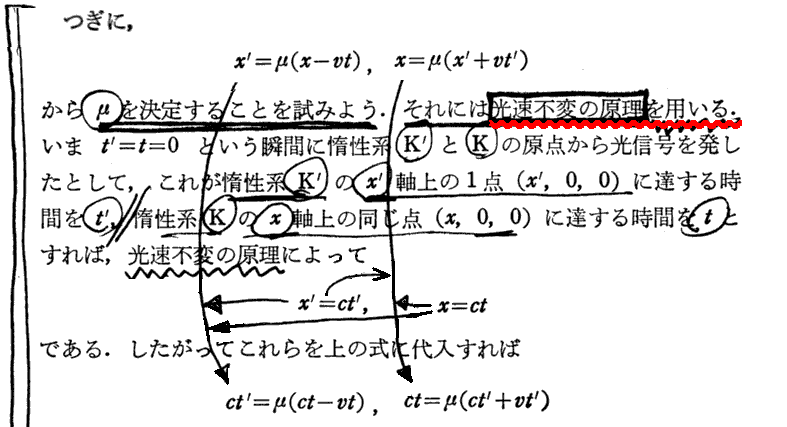

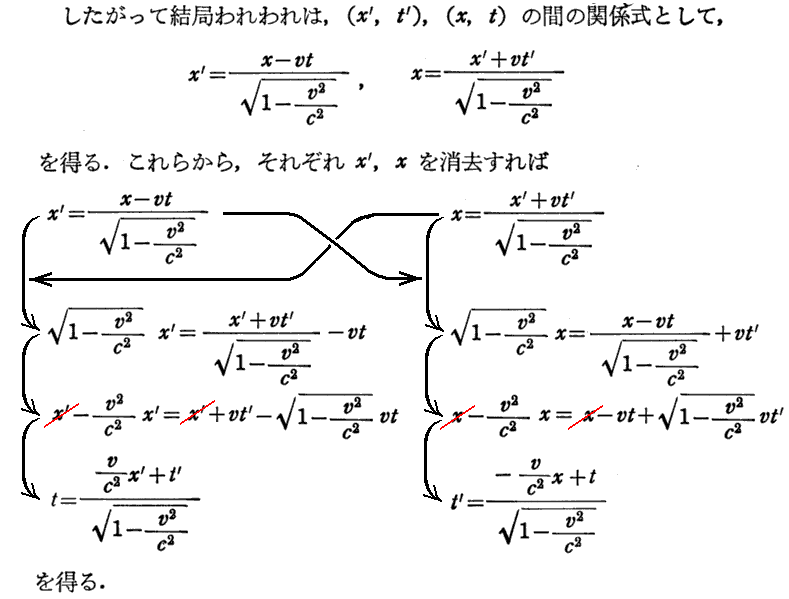
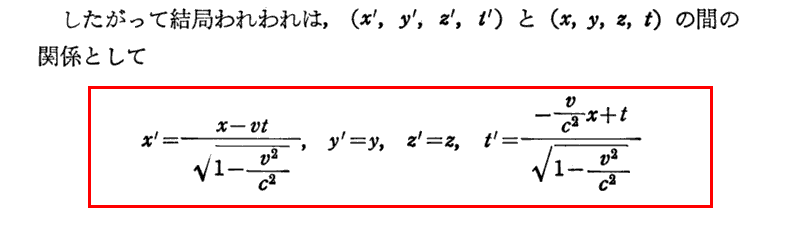

[補足説明1]
上記“互いに他を解いた形になっている”とは、未知数x,tの二元連立方程式を解いた形になっているということです。
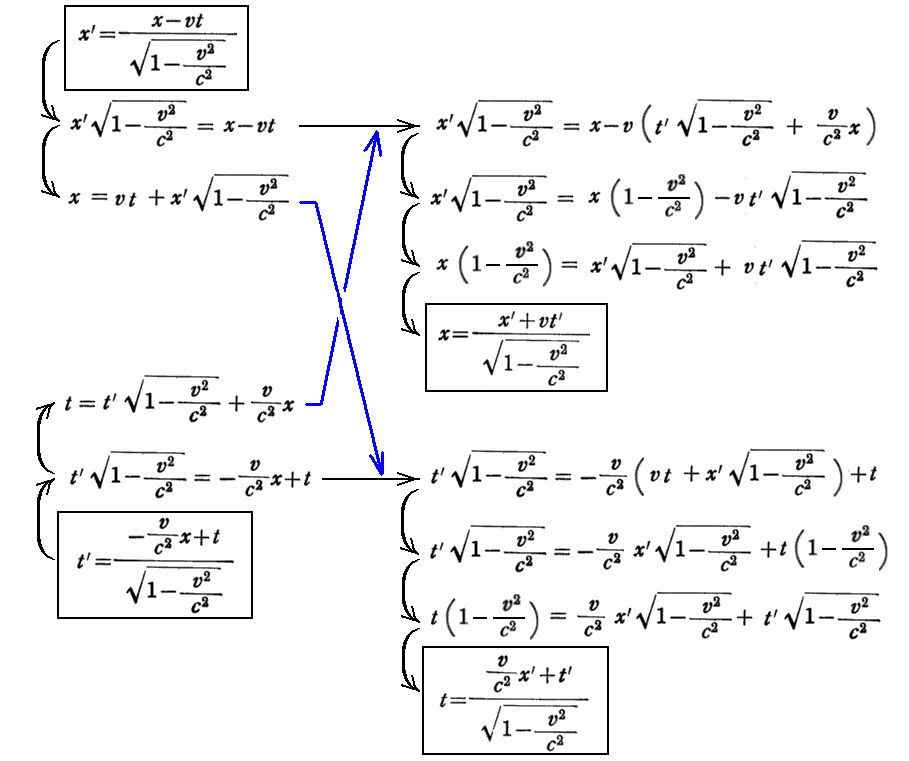

上記“のちに詳しく論じることにする”はこちらのことです。また以下で述べている事はEinsteinが原論文§5.で述べている群に付いての説明を先取りした説明です。



[補足説明2]
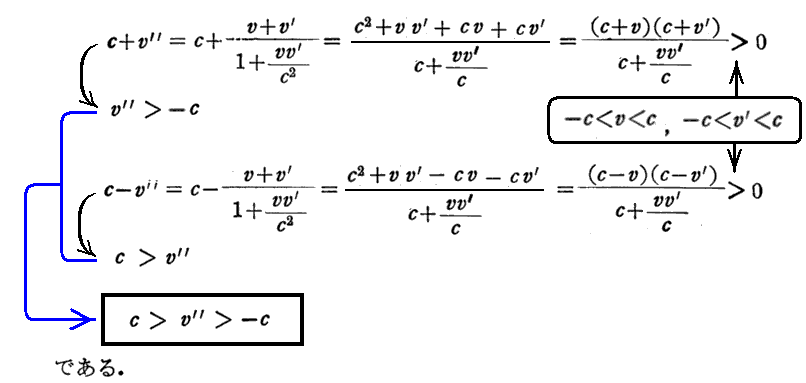
上記の式変形を補足する。下図の様に静止系Kに対してX軸方向に速度vで移動するK’系と、そのK’系に対してさらにX’軸方向にv’で移動するK”系を考える。そのときK系からみたK”系の移動速度をv”とする。
このときv”が単純にv+v’となるわけではない事に気付くことが重要です。
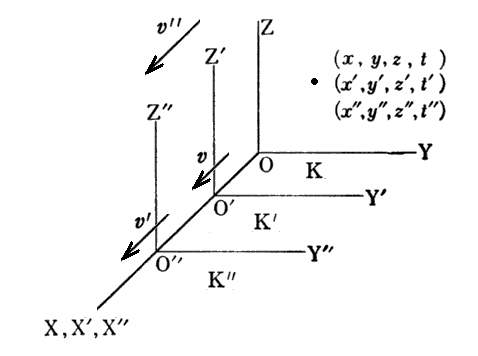
そのとき、ローレンツ変換

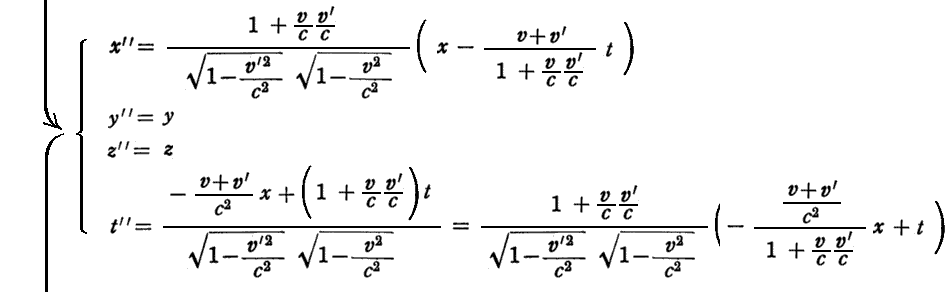
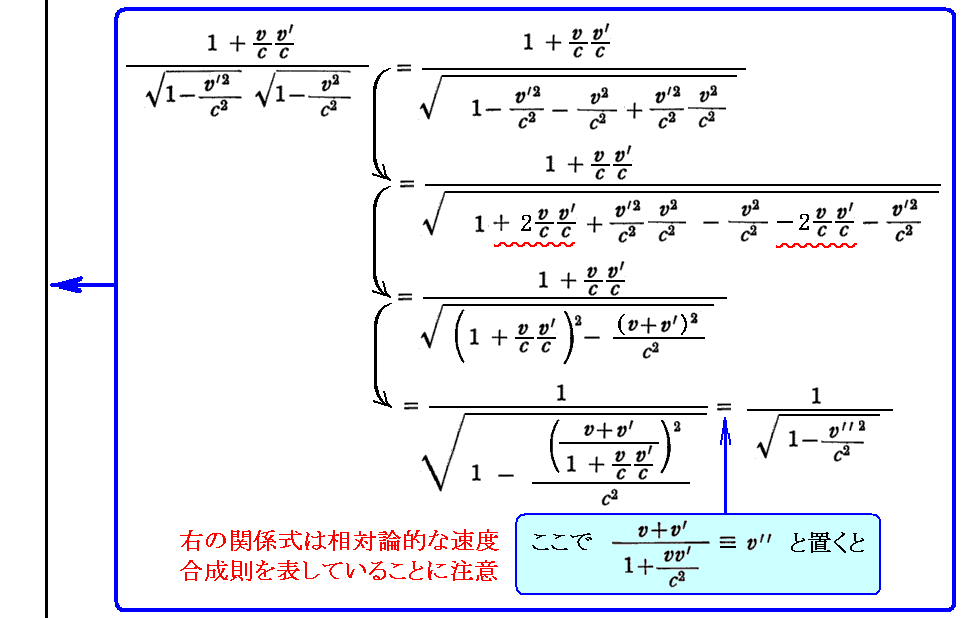
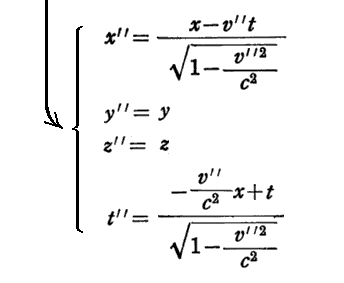
となります。このとき、速度vと速度v’の和は、相対性理論に従うと上記で表されるv”になる事を示している。

[補足説明3]
上記の“vの代わりに-vを代入したものが逆変換(つまり群論で言う逆元)である”ことの証明は、vに関係したローレンツ変換に引き続いて、-vが関係したローレンツ変換を行うと、それが恒等変換(群論で言うところの単位元)となることを言えば良い。
それは上記の[補足説明2]の変換式のv’を-vに置き換えればv”=0となることから簡単に確かめられる。
[補足説明4]
ここで群について説明する。(岩波「理化学辞典」より引用)
集合Gの任意の元a、bに関して算法(law of composition)c=ab、c∈Gが定義され、次の3法則を満たすときGは“群”であるという。
1.Gの任意の元a、b、cに対して(ab)c=a(bc)となる(結合法則)
2.Gに元eがあって、Gの任意の元aに対しae=ea=aとなる。eをGの単位元(unit element)という。
3.Gの任意の元aに対しある元a’がGにあって、aa’=a’a=eとなる。a’をaの逆元といい、ふつうa-1と書く。
この3法則のもとでは単位元eもaの逆元a-1も一意に定まる。さらに可換法則ab=baが成り立つときは可換群という。算法が加法である可換群を加群という。群Gが有限個の元からなるときは有限群、そうでないとき無限群という。Gの部分集合HでGの算法に関して群になるものをGの部分群(subgroup)という。
Gの任意の部分集合Sに対し、Sの元のべきSn(n=0、1、…)全体はSを含む最小の部分群である。これをSによって生成された部分群という。SがGの1つの元からなる場合は巡回群である。群Gの元の個数をGの位数(order)といい、元aによって生成される巡回群の位数をaの位数という。
環、体、線形空間などの代数系や線形変換などの変換は、いずれも“群”の性格をもつ。




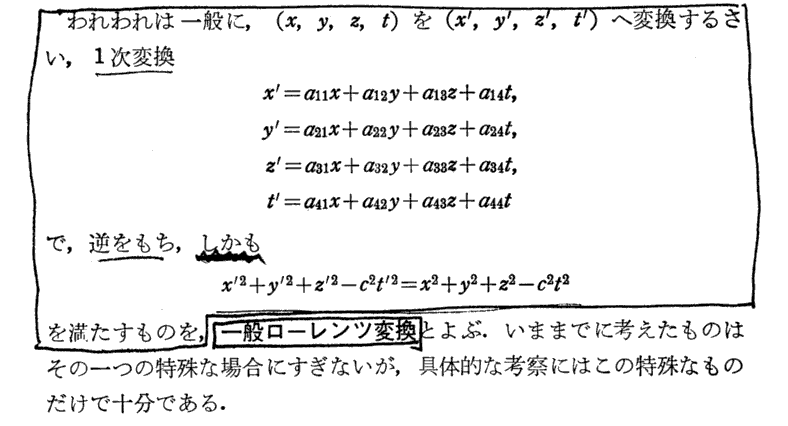
“一般ローレンツ変換”に関しては別稿「特殊ローレンツ変換から一般ローレンツ変換へ」をご覧下さい。
(6)原論文§4
ここから、再びEinsteinの文献103.からの引用。
1.長さの縮み





[補足説明1]
長さの収縮を表す式の意味は非常に解りにくい。アインシュタインの文献108.第Ⅰ部12章の説明をご覧下さい。
[補足説明2] 文献301.より
Lorentzの収縮は非常に理解しにくい所です。この収縮が“実際に起こる”ことなのか、あるいは“見かけ上のもの”なのかと言うことがしばしば問題とされるが、この問いは相対性理論に於いて、相互に運動している二つの物体のどちらが静止していて、どちらが運動しているのかと問うことと同様に意味の無いことです。
今までの議論で静止系とか、それに対して速度vで運動する運動系と言ってきたのは、単に言い表し方を簡単化するために言ってきただけであって、本来どちらが止まっていてどちらが運動しているかを判定するすべはなかったことを思い出して下さい。
自分に対して動いている物の長さを測ると確かに収縮しているのだと言うことです。そのとき、自分に対して動いている物の長さを測るには前記の§2.長さと時間の相対性で説明されているような方法(あるいは1.(5)で引用した方法)を用いるしか無いことに注意して下さい。
[補足説明3]
Paisは文献502.p183で、アインシュタンイの論文 Phys. Zeitschr. 12, 509. 1911年 の次の言葉を紹介している。
『ローレンツ収縮が存在するのか、しないのかという問題は、人々を混乱させる。それは[棒とともに]動く観測者にとって存在しないという意味において、“本当には”存在しない;けれども原理的には静止観測者によってそれが示されうるという意味で、“本当に”存在する』
Pauliは文献501.p51で、この1911年論文中のEinsteinの思考実験を紹介している。

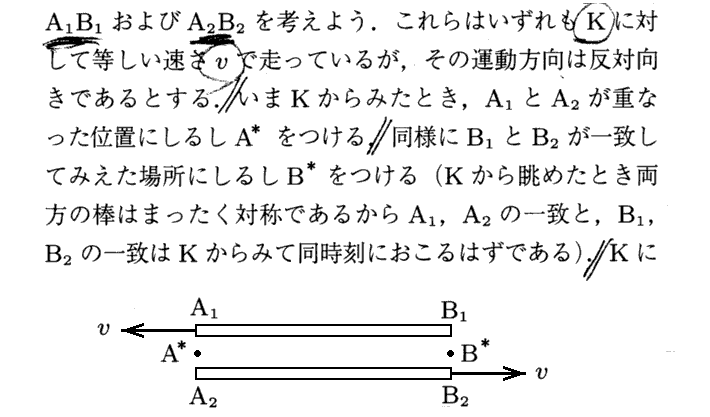

[補足説明4]文献301.より
ここで述べられている様に、運動している半径aの球は、運動方向の短軸が
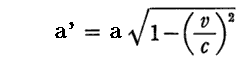
となる回転楕円体に扁平化してしまう。これに基づいて、1903年にLorentzは、電子論に関する大論文(Enzyklopa¨die der Math
Wiss,Ⅴ巻,p277~279)の結論として、変形可能な電子の仮説を提唱した。
[この大論文はネットから無料ダウンロード可です。]
2.時間の遅れ


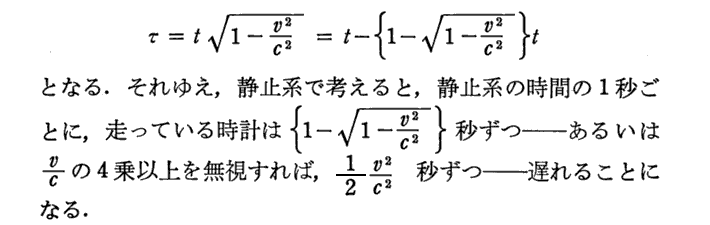


[補足説明1]
時間の収縮を表す式の意味は非常に解りにくい。アインシュタインの文献108.第Ⅰ部12章の説明をご覧下さい。
またこのことは、時計を持ち運ぶことにより離れた地点における時刻を揃える方法は、一般的に不可能であることを意味している。運搬速度がゼロの極限でのみ、それは正しい結果を与えるのだから。
[補足説明2]
下記の“平衡輪式時計”と言う言葉は、同じメカニズムの二つの時計というときの時計が“振り子時計”の様なものでは無いのだと言うことを表すために用いられています。要するに、時を刻むメカニズムが周囲の状況・環境に影響されない、原子固有の振動数などを用いる今日の原子時計の様な、ものを想定している。
アインシュタインは後の1913年に出版された相対論関係の論文集[Einstein,Lorenz,Minkowski;Das relativitatsprinzip
: eine sammlung von abhandlungen; mit Anmerkungen von A. Sommerfeld und
Vorwort von O. Blumenthal (Fortschritte der Mathematischen Wissenschaften
in Monographien),B.G. Teubner 1913年]の該当ページに脚注として『赤道と極では重力加速度が異なるために、重力を利用した振り子時計の様なものは地球と一緒になって一つの物理系と見なすべきもので、ここでの議論からは除外しなければならない。』という趣旨の記述を付け加えている。



[補足説明3]
この時点でのアインシュタインはまだ気付いていないのですが、上記の地球を周回する時計の例には注意すべき点が多々あります。
アインシュタインは後に互いに加速度運動をする系に対しても成り立つ一般相対性理論を発見するのですが、この例の様に互いに加速度運動をする時計の遅れを、特殊相対性理論によって見積るには注意が必要です。また、一般相対性理論では重力場中に存在するだけで時間が遅れるのですから、更に注意深い考察が必要です。
この事に関して、文献203.のメラーの説明を引用しておきます。
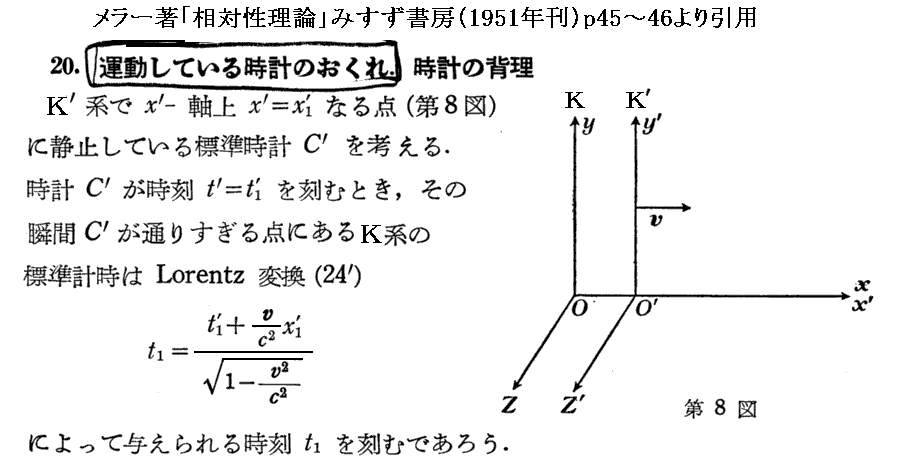



一般相対性理論によらないと正確に説明できないのですが、文献207.§2.4.3で江沢先生がとても解りやすく解説して下さっていますので別稿で引用しておきます。理解するにはミンコフスキー座標を利用するのが得策なのでその説明§2.4.1も合わせて引用します。ミンコフスキー座標についてはBorn文献第Ⅵ章の説明も秀逸です。また、文献214.§4(d)の内山先生の説明も解りやすく秀逸ですので合わせてご覧下さい。
また、この問題については、別稿「双子のパラドックスと一般相対性理論」もご覧下さい。
実際、HafeleとKeatingは、1971年に航空機で運んだ原子時計と地上で静止したままの原子時計との間に発生する時間のズレが理論と誤差の範囲で一致することを確かめた。このことについての解説は別稿§3-2を参照されたし。この実験については戸田先生の解説が解りやすいので別ページで引用。
同様な実験が1975年9月~1976年1月にかけてメリーランド大学のC.アレーの研究グループによりさらに高精度で行われた。それにより特殊相対性理論による時間の遅れの効果と、一般相対性理論による時間の進みの効果がきわめて正確に確かめられた。このことの詳しい解説は別稿§3-2-2を参照されたし。
(7)原論文§5


[補足説明1]
上式を導く。ローレンツ変換式を変形すると
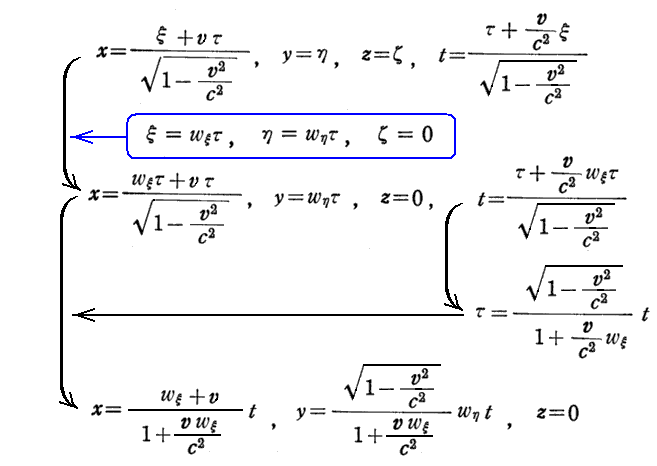
が得られる。
この式は、更に次のように変形できる。
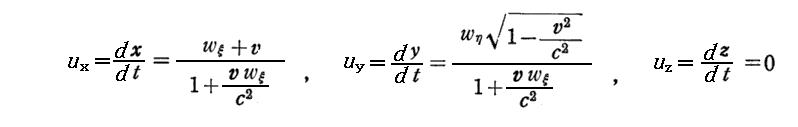
これが、普通の教科書に書かれている速度変換公式に対応する式です。たとえば、2.(8)3.[補足説明1]で説明した式と比較検討してみられたし。
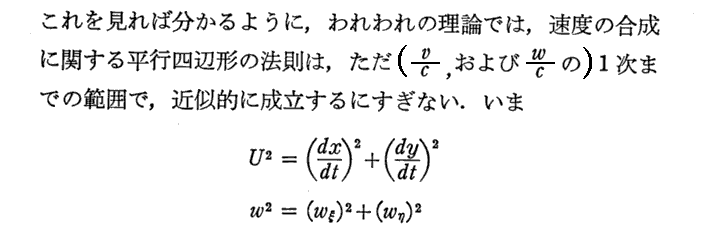

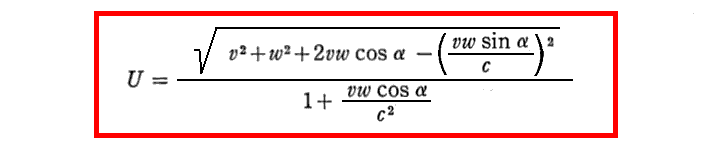
[補足説明2]
上式の導出は下記参照
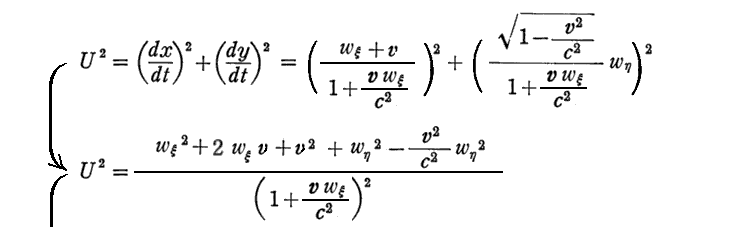
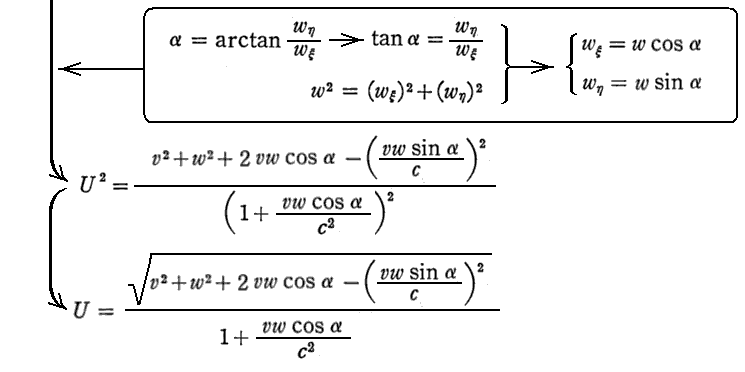


[補足説明3]
ここは、相対性理論で最も不思議なところですので、通俗書の式変形を用いて補足しておきます。今、K系のx軸方向にk系は速度vで動いている。そのときk系のx’軸(論文ではX軸orΞ軸となっている)はx軸方向とする。k系から見てx’軸の正方向に速度wで動く物体をK系から見たら上記のUで動くように見える。
このときUをcで割った式を変形すると
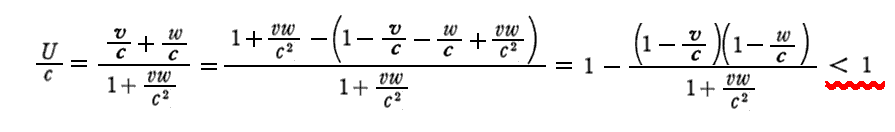
となる。このときw、vが正でかつ<cである限り、右辺の第二項の分子の両因子は常に1より小さく、分母は常に1より大きいので、第二項は1より常に小さくなる。そのため右辺は常に1より小さくなり、U<cが成り立つ。これはwとvが両方とも0.5cよりも大きくても成り立つので常識で推し量るととても不思議なことです。
ついでにもう一つ補足しておく。前記の公式
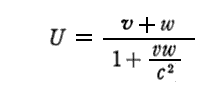
を下式左辺のUに代入して展開計算すると直ちに右辺の式に関係付けられる。
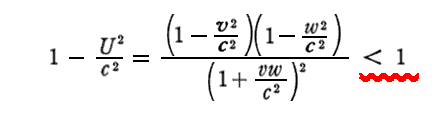
これも、種々の公式の証明に使える便利な関係式です。

[補足説明4]
このことが、別稿「フィゾーが運動媒質中の光速度(随伴係数)を測定した方法(1851年)」4.(2)5.[補足説明]で注意した事柄です。
アインシュタインは光速度が示すこの性質に驚嘆します。おそらくそのために、2.(3)で説明した“光速度不変の原理”の定義文に、“光速度は光源の運動に無関係”というただし書きと“光速の測り方”の注意書きを付け加えたのだろう。
ただし、光速度が光源の運動に無関係であることが実験・観察により検証されるのは、別項で説明した様にもっと後になってからのことです。


[補足説明5]
上記赤波線部分については、矢野文献108.から引用した2.(5)の後半部を参照されたし。特にそこの[補足説明2]がEinsteinが上で説明している事柄です。
アインシュタイン原論文のⅠ.“運動学の部”は以上です。以下の(8)~(11)節は他文献からの引用です。
まず、矢野文献205.第2章§5(p39~45)から引用して上記§4、§5の内容をもう一度説明します。原論文の(ξ,η,ζ,τ)が(x’,y’,z’,t’)に置き換えらていることに注意されてお読み下さい。
(8)矢野文献205.の説明
1.長さの縮み
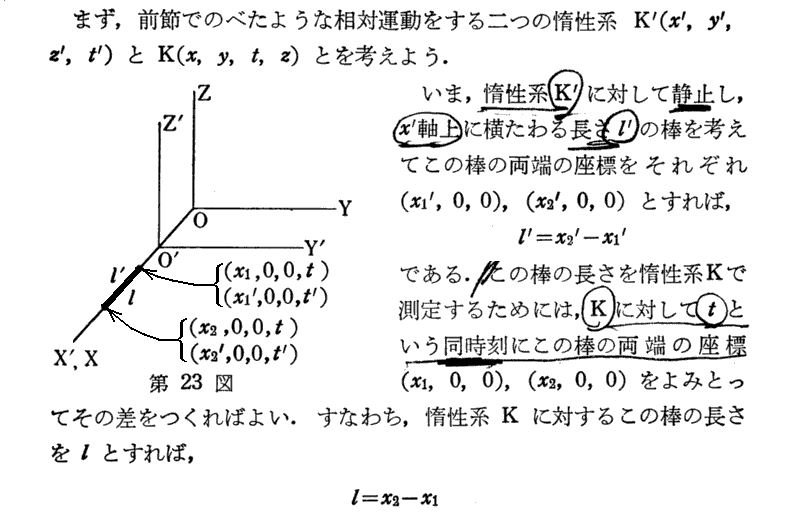
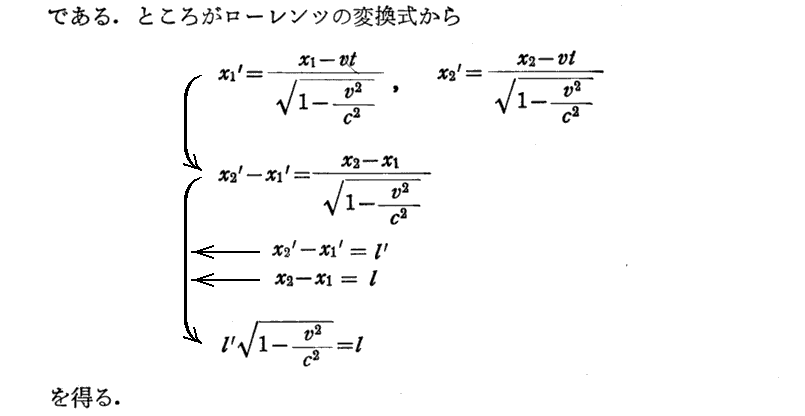





2.時間の遅れ

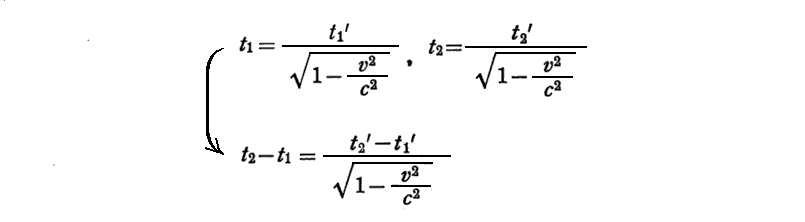

3.速度の合成
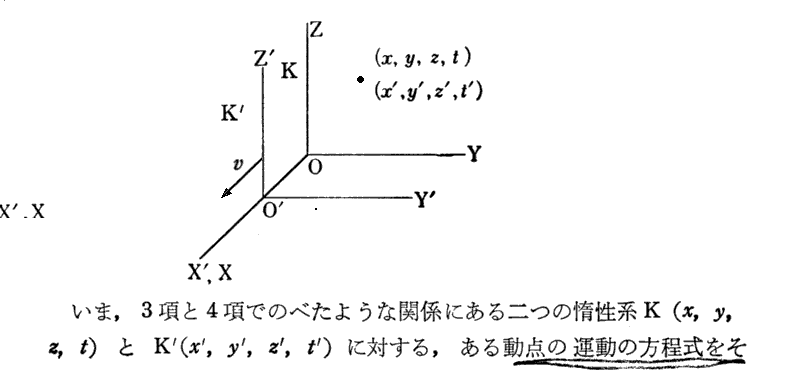

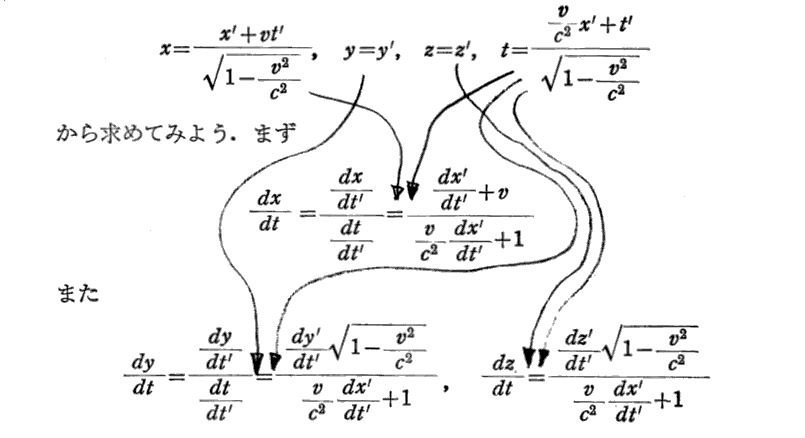

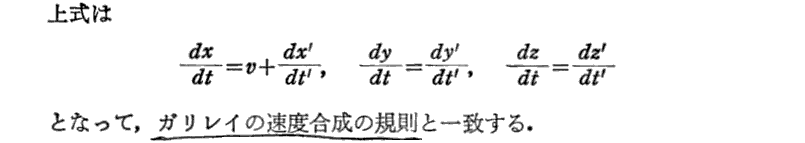
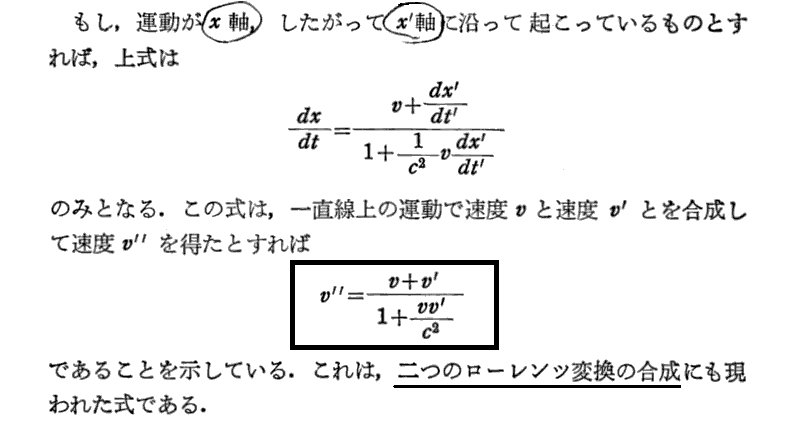
上記“二つのローレンツ変換の合成”とはこちらの説明の事です。
[補足説明1]
上記の式は、多くの本で
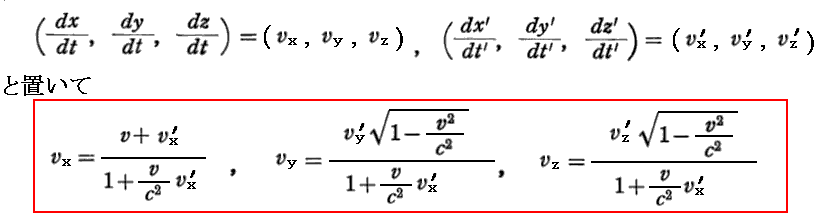
と表されているものです。これはK’系から見て(vx’,vy’,vz’)で動いている物体は、K系から見ると(vx,vy,vz)で動いているように見えることを意味しています。
あるいは上式を逆に解いて
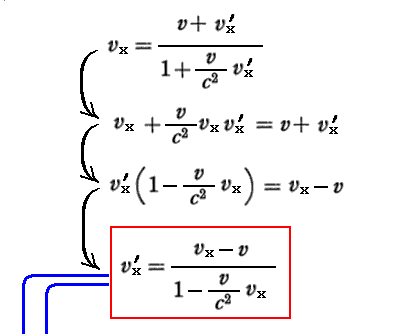
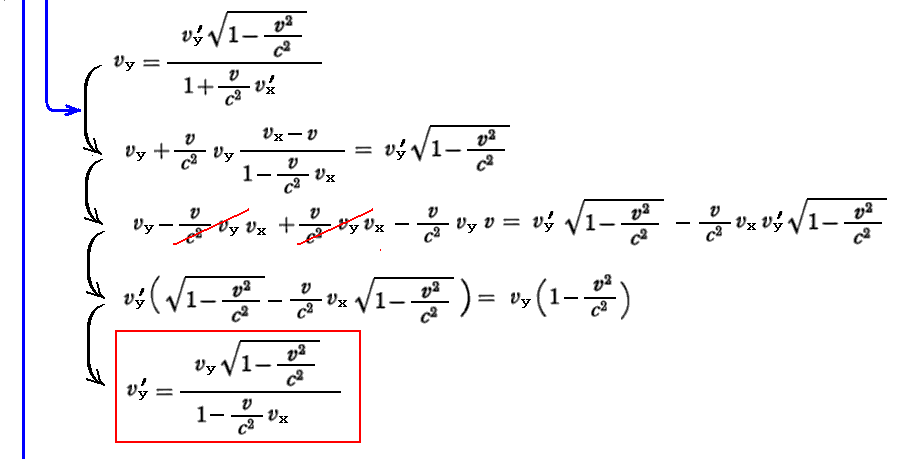
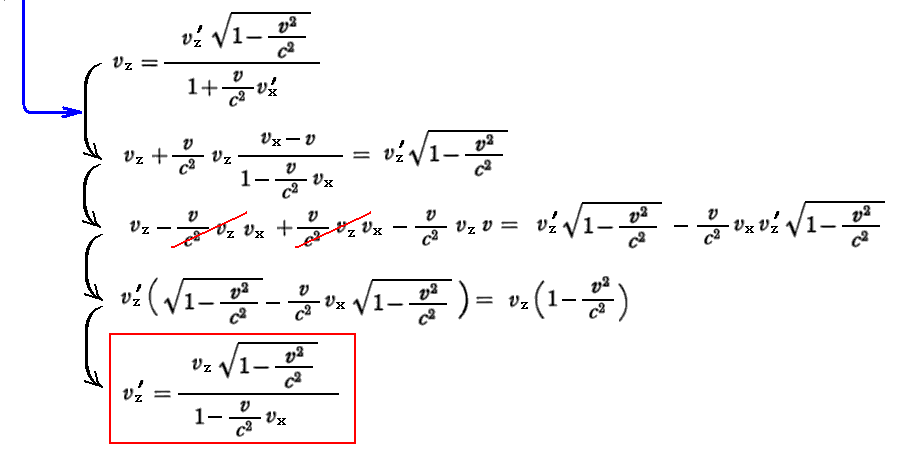
と書くと、これはK系から見て(vx,vy,vz)で動いている様に見える物体は、K’系から見ると(vx’,vy’,vz’)で動いているように見えることを意味しています。
これはもちろん前出の式に於いてK’系が静止しており、K系がK’系のx’軸方向に-vで移動しているときに得られる式
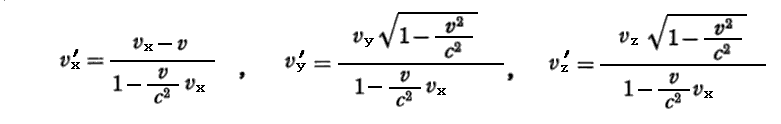
に一致します。
このとき、これらの式中の v はK系から見たK’系のx軸方向への移動速度であることを忘れないでください。(vx,vy,vz)と(vx’,vy’,vz’)のどちらでもありません。
さらに、K系に対するK’系の移動方向に垂直な方向の速度成分vyやvzも、K’系から見ると変化します。K座標系からみたK’座標系はx軸方向しか縮まないのに、y方向やz方向に関しても変化するのは不思議に見えますが、これはK’系の時計がK系からみ見ると遅れるためです。
[補足説明2]
この速度の合成則も解りにくい所ですから補足しておきます。
2.(2)[補足説明2]で述べたようにアインシュタインの言う空間座標とは以下のことでした。
例えば、速度の合成則に於いて“地面に静止する観測者”や、地面に対して速度vで移動する“列車に静止している観測者”や、列車に乗っている観測者から速度v’で“前方に投げ出されたボール”というような物体が議論されます。そのとき、観測者が立っている地面に設置している(縦、横、上向きの)物差しの棒のセット、列車に設置してある同様な物差しの棒のセット、ボールそのものにくっついている物差し棒のセットが空間そのものを意味します。それらの物差し棒のセットで測られる座標値がそれぞれの空間ということです。
同じ物差し棒のセットを三組準備して、互いに静止している時に地面、列車、ボールのそれぞれにくっつけます。また同じメカニズムで時を刻む時計を三個準備してそれぞにくっつけます。その後に、地面に対して速度vで列車を動かし、さらにその列車から見て速度v’でボールを投げ出す。
そのとき、速度 v は静止した地面の物差し棒のセットと地面にある時計で測られた列車(あるいは列車に付随している物差し棒セット)の速度値であり、速度 v’ は列車にくっついている物差し棒のセットと列車に乗せてある時計で測られたボールの速度値です。そのとき、同じボールを地面に設置してある物差し棒と地面にある時計で測ったボールの速度がv”だと言うことです。
相対性理論に従うと動いている物差し棒は縮むし、時計は遅れるのですから、そのことを考慮すると速度の合成則に示すような関係が成り立つということです。
この当たりについて、ミンコフスキー図を用いた解りやすい説明を別項「Born“アインシュタインの相対性理論”第Ⅵ章」6.(2)[補足説明]でしていますのでご覧ください。
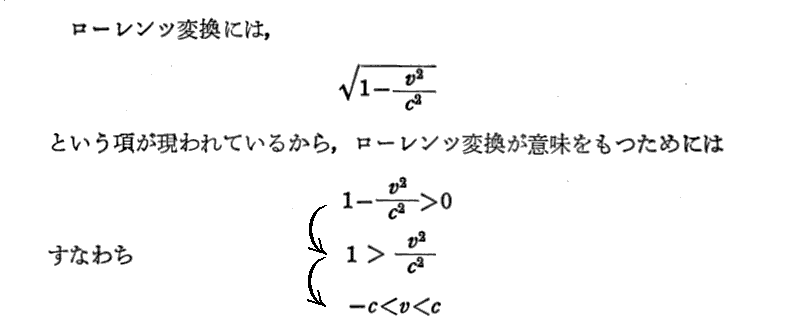

4.世界距離のローレンツ変換不変性
ガリレオ変換では“距離の長さ”が不変に保たれたのですが、ローレンツ変換では時間間隔を含めた“世界距離”という量がローレンツ変換不変性を保ちます。これは2.(4)[補足説明3]で述べた事柄をもう少し一般的に言い換えたものです。
K系において質点が時刻t1に場所(x1,y1,z1)に存在し、時刻t2に場所(x2,y2,z2)に移動したとする。そのとき
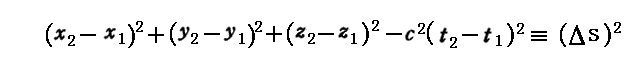
で定義される量Δsを“世界距離”と呼ぶ。
このとき、k系において対応する状況は質点が時刻t1’に場所(x1’,y1’,z1’)に存在し、時刻t2’に場所(x2’,y2’,z2’)に移動することである。k系において対応する世界距離Δs’は
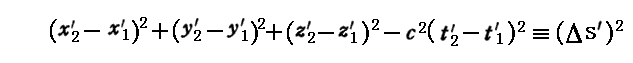
となる。
このとき、“世界距離”Δsはローレンツ変換に対して不変でその二乗に対して (Δs)2=(Δs’)2 となる。
その証明は簡単です。
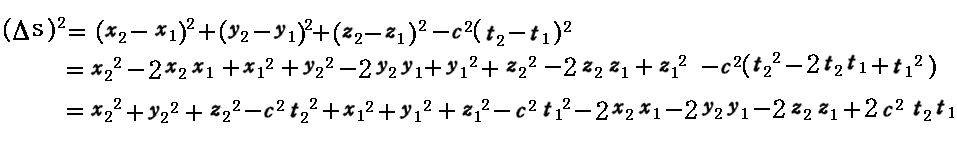
において、すでに証明したようにx2+y2+z2-c2t2はローレンツ変換に対して不変であった。またyとzはそのままy’とz’に変換されるので結局
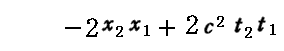
がローレンツ変換に対して不変である事を証明すればよい。これはローレンツ逆変換を用いれば簡単に証明できる。

以下の(9)~(10)節で取り上げる内容は、後ほど解説するアインシュタイン原論文のⅡ.“電気力学の部”に出てきます。後のその部分の解説の準備も兼ねてSommerfeldの文献402.「光学」§10、§11、を紹介します。
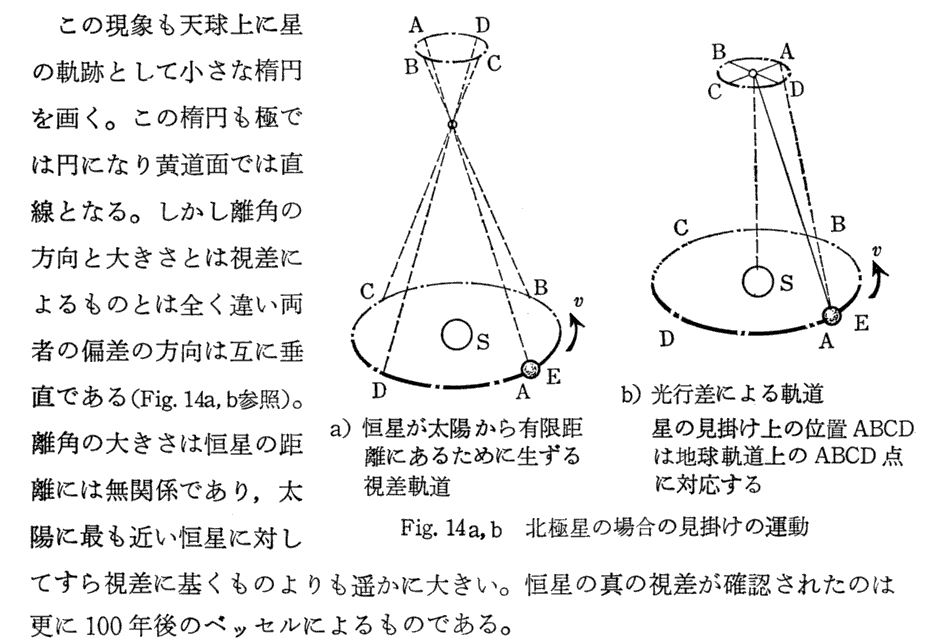
(9)光行差(Sommerfeld文献402.)
アインシュタインは1905年論文のⅡ.“電気力学の部”で光の電磁波説にもとずく波動論で光行差の現象を説明しています。アインシュタインが光行差を第Ⅱ部で論じたのは、波面と波のエネルギーの進行方向との関係についての深い考察にもとづくためだと思われます(その当たりについては3.(2)3.[補足説明5]を参照)。
しかし、光はアインシュタインが発見(彼は直前に光量子の論文を発表)した“光量子説”にもとずく粒子であると見なすこともできます。
そのとき、光を光速度で移動する粒子であると考えると、電磁気学を持ち出さなくても、ここまでに説明した相対論的な運動学的知識のみで光行差の現象は完璧に説明できます。
別稿「ブラッドリーが光行差を見つけた方法」4.(2)で説明したようにブラッドリーは元々粒子説で説明していたのですが、ここで説明する光粒子は古典的な粒子ではなくて、どの座標系から見ても光速度cで移動する(相対論的な速度合成則を満足する)粒子であることに注意してください。
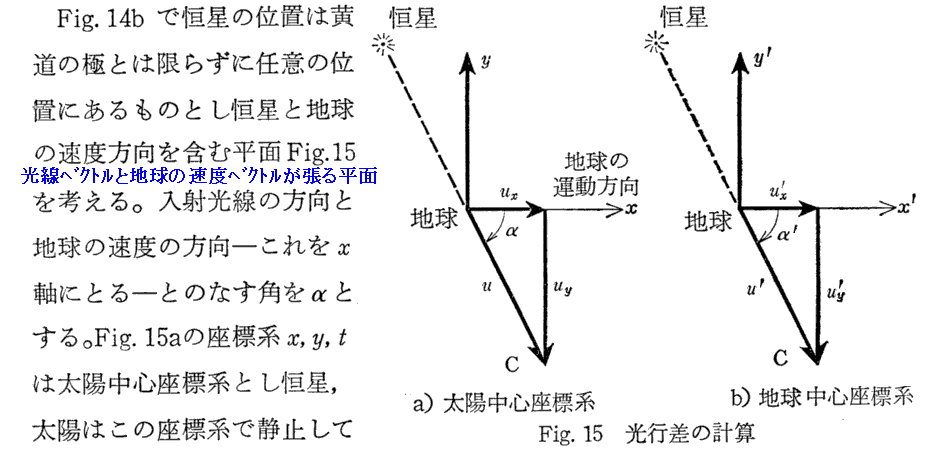
以下はSommerfeldの文献402.からの引用です。下記の(3)式は2.(8)3.ですでに導いた式であることに注意されてお読み下さい。


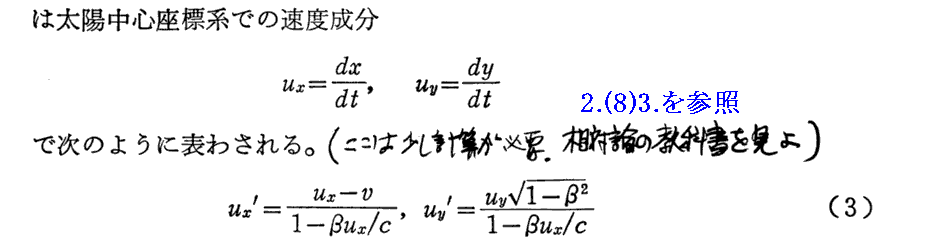
上記の2.(8)3.はこちらです。

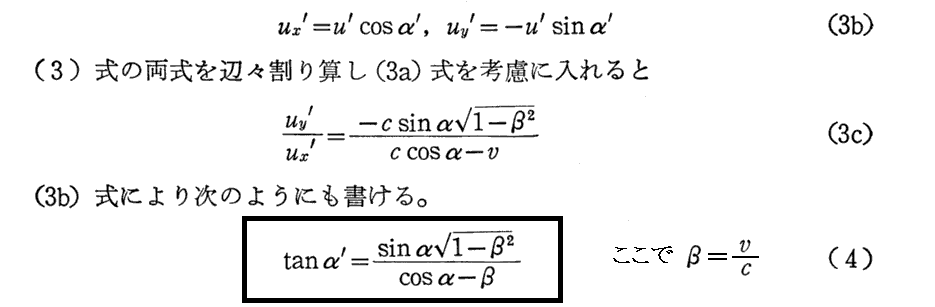
[補足説明1]
ここは何を言っているのか解りにくいが、要するに2.(8)3で説明した速度に関するローレンツ変換を実施しているだけです。そこの(vx,vy,vz)を(ux,uy,uz)へ、(vx’,vy’,vz’)を(ux’,uy’,uz’)へ置きかえた式を用いればよい。
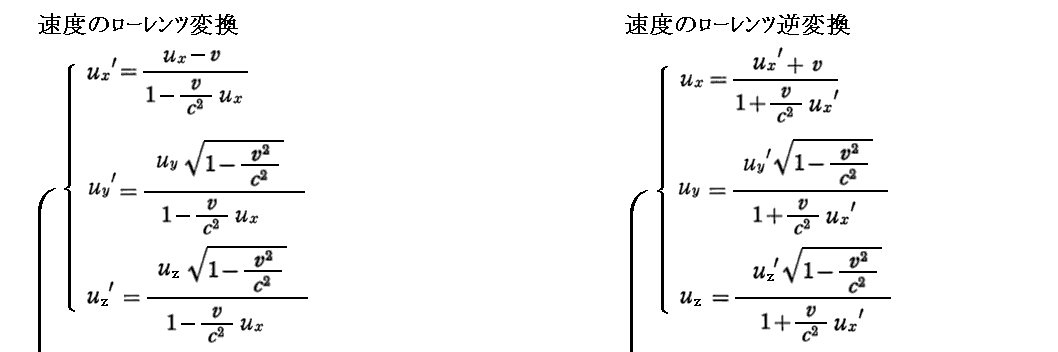
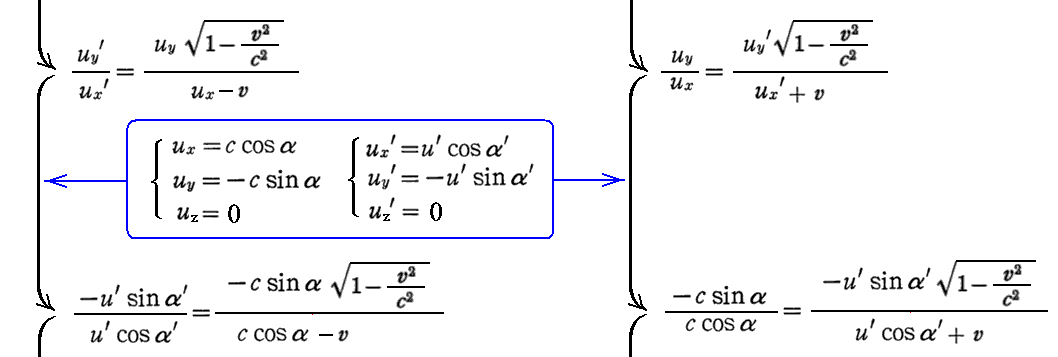
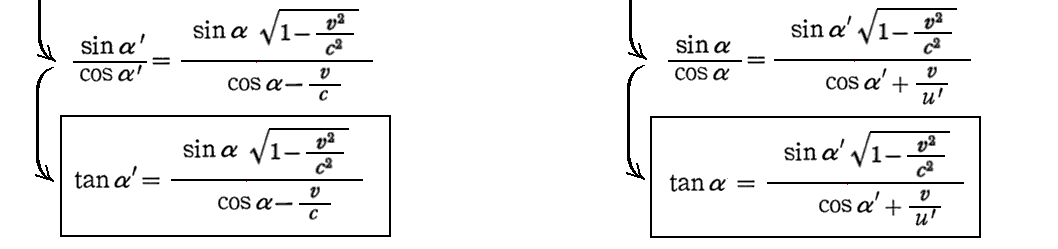
このとき注意して欲しいことは、ローレンツ逆変換を用いて得られる上記右側の式は、次で証明する u’=c であることを考慮すると、左側のローレンツ変換から得られる式のvを-vに置き換えでαをα’に置きかえた式になっていることです。つまり、光源が動いて観測者が静止しているとみなしてもまったく同じ結論が得られる“相対性原理”を完全に満たしている。
もちろん、下記に示すように左側の式を直接逆に解いても右側の式が得られる。
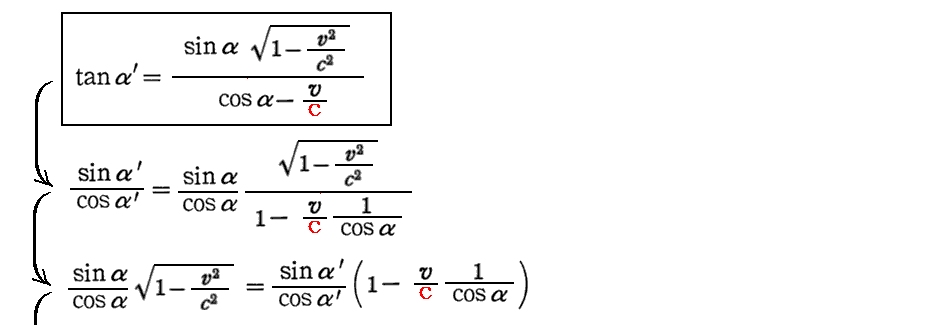
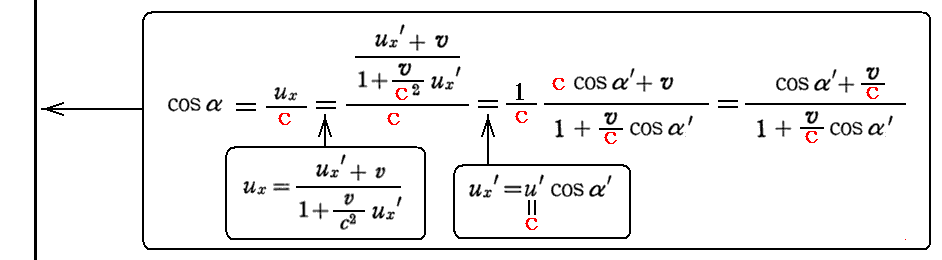
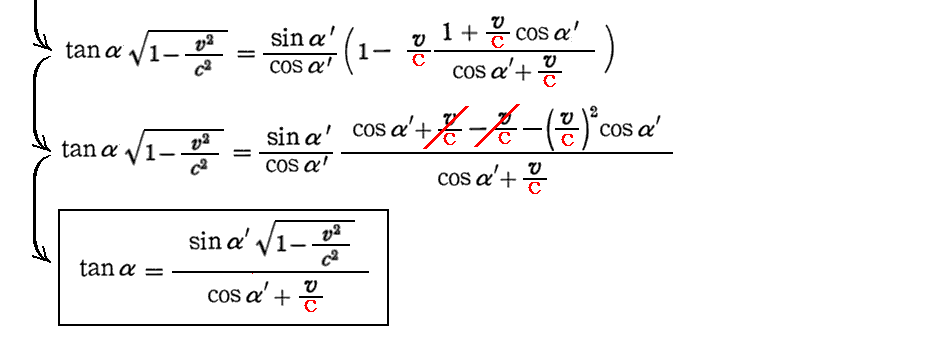
これは、ガリレオ変換に従う古典的な光行差理論の結論とは異なっています。(3.(2)3.[補足説明3]を参照)。


ここは日本語訳の訳文が良くないのだろう。おそらく、Sommerfeldは、この結果は、“光速不変の原理”から言えるということを言いたいのだろう。


これが初等的光行差理論で習う式です。


この説明は解りにくいが、別稿1.(3)の様に見えるということです。

[補足説明2]
Sommerfeldが粒子論によって求めた結論(4)式は、次節§11で求める波動論による結論(7a)と一致します。もちろんこれは、3.(2)3.でEinsteinが波動論によって求めた結論とも一致します。実際、(4)式を変形すると
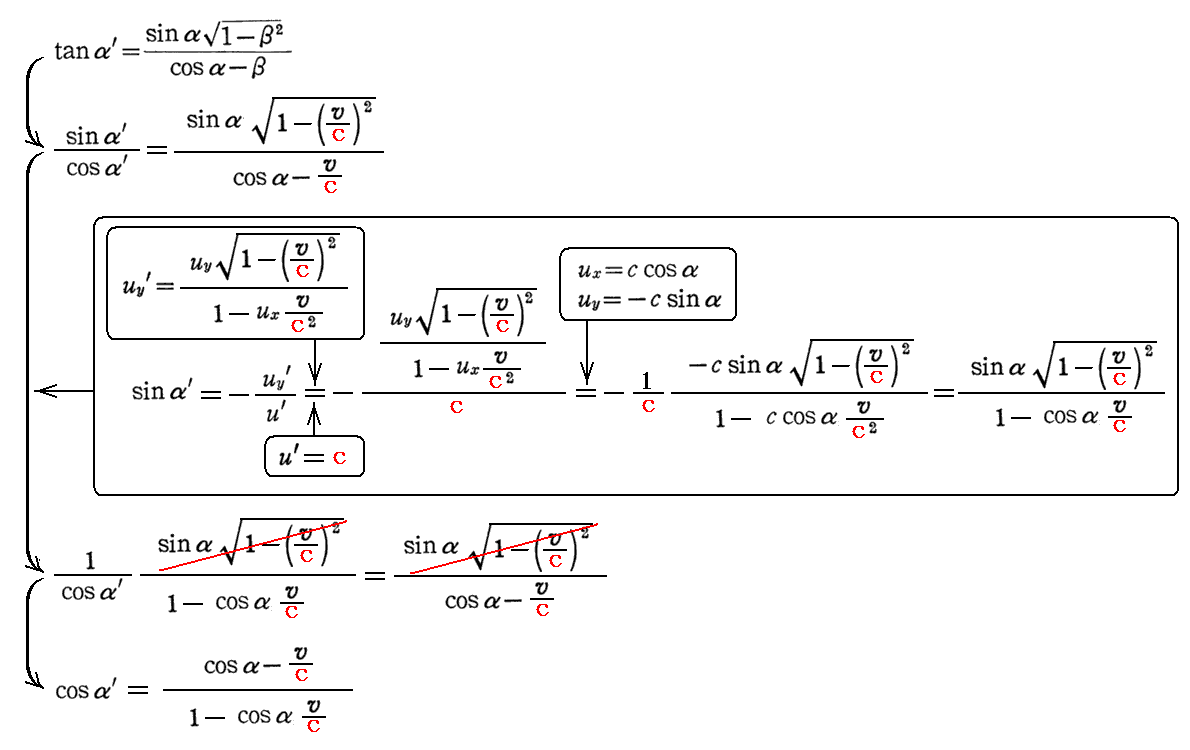
となるので、α→φ、α’→φ’を考慮すると、Einsteinが求めた結果と完全に一致する。
[補足説明3]
ここでは、光を粒子と見なして、相対論的な運動学の結論を用いて、光行差の現象を相対論的に説明しました。
そのとき、この光はNewtonの光粒子説の粒子とは根本的に異なる事に注意してください。この光粒子は、光を放射する物体(恒星)の運動速度によらず、つねに光速度cで進む。つまり、相対論的な速度合成則 c+v=c(c;光速度、v;光源の速度)が成り立つ粒子です。
Sommerfeldが文献301.の§27-I.で注意しているように、Newtonの光粒子説が今日光量子説として復活できたのは、まさにこの相対論的速度合成則による。
(10)ドップラー効果
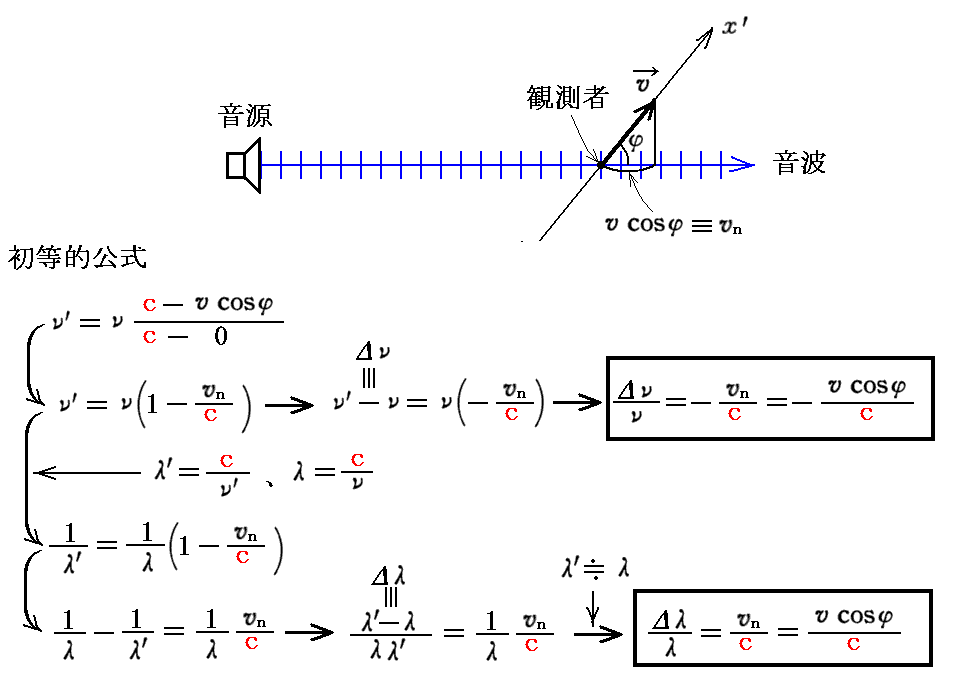
1.波動説による説明(Sommerfeld文献402.より)
Sommerfeldの説明を引用。これは光の電磁波説に基づくものですが少し難しい。そのため、アインシュタインの1905年論文第Ⅱ部§7[3.(2)1.~2.波動説によるドップラー効果の説明]を平行して読まれることを勧めます。そちらの方がより明快で解りやすい。
以下の古典論の部分は、高校物理で習う音のドップラー効果の公式(説明1、説明2、説明3)を思い出しながらお読み下さい。



観測時間 t を任意にしているので解りにくいが、t=1秒にすればt/τ→1/τ=振動数 f になります。こちらの表現にした方が解りやすいかも知れません。

上記の部分の訳文は解りにくい。Sommerfeldが言いたいのは次の事です。
・・・・光は絶対静止空間に静止するエーテルの振動であるとする古典論では、(1)式と(2)式は厳密に一致しない。だから、観測する振動数の違いを計測すれば、観測者が波源(光源)に近づいているのか、あるいは波源(光源)が観測者に向かって近づいているのかを判別できる事になる。つまり絶対静止空間(エーテル空間)の存在を検知できる。
ところが、本稿で論じている“相対性原理”と“光速不変の原理”が正しいのなら、本来観測者が波源(光源)に近づくことと、波源(光源)が観測者に近づく事は区別できないはずである。つまりドップラー効果を表す公式の形はどちらの場合も同じになるはずである。・・・・
ここでの話はあくまで波源が(光源)の場合です。波源が(音源)の場合には音を伝える媒質が存在しますので、相対論的に論じた場合でもドップラー公式が相対性原理を満たす公式になるわけではありません。その当たりは別ページの説明をご覧下さい。ここは難しい所ですので、後の3.(2)2.[補足説明4]でもう一度詳しく説明します。

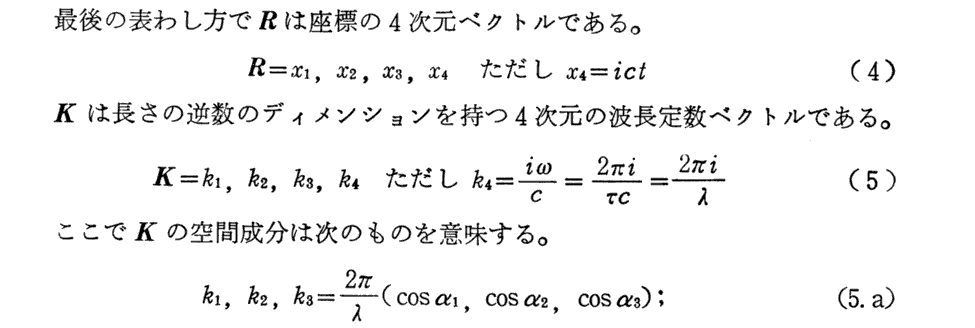
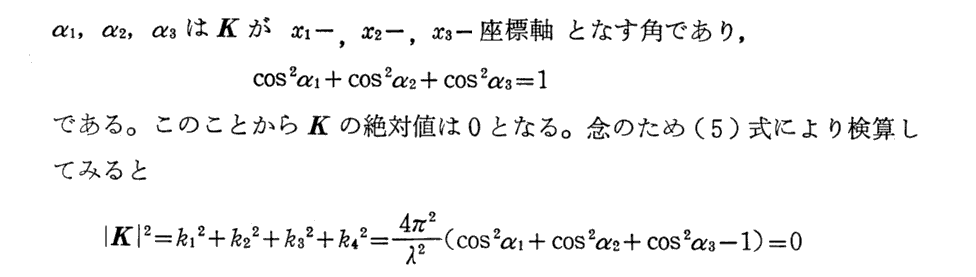

変換式(6)は後の3.(2)1.[補足説明7]でも導きます。そのとき解る様に虚数単位 i を導入しなくても同様な議論ができます。Sommerfeldは、ミンコフスキー(H.Minkowski)の業績を尊重して虚数単位
i を用いているだけです。
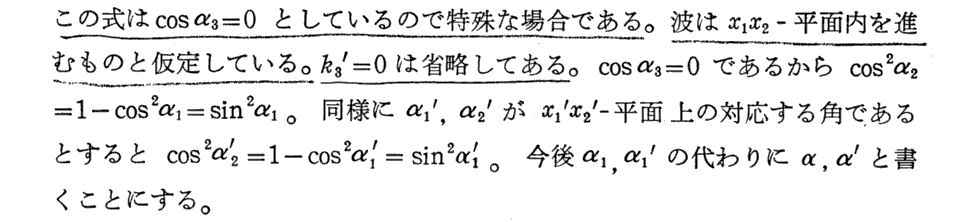

上記の(10.4)式とは2.(9)の(4)式のことです。また、2.(9)[補足説明2]で注意したように、(7a)式は3.(2)3.でEinsteinが波動論によって求めた式と一致します。
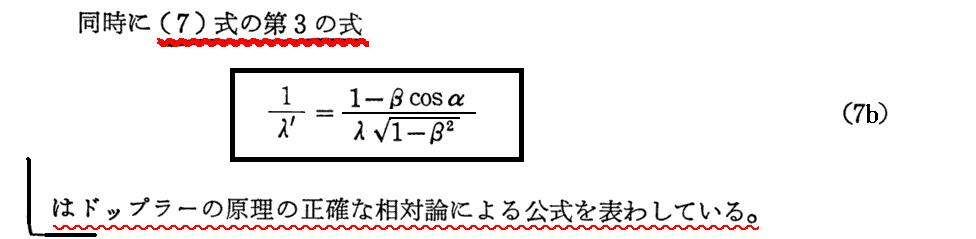

この方法が、3.(2)1.~2.でEinsteinが用いた方法です。

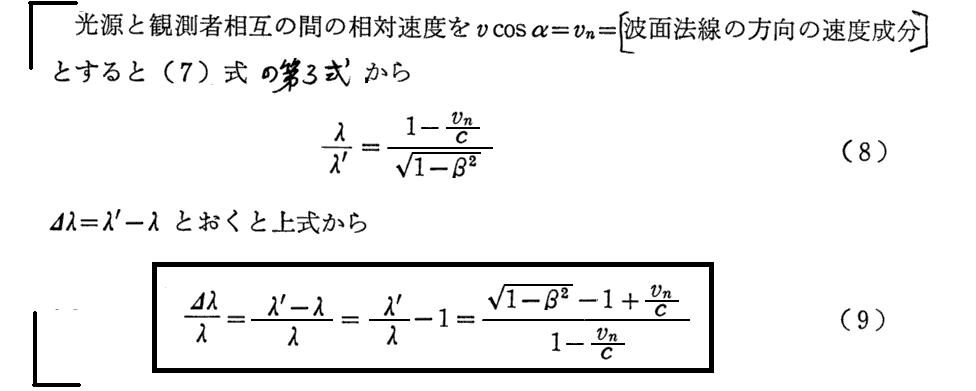

“初等的ドップラー効果の公式”(10)式に付いては[補足説明2]を参照。

上記の“横ドップラー効果”の公式は光源が存在する静止系から見てα=90°の場合の式であって、観測者の系から見てα’=90°の場合の公式は異なります。そのことに関して注意深い考察が必要です。3.(2)2.[補足説明3]をご覧下さい。
[補足説明1]
Sommerfeldが導いている相対論的結論である(7)式の第3式
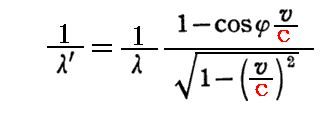
は、Einsteinが3.(2)2.で“光速不変の原理”と“運動している波源や観測者の時間が遅くなる”ことから導いている
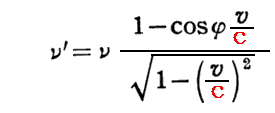
とまったく同じです。
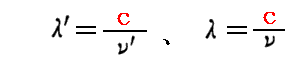
なのですから。
このことについての詳細は3.(2)2.[補足説明4]を参照されたし。
[補足説明2]
上記の“初等的ドップラー効果の公式”(10)を高校物理で習う相対論以前の古典的な波動論によるドップラー効果の公式(説明1、説明2)で確認しておきます。
下記は波源は静止して観測者が動く場合を説明していますが、波源が動いて観測者が静止している場合(説明3)も同様な結論が得られます。
2.時間の遅れ(横ドップラー効果)の検証実験
<1>横ドップラー効果(Sommerfeldの文献301.より)
横方向のドップラー効果の測定実験について文献301.からの引用です。





[補足説明]
上記のIvesの実験の説明は解りにくい。このことの正確な意味については3.(2)2.[補足説明3]をご覧下さい。また、上記のIvesとStilwellの1938年論文と1941年論文はこちらを参照。
この話題の詳細については下記のページを参照されたし。
http://gsjournal.net/Science-Journals/Research%20Papers-Relativity%20Theory/Download/727
<2>μ粒子の時間の遅れ(Sommerfeldの文献301.より)
μ粒子観測による時間の伸びの観測の報告です。前項Sommerfeld文献301.「電磁気学」§27Dの続きです。原論文はRossi_Hall_1941年、Rasetti_1941年を参照されたし。

Rasettiの測定に関しては<3>の説明をご覧下さい。



[補足説明]
今日ではμ中間子という呼び方はしない。レブトンの一種で“μ粒子”(ミューオン)と呼ぶ。
また、湯川の予言した中間子は“π中間子”と呼ばれているが、その固有寿命はμ粒子よりも二桁短い(約2.6×10-8s)。そのため<3>の説明の様にμ粒子と違ってパイ中間子は地表までほとんど届きません。π中間子については<4>を参照。
宇宙線に付いては別稿朝永振一郎著「宇宙線の話」を参照されたし。特にp59の図1をご覧下さい。
地上まで届く宇宙線のほとんどはμ粒子です。これは透過性が高いためかなりの厚さの岩盤も透過します。そのことは最近(2016~2017年)、その透過性を用いてエジプトのクフ王のピラミッドを透視して内部に隠された空間があることが発見されたことで話題になった。名古屋大学PressReleaseその1、その2、その3、Nature. 21. Nov. 2017年
<3>μ粒子の時間の遅れ(竹内淳の文献211.より)
同じくμ粒子の崩壊時間の変化についての説明です。






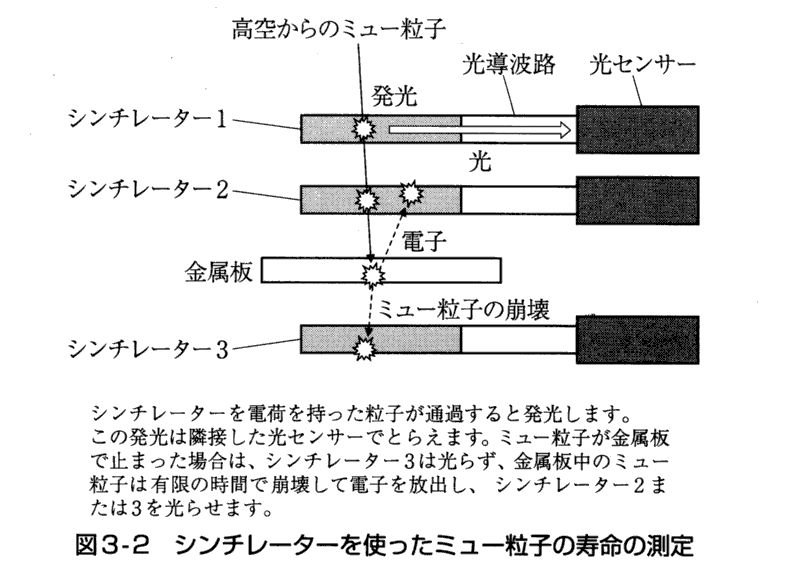





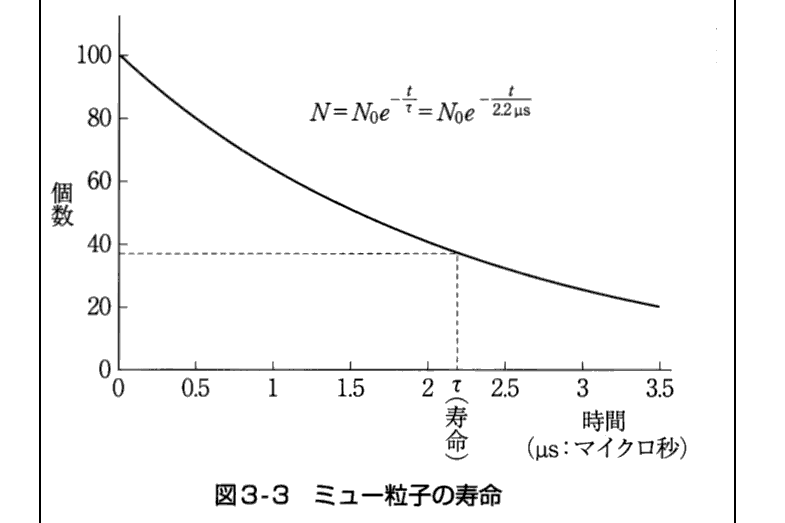

<4>π中間子の時間の遅れ(文献406.より)
下記はμ粒子ではなくてπ中間子の時間の遅れの観測結果の報告です。






3.粒子説によるドップラー効果の説明(Sommerfeld文献403.より)
ドップラー効果が光の粒子説に基づいても説明できることを最初に示したのはシュレーディンガーです。
光の粒子説による相対論的なドップラー効果は
A.Sommerfeld著「理論物理学講座Ⅳ 光学」講談社(1969年刊)の第Ⅱ章§16.p88~89
で説明されているのですが、
A.Sommerfeld著「原子構造とスペクトル線Ⅰ(上巻)」講談社(1973年刊)の第1章§7.p56~58
の説明の方がより解りやすいので、こちらから引用します。

この(1)式については、2.(10)1.[補足説明2]に記した(説明3)を復習されたし。

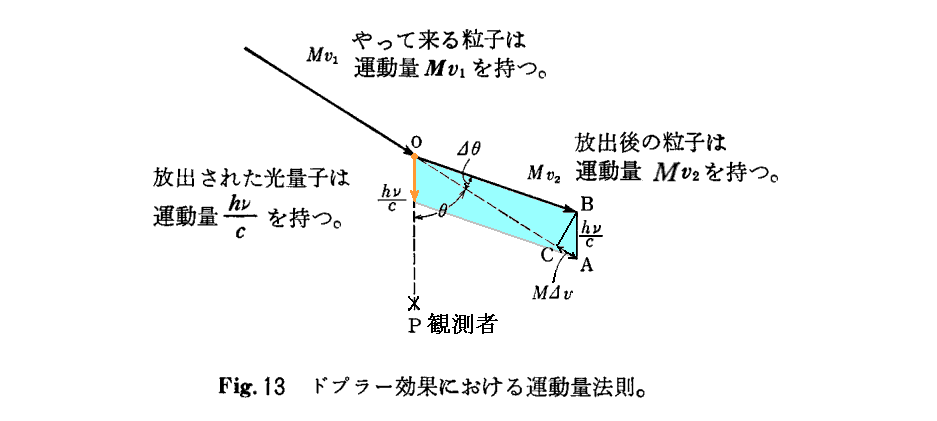



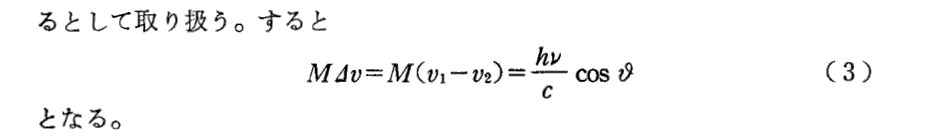

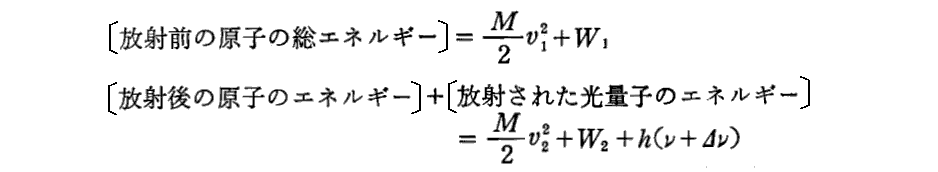
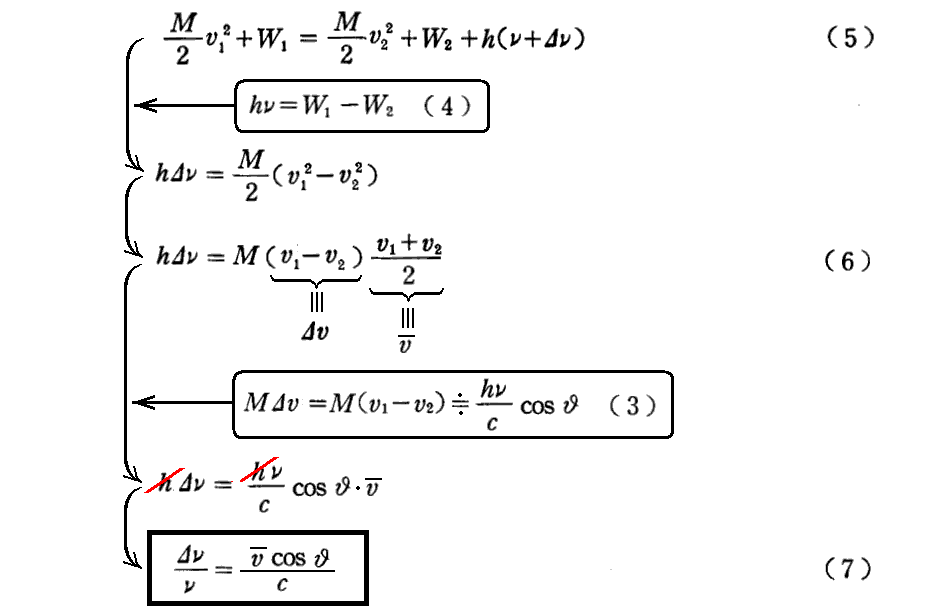




脚注(‡)で示されている“相対論的な意味で厳密なドップラー公式”は、波動説に基づいて2.(10)1.の(9)式ですでに導いています。粒子説に基づく厳密な証明は3.(3)1.[補足説明6]で行います。
[補足説明]
このように、光行差やドップラー効果は、“光量子”としての光に相対性理論を適用することで極めて旨く説明できる。この事は特殊相対性理論が量子論と完璧な整合性を持っていることを示している。
実際、アインシュタインは、1905年論文第Ⅱ部§8で、“光の集まりのエネルギーと振動数とが同じ法則に従って観測者の運動状態と供に変化することは、注目に値する。”と言っています。
次の(11)節は、アインシュタイン原論文(1905年)では取り上げられていない、“フレネルの随伴係数”に関する説明です。Pais文献502.、Sommerfeldの文献402.「光学」§12.、Einsteinの1917年文献108.、などから引用して説明します。
(11)フレネルの随伴係数
1.Pais文献502.の説明
この事について、パイスは文献502.p184で次のように述べている。
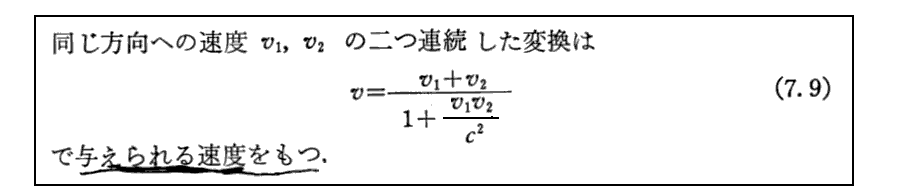
(7.9)式はすでに何度も出てきた相対論での速度合成則です。以下の議論に用いるので引用しているだけです。




上でPaisが述べているLaue論文(Annalen der Physik, ser.4, vol.23, p989~990, 1907年)はこちらを参照。
動力学的計算で(7.13)式を導くことを示している[P5]とはW.K.H.Panofsky and M.Phillips共著“Classical Elictricity and Magnetism”Addison-Wesley,Reading,Mass.,1955年(訳本は文献303.)のChap.11の事。
2.Sommerfeld文献402.の説明
前記のように、“フレネルの公式”の相対性理論による説明はラウエによって最初に与えられた。その詳細をSommerfeldの文献402.から引用して紹介します。

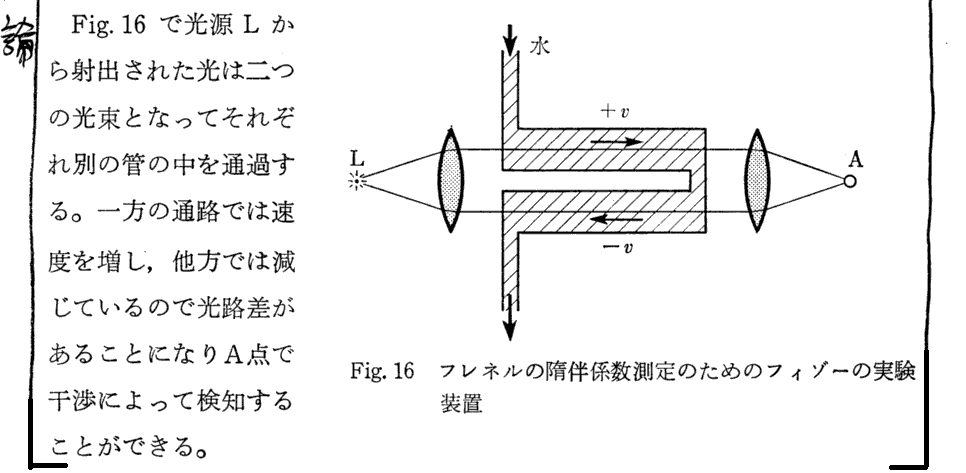

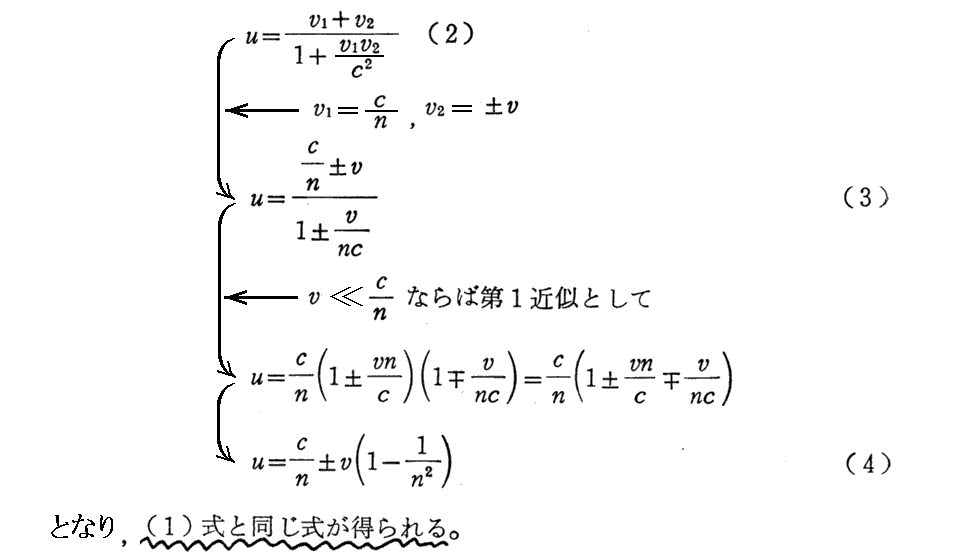




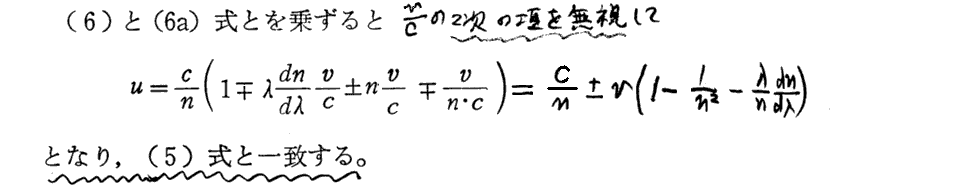




[補足説明]
上記引用文の最後にSommerfeldが述べていることを補足しておきます。
媒質中で光速度が遅くなるメカニズムの電子論的な説明は別稿「フィゾーが運動媒質中の光速度(随伴係数)を測定した方法」1.(2)[補足説明2]あるいはファインマン物理 第Ⅱ巻 第6章の様になります。だから随伴係数を相対性理論を用いた電子論的で厳密な証明をするには、媒質中の光の位相速度がc/nとなる様に重ね合わさる二次波を放出する原子の移動速度に相対論的な速度合成法則を適用することになります。
しかし、元々の二次波を出す原子と同じ速度で移動する観測系から見て媒質中の速度がc/nになることは二次波を出す原子の存在によって生じたのですから、媒質中の速度がc/nになるという事実に二次波を出す原子の運動学を相対論的に考慮すればそれで完全に正しい結論が得られるのです。
分散性媒質に付いても同様です。
3.アインシュタインの説明
アインシュタイン自身は、後の文献108.§13.(1917年刊)で、以下のように説明している。





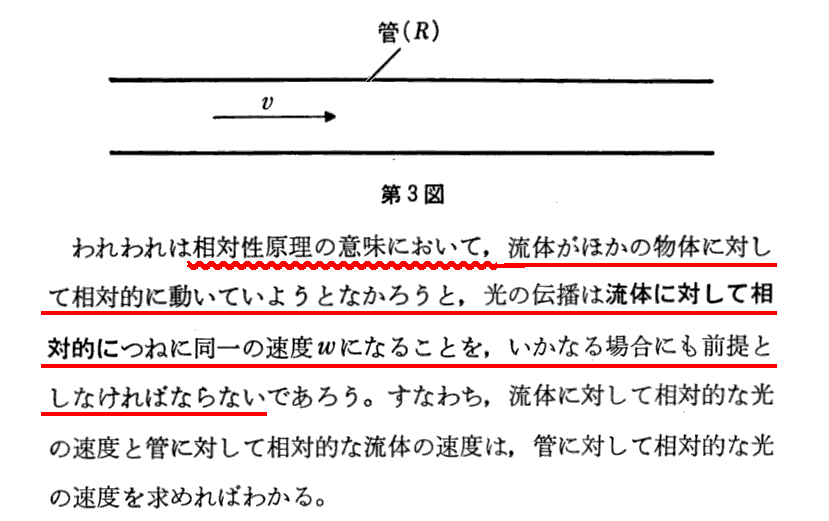





アインシュタインの説明と同じなのですが、佐藤文隆先生の説明も以下に引用。



[補足説明1]
アインシュタインは、このフィゾーの実験結果を完璧に説明できたことこそが、相対性理論の明白な実験的証拠と考えていたようです。実際、後に彼はShanklandの質問に対して“光行差とフィゾーの実験(フレネルの随伴係数)を相対性理論が説明できた事が、その理論の正当性を確信する上で充分でした(were enough)”と語っている。(文献510のホルトンp88_89の引用も参照)
そのことからも、1905年の論文を書いた時点でラウエの指摘は当然気付いていたでしょう。それなのになぜ論文中に書き込まなかったのでしょうか?
私の推察ですが、フィゾーの実験が相対性理論によってあまりにも簡単かつ完璧に説明できたことに半信半疑だったのではないでしょうか。あまりにも自明だったので論文に書かなかったか、あるいは、この事を正確に説明するためには先の2.(11)2.[補足説明]で説明した電子論的な説明をしてから、その二次電磁波の出す原子の相対論的速度合成則に持って行かねばならない面倒さ故に書かなかったのでしょう。実際、アインシュタインはローレンツが1895年の冊子で展開しているフィゾーの実験結果およびフレネルの随伴係数を電子論で説明するメカニズム(2.(11)2.[補足説明]参照)を完璧に理解していたのですから。
このフィゾーの実験の説明は後(1907年)にラウエによって指摘されるのですが、アインシュタインは他人の業績に対してとやかく言うような了見の狭い人ではなかったので、この事を論文に書かなかったことについて言い訳したりすることはありませんでした。しかし、本当の所は上記の通りだったのではないかと思います。
アインシュタインは1907年の総説論文(文献113)でフィゾーの実験を取り上げるのですが、前書き(p68~69)で、“これはラウエ氏によって気付かされた”とラウエを讃えています。アインシュタインらしいですね。ただし、この言い方を深読みすると、アインシュタインはラウエ以前にすでに気付いていた事を伺わせます。
[補足説明2]
ラウエについて補足する。彼はアインシュタインと相対性理論について討論するためにベルンを訪問した最初の物理学者であり、また相対性理論の解説本を最初に(1911年)書いた人です。
プランクおよびラウエとアインシュタインの初期の関わりについては、アーミンの文献504.が興味深いので引用する。
3.相対論的電磁気学
この部分は、1905年論文のメインテーマです。文献103.は単位系を電磁単位系に改竄しているので、ここは原論文のGauss単位系を踏襲している文献101.から引用して説明します。
ただし、原論文中の光速Vをcで、(ξ,η,ζ,τ)を(x’,y’,z’,t’)で、電場をE=(Ex,Ey,Ez)で、磁場をH=(Hx,Hy,Hz)で書き換えています。
このとき、光速cを波の進行方向の余弦(a,b,c)のcと混同しないように赤記しています。同様に、エネルギーEと運動量Pも、電場ベクトルEや圧力Pと混同しないように赤記することにします。
なぜGauss単位系を採用するのかは、この稿の最初で説明しました。相対性理論が難しくて解りにくいのも単位系の混乱にあるように思いますので、もう少し補足します。
[補足説明]
Gauss単位系ではEとDは全く同じ次元となり、さらに同じ数値となります。HとBも同様に同じ次元、同じ数値となります。そのためDや、HとBの両方を導入する必要は無くなります。それゆえに静電単位系やMKSA単位系で出て来る、電磁気学で最も解りにくい、E-H対応系かE-B対応系かは問題になりません。全ての場がEとH(or B)の二つの量で議論できるからです。
そのためこの稿では電場をE=(Ex,Ey,Ez)で表し、磁場をH=(Hx,Hy,Hz)で表すことにします。ここではDやBを導入する必要はなくて全てEとHで論じることができます。この事については別稿「電磁気学の単位系が難しい理由」5.(3)を参照されて下さい。
そこでも説明しましたように、Gauss単位系ではローレンツ力をF=qE+q/c[v×H]あるいはF=qE+q/c[v×B]のどちらの形で表しても良いのですが、この稿では磁気的な場としては“磁束密度”Bではなくて“磁場”Hを採用していますので全て前者の表現を採用する事にします。
上記の様に二つの量EとHで電磁気学が表現できることは、ローレンツがあらゆる電磁気現象を真空中の場と電荷のみに還元したことによります。それまで電磁気学を混乱させていたMaxwell、Hertz以来の電媒質、磁媒質を排除して真空中の場と電荷のみで電磁気学が書きあらわせたことが、相対性理論の発見に本質的な役割を果たしたようです。
この事は別稿「電磁気学の単位系が難しい理由」5.(3)2.で引用したアインシュタインの文章の赤波線の部分や別稿で引用したShanklandの文章中のアインシュタインからの手紙(手紙の全文はこちらを参照)の内容に関係します。
これらの文章を読むと、アインシュタインが特殊相対性理論を建設できた要因として、彼が“ローレンツの電子論を深く学んでいたこと”が、もう一つの“時間の相対性に気付いたこと”と並んで極めて重要であったことが解ります。EやHに付け加えてDやBも絡んでいたら、とても特殊相対性理論の認識には至らなかったでしょう。
Bornの「アインシュタインの相対性理論」、Planckの「理論電気磁気学」、ランダウ・リフシュツの「場の古典論」が(非有理化)Gauss単位系を採用しているのも、この当たりの見通しを良くするためだろうと思われます。補足しますとローレンツは有理化したGauss単位系を用いています。
この当たりに関しては、Sommerfeldの文献301.§8の解説をお読み下さい。
相対性原理が成り立つのはガリレオ変換に対してではなくて、ローレンツ変換に対してなのだということを確定する現象が、§6.で証明されている、真空に対するMaxwell-Hertz方程式のローレンツ変換不変性ですから、Einsteinはまずこのことから話を始めます。
このとき導かれるローレンツ変換共変の電磁場変換則が、それまでに知られていた電磁気学における不可解な現象を完璧に説明してくれます。
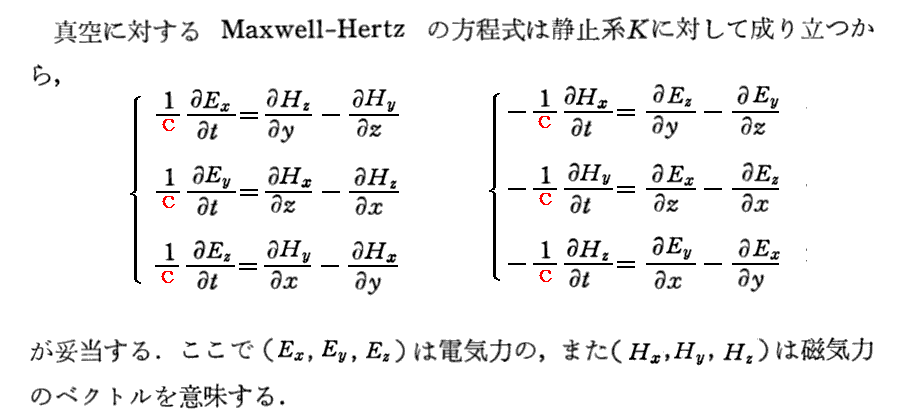
(1)原論文 §6.Maxwell方程式のローレンツ変換不変性の証明
ここでは、前述の様に記号を置き換えて引用していますが、アインシュタインの元論文では、電場E=(Ex,Ey,Ez)が(X,Y,Z)で表され、磁場H=(Hx,Hy,Hz)が(L,M,N)で表されています。アインシュタインが電場、磁場を(X,Y,Z)、(L,M,N)と表したのは当時の慣習にしたがったからです。ヘルツ、プランク、ポアンカレ、ローレンツなどが書いた当時の論文では皆その様に表しています。
また、K座標系(x,y,z,t)に対して速度vで動いているk座標系での変数(x’,y’,z’,t’)は(ξ,η,ζ,τ)で表されています。そのため以下の説明を源論文と比較されるときには注意して下さい。

電荷・電流が存在する場合の議論は3.(4)§9.で行われます。

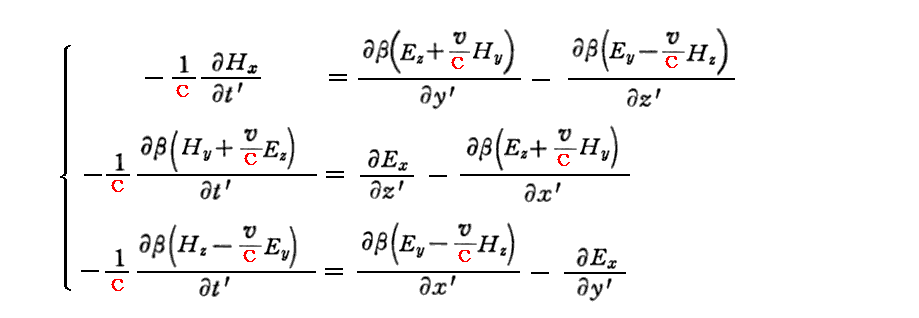
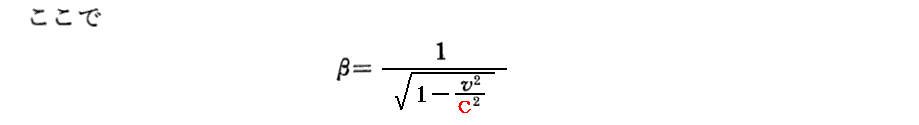
[補足説明1]
t’は(x,y,z,t)の関数、x’、y’、z’も(x,y,z,t)の関数だから、微分法の性質より
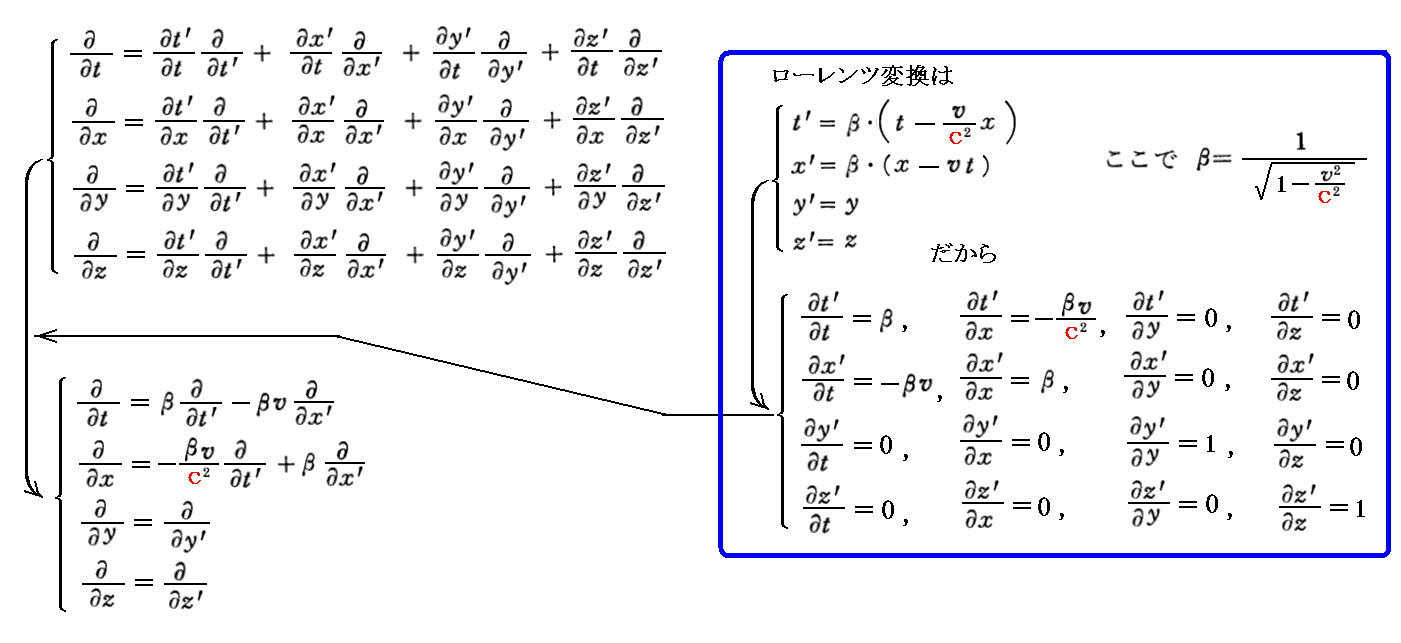
が成り立つ。
[補足説明2]
“電荷が存在しないとき”にはdivE=0、divH=0が成り立つので上記の公式を用いると
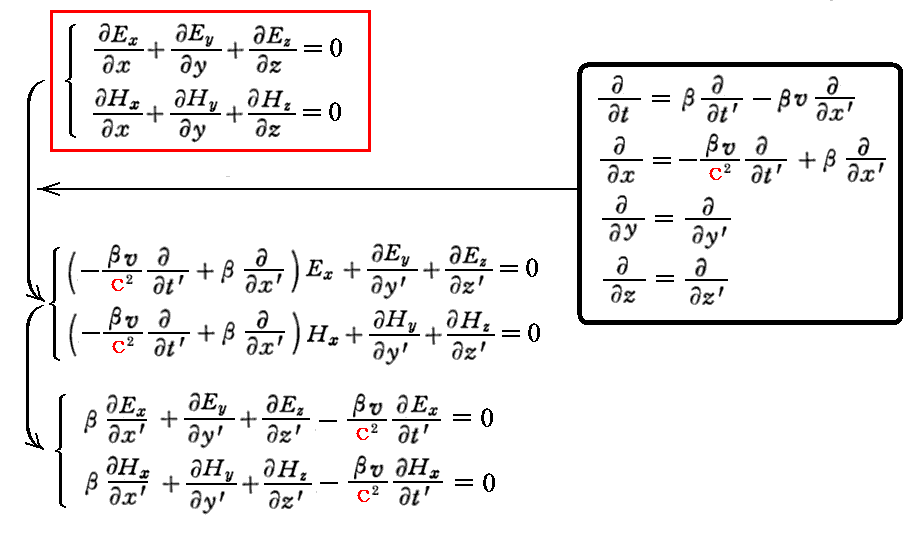
が言える。
[補足説明3]
上記の関係式を用いるとマックスウェルが拡張したアンペールの法則は
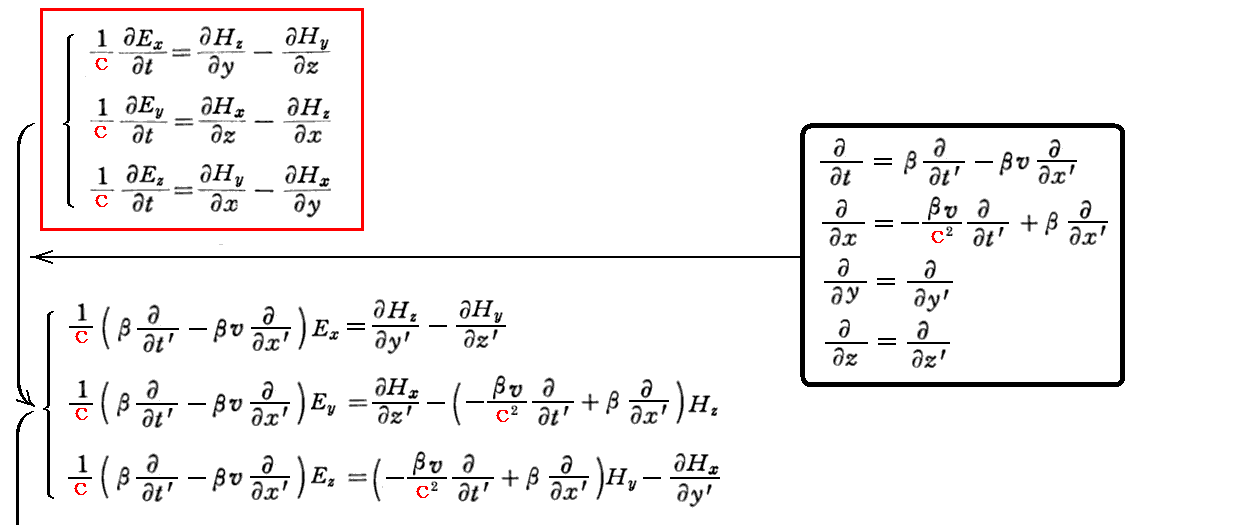
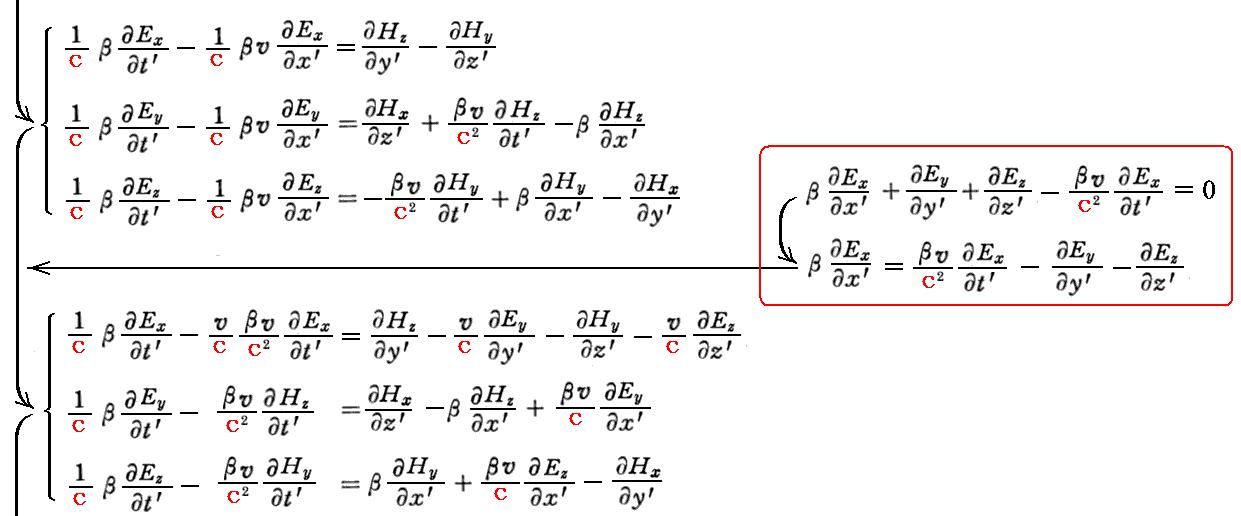
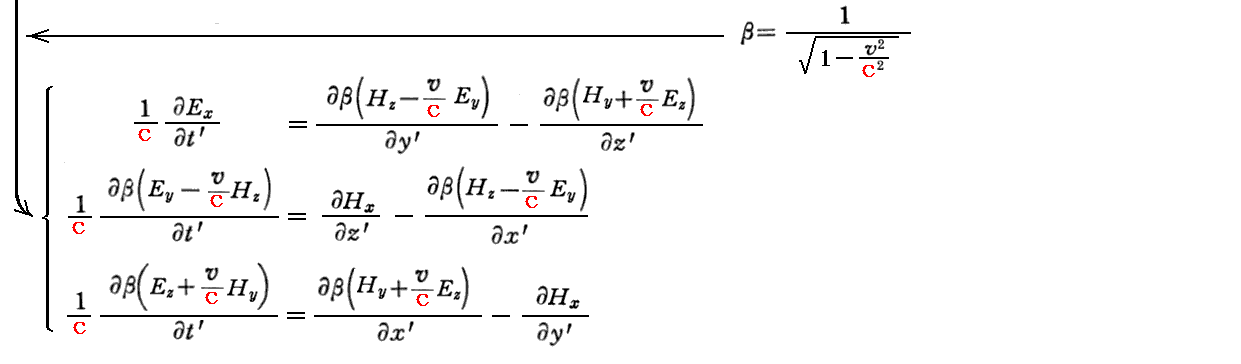
となる。
まったく同様(詳細は3.(4)[補足説明3]参照)にしてファラデーの電磁誘導の法則は
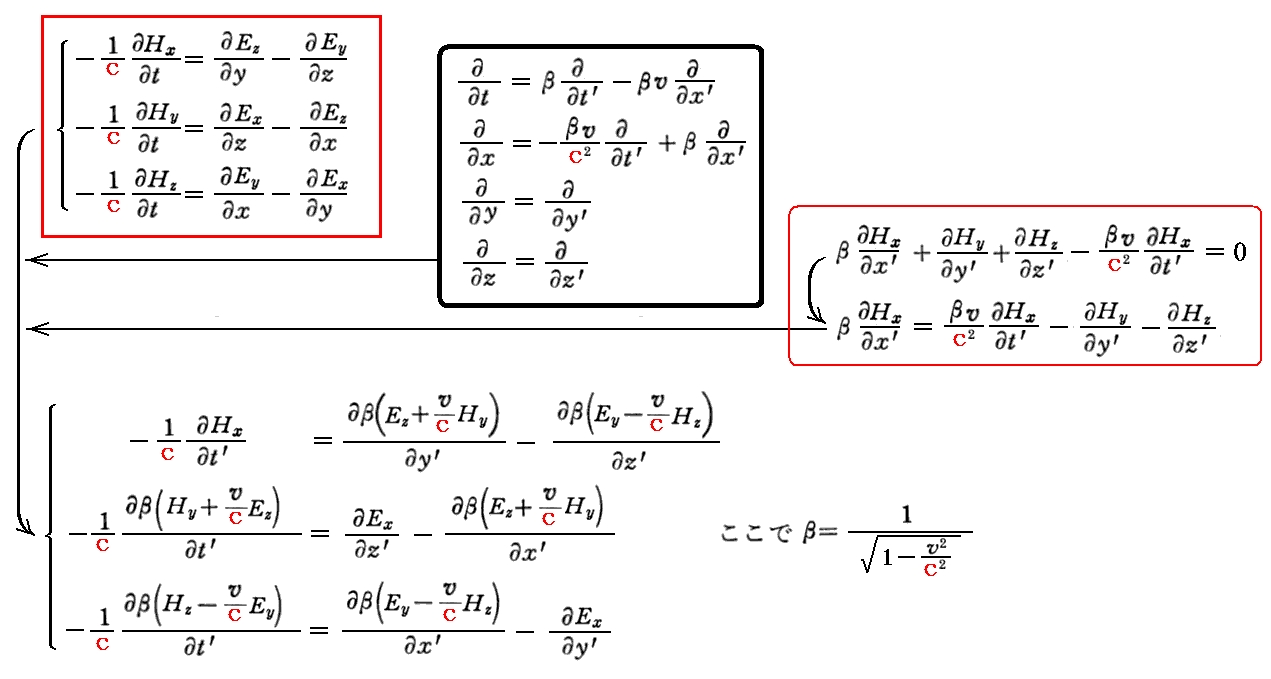
となる。
[補足説明4]
前記[補足説明3]で得られた式を用いると、divE=0は

となる。
まったく同様にして、divH=0は
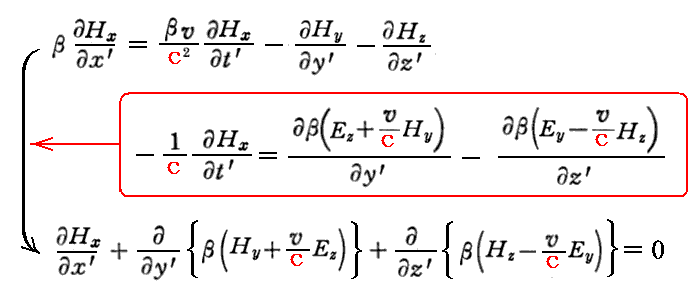
となる。
このとき、後で求まるローレンツ変換に対する電場・磁場の共変式
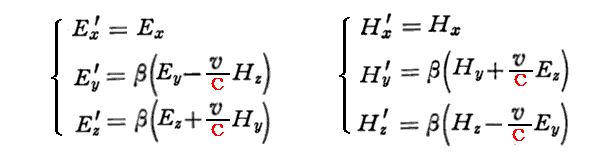
を用いれば、上記の結論は
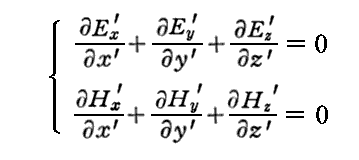
となり、これらの方程式もローレンツ変換不変であることが確認できる。
電荷が存在する一般的な場合は、3.(4)[補足説明2]および3.(4)[補足説明3]で説明します。


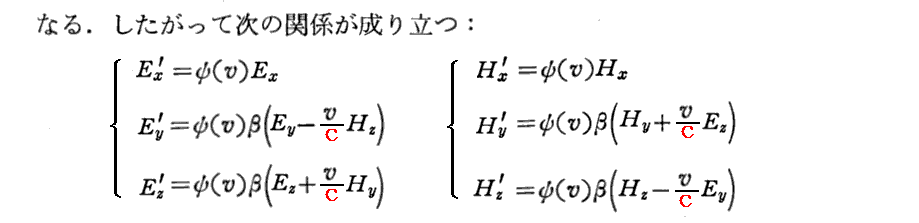

[補足説明5]
上記関係式を補足する。まず、前記の関係式を(Ex,Ey,Ez)、(Hx,Hy,Hz)に付いて解くと
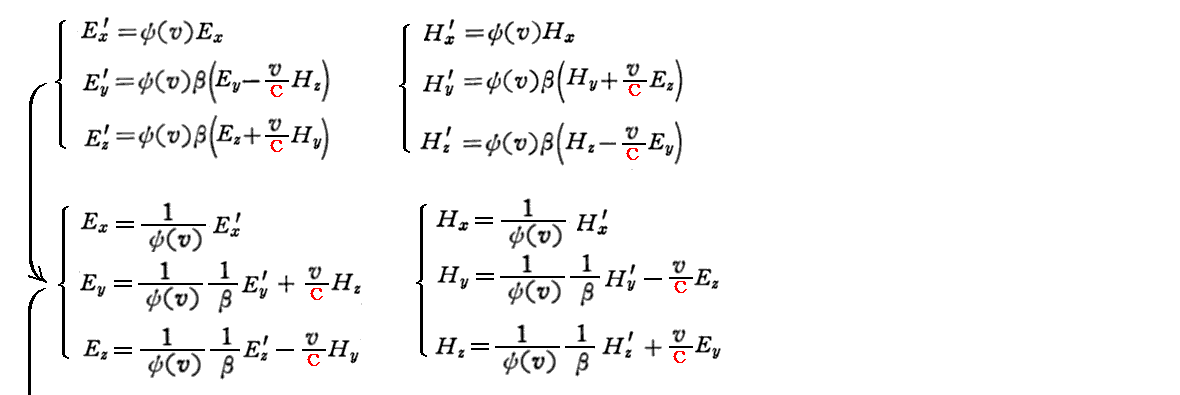
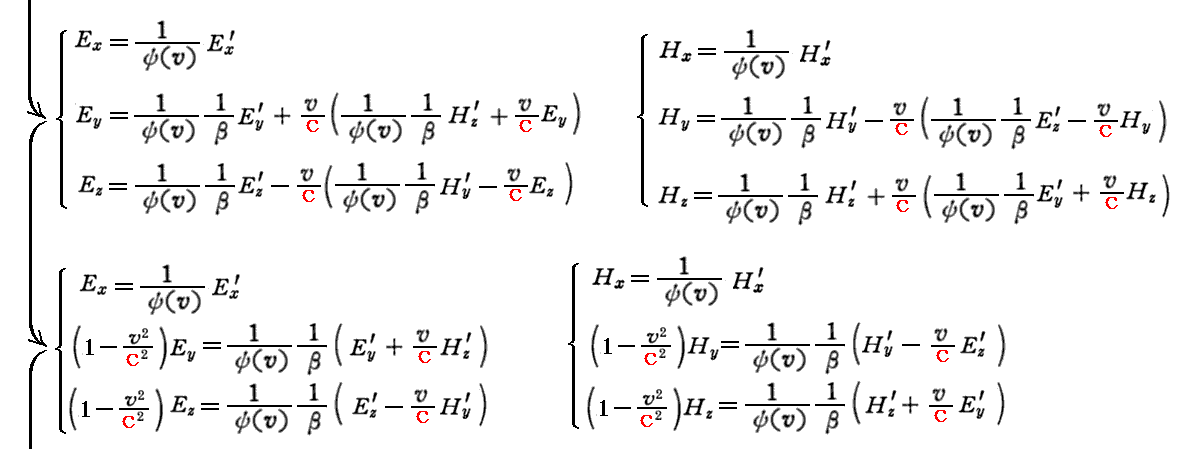
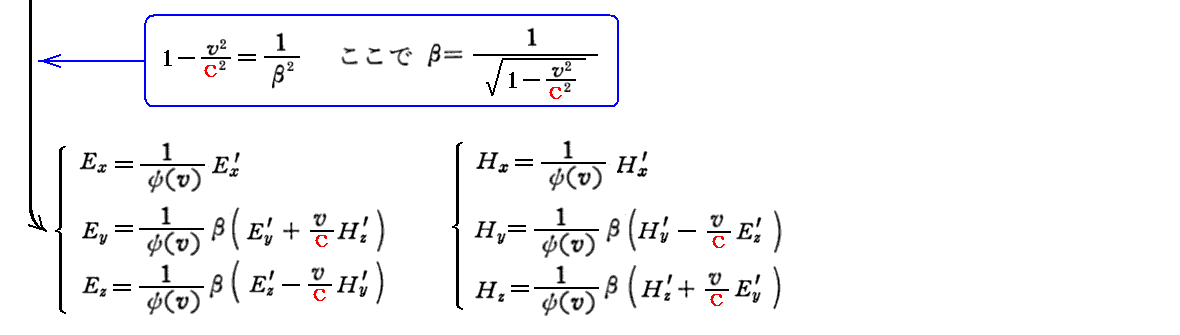
が得られる。
一方、最初の式のvを-vに置きかえ、ダッシュ’つきの量から’を取り除き、’が付いていない量に’をつけるとk系からK系への変換式として
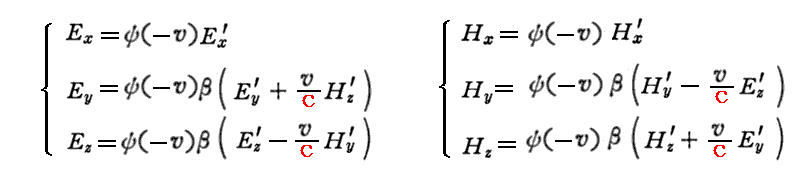
が得られる。
上記二つの表現は等価でなければならないので
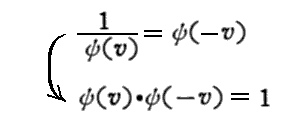
が得られる。

[補足説明6]
“対称の理”についての脚注 1)を補足する。
アインシュタインは、上記の関係式を導くための例として(Ex,Ey,Ez)=(0,0,0)、(Hx,Hy,Hz)=(0,0,Hz)の場合を取り上げている。
このとき、前記のローレンツ変換式により(Ex’,Ey’,Ez’)、(Hx’,Hy’,Hz’)求めると
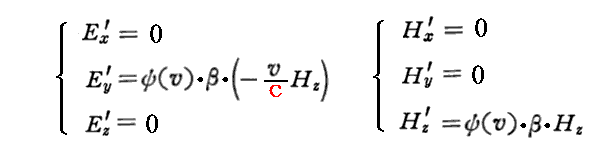
となるのであるが、電荷の運動方向が反対の場合に、それぞれの電荷ρが静止している座標系に移ると
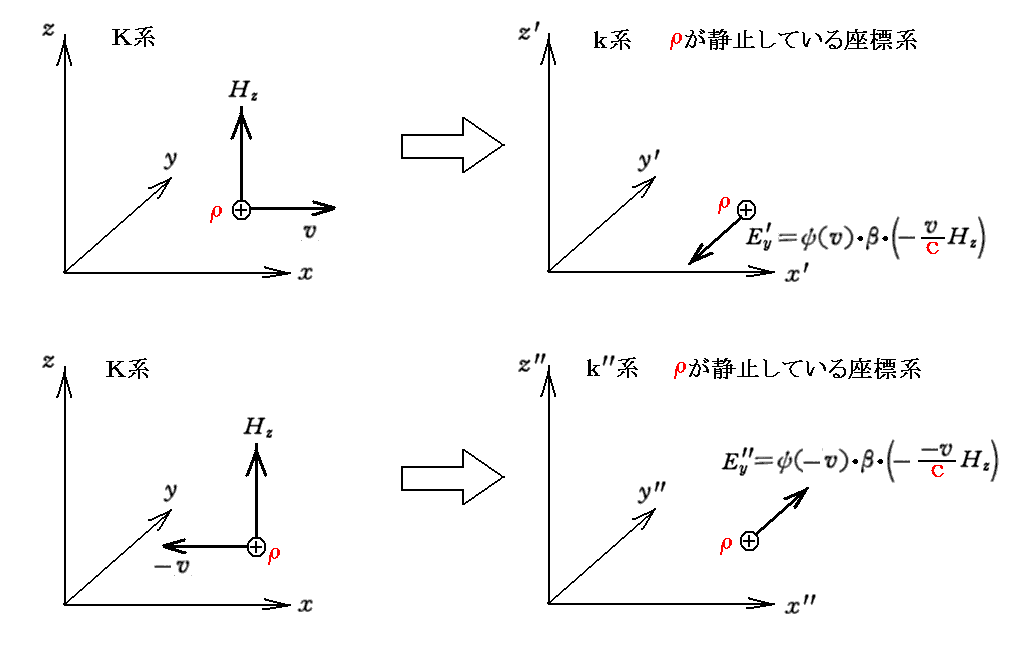
となる電場が生じる。
このとき、生ずる電場の方向は、よく知られている“ローレンツの力の法則”を満たすためには上図の様に成らねばならない。そのため以下の等式が成り立つことが解る。
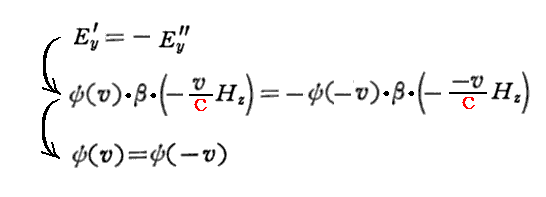
よって前記の関係式が導かれる。




[補足説明7]
上記赤波線アンダーラインの“はじめの3つ”とは
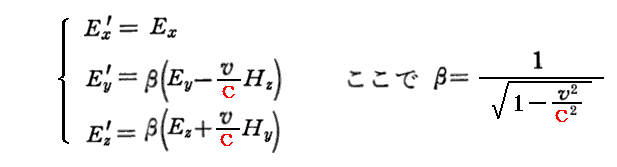
のことです。
この関係式は、以下のベクトル関係式を表している。実際、 v≪c で β≒1 と於ける場合には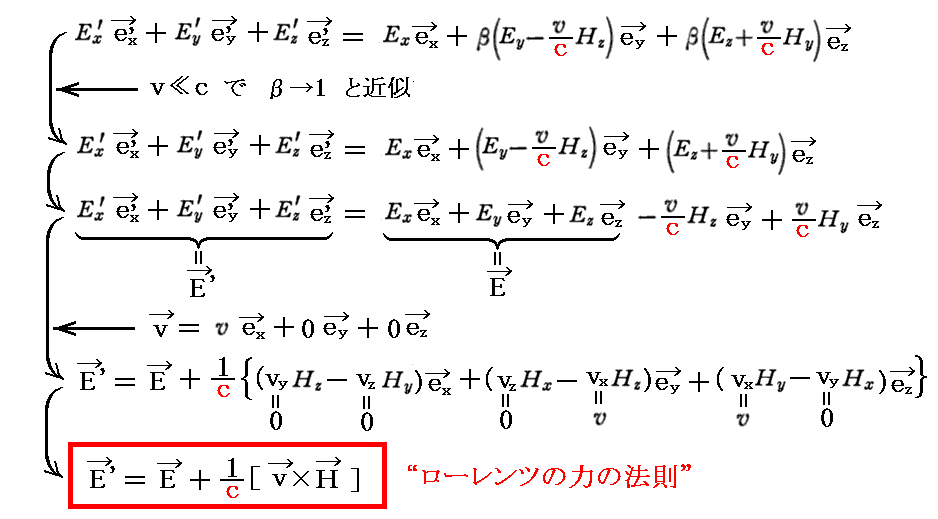
となります。
つまり、
1.(古い表現法)は上記の右辺を意味する。そのため、1.の文中の“電気単位極には電気力の外に「動電力」が働き”の“電気力”は上記に電気量ρを乗じたρEの部分であり“「動電力」”はρ/c[v×H]の部分を意味する。
また、
2.(新しい表現法)とは上記の左辺を意味する。そのため、2.の文中の“それに作用する力は、単位極の場所に存在する電気力に等しい”は、左辺のぺクトルE’にρを乗じたρE’を意味する。
すなわち、
アインシュタインは、当時ローレンツにより発見された“ローレンツの力の法則”が、特殊相対性理論の必然の結果として導き出されることを注意している。
また、次の文節で同様なことが
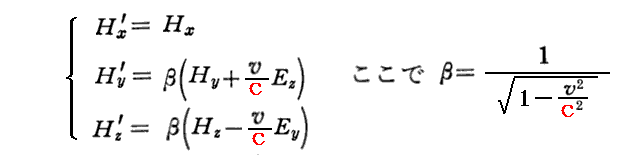
中の“「動磁力」”=m/c[v×E]についても成り立つと説明しています。ただし、単極の磁荷mは存在ないのでそこは注意が必要です。
[補足説明8]
“ローレンツ力”について補足する。
2.(1)[補足説明1]で説明したように、Gauss単位系で表現した電磁気学の法則は
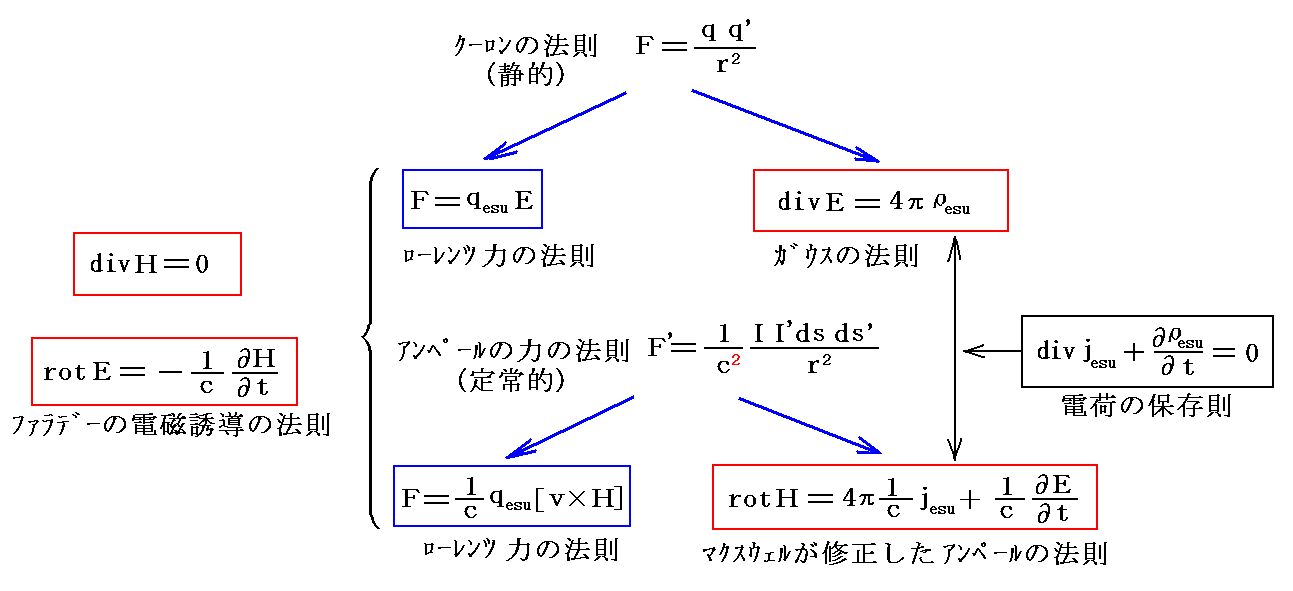
となる。
この事から明らかな様にマックスウェルの電磁場方程式
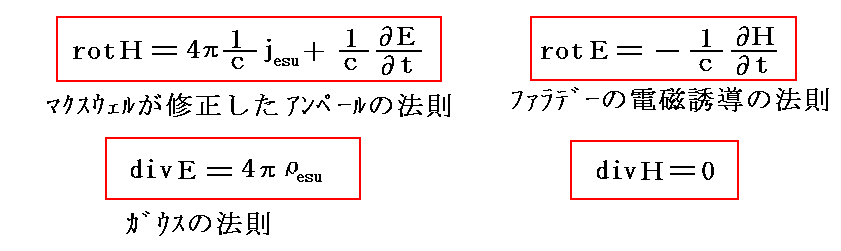
に現れる電荷や電流は場を生ずる源として存在するのであって、場がそれらの電荷や電流にどのような力を及ぼすのかは示していません。
もちろんその力の法則は、元々の“クーロンの法則”や“アンペールの電流要素間に働く力の法則”の中には含まれているのですが、その力の法則を電磁場方程式とは独立なものとして導き出したのがローレンツの電子論です。
そうしてこそ、電媒質、磁媒質の複雑な場の中に埋もれていた電磁気学現象を真空中の電磁場とそれを生みだし克つ、それから力を受ける電荷・電流に分離して極めて明快な形に電磁気学を組み立て直すことができたのです。
だから“ローレンツの力の法則”
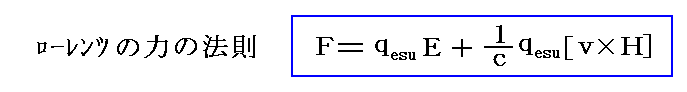
は、元々“マックスウェルの電磁場方程式”とはまったく独立な法則です。
そのとき、アインシュタインの特殊相対性理論によると、“マックスウェルの電磁場方程式系”が“相対性原理”を満たす(つまりローレンツ変換に拠って不変である)事を要請すると必然的に“ローレンツの力の法則”を導き出せる。
すなわち、相対性理論の整合性が見事に成り立っている実例であるとアインシュタインは述べている。アインシュタインがこの論文に「運動物体の電気力学について」という題目を付けた理由です。


[補足説明9]
上記“単極機械”とは“ファラデーの単極発電機”のことです。ファラデーは1821年に、下図の実験をして下記(1)~(3)の現象が生じる事を発見した。
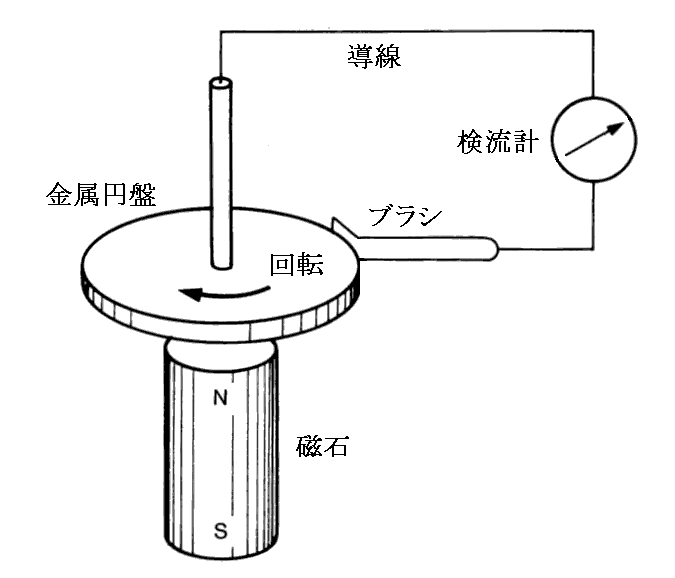
上図の装置の磁石または金属円盤を回転させると
(1)円盤を固定して磁石を回転すると誘導電流は流れない。
(2)磁石を固定して円盤を回転すると誘導電流が流れる。
(3)磁石と円盤を一緒に回転すると誘導電流が流れる。
という現象が生じる。
このとき (1) と (2)、(3) の関係は不思議で、2.(1)[補足説明1]で述べた“相対性”に矛盾するように見えます。これも当時の物理学者を悩ました問題でした。
しかし、アインシュタインは、以下のように考えればこの現象は明らかだと言っている。
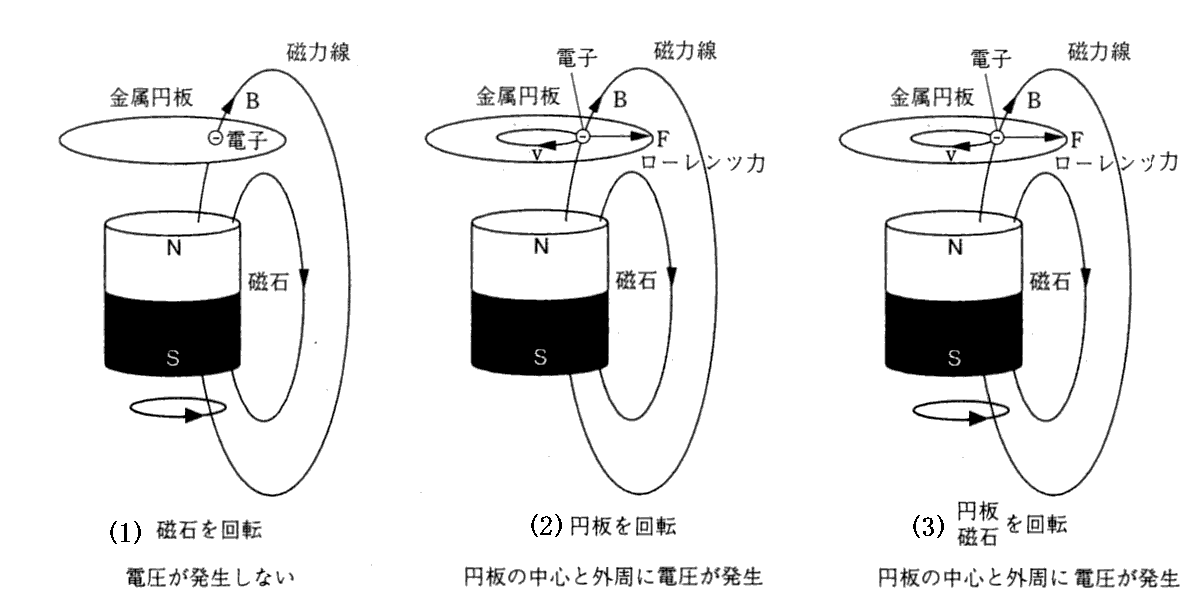
磁力線は磁石から出ているのですが、磁力線そのものものが磁石と一緒に回転するという考え方は間違っている。磁場というのはまさに場そのものであり、上記の例で磁石が回転しても磁場が回転するわけではない。そのため磁石が回転してもしなくても、磁場の様子は上記(1)~(3)の場合に全て同じになり、時間的に変化するわけではない。その時、金属円盤が回転するかしないかの違いが重要であって、金属円盤が回転する場合には“ローレンツ力”により円盤と外周の間に電位差が生じて電流が流れる。
こちらの引用文もご覧下さい。また、この当たりについてはファインマン文献407.第Ⅲ巻§13-1~6 や§17-1~4 の説明が興味深いのでご覧下さい。
§7.は、Einsteintに相対性理論の正しさを確信させた現象の説明です。
古典的なDoppler効果と光行差の公式は相対性原理を満たしていないのですから、相対性理論(ローレンツ変換)によって相対性原理を満たす公式が得られることが、Einsteinに相対性理論の正しさの大きな自信を与えた。この事はEinstein自身が後に繰り返し述べていることです。
(2)原論文 §7.Doppler効果と光行差
1.光の波動解のローレンツ変換

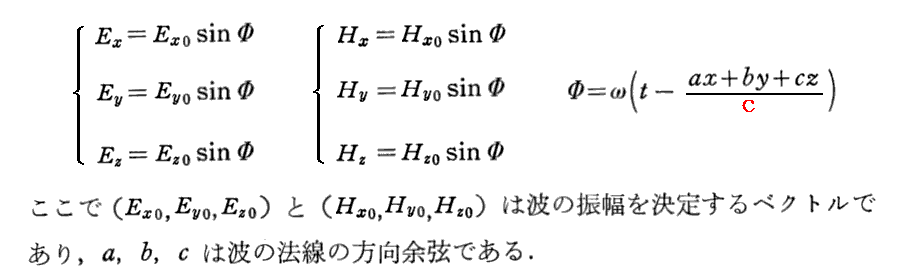
[補足説明1]
上記の解は、“Maxwell方程式”を変形して得られる“波動方程式”を解くことにより得られる。
波動方程式は、電荷が存在しない場合のMaxwell方程式
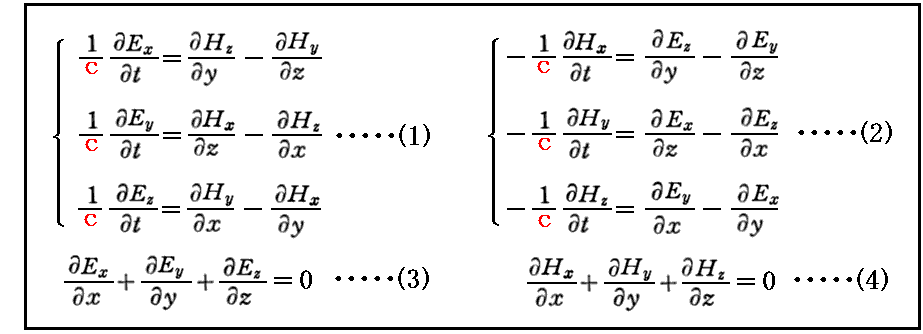
を変形すれば導ける。
(1)式の両辺を t で偏微分した後に(2)、(3)式を用いて変形する。
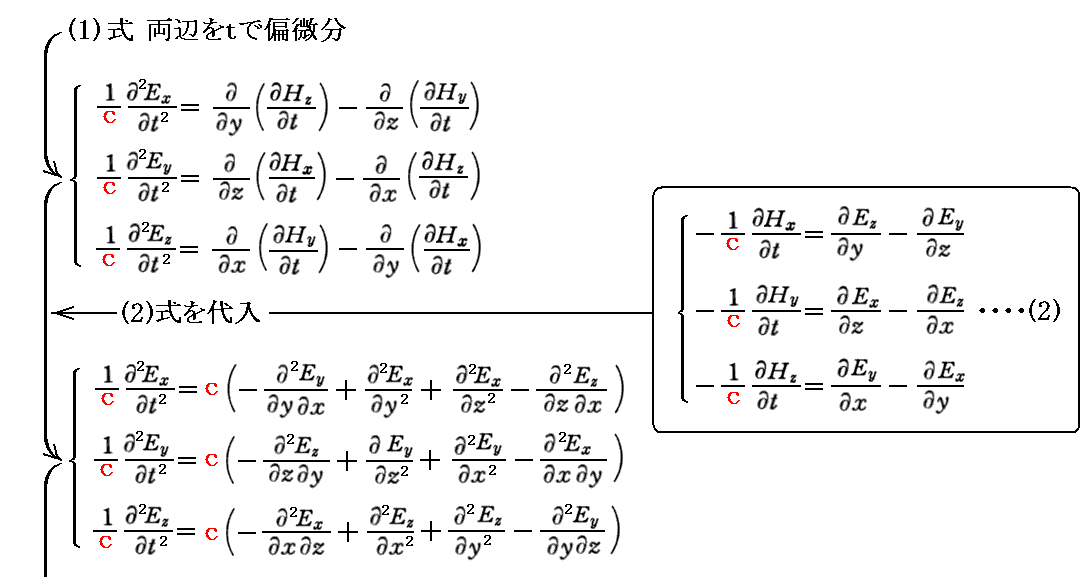
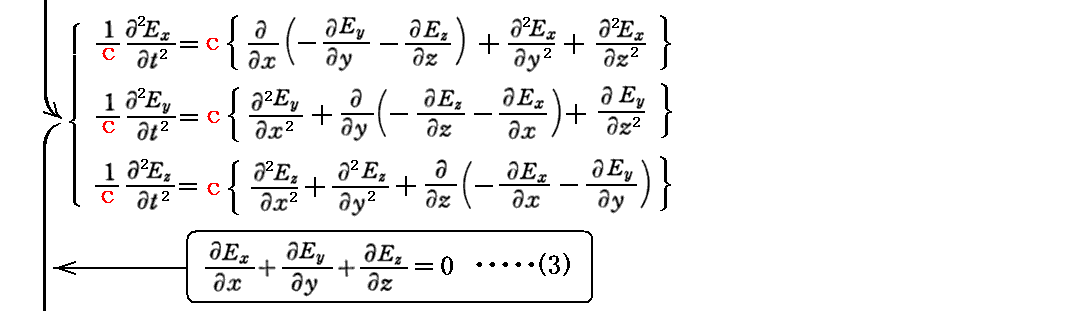
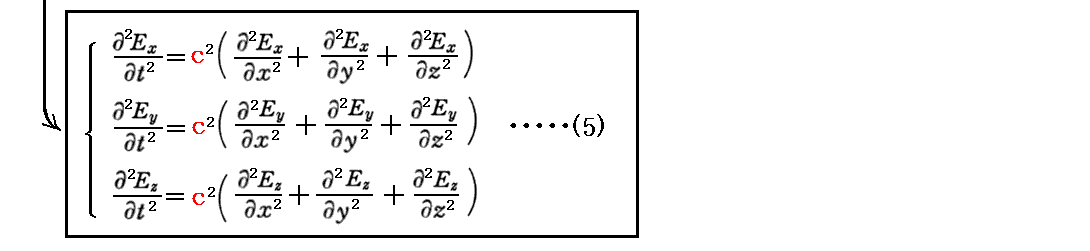
同様に、(2)式の両辺を t で偏微分したものに(1)、(4)式を適用すると
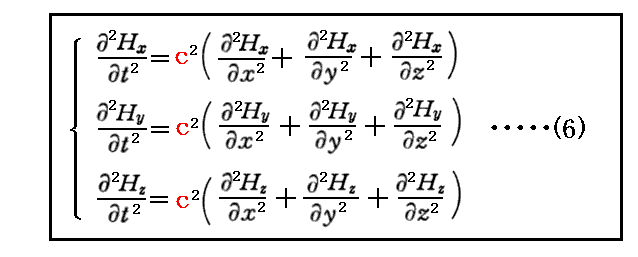
が得られる。
(5)、(6)式は、別稿「波動方程式と一般解」3.で説明した“波動方程式”の形をしている。そのため、この解として位相速度cで伝わる“平面波”解が存在する。
ここで以下の事に注意して欲しい。前節で証明したようにMaxwell方程式はどの慣性系でも同じ形に表された。ここで導いた波動方程式はMaxwell方程式から導かれるものですから、波動方程式もどの慣性系で見ても同じ形になる。この事は、波の位相速度を表すcはローレンツ変換に対して不変の定数だから、光の伝播速度がどの慣性系で見ても同じであることを意味する。
さらに補足しておきます。ここの波動方程式は、電荷・電流が存在しない場合のMaxwell方程式系から導きましたので、“同時波動方程式”になりましたが、電荷・電流が存在する場合のMaxwell方程式系を用いれば電荷・電流項を含んだ電磁場の“非同次波動方程式”が得られます。その当たりにつきましては別稿「電磁場の非同次波動方程式」2.(2)を御覧下さい。
[補足説明2]
“波動方程式”(5)の解として
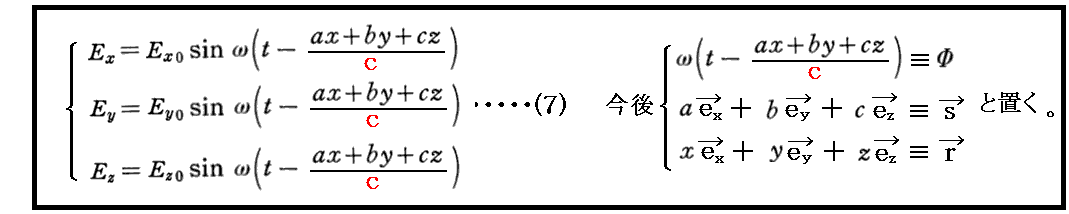
を仮定しよう。
ここで、(Ex0,Ey0,Ez0)は波の振幅ベクトルのx,y,z成分であり、(a,b,c)は波面の法線方向を表す単位ベクトル(sと置く)のx,y,z成分(法線の方向余弦)です。そのとき方向余弦に関しては、ピタゴラスの定理により、a2+b2+c2=1が成り立つ。
解(7)式が波動方程式(5)式を満足することは代入してみれば直ちに確認できる。例えば(7)の第1式を(5)の第1式に代入すると
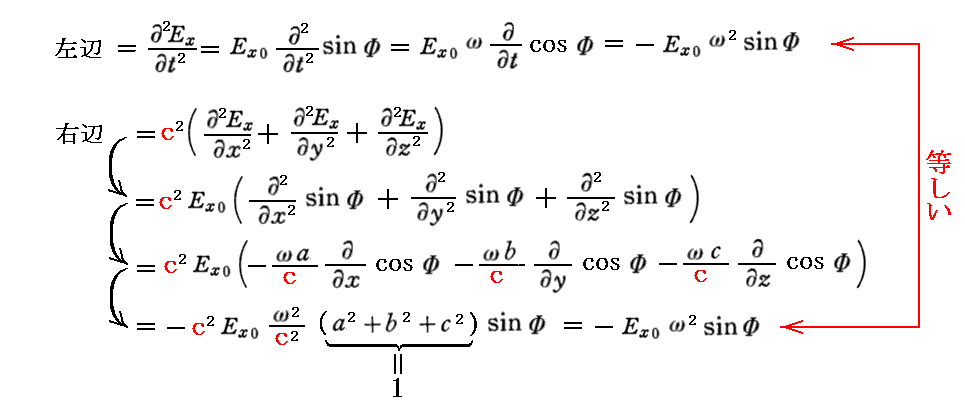
となる。他の成分についても同様に確認できる。。
同様に、“波動方程式”(6)の解として
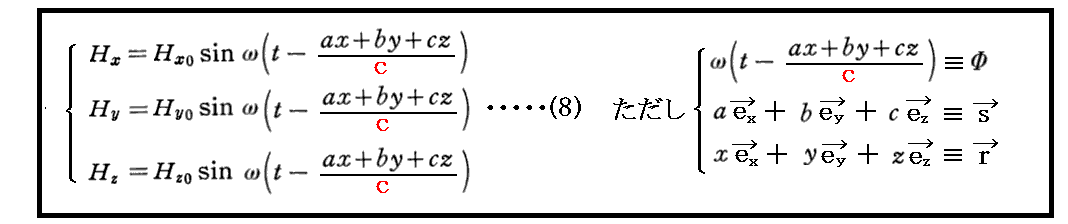
が得られる。ここで、(Hx0,Hy0,Hz0)は波の振幅ベクトルのx,y,z成分であり、(a,b,c)は波面の法線方向を表す単位ベクトルsのx,y,z成分(方向余弦)です。当然a2+b2+c2=1が成り立つ。
ここで位相Φの表し方について補足します。多くの本では位相Φを
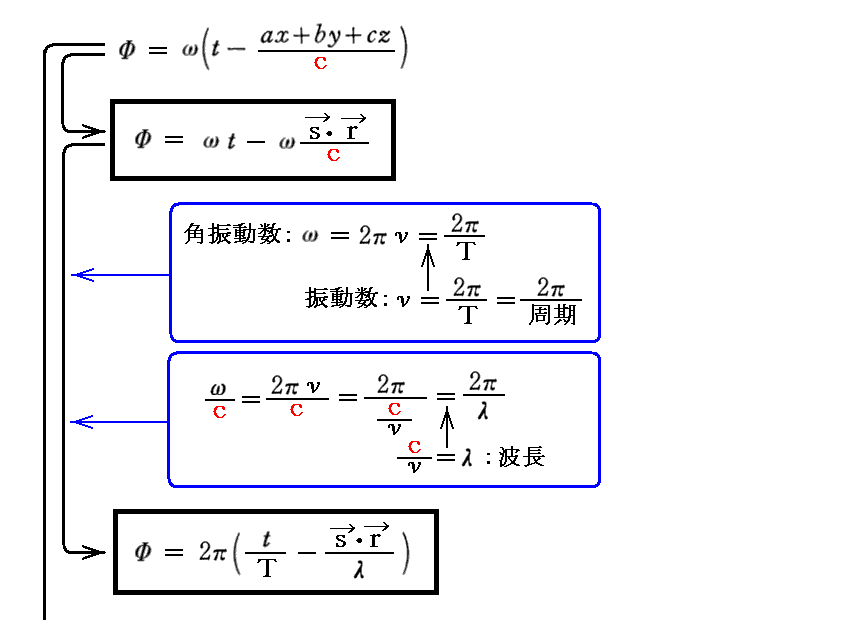
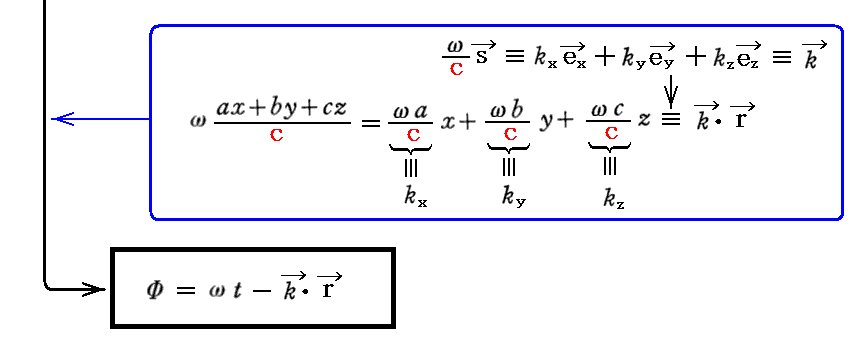
の様に表している。これらの表現は2.(10)1.で引用したSommerfeldの本や、別稿「偏光とは何か」2.や、「慣性重力波とロスビー波、そして赤道波」2.(3)3.でも利用しています。
前記の解(7)、(8)式は、波の伝播方向を表すベクトルsに垂直な平面内で波の位相が全て等しい“平面波”を表す。実際、位置(x,y,z)の時刻tに於ける位相Φ1は
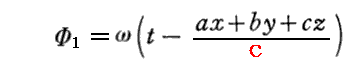
となるが、ベクトルsに垂直に(x,y,z)から任意距離(Δx,Δy,Δz)=Δr離れた点の時刻tに於ける位相Φ2は下記の様に常にΦ1と一致する。
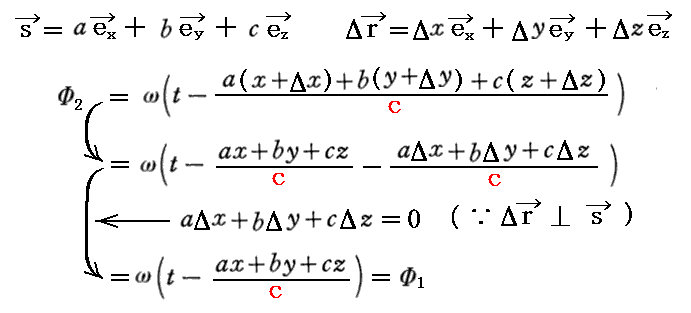
このとき“二つのベクトルが直交すれば、その内積はゼロとなる”(別稿「ベクトルの内積と外積の成分表示」を参照)を用いた。
[補足説明3]
前記の解(7)、(8)式は、“Maxwell方程式”(1)~(4)式も満足しなければならない。つまり
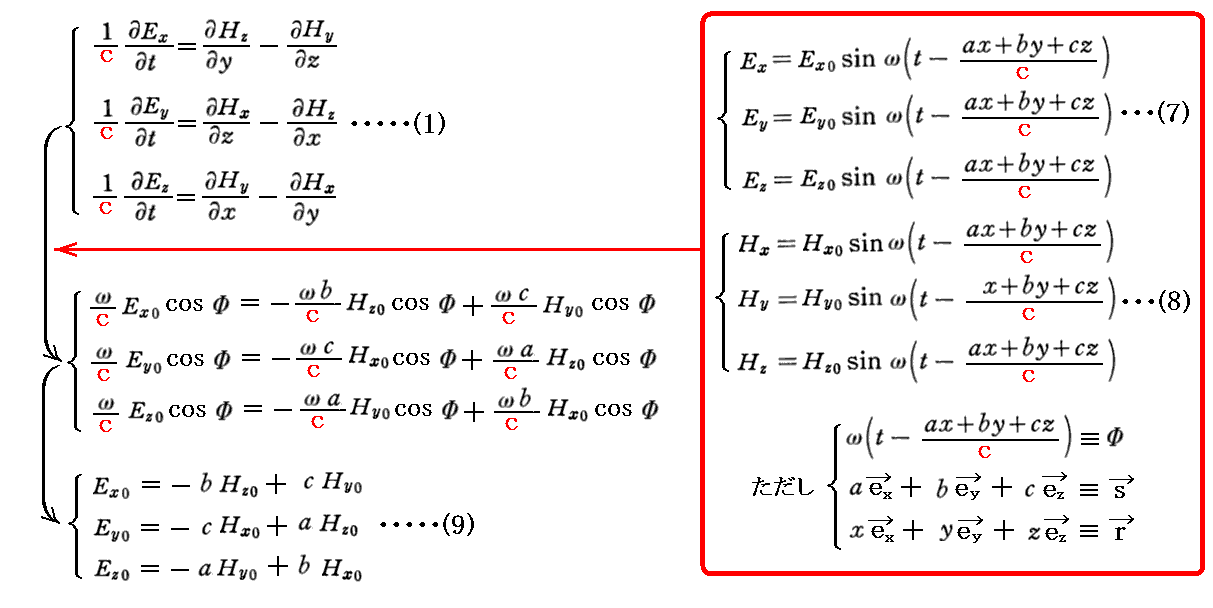
の関係を満たさねばならない。
同じく、(2)式に(7)、(8)式を代入して
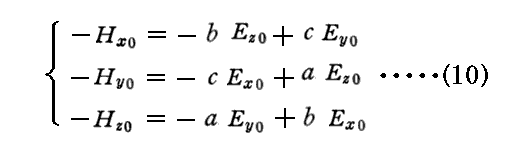
の関係式が得られる。
[補足説明4]
前記の関係式(9)、(10)式から、以下の事柄が証明できる。
(1) E0⊥s かつ H0⊥s
電場振幅ベクトルE0と磁場振幅ベクトルH0は波面の法線方向を表す単位ベクトル(a,b,c)=sに垂直。
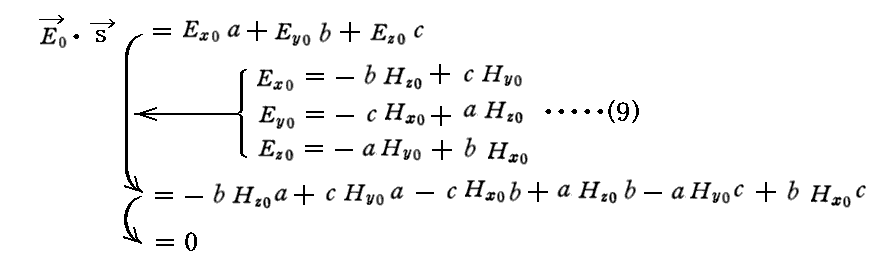
同様に
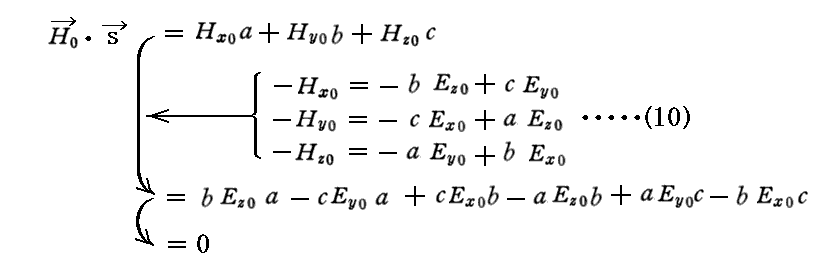
(2) E0⊥H0
電場振幅ベクトルE0と磁場振幅ベクトルH0は互いに垂直。
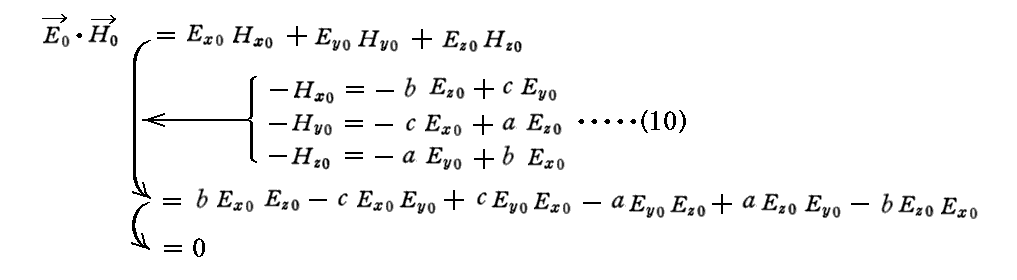
(3) [E0×H0]=|E0|・|H0|s
電場振幅ベクトルE0、磁場振幅ベクトルH0、法線ベクトルsの位置関係は、ベクトルE0からベクトルH0へ右ねじを回したときネジが進む方向がsベクトルの方向になっている。
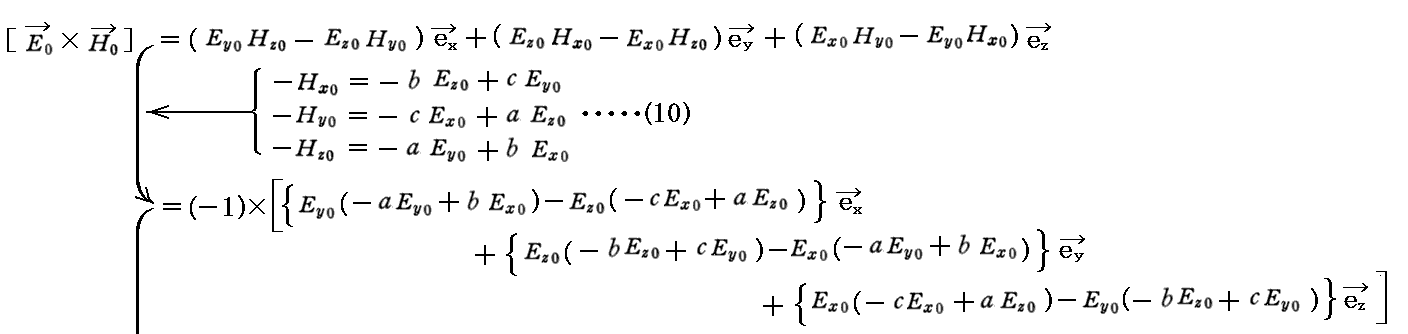
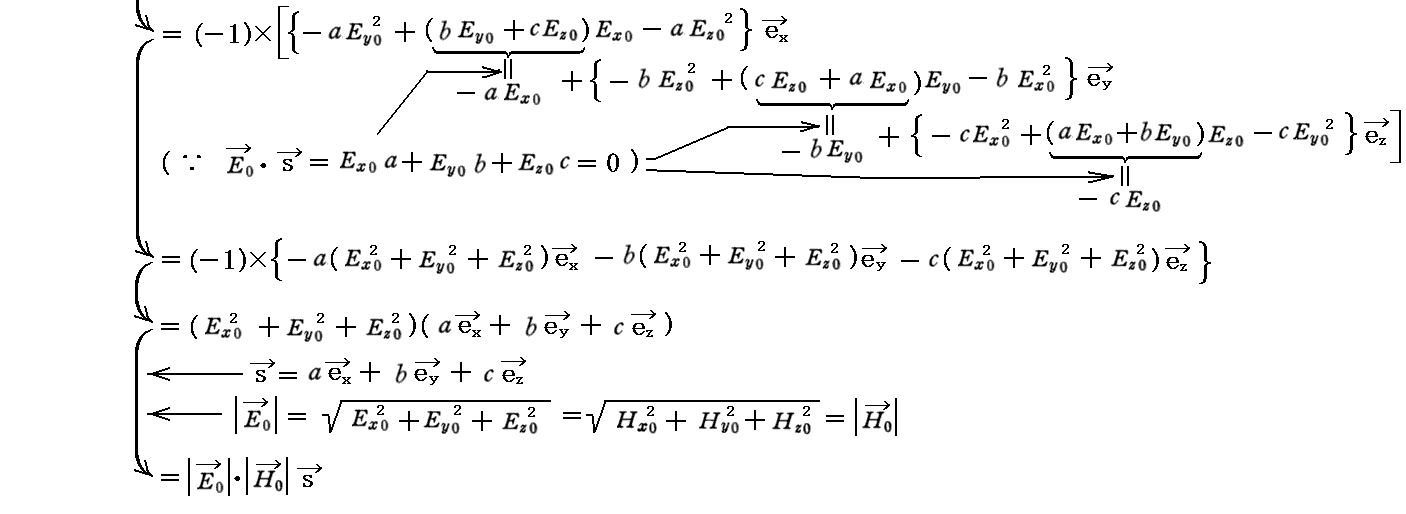
これらの関係式は光(電磁場)が横波であることを示している。光についてはフレネルが、電磁波についてはヘルツが独創的な実験・考察に基づいて明らかにした。
(4) |E0|=|H0|
電場の振幅ベクトルE0の絶対値と磁場の振幅ベクトルH0の絶対値は等しい。
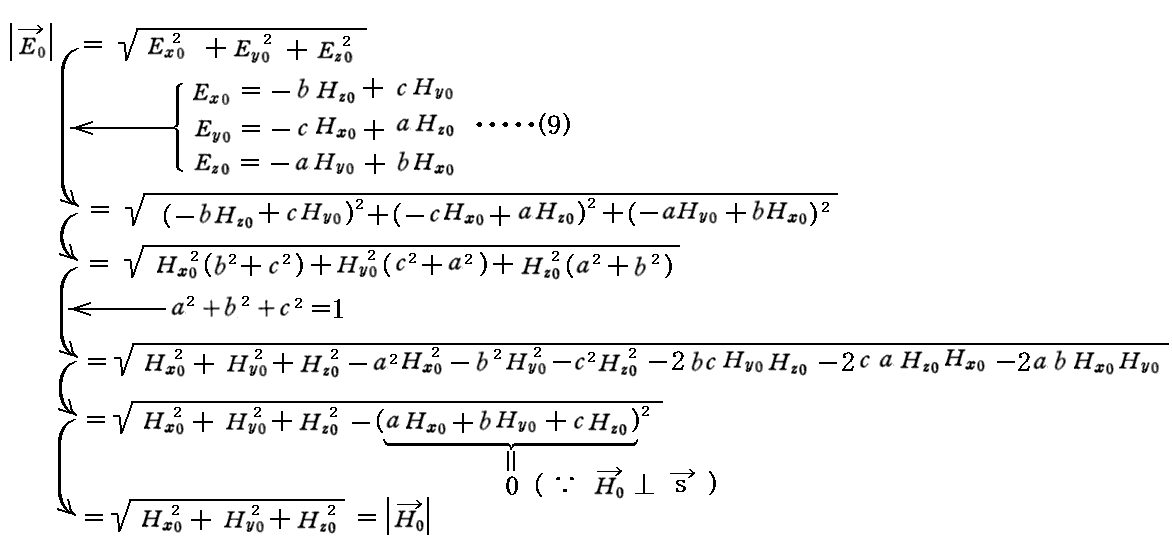
この事はGauss単位系の場合に言えるのであって、他の単位系ではc倍が絡んできます。
これらの事柄の簡単な場合の証明は別稿「電磁波の伝播」3.ですでに説明していますのでご覧下さい。

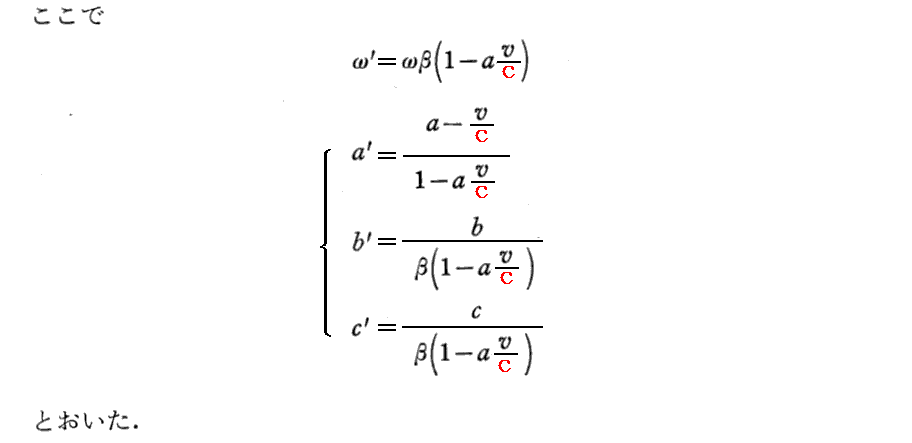
[補足説明5]
上式を導く。まず位相を表す式にローレンツ逆変換を適用すると

となるが、これは当然k系での位相を表す式
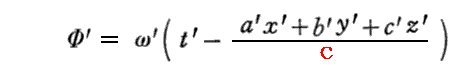
と一致する必要がある。このことから
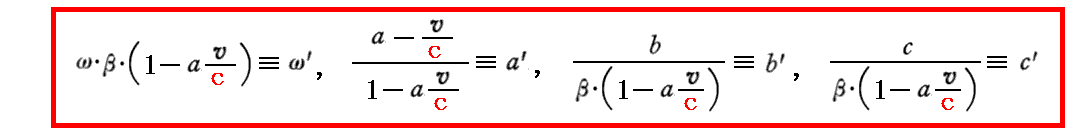
が成り立たねばならない。
このとき、ω’は系kにおける波の角振動数、(a’,b’,c’)は系kにおける波の進行方向を規定する単位ベクトルs’と解釈できる。実際
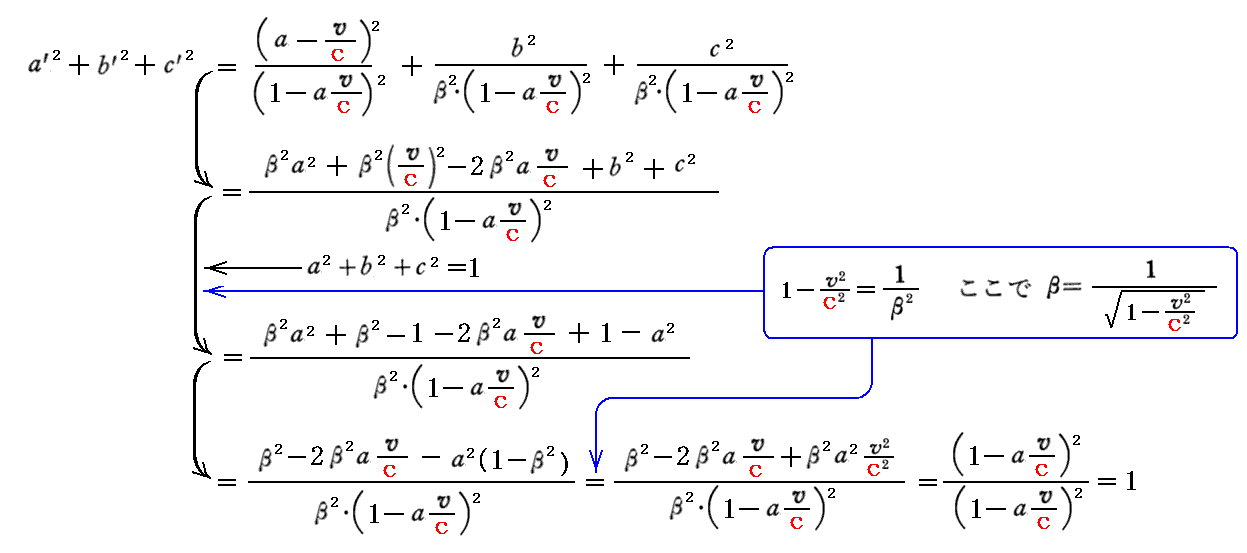
となるので、(a’,b’,c’)が単位ベクトルであることは直ちに確認できる。
[補足説明6]
同一の電磁波をK系とk系で観測するのですから、どちらの系から見てもその波の位相は同じはずです。つまりΦ=Φ’です。Φは(x,y,z,t)で表され、Φ’が(x’,y’,z’,t’)で表されているということであって両者は同じものです。
これは丁度、同じ質点の位置をK系とk系で観測したときどちらも同じ位置を示しているのですがそのときの座標値がK系で(x,y,z,t)で表されk系で(x’,y’,z’,t’)で表されることと同様です。
したがって
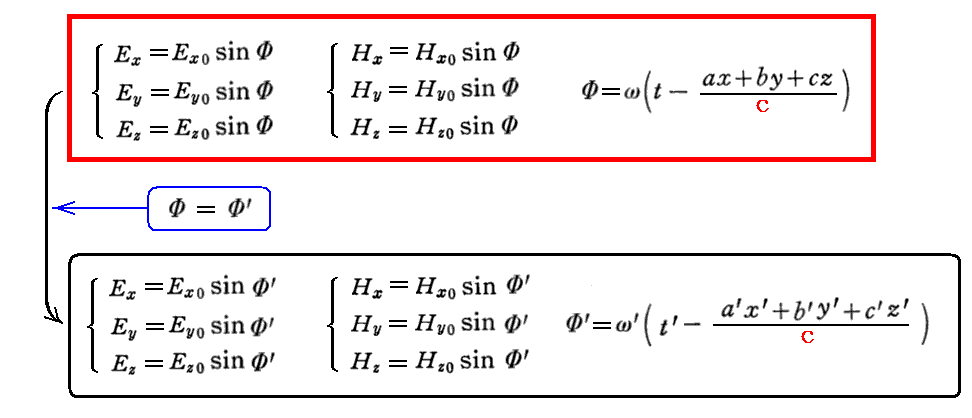
となる。
これを用いると
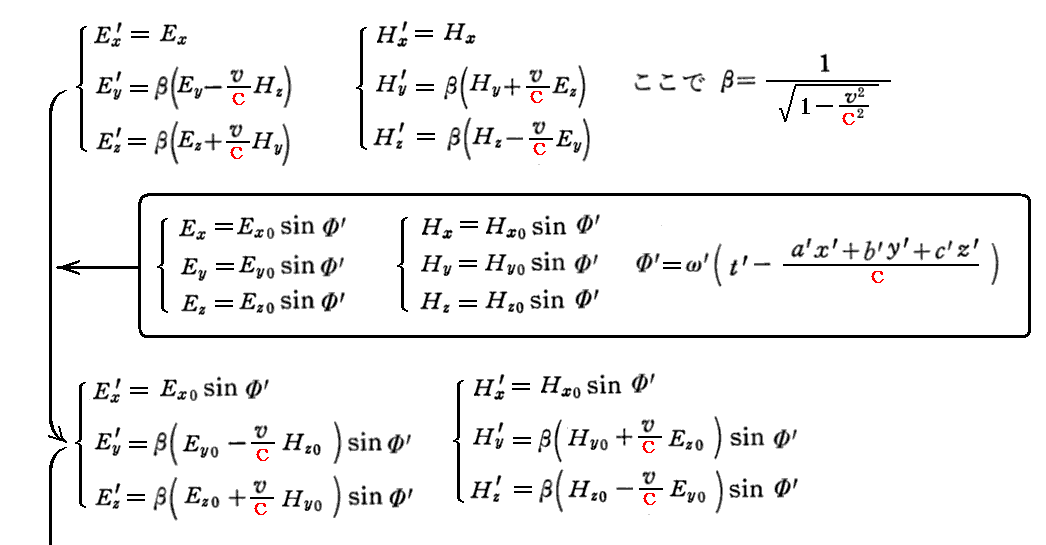
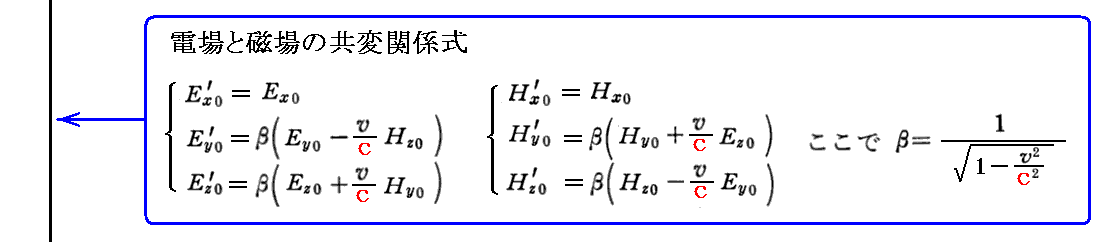
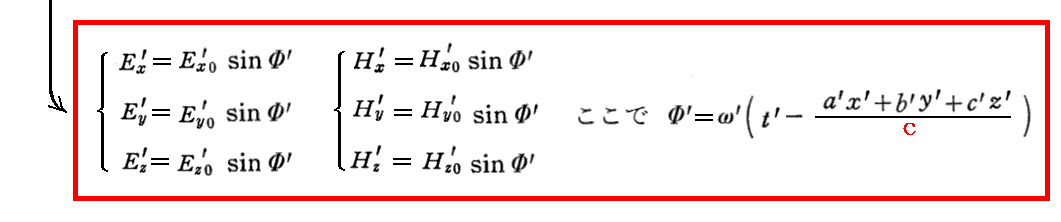
となり、波動方程式の共変的な解が得られる。
[補足説明7](2018年3月追記)
3.(2)1.[補足説明2]で位相Φを角振動数ωと波数ベクトル(kx,ky,kz)で表すことを紹介した。すなわち
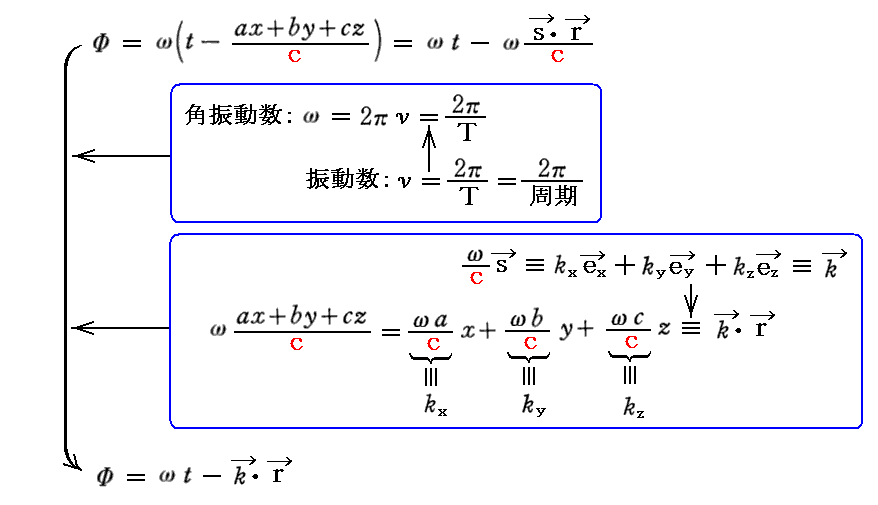
とするやり方です。
このやり方で定義すると、前述の位相Φを表す要素のローレンツ変換共変の変換式は
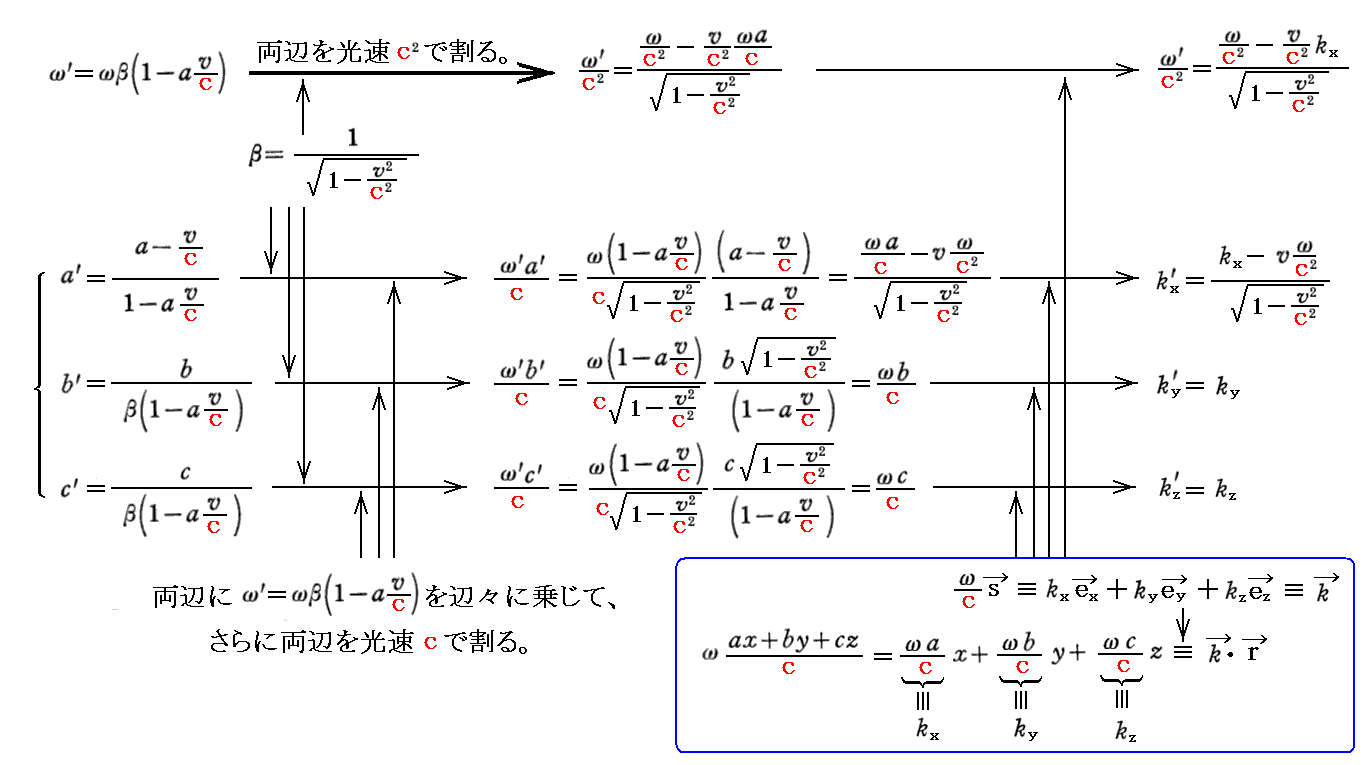
となる。
もちろんこれは、“相対性原理により位相 Φ=ω・t-k・x がローレンツ変換に対して不変の形を保つべき”から直接導けます。すなわち
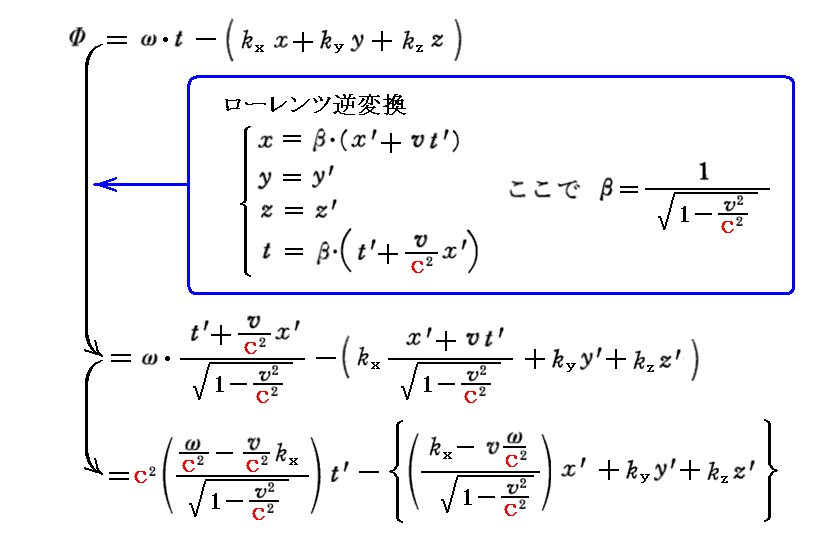
となりますが、これが
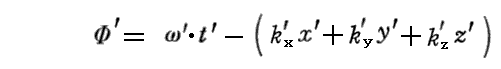
と一致するためには
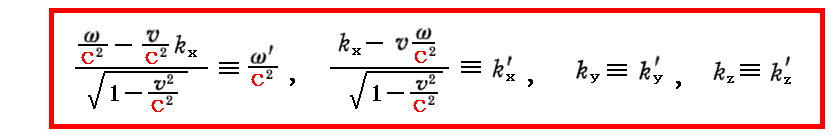
でなければ成らないことが導ける。これは (a,b,c,ω) の変換法則を求めるときにアインシュタインが用いた方法です。
いずれにしても、この変換則は(kx,ky,kz,ω/c2)が時空座標(x,y,z,t)と全く同じローレンツ変換に従う事を示している。つまり、“波数ベクトル”kは“角振動数”ω/c2と一緒になって“4元ベクトル”を構成する。
“4元ベクトル”に付いては別稿「4元速度、4元加速度と4元力」で詳しく説明します。
2.ドップラー効果
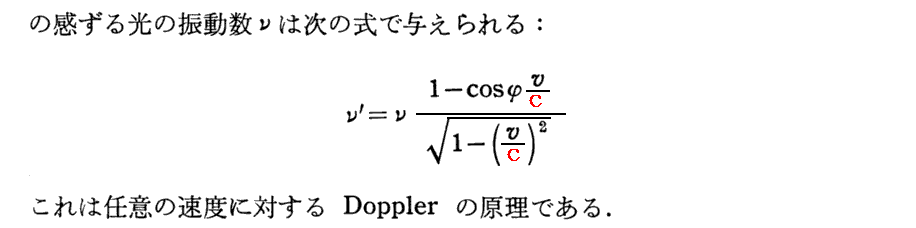
前項で求めたω→ω’は静止系Kから運動系kへ移ったときに光(電気力学的波)の角振動数が変化すること表している。これは波を動きながら眺めたときに波の振動数が変化したように見える“ドップラー効果”そのものを表している。そのことに関してアインシュタインは以下の様に説明している。

[補足説明1]
上式の導出は以下の通り。前項で求めた“角振動数”のローレンツ変換式を“振動数”の関係に直すと
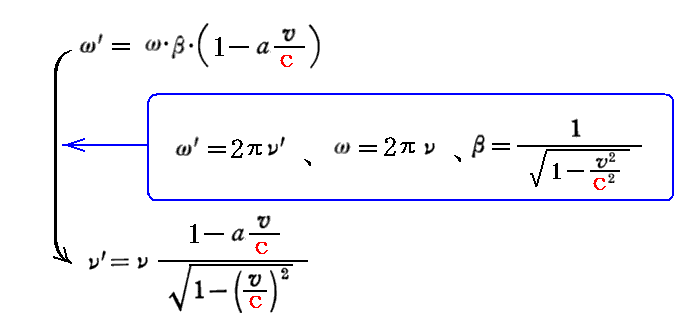
となる。
今は、静止系であるK系に対して観測者(k系)が速度vで動く方向をx軸の正方向としている。K系に於いてk系の原点にいる観測者に向かって進む光の伝播方向ベクトルsとK系のx軸が成す角度をφとするとa=cosφだから
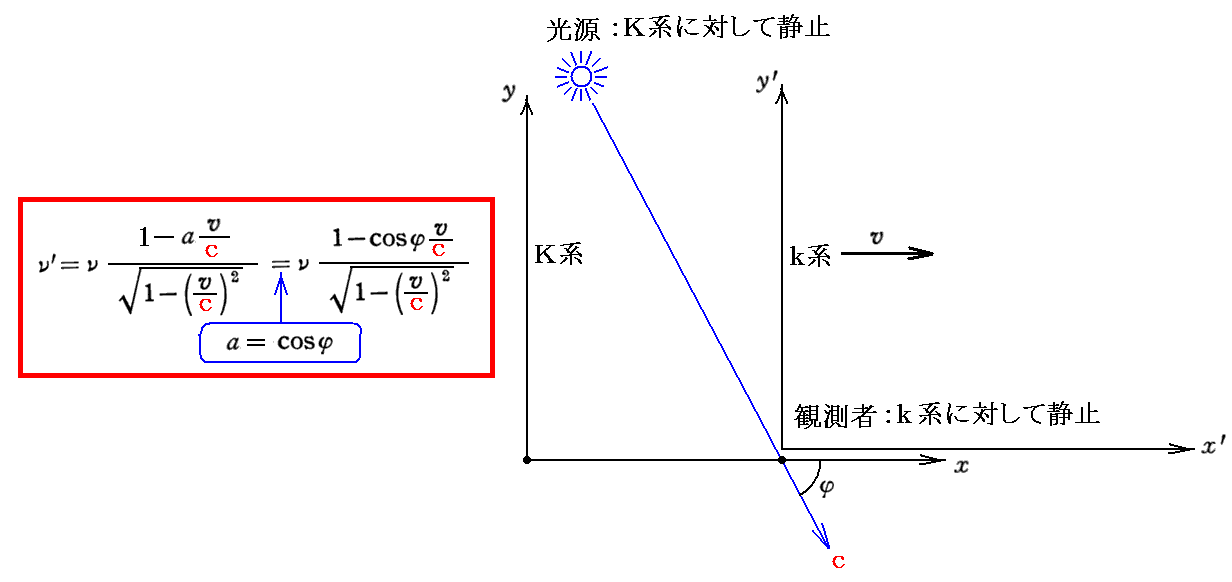
となる。これが論文中の式です。
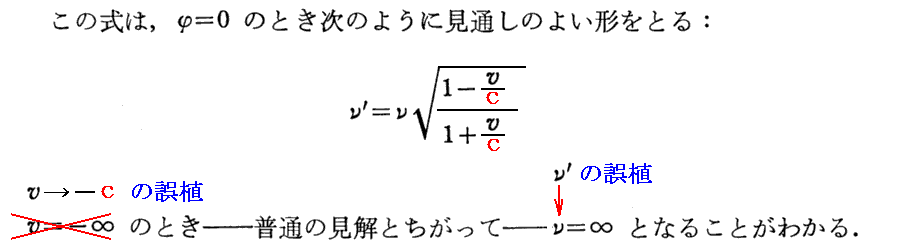
ここで、φ=0°(光源と観測者が互いに遠ざかる)の場合にはcosφ=1だから
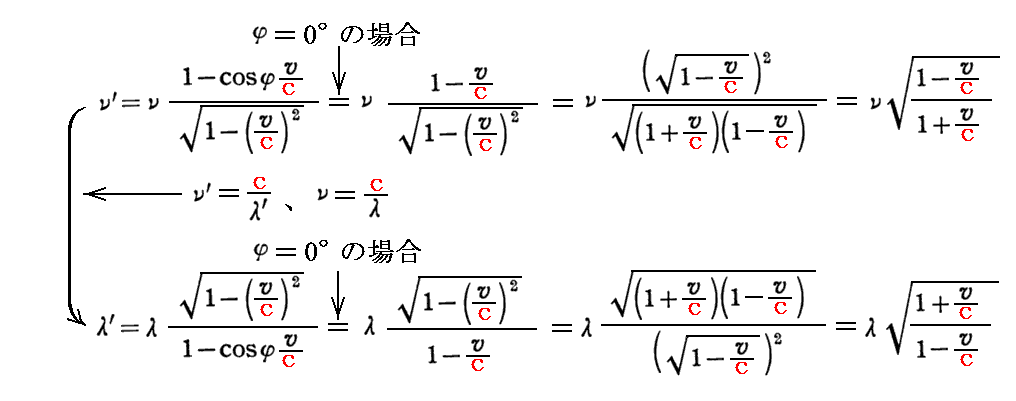
となる。この場合光の振動数は小さくなり、波長は長くなる“赤方偏移”となる。
更に、φ=180°(光源と観測者が互いに近づく)の場合にはcosφ=-1だから上記の公式のvを-vに置きかえた式になることに注意されたし。この場合光の振動数は大きくなり、波長は短くなる“青方偏移”となる。
論文中に注意されているように、ここで v→-c となると、ν’→∞ となる。つまり、観測者が光源に光速度で近づくと観測する光の振動数は無限大になることを意味する。これは古い絶対静止空間のエーテル理論から得られるドップラー公式の示す結果と異なる。古いエーテル理論(説明1、説明2、説明3)では、v→-cとともにν’→2νとなるだけです。
[補足説明2]
上記の式と古いエーテル理論のドップラー公式との関係を補足する。上式で v≪c が言えるときには
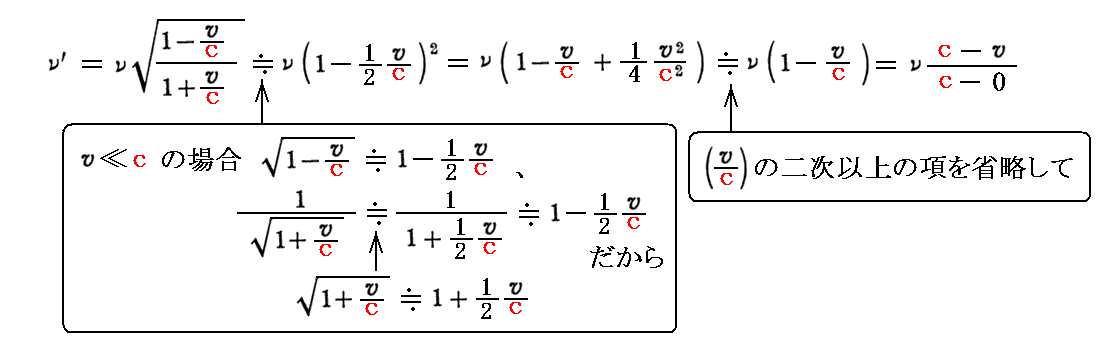
となる。これは、高校物理で習う音のドップラー効果の公式(説明1、説明2、説明3)を思い出せば解るように、古典的な絶対静止空間のエーテル中に静止した光源に対して、観測者が(エーテル中を)速度vで遠ざかる場合の公式に一致する。
それ故に、ドップラー効果の観測で相対性理論とエーテル理論の優劣を確かめるには、v/cの二次以上の観測精度が必要です。

下記のIvesとStilwellの1938年論文と1941年論文はこちらを参照。
また(11.21)から(11.23)を導く所を補足すると
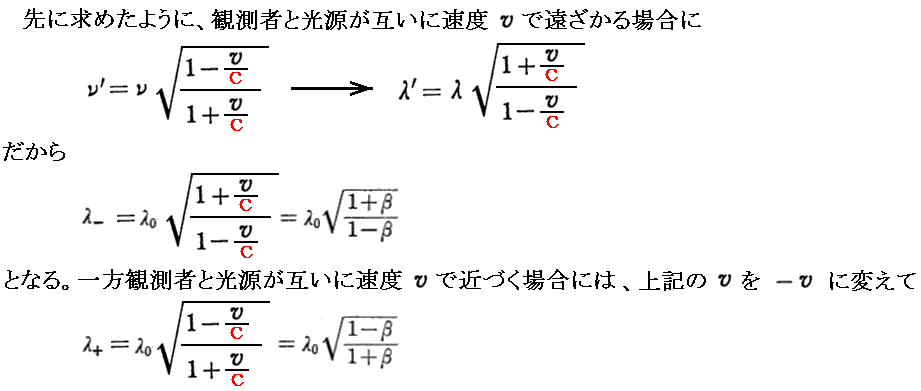
となる。


ちなみに、古典的エーテル理論のドップラー公式によると(説明2の記号で)
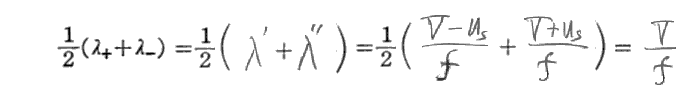
となりますから、波長のずれはありません。
[補足説明3]
ここで更に注目すべきはφ=90°の場合です。観測者が光線の進行方向に対して直角に動いている場合にも
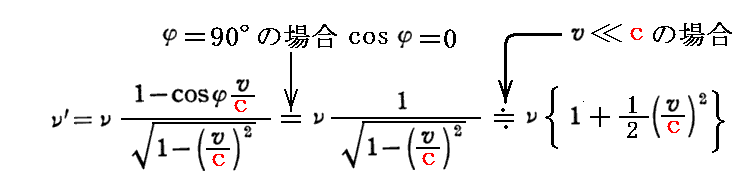
となり、v/cの二次の効果に伴う“横方向のドップラー効果”が現れる。ただし、上記の式はK系で見た光の伝播方向とx軸とが成す角φが90°の場合で“青方偏移”となる。
このとき、次の光行差の項で説明するように、観測者が動きながらK系の光源を見る場合v/cの一次の大きさで光のやってくる方向が変化します。だからk系から見て、k系のy’軸に沿ってk系の原点にいる観測者にやってくる光(つまりk系での角度φ’=90°の場合)のドップラー効果は上式とは異なります。
φ=90°で見るのか、φ’=90°で見るのかはv/cの二次のオーダーで異なりますから、“横方向のドップラー効果”を調べるためにはその当たりを厳密に論じなければなりません。この点を明記していない解説書もあり、混乱を招くところですので注意されて下さい。
φ’=90°で見る場合に上記の公式を書き換えるには、前記の公式の a を a’ に変換すればよい。つまり
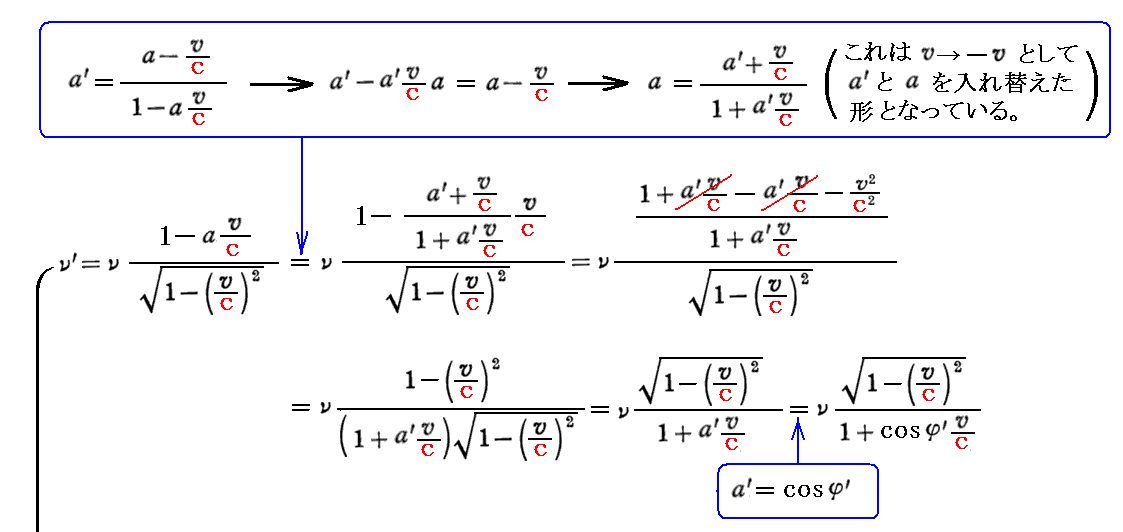
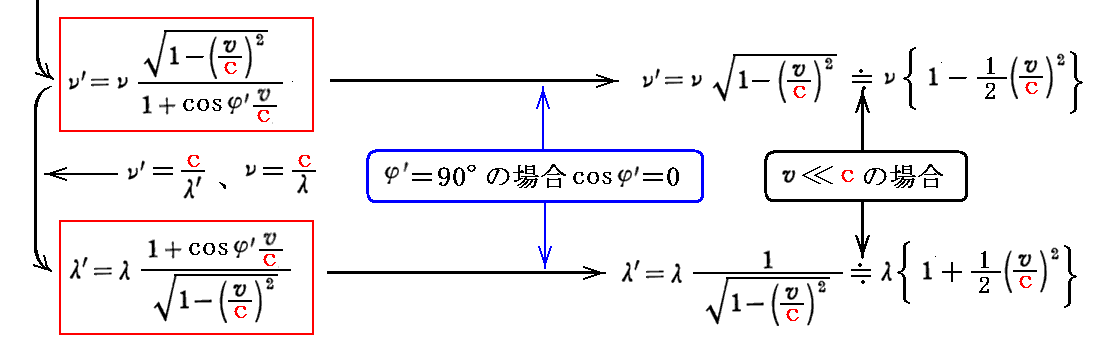
が得られる。つまり厳密にφ’=90°の方向から運動光源を見たとき“赤方偏移”のドップラー効果が見られることになる。
このとき、k系のx’軸からφ’=90°の方向の(つまりy’軸の正方向からy’軸に沿ってやってくる)光線を見ることになるのですが、K系からみると静止していた光源はk系から見るとk系のx軸の負方向に速度-vで動いています。つまり、k系の観測者にやってくる光線の方向に対して厳密に直角方向に動いている光源からやってくる光を観測することになります。
上記の
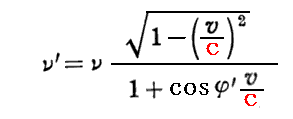
は、最初に求めた
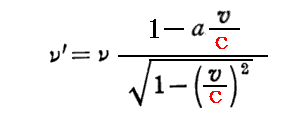
をνについて解き、その式のvを-vにして、νとν’を入れ替え、aをa’としたものに等しいことに注意されたし。これは観測者がいる系を静止系Kと見なし、光源がK系に対して-vで移動している運動系kに静止していると見なした場合のドップラー効果を現す式です。この意味でも相対性理論の整合性が確認できる。
このようにk系に於いて光がやってくる方向から厳密に90°の方向に動きながら見た場合(k系の観測者にやってくる光線の方向に対して厳密に直角方向に動いている光源からやってくる光を観測する場合と言っても良い)、ν’はνよりも小さくなり“赤方偏移”を生じる。これが真の“横方向のドップラー効果”です。
これは動いている物の時間が
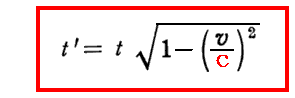
に従って伸長する(時間がゆっくり進む)ために生じる。これは古典的なエーテル理論では決して現れない効果ですからこれが確かめられれば相対性理論の実験的証拠となる。
古典的エーテル理論で現れないことは古典的なドップラー公式(説明3)を復習すればすぐに解ります。そこの説明ではvが逆ですから、そこの公式のvを-vに置き換えた式が上記の相対論的ドップラー効果の式に対応します。古典的な式は相対論的な式で
v/c の二次の項を省略したものになっており、相対性理論は古典的な理論の自然な拡張になっています。
実際、Einsteinは1907年に陽極線(カナル線)を用いれば横ドップラー効果を検証できるかもしれないと提案した
“Über Möglichkeit einer neuen Prüfung des Relativitätsprinzips”,Annalen
der Physik. 23, p197~198, 1907年
この論文はwikiからdownlordできます。また、陽極線そのものについてはBornの文献202.§8のp126を参照されたし。
しかし、横ドップラー効果の測定は極めて困難です。その理由は、観測方向がカナル線に対して直角からわずかに狂っても縦のドップラー効果の寄与が生じて来て、横ドップラー効果を覆い隠してしまうからです。角度がどの程度厳密に90°でなければならないのかは先に説明しましたが、この困難さから長い間測定できなかった。
横ドップラー効果は、IvesとStilwellが1938年に、Ottingが1939年に、カナル線(陽極線)を用いて確かめたのですが、特別な工夫をすることで成功した。
彼らの工夫とは、カナル線から互いに反対方向に放射される光線に対する縦ドップラー効果の寄与は、大きさは等しく反対に作用することに着目して、カナル線から互いに反対方向に放射される光線を同時に測定して平均を取って縦ドップラー効果の影響を消去してしまうというものです。これが、2.(10)2.<1>で引用した文献301.§27DでSommerfeldが説明している事柄です。また前記[補足説明2]で説明したものです。この方法に拠って、横ドップラー効果は確かめられた。また時間の伸長も直接的に確かめられた。
[補足説明4]
相対論以前の古典的なドップラー公式(説明1、説明2、説明3)は、光源が動く場合と観測者が動く場合では異なる結果を与えた。しかし相対性理論では光源と観測者の相対的な速度vのみに関係してどちらが動いていて、どちら静止しているかには関係しない。これこそが特殊相対性理論が言っていることで、ドップラー効果をいくら観測してもどちらが静止していて、どちらが動いているのかを決めることはできないのです。
[補足説明1]では光源が静止した系に対して観測者が速度vで動くとしてこれらの公式を導いたのですが、相対性理論では、これらの公式は観測者が静止していて、光源が動いている場合でも同じになります。以下でその当たりを補足する。
相対性理論によると光はどの慣性系からみても同じ光速度で伝播する。この事実がドップラー効果に於いてどのように説明されるのかを確認する。“観測者(observer)”と“光源(source)”が相対速度vで互いに遠ざかる場合と、互いに近づく場合に分けて考察する。ここでは古典論の(説明1)のやり方で説明するが、古典論の(説明2)のやり方でも同様です。
(1)観測者と光源が相対速度vで遠ざかる場合
(a)観測者が静止している系から眺める。(つまり静止している観測者から光源が速度vで遠ざかる場合)
このときには、光源が速度vで動いているために、光源の時間は遅れて見える。そのため光源の発する光の振動数は本来のν0よりも小さいνとなる。観測者に取ってその小さくなった振動数νの光を発しながら光源は速度vで遠ざかるのです。そのため観測者が観測する振動数ν’は下記のようになる。そのとき光の信号は観測者に対して光速度cで伝播してくることに注意。
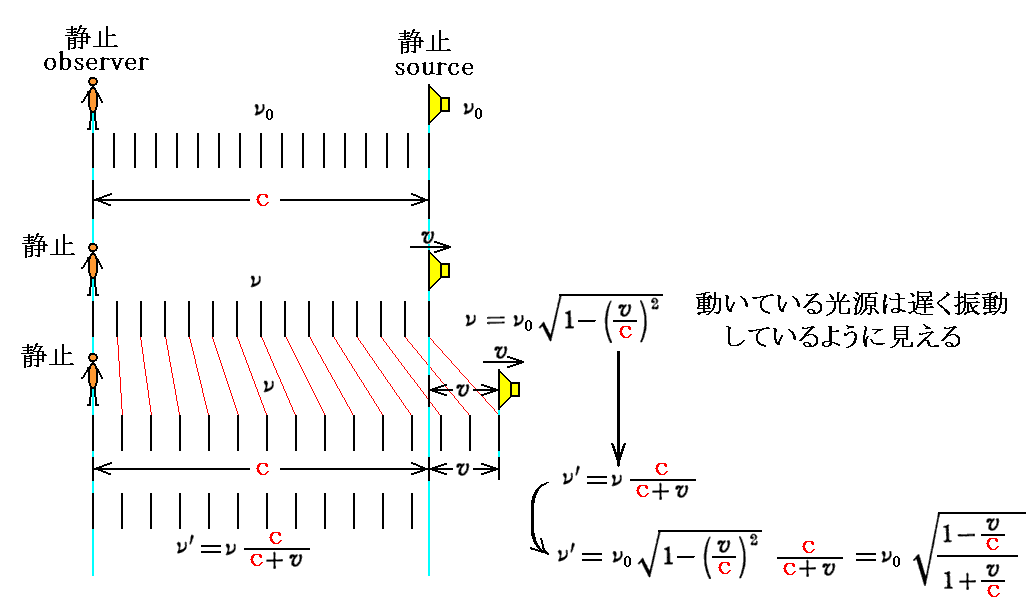
(b)光源が静止している系から眺める。(つまり静止している光源から観測者が速度vで遠ざかる場合)
このとき光源の時間で1秒経つ間に観測者が観測する波の数はνとなる。ところがこのとき、光源が静止している系(光はその系で測ってcで進む)から動いている観測者を見ると、観測者の時計はゆっくりと時を刻む様に見える。だから観測者にとっては、光源の1秒よりも少ない時間しか経っていない。観測者にとっての1秒間に観測する波の数 ν’ は ν を
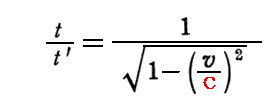
倍したものとなる。そのため観測者の時計で1秒間に観測する波の数ν’は下記のようになる。
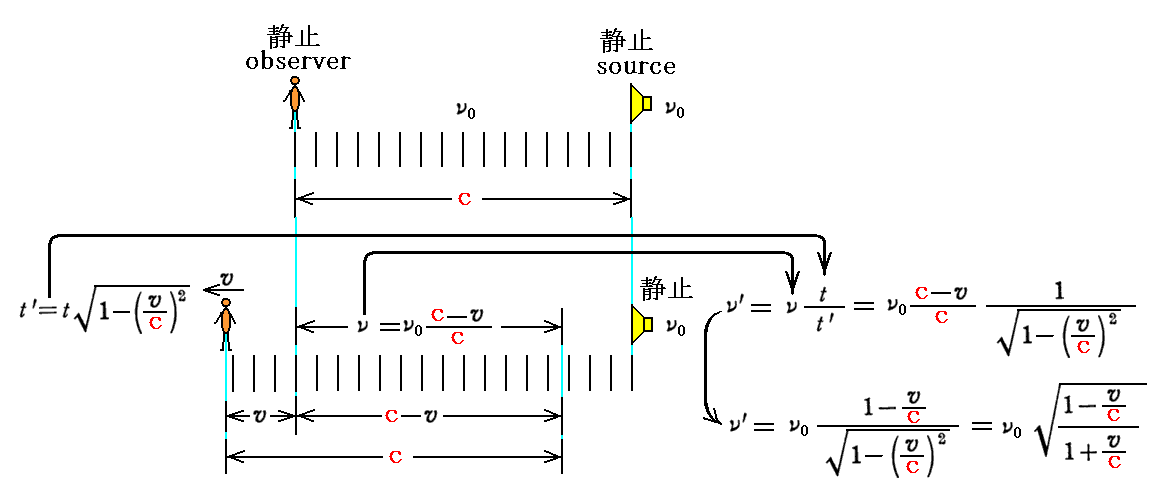
上記の(a)と(b)はまったく同じ答えを与えることに注意されたし。
このとき、観測者から見ると光源に対する光の速度はc+vになっているように見えますが、相対性理論に拠ると光源から見た光の速度はcであることは何度も注意[2.(7)や2.(8)3.]しました。
相対性理論の速度合成則によると観測者から速度vで動く光源に移って見たときの光速度がcのとき、同じ光の伝播を観測者から見るとcで伝播するように見えるのです。
例えば別稿「フィゾーが運動媒質中の光速度(随伴係数)を測定した方法(1851年)」4.(2)5.[補足説明]を復習して下さい。そこのエーテル空間を光源と置きかえれば理解していただけると思います。
(2)観測者と光源が相対速度vで近づく場合
(a)観測者が静止している系から眺める。(つまり静止している観測者に光源が速度vで近づく場合)
このときには、光源が速度vで動いているために、光源の時間は遅れて見える。そのため光源の発する光の振動数は本来のν0よりも小さいνとなる。観測者に取ってその小さくなった振動数νの光を発しながら光源は速度vで近づくのです。そのため観測者が観測する振動数ν’は下記のようになる。そのとき観測者に対して光の信号は光速度cで伝播してくることに注意。
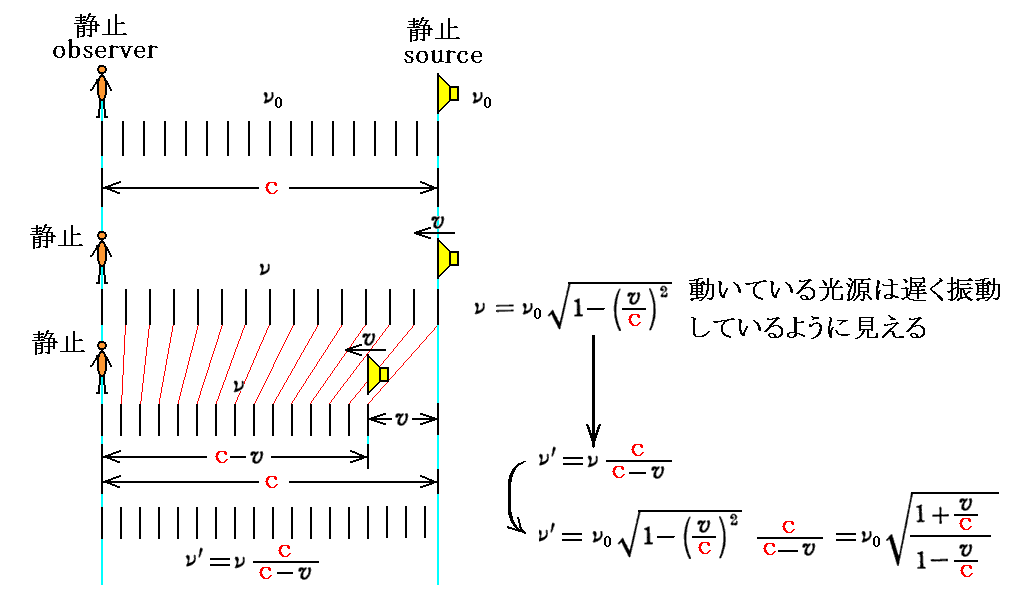
(b)光源が静止している系から眺める。(つまり静止している光源に観測者が速度vで近づく場合)
このとき光源の時間で1秒経つ間に観測者が観測する波の数はνとなる。ところがこのとき、光源が静止している系(光はその系で測ってcで進む)から動いている観測者を見ると、観測者の時計はゆっくりと時を刻む様に見える。だから観測者にとっては、光源の1秒よりも少ない時間しか経っていない。観測者にとっての1秒間に観測する波の数
ν’ は ν を
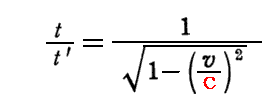
倍したものとなる。そのため観測者の時計で1秒間に観測する波の数ν’は下記のようになる。
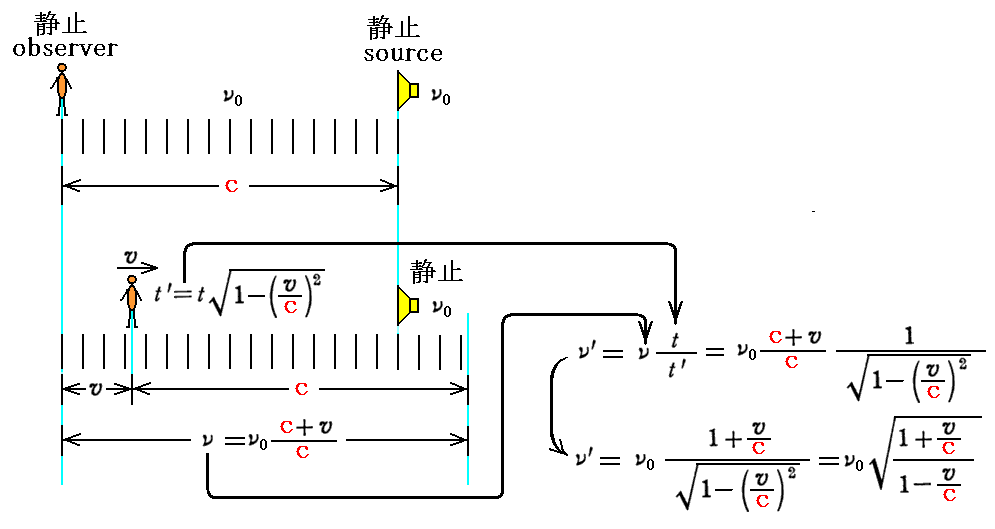
上記の(a)と(b)はまったく同じ答えを与えることに注意されたし。また、(1)と(2)の関係はvを-vで置きかえたものになっていることに注意されたし。
これらの事実は、ドップラー効果の現象をいくら詳しく解析しても光源と観測者のどちらが動いていて、どちらが静止しているのかを判定することはできないことを意味します。これこそが、相対性理論が主張していることです。
相対性理論以前の古典的ドップラー効果の公式では、音源と観測者の相対的な速度vは同じでも、波を伝える空気に対して音源が動く場合と観測者が動く場合では、νの観測結果は異なったことに注意して下さい。そのため古典論によるとドップラー効果の観測から空気層の存在を知ることができるし、その空気層に対して観測者がどのように動いているのかを知ることができたのです。
ところが、相対性理論に拠ると光を伝えるエーテル空間(絶対静止空間)を知ることはできないのです。このとき、さらに、観測者あるいは光源が静止している“それぞれの慣性系に於いて光速度が一定”であるという事実と“時間の相対性”が旨く整合的に関係していることに注意されたし。
補足しますと、音波に対するドップラー効果に付いては、相対論的に厳密なドップラー公式から空気層に対して音源と観測者のどちらが動いているのかを判別することができます。ここは勘違いしやすいところですので、2.(10)1.における別ページの説明を復習されて下さい。
[補足説明5]
相対論的なドップラー効果は、膨張宇宙の発見に於いて、重要な役割を果たした。このとき、波長のずれの相対的な変化を“赤方偏移”zといい

で表す。
ここではφを
のように定めている。
そのとき、膨張宇宙論では遠くの銀河は常に天の川銀河からの視線方向に遠ざかっているため
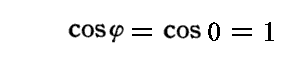
となります。
そのため、前述の式より
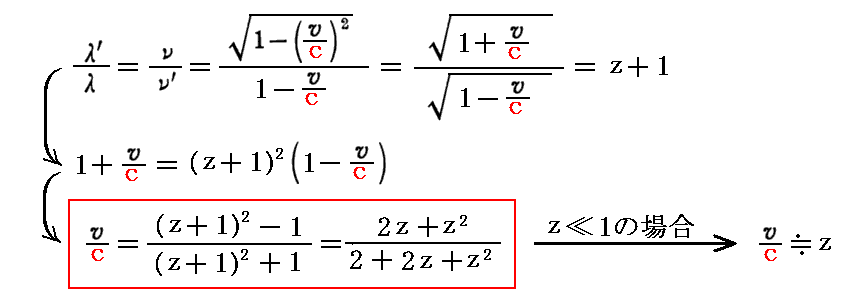
が成り立つ。この式を用いれば“赤方偏移”zの観測値から銀河の遠ざかる速度vが計算できる。
[補足説明4]で注意したようにドップラー効果の赤方偏移には、銀河が運動していることに伴う時間の遅れの効果が含まれている。遠方銀河の時間は遅れて見えることに注意されたし。
また、そのとき何度も注意したように、遠方銀河が速度vで動いているのか、天の川銀河が速度-vで動いているのかの違いは判別できません。
[補足説明6]
“宇宙の背景輻射”は観測方向によってドップラー遷移することが知られている。この事を用いると、背景輻射の中での太陽の運動方向とその速度を知ることができる。そのことの解りやすい説明が江沢文献207.§2.3.6に在りますので別稿で引用しておきます。
実際、スムート(Smoot)、ゴレンシュタイン(Gorenstein)、マラー(Muller)は観測によって、太陽は背景輻射に対して390±60km/sの速さで獅子座の局部銀河団に向かって動いている事を確かめた。
“Ditection of Anisotropy in the Cosmic Blackbody Radiation”, Phys. Rev. Lett., 39, p898~900, 1977年
https://ned.ipac.caltech.edu/level5/March03/Weiss/Weiss_contents.html
この太陽の速度(地球から観測する場合には、太陽のまわりを公転する地球の速度30km/sも考慮する)を打ち消す速度で走る検出器から見れば、背景輻射は1/3000の精度で等方的で、温度2.7Kのプランク分布によく合うことが確かめられた。
1989年に打ち上げられた衛星COBEは、宇宙マイクロ波背景放射の赤方変位量の双極子成分をさらに精度良く観測して、ビッグバンに起源を持つ宇宙マイクロ波背景放射に対して太陽系は速度370km/sで、銀河系は速度550km/sで動いていることを明らかにした。(杉山直著「相対性理論」講談社2010年刊より)
これは一見すると、絶対静止空間(エーテル空間)が検出できて相対性原理に矛盾するように見えますがそんなことはありません。それは以下の例を考察すれば了解できます。
下図の様に光源AとBが一定距離だけ離れて静止して、それぞれが原子中電子のエネルギー順位間遷移に伴って放出される特定振動数の光を発しているとする。
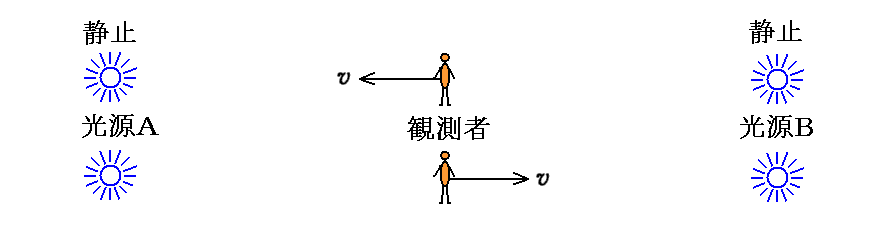
その中間にいる観測者がAの方に速度vで動いている場合と速度vでBの方に動いている場合では、それぞれの光源から来る光のドップラー遷移の様子は異なる。その違いから観測者が光源AとBのどちらに向かっていくらの速度で動いているかは検出できます。

一方、相対性理論は、観測者が静止していて、光源AとBが一緒にAからBの方向、あるいはBからAの方向に速度vで動く場合でもまったく同様な結果を与えます。
つまり、観測者がA、Bに対して相対的にAの方へ動くのかBの方へ動くのかは検出できるが、観測者が動いているのか、あるいはA、Bが動いているのかの判別はできないのです。光源AとBが背景輻射の場だと考えれば同じことです。
そのとき、相対論以前の古典的なドップラー効果の理論では、観測者が動く場合と光源が動く場合では、ドップラー効果の現れ方が異なります。そのためどちらが動いているかが判別できる(つまり絶対静止のエーテル空間が識別できる)のでした。そのこととの違いに注意して下さい。
[補足説明7]
光束(光子)の“ドップラー効果”に就いて重要な補足をします。
特殊相対性理論(とくにその“光速不変の原理”)によると、光がやってくる方向(光源の方向)へ速度vで移動している観測者が観測する光束(光子)の振動数をν’は、静止した観測者が観測する光束(光子)の振動数ν0に対して
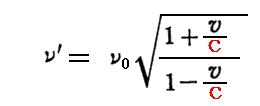
と表される。
また、その逆に観測者が光源から遠ざかる場合に観測する振動数ν’は
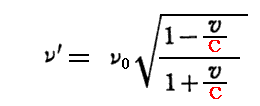
となる。
このとき、Planckの公式(あるいはそれを更に発展させたEinsteinの光量子説)によると光束(光子)の持つエネルギーはE=hν’ですから、光束(光子)を見る観測者に取って、その光束(光子)の持つエネルギーは光束(光子)がやってくる方に向かって動きながら観測するとエネルギーが増大して見えることになり、光束(光子)がやってくる方向から遠ざかるように動く観測者に取っては光束(光子)のエネルギーは減少して見えることになります。このとき光束(光子)の速度はどちらの観測者に取っても一定値cであることは忘れないで下さい。
上記の事実は可秤量物体(普通の物質)に於ける特殊相対性理論の結論と整合性があります。実際、一定速度Uで運動する質量m0の物体に対して速度vで近づきながら観測する(そのとき可秤量物体は観測者に対して相対速度U+v=U+で近づく)と、その可秤量物体のエネルギーは

となり、静止して観測する場合に比較してEからE’へ増大したように見える。逆に可秤量物体の進行方向とは逆に速度vで遠ざかりながら観測する(そのとき可秤量物体は観測者に対して相対速度U-v=U-で近づく)と、その可秤量物体のエネルギーは

となり、静止して観測する場合に比較してEからE’へ減少したように見えるのでした。
その様に整合性が成り立っている事は、本稿の3.(3)1.の最後段落、あるいは3.(3)1.[補足説明7]で説明します。さらに、別稿「相対論的力学」3.(4)[補足説明5]に続く文節で説明していますので、ご確認下さい。
以下は、村上陽一著「ルイ・ド・プロイ(1892~1987)の功績」(http://www.wattandedison.com/deBroglie.pdf)から引用。
ド・ブロイが物資が波動であるという着想を得たのは、1922年~1923年9月の間であると言われていますが、その理論構成の特徴は“殊相対性理論”を指導原理としたことにあります。
すなわち、ド・ブロイは当初“プランクのエネルギー量子の表現式”
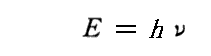
と“アインシュタインの特殊相対論のエネルギー質量公式”
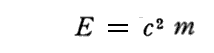
とを関連付け、質量mを持つ可秤量物体粒子は
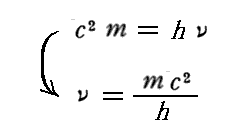
の振動数の波動であると考えた。
しかし、この考え方には大きな困難があります。なぜなら、在る固有振動数ν0で振動する振動体が運動を始めると、その運動体の固有時の進みはゆっくりとなりますから、外部から見た時の振動体の振動数νはν0より減少します。なぜなら

となるからです。一方、速度Vで運動する可秤量粒子のエネルギーは特殊相対性理論によると
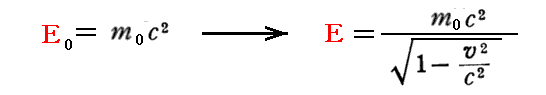
となります。
つまり可秤量物体粒子に付随させた波の振動数νと、可秤量物体粒子の質量m(=E/c2)は互いに逆向きに変化することになります。これは光束(光子)の場合に成り立ったν(光子の振動数)とm(光子の慣性質量=hν/c2)が、同一のローレンツ変換によって変換されるという考え方と“矛盾”する事を意味します。
この“矛盾”については別稿「ド・ブロイの学位論文」1.(1)[補足説明1]の前半も参照されて下さい。
1923年9月に、ド・ブロイはこの困難を回避する画期的な方法を発見します。「そのとき、大いなる光が頭の中で輝きわたった」のです。
彼はまず、可秤量物質粒子には内部の振動と同じ位相を持つ空間的に広がった波動が結びつけられているとします。そして彼は、静止系K0における観測者が見た静止系に静止する可秤量物体粒子には、次式で示される“随伴波”
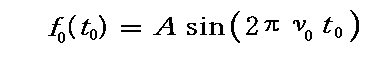
が結びっており、その随伴波は場所に依らずすべての場所で同一の位相で振動(振動数ν0で)しているとします。
次に、この波を、静止系K0に対して相対速度 v で移動しているK系から眺めます。そうすると前記の可秤量物体粒子は速度 v で移動している事になる。そのとき、K系での時間 t 及び位置 x はK0系での時間 t0 とローレンツ変換で結び付けられますので
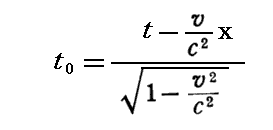
となり、K系での“随伴波”は
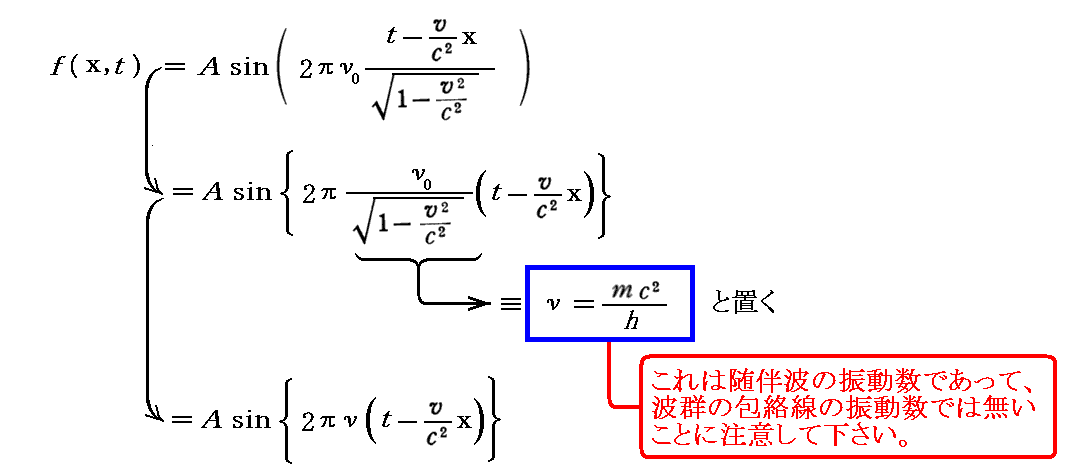
の様な、位相が場所により異なる波となります。これはK0系に対して相対的に動いている K系 に於いては同時性が崩れる為です。そのため、 K系 から見た“随伴波”は下記で説明する“伝播速度”(位相速度) V を持つ進行波となります。このとき、上記の様に定義(mc2/h≡ν)する ν が、 K系 から見ると速度 v で動く様にみえる可秤量物体粒子の“随伴波”の振動数となる。この振動数νは粒子の速度vが増せば増大することに注意して下さい。なぜなら上記の ν=mc2/h 中の m は“移動速度”vと共に増大するのですから。そのため先ほど述べた“矛盾”は解決されたことになる。
そのとき、その“随伴波”の関数形から解るように、随伴波はx方向に“伝播速度”(位相速度) V
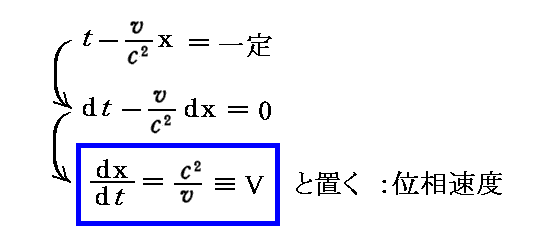
で移動していく進行波を表しています。このとき“随伴波”の“伝播速度”(位相速度) V は、一般に光速度 c ょりも大きくなります。ここで、【可秤量物質粒子の“移動速度”】 v と、その物質粒子に付随する【随伴波の“伝播速度”(位相速度)】 V は【光速度】 c を仲介にして以下の関係にある事に注意して下さい。
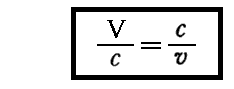
さらにこのとき、この“随伴波(位相速度Vで進行する波)”の速度vで移動する可秤量物質粒子の位置に於ける位相は、上の進行随伴波を表す式の x に x=vt を代入した
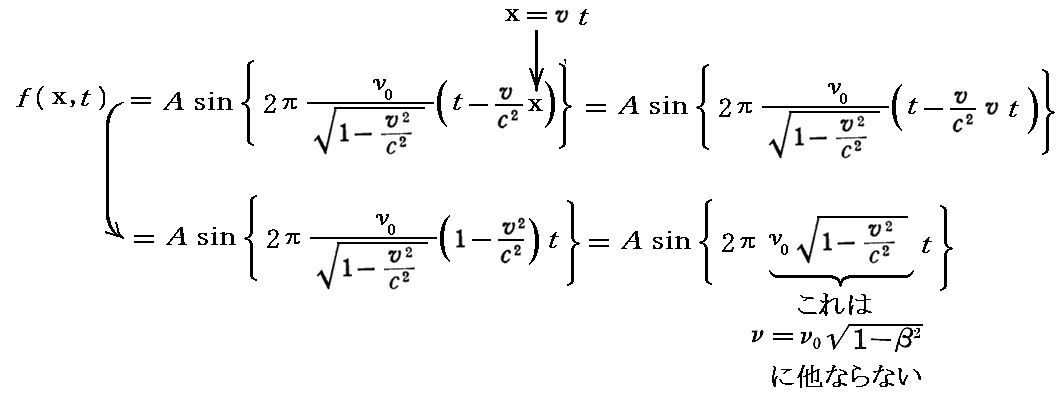
の式で決定さることになります。つまりK系から見た“随伴波(速度Vで移動する進行波)”のちょうど可秤量物質粒子の位置に於ける“随伴波”の振動の振動数は先ほど求めた
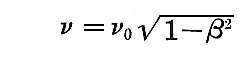
となるのです。従って、先ほど述べた“矛盾”が解決された事になる。
この事については別稿「ド・ブロイの学位論文」1.(1)[補足説明1]の後半の『位相一致の定理』についての説明を参照されて下さい。
この“随伴波の波長” λ は当然、その随伴波の“伝播速度”(位相速度)V を随伴波の“振動数” ν で割った
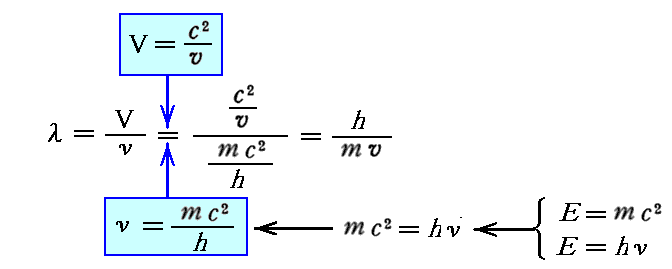
となります。
この随伴波の波長λを可秤量物体粒子の 質量 m と 移動速度 v に プランク定数 h を仲介にして関係付ける式
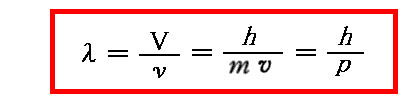
が有名な“ド・ブロイの物質波の関係式”です。この関係式に就いては別稿「相対論的力学」3.(4)[補足説明4]で再度説明します。
もちろん、この“随伴波”の“伝播速度”(位相速度)V は光速度を越えていますので、現実的な波とは考えられません。そのためド・ブロイはこの“随伴波”(位相速度V)の重ね合わせで実現される“波束”(波群)の示す“群速度”が可秤量物体粒子の“移動速度”vに成るのだと理論を進めていきます。
ただし、その当たりの説明は別稿で行う予定ですので、ここでは取り上げません。
3.光行差
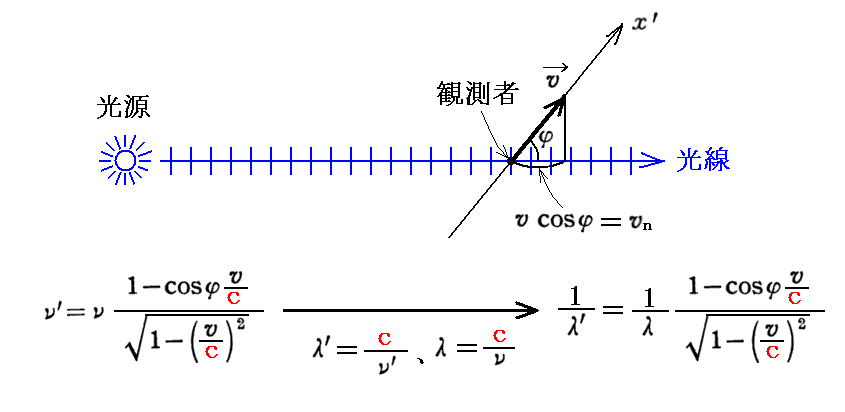
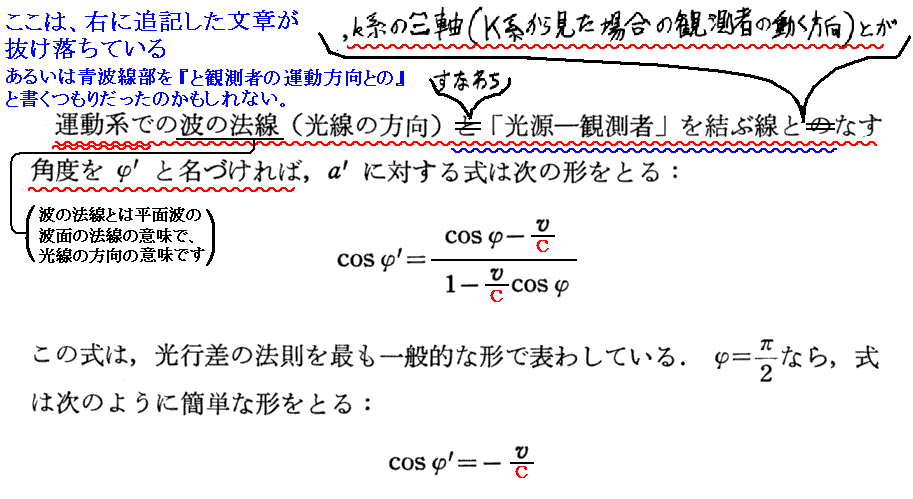
前項で求めた(a,b,c)→(a’,b’,c’)は静止系Kから運動系kへ移ったときに光(電気力学的波)の進行方向が変化する事を表している。これは波を動きながら眺めたときに波がやってくる方向が変化して見える“光行差”の現象を表している。そのことに関してアインシュタインは以下の様に説明している。
[補足説明1]
上記説明でEinsteinの言う角度φ’とは下右図の角度φ’のことで、上式の右辺に出てくるφは下左図の角度φのことです。このφが前項ドップラー効果の公式で出てきたφです。この両者の関係については2.(10)1.の(7a)式と(7b)式を復習して下さい。
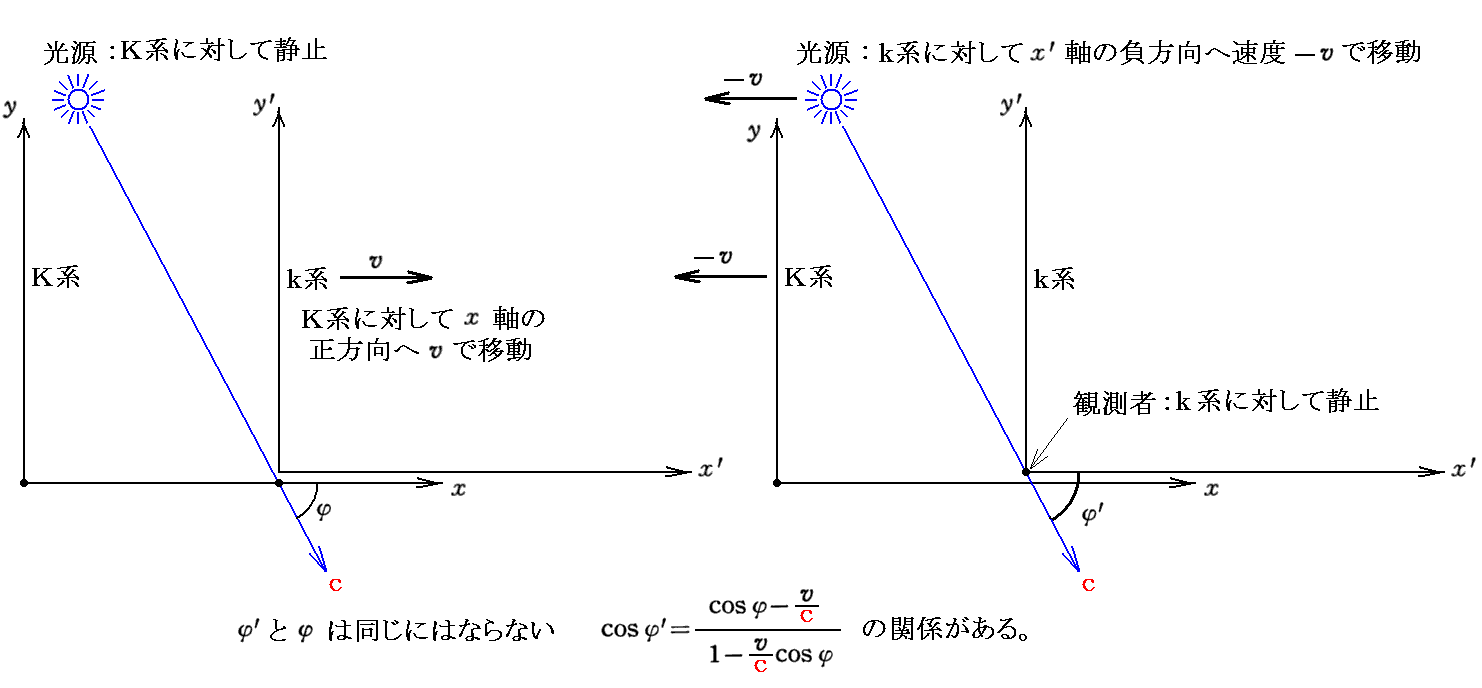
上記関係式を導くには、3.(2)1.[補足説明5]で求めた関係式
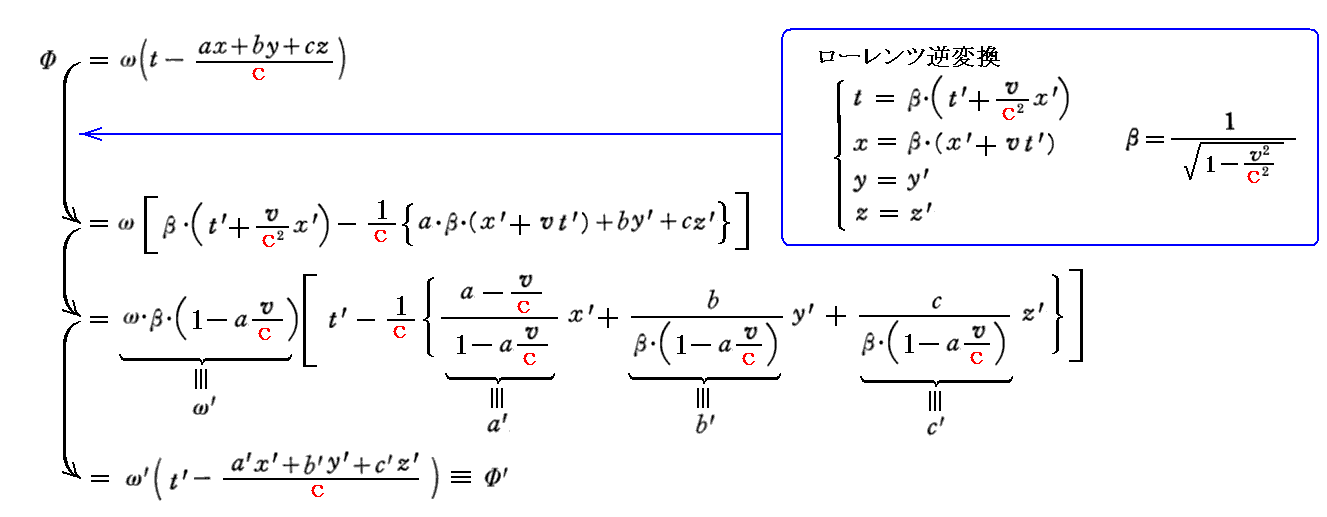
すなわち
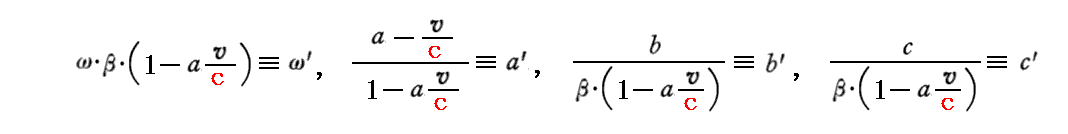
の第2式を用いればよい。ここで、a=cosφ、a’=cosφ’だから
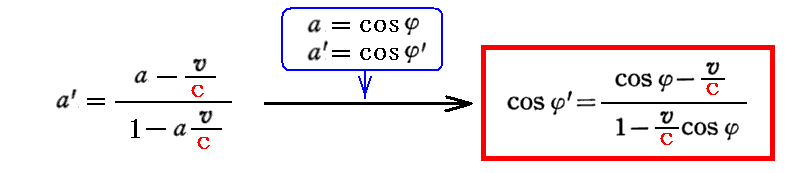
が得られる。これは静止系Kに静止する光源を運動系kから見た場合に光りがやってくる方向が見かけ上変化する“光行差”の現象を表している。
このとき、φ=90°(つまりcosφ=0)の場合には
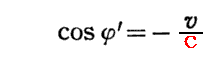
となる。
[補足説明2]
このとき、この式をcosφについて解くと
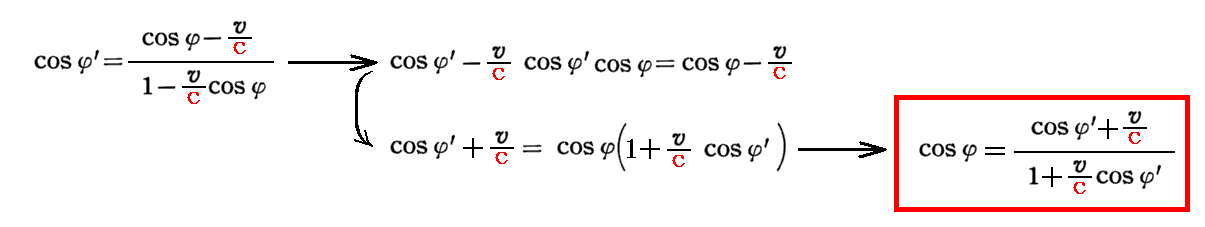
となるが、これは最初の式のvを-vで置きかえてφとφ’を入れ替えた式になっていることに注意されたし。
これは
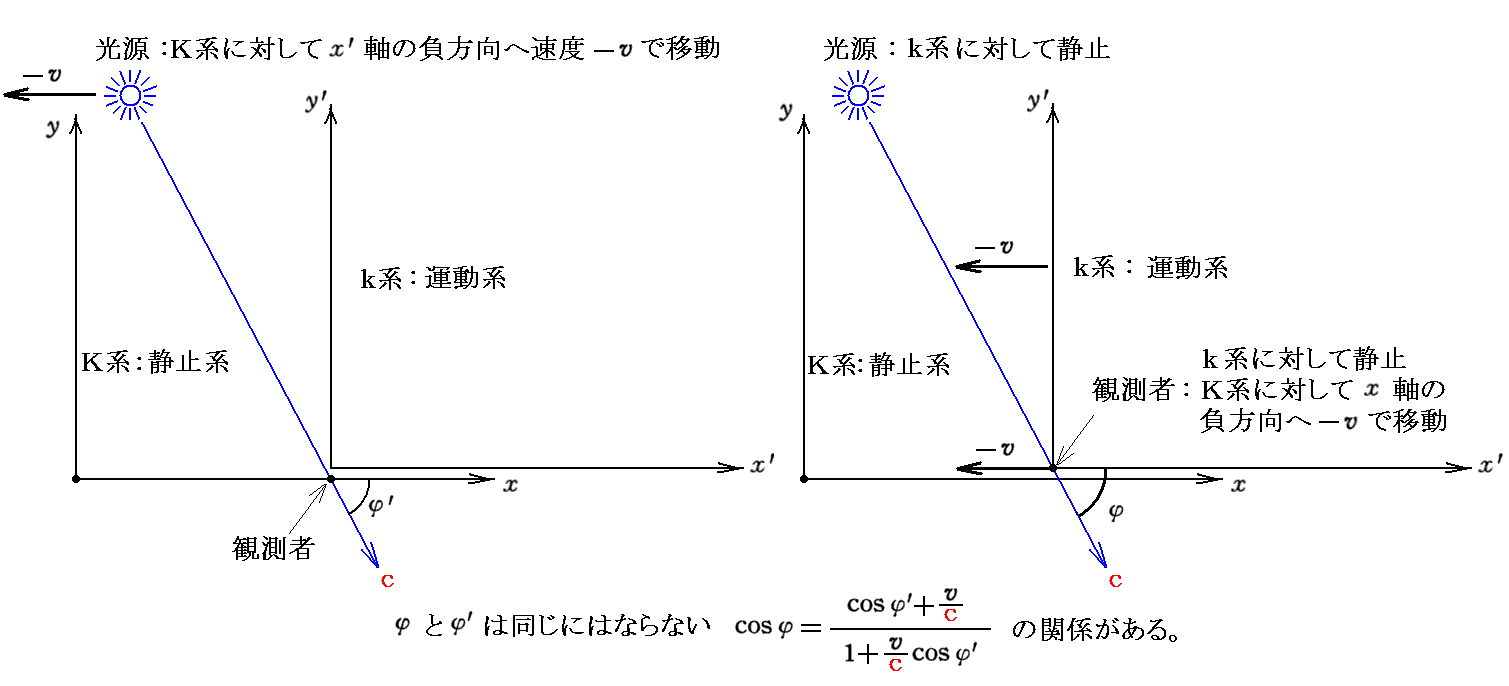
の関係を意味しています。
つまり、光行差の現象は完全に“相対的”で、光行差の現象からは絶対静止空間(そこをエーテルは満たす)を検出することはできないのです。これが別稿「マイケルソン・モーリーの実験」1.(2)で述べた“レーナルトの批判”に対する答えです。すなわち、Maxwell方程式、およびそれから導かれる波動方程式はローレンツ変換に対して不変だから、光行差の現象が絶対静止空間(そこをエーテルが満たしており、光速度はそのエーテル中を一定速度で伝わる)を見つける方法を与えることは無いということです。このことは2.(9)[補足説明1]ですでに説明しました。次の[補足説明3]もご覧下さい。
[補足説明3]
古典的なエーテル理論ではどうなるかを補足しておきます。
まず、別稿「ブラッドリーが光行差を見つけた方法」1.(2)で説明した図(ここでは光を伝える媒質であるエーテルが存在する絶対静止の空間があり、地球はそれに対して動いている)
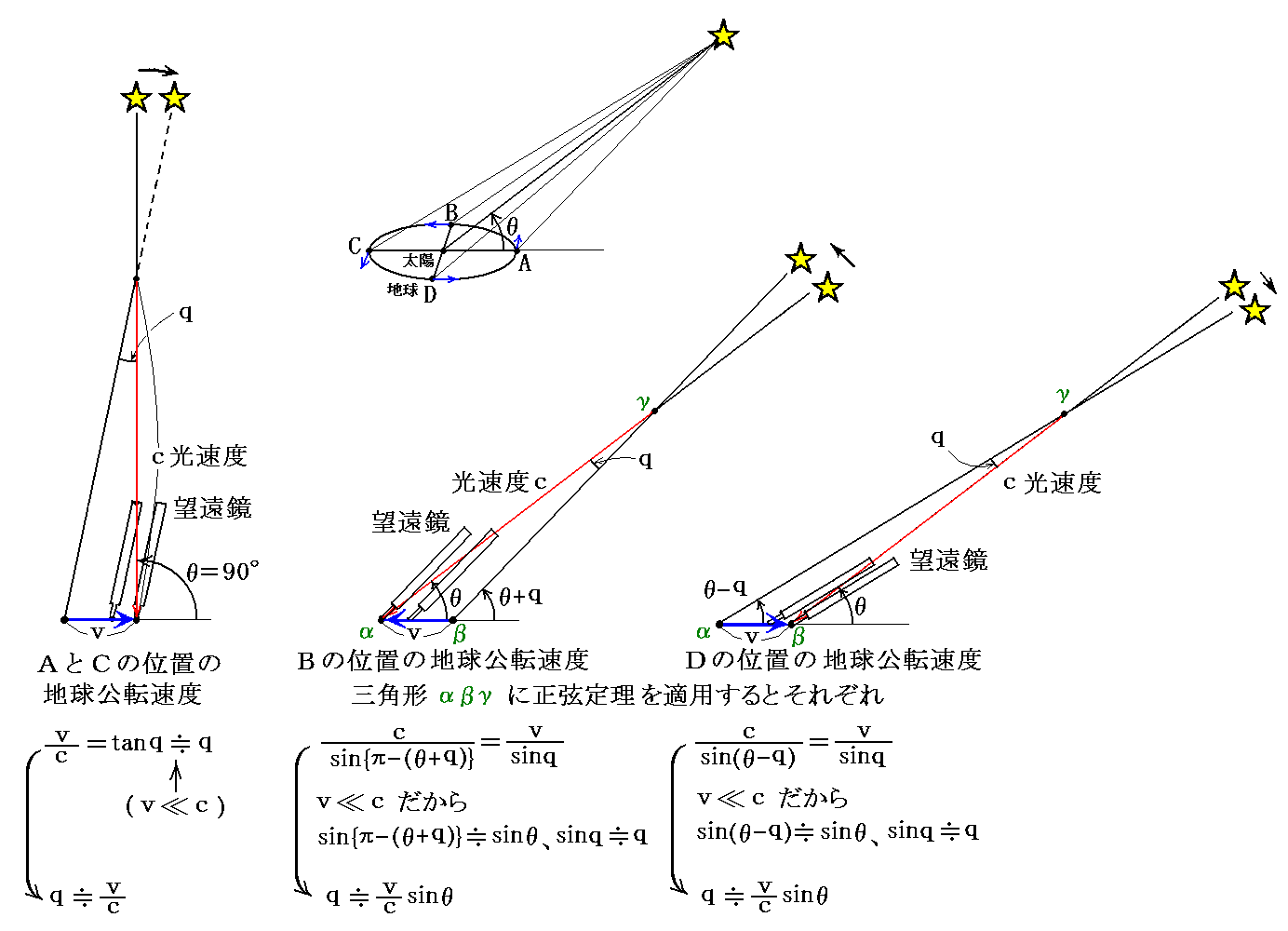
を用いて古典論の厳密解を求める。上中央図の左右を反転させて、さらに θ 、 θ+q 、 q をここでの記号 φ 、 φ’ 、 φ’-φ に変更すると下記の式が得られる。
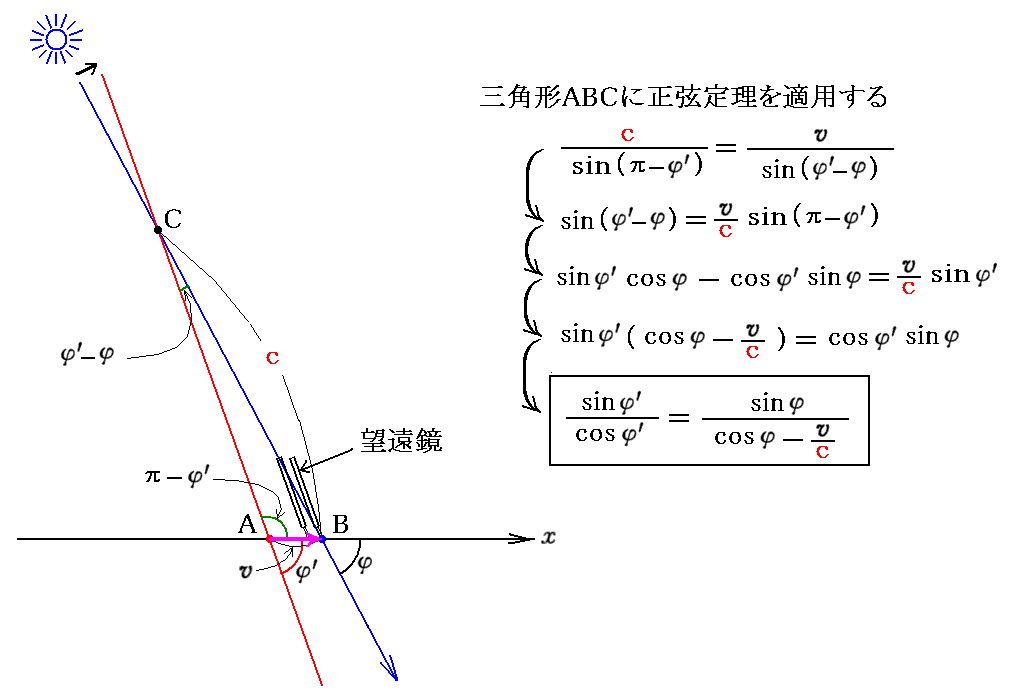
これは“ガリレオ変換”で得られる式であることに注意して下さい。実際にガリレオ変換を用いると
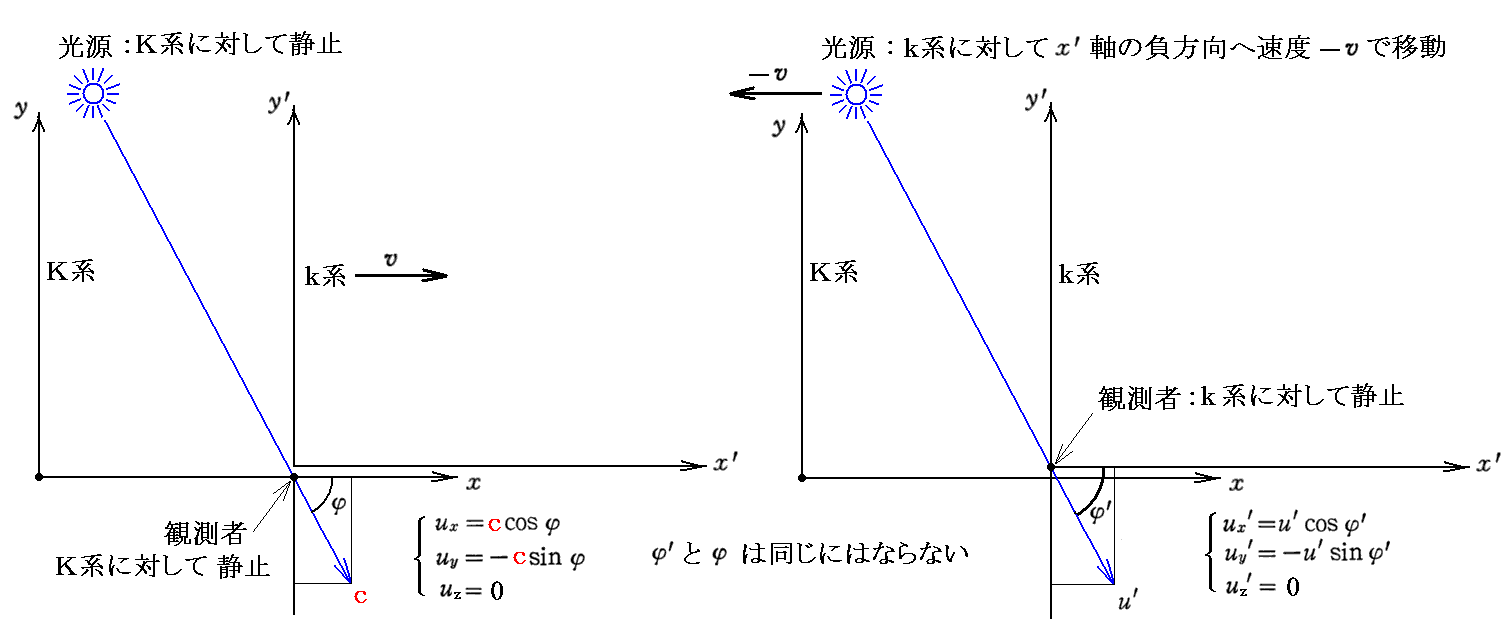
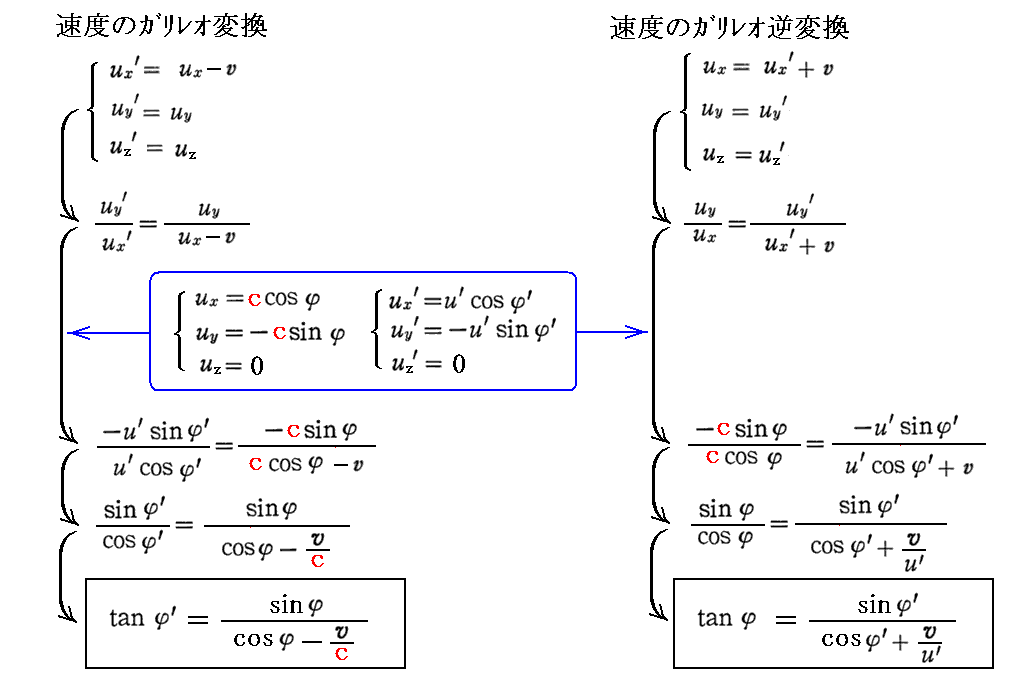
となります。
このとき注意して欲しいことは、ガリレオ逆変換を用いて得られる上記右側の式は、一見すると左側のガリレオ変換から得られる式のvを-vに置き換え、φとφ’を入れ替えた式になっている様に見えます。
しかし、

となる。あるいは、光線のz(or z’)成分がゼロで、光線がxy(or x’y’)平面内に限られるときには
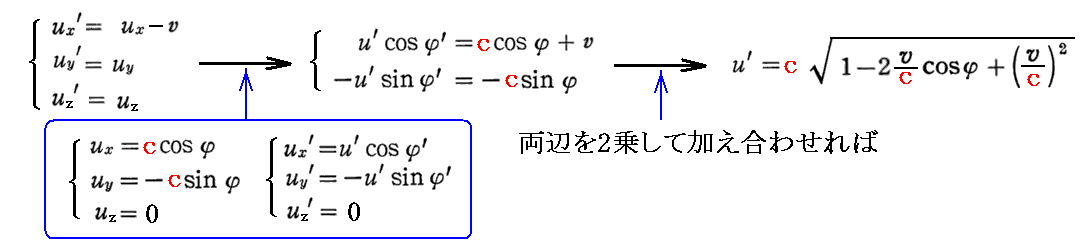
となります。いずれにしても u’≠c となり、等しくないのです。
すなわち、Maxwell方程式、およびそれから導かれる波動方程式は“ガリレオ変換”に対して不変ではないから、光源が動いて観測者が静止しているとみなすと同じ結論が得られません。だから、もし光行差の現象を極めて精度良く観測できて、観測値が厳密にこの式に従って角度変化するのなら絶対静止空間を検出することができます。
もちろん恒星には銀河系内の運動に伴う固有運動がありますし、年周視差の動きもあります。それらが光行差楕円に重なって現れます。しかし、普通の恒星では、1年あたりの固有運動量や年周視差は光行差楕円の半長軸20.5”に比べてはるかに小さい。
さらに補足しますと、上記光行差楕円の天球上での変動には、地球の地軸のフラつきに伴う“歳差”(20”/年程度)と“章動”(1”/年程度)も重なってきます。ただし、これらの年当たり変化量は正確に計算できて解っていますから、観測値からそのその事による変動量を差し引いておくことができます。
【ここは非常に解りにくい所です。別稿「光行差観測による特殊相対性理論の検証」で解りやすく説明しておりますのでご覧下さい。】
ブラッドレーの観測(1727年)以来、Einsteinが特殊相対性理論を提案した1905年までに、170年以上光行差の観測は積み重ねられてきました。そのとき過去のどの観測結果を見なおしても、光行差楕円の位置がずれる様な観測結果は無かったのです。
実際、ブラッドレーは光行差楕円の絶対赤緯の測定の年変化から、逆に“章動”の現象を発見したのですから、光行差楕円の位置のずれが無い事はブラッドレーの時代の観測からすでに確認されていたと言っても良いのしょう。とにかく、すべての観測結果が別稿「年周光行差と年周視差による星の位置変化」1.(3)で説明した図
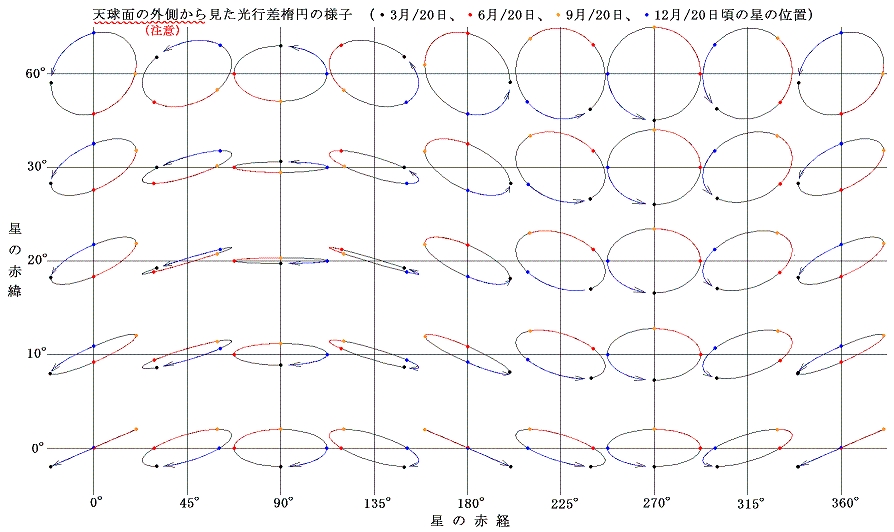
の様な楕円だったのです。
もちろんこれは、地球の公転軌道が絶対静止空間(エーテル空間)内をスライドする事無く公転している場合、古典論的に正しい結果ではあります。実際、上記別稿の計算はその様に仮定して古典論的に計算したものです。
しかし、当時銀河系が回転しており銀河自体も宇宙空間内を高速で移動している事は解っていましたから、その結論は問題になりません。
上記の事柄は、当然Einsteinの認識の中には在ったと思います。それだからこそ、特殊相対性理論の正当性を確認する重要な例として光行差の現象を取り上げたのでしょう。
方程式系が不変かどうかは、真に正しい“ローレン変換”に対してであって、残念ながら“ガリレオ変換”に対してではありません。そのとき、2.(9)[補足説明1]で証明したように、ローレンツ変換に対して不変になる相対論的に正しい光行差公式からは、楕円の位置変化は検出できません。そのため絶対静止空間(その空間を光は一定速度cで伝播する)を検出することはできません。
[補足説明4]
別稿「ブラッドリーが光行差を見つけた方法」1.(2)[補足説明]で、次のように説明しました。
「今日、地球は太陽のまわりの公転運動のみならず、太陽系の銀河回転運動に伴う速度や、銀河自体の移動に伴う速度ベクトルが重なった運動をしていることが解っています。もちろん、観測する恒星も銀河系内を高速で移動しています。そのため、光行差を観測する1つの星に対して地球は単純な円運動をしているわけではありません。そのとき、上記の様に光行差の観測値が地球の公転運動(つまり問題の恒星と地球の相対的な運動)にのみ関係している様に見えるというのはとても不思議な事です。」
この事をもう少し補足すると、文献510.に収録されている広重論文「エーテル問題・力学的世界観・相対性理論の起源」p177~178によると、19世紀に入ると恒星位置をまとめた星表の編纂において、その位置精度を高める補正因子として、大気による屈折の影響はもちろんのこと、[光行差]、[宇宙空間内における太陽系の運動]、[恒星自身の固有運動]が重要であることが、明確に認識される様に成った事が紹介されている。
つまり光学理論において光源・観測者・媒質の三者相互の間の運動が存在するときの光の伝播の仕方を明らかにすることは極めて重要な問題となっていたのです。
ここでの議論を読まれれば上記の疑問が相対性理論で完璧に解決されることが解ります。光行差に伴う恒星の見え方の変化は、恒星と地球の相対的な運動のみに関係していて、恒星や地球が銀河系や宇宙空間の中でどのような動きをしているかにはまったく関係しないのです。つまり、恒星と地球がやり取りする光のやり取りの様子は恒星と地球の相対的な関係のみに関係しているのです。これはとても不思議ですが、光はその様な性質をもっているのです。
[補足説明3]で述べた様に、光行差楕円の位置変化が無い事は、丁度マイケルソン・モーリーの実験装置を回転させても、干渉縞の移動が生じなかったことに対応します。すなわち、光行差楕円の観測結果はマイケルソン・モーリーの実験の観測結果の天文版です。
そのとき、光行差の観測結果が与えた結論、つまり絶対静止空間(エーテル空間)が検出できないということに対して、特殊相対性理論は完璧な解決を与えています。
このことが、アインシュタインが“光行差 と フィゾーの実験(フレネルの随伴係数) を相対性理論が説明できた事が、その理論の正当性を確信する上で充分でした(were enough)”と言った理由です。
上記のアインシュタインの述懐についてはPais文献6.のp145~147を参照されて下さい。
[補足説明5]
別稿「マイケルソン・モーリーの実験」1.(2)[補足説明2]で、つぎのように説明しました。
・・・・・エアリーの実験(1871年)が示す“望遠鏡の鏡筒を水で満たしても光行差の角度が変化しない”という事実は、パウリ著「相対性理論」第Ⅲ編§36に拠ると、『・・・相対性理論の立場に立ってエアリーの実験を眺めれば、この結論は当然である。いま望遠鏡を恒星の見かけの位置の方向に向ければ、その恒星から発射された光は望遠鏡の方向に平行に鏡筒内に入射してくる。鏡筒を水で満たしていても、光はレンズに垂直(従って水面にも垂直)に入射するのだから、光は鏡筒の内部に水が無かったときと同じ方向に進む。つまりエアリーの実験の観測者(地球)の静止系からながめれば、それは“入射角が0の入射光の屈折角は0である”という周知の事実を表しているにすぎない。・・・』と説明される。・・・・・
パウリの説明は難解ですが、以下の事を言っている。別稿で引用したBornの文献202.の第Ⅳ章§10で説明されている様に、“エーテル理論では、エーテルに対して移動する観測者にとって光線の方向(つまり波のエネルギーが伝播する方向)は波面が伝播する方向(つまり波面に垂直な方向)とは必ずしも一致しない。”
これは古いエーテル理論が抱える大きな疑問点でした。ところがこの節で見てきたように、相対性理論では、全ての慣性系の観測者にとってエネルギーが移動する方向である光線の方向は波面に垂直となる。従って上記の疑問点は完璧に解決される(ここはBornの文献202.のp298を参照)。
これは、Maxwell方程式および波動方程式はローレンツ変換不変だから、k系での波動解

をk系でのMaxwell方程式に代入すれば、3.(2)1.[補足説明3]の(9)、(10)式に相当する式が成り立ち、3.(2)1.[補足説明4]と同様な手順で E0’⊥s’ and H0’⊥s’、E0’⊥H0’、[E0’×H0’]=|E0’|・|H0’|s’、|E0’|=|H0’| が、k系での波動解についても成り立つからことから言えることです。
この事も アインシュタインが“光行差を相対性理論が完璧に説明できた事が、その理論の正当性を確信する上で充分でした”と言った理由だと思います。
[補足説明6]
最後に、“相対性理論の光行差公式”と別稿「ブラッドリーが光行差を見つけた方法」1.(2)で説明した古典的な“エーテル理論による光行差公式”との関係を補足します。
相対論的光行差の公式として、前記のEinsteinの求めた形ではなくて、2.(9)で説明したSommerfeldの形
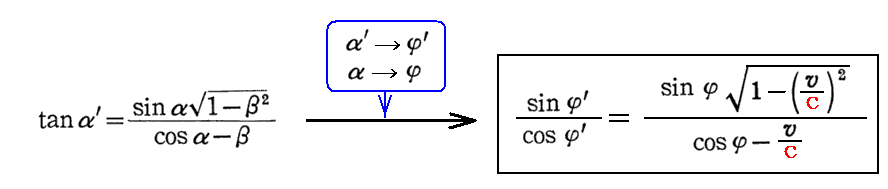
を用いる。これが前記のEinsteinが求めた公式表現と等価であることは2.(9)[補足説明2]で証明した。
この式でv/cの二次の項を省略すれば、3.(2)3.[補足説明3]で求めた“エーテル理論(ガリレオ変換)による光行差公式の厳密解”
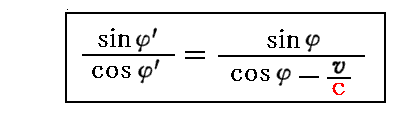
となります。
つまり、v≪cの場合には、相対論(ローレンツ変換)とエーテル理論(ガリレオ変換)との差はほとんどなくなります。そのため、別稿で説明した古典論の結果が近似解としてそのまま得られます。ただし、記号φ、φ’とそこでの記号θ、θ+qとの対応関係に注意して下さい。
4.光の振幅の変化


[補足説明1]
上記関係式を証明しておく。
K系における電気力(電場)の振幅をAとすれば
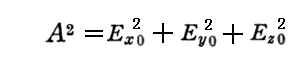
で表される。
同様にk系における振幅をA’とすれば
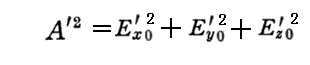
となる。3.(2)1.で得た電磁場の変換式を用いるとk系における値をK系における値と関係づけることができる。
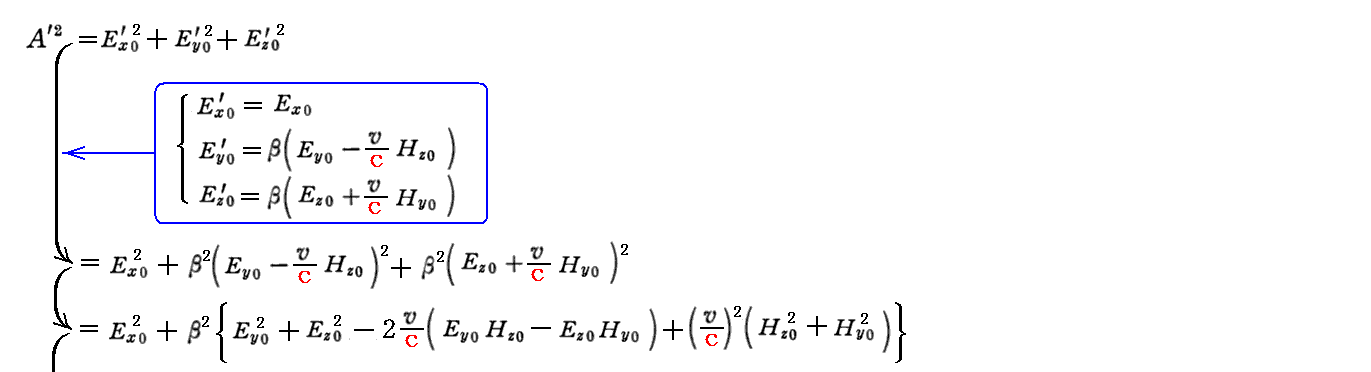


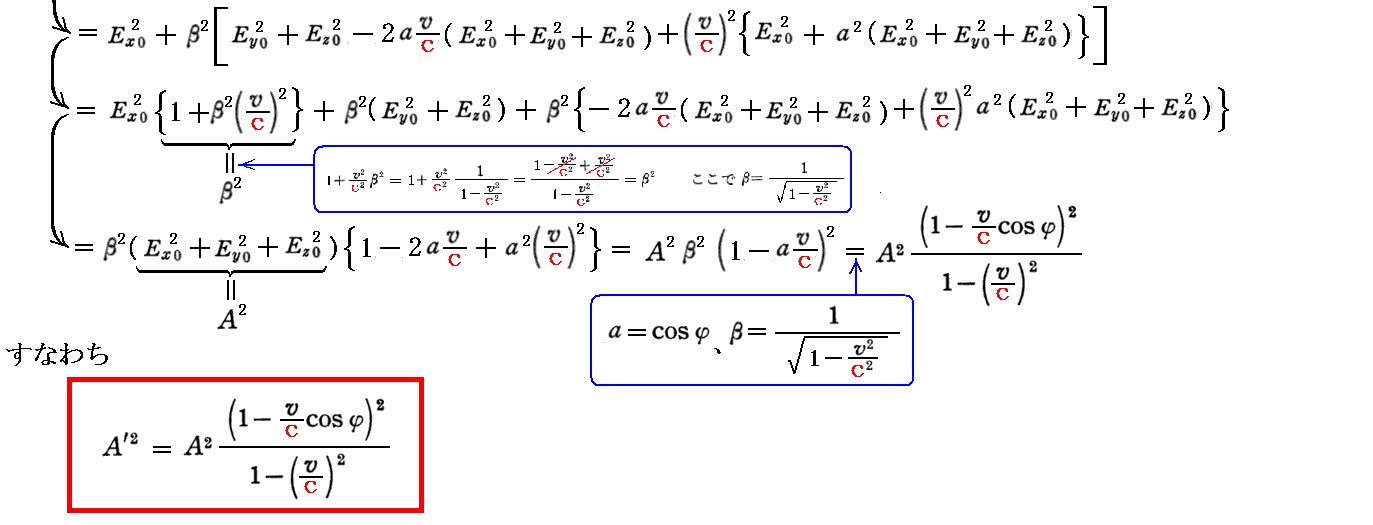
磁気力(磁場)の振幅に付いても同じ関係
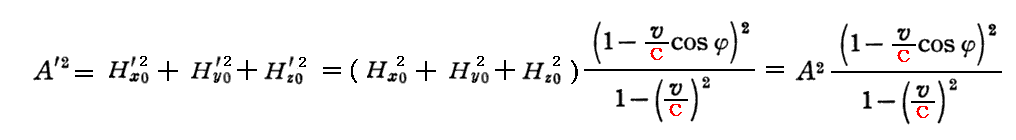
が成り立つことは、同様にして証明できる。
[補足説明2]
観測者が光源から遠ざかる場合はφ=0°だからa=cosφ=cos0°=1となるので、前記の式は
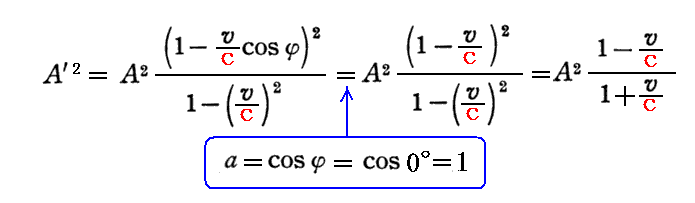
となる。そのため、観測者が遠ざかる速度vが光速cに近づくと、A’→0なり、光源は限りなく暗くなる様に見える。
一方、観測者が光源に近づく場合はφ=180°だからa=cosφ=cos180°=-1となるので、前記の式は
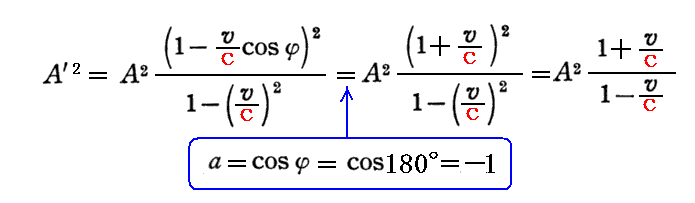
となる。このとき前記のvを-vに置きかえれば後記の式となり、この場合も“相対性原理”を完璧に満たしていることに注意されたし。
そのため、近づく速度vが光速cに近づくと、A’→∞となり、光源は無限の強度で輝く様に見える。
これらの予言は古典論からは決して出てこないもので、相対性理論の驚くべき成果です。このとき、観測者に向かって伝播してくる光の速度は、光源に対する観測者の運動状態によらず常に一定値cであることに注意して下さい。この事を考慮すると、“エネルギー保存則”に矛盾しないためには上記の様にならなければならい。実際、光源が遠ざかる場合と近づく場合では、その光源から単位時間に観測者に届くエネルギー量に関して上記の関係が成り立たないとおかしな事になります。
このことは、膨張宇宙の発見と相まって、宇宙論における大問題であった“オルバースのパラドックス”を完璧に解決する。
更に補足しますと、今日オルバースのパラドックスの解決には宇宙が膨張している事よりも、宇宙の年齢が有限であるため観測できる銀河の数が有限でその年齢も宇宙年齢より短いことが大きいようです。つまり宇宙には夜空を明るくするほど多くの星(銀河)が存在しているわけではないことがオルバースのパラドックスを解決するようです。
§8.は、この論文の中で特に重要な所で、Einsteinが最も力を込めて説明したかったことだと思います。おそらく直前(3月)に発表した光量子仮説の論文をおおいに意識して書いたと思われます。
ただし、Einsteinは極めて簡潔に説明していますので、解読するのは大変です。
(3)原論文 §8.光線のエネルギーと輻射圧
1.光のエネルギーの変換則



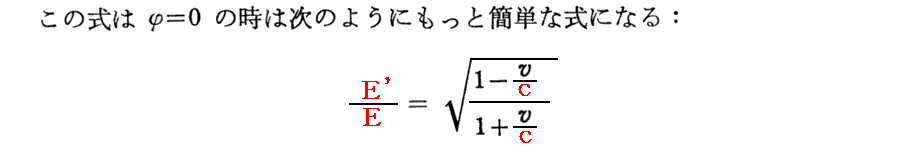

[補足説明1]
上記文中の関係式を以下で順番に説明していく。
光線の束が持つエネルギー密度(単位体積当たりの光のエネルギー)は別稿「光の圧力(輻射圧)」2.(5)1.で
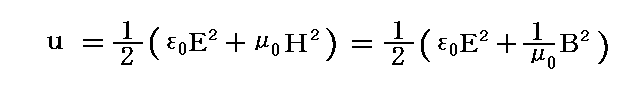
となることを説明した。
これを、この稿で用いている有理化されていないGauss単位系(別稿「電磁気学の単位系が難しい理由」5.(3)3.の対応表を参照)で表すと
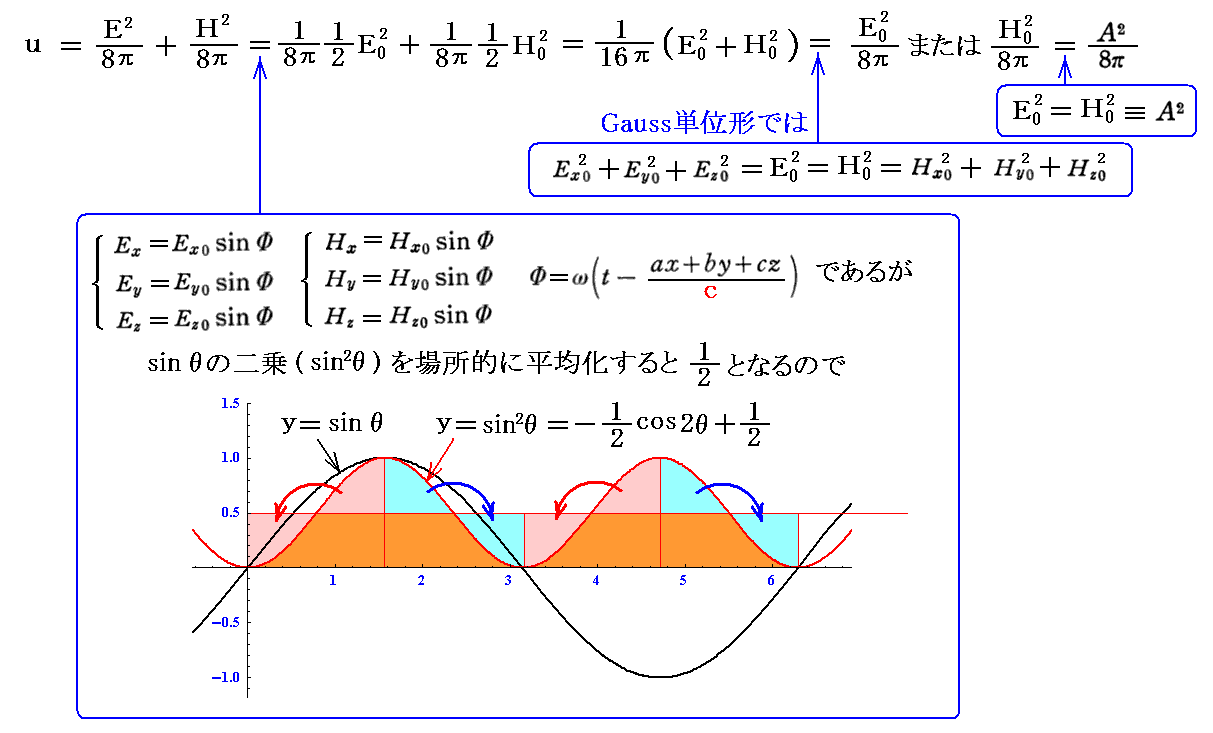
となります。
[補足説明2]
(a,b,c)を静止系Kにおける光の法線方向の単位ベクトルとすると、光速度cで動いている球体表面は
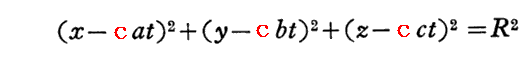
で表される。
この球体表面は下図の様なものです。ここでの球体の半径は時間的に変化しません。
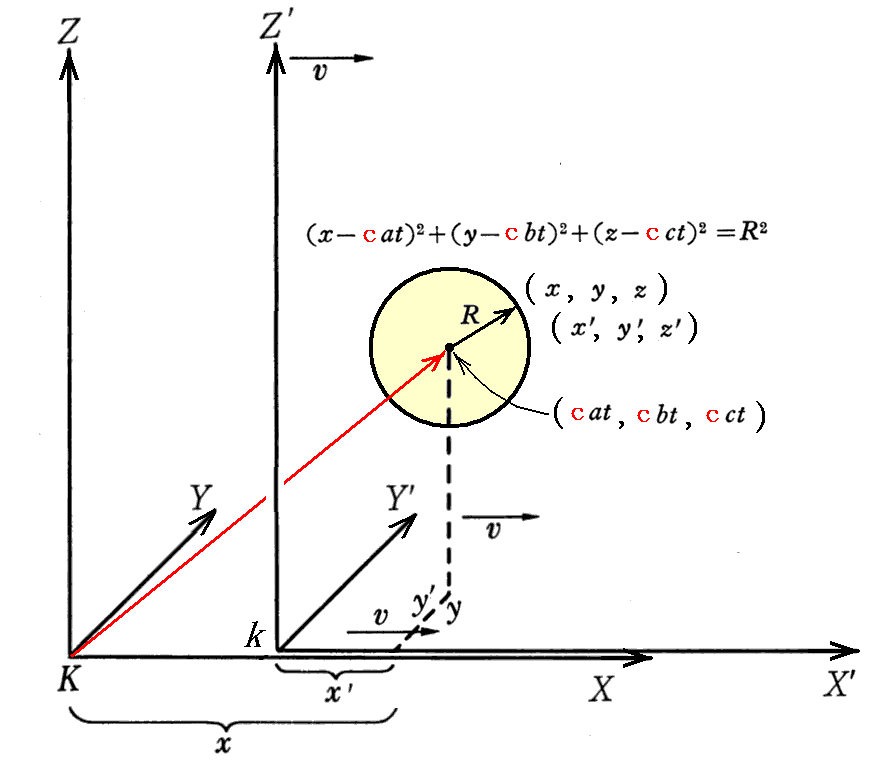
この“球体表面”を、2.(4)[補足説明3]で紹介した文献211.に於ける“球面波”
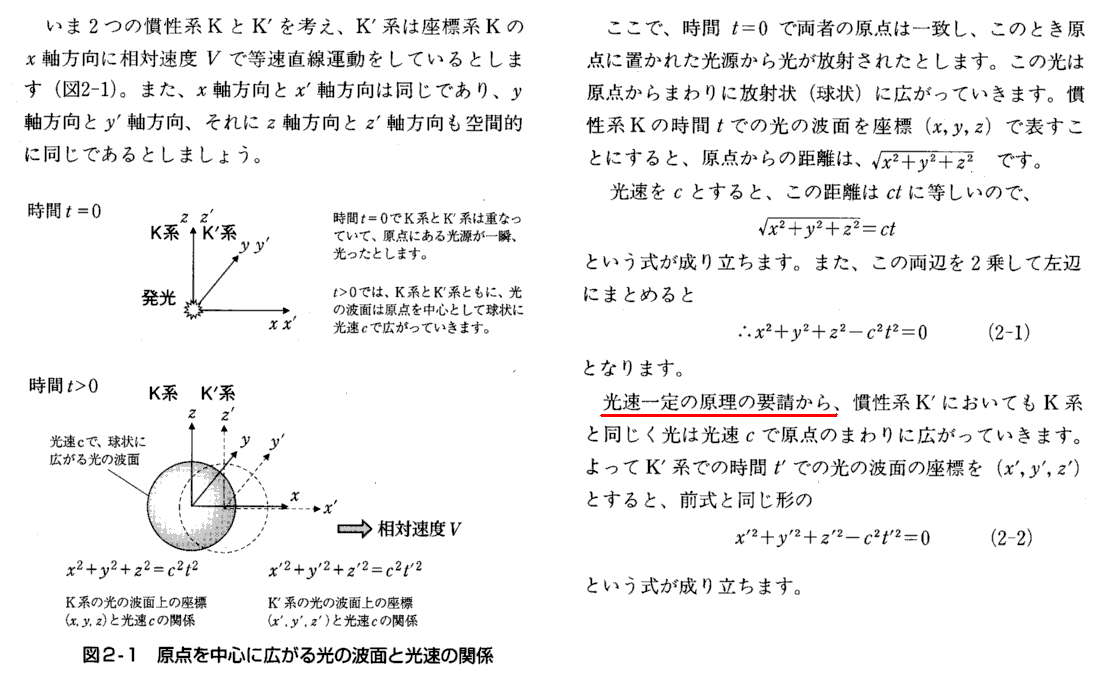
と混同しないで下さい。こちらの“球面波”の半径は時間と共に増加していきます。
上記の“球体表面”を運動系kから眺めるとどのように表されるかを調べる。K系からk系へ変換するのにローレンツ逆変換を用いるのであるが、計算を簡単にするためにt’=0における形を調べる。すなわち先ほどの図で t=0 で球面がKの原点に存在するときの状況を調べる。すると

となる。これは最初の項中のx’の前にβが掛かっていることから解る様に、一つの楕円体曲面を表す。
[補足説明3] 以前、この補足説明の内容は別ページのような説明ですましていました。今回、そこで省略されていた計算をすべて実行して説明します。(2021年7月改訂)
文中に記されている光の球体の変形を論じるのですが、光球体の移動方向をxy平面上に限定して論じても一般性を失わないので、その場合に限って説明します。つまり (a,b,c)=(a,b,0) であり a2+b2+c2=a2+b2+02=1 の場合です。
その為、K系からみて方向余弦(a,b,c)方向に進む光の球体をk系から見ると、z方向についてはそのまでy方向とx方向で縮んだ楕円体になります。すなわち
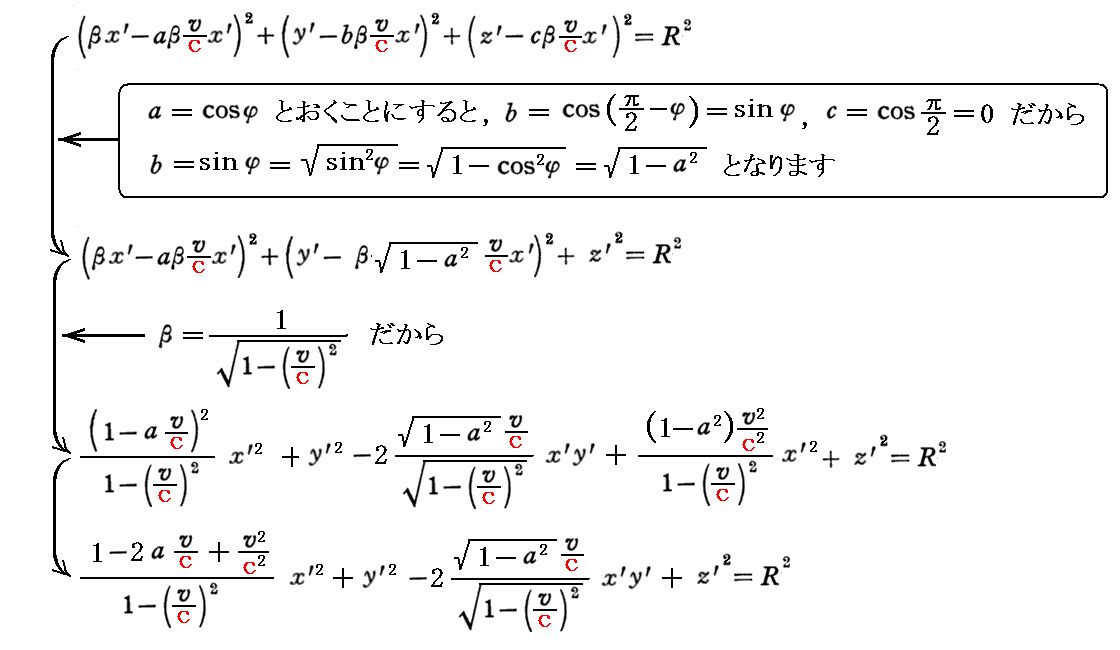
となります。
この楕円体を表す二次形式を標準形に変換するにはこちらの別稿の手順に従えば良い。
まず上記の“二次形式の係数”を行列表示すると
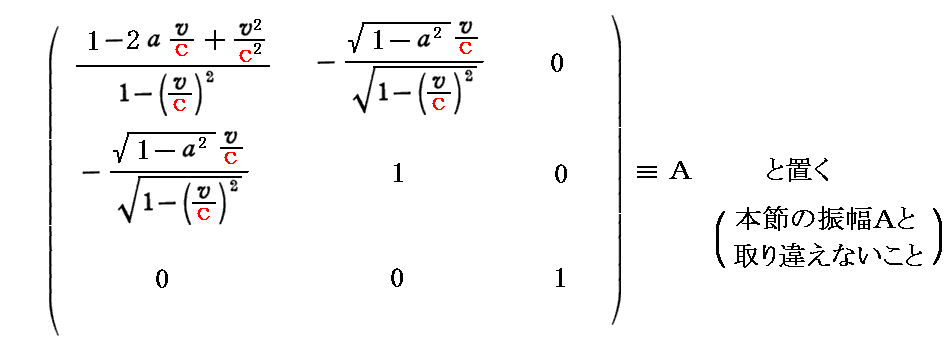
となります。
これを対角化したときの対角行列の“対角要素”は、次のλに関する3次方程式
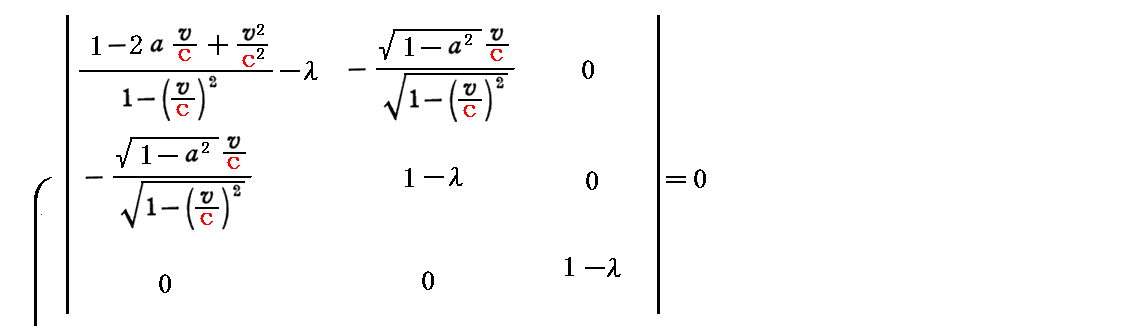
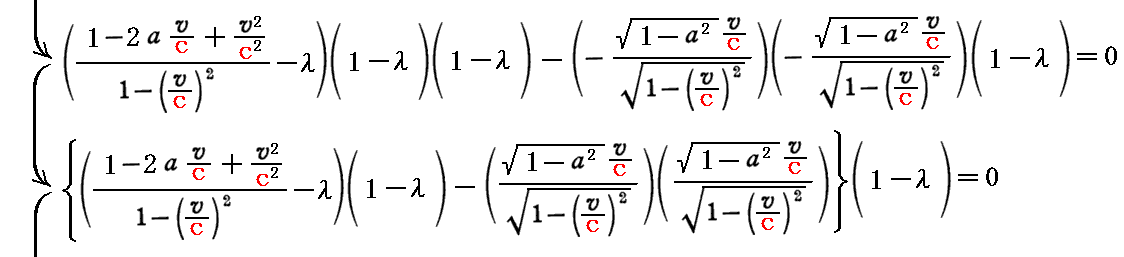
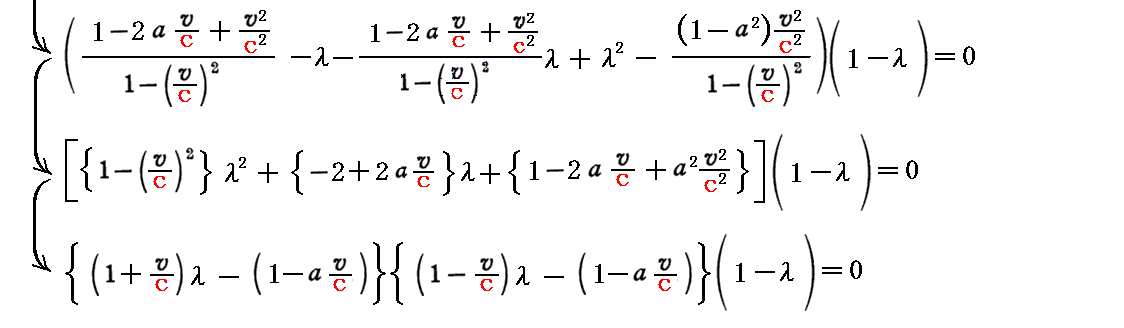
の根となります。すなわち
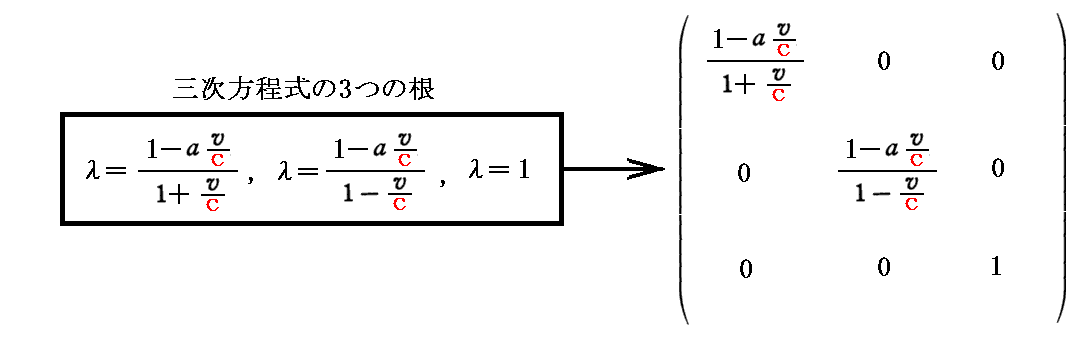
です。
このとき、上記の対角化を行うための(x’,y’,z’)→(x”,y”,z”)への“座標変換行列”は、以下の連立方程式を解くことによって得られる。
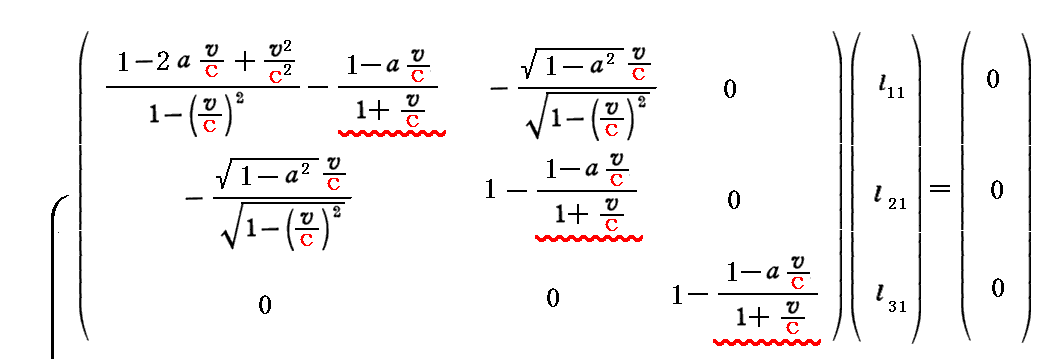
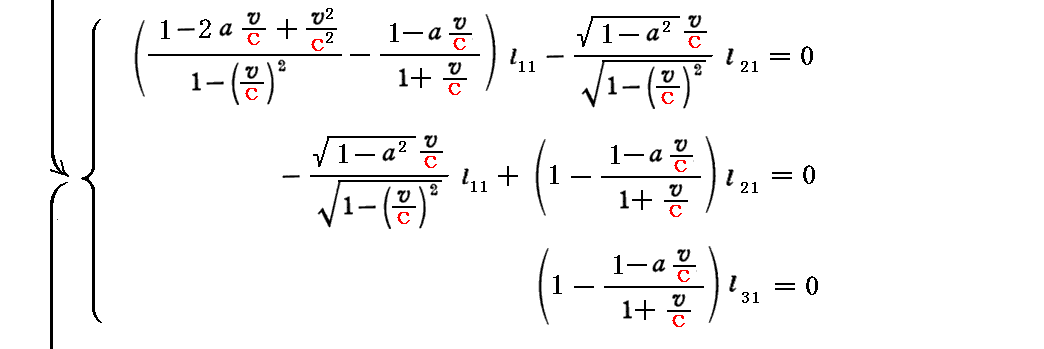

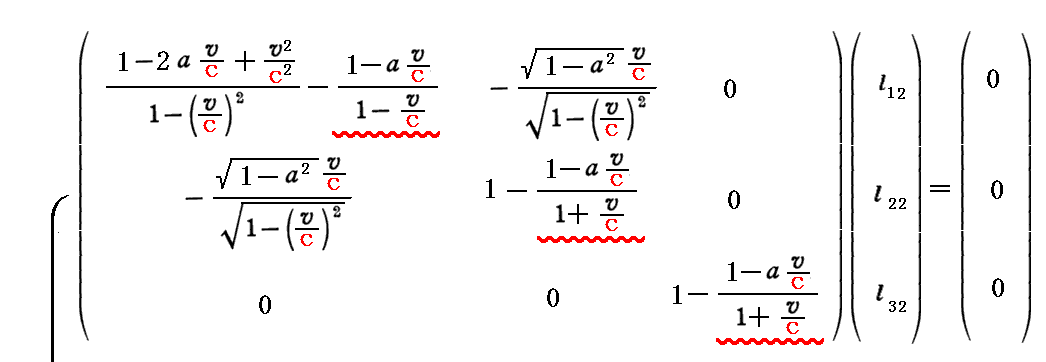
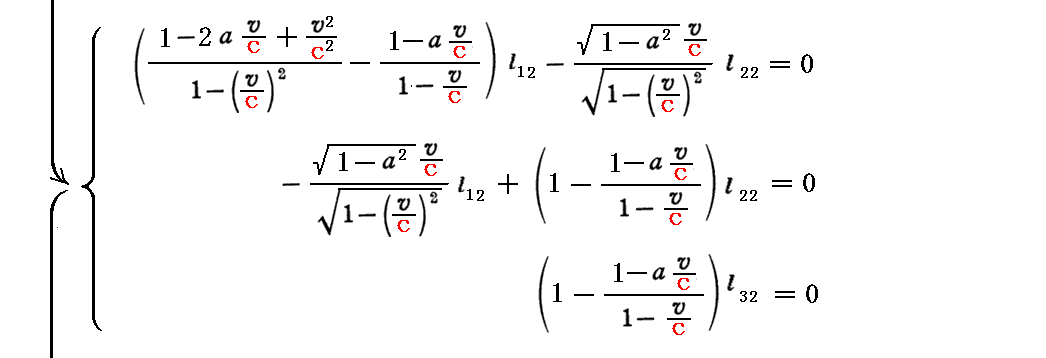
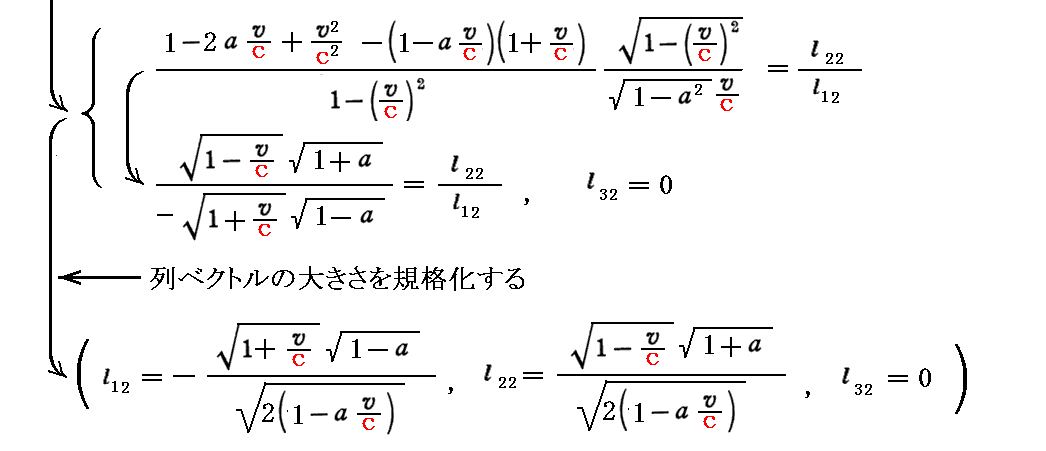
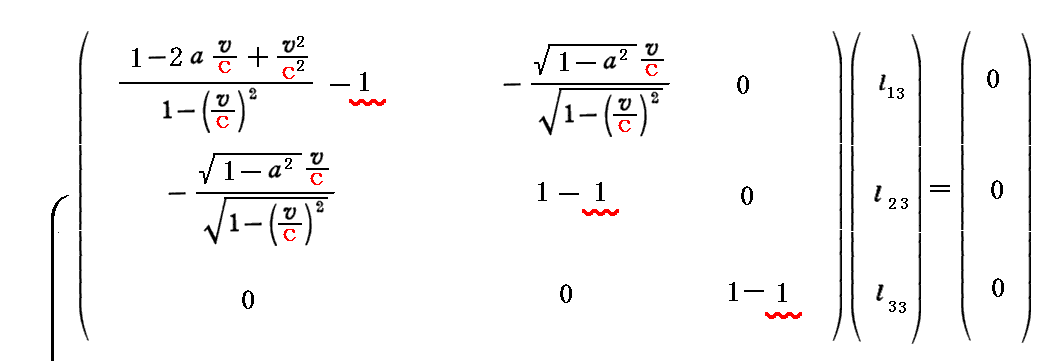
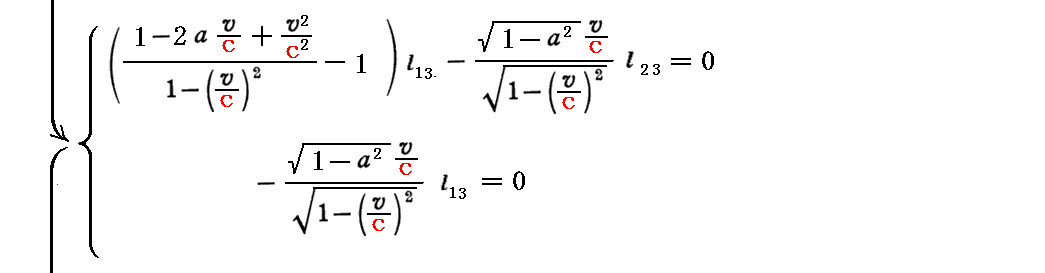

すなわち、こちらの別稿で言うところの二次形式を標準形にする為の “座標変換行列”Lは、上記3つの列ベクトルから構成される行列
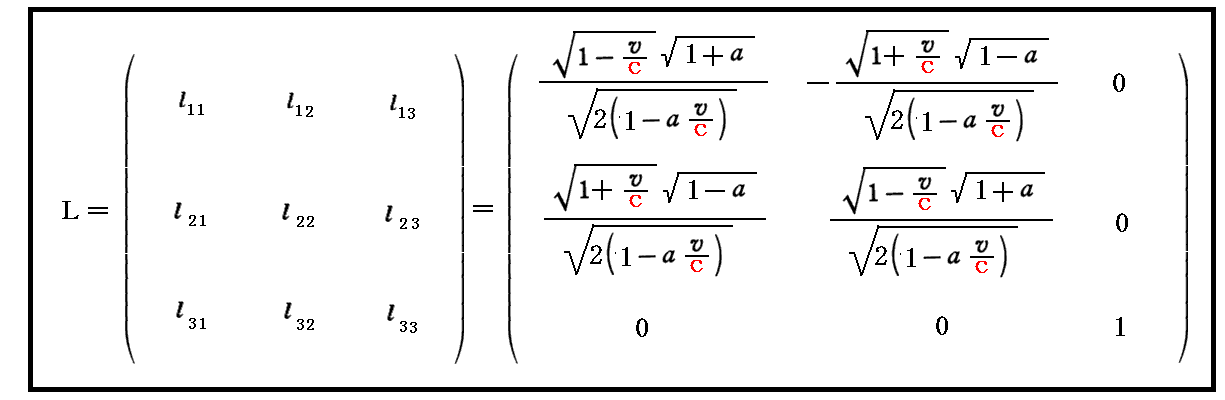
となります。
この “行列” L に対して以下の関係式が成り立つ。
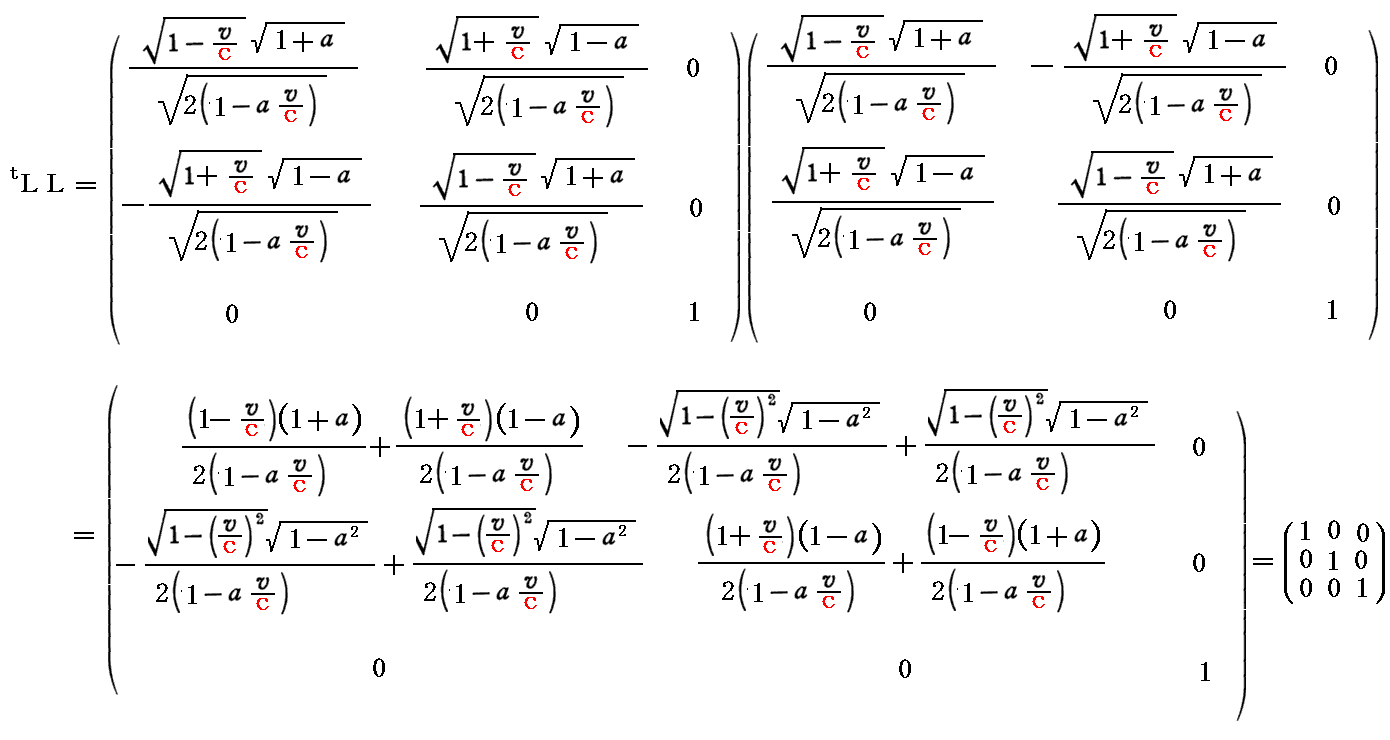
これを、最初の“係数行列式”Aに対して以下の様に適用すれば行列要素を対角化できる。
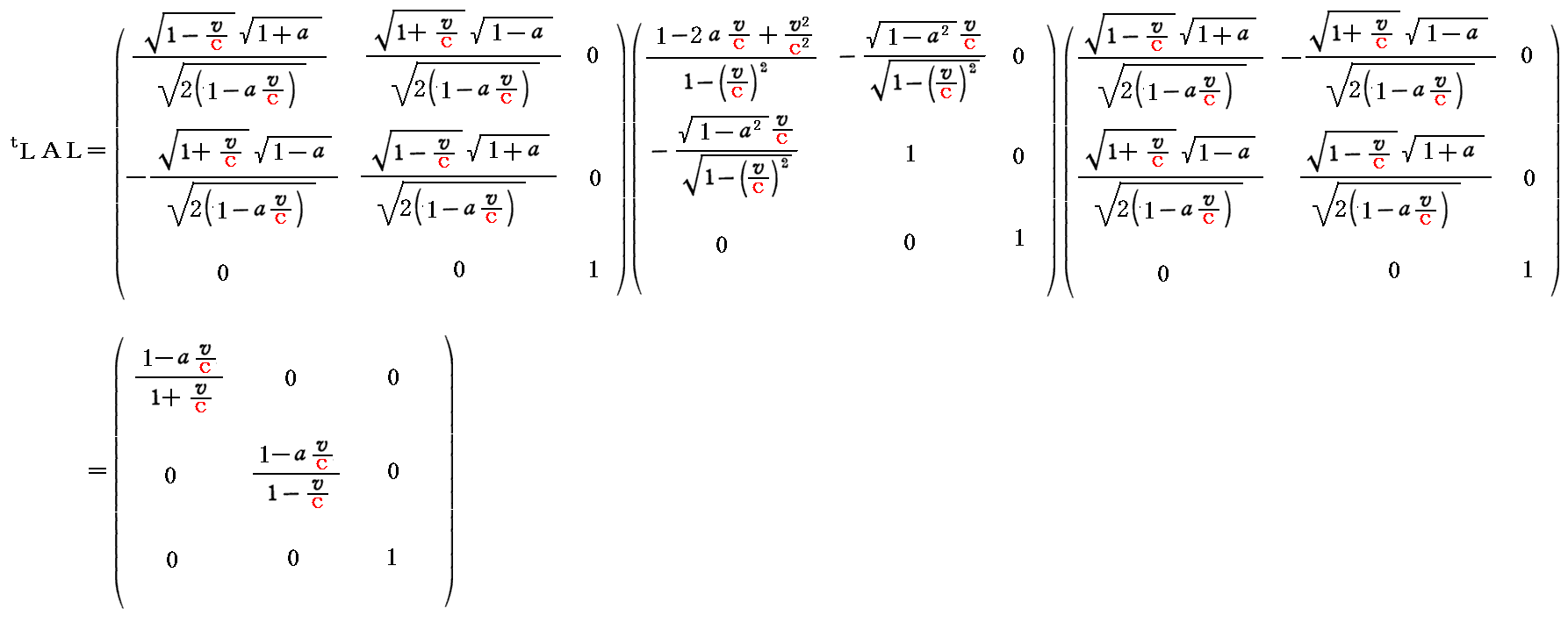
これらの確認は結構面倒ですが、別稿2.(1)4.“行列の乗法”の定義に従って計算すればできます。
以上の関係から標準形で表した三次元楕円体曲面の方程式は
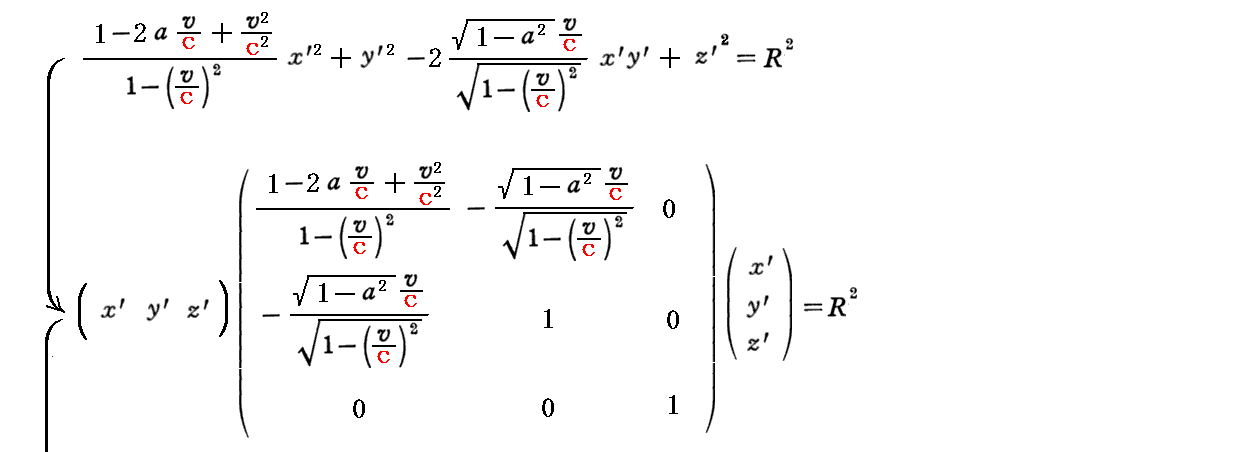
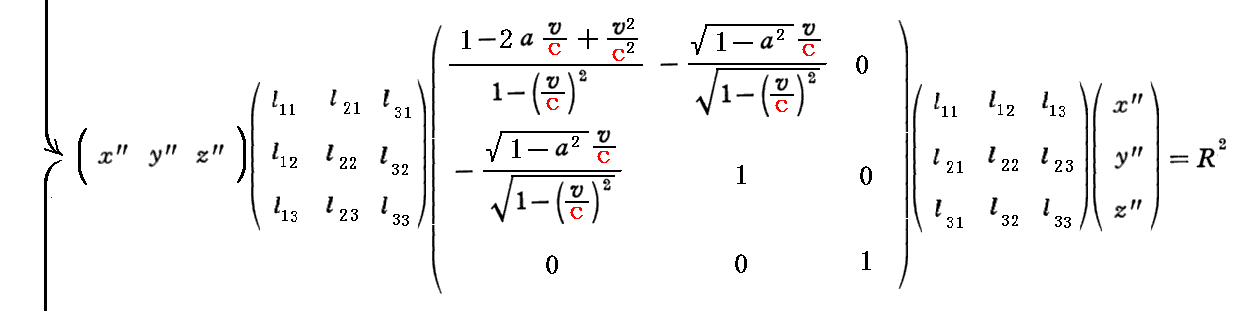
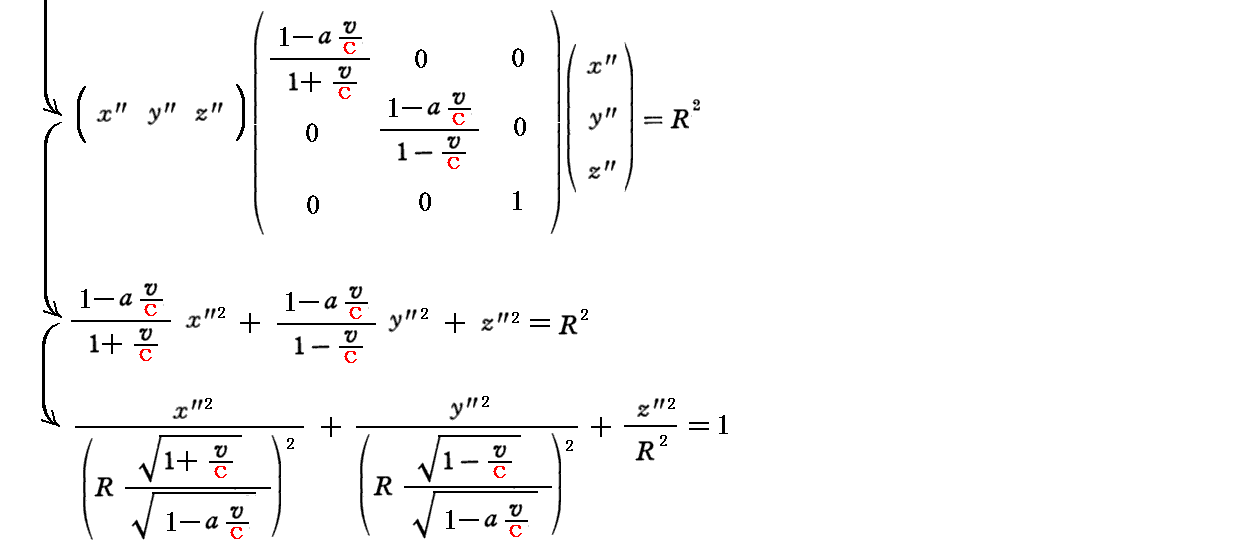
となります。
標準形に直すことができれば、楕円体の体積公式は
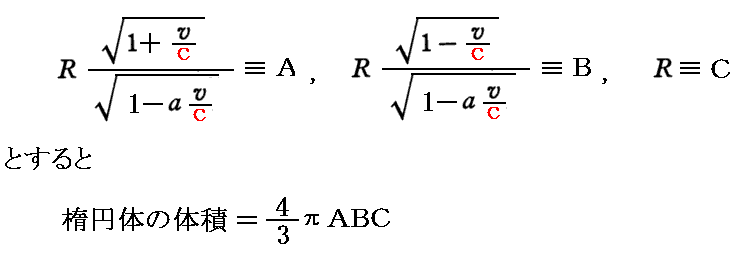
ですから、楕円体のk系における体積S’は
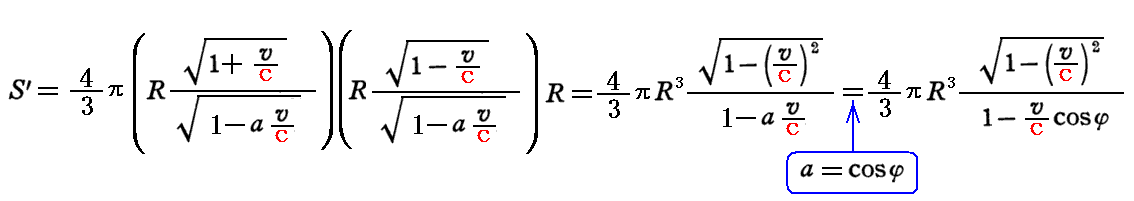
となります。
一方、K系における球体の体積Sは
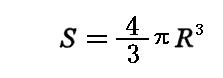
となる。
これらを用いれば文中の
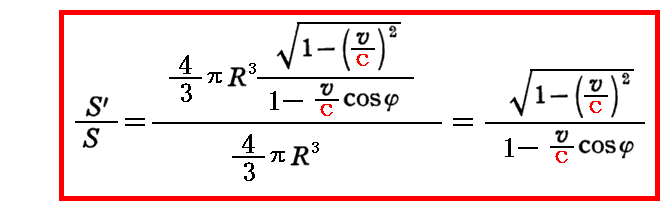
が求まる。
======= 蛇足ですが、以下の事に注意して下さい。=======
読者の中には、座標変換(x’,y’,z’)→(x”,y”,z”)としてz’軸の周りにx’y’座標軸を角φだけ回転すれば、三次元楕円体曲面方程式を標準形に変換できるのではないかと思われる方がおられるかも知れません。つまり下記の様にする?
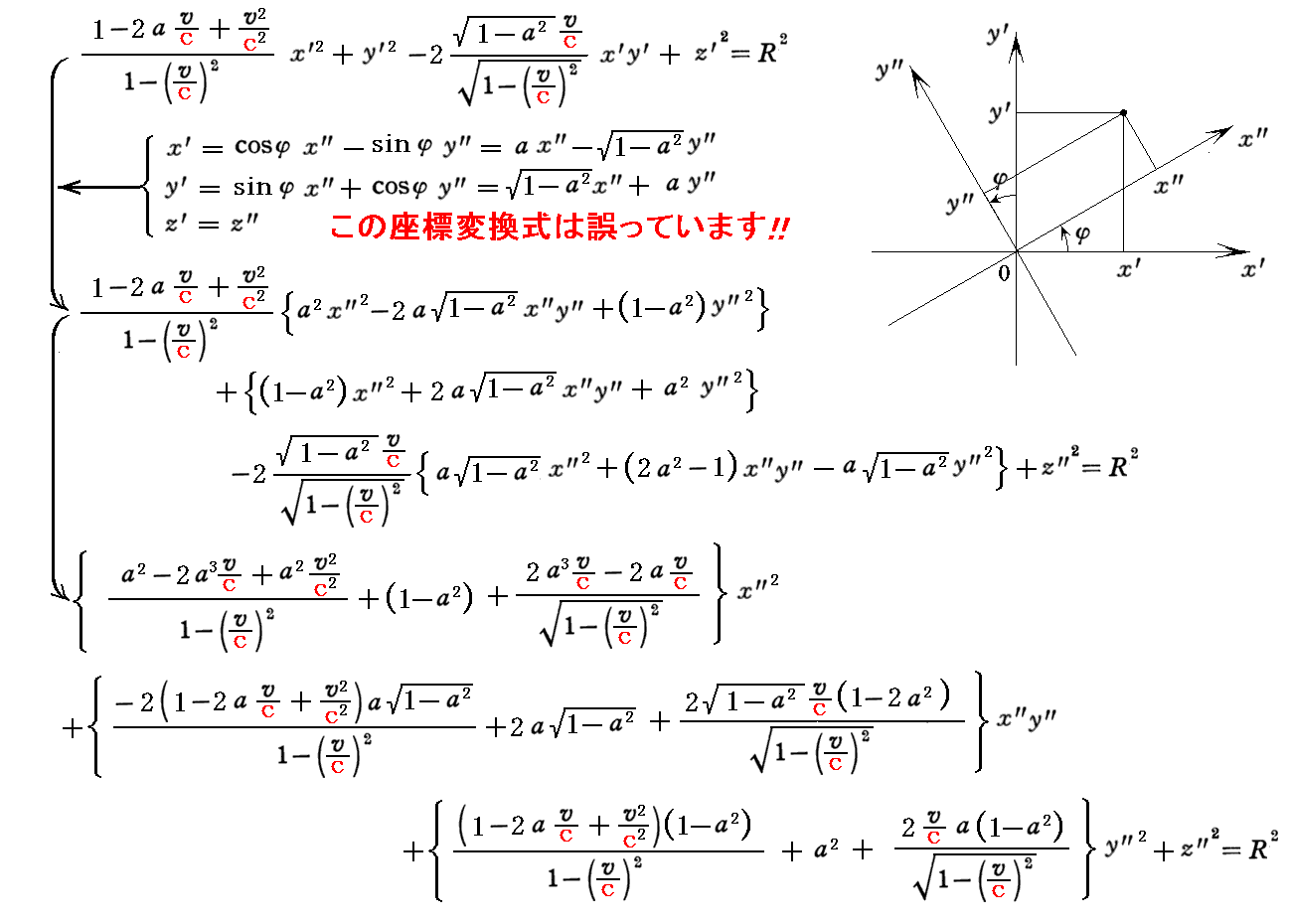
しかし、上記の座標変換では、x”y”項の係数はゼロにならず、標準形になりません。このやり方は誤りです。
なぜなら、“光球体”が変形するのは、光塊(光子)が方向余弦(a,b,c)方向に光速度で移動するから変形するのではなくて、K系に対して(そのx軸方向に)速度vで移動しているk系から見るから変形するのですから。
くれぐれも、このことを、3.(4)[補足説明5]で出てくる事柄と取り違えないで下さい。そこでは、静止系Kから見るとK系のx軸方向に速度vで動いている“帯電球体”は、相対論的な長さが縮む効果によりx軸方向に縮んだ楕円体に見えるのです。すなわち
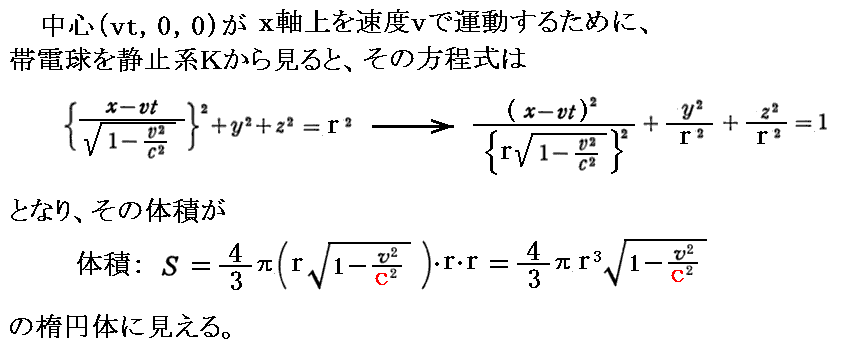
これは、今ここで議論している状況とは全く異なります。実際、ここでの結論において(a,b,c)=(1,0,0)としても
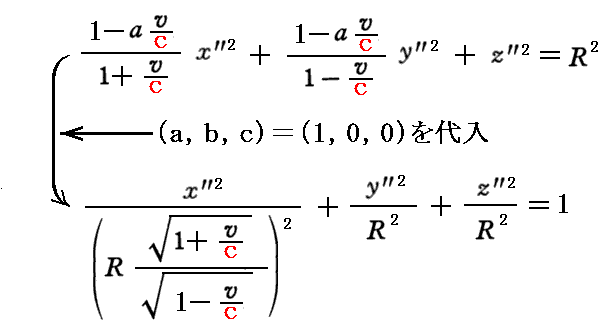
となりますので、標準形の方程式も全く異なります。
[補足説明4]
この文節の最後で、Einsteinはエネルギーの変換則
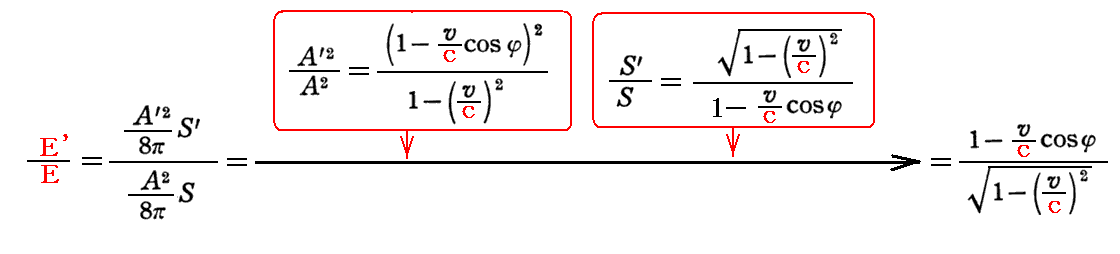
が、すでに求めた振動数の変換則
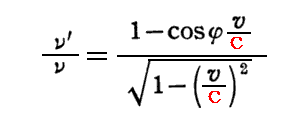
と完全に同じである事を注意している。このことに関してPais文献502.(p186~187)7-5の解説は興味深い。
これは、“相対性理論”が(Einsteinがこの論文の直前に発表した)“光量子仮説”や(Planckが1900年に発表した)“エネルギー量子仮説”におけるE=hν(hは普遍定数)と完全な整合性を持っていることを示している。
つまり、『相対性理論に従って現在の座標系から運動する座標系に移されていくとき、長さ・時間・エネルギー・振動数などのあらゆる量が変わるのだが、“プランクの作用量子h”は不変量のままである。』 おそらく、Einsteinの論文を注意深く読んだPlanckは、この事に強く引きつけられたに違いない。
この当たりについてPais文献502.p191~192で次のように説明している






上記文中のラウエの[L1]論文はこちらを参照、プランクの[P6]論文はこちらを参照。また、ルイスとトルマンの[L5]論文についてはこちらを参照。
[補足説明5]
ここで得られた式

は静止系Kから見た“光線塊”の持つエネルギーEは運動系K’から見るとE’の様になるということを言っている。つまり同じ“光線塊”の持つエネルギーでも、それを観測する慣性系に拠って異なると言っている。これは古典論からいくと不思議なことですが、相対性理論からいくと当たり前で、そうでなければなりません。なぜなら、相対性理論の大原理は光の速度はどの慣性系から見ても常に一定値cだからです。
例えばK系で見た“光線塊”がx軸に沿って速度cで移動しているとします。今はK’系はK系のx軸方向に速度vで動いているとしていますので、上記式中の光線の進行方向とx軸との角度を表すφは0でcosφ=1となり、EとE’の差はφ=0のとき一番大きくなります。
“光線塊”のエネルギーが観測する慣性系に拠ってことなることは、次の事実を考えたら明らかです。同じ“光線塊”をK系とK’系で観測します。そのときK’系に静止しているx’軸に垂直な面(K系では当然x軸の正方向へ速度vで移動する面となる)を考える。その同じ面を単位時間に通過するエネルギーはK系から見ても、K’系から見ても同じでなければなりません。もちろん同じ事象をK系の時計で計った時間とK’系の時計で測った時間は異なりますから正確に論じるにはそのことも考慮しなければなりませんが。
そのとき“光線塊”の速度はK系でもK’系でも同じ速度cです。ところが透過する面はK系では遠ざかり、K’系では静止しています。光線塊の移動速度が両系で同じcで在ることを考慮すると、この事はまさに“光線塊”のエネルギーがK系で見た場合の方がK’系で見た場合よりも大きくなければならない事を言っています。このことは3.(2)4.[補足説明2]すでに注意したことです。
つまり、K系から見た“光線塊”がx軸の正方向へ速度vで遠ざかっている同じ面を同じエネルギー量で通過するためには、光線塊のエネルギー量は当然K’系で見た場合より多くなければならないのです。このように考えれば、φ→90°(つまりcosφ→0)となると、E’→E(1-v2/c2)-0.5へ近づく理由も明らかです。ここで、E’→Eでは無いのはもちろん時間の相対性に因ります。
つまり、“エネルギー”、“振動数”、“振幅”などがローレンツ変換に対して不変ではないのは、“光の速度がどの慣性系から見ても同じ速度cで伝わる”としたからです。【エネルギー保存則】がどの慣性系から見ても成り立つためにはそうでなければならない。
“光速不変の原理”は、常識では理解できませんが、これこそが相対性理論を理解する鍵です。最初に説明した、あるいは別稿でも説明する、Bornの文章の『この中間で生ずることは純粋に仮想的であり、あるいはもっと正確に表現すれば、任意的である。このことは、理論家はその判断にしたがって、位相、場あるいは類似の量を、物質について観測される変化に簡単明瞭な関係をうちたてるのに役立つという制限のもとで、真空に賦与することができることを意味する。』、
あるいはSommerfeldの文章の『我々の目は“光波をみる”と学校で教えられたが、それは迷信である。われわれの目がみるのは、入射光量子の大きさhνに従ってわれわれの視覚的印象の多色の世界を生ずる網膜での光電過程である。』をもう一度噛み締めて下さい。
こういった事柄は光速不変の原理からいくらでも出てきます。アインシュタインは相対性理論が予言するこれらの事実に気づき・驚いたに違いない。彼は、(ローレンツ変換によって)時間の相対性を発見した後の論文発表までの5週間に、おそらく寝る間も惜しんで、それらの驚嘆すべき事柄の確認計算を実行したと思われます。
この事から“質量”という属性もローレンツ変換に対して不変では無いことが証明できます。さらにこの事からアインシュタインの有名な公式 E=mc2 が証明できます。これらは別稿「アインシュタインの公式
E=mc2 の証明」で説明します。
[補足説明6]
本文の最後に出てきた式はアインシュタインの“光量子説”で言うところの“光子”のエネルギーについても成り立つ。
つまり、そこでの“光束(光塊)”を“光子”と見なすこともできて、K系でみた光子のエネルギーEと、同じ光子をK系に対して速度vで動くk系から見たときのエネルギーE’の関係を表していると解釈することもできる。
この事については別項「相対論的力学」3.(4)もご覧下さい。
そのとき、アインシュタインの光量子説に従ってそれぞれのエネルギー表現E=hνとE’=hν’を適用すると
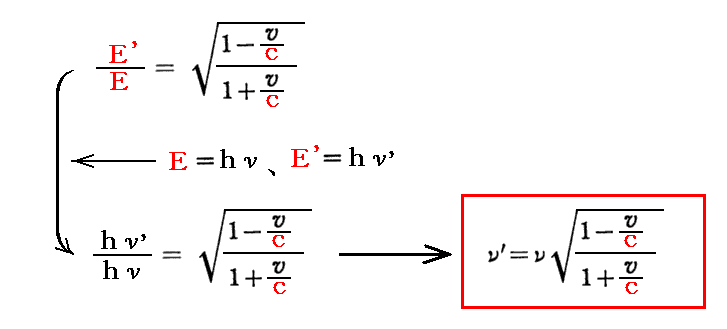
となる。これは波動説に基づいて3.(2)2.ですでに求めている“Doppler効果の公式”と同じです。
すなわち、光のドップラー効果は波動説のみならず、光の粒子説でも完璧に説明できます。この事はすでに、2.(10)3.で説明して注意しました。
上式は光の進行方向と光源(又は観測者)の運動方向vが同一の場合でしたが、光速cとvが角度φを成す一般的な場合には、前記式の一つ前の式を用いればよい。すなわち
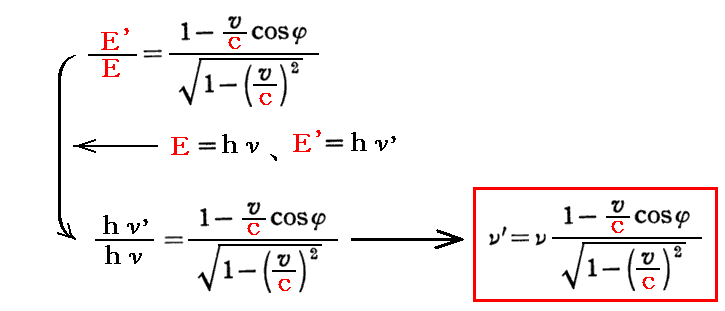
となる。これはもちろん3.(2)2.で、波動説に基づいてすでに求めている式に一致します。
これを用いると
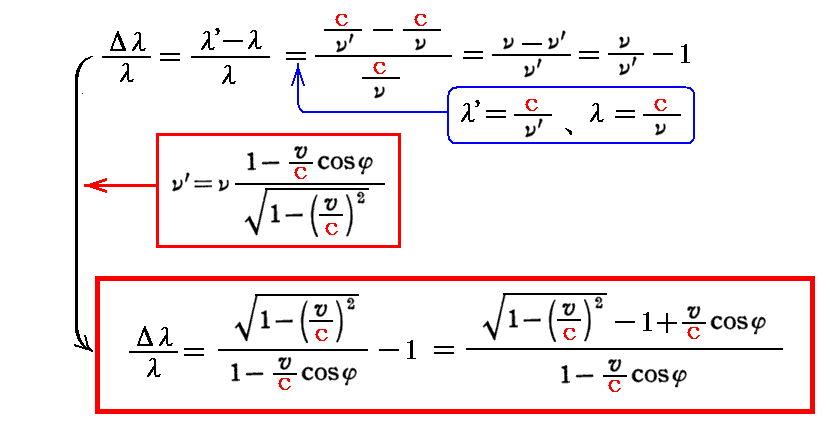
が得られます。これは、シュレーディンガーが2.(10)3.[脚注(‡)]で強調した粒子説から導いた“相対論的に厳密なドップラー公式”です。そこのvnはここのv・cosφのことです。
[補足説明7]
本文の最後に出てきた式
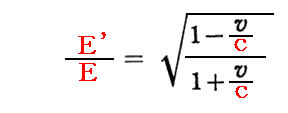
についてもう少し補足します。これは後に明らかになる(運動量ベクトル、質量[エネルギー])四次元量に対するローレンツ変換式
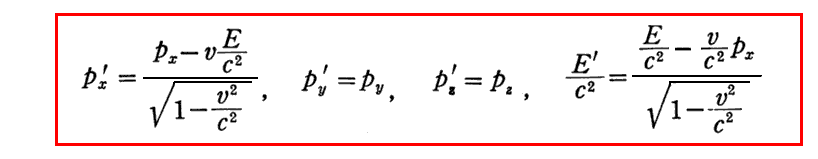
からもっと一般的に導くことができます。この式の導出は別稿「相対論的力学」3.(4)の(88’)式をご覧下さい。
この式をx’軸の正方向に速度cで動く光塊に対して適用する。その光塊の運動量ベクトルとエネルギーを測定するk系は静止系Kのx軸の正方向へ速度vで動いているとする。
“光塊”に対しても上記の(運動量、質量)四次元量に対するローレンツ変換は正しい。そのため
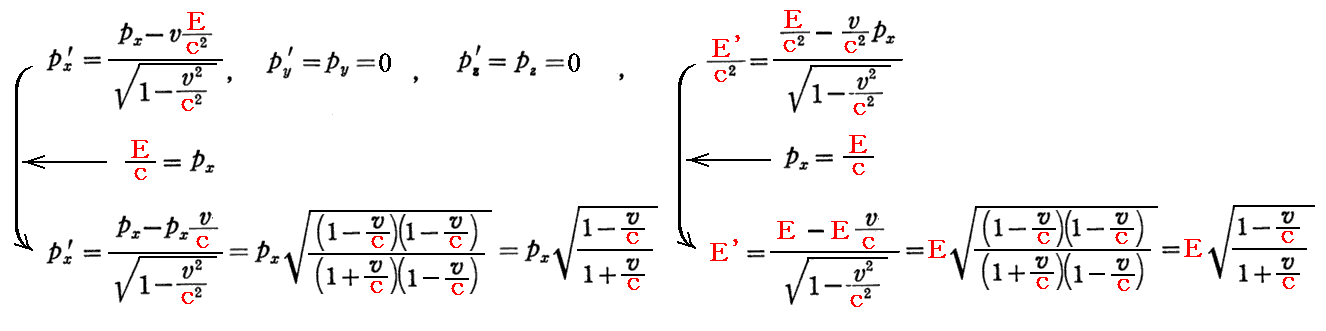
となり、前記の結果が得られる。なおここで用いたpx=E/cの証明も別稿「相対論的力学」3.(4)を参照されたし。
ここで求めた式は、素粒子論でとても重要な現象の現れ方を予言します(別稿「相対論的力学」3.(4)あるいは4.(4)を参照)。また、この式は後にアインシュタインが一般相対性理論構築のヒントを得た考察(1911年)でとても重要な働きをします。
2.光の圧力

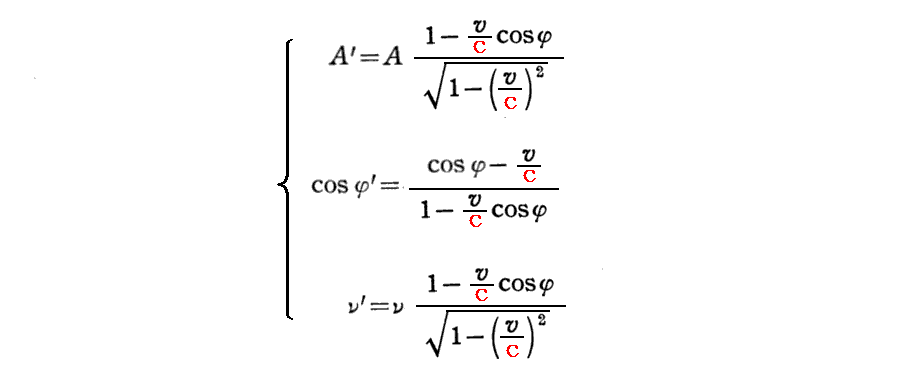





[補足説明1]
上記文節の内容を順番に補足する。
最初に、後で必要になる[k系からK系への“振幅”と“角度”と“振動数”の変換公式]を導く。
左端の式は 3.(2)4.[補足説明1]、 3.(2)3.[補足説明1]、 3.(2)2.[補足説明1] ですでに求めているので、これらを逆に解けば良い。
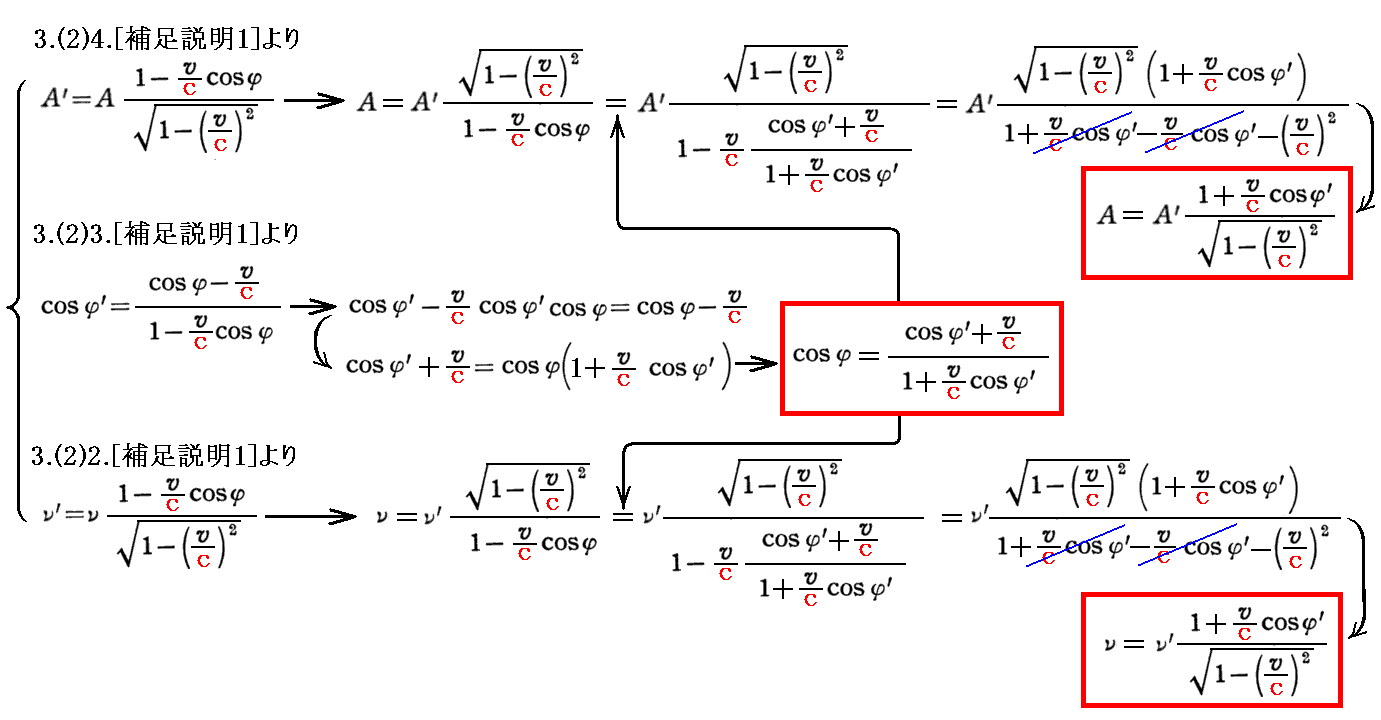
これらの式は、3.(2)2.[補足説明4]、3.(2)3.[補足説明2]、3.(2)4.[補足説明2]で繰り返し説明したように、相対性原理を満たしていることから、左端の式のvを-vに置きかえて、A’とA、φ’とφ、ν’とνを置きかえたものになっている。
[補足説明2]
次に、K系における反射光の状況を入射光の値で表すのだが、文中のφ、φ’、φ”、φ’”の関係を確認しておきます。
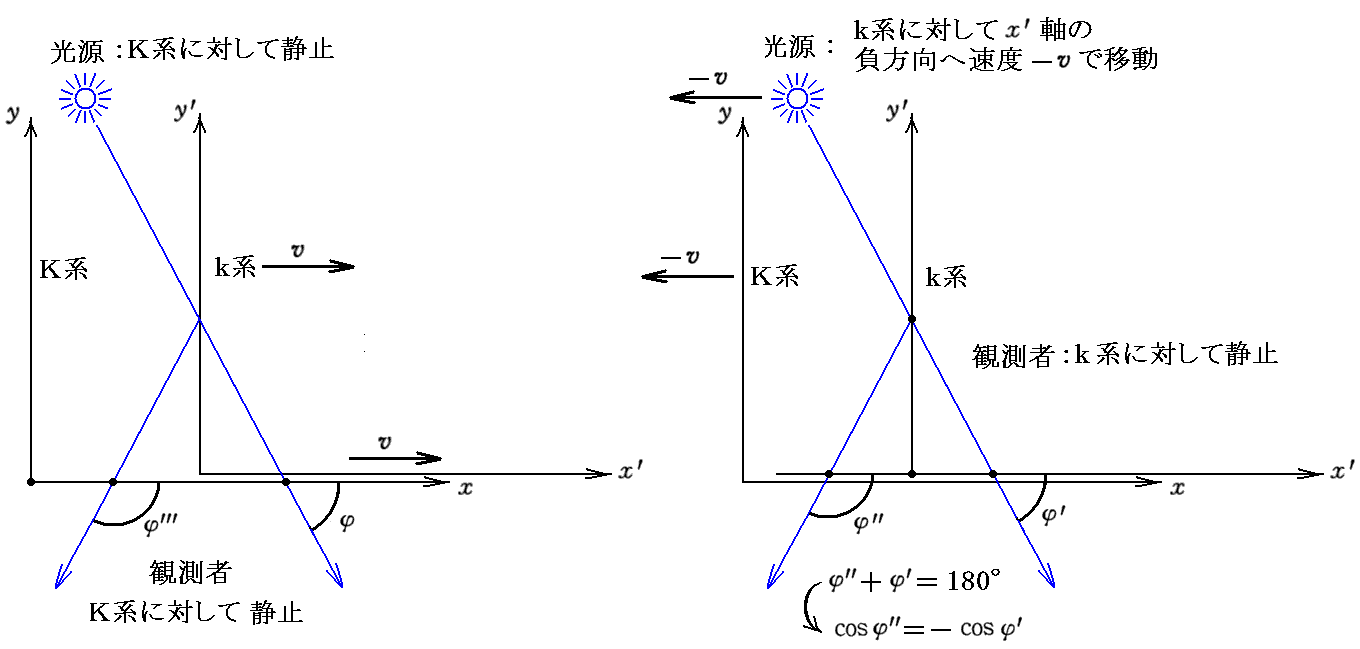
[静止系Kにおける入射光と反射光(AとA’”、φとφ’”、νとν’”)の関係式]を求めるためには、[補足説明1]であらかじめ求めておいた[k系からK系への変換式]の A,φ,ν を A’”,φ’”,ν’” へ、 A’,φ’,ν’ を A”,φ”,ν” へ置き換えた式から出発すれば良い。
下記左端の式がそれですが、この関係式を、[k系での入射波と反射波の関係式]と、最初に求めた[K系からk系への変換式]を用いて変形すれば良い。そうすると
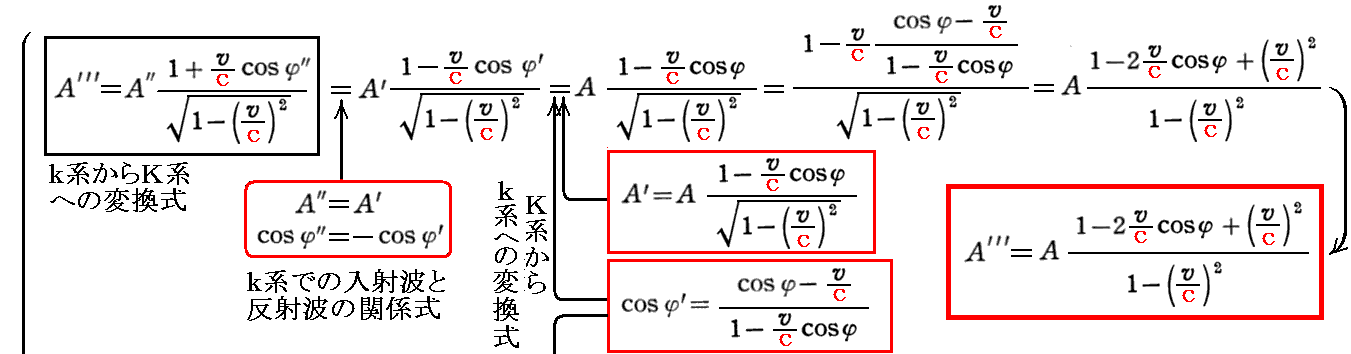
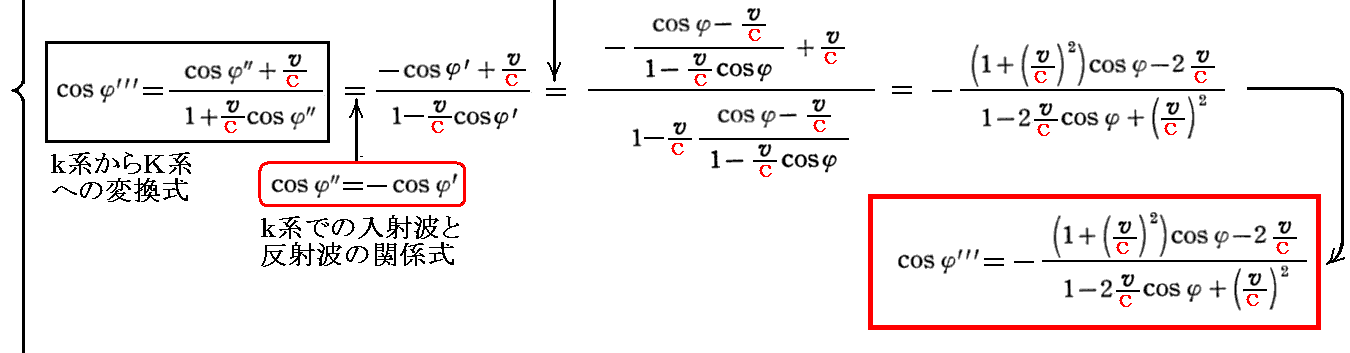
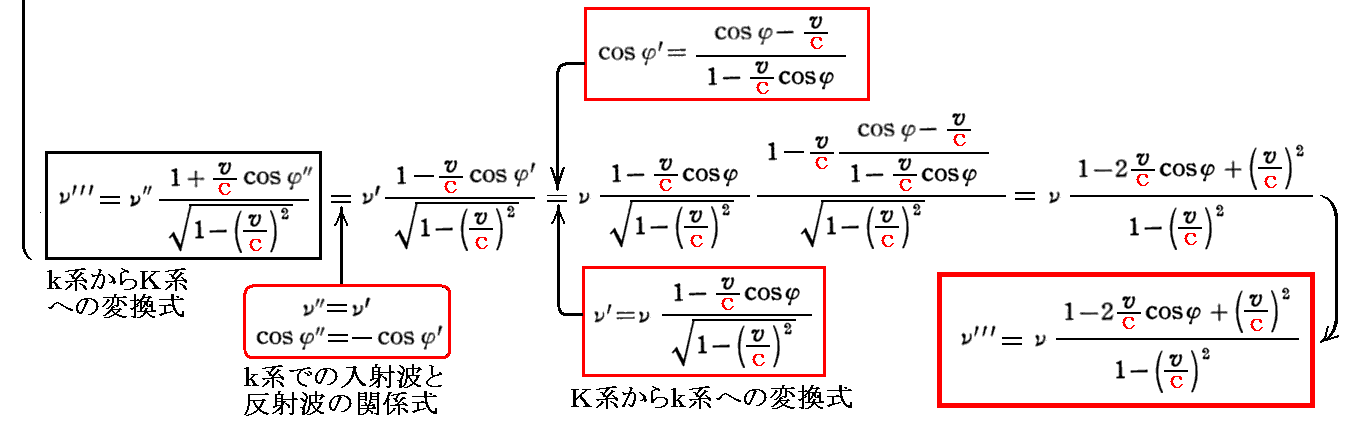
が得られる。
すなわち、K系で見たときの入射光の値(A’”,φ’”,ν’”)と、K系から見て動いている鏡で反射された後の反射光の値(A,φ,ν)との関係
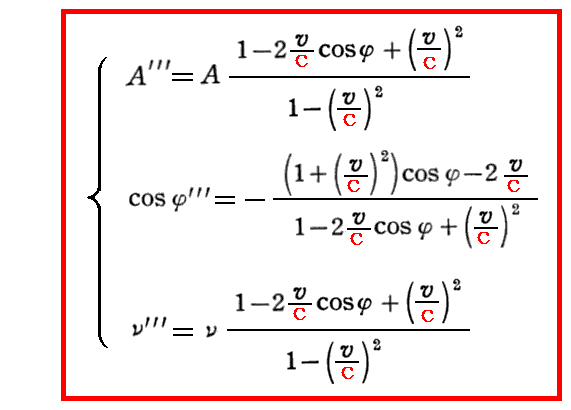
が得られる。蛇足ですが、上記三式を3変数 A,cosφ,ν の三元連立方程式と見なして解くと
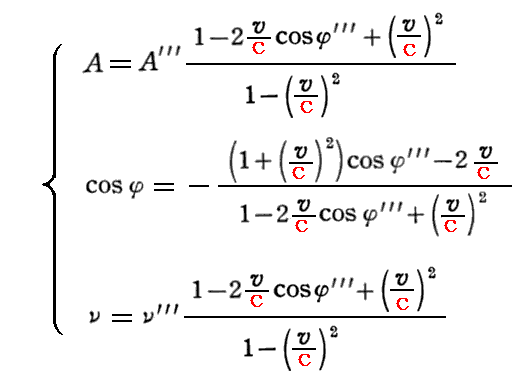
の様に元の式と全く同じ関係式が得られます。これは当然といえば当然なのですが、ここの議論の正当性を保証しているとも言えます。
これらの関係式の中で振動数の変換式については、“非相対論的”な関係式を別稿「ウィーンの変位則」3.(1)ですでに求めています。そこの関係式が“相対論的”な関係式の(v/c)2項を省略した形であることに注意されたし。
アインシュシタインは淡々と説明していますが、ここの 「動く完全反射鏡による光の反射」 と 「動く鏡に及ぼす光の圧力」 は、当時の物理学にとって極めて重要な問題であった“輻射の熱力学”に関係しています。相対性理論はそれに対して完璧な解答を与えた。
[補足説明3]
最後に、本文中の入射光と反射光のエネルギー差を計算する。
[補足説明2]の最初に注意した入射角φと反射角φ’”の違いを考慮すると
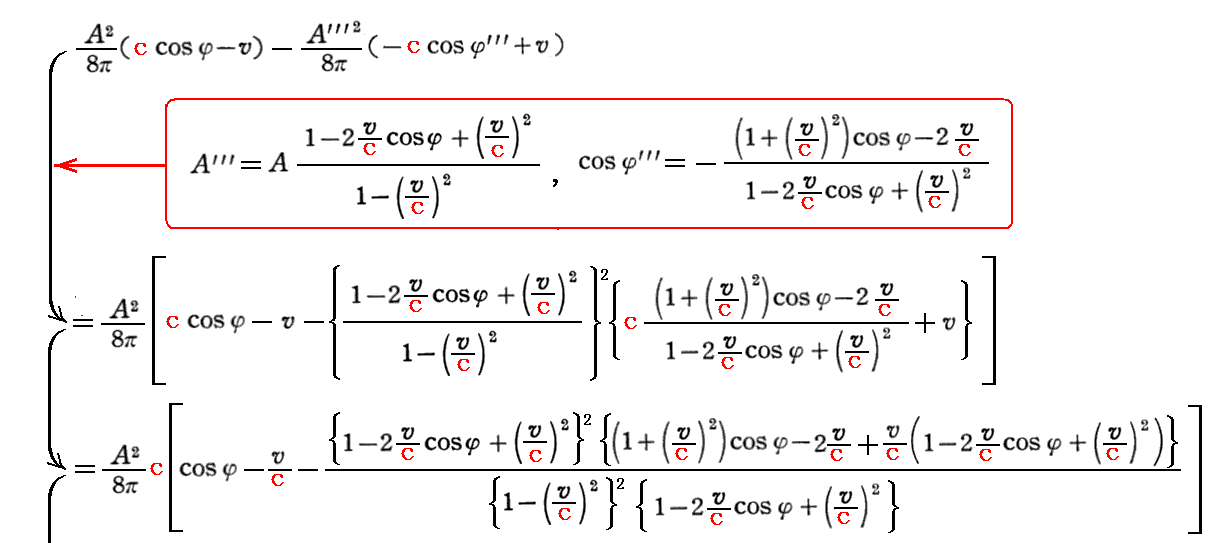
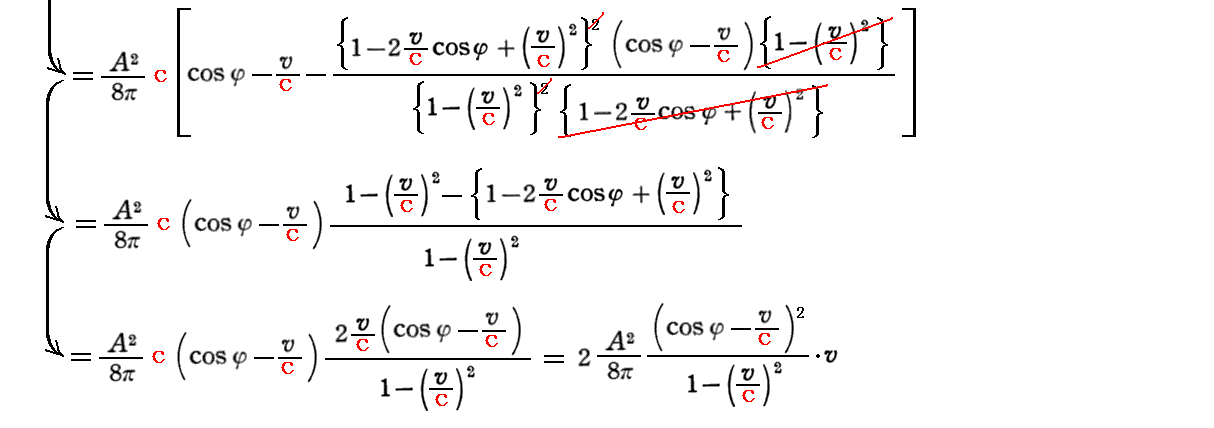
となる。
これは、エネルギー原理によれば、“光の圧力”Pが鏡に対して“単位時間にする仕事”P・vに等しい。そのため“光の圧力”として

が得られる。
v≪c で鏡が静止している(つまりv=0)の場合に成り立つ式(ただしMKSA有理化単位系表現)は別稿「光の圧力」1.(4)3.ですでに求めているので参照されたし。そこの結論と完全に一致します。
[補足説明4]
ここでの議論の本質は以下の事柄にあります。
鏡と供に運動する系で反射の現象を観測すると入射光と反射光の関係は
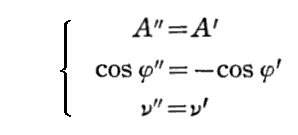
でした。そのため入射光と反射光との間にエネルギーの変化はない。またそのとき鏡も動いていないので鏡に対して成される仕事P・vはゼロです。仕事はゼロですが、圧力Pは働きます。実際、上記のエネルギー差を表す式に於いてv→0となっても、圧力を表す項が0になるわけではないことに注意して下さい。v→0のときの圧力は古典論の非相対論的議論における値と一致します。
また、普通の粒子が(動く)反射壁にぶつかって反射される場合には、速度の大きさは変化します(別稿「断熱膨張の気体分子運動論」を参照)。しかし、光が動く鏡にぶつかって反射される場合には相対性原理により反射光もまた光速度cで進みます。相対性理論では、光のエネルギーが変化するのは光速度が変化するのではなくて振幅と振動数が変化することで変化します。真に正しい相対性理論では上記の様な議論をしなければならないと言うことです。
非相対性理論による議論では、鏡の中の電荷と入射電磁波との相互作用から圧力が導き出された。そのとき別稿「光の圧力」2.(5)3.[補足説明2]や「シュテファン・ボルツマンの法則」2.(5)の様な説明が必要だった。しかし、相対性理論ではその様な不明瞭さは一切ない。極めて明快であることに驚嘆します。
[補足説明5]
最後の赤波線アンダーラインの部分は、“前書き”で述べられている『・・・“光を伝える媒質”に対する地球の相対的な速度を確かめようしとして、結局は失敗に終わったいくつかの実験・・・』や、マイケル・モーリーの実験や、熱輻射論、等々・・・を含めた対処法を述べているのですが、あまりにもあっさりとした説明なので、具体的にどこまで見通しているのか測りかねます。
いずれにしても、Einsteinは本節で得られた結論が最も重要だと考えていたのでしょう。この論文のタイトルを「運動物体の電気力学について」としているのですから。
§6.で真空に対するMaxwell-Hertz方程式のローレンツ変換不変性を論じたのですが、§9.では電荷や電流の存在するMaxwell-Hertz方程式のローレンツ変換不変性を論じます。
その考察過程で、Einsteinは電荷の持つ電気量という属性がローレンツ変換不変であることを発見します。粒子の持つ質量という属性はローレンツ変換不変ではないのですから、両者の違いはEinsteinにとって驚愕の事実だったでしょう。
ここも、極めて簡潔に記されていますので、解読するのは大変です。
(4)原論文 §9.電荷の不変性
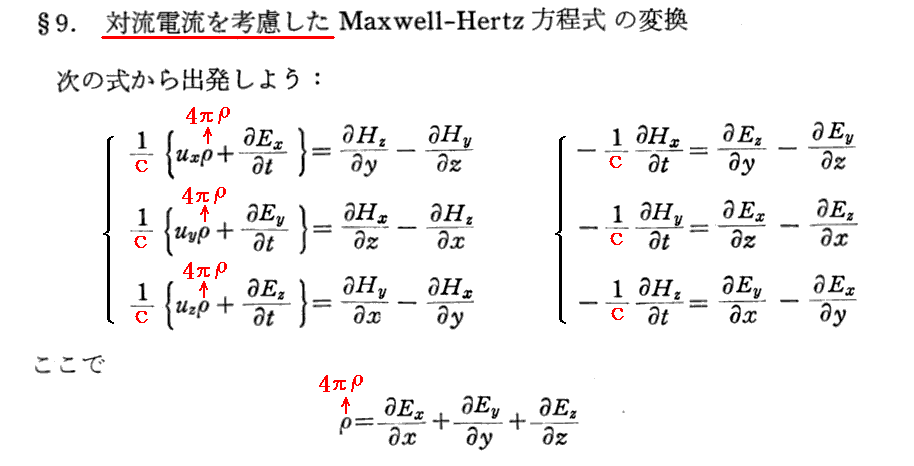

[補足説明1]
上記赤波線部分の説明は解りにくいので補足します。
アインシュタインが影響を受けたと様々な機会(あるいはPais文献6のp146)にのべているローレンツの1895年の冊子は有理化されたGauss単位系で記述されています。しかし、本論文は普通の(有理化されていない)Gauss単位系で記されていますのでdivE=4πρとなります。そのため上記の説明を付け加えている。ここは3.[補足説明]と、別稿「電磁気学の単位系が難しい理由」5.(4)1.などを復習されて下さい。
ここは混乱しやすいところなので、以後は4πを付け加えた普通の表記に変換して(つまりアインシュタイン論文中のρを4πρで置きかえて)説明します。
ついでに補足しますと、この時代は動電気学や電気工学の発展に伴い電磁気学単位系の主流は、“静電単位系”から“電磁単位系”に置き換わった時代です。実際、当時の実験物理学の論文のほとんどは電磁単位系を用いて書かれています。
そのなのにアインシュタインがローレンツの流れを汲んだ“Gauss単位系”を用いたのは、それなりに深い意味があるのでしょう。それにしても26歳のアインシュタインは電磁気学およびその単位系について完璧に理解していたようですね。
さらに、上記赤二重線部分は、次の文節の最後で背景を薄赤着色している記述に関係します。
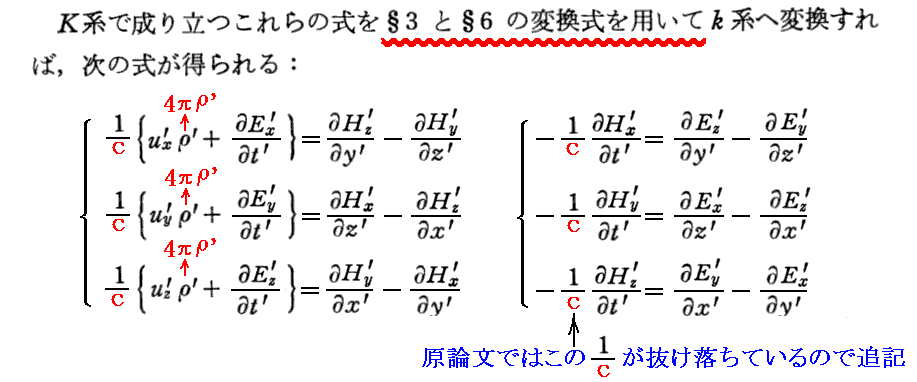
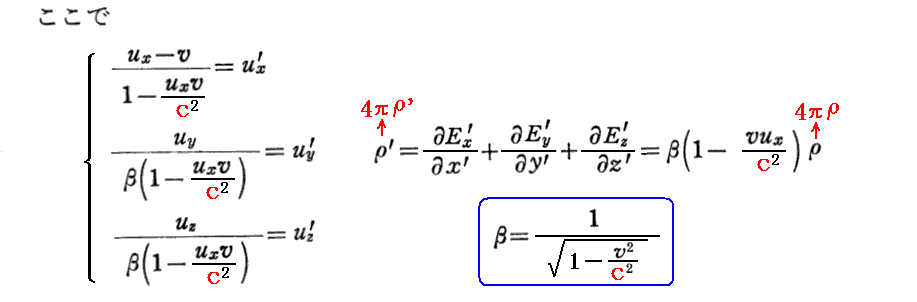


[補足説明2]
ここで取り上げている対流電流を考慮したMaxwell-Hertz方程式のローレンツ変換不変性の証明は結構込み入っています。
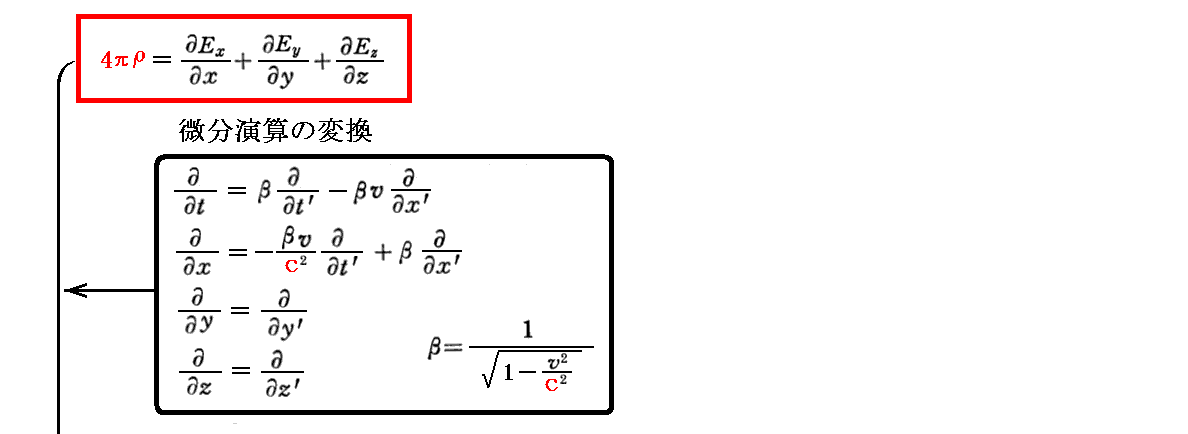
以下で順番に説明しますが、Einsteinが文中で述べている§3.の変換式とは“ローレンツ変換式”のことです。また、§6.の変換式とはローレンツ変換を用いて得られる3.(1)[補足説明1]の“微分演算変換式”と§6.の最後で導く“電磁場の共変変換式”のことです。
最初に “4πρ=divE” の変換式を求める。
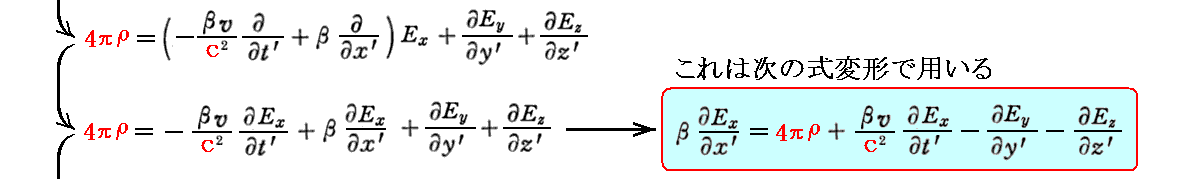

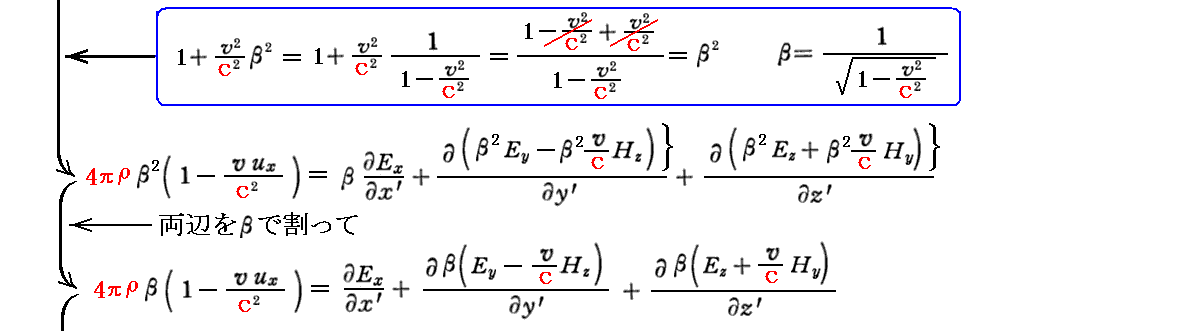

次に “マックスウェルが拡張したアンペールの法則” の変換式を求める。


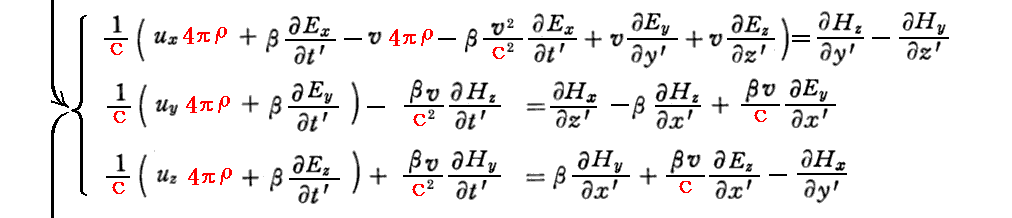



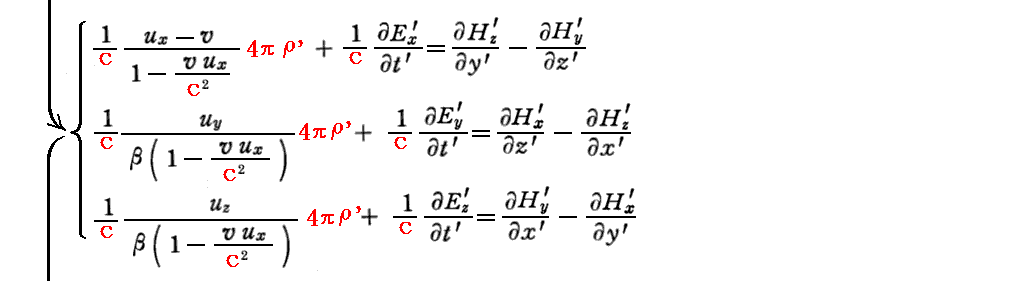
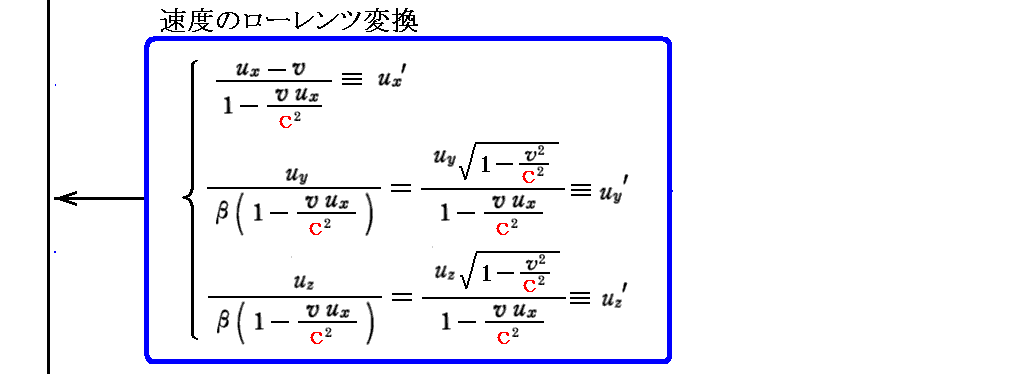
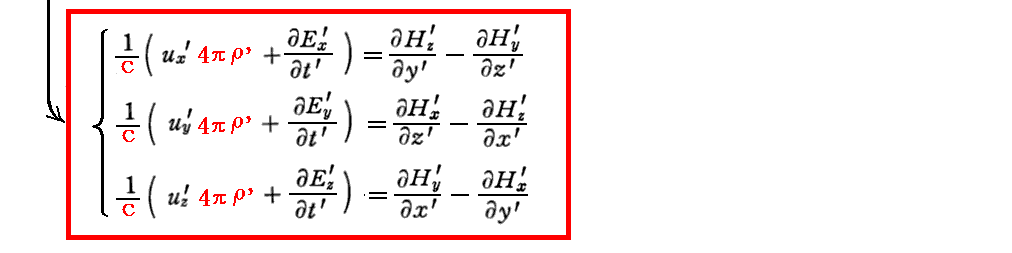
変換式を求めるのに必要な式が互いに錯綜しています。こちらの一覧表示でご確認下さい。
結局、運動系kにおいて電荷密度ρ’であるものを静止系Kからみると
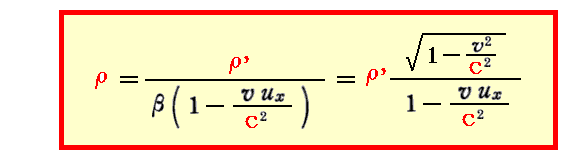
の様に見えるとすれば、電荷、電流が存在する場合のMaxwell-Hertz方程式も、ローレンツ変換に対して不変であることが証明できたことになる。
この式の意味は非常に解りにくいが、長さや時間や速度(2.(8)3.[補足説明2])といった物理量測定と同様に考えればよい。このとき、K系に対するk系の運動方向vに対して電荷の運動方向uはまったく独立に任意の方向を向いていて良いことに注意して下さい。その場合でも速度uに対してローレンツ変換を施せば、“電流密度”(ρu)を含むMaxwell-Hertz方程式がローレンツ変換に対して不変であることが導けるのです。
“電流密度ベクトル(jx,jy,jz)”と“電荷密度ρ”がローレンツ変換によってどのように変換されるかは、別稿「相対論的力学」3.(5)で説明していますので参照されてください。そこで明らかになるように、これらは“位置ベクトル(x,y,z)”と“時間t”を合わせた4元量のローレンツ変換式とまったく同じ形で変換されます。
実際、上記の結論は
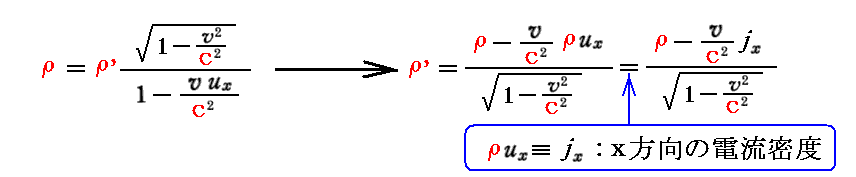
となりますが、“電荷密度”は“電流密度ベクトル”と一緒になって4元量を構成します。
つまり、電流密度ベクトルは、速度のローレンツ変換を用いると
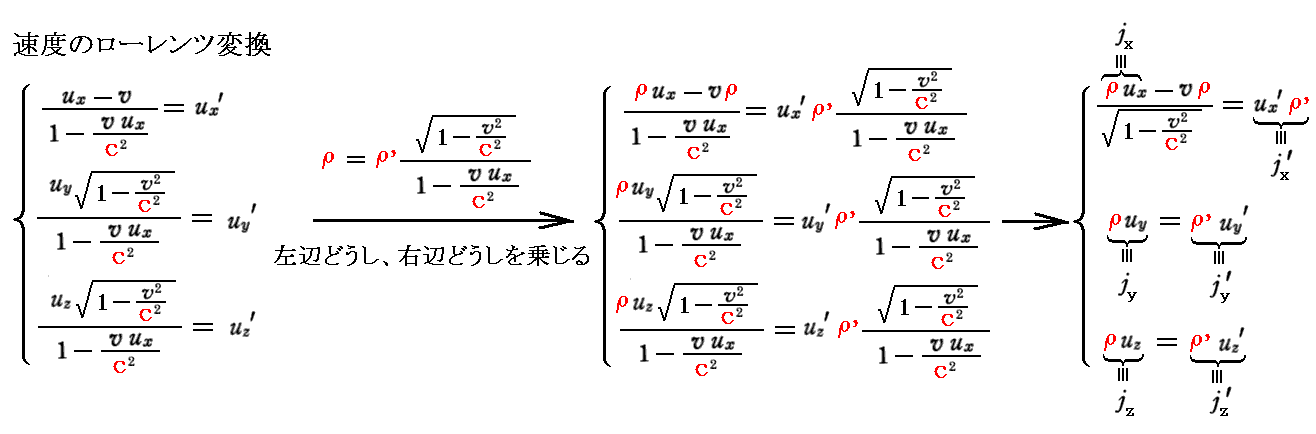
の様に変形できるが、これは[電荷の不変性](これは[補足説明5]で説明)と[相対論的運動学]から導かれる[電流密度・電荷密度]4元量のローレンツ変換公式そのままです。
上記の結論は[Maxewll方程式のローレンツ変換不変性から導かれた]ものですが、このことからも“電荷の不変性”は相対性理論から導かれる必然の結果であると言える。
ここで注意して欲しいことは、[電荷不変の原理]はアインシュタインによって[光速不変の原理」と[自然法則の相対性原理]の二つの原理から導かれたのですが、[電荷不変の原理]は、その後のあらゆる実験・観察によって正しいことが確認されています。だからこれは、[光速不変の原理」と[相対性原理]という二つの原理と並び立つ第三番目の原理と言っても良い。
[光速不変の原理」が実験・観測事実から原理として採用されたのと同様に、[電荷不変の原理]を実験・観測事実からの原理として採用すれば、[電荷不変の原理]と[相対論的運動学]から電流密度・電荷密度のローレンツ変換則は簡単に導かれます。
このとき、くれぐれも“電荷”と“電荷密度”を混同しないで下さい。電荷はどの様な慣性系から見ても不変ですが、電荷密度は慣性系が変われば、電流密度と共に変化します。それは慣性系が変われば距離が変わり体積要素が変化しますし、速度ベクトルも変化するからです。
[補足説明3]
まったく同様に “0=divH”のローレンツ変換不変性が導けます。

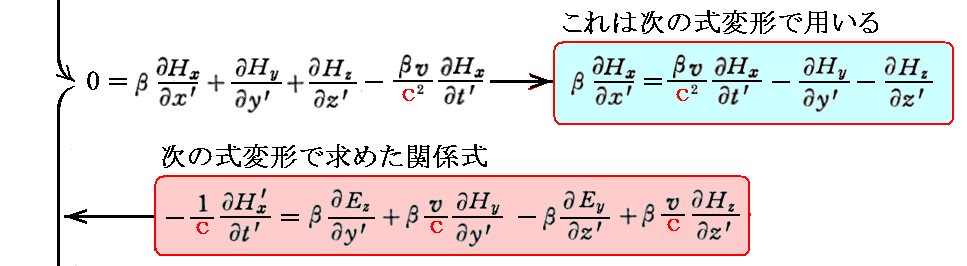
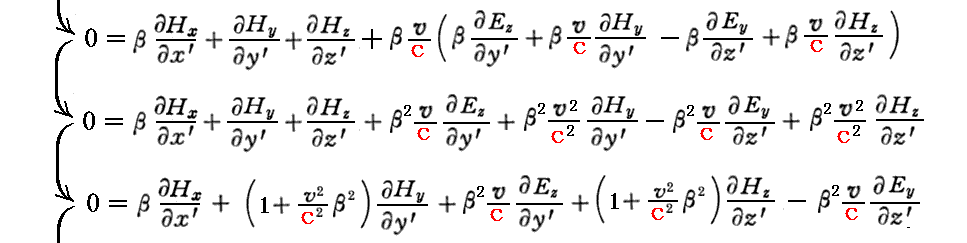
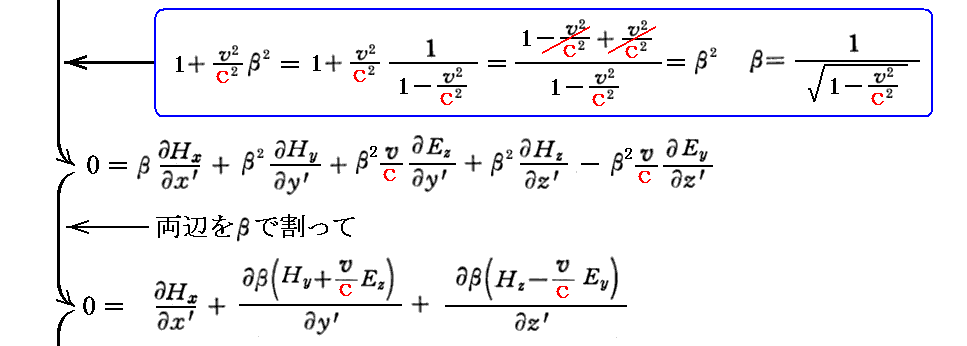
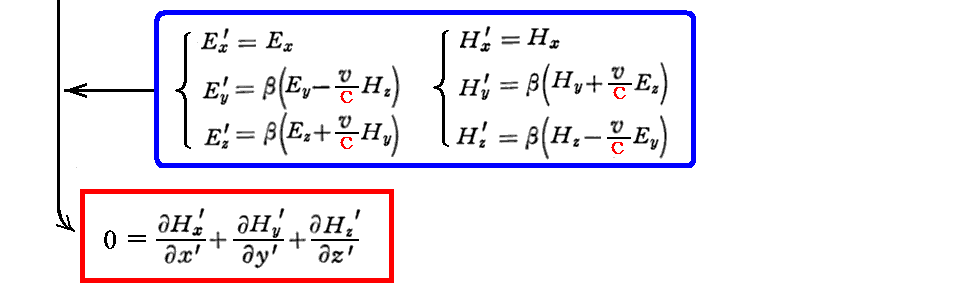
さらに “ファラデーの電磁誘導の法則”のローレンツ変換不変性の証明は以下の通りです。
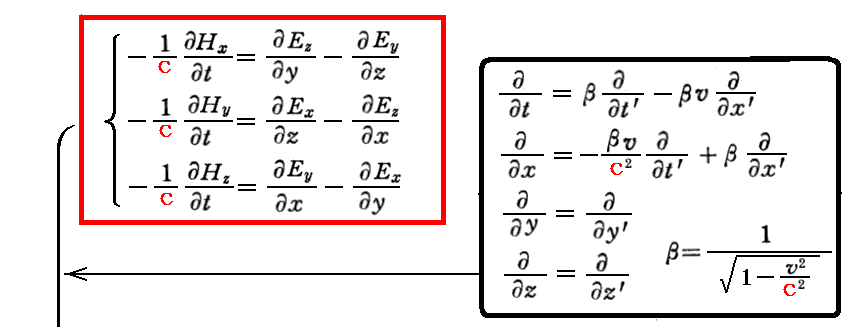

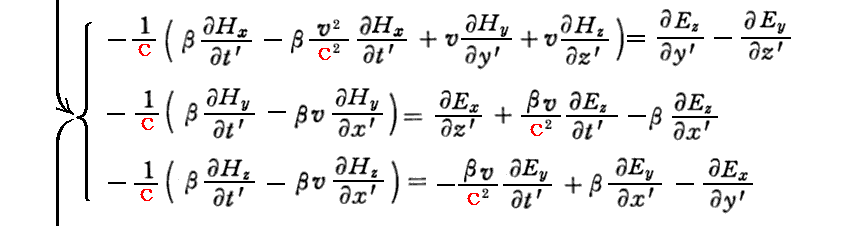
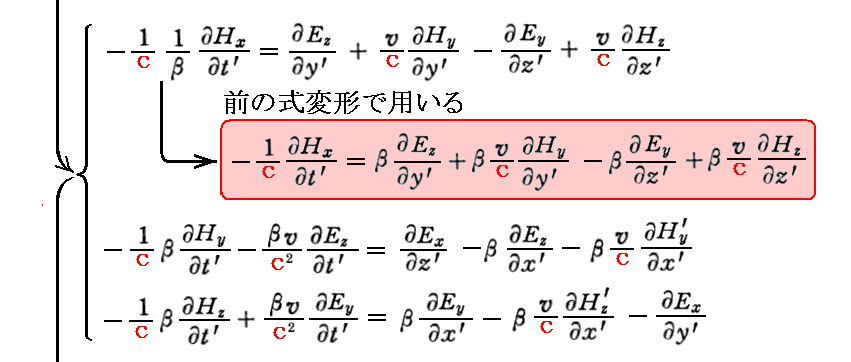


証明に必要な式の互いの依存関係についてはこちらの一覧表示でご確認下さい。
[補足説明4]
別稿「マクスウェルによるアンペールの法則の拡張」(2)で説明した様に、Maxwell方程式(アンペールの法則とガウスの法則)から“電荷の保存則”が導ける。
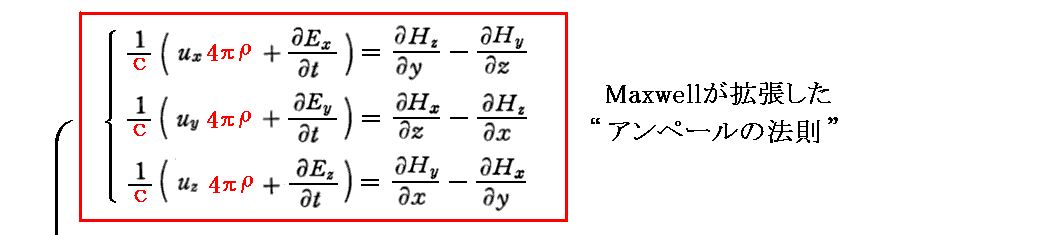



別稿「Maxwell方程式系の先見性と電磁ポテンシャル」5.(2)[補足説明4]に於いて、上記の式変形を相対論的にもう少し見通しの良い形で行っていますのでどうぞご覧下さい。
このとき、[補足説明2]で求めた“電荷密度”の共変関係式を用いれば“電荷の保存則”もローレンツ変換不変であることが確認できる。
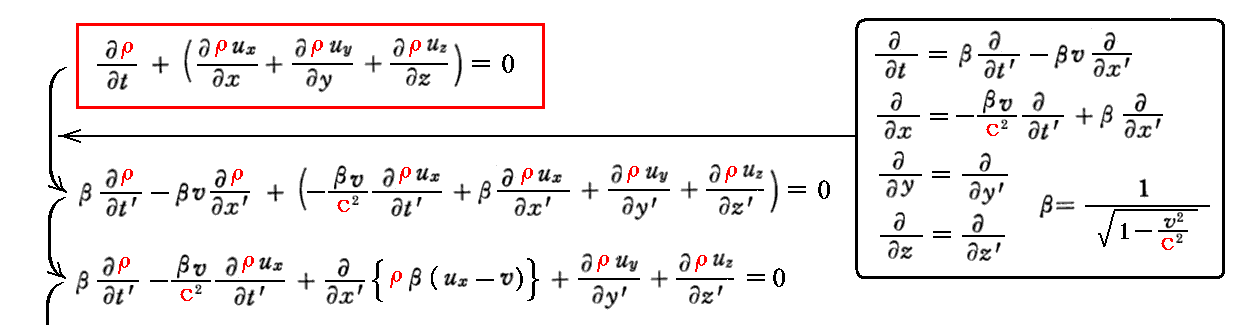
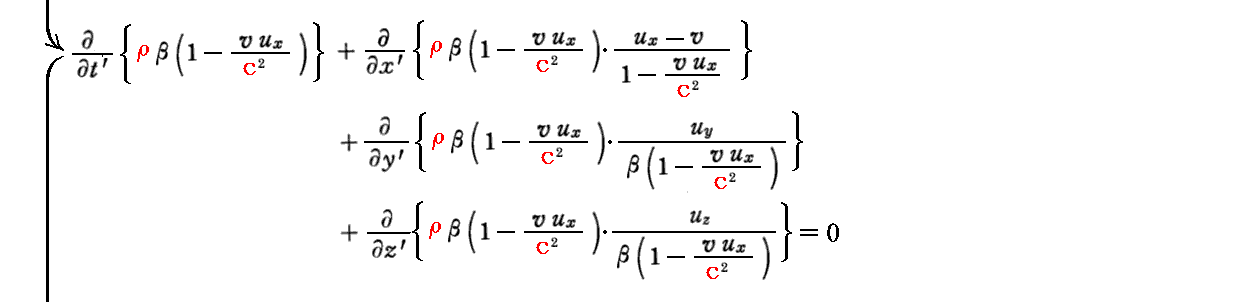
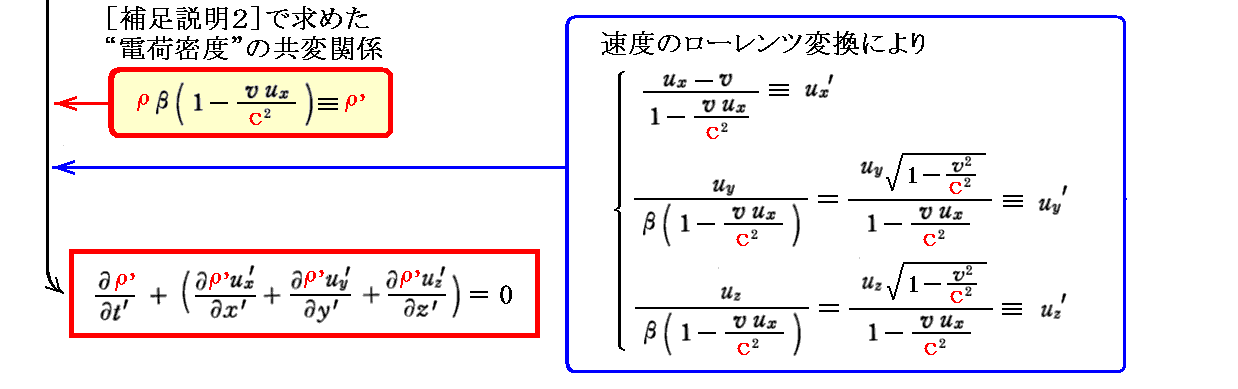
この事を逆に解釈すれば、“電荷の保存則”がローレンツ変換不変でなければならない事から“電荷密度”の共変関係式が導けるということです。このとき、[補足説明2]では“Maxwell方程式”のローレンツ変換不変性より“電荷密度”の共変関係式を導いたことを思い出されたし。
このことをもっと一般的に言えば、“電荷の保存則”が電荷密度と電流密度ベクトルが一緒になって“4元電流密度”を構成することと表裏一体の関係である事を示しています。このことについては、別稿「4元速度(4元運動量、4元電流密度)、4元加速度と4元力」3.(2)[補足説明4]を参照されたし。
[補足説明5]
アインシュタインが段落の最後の文節で述べている“電荷の不変性”について補足する。
ここの訳文は解りにくいのですが、アインシュタインはここで、“電荷密度は長さや質量と同様にローレンツ変換不変ではないが、電荷自体(任意の物体が持つ電気量)はローレンツ変換不変量で静止していても動いていても変化しない。”と言っています。
いつものように静止系Kに対して、そのx軸方向に速度vで移動する移動系kを考える。k系の原点に静止して存在する半径rの球

が持つ電気量は

となる。
一方、この球を静止系Kから見ると、(2.(6)1.で説明したように)中心(vt,0,0)がx軸上を速度vで運動する楕円体
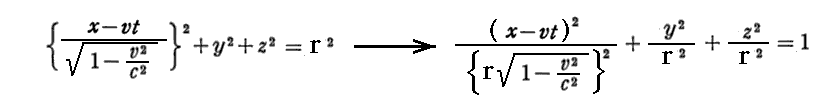
となる。この楕円体の体積が
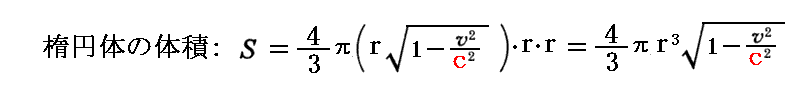
であることと、K系における電荷密度がρであることを考慮すると、この楕円体の持つ電気量は

となる。このときK系に対して帯電した楕円体は速度vで動いていることに注意されたし。
[補足説明1]で説明したuxがvと等しい特別な場合を考えると、前述の電荷密度の変換式は

となる。特に右側の式は、静止しているときの電荷密度がρ’の帯電物質が速度vで移動すると、電荷密度がρ(すなわちρ’の(1-v2/c2)-0.5倍)に増大したように見える事を意味する。
ところで帯電物質の体積は運動すると、静止したときに比べて(1-v2/c2)0.5倍に縮んだように見えるのでしたから、この両方の効果を考慮すると、最初静止していた時に持っていた帯電物質の全電気量は、それが動いても同一の電気量を保持することになる。すなわち
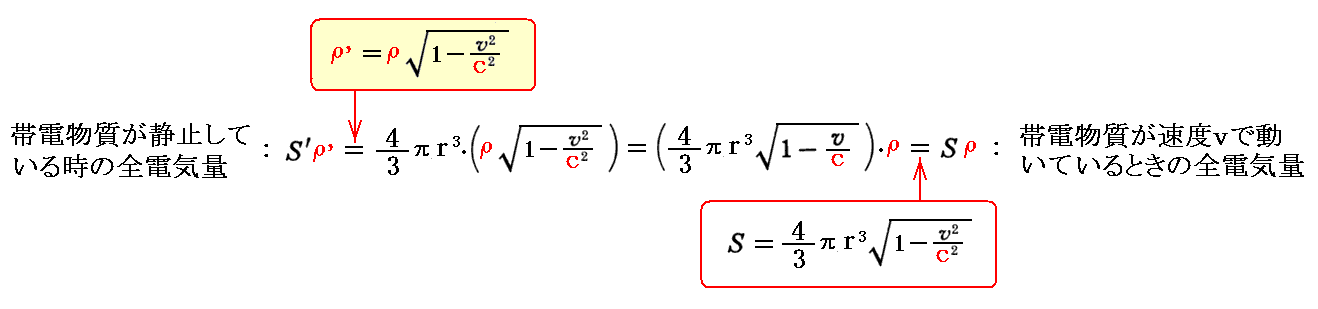
電荷とともに運動する座標系kから見て電荷の電気量が不変ならば、静止系Kから見て電荷の電気量は常に一定である。これは静止系Kで任意の速度で運動する電荷の電気量が運動速度に依存して変化することは無いことを言っている。
後で解る様に物体(質点)が持つ“質量”という物理量は運動すると増大することが解りますが、物体(質点)が持つ“電気量”という物理量にはその様な変化は生じないという極めて重要な性質を導いたことになる。
[補足説明6]
上記の結論は重要です。これは『電子や陽子などの荷電粒子が持つ“電荷(電気量)という属性”はそれらの運動状態が変化しても不変である。』ことを意味します。これは後で説明する『電子や陽子などの粒子が持つ“質量という属性”は運動状態によって変化する。』とは異なっています。
そのとき、質量が運動状態によって変化することが多くの実験・観察によって検証されていると同様に、電荷が不変量であるということも多くの実験・観察から検証されています。この検証実験については文献406.「力学」p445の説明や、文献304.Purcell著「バークレー物理学コース2 電磁気学(上巻)」§5.3“動いている電荷の測定”、§5.4“電荷の不変性”の説明をご覧下さい。
アインシュタインは『電子や陽子などの様々な荷電粒子の持つ電荷はローレンツ変換不変である。』を、対流電流を考慮したMaxwell方程式のローレンツ変換不変性から導いたのですが、これは3.(3)1.[補足説明4]で説明したように、『“プランクの作用量子h”が不変量である。』が相対性理論から導けるのと同様に相対性理論の整合性が確認できる極めて重要な結論です。
電子や陽子などの荷電粒子が分布する物質の体積要素、あるいは存在する空間領域が荷電粒子と共に動くと、相対性理論により、その体積は縮小します。そのとき電子や陽子などの様々な荷電粒子の持つ電荷がローレンツ変換不変であるということは、その体積要素における電荷密度は体積の減少に逆比例して増加する事を意味します。[補足説明2]の最後で注意した事や[補足説明5]はそのことを言っています。
また、電荷がローレンツ変換に対して不変である事は、荷電粒子が発生する電場を異なった座標系で観測するとどのように変化するかという、電磁場のローレンツ変換に対する共変関係を規定します。
つまり、電荷のローレンツ変換不変性を用いれば、3.(1)で導いた
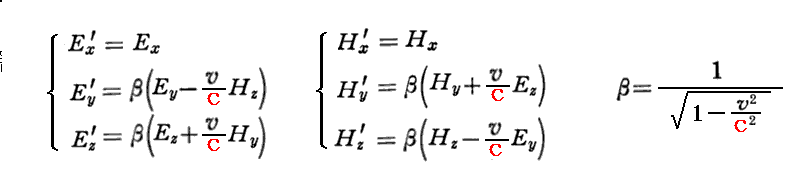
が逆に導けるのです。その当たりについて文献304.Purcell著「バークレー物理学コース2 電磁気学(上巻)」§5.5“異なった座標系において測定される電場”、§5.6“一定速度で動いている点電荷の場”の説明はとても教訓的ですのでご覧下さい。このことは、別稿「電磁場の相対性」で解りやすく説明していますので参照してください。
最後にもう一度強調しますが、上記の話は“電荷”がローレンツ変換に対して不変であることを言っているのであって、“電荷密度”や“電流密度”についてではないことに注意してください。このことについては別稿「相対論的力学」3.(5)を是非参照されたし。
§10.でいよいよ電子の相対論的運動方程式(すなわちローレンツ変換不変な運動方程式)が導かれます。
ここでEinsteinが展開している(古典的方程式から相対論的方程式を見つけるための)手法は独創的なもので、後のすべての教科書の説明で踏襲されています。
ただし、Einsteinが導いた方程式は、正しいにもかかわらず、この論文で唯一歯切れの悪い所です。後にPlanckによって改良される余地を残しています。
(5)原論文 §10.電子の力学



[補足説明1]
上記赤波線アンダーラインの注記は重要です。後で解るのですが、粒子の質量はその運動状態によって変化します。その可能性もあるので今はゆっくり動いている状況を考えている。
またその粒子に力が働くと加速されてその運動速度が大きくなります。その場合、電子がk系において静止し続けているという条件を満たさなくなります。だから静止しているという条件が成り立つごく最初の瞬間を考えている。
アインシュタインは、ここで相対論的な力学を論じようとしている。ニュートンの運動方程式はガリレオ変換に関して不変だが、ローレンツ変換に関して不変ではありません。そのとき、v≪cの場合にローレンツ変換がガリレオ変換に近づいた様に、、v≪cの場合には未知の真に正しい力学の運動方程式もニュートンの運動方程式となるであろう。そのためローレンツ変換不変となる運動方程式がどのようになるかを、質量(可秤量物体)が静止しているk系でのニュートンの運動方程式から出発してK系で、しかもv≪cの場合にどのようになるかを推測しようとしている。
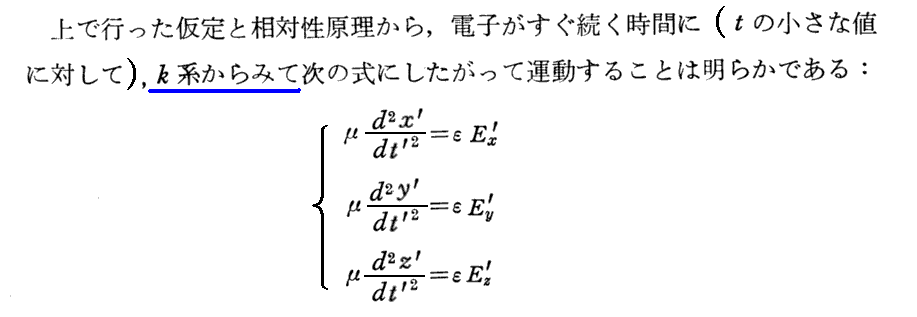


[補足説明2]
上記(A)式の導出を補足する。
まずローレンツ逆変換式より
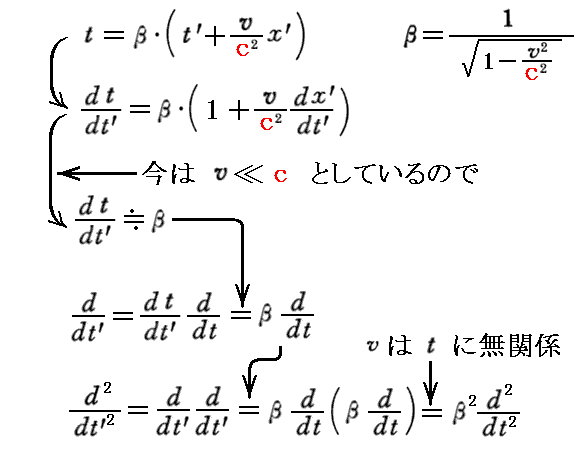
となる。
これらを用いると
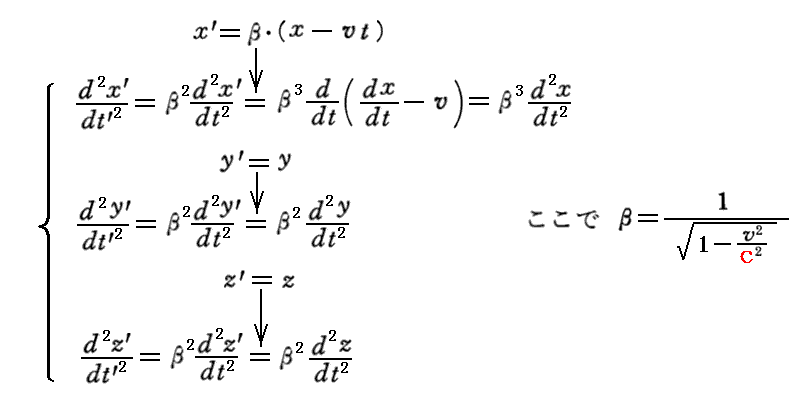
が言える。これと電磁場のローレンツ変換共変式を最初の式に適用すれば、本文の(A)式が得られる。

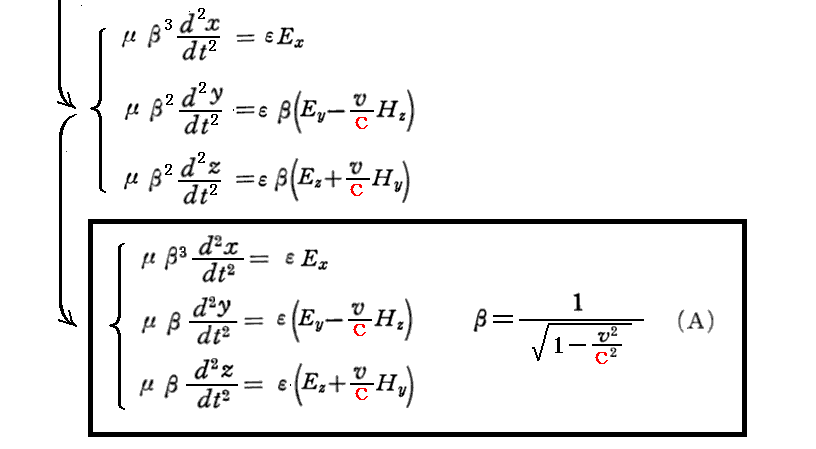
ただし、上記の(A)式は後で説明する[補足説明4]の内容を見越した形で記しています。上式はあくまで、x軸の正方向に速度vで動いている瞬間の質量μ、電荷εの電子に対する相対論的な運動方程式です。
右辺に磁場の存在に伴うローレンツ力の項が現れていますが、今はx軸方向の速度成分しかない時ですから、ローレンツ力を生じるのに必要な項のみが現れています。
[補足説明3]
§10.の本質は、如何にして、ローレンツ変換に対して不変な“相対性原理”を満たす運動方程式を導くかです。ここでEinsteinが説明している手法が本質であり、独創的なものです。
その独創的な考察で導いた(A)式は“相対性原理”を満たしており相対論的に正しい運動方程式です。今日のどの教科書もEinsteinの方法を踏襲しています。その当たりを説明している文献を幾つか引用しておきますのでご覧下さい。
江沢文献405.§4.4
内山文献103.補足説明[23.]
『放射能学および電子学年報』(1907年)の総説論文のⅢ.質点の力学(電子)これは、Einstein自身が少し改良したものです。
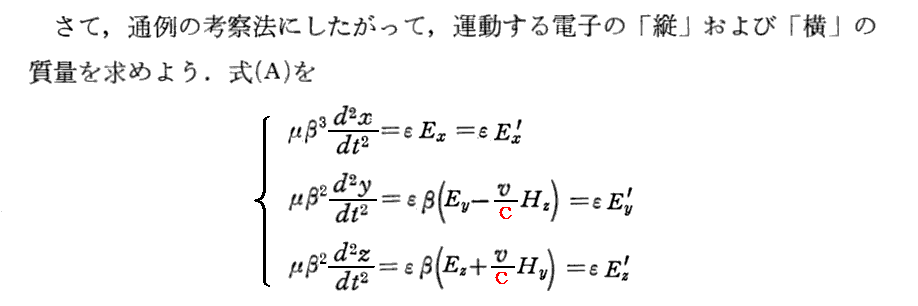



[補足説明4]
直前文の赤波線アンダーライン部分は重要です。先の部分は当時話題となっていた電子の電磁質量の速度変化に付いてのKaufmannの実験とその説明理論を意識しての注意だろう(広重文献509.p205)。また、次の部分で、これが一般の質量を持つ物体に対する相対論的な力学方程式を与えると注意している。
しかしここは、間違いではないのですが、この論文で唯一歯切れの悪い所です。電子に作用する力は運動系kで測定し、加速度は静止系Kで測定するという解りにくい説明をしています。つまり、力の定義が相対論的でないのです。本来のK系での力を用いるべきで、そうするとy、z成分の運動方程式の両辺のβが消去できて、左辺にβの一乗のみが残る。これが本来の式です。
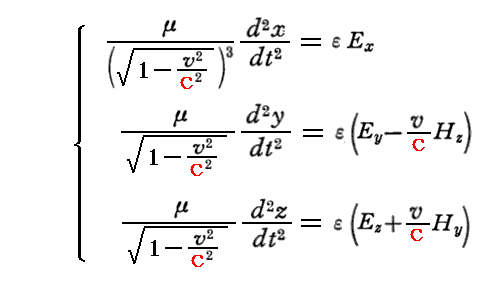
また、この論文の1913年再掲載版(Sommerfeld編集)の上記力の定義の所に『プランク(M.Planck)が最初指摘したように、このような力の定義は便利ではない。運動量とエネルギーの法則が最も簡単な形をとるように力を定義する方が適切である。』と“注記”されている。
この論文集はSommerfeldの提案で、アーヘン時代の同僚であるO.Blumenthalの骨折りで(1913年に)出版されたものです。この論文集の1905年Einstein論文には(別の編集人により後に繰り返し出版される相対性理論関係の論文集にも収録されることになる)“有名な注記”が数カ所に渡って成されています。
これらはかなり本質的な注記ですから、編集者が勝手に書き加えたものではなくて、おそらくSommerfeldの依頼を受けてEinstein自身が書き加えたものでしょう。Sommerfeldは他人の業績をとても尊重する人ですから、Sommerfeldが書き加えたのなら必ずその事を銘記したはずです。
文献507.に紹介されているSommerfeldとEinsteinの文通の様子などから推察するに、この論文集に収録する論文の選定についてもEinsteinは相談を受けたでしょう。
上記の“有名な注記”については、文献104.Ⅲ章末でスタチェルが説明していますので、別ページで引用しておきます。
論文集の再編集版に付け加えられた上記の注記の意味は解りにくいが、要するに力の定義を本文のようではなくて、Planckが指摘した様に

と定義した方が適切であったと言っている。
こうすると相対論的(つまりローレンツ変換に対して不変)な力学運動方程式は、今日的な表現である
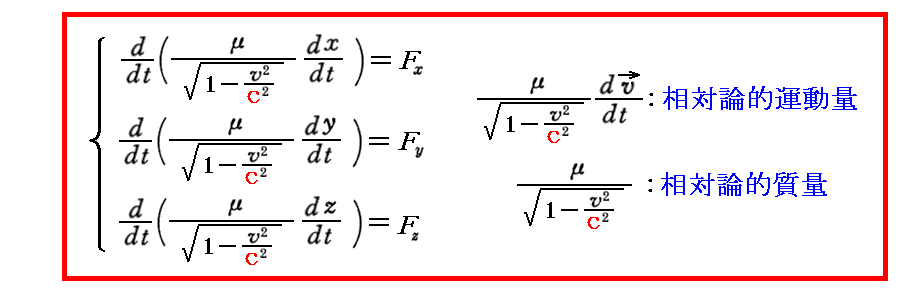
という形になる。この導出はPlanckの1906年3月論文あるいは、Einsteinが1907年12月に『放射能学および電子学年報』に寄せた総説論文のⅢ.質点の力学(電子)をご覧下さい。
このときv≪cの場合には
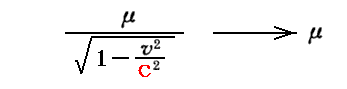
となり、μは定数だから、時間微分の前に出せて古典的なニュートンの運動方程式
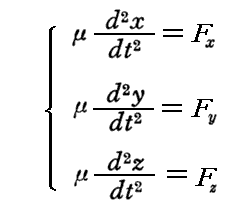
に移行し、上記の相対論的な運動方程式が自然な拡張となっていることが解る。
このように、運動量pを用いて運動方程式を表現すれば、上記の様に定義される“相対論的質量”が運動方程式中において方向によって変化することはない。
つまり、これをさらに時間微分を実施して
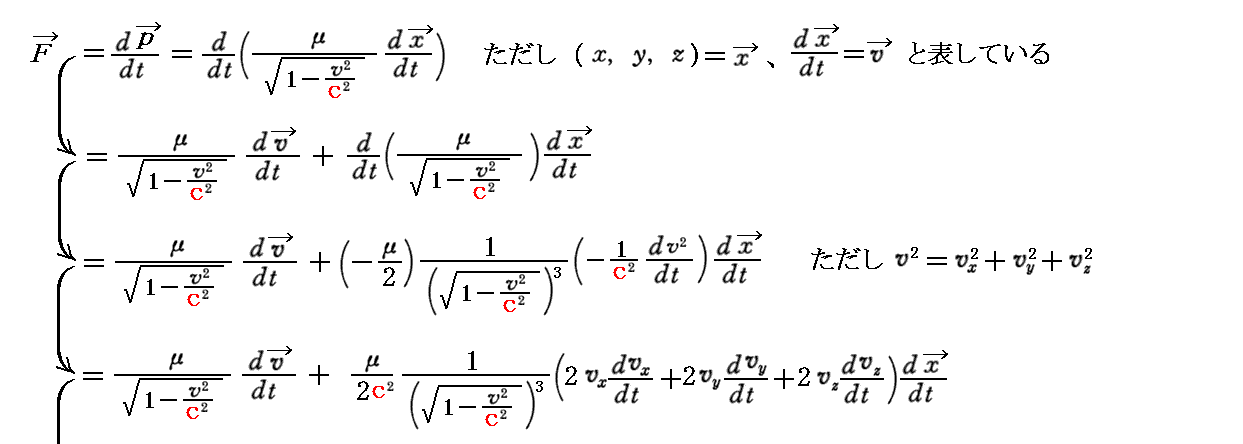
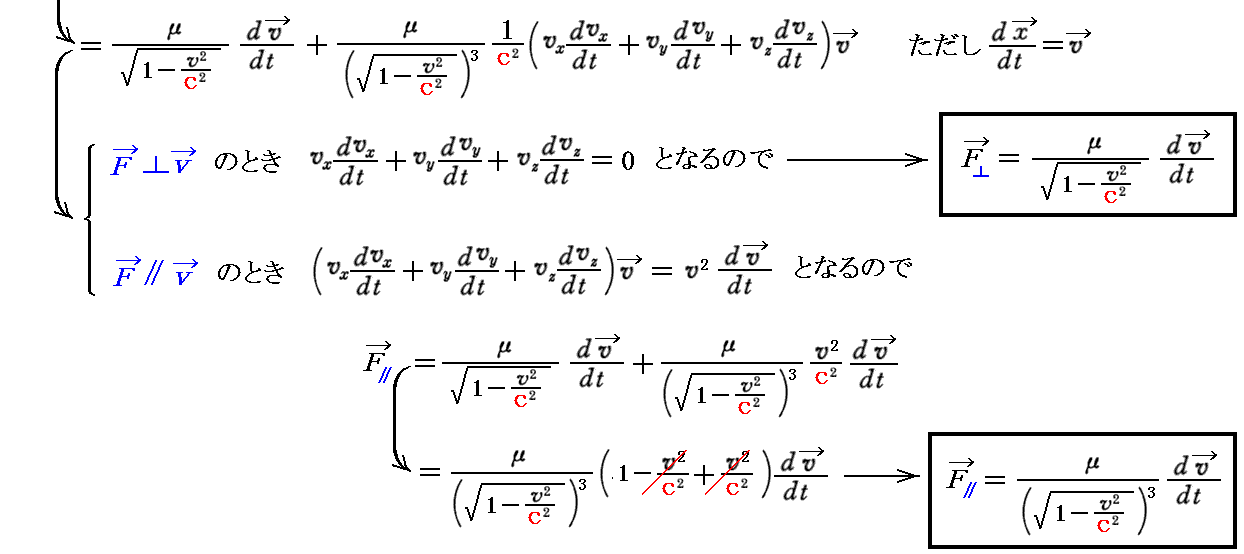
のように変形して、無理に古い形のニュートンの運動方程式に対応させようとするから、“縦質量”と“横質量”の違いが生じてくるのであって、“運動量の時間変化が力に比例する”という新しい表現のままで置いておけば、その様な不条理は無くなる。
やがて解りますが、相対論的運動量と相対論的質量は一緒になって、ローレンツ変換によって変換される相対論的4元運動量ベクトル(px,py,pz,E/c2)を構成します。
このことに付いては別稿「相対論的力学」3.(4)や、別稿「4元速度、4元加速度と4元力」3.(1)で説明します。
[補足説明5]
相対論的な運動方程式の完全な形を求めたのはM.Planckです。Planckは、1906年3月の論文で、上記の[補足説明4]の趣旨にそった修正をして、さらに得られた方程式がLagrange形式で書ける事を示して、相対論的な力学方程式の正しさを基礎付けた。
詳細については、別稿「相対論的力学」2.で引用・解説しているPlanck論文「相対性原理と力学の基本方程式」をご覧下さい。
また、今日の多くの教科書で説明されている、運動量保存の法則から相対論的運動方程式を導く方法は、N.LewisとC.Tolmanの論文「相対性原理と非Newton力学」(1909年)で示された。これについても別稿「相対論的力学」3.をご覧下さい。

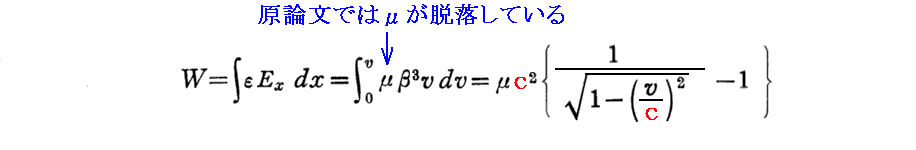

[補足説明6]
上記の積分を補足する。
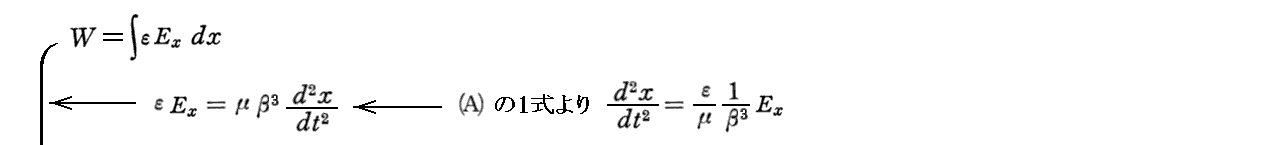
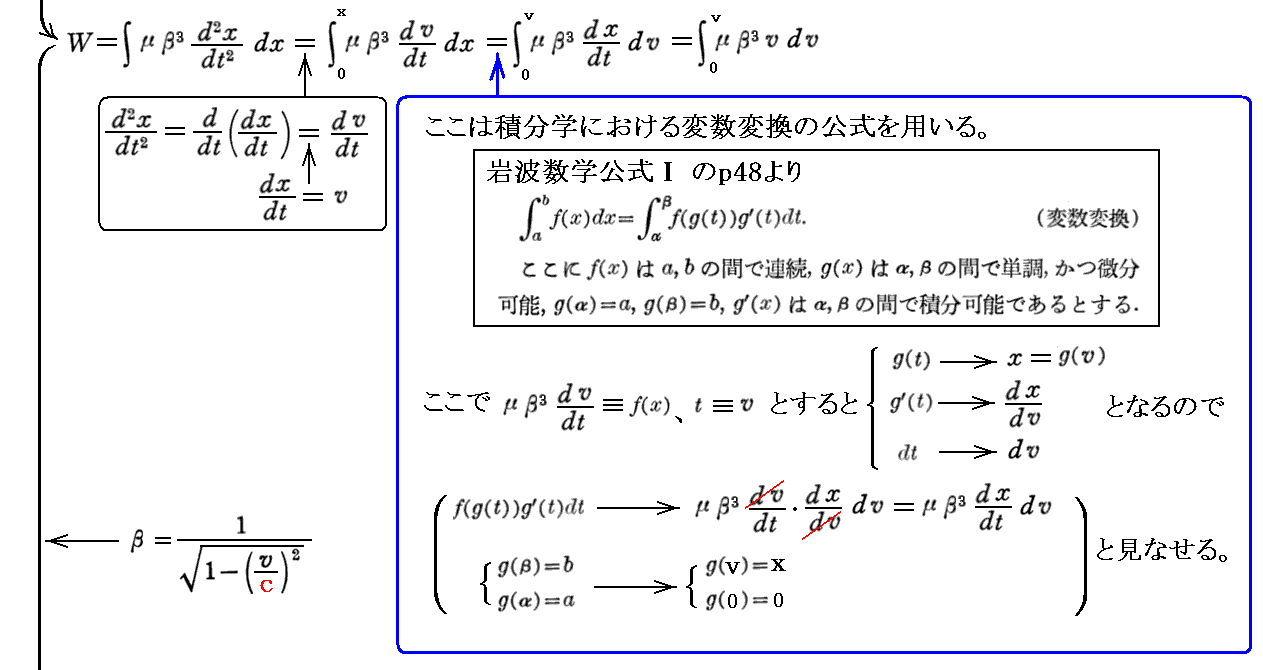
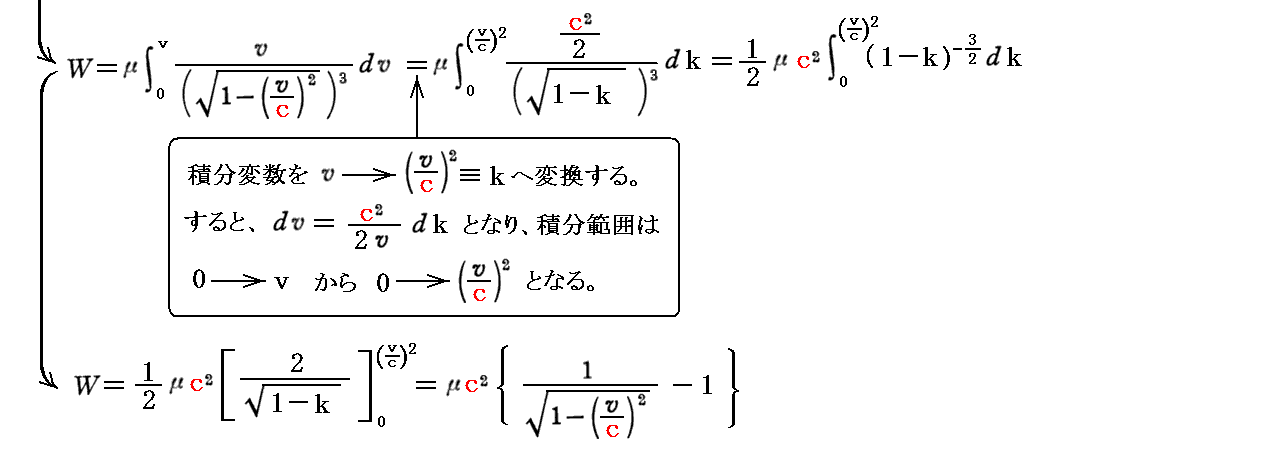
この式のWは静電気力の場が電子に与えた仕事ですから、電子が得た運動エネルギーであると解釈することができる。このとき、v≪c と見なせる場合には上式は
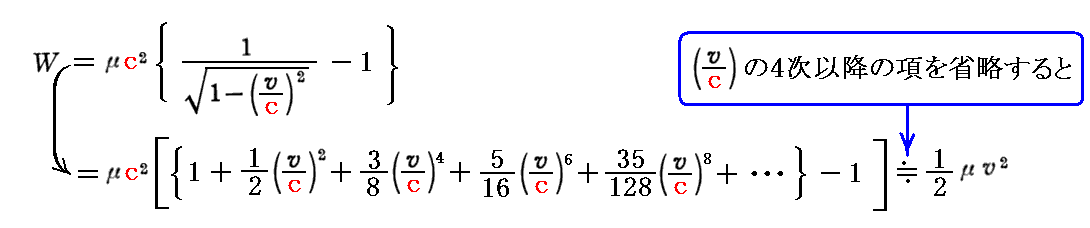
となり、確かに通常の運動エネルギーの式となる。
最後の文節の赤波線アンダーラインの部分で、ここで導いた式は電子に限らず、一般の物質(可秤量物体)についても成り立つと注意しているのですが、この式には後に有名になる E=mc2 に繋がるヒントが隠されています。
この論文を発表した6月の時点のアインシュタインはまだ気付いていないのですが、すぐ後にその重大性に気付いて9月に追加の論文「物体の慣性はそのエネルギーに依存するか?」を発表します。この論文については別項「アインシュタインの公式
E=mc2 の証明」をご覧下さい。



[補足説明7]
ここは、磁気的な屈曲Amと電気的な屈曲Aeの定義が明記されていないので解りにくい。文面から推察するに(A)式において、EyとHz成分のみがゼロでない状況を考えている。そのため
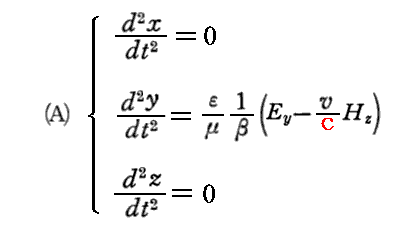
となるが、電子はx軸の正方向へ運動しているとしているので、EyとHzの大きさを適当に調節すれば電子の運動に屈曲作用が生じない状況を探すことができる。そのとき、電子の速度vを別な方法で測定して、その速度vとEy、Hzの大きさが以下の関係式
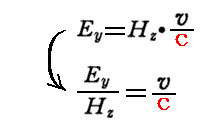
を満たすことが解れば、ローレンツの力の法則を確認できると言っている。そのように考えると、Ae、AmはAe∝1/Ey、Am∝1/Hzに関係する量を意味するのだろう。
アインシュタインは1907年に『放射能学および電子学年報』に寄せた総説論文のⅢ.質点の力学(電子)§10カウフマンの実験の項で電気的屈曲Aeおよび磁気的屈曲Amの定義を与えていますので、詳しくはそちらを参照して下さい。
これは次に述べるような相対性理論が予言する新たな効果を確かめる実験ではないが、ローレンツの力の法則が相対性理論に於いても成り立っている事を確認する実験です。
この事は相対性理論以前の電磁気学で当然成り立っているのですが、電磁気学のMaxwell方程式がもともと相対性理論を満たしていることを考慮すれば、その意味において相対性理論(電磁場のローレンツ変換共変性)を確かめる実験であると言える。
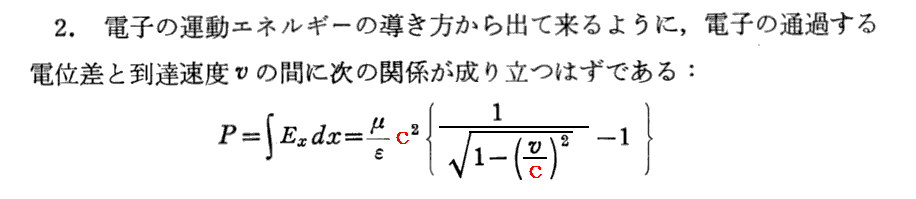
[補足説明8]
これは、前記Wに関する式から直ちに出て来る結論です。加速電圧が大きくなれば到達速度は大きくなるのですが、到達速度vがcに近づくと、いくら加速電圧を大きくしても到達できる速度が頭打ちになることを示している。これは後に多くの素粒子加速実験で確かめられることになる。

[補足説明9]
いまK系には電気力は存在せず、磁気力Hzのみが存在するときには(A)式より
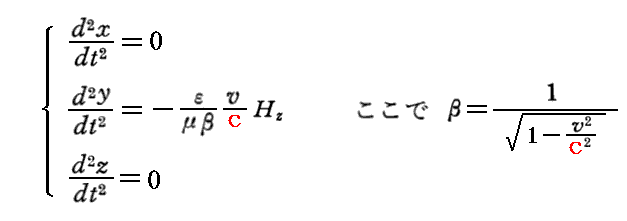
となる。所で電子はx軸の正方向へ速度vで運動しているので、上記の式は電子にy軸の負方向への偏向力が働くことを示している。次の瞬間には電子の運動方向は変化するが、その方向に垂直に偏向力は働き続ける。そのため電子の描く軌道は円軌道となる。高校物理で習うように、円運動を続ける為に必要な向心加速度aと円運動の半径Rと運動速度vの間には
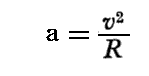
の関係がある。これが上記第2式の右辺と等しくなければならないので
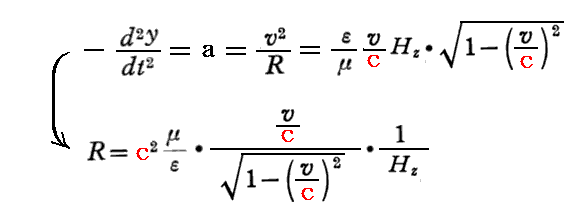
となる。
これも、相対性理論以前の式
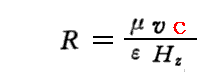
とは異なるので、Hz、v、Rを測定すれば相対性理論の実験的な裏付けが得られるはずだと言っている。これは後に円形電子加速器で実際に確認される。つまり、電子加速器は相対性理論に従って設計されているということです。詳しくは別稿「相対論的力学」4.(3)などを参照されたし。

[補足説明10]
最後に謝辞を捧げているM.Bessoに付いては、1.(2)[補足説明2]をご覧下さい。
ここまでの説明でかなりのページ数を費やしましたので、“アインシュシタインの有名な公式 E=mc2”については別稿「アインシュタインの公式 E=mc2 の証明」で説明します。また、“相対論的力学”に付いては別稿「相対論的力学」をご覧下さい。
[補足説明11]
アインシュタインは多くの機会に“同時性の矛盾を解決する事こそが全ての鍵であった。これが解った後は5週間程度で(特殊)相対性理論の論文を書くことができた。”と言っている。[例えば文献107のp83参照]
おそらく同時性の矛盾を解決できた後は、速度の合成則で説明したローレンツ変換が群を成していることの確認計算や、Maxwell方程式のローレンツ変換不変性を確かめるための計算などを次々と実行していったのだろう。それらと同様な計算を様々な現象に対して繰り返して、全ての辻褄が合うことをチェックする事が主な作業だったに違いない。
上記の5週間の間に行った計算で全てが矛盾無く辻褄があっていることが確認されていく過程は、彼自身にとっても相対性理論(すなわちローレンツ変換)の示す威力にワクワクする思いだったにちがいない。まさにローレンツ変換に依って、それまで存在していた矛盾の全てを一気に解決できたのですから。
アインシュタインは“時間の相対性(ローレンツ変換)の仮説”を“ローレンツの電子論が示す新しい解釈の電磁気学”に適用して全ての矛盾を解決できたのですが、それはちょうど別稿で説明したプランクが“エネルギー量子仮説”を“エントロピーのボルツマン流統計力学による新しい解釈”に適用して黒体輻射の観測値を完璧に説明できた時に感じたのと同様の感慨をアインシュタインにもたらしたに違いない。
プランクは数週間の計算の後に全ての辻褄が合うことを確認したときの感慨をノーベル賞講演で
“・・・・・・しかしながら、たとえこの輻射公式が絶対に正確だと保証されるにしても、それはただうまくあたった内挿式だという意味で、あくまでもまったく制限された価値をもつにすぎないだろう。
従って私は、この式を立てたその日から、それにほんとうの物理学的な意義を付与するという課題に没頭したのであり、そしてこの問題は、私をおのずからエントロピーと確率の関係についての考察に、こうしてまた、ボルツマンの思考過程へと導くことになった。
私の生涯で最も緊張した研究作業の数週間がたって、ついに暗闇はしらじらと明け、新しい、思いもかけなかった遠景が姿を見せはじめた。・・・・・・”
と述べているが、アインシュタインも同様な感慨であったでしょう。
実際、アインシュタインはそのときの気持ちを京都公演で
“・・・・・・私の解というのは、それは実に時間の概念に対するものであったのでした。つまり時間は絶対的に定義せられるものではなく、時間と信号速度との間に離すことの出来ない関係があるという事柄です。以前の異常な困難はこれで初めてすっかりと解くことが出来たのでした。
この発見の後、5週間で今の特殊相対性理論が成り立ったのです。私はそれがまた哲学的に見てもはなはだ至当の物であることを疑いませんでした。そしてそれはマッハの論とも一致すべきことを見ました。
もとよりここでは、後に一般相対性理論によって解かれたことのように、直接にはマッハの言説とは関係してはいませんけれども、しかし彼が多くの科学上の概念を明らかに解析した中に、間接にはそういう関係を持っているといってもよいのでありましょう。
かようにして特殊相対性理論は生まれたのでした。・・・・・・”
と語っているが、これがアインシュタイン流の自分の気持ちの表し方なのでしょう。上記の“時間と信号速度との間に離すことの出来ない関係がある”の意味はこちらを参照。
私自身、アインシュタインの1905年論文を読む過程で、本稿中の[補足説明]として記したローレンツ変換を様々な現象に適用する計算(おそらくこれが5週間の間にアインシュタインが実際に行った計算)を追体験してみて、全ての辻褄が合うことにワクワクする驚きを禁じ得ませんでした。
特殊相対性理論のページを作っての独り言5
4.参考文献
アインシュタインの1905年論文についての解説本は近年沢山出版されています。本稿は多くの既存書を読み比べて参考にし、説明の繰り返しをいとわず、できるだけ解りやすくなることを心がけて作りました。参考にした本を下記に挙げています。刊行年は私が持っている本の印刷年ではなくて、参考にした本と同じ版が最初に出版された年を記しています。
最初に挙げているのは、アインシュタインの論文・著書・講演、あるいはそれらを引用した解説本です。そのあとが一般の解説本です。
1.アインシュタインの論文・著書・講演。およびそれらを引用した解説本
- 物理学史研究会編「物理学古典論文叢書4 相対論」東海大学出版会(1969年刊)
日本語で読める最も基本的な文献集です。本稿の3.章はこの中の第1論文から引用。他の第2論文、第3論文、第6論文、第7論文、第8論文、第9論文は別稿で引用紹介しています。
- 湯川秀樹監修、中村・谷川・井上訳編「アインシュタイン選集1《特殊相対性理論・量子論・ブラウン運動》」共立出版(1971年刊)
- 内山龍雄訳・解説「アインシュタイン 相対性理論」岩波書店(1988年刊)
本稿の2.章はこれから引用。この本はGauss単位系を電磁単位系に変換して引用しているので注意されたし。
- ジョン・スタチェル篇(青木薫訳)「アインシュタイン論文選 「奇跡の年」の5論文」筑摩書房(2011年刊)
第Ⅲ章の編者解説と、その章末の編者注(p294~250)を引用。
- 唐木田健一訳・解説「原論文で学ぶ アインシュタインの相対性理論」筑摩書房(2012年刊)
本文中に挿入した[補足説明]の計算の多くが詳しく展開されています。本稿の確認計算の多くはこの文献に導かれて書きました。
- A.Einstein著(中村誠太郎、五十嵐正敬訳)「自伝ノート(1947年)」東京図書(1978年刊)
アインシュタインが晩年に記した覚え書きですが極めて含蓄深いものです。この中の特殊相対性理論(第4段落)を引用。
これは、金子務編訳「未知への旅立ち(アインシュタイン新自伝ノート)」小学館(1991年刊)の中にもドイツ語原文からの新訳があります。この新訳もどうぞ参照されて下さい。
- 石原純著、岡本一平画、「アインシュタイン講演録」東京図書(1971刊)
この中の京都講演(1922年12/14)と東京帝大特別講演(1922年11/25~12/1)を引用
- A.Einstein著(金子務訳)「わが相対性理論」白揚社(1973年刊 原本は1917年刊)
原本はU¨ber die spzielle und allgemeine Relativia¨tstheorie(1917年刊)
簡単な数式しか用いていませんが、極めて含蓄深い本です。ただし、アインシュタインが前書きに述べている様にこの本を読みこなすには、かなりの忍耐力と意志力が必要で簡単に読める本ではありません。“明鏡止水”の境地で、“虚心坦懐”な心を持ってお読み下さい。
この中の第1部「特殊相対性理論について」、附録1「ローレンツ変換の簡単な導き方」、附録2「相対性と空間の問題」等々を引用。第2部「一般相対性理論について」は別稿で引用しています。
これは近年、「特殊および一般相対性理論について」白揚社(2004年刊)として再版されています。訳文も改良されているようです。ただしこちらは版組が縦書きなので、旧版の方が読みやすい。
- A.Einstein著(矢野健太郎訳)「相対論の意味」岩波書店(1958年刊)
1921年にプリンストン大学で行った講義を出版(1922年)したものです。内容は高度で難しい。第3回講義の前半だけ別ページで引用。
Einsteinが1922年に来日した際に東京帝国大学で専門家向けに行った6回の特別講義は、前年に出版されたこの本と同じ内容だったと石原純は文献107.の中で説明してます。
文献114.「アインスタイン全集 第1~4巻」改造社(1923年刊)の第4巻中にも邦訳が収録されています。矢野訳版と読み比べて見られると良いでしょう。
- 「ノーベル賞講演 物理学3(1915~1922年)」講談社(1980年刊)
A.Einstein(1923年7月11日講演)“相対性理論の基本的な考え方と問題点”
近年開示された、ノーベル賞選考過程の議論によると、アインシュタインのノーベル賞が「相対性理論」ではなくて「光電効果」に対してとなったのは、相対性理論に対する評価がこの段階でも確定していなかったからだという事情もあったようです。しかしアインシュタインに取っては相対性理論こそが重要な業績だという思いだったのでしょう。記念講演の題目がそうだったのですから。
- A.Einstein著(石井友幸, 稻葉明男共訳)「我が世界観」白揚社(1935年刊、1947年再販)
1922年~1934年にいたる講演・諸寄稿を含む。グラスゴー講演(1933年)を別稿で引用。また河川蛇行形成理論を別稿で引用。
- A.Einstein著(中村誠太郎,南部陽一郎、市井三郎訳)「晩年に想う」講談社(1971年刊)
1934年~1950年にいたる講演・諸寄稿を含む
- Einstein,“U¨ber das Rela¨tivitatsprinzip und die aus demselben gezogenen
Folgerungen”, Jahrbuch der Radioaktivita¨t und Elektronik, vol.4, p411~462,
vol.5, p98~99, 1907年12月 にアインシュタイン自身が特殊相対性理論を解説した総説論文。下記URLにあり。日本語訳が文献114.に在る。
http://www.soso.ch/wissen/hist/SRT/E-1907.pdf
- A.Einstein著(石原純、他3名訳)「アインスタイン全集 第1~4巻」改造社(1923年刊)
この第1巻に、特殊相対性理論関係論文の日本語訳が在ります。各県の県立図書館は所蔵していると思います。アインシュタイン全集ではなくて“アインスタイン全集”で検索してみてください。
この中の多数の論文を、別稿「・・・への道程」と、別稿「・・・重力場方程式」で引用しています。
[追記2020年3月]
- A.Einstein著「自伝スケッチ(1955年)」
この一文は、Einsteinが亡くなる一ヶ月前の最晩年に、マルセル・グロスマンに対する感謝の気持ち込めて、書いたものです。この後半部分を金子努編訳『未知への旅立ち』(アインシュタイン新自伝ノート)小学館(1991年刊)のp154~160より引用。
2.相対性理論の解説本
- M.Born著(林一訳)「アインシュタインの相対性理論」東京図書(1968年刊 原本のドイツ語初版は1920年刊)Gauss単位系
一般向けの解説書としては、文献108の次に出版されたものです。名著の誉れ高いものです。
- M.Born、W.Biem著(瀬谷正男訳)「アインシュタインの相対性原理」講談社(1971年刊 原本は1964年刊)Gauss単位系
文献201の改訂版です。Ⅵ章、Ⅶ章はかなり書き換えられています。しかし、この部分は初版の方が解りやすい。第Ⅲ章、第Ⅳ章§7~11、第Ⅴ章、第Ⅵ章を別稿で引用。
- C.メラー著「相対性理論」みすず書房(1959年 原本は1951年刊)
この本の第Ⅰ章“特殊相対性理論の基礎、歴史的概観”は秀逸です。丁寧に書かれていますが、全般的に少し難しいので、本稿をご覧の後にお読み下さい。有理化Gauss(Lorentz-Heaviside)単位系(磁場H)
- P.G.ベルグマン著「相対性理論序説(新訂増補版)」秀潤社(1978年刊 原本は1942年刊)Gauss単位系(磁場H)
専門家向けとしては割と早い時期に刊行された教科書です。
- 矢野健太郎著「近代数学新書 相対性理論」至文堂(1967年刊)有理化Gauss(Lorentz-Heaviside)単位系(磁場H)
著者は微分幾何学が専門の数学者です。この本は、日本人が書いた相対性理論の教科書としては、草分け的なものだと思います。この第2章§6、第3章、第4章は「ミンコフスキーの4次元世界」で、第5章はこちらで、第6章は“テンソル解析学(絶対微分学)”で、第7章は“テンソル解析学の一般相対性理論への応用”で引用。
- 平川浩正著「相対論(第2版)」共立出版社(1986年)MKSA有理化単位系
この本の内容は214の参考書案内で内山先生が評されている通りです。この中の4.“Riemann幾何学”を引用。
- 江沢洋著「基礎物理学選書27 相対性理論」裳華房(2008年刊)MKSA有理化単位系
含蓄深い本です。この本のp54~67背景輻射の観測、ミンコフスキー空間、双子のパラドックスを引用。
- 中野董夫「物理入門コース9 相対性理論」岩波書店(1984年刊)
Bornの本と一緒に平行して、最初に読まれると良いかも知れません。この中から第9章“一般相対性理論の概要”を引用しています。
- 杉山直著「講談社基礎物理学シリーズ 相対性理論」講談社(2010年刊)
この中から一般相対性理論に関係する第10章を引用。
- ランダウ、ジューコフ著(鳥居一雄、広重徹訳)「相対性理論入門」東京図書(1963年刊 原本は1959、1961年刊))
この本はきちんと書かれていますので、読みこなすにはかなりの努力が必要です。この中の主な所は別項で引用。
- 竹内淳「高校数学でわかる相対性理論」講談社(2013年刊) p63~68を引用
- 佐藤勝彦著「相対性理論アインシュタイン(時間は、絶対ではない)」NHK出版(2014年刊) p44~50、p51~65を引用。
- 佐藤勝彦著「相対性理論を楽しむ本」、「『相対性理論』の世界へようこそ」PHP研究所
[2019年5月追記]
- 内山龍雄著「相対性理論」岩波書店(1977年刊)
最近(2019年4月)読んだので紹介が遅くなりました。最初に読む本としては書き方が難しいです。文献208.の中野先生の様な書き方の方が読みやすいです。しかし、著者が自慢しておられる様に簡潔・明快に書かれている名著です。双子のバラドックス(p20~27)、固有時(p88~89)、第Ⅴ章“一般相対性理論”(p111~123)を別ページで引用。
- 藤井保憲著「時空と重力」産業図書(1979年刊)
これも最近読みました。§2“波動方程式の共変性”、§4“時空概念”、§5“固有時”、§15“接続の意味”、§19“測地運動方程式”、§20“重力場方程式”を引用。
3.相対性理論の解説を含む電磁気学本
- A.Sommerfeld著「理論物理学講座Ⅲ 電磁気学」講談社(1969年刊 原本は1948年刊) MKSA有理化単位系
有名な教科書ですが、内容はかなり難しいです。本稿をご覧の後にお読み下さい。
§1.歴史的回想と§38.一般相対性理論(p352~369)を別稿で引用。また、第Ⅰ章は電磁気学の成り立ちを考えるときには必読ですので別稿で引用しています。
- ランダウ、リフシッツ著「場の古典論(増訂新版)」東京図書(1964年刊) Gauss単位系(磁場H)
この中から第1章§1、§2の導入部を引用。本稿をご覧の後に第1章§1~§7と第2章§8、§9をお読みになる事を勧めます。第3章§15、§16、§17、§18、§19、第4章§32~35、第10章§81、82,87も別ページで引用しています。
- W.K.H.Panofsky、M.Phllips著(林忠四郎、西田稔訳)「電磁気学 第2版(上)(下)」吉岡書店(1968年刊)
MKSA有理化単位系、原本の第1版は1955年刊、第2版は1961年刊。
- Edward M. Purcell著「バークレー物理学コース2 電磁気学(上巻)(下巻)」丸善(1970年刊)
Gauss単位系、意欲ある高校生・理系大学新入学生に勧めます。この中の5章“動いている電荷の場”と6章“磁場”を引用しています。これは秀逸です。
- 砂川重信著「理論電磁気学(第3版)」紀伊国屋書店(1999年刊)第10章、第11章
MKSA有理化単位系、第10章に、Hertzの理論と実験との比較が詳しく説明されている。
4.相対性理論の解説を含む物理学本
- A.Sommerfeld著「理論物理学講座Ⅰ 力学」講談社(1969年刊 原本は1942年刊)
発刊が少し古いのですが、含蓄深い教科書です。§4.“質量の変化する場合”と、§6.“自由運動質点の動力学 ケプラー問題とポテンシャルエネルギーの概念”を引用。
- A.Sommerfeld著「理論物理学講座Ⅳ 光学」講談社(1969年刊 原本は1949年刊)
有名な教科書です。内容は含蓄深くかつ難しいです。この中から§10、§11、§12を引用。
- A.Sommerfeld著「原子構造とスペクトル線Ⅰ(上巻)(下巻)」講談社(1973年刊 原本初版は1919年刊)
繰り返し改訂された有名な教科書です。この中から第1章§7を引用。
- Goldstein著「古典力学」吉岡書店(1959年刊)
- 江沢洋著「現代物理学」朝倉書店(1996年刊)
これからp124~128を引用。この引用文は秀逸ですから熟読される事を勧めます。
- Kittel、Knight、Ruderman著「バークレー物理学コース1 力学(上巻)(下巻)」丸善(1975年刊)
Gauss単位系、一見すると解りやすく易しそうですが、中身はかなり高度で難しいです。第13章“相対論力学の問題”、第14章“等価原理”を引用。引用していませんが、第12章の相対論的力学の説明も教育的です。
- ファインマン、レイトン、サンズ著「ファインマン物理学 Ⅰ~Ⅴ巻」岩波書店(1968年~1972年刊))
MKSA有理化単位系、理系大学に進まれた全ての新入生に全巻を読まれることを勧めます。ただし全てを読みこなすにはかなりの努力が必要です。
この歳になって解って来たのですが、この本は一見すると解りやすく易しそうですが、要点のみを挙げて簡潔に説明しているので中身はかなり濃密で注意深く読まないと理解するのは難しいです。実際、もう少し解りやすく説明できるだろうと思うところも多々あります。
5.相対性理論の歴史解説本
- W.Pauli著(内山龍雄訳)「相対性理論(上)(下)」筑摩学芸文庫(2007年刊)
原書は1921年刊です。上記訳本の元本は1974年に講談社から刊行されたもの。熟読する価値があります。
- Abraham Pais著(西島和彦、他共訳)「神は老獪にして・・・(アインシュタインの人と学問)」産業図書(1987年刊)
原書は1982年刊。この解説は秀逸です。第6章と第7章を引用。一般相対性理論に関係する章も別稿で引用しています。
- C・ゼーリッヒ著(広重徹訳)「アインシュタインの生涯(新訳版)」東京図書(1974年)
訳者が後書きに書かれている事を心に留めてお読み下さい。
- アーミン・ヘルマン著「アインシュタインの時代」地人書館(1993年刊)
この中の第2章“特殊相対性理論-空間と時間の変換”を引用。
- B・ホフマン、H・ドゥカス共著(鎮目恭夫、林一共訳)「アインシュタイン-創造と反骨の人-」河出書房新社(1974年刊)
- P.C.アイヘンベルク、R.U.ゼクスル編(江沢、亀井、林 共訳)「アインシュタイン」岩波書店(1979年刊)
アインシュタイン生誕100年を記念して出版された論文集です。1905年論文については第8章のA.I.Millerの解説を参照されたし。
- アーミン・ヘルマン編・著「アインシュタイン/ゾンマーフェルト往復書簡」法政大学出版局(1971年刊)
この中から、EinsteinからSommerfeldへの書簡(1912年10月29日付 、1915年11月28日付、1915年12/9、1916年2/2付)を別ページで引用。
- ボルン編・著「ボルン/アインシュタイン往復書簡集」三修社(1981年刊)
これには学術的に興味深い書簡が沢山収録されています。しかし、この中から、BornからEinsteinへの書簡(1953年9/26)と、これに対するEinsteinからBornへの返信(10/12)のみを別ページで引用します。
- 広重徹著「相対論の形成」みすず書房(1980年刊)
興味深い論文が多数収録されています。各論文末に記されている歴史的資料の文献表は貴重です。
- 西尾成子編(広重徹、G・ホルトン、M・クライン、T・クーン)「アインシュタイン研究」中央公論社(1977年刊)
この中から、ホルトン論文「アインシュタイン・マイケルソン・決定的実験」の§5、§9、著者注釈を引用。またこの中の、広重論文「エーテル問題・力学的世界観・相対性理論の起源」はとても面白い。是非お読みになることを勧めます。
- 広重徹著「物理学史Ⅰ、Ⅱ」倍風館(1968年刊)
- 吉田伸夫著「思考の飛躍(アインシュタインの頭脳)」新潮社(1964年刊)
この中の一部(p24~39)を別稿で引用
- 霜田光一著「歴史をかえた物理実験」丸善(1996年刊)
この中の5章の一部と6章を別稿で引用。
- L・インフェルト著(武谷三男、篠原正瑛訳)「アインシュタインの世界」講談社(1975年刊)
第Ⅰ部のp47~53、p84~87、p88~90を別ページで引用。
第Ⅱ部“アインシュタインの思い出”は貴重です。アインシュタインの人柄が良く解ります。p244~251、p256を別ページで引用。
- J.S.リグデン著(並木雅俊訳)「アインシュタイン奇跡の年1905」シュプリンガー・フェアラーク(2005年刊)
- Abraham Pais著(西尾成子、今野宏之、山口雄仁共訳)「ニールス・ボーアの時代1」みすず書房(2007年刊)
原書は1990年刊。この第4章“20世紀に向かって(古代の光学から相対論へ)”に特殊相対性理論がその歴史的背景も含めて簡潔・明快に説明されています。
[追記2019年8月]
- 松田卓也、木下篤哉著「相対論の正しい間違え方」丸善(2001年刊)
話には聞いていたのですが最近(2019年8月)やっと読みました。相対性理論で勘違いしやすいところが歴史的な説明を織り交ぜながら解りやすく説明されています。とても面白い本ですのでご覧下さい。当HP(本稿)と平行して読まれるとさらに良く解るかもしれません。