目次付フレーム版　　詳細目次付フレーム版　　NOフレーム版

プランクの熱輻射法則（1900年）

　熱輻射法則を見つけるためにプランクが利用した方法は以下の着想に基づいています。
　熱輻射もまた熱力学第二法則を満たしていること、たとえば異なった温度の物体が相互に行う輻射放出は常にその温度を均質化する向きに起こるであろうこと、は常に成り立つとして良いであろう。すでにキルヒホッフは物体の輻射能、吸収能についての理論を、この法則によって基礎づけている。またシュテファン・ボルツマンの法則やウィーンの変位則もこの法則に基づいて導かれたものです。そのためここで考察する熱福射の分布則も、おそらく熱理論の第二法則を輻射熱に適応することで解決されるであろう。これがプランクが追求した方法です。
　すなわち、彼は［熱力学におけるエントロピーの概念(熱力学第二法則)を輻射場に適応して、エントロピーについての深い考察から熱輻射の観測値を旨く説明する内挿公式を見つけた］。そして、その公式を、［ボルツマンの統計力学に現れるエントロピーの表現形式を自分流に書き換えたもの］と［ウィーンの変位則］を用いて、解釈し直すことでエネルギー量子ε＝ｈν（作用量子ｈ）を発見したのです。
　
　このページは、プランクの解説文12．と13．を導きの糸にして原論文1．〜９．と著書10．と１１．を参考にしながら、彼自身がたどった発見への過程を紹介するものです。解説文12． と 解説文13． を常時参考にされながらお読み下さい。

［2023年1月追記］
　本稿を最近改訂しました。内容は同じなのですが、かなり読みやすくしました。
　この稿はプランクの思考過程をできるだけ忠実に追うことを目的としています。そのため、最初から順番に読まれるのはかなりしんどいと思います。
　プランクの得た成果は良く知られていますので、逆に最後の章の“まとめ”から読まれて、一章ずつ前にさかのぼって読んで行かれると解りやすいと思います。　

１．線型振動子の振動方程式（原論文1．と２．、著書10．§104〜111）

　プランクは上記の指針に従って研究に着手したのですが、その前提として輻射熱の放出と吸収の現象を電磁的な成り行きとして理解することが必要であると考えました。熱輻射線の放出は、物質原子で構成される何らかの要素的な振動子（共鳴子）によって送り出される電磁波であり、輻射熱の吸収とは上述の共鳴子に当たる電磁波によって引き起こされる共鳴振動であると理解して良いであろうとして、その様な共鳴子と電磁波の相互作用の考察から始めた。
　
　この章は参考文献に揚げたプランクの原論文1．と２．、および著書10．の§104〜110で説明されているもので、H.Hertzの偉大な研究「Maxwell理論による電気的振動の力」（1889年）に基づいています。プランクはヘルツと同じように直交座標・ガウス単位系を用いて説明しているのですが、それは今日の目から見ると込み入っていて解りにくいので、ここはゾンマーフェルト著「理論物理学講座�V 電磁気学」§19，§36を参考にして球座標・MKSA有理化単位系に直しています。

　熱輻射論の重要な問題は、黒体輻射のエネルギースペクトル分布を導き出すことです。これは“ウィーンの変位則”で未知のままに残されていた関数Ｆ（ν／Ｔ）を見いだすことです。
　そのときの出発点は“キルヒホッフの法則”です。それによると、「鏡のように反射する壁によって囲まれた真空は、その中に任意の放出吸収物質が任意の配置でおかれているとき、時間を経ると黒体輻射の定常状態になる。それは一つのパラメーター温度によって完全に決められ、物体の配置や性質には依存しない。つまり、黒体輻射の性質を調べるためには、真空中に存在すると仮定される物体がどんな種類かということはどうでもよく、任意に選ばれた特定の放出・吸収系に対して、完全な安定性によって他と区別される輻射状態を示すこに成功しさえすれば、その状態こそ黒体輻射といえる。」
　この法則によって保証される無拘束性を利用して、すべての放出・吸収系の中で最も簡単な系、すなわち静止したある一つの振動子を選ぶ。それは反対符号の当量の電気を帯びた二つの極から成り、それらは固定した直線上を互いに振動運動する。
　運動は本来三次元的なものであるが、空間的な運動を互いに垂直な直線成分に分解すれば一成分の運動に限って扱うことができるであろう。そのため以下の状況を考察する。

（１）線形振動子（著書10．§104〜105）

　任意の電磁波に満たされた真空中に線形（ｚ軸方向にのみ振動する）の電気的共鳴子が存在しており、その固有振動数は共鳴子の一次元の大きさに比べて十分大きい波長の光の振動数νに対応しているとする。また、その振動の振幅は定常電流の抵抗とか、共鳴子内部で作用する摩擦のようなものではなくて、ただ周囲の空間に輻射としてエネルギーを放出することによってのみ減衰するものとする。
　つまり、プランクは輻射場の中へ、これといくらか作用し合う一次の振動子を入れた。それは決まった固有振動数ν₀を持つヘルツ双極子で、その大きさは問題とする波長よりも十分小さいとした。この振動子の状態は、そのモーメントｆ（ｔ）＝［軸の正方向にある極電荷：ｅ］×［極間距離ｚ］、及びその時間微分

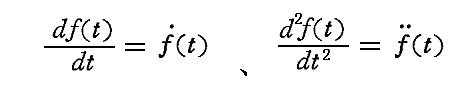
によって完全に決められよう。そのとき“振動子のエネルギー”は力学的考察から

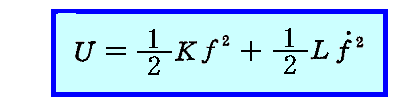
であろう。ここでＫとＬは振動子の性質に依存する正の定数である。ここでエネルギーが保存される場合には ｄＵ＝0 となるので

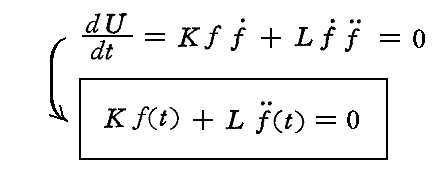
なる微分方程式を満足することになる。この解はよく知られているように

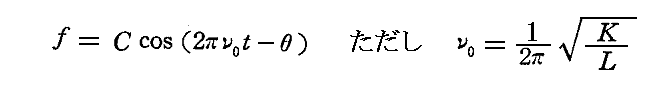
となるるここでＣおよびθは積分定数、ν₀は振動子の固有振動数と言われるものです。これは、周囲の電磁場に影響されず、また周囲に輻射線を放射しない場合の解です。

［補足説明１］
　ここで振動運動の一般的考察から運動エネルギーと位置エネルギーの時間的平均値は等しいと考えられるので

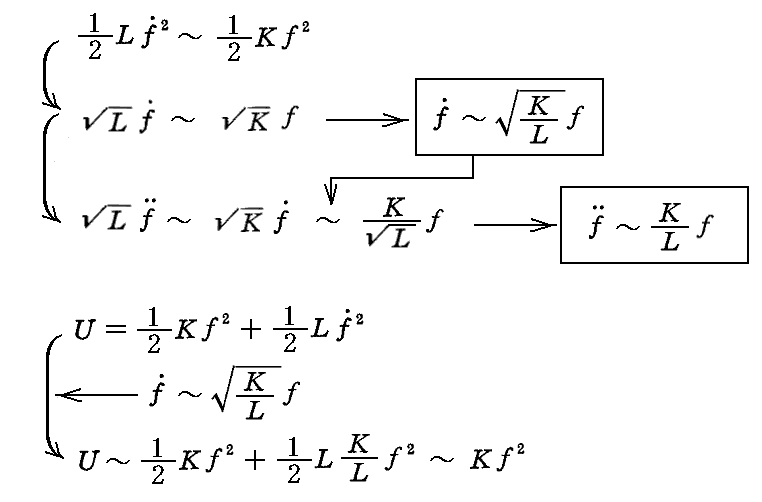
が言える。これらの関係はこういったタイプの振動について一般的に成り立つ。

［補足説明２］
　プランクはできるだけ一般的に議論するために、Ｋ、Ｌ、ｆ（ｔ）を用いて論じていますが、最も簡単な場合にはＫ＝ｋ／ｅ²、Ｌ＝ｍ／ｅ²、ｆ（ｔ）＝ｅ・ｚとすれば良い。ｋはバネ定数、ｍは質点の質量、ｅは質点の持つ電気量です。ここのｚをｘと見なせば、別稿「調和振動子」２．で論じたものに他なりません。
　また、この簡単な場合では、［補足説明１］の内容は次の関係を意味する。すなわち運動エネルギーと位置エネルギーの時間的平均は等しいので

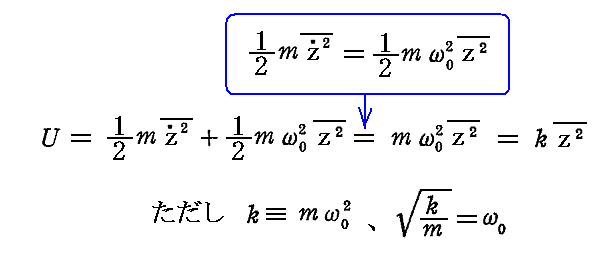
となる。

（２）電磁波の放射がある場合の運動方程式（著書10．§106〜109）

　Maxwell理論によると、電荷を持った振動子は、その振動のためにあらゆる方向に球面電磁波を送り出す。それは別稿「線型振動子による電磁波の放出」２．（３）で求めたように、球座標の（ｒ，θ，φ）の位置での電磁波の強度は

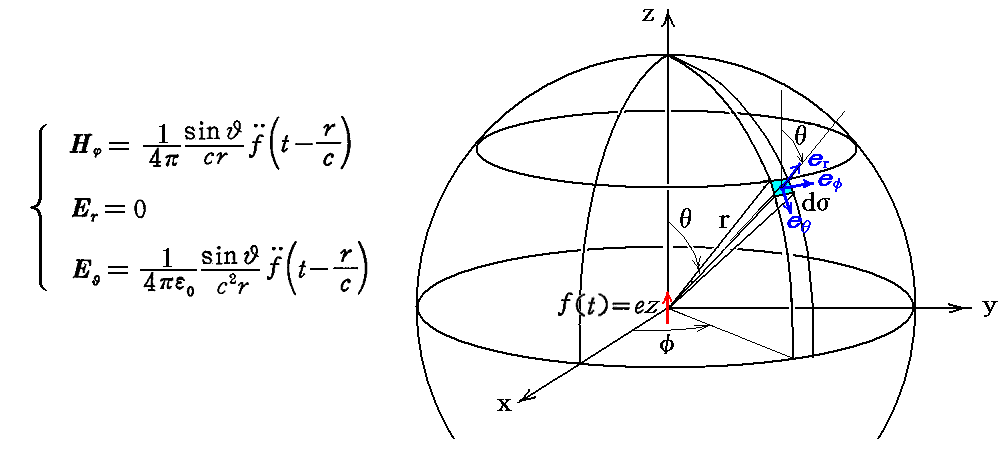
となる。ここで ｒ は振動子と放出された電磁波を観測する点の距離、ｃは光速度、ε₀は真空の誘電率、θは動径ベクトルｒ が振動子の軸（ｚ軸）となす角です。“ヘルツベクトル”ｐ（ｔ）は、ここでの表現式ｆ（ｔ）に置き換えてある。
　Poyntingの定理に従うと、ｄｔ時間に球面要素ｄσ＝ｒ²ｄΩ＝ｒ²ｓｉｎθｄθｄφを通って外に流れ出るエネルギーは

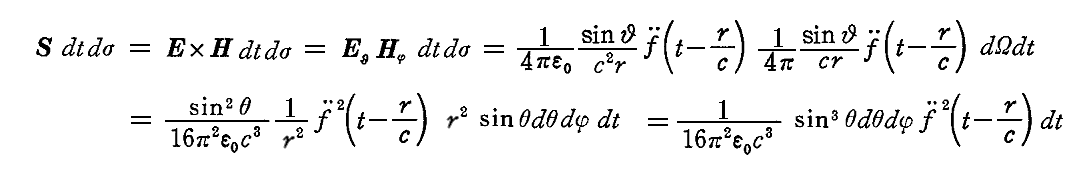
となります。
　従って、全球面（φ：0〜2π、θ：0〜π）について積分すると

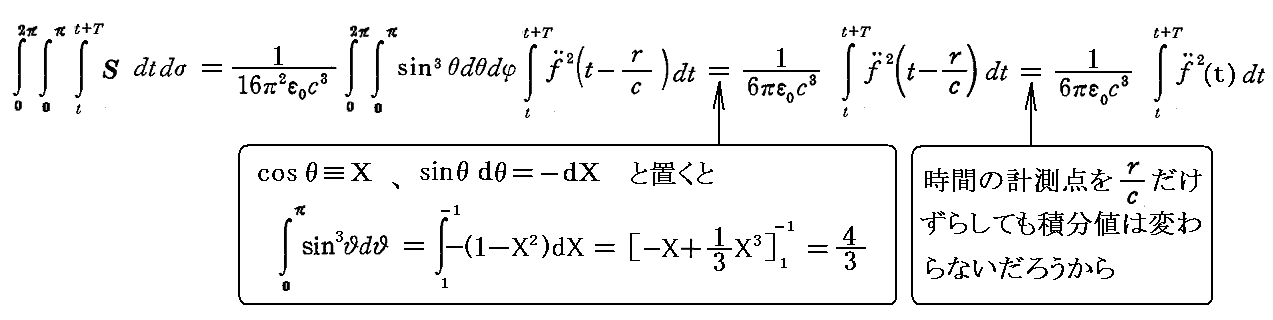
であるから、ｔ〜ｔ＋Ｔの時間に振動子から“流出するエネルギー”は

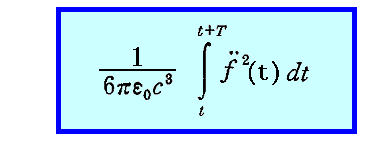
となる。

　“エネルギー保存原理”によると、Ｔ時間に放射されるエネルギーは、同じ時間に生じる振動子の振動エネルギーＵの減少に等しいので

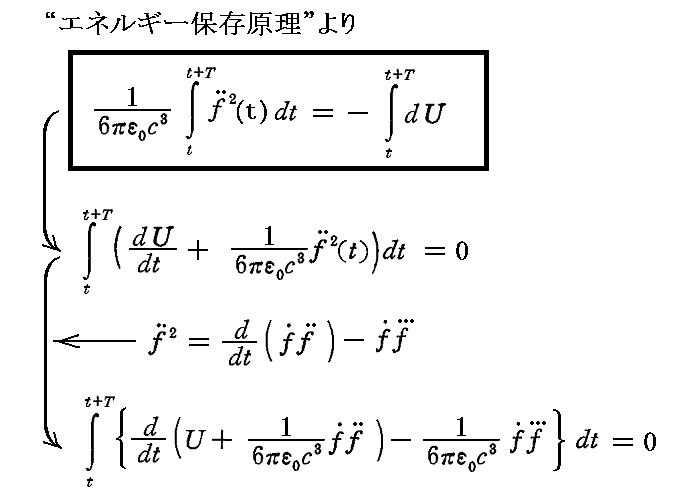
となり、非線型の微分・積分方程式が得られる。
　このとき１．（１）［補足説明１］で説明した事実を用いると

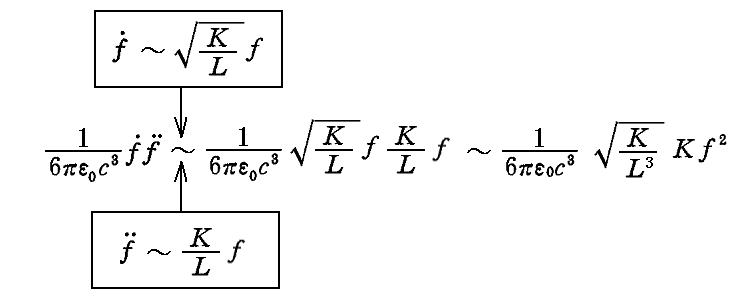
となるが、ここで

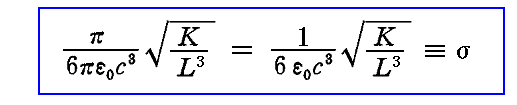
と置くと、このσは１より極めて小さな値となるので

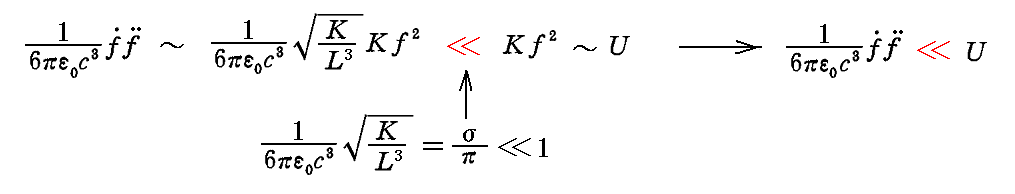
となる。σが１より極めて小さな値となることは次節の［補足説明２］で確認します。
　そのため前記の非線型の微分・積分方程式は線形に簡単化されて

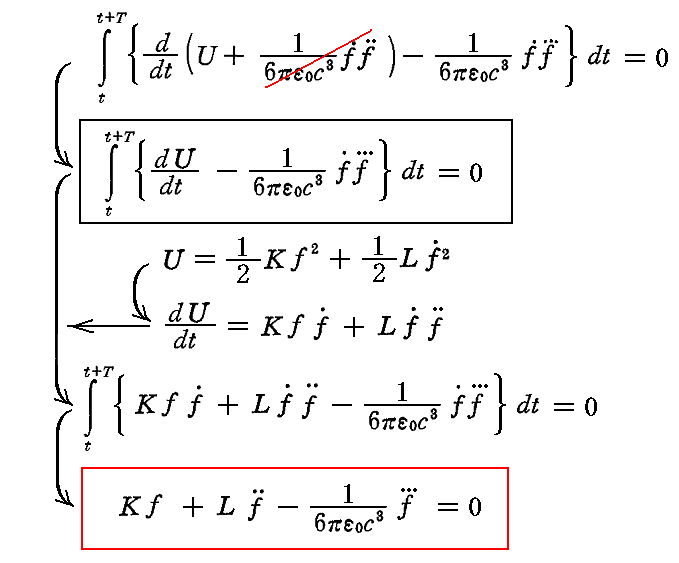
となり、同次線形微分方程式が得られる。
　ここで注意して欲しいことは、もともとの式が比較的長い時間間隔 Ｔ に対して成り立つ微分・積分方程式であったので、個々の時刻 ｔ に対して成り立つ振動子の運動方程式とすることに対して、必ずしも明確な根拠があるわけではない。
　しかし、この稿での議論を検証する物理的測定は、最も精密なものでも常に１振動周期の間隔に比べて著しく長い時間間隔で行われる。そのため、もともとの微分・積分方程式に矛盾しないｆ（ｔ）についての微分方程式なら、いずれも振動子に対して許される振動法則を与えると考えても良いであろう。
　そのため今後は上記の同次線形微分方程式を用いて議論を進めることにする。

［補足説明１］
　この微分方程式でＫ＝ｋ／ｅ²、Ｌ＝ｍ／ｅ²、ｆ（ｔ）＝ｅ・ξと置き換えてみれば、別稿「線型振動子による電磁波の放出」４．（２）１．の（３４）式と同じになります。ｋはバネ定数、ｍは質点の質量、ｅは質点の持つ電気量です。
　また、非線形の方程式を線形の方程式に簡単化するためにここで用いた手順は、別稿「線型振動子による電磁波の放出」４．（１）で用いたものと同じです。つまり、σ＜＜１の仮定は、1振動周期程度の時間間隔では振動がほとんど減衰しない事を意味します。

（３）同次線形微分方程式の解（著書10．§110）

　前節の同次線形微分方程式の解としては

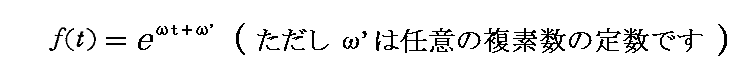
の形のものが考えられる。これ微分方程式に代入すると

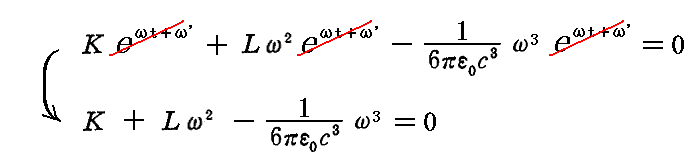
なるωの三次方程式が得られる。このωの方程式は一つの正の実根と二つの複素数根を持つ。第一の正の実根は関数ｆ(ｔ）が時間と共に途方もなく大きな値になるので物理的に何ら意味を満たず省略して良い。従って複素根のみに着目して、改めて

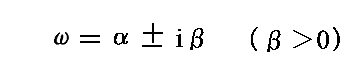
と置いて上式に代入すると

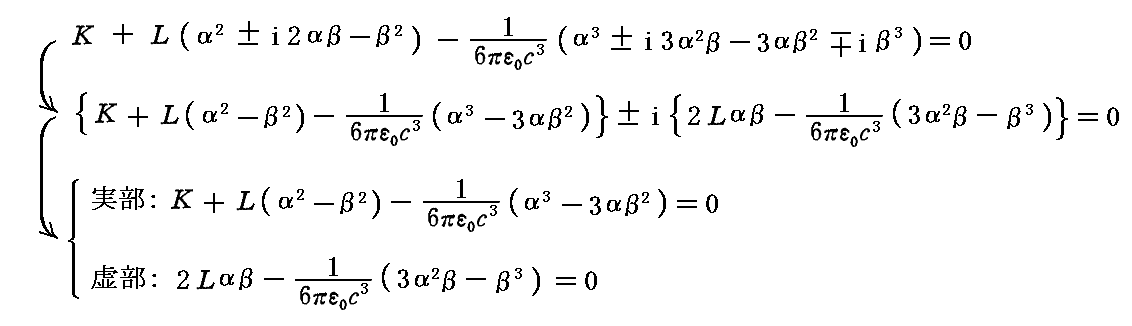
の二式が得られる。第二の式より

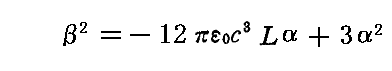
となるので、これを第一の式に代入すると

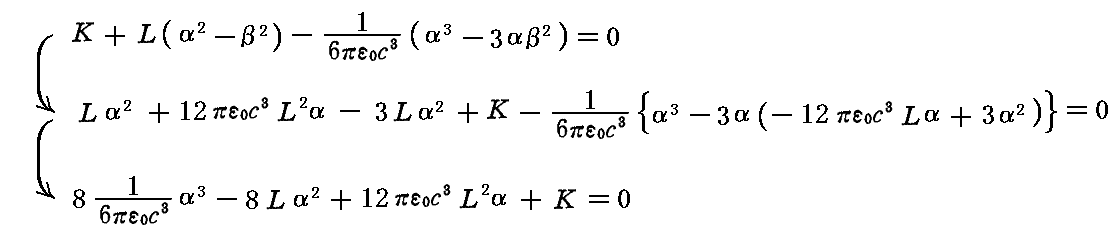
となる。ここで、先ほど定義した様に

であるが、σが小さい数であることを考慮して三次方程式の係数値を比較すると、実根αはαの高次の項を省略した

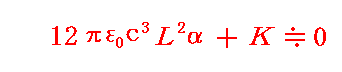
の解と考えて良い。この様に近似できる事は［補足説明３］で確認します。
　上式を解いて

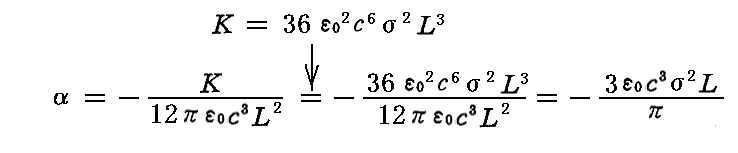
となる。ここでαは負の値であることに注意。これを前記のβ²の式に代入すると

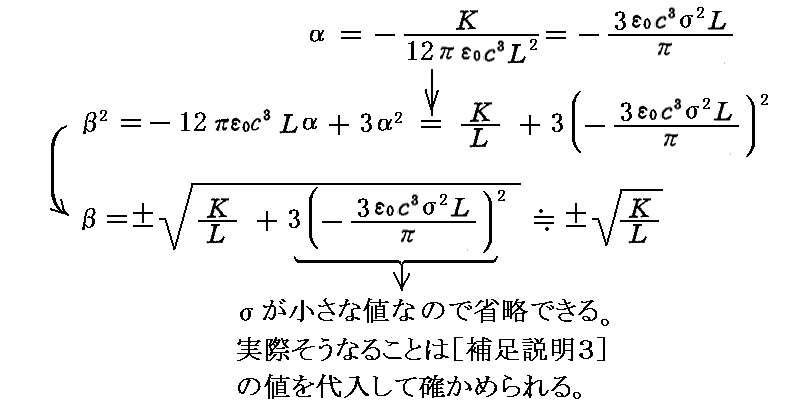
が得られる。
　このαとβを最初の式に代入して、定数項ω’を適当に調整すると

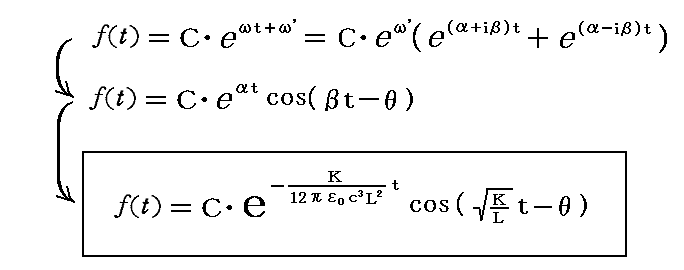
が得られる。従って振動子はその振幅をわずかずつ減衰［ｔ〜1／α経つと1／ｅになる］しながら角振動数βで振動する解が得られる。振幅Ｃと位相定数θは初期条件に依存する。

　式の形から明らかなように振動数は

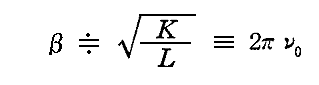
の関係がある。これは１．（１）で述べた非減衰振動の場合と同じなので、そこで説明し振動子の固有振動数ν₀に関係づけられる。
　また

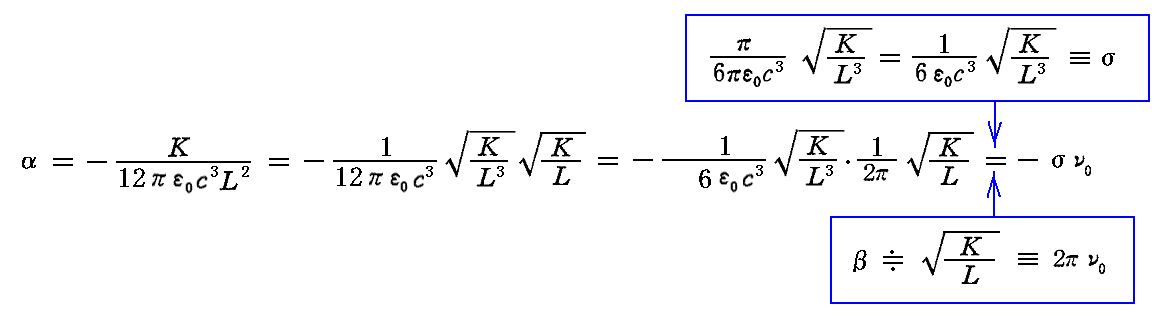
となりσとν₀と関係づけられる。
　エネルギー定数ＫおよびＬの代わりに振動子の固有振動数ν₀と減衰係数σを用いると、振動子の解は

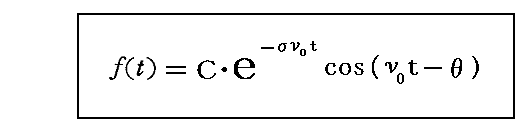
となる。
　この式から１．（２）で導入した σ は次の様な物理的意味を持つことが解る。すなわち時間が１振動周期＝1／ν₀経つと振幅が ｅ^-σ倍 に減少する事を意味する。そのためこの σ の事を今後“対数的減少率”と呼ぶことにする。１振動での減衰率ｅ^-σの自然対数を取り符号を変えたものが σ だからそう名付けたのです。
　この事から、以前設定した σ が小さい［ゼロに近い］と言う仮定は ｅ^-σ がほぼ１に近く、１振動周期程度の時間では振幅の減少はわずかである事を要請した事と同じです。実際この事は次の［補足説明２］で確認される。

　最後に Ｋ、Ｌ と σ、ν₀ の関係を導いておく。

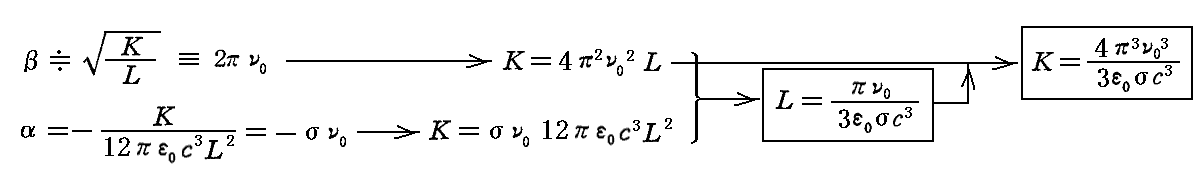
となる。

［補足説明１］
　Ｋ＝ｋ／ｅ²、Ｌ＝ｍ／ｅ²、ｆ（ｔ）＝ｅ・ξと置き換えてみれば、別稿「線型振動子による電磁波の放出」４．（２）２．で得られものと同じになります。ｋはバネ定数、ｍは質点の質量、ｅは質点の持つ電気量です。
　これらの値を用いれば“対数的減少率”σは

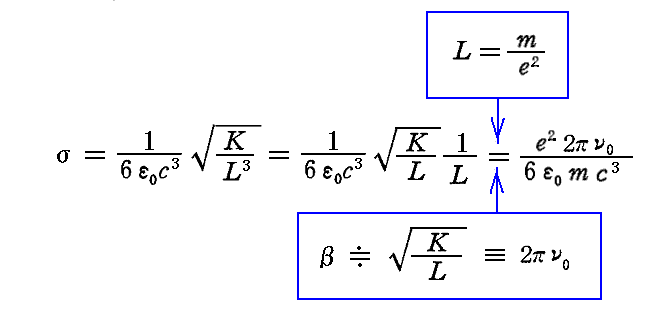
と表されます。実際このσの値を前記のＫとＬの表現式中のσに代入するとＫ＝ｋ／ｅ²、Ｌ＝ｍ／ｅ² になることが確認できます。

［補足説明２］
　σをν₀倍したものは

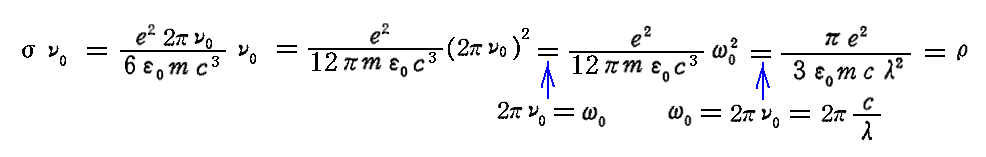
となりますので、これは別稿「調和振動子」４．や別稿「線型振動子による電磁波の放出」４．（３）で出てきたρに相当します。
　ここで振動子の固有振動数ν₀が光の青色可視光（λ＝4×10^-7ｍ）程度と仮定できる場合、ν₀＝ｃ／λ＝3.0×10⁸ｍ／ｓ÷4×10^-7ｍ＝7.5×10¹⁴Ｈz／ｓとなりますので、σν₀は

となります。
　つまり、σν₀自体はかなり大きな値（〜10⁸程度）です。そのため強制力が働かない自由振動の振幅は電磁放射でエネルギーを失ってかなり短い時間（σν₀の逆数〜10^-8秒程度）で１／ｅ倍に減衰してしまいます。
　ただし、振動子が１振動する時間は１／ν₀〜10^-15秒程度ですから１／ｅ倍に減衰するまでに莫大な回数の振動をしています。そのため１振動周期（〜10^-15秒）程度では振幅はほとんど減衰しないと言って良い。
　このときν₀〜10¹⁵Ｈz／ｓ程度ですからσ自体は10^-7程度になり１に比較して極めて小さな値になります。そのため１．（２）でσに対して行った仮定の正当性が裏付けられます。
　ここで説明した

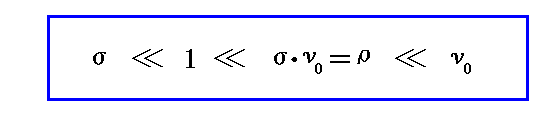
の関係は今後の議論で重要になりますので注意して下さい。

［補足説明３］
　上記の値を用いるとαの三次方程式を求めるとき設定した仮定の正当性が評価できます。すなわち

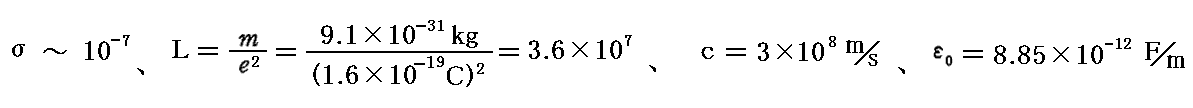
ですから、三次方程式の係数のオーダーはそれぞれ

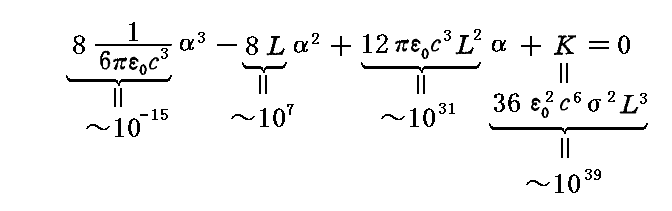
となります。そのためαの高次の項は省略できて、αの一次の項と定数項から −α〜10⁸／ｓ程度 が得られたのです。

（４）非同次線型微分方程式（著書10．§111）

　これまでは、外からの作用がなく、任意に与えられた初期振動が自然に減衰していくような振動子を考察してきた。これからは振動子が電場中に存在するために振動子に強制力が働く場合を考える。この場合、１．（２）で考察したエネルギー方程式

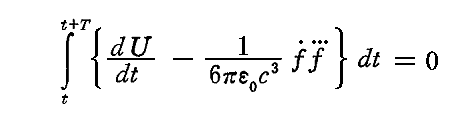
は拡張されて、振動子のエネルギーＵは、電磁波によるエネルギー放射の他に、外部電場が振動子にする仕事によって変化することになる。
　電気双極子の軸がｚ軸と一致しているから、［時間要素ｄｔになされる仕事］＝［力］×［速度］×ｄｔ　は

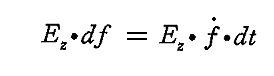
となる。ここでＥ_zは振動子の場所での外部電場の強さ、すなわち振動子がなかったらその場所に存在するであろう電場の強さのｚ成分です。外場のその他の成分は振動子の振動になんら影響を与えない。
　このとき振動子のエネルギーＵは時間要素ｄｔに外から成された仕事の量だけ増大するから、十分長い時間間隔Ｔに振動子よって“吸収されるエネルギー”は

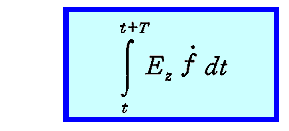
となる。
　これを追加したエネルギー方程式から導かれる運動方程式は

となる。
　ここで定数Ｋ、Ｌを定数ν₀、σで表すと

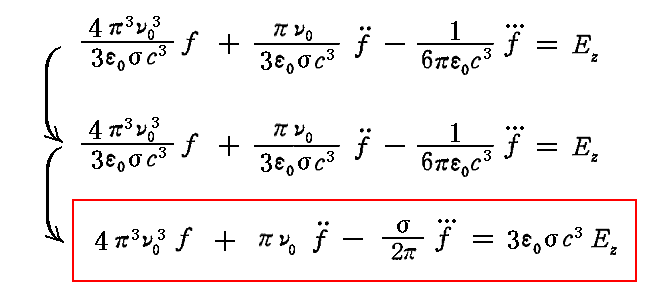
となる。
　この非同次線型微分方程式から、与えられた初期条件と外部電場の強さＥ_zを用いて振動子の振動関数ｆ（ｔ）が計算される。解が求まれば、振動子の外部電磁場への反作用も決めることができる。それは、振動子の外部でもともと与えられた電磁場成分と振動子によって放出される球面電磁波を単純に重ね合わせたものによって、あらゆる時間における状態が一義的に決められるからです。

［補足説明］
　最後の式に、具体的な電子の電気量ｅと質量ｍで表したσと ｆ（ｔ）＝ｅ・ｚ（ｔ） を代入すると

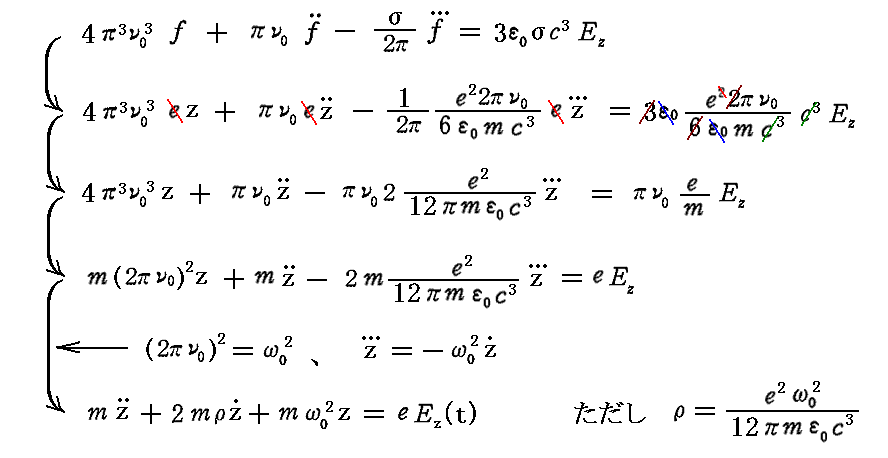
となり、別稿「線型振動子による電磁波の放出」３．（２）１．で考察した運動方程式と同じであることが解る。

２．任意の輻射場における１個の振動子（原論文3．§1〜10、著書10．§175〜182）

　プランクは前章で求めた関係式を、ここで追求しようとしている問題　“容器に囲まれた空間を満たしている全く任意のエネルギー分布の輻射が物質(振動子)との相互作用を通じて、どの様な仕方・どの様な過程によって熱力学的な平衡状態に移行していくのか？”という不可逆な過程に適用します。
　それは、容器の中に閉じこめられた気体が初め任意に与えられた流れ(任意の速度分布)と温度差のある状態から除々に静止した等温状態における速度分布に移行する過程を明らかにするのと同じことです。
　プランクは、その過程を調べれば、エントロピー極大に対応する状態のエネルギー分布として黒体輻射のエネルギー分布則が導かれるのではないかと期待するわけです。

（１）振動子の方程式（原論文3．§1、著書10．§108〜111）

　ここでは場所的にも時間的にも任意に変わりうる輻射場の中に存在する振動子（共鳴子）を考察する。輻射場は可能なすべての方向に空間中を横切る輻射線によって満たされているとする。

　このとき“エネルギー保存原理”により振動子の持つエネルギーＵのｔ〜ｔ＋Ｔにおける変化分について、1.（2）と1.（4）の結論を用いると、次の“エネルギー方程式”が成り立つ。

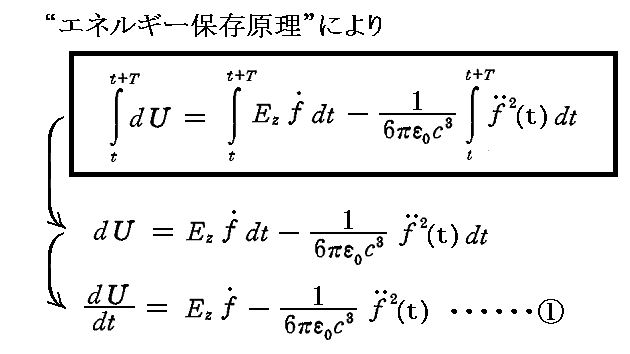
この式の各項は、前章で説明したように

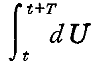• は振動子の持つエネルギーの ｔ〜ｔ＋Ｔ の時間での変化量
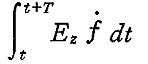• は時間Ｔの間に振動子が外部電磁場から吸収エネルギー
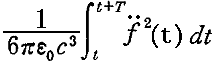• は時間Ｔの間に振動子から外部へ放出されるエネルギー

を表す。

　また“振動子のエネルギー表現式”は

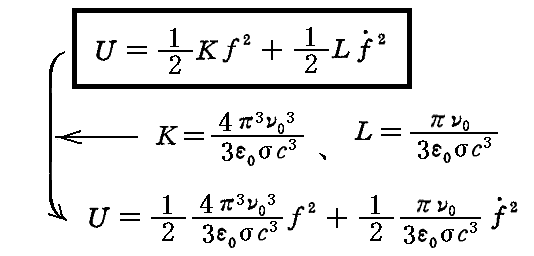
で表される。右辺の各項は

• 第１項は振動子のポテンシャルエネルギー
• 第２項は運動エネルギーを表す。

の意味を持つ。これから

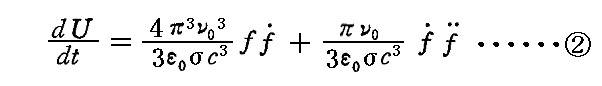
が得られる。

　更に、以前1．（2）で利用した関係式

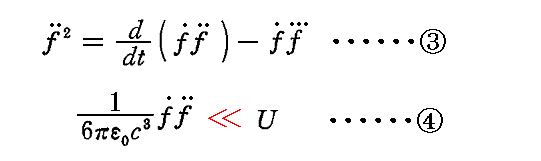
がある。

　�A、�B、�C式を“エネルギー方程式”�@に適用すると


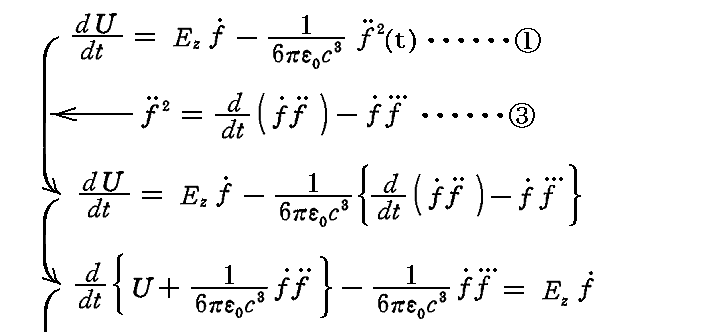
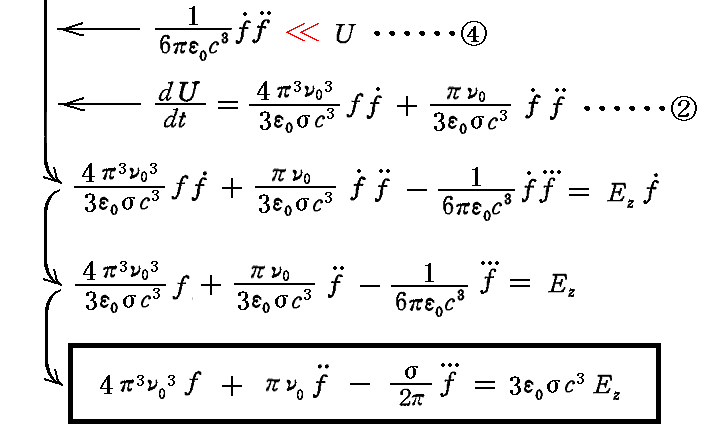
となり、前章ですでに求めているものが得られる。
　これが、振動子の状態を決定する“運動方程式”［非同次線型微分方程式］ですが、ｔ＝0における初期条件の元でこれを解けば良い。式中の記号は下記の意味を持つ。

• ｆ（ｔ）　：時刻ｔでの線形振動子により表される電気的双極子。
• Ｅ_z（ｔ）：振動子の位置につくられる外部電磁場の強さの振動子の軸方向の成分。
• ν₀　：共鳴振動子の固有振動数。
• σ　：対数的減少率で、時間が１振動周期＝1／ν₀経つと振幅がｅ^-σ倍に減少する事を表す量。
  　　　　今取られている前提からすれば１より非常に小さなゼロに近い値です。
• ｃ　：光速度。
• ε₀：真空の誘電率（ここではMKSA有理化単位系を用いている）

　別稿で説明したように、［エネルギー保存則（エネルギー方程式）］、［エネルギーの表現式］、［運動方程式］は同等な内容を異なった形式で表している。上で説明した様に一方から他方を導くことができる。そのため、この三つの形式を同等と見なして今後の議論を進めてゆく。

（２）振動子の振動（原論文3．§2〜5、著書10．§175〜177）

１．励起振動をフーリエ積分表示した場合の振動解（原論文3．§2〜3、著書10．§175）

　励起電磁場には様々な振動数の電磁波が含まれるので、有限な時間間隔（例えばｔ＝0〜Ｔ）に対して、励起振動Ｅ_z（ｔ）は次のように書かれるであろう。

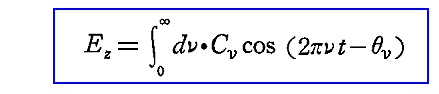
ここで、Ｃ_ν（正）及びθ_νは正の積分変数νの関数であり、その値はｔ＝0〜Ｔを越えてそれ以前の過去の状況に依存する。Ｅ_ｚの角振動数に対する振幅の分布が時間的にどの様に変化するかは後ほど示される。
　このとき、１．（３）で説明したようにｔ＝0における初期状態に依存する解

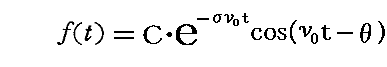
は、Ｔを十分大きく取ってσν₀・Ｔが１より十分大きくなるようにすれば、ゼロに減衰する。そのため今後 Ｔ として振動子の初期状態（ｔ＝0に対する）をまったく度外視しうるほど十分大きな値を取ることにする。
　その場合、非同次線形微分方程式

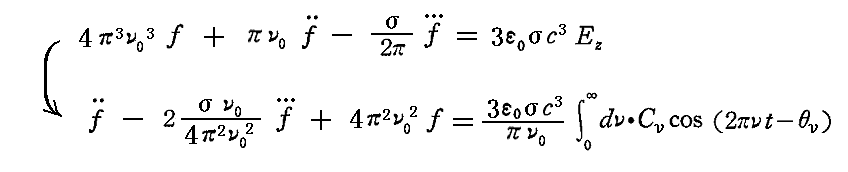
の解として

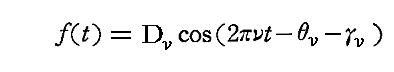
の形が考えられる。このように考えるのは微分方程式が線形だから励起振動 Ｃ_νcos（2πνｔ−θ_ν） の部分の解を考えて、それらをνに関して積分すればよいからです。
　この形の解を励起振動 Ｃ_νcos（2πνｔ−θ_ν） の微分方程式に代入すると

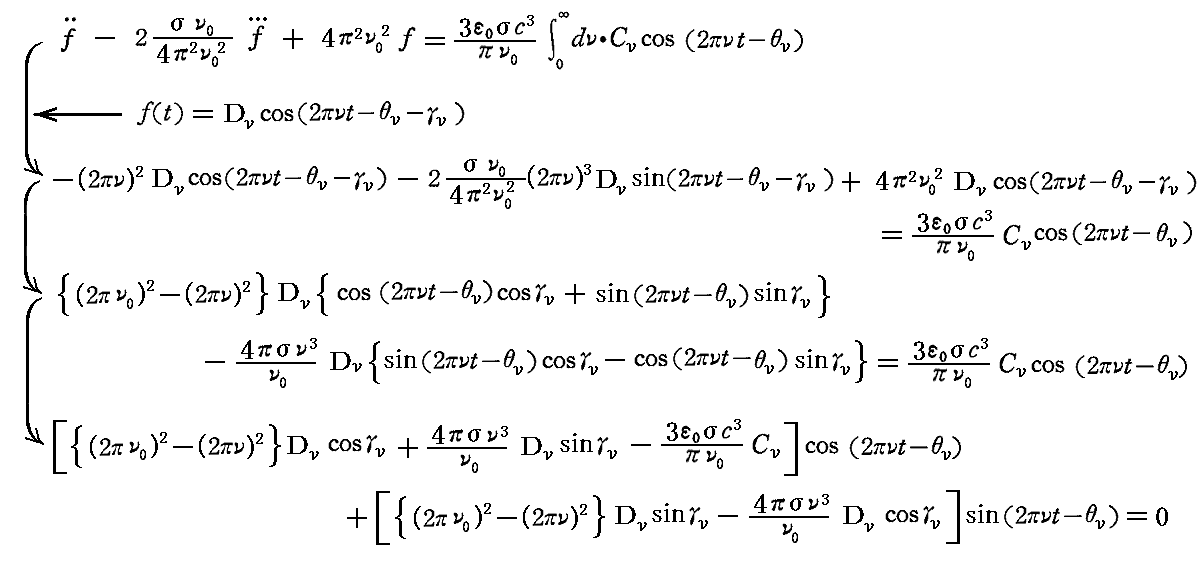
となる。ここで任意のに時間ｔに対して上式が成り立つためには cos（2πνｔ−θ_ν） の項の係数と sin（2πνｔ−θ_ν） の項の係数がそれぞれ独立に0とならなければならないので

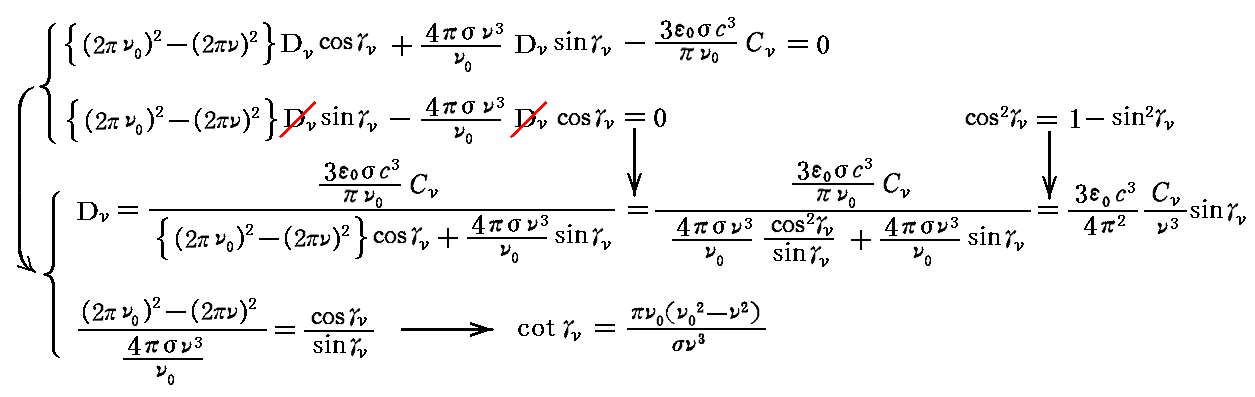
が得られる。そのため振動方程式の一般解として

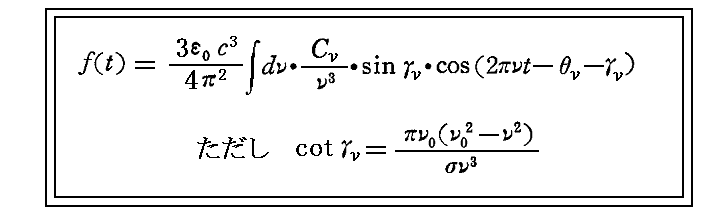
が得られる。ここで Ｃ_ν は励起振動Ｅ_zの振動数ν成分の振幅です。微分方程式が線形だからそれらの各励起振動に対応する解の重ね合わせ（ｄνでの積分）で表現できるわけです。ここでさらに、γ_νを一義的にするために　0＜γ_ν＜π　と決めておくことにする。
　σが小さいので、νがν₀より少しでも小さくなるか大きくなれば cotγ_ν の値は、正か負の大きな数となる。従って ν＝ν₀ のとき γ_ν＝π／2 となるが、νがν₀から少しでも小あるいは大のいずれかに外れると角 γ_ν は 0 かあるいは π に近い値なる。それはフーリエ積分の指数νが振動子の固有振動数ν₀に近いときのみsinγ_ν／ν³はゼロと異なる値になり、それ以外ではほとんどゼロと考えて良いことを意味する。そのため、多くの場合で積分量νをν₀によって置き換えることができる。以下ではしばしばそれを使用するであろう。

［補足説明１］
　この当たりの計算は別稿「調和振動子」５．の議論とほぼ同じですのでそこの議論とδのグラフを参照されて下さい。ただしそこでのδがここでのγ、そこでのρはここでのσ・ν₀に相当します。またω＝2πνですが、減衰項が時間の一次微分から三次微分になっていることに伴う表式の違い（ν／ν₀だけ）がありますので、その点に注意して比較してみて下さい。

２．励起振動の強さ（原論文3．§4、著書10．§176）

　時間ｔの関数としての励起振動の強度 Ｊ は、 ｔ〜ｔ＋τ までの時間間隔における Ｅ_ｚ² の平均値のε₀倍として定義される。
　ここで、τ は時間 Ｔ と比べてできるだけ短く、しかし振動子の固有振動周期（＝１／ν₀）に比べて常に長くとる。τ をあまり短く取ると平均値としての Ｊ の値を決めることはできない。そのような場合に励起振動の強度を問題にすることはできない。しかし振動強度の振幅は１振動程度の時間間隔ではほんのわずかしか変化しないので、τ をそれよりも十分長くとり、時間 Ｔ よりも短く取れば時間 ｔ にのみ依存する Ｅ_ｚ² の平均値があるような過程として考察できる。
　今後一般解にふくまれる Ｃ_ν は ν₀ に比べて低い ν のすべての値に対しては無視できるほど小さいとする。つまり固有振動の振動周期よりも長い周期の励起振動は含まれないとする。

　励起振動の強度 Ｊ を計算するために前節の Ｅ_z（ｔ） のフーリエ積分表示から Ｅ_z² をつくり、この値の平均値を ｔ について ｔ〜ｔ＋τ まで積分して τ で割り、 τ を十分小さくして極限移行することによって決める。まず

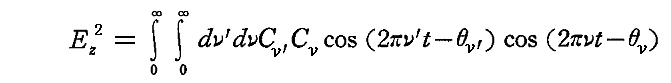
が得られるが、νとν’を交換しても積分記号のもとで関数は変わらない。従って

と決めて積分し、それを二倍する。そうすると

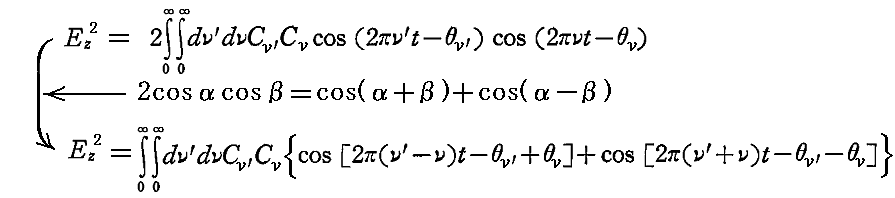
となるので、

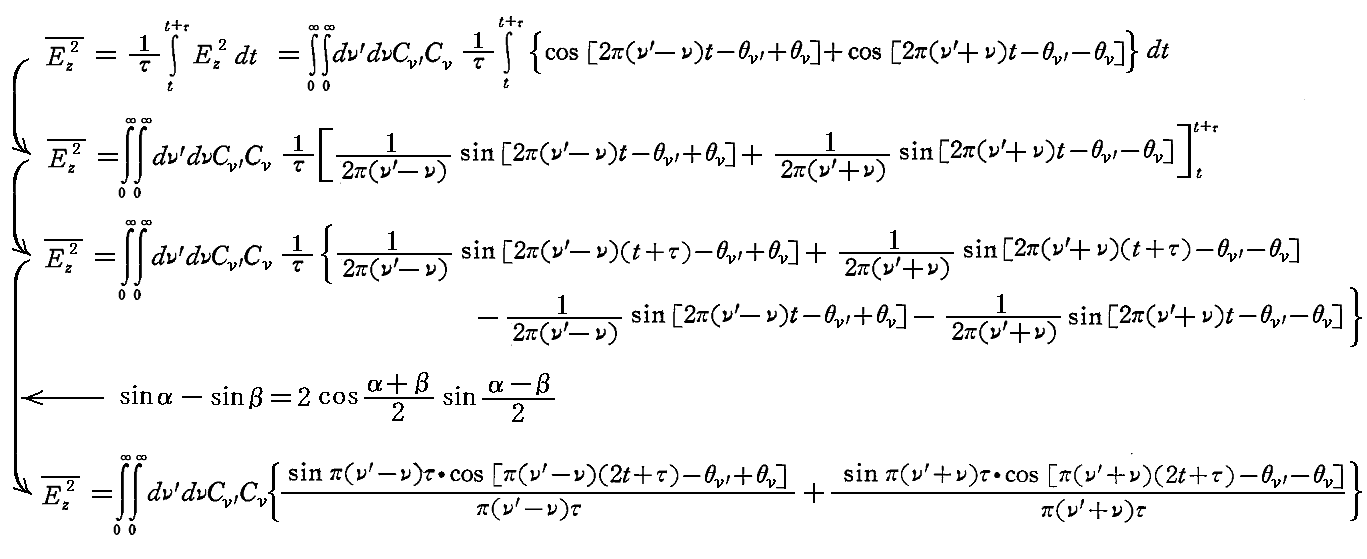
　上で行った仮定によると、ν₀に比べてνが小さい場合にはＣ_νはゼロと見なせるので、上の式のνもν’もν₀と同じかあるいはそれ以上の大きさと見なすことができる。
　ここで、τをどんどん短くしていっても、ν₀τは十分大きい値であるという条件に従って、第１項の分数分母の(ν’−ν）τはτの減少とともに有限の値以下に低下しうるが、第２項の分数分母の(ν’＋ν）τはτが減少しても大きな値のままにとどまる。
　従って (ν’−ν） が十分小さな値のとき積分は第一項のみが残る。そのとき sinπ(ν’−ν）τ／π(ν’−ν）τ〜１ と見なせるので

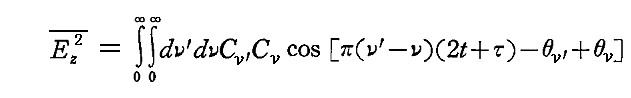
となり、実際には τ には依存しなくなる。
　(ν’−ν）が大きな値(時間と共に速く変化する)のときに対応する二重積分の残りの項は一般に τ に依存する。しかし、強度 Ｊ が τ に依存しない為には第二項は消えねばならない。その場合にも残る第１項については

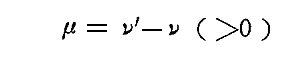
を ν’ の変わりに第二の積分変数として用いると

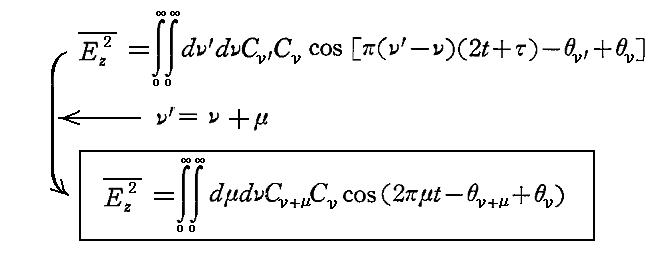
となる。これにより、励起振動の強度Ｊ は時間の関数としてFourier積分の形に表される。

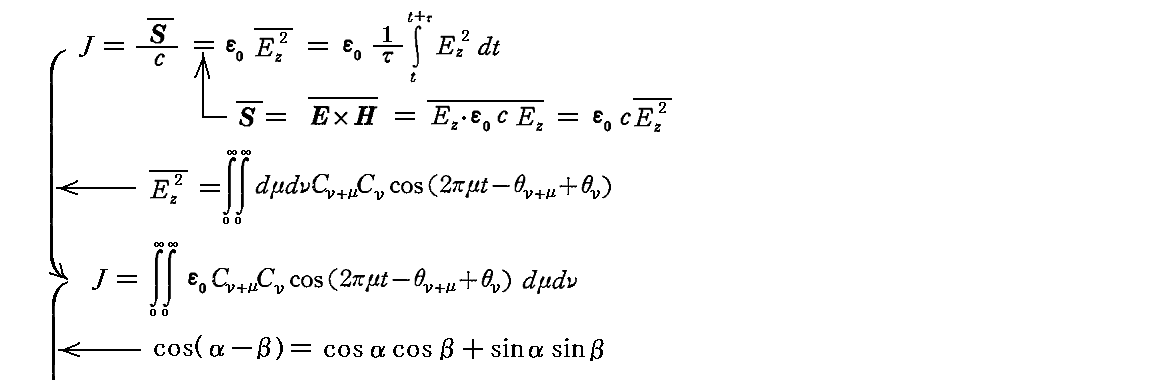
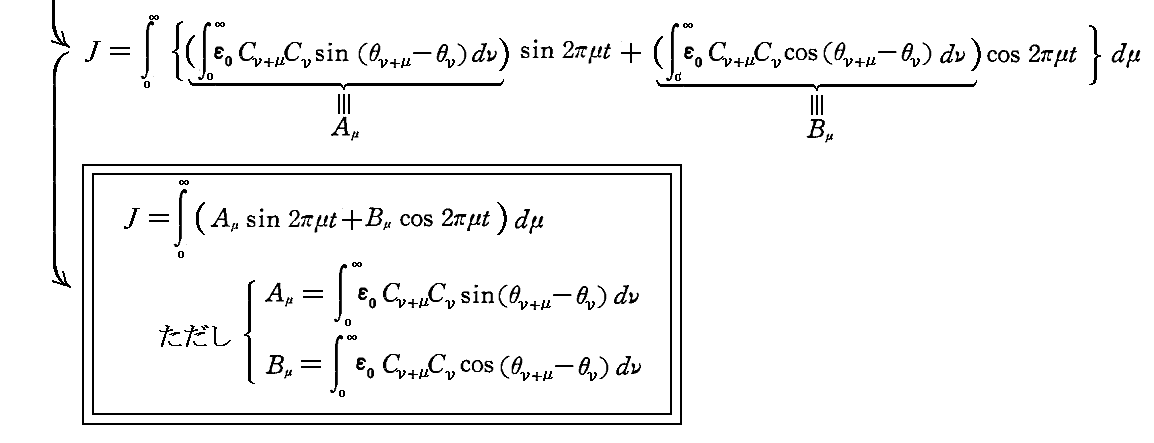
３．急速に変化する量とゆるやかに変化する量（原論文3．§5、著書10．§177）

　もともと励起振動の強度Ｊ の時間的変化は Ｅ_ｚ（ｔ） の振動自身よりずっと緩やかに変化すると仮定している。実際、前節の Ｊ の計算式に於いて任意の Ｃ_ν と Ｃ_ν’ の組みに対して平均を取るときの ν・τ や ν’・τ は大きく、それに対して (ν’−ν）・τ は小さい。そのとき

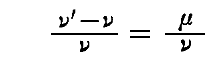
はなおさらのこと小さいのだから。
　そのため Ｅ_ｚ（ｔ） と Ｊ（ｔ） は時間的にまったく異なった仕方で変化する。そのため Ｅ_ｚ（ｔ） と微分方程式で結びつけられている振動子の振動を表す関数 ｆ（ｔ） のように“速く変化する”量と、Ｊ（ｔ） や振動子のエネルギー Ｕ（ｔ） のように“ゆるやかに変化する”量は明確に区別されねばならない。

　Ｕ の値については後で計算するが、上記の量の時間的変化における違いは相対的なものです。なぜなら、 Ｊ(ｔ） や Ｕ（ｔ） の時間微分の大きさは、時間単位の大きさに依存し、これを適当に選べば任意に大きくすることができるからです。従って Ｊ(ｔ） や Ｕ（ｔ） が絶対的な意味で時間的にゆっくり変化する関数であると決めつけることはできない。時間的にゆっくり変化するという言い方は、関数 Ｅ_ｚ（ｔ） や ｆ（ｔ） の特異的な振る舞いに対しての相対的な意味で使われる。

　しかし、θ_ν の指数 ν への依存性については絶対的な意味で“速く変化する”特質を持つことが必要です。なぜなら、μ が ν に対して小さくとも、θ_ν+μ−θ_ν の差は一般に小さくはないことが必要だからです。θ_ν+μ−θ_ν の差がいつも小さなものであれば Ａ_μ と Ｂ_μ が特別な値を持つことになるからです。
　(∂θ_ν／∂ν)・ν は大きな数であることが必要で、この事が満たされれば、時間単位を変えたり、時間の出発点を移動しても、以下の議論に根本的な変化を生じることはない。
　位相定数θ_ν や 振幅Ｃ_ν が ν の変化に対して“急速に変化する”ことは、決まった振動強度 Ｊ が存在するための必要条件です。

（３）振動子のエネルギー（原論文3．§6〜7、著書10．§178〜179）

　前節で速く変化する量とゆるやかに変化する量の違いについて注意したが、今後はもっぱら、ゆるやかに変化する量について考察する。それは光学や熱輻射の問題に於いて実験的に測定できるのはゆるやかに変化する量についてのものだからです。ここではゆるやかに変化する量のなかで最も重要なもの［振動子のエネルギー］と［振動子によって放出されるエネルギー量］、［振動子によって吸収されるエネルギー量］を計算する。

１．振動子のエネルギー（原論文3．§6、著書10．§178）

　振動子のエネルギーは２．（１）で述べたようにポテンシャルエネルギーと運動エネルギーからなる。そのとき Ｋ と Ｌ に付いての関係式と ｆ（ｔ） の関係式を用いると両方のエネルギーの時間的平均は同一であることが解る。

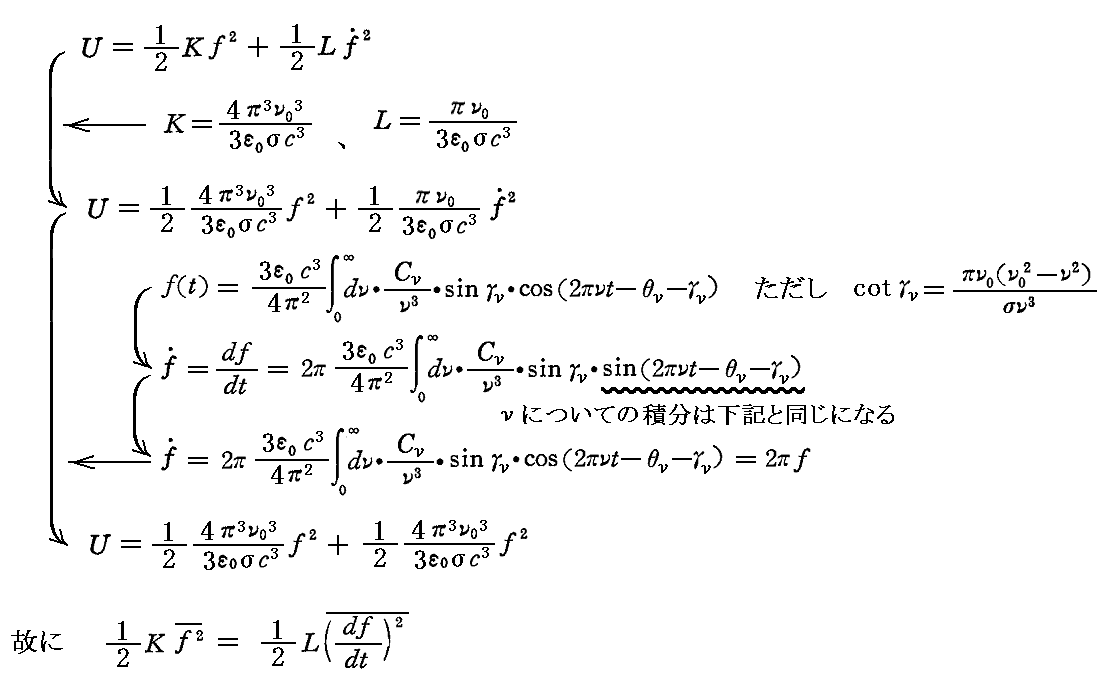
そのため

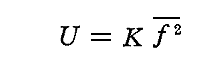
と書くこともできる。(ここは1．（１)［補足説明１］で求めている程度の証明で良いのかも知れない。)
　このとき、振動子のエネルギーは“ゆるやかに変化する量”としてｔ〜ｔ＋τの間の時間平均として表されるのであるが、その計算は２．（２）２．でＥ_ｚ²の時間平均を求めたのとまったく同様なやり方で行えばよい。
　ｆ（ｔ）とＥ_ｚ（ｔ）は、振幅の違いを除くとまったく同じ形をしている。

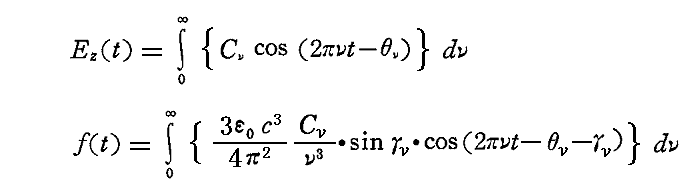
　そのためそこで求めたＥ_ｚ²の時間平均の計算結果の Ｃ_ν を （3ε₀ｃ³Ｃ_νsinγ_ν／4π²ν³） で、 θ_ν を （θ_ν＋γ_ν） で置き換えればよい。そのとき、 μ が ν に比べて小さく、積分には ν が ν₀ に近いような項のみが著しく考慮されるということ （ν₀／ν〜1） を用いると

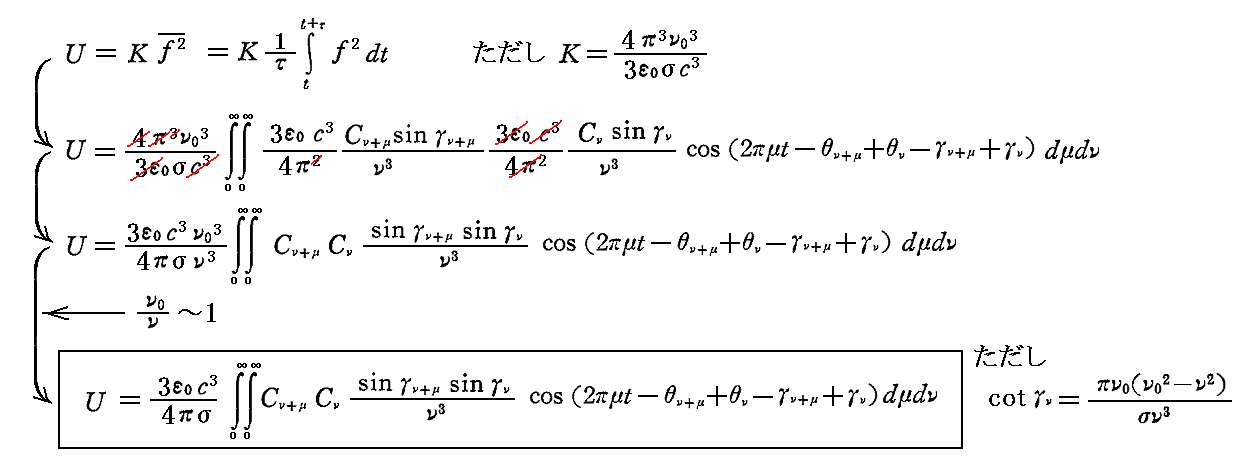
となる。これはさらに次のように書くこともできる。


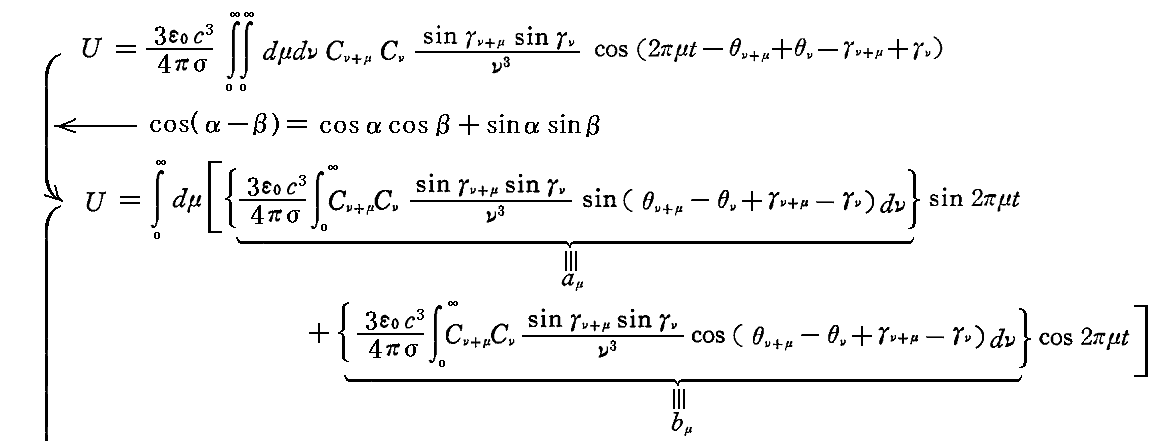
　ここで Ｃ_ν も θ_ν も絶対的な意味でνとともに“速く変化する”。また

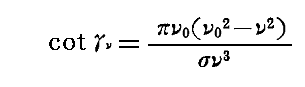
であるから γ_ν も絶対的な意味でνとともに“速く変化する”。それ故に、たとえ μ が ν に比べて小さくとも、角 γ_ν+μ を γ_ν にほぼ等しいと置くことはできない。 μ が σν₀ と同程度もしくはそれ以上の大きさのときにはそうはならないからです。

２．共鳴子によって放出されるエネルギー（原論文3．§7、著書10．§179）

　振動子によってｄｔ時間に放出されるエネルギー量は、“ゆるやかに変化する量”として、２．（１）で説明した量のｔ〜ｔ＋τの時間平均を取ったもの、すなわち

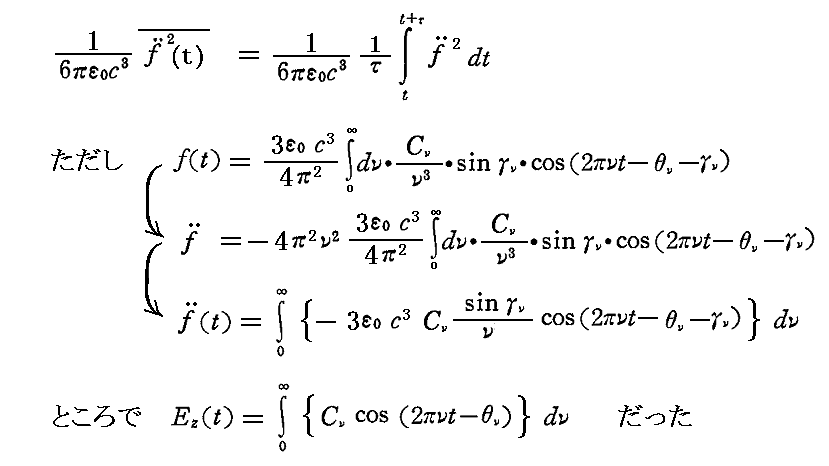
のｄｔ倍とすればよい。上記の平均操作は、２．（２）２．でＥ_ｚ²の時間平均を求めたのとまったく同様なやり方で行えばよい。（ｄ²ｆ／ｄｔ²）とＥ_ｚ（ｔ）は振幅の違いを除くとまったく同じ形をしている。そのためそこで求めたＥ_ｚ²の時間平均の計算結果のＣ_νを（3ε₀ｃ³Ｃ_νsinγ_ν／ν）で、θ_νを（θ_ν＋γ_ν）で置き換えればよい。そうすると

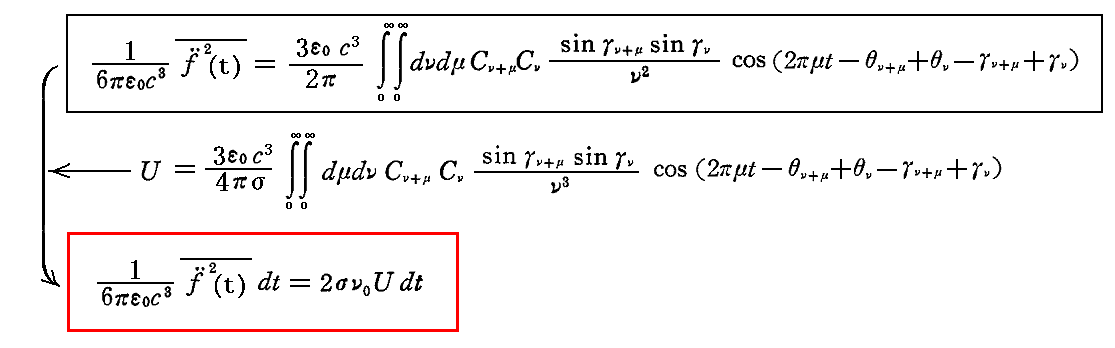
ここで、Ｕのｔ〜ｔ＋τの時間平均値の表現式と比較して最後の表現が得られる。ただしν〜ν₀の近似を用いている。

　すなわち、［時間要素ｄｔ内に振動子によって放出されるエネルギー］は、［振動子のエネルギーＵ］、［振動子の固有振動数ν₀］、［対数減衰率σ］に比例する。

３．共鳴子によって吸収されるエネルギー（原論文3．§7、著書10．§179）

　振動子によってｄｔ時間に吸収されるエネルギー量は、“ゆるやかに変化する量”として、２．（１）で説明した量のｔ〜ｔ＋τの時間平均を取ったもの、すなわち

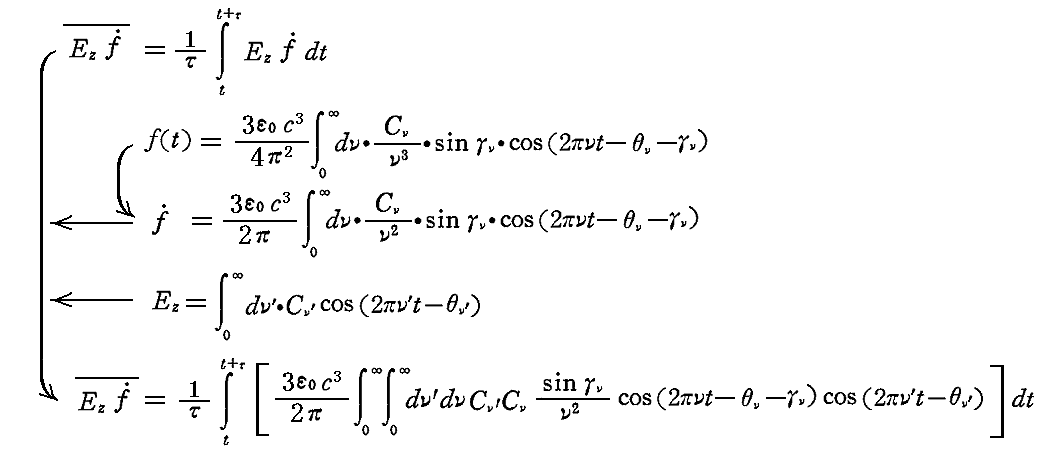
を計算することで求めることができる。

　しかし、ここではすでに計算したＵの結果をエネルギー保存則に適用することで求めよう。エネルギー保存則によれば、時間要素ｄｔ内に振動子によって［吸収されるエネルギー］はその時間要素内に［生じたエネルギーの増加ｄＵ］と［放出エネルギー2σν₀Ｕｄｔ］の和に等しいので


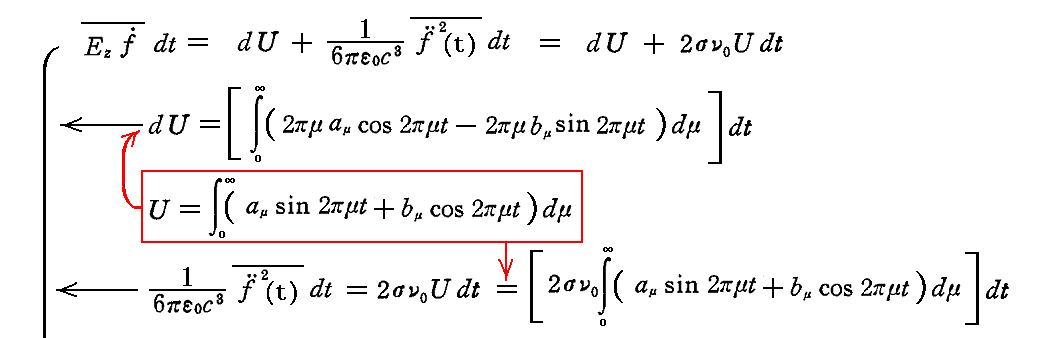
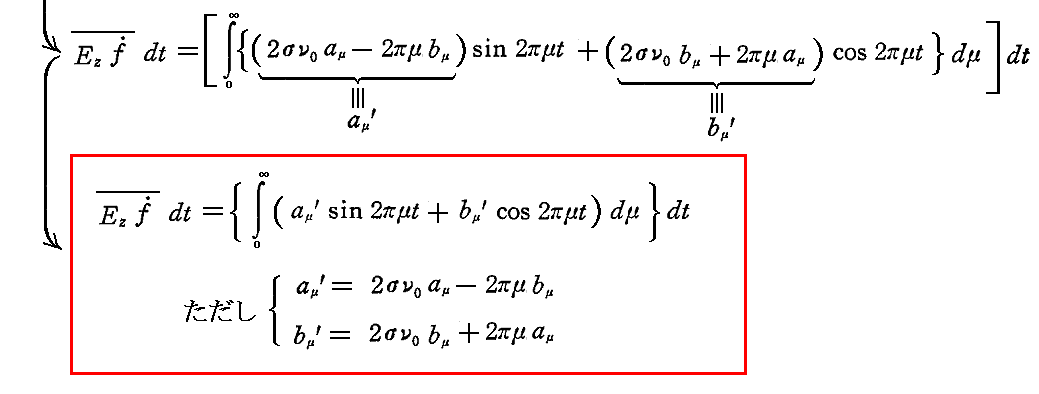
となる。この式に於いてもμとσ・ν₀の比が任意に大きい場合でも、小さい場合でも取り得ると考えなければならない。

（４）励起振動の強さのスペクトル分解（原論文3．§8〜10、著書10．§180〜182）

　これまでの議論に現れたエネルギー量の内、我々が直接測定できるのは［励起振動の強さＪ］と［振動子のエネルギーＵ］のみである。このとき、この両者の間に成り立つ関係式は一般的に簡単なものではない。振動子のエネルギーＵは励起振動Ｅ_zの全体の強度Ｊによるばかりでなく励起振動Ｅ_ｚのスペクトル分布特性にも関係しているからである。
　そのため、励起振動の性質を知るには、励起振動の各スペクトル領域と様々な振動子との相互作用をさらに詳しく調べる必要がある。このとき、振動子が受け取るエネルギー量こそ励起振動の強さそのものである。

１．振動数νの励起振動の強さＪ_ν（原論文3．§8、著書10．§180）

　全強度Ｊに含まれる一定の振動数νの強度Ｊ_νを次式で定義する。

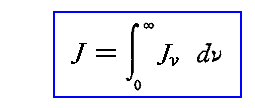
このときＪ_νは、振動数νの共鳴子が励起振動Ｅ_zのもとで取り入れるエネルギーによって測定・定義される。このときＪ_νは変数νとｔに関して“ゆるやかに変化する量”と考えることができる。
　このとき、振動Ｅ_ｚによって励起される振動子のエネルギーは、その固有振動ν₀のみならず、その減衰係数σにも依存する。そのため、強さＪ_νの測定に利用される振動子の減衰係数σを適当に選ぶことも重要です。
　振動子が、励起振動スペクトル分布の有限の幅に対しててはなく、ある一定の振動のみにはっきり反応するためには、その対数的減少率σが小さくなければならない。実際、減衰率σのν₀倍は別稿「調和振動子」５．（３）や別稿「線型振動子による電磁波の放出」４．（３）で議論した減衰項ρを意味し、ρは共鳴振動の波長変化の半値幅を与えるので、上記の事情を満たすためにはσν₀はかなり小さな値でなければならない。そして１よりも十分大きく無ければならない。
　ただし、σが極端に小さい場合、振動が弱まるのに長い時間かかり、そのような振動子は、これを励起する励起振動（時間と共に変化する）との同一時刻性を規定できなくなり、過去の励起振動場のスペクトル分布の様子にも依存するようになるからです。
　そのとき振動子のエネルギーは強さＪ_νそのものではなくて、Ｊ_νの比較的長い時間間隔の平均値で表現される。

　以上の事情を考慮して、励起振動Ｅ_ｚの解析に使うすべての振動子の対数的減少率σ_νは、１よりも非常に小さいが、σ_ν・ν₀は１よりも十分に大きくなるようにする。またσ_ν・ν₀はすべてのμ＝ν’−νに対しても大きくなるようにする。この事は

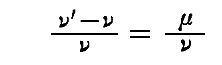
よりμがνより小さいので常に可能です。この当たりについては１．（３）の［補足説明２］を参照。

　そうすれば、解析の対象となる１個の振動子（固有振動数ν₀）の状態は、励起振動の同一時刻の性質によって完全に決定される。またそのとき、振動子は励起振動の強さのゆらぎすべてを時事刻々に体現・表示すると言って良い。
　前節の最後で求めた、振動子によってｄｔ時間に吸収されるエネルギー量の表現式

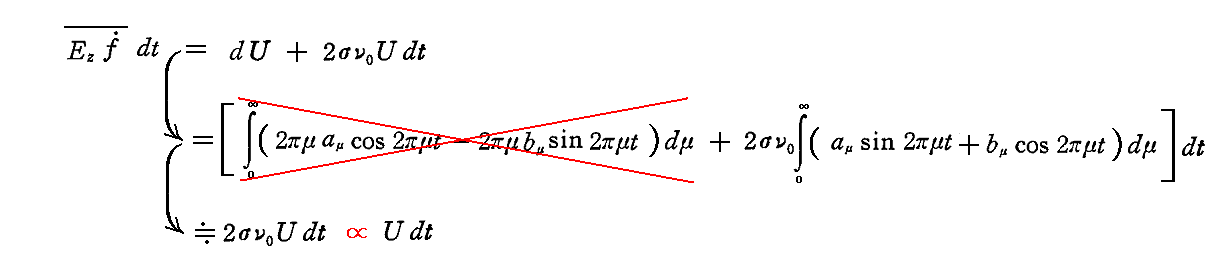
に於いて、σの変わりにσ₀（添え字0は固有振動数ν₀の振動子に関する減衰率という意味）と置けば、ここでの仮定はμの因子を持った項はσ_ν・ν₀の因子を持った項に比べて無視して良いほど小さいこと意味する。この事はまた、振動子によって吸収されるエネルギー量は、その瞬間の振動子のエネルギーＵに比例することを示している。もちろん、この事は振動子の状態が、励起振動の同一時刻の性質だけに依存している場合のみ可能である。

　これまで説明してきた前提のもとに、励起振動全体の強さＪに含まれる振動数ν₀の強さ（これを簡単にＪ₀で表す事にする）を求めよう。振動数ν₀の励起振動の強さＪ₀こそ、固有振動数ν₀の振動子によって吸収されるエネルギー量に他ならない。そしてこのエネルギー吸収量は上に述べたように振動子のエネルギーＵに比例するのだから、２．（３）１．で求めたＵの表現式を用いると、振動数ν₀の励起振動の強さＪ₀は時間ｔの関数として

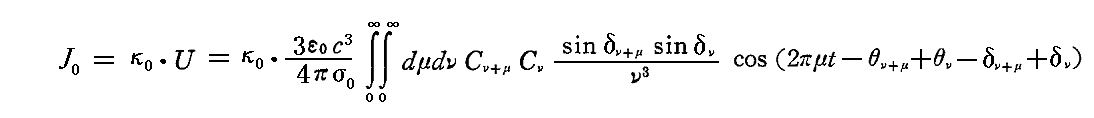
が得られる。ここでκ₀はν₀に依存しており、今から決定しなければならない比例因子です。またここでは、σはσ₀に、γ_ν、γ_ν+μはδ_ν、δ_ν+μに置き換えてある。そのとき

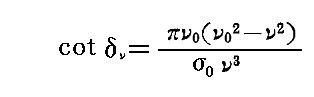
である。ここでμ＝ν’−νがσ_ν・ν₀に比べて小さいからδ_μ+ν＝δ_νと置けて

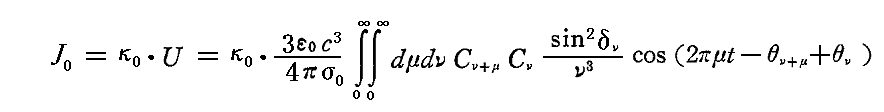
となる。
　比例因子κ₀は［Ｊ_νの定義式］と［上式のＪ₀表現式］及び［２．（２）２．で求めたＪ表現式］から求まる。

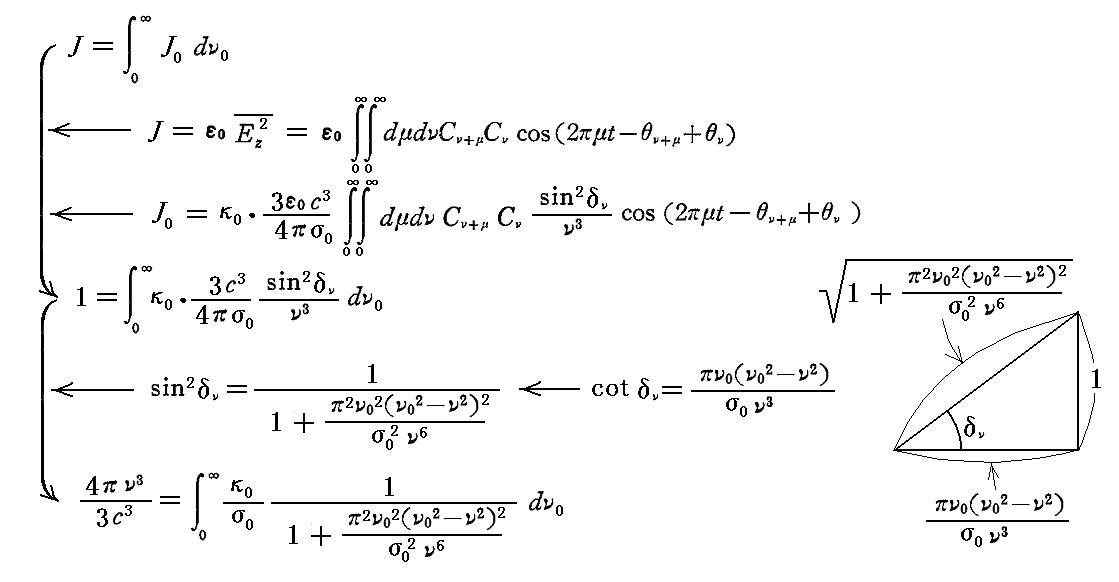
ここで、σ_νは１よりも非常に小さな値だから、積分記号中の関数の値はν₀がほとんどνに等しいようなものだけを考慮すればよい。すなわち

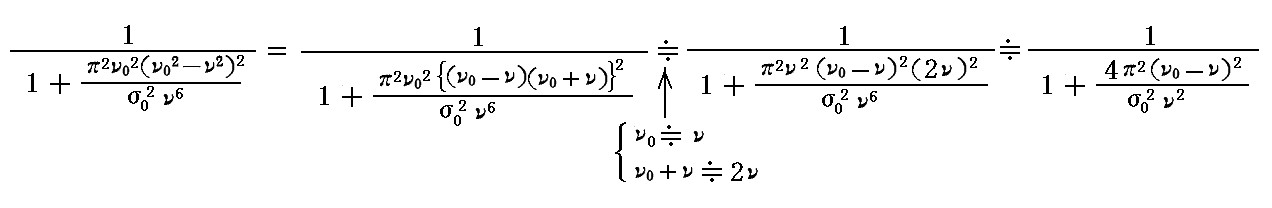
と置けるので上記の積分は

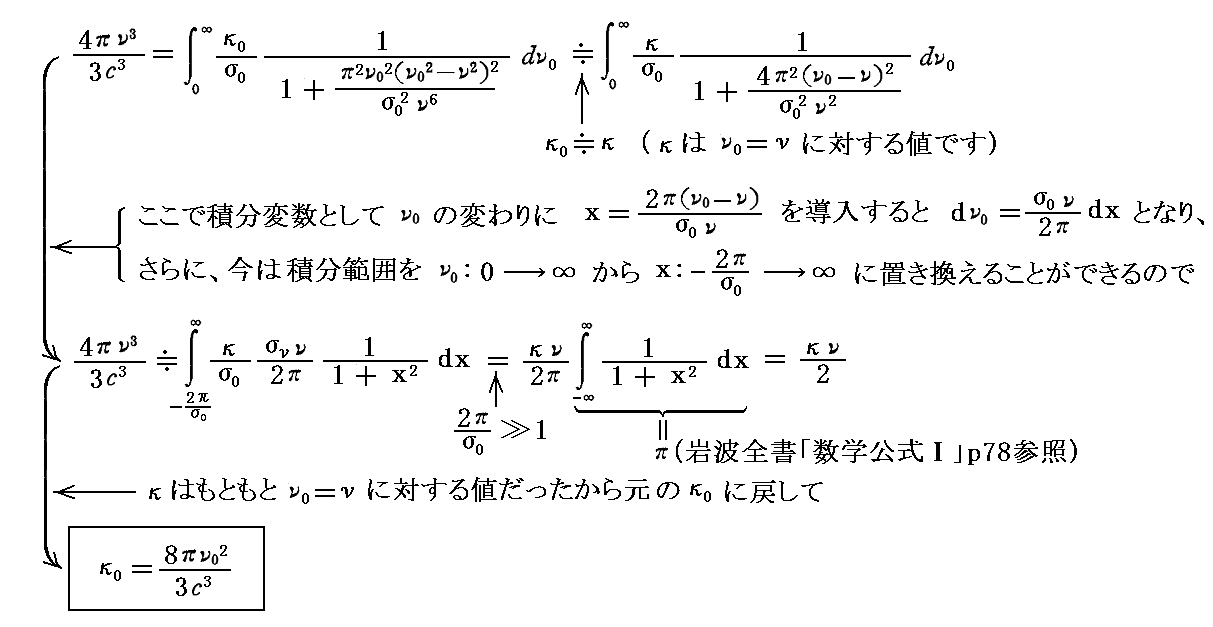
となる。
　従って、振動数ν₀の強さＪ₀は次のようになる。


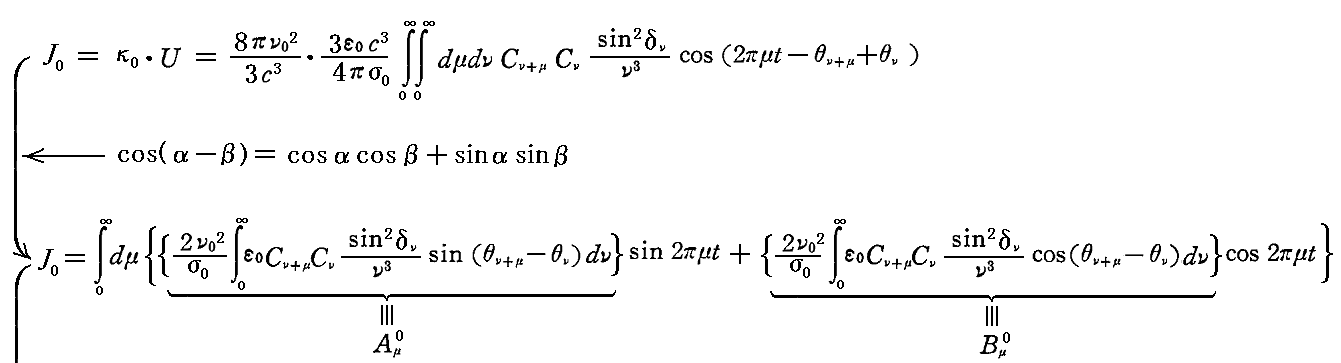
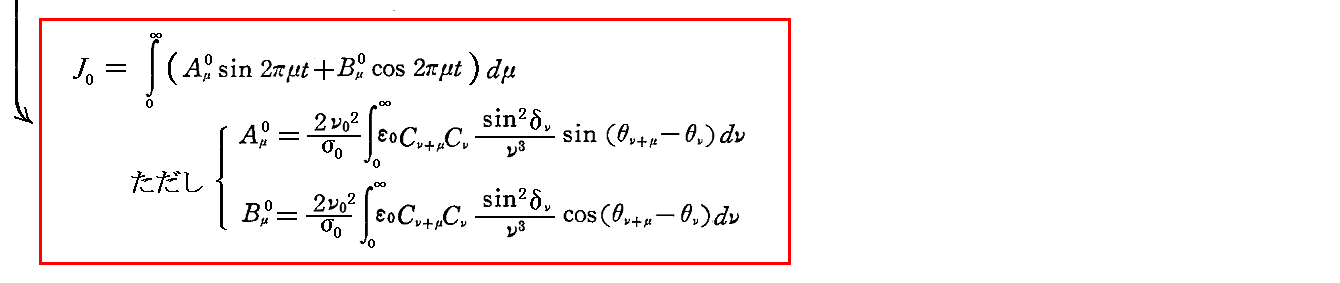
　一般にＡ_μ⁰とＢ_μ⁰の値はまだσ_νに多く依存するであろうから、確定的な意味に於いて振動数ν₀の強度Ｊ₀について言うことはできない。
　ここで、先の議論の為に以下の仮定をする。すなわち

　各振動数νは、測定に用いられる量σ_νに無関係な、時間と共に“ゆるやかに変化する”一定の振動強度Ｊ_νをもつとする。また、その振動強度については２．（２）２．で導入した条件が満たされて、励起振動Ｅ_zの全体の強さＪは

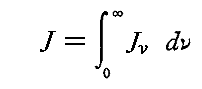
の関係を満たすとする。

２．自然輻射の仮定（原論文3．§9、著書10．§181）

　ここまでの議論で、“速く変化”して直接測定することが不可能な励起振動Ｅ_zを分析して、測定可能な振動数νの振動強度Ｊ_νの和で全体の強度Ｊを表すことが可能になった。
　しかしながら、“速く変化する”励起振動Ｅ_zに付いてハッキリと解ったと言える性質はほとんど無い。関数Ｃ_νやθ_νはνに依存するがその実態については未知のままである。
　ここでさしあたり、時間ｔの“ゆるやかに変化する”関数である振動数ν₀の強度Ｊ₀を測定することにより知ることができる“速く変化する”量Ｃ_νおよびθ_νについての性質についてまとめておこう。前節に出てきた式のＡ_ν⁰とＢ_ν⁰はすべてのμの値に対して測定可能と考えられる。ここで仮に

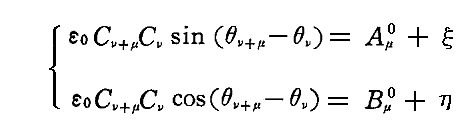
と置けるとする。つまり、ここＡ_ν⁰とＢ_ν⁰は測定可能な“ゆっくり変化する”量であったが、“速く変化する”量である左辺が、その“ゆっくり変化する”量にその変分として“速く変化する”量ξやηとの和で表されるとするのです。ξやηはνおよびμの“速く変化する”関数です。
　その様に置けるとすると

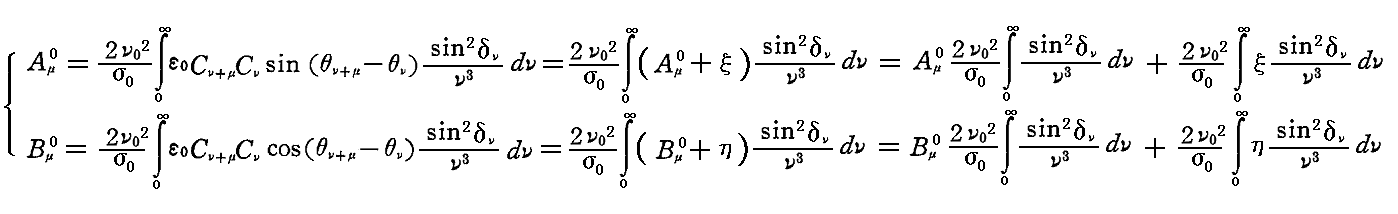
となる。
　ここで

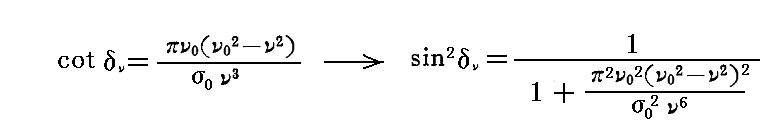
を考慮すると

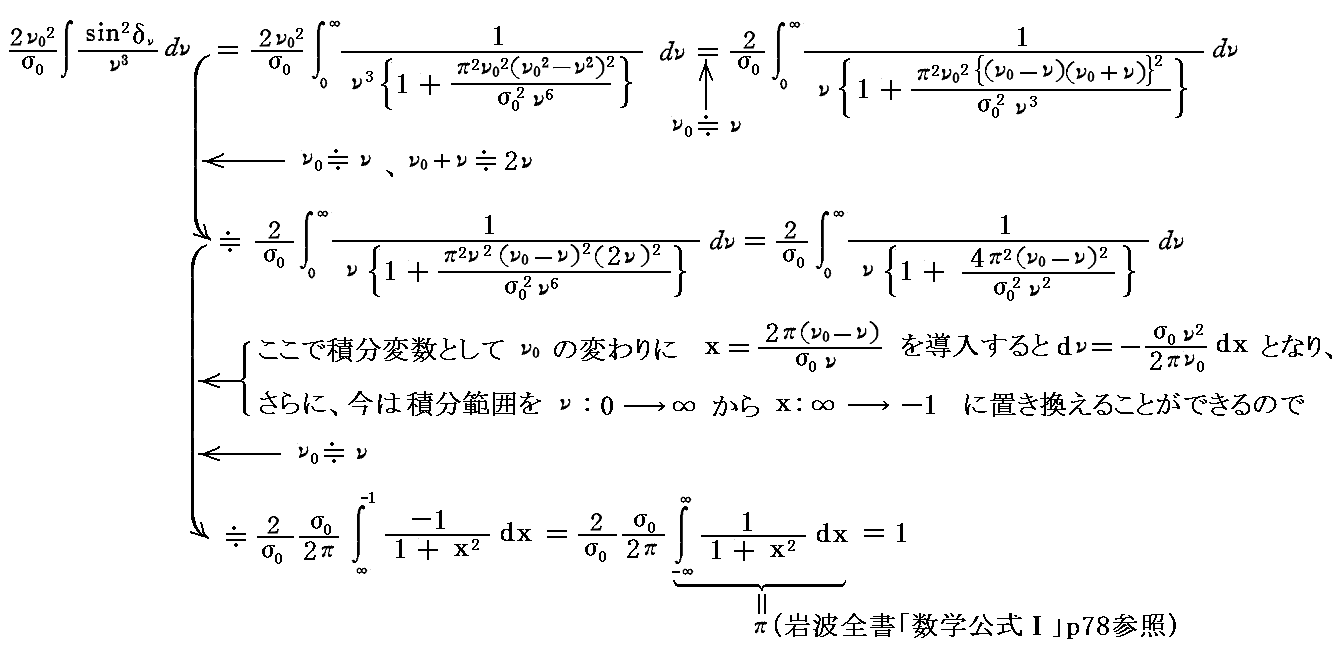
となる。従って前記の式が成り立つためには

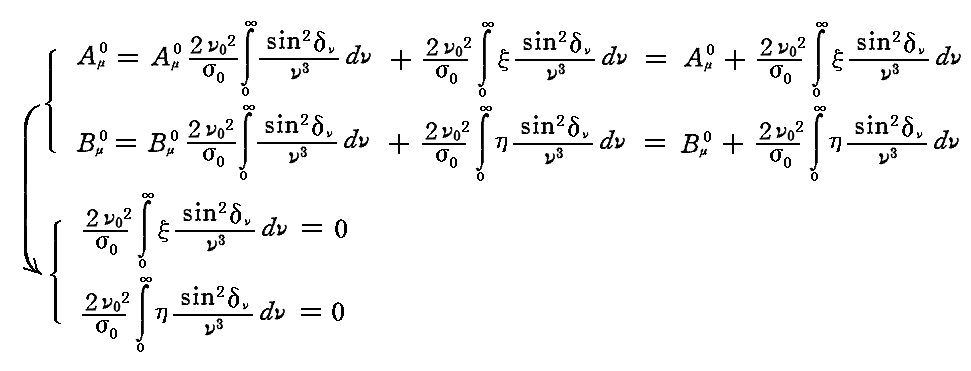
でなければならない。つまり変分としてのξやηの時間的平均はゼロになると言うことです。ここでの計算に於いて、sinδ_ν／νはνがν₀にごく近い所を除いて極めて微小である事実を用いて積分を実施している。
　結局のところ、量Ａ_ν⁰は“速く変化する”量ε₀Ｃ_ν+μＣ_νｓｉｎ（θ_ν+μ−θ_ν）の、ν₀に近いνに対する、“ゆるやかに変化する”平均値を表す。同様にＢ_ν⁰は“速く変化する”量ε₀Ｃ_ν+μＣ_νｃｏｓ（θ_ν+μ−θ_ν）の平均値を表す。

　ここで振動数ν₀、減衰度σ_νの振動子の研究にもどると、励起振動Ｅ_zの振動子へ及ぼす影響を計算するためには、一般に平均値Ａ_ν⁰とＢ_ν⁰についての知識では十分ではなくて、量Ｃ_νおよびθ_νを知る必要があることが、直ちにわかる。
　実際、振動子のエネルギーＵは、その表式

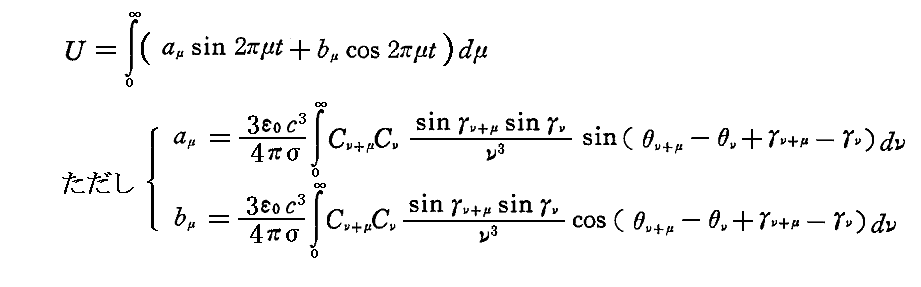
から解るように、Ｕの値はνがν₀に近いときのε₀Ｃ_ν+μＣ_νｓｉｎ（θ_ν+μ−θ_ν）およびε₀Ｃ_ν+μＣ_νｃｏｓ（θ_ν+μ−θ_ν）の値をそれぞれ与えることができて初めて正確に計算される。言いかえれば、励起振動に含まれる振動数ν₀の強度Ｊ₀はたとえそれがあらゆる時刻について知られいていても、一般にその振動に当たった振動子のエネルギーＵを決定しない。

　従って、量ＵおよびＪ₀の間の一般的関係を確立することを断念するか、あるいは、新しい仮説を導入してそこに存在する亀裂の橋渡しをする以外にはない。実際、物理的事実は第二の方法で行くしかないことを示唆する。
　その仮説は、いま最も手近でおそらく唯一の可能なものとして導入され、以下の議論でのすべてで保持されることになるものす。その仮説とは

　前記の式により振動子のエネルギーＵを計算するとき、係数ａ_μおよびｂ_μの値を与える積分において、“速く変化する”量ε₀Ｃ_ν+μＣ_νｓｉｎ（θ_ν+μ−θ_ν）およびε₀Ｃ_ν+μＣ_νｃｏｓ（θ_ν+μ−θ_ν）の代わりに、“ゆるやかに変化する”それらの平均値Ａ_ν⁰およぴＢ_ν⁰を用いることができる。

というものである。従ってＪ₀からＵを計算するという課題は測定によって確かめることができる完全に定まった解を得る。上記の仮説が適合するような輻射を“自然輻射”とよび、上記の仮説を“自然輻射の仮定”と呼ぶことにする。
　自然輻射の仮定とは結局のところ、測定不可能な“速く変化する”量であるε₀Ｃ_ν+μＣ_νｓｉｎ（θ_ν+μ−θ_ν）、等々の、測定可能な“ゆるやかに変化する”平均的な量Ａ_ν⁰、等々からの変分が完全にアトランダム（不規則）に起こるとすることと同じです。

３．拡張された理論の基礎方程式（原論文3．§10、著書10．§182）

　前節で導入された仮説に従って振動子のエネルギーＵを計算するときのｄνに関する積分係数は


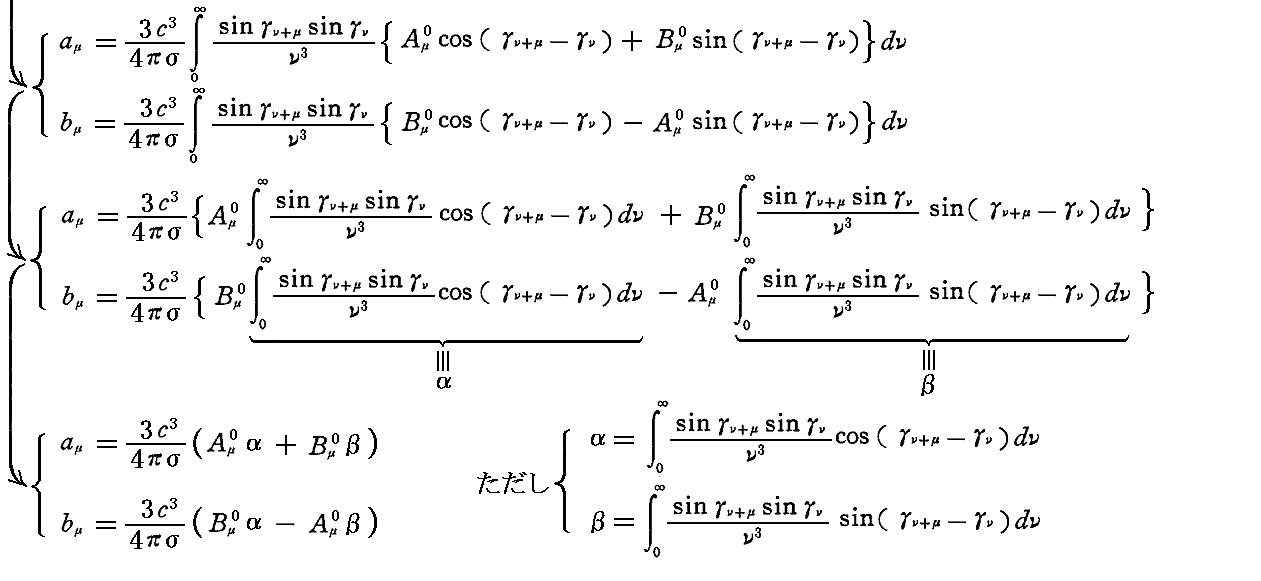
となる。そのためＵは

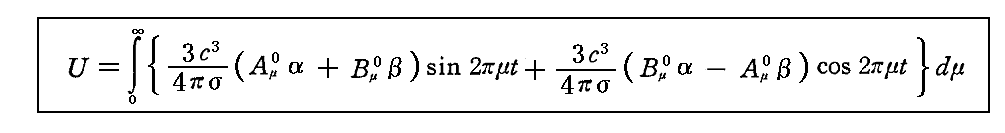
となる。
　ここで、σが小さく、一般的にμが最大でもσν₀と同じ大きさの程度か以下であるから

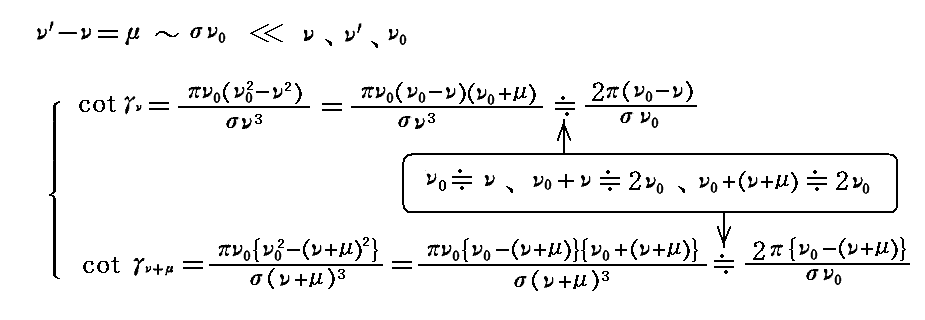
とおける。そのため

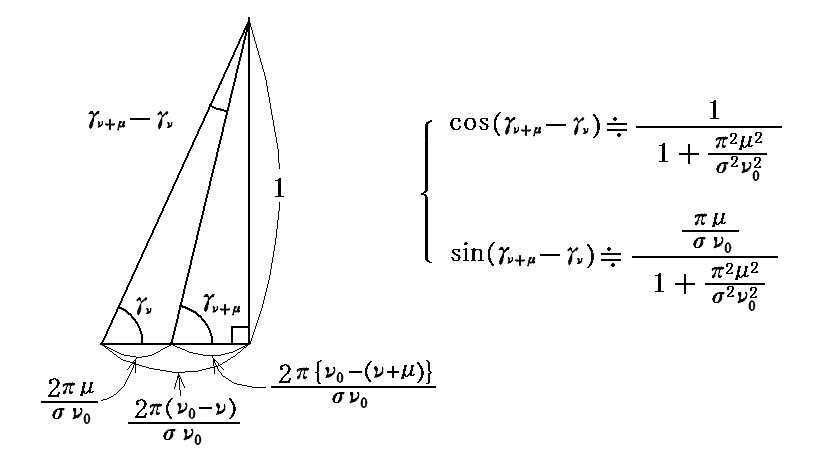
となる。

［補足説明１］
　正直なところ、上記の式変形が旨くたどれないのです。cos（γ_ν＋μ−γ_μ）もsin（γ_ν＋μ−γ_μ）も、こことは少し違った形になると思うのですが、後の式変形を考慮して、その当たりは積分変数μの任意性に負わせてあえてこの形にしたのかも知れない。たしかにその様にすることは可能だとは思うのですが？

　このことを考慮すると、いままで何度か考察してきたのと同じように考えて初等的な積分操作を実施すると

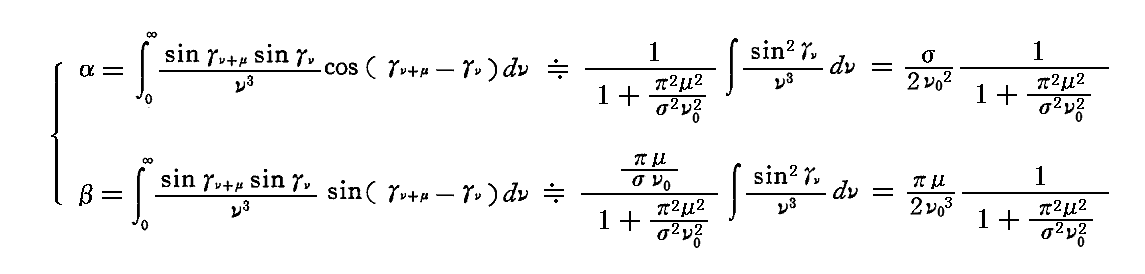
が得られる。したがって

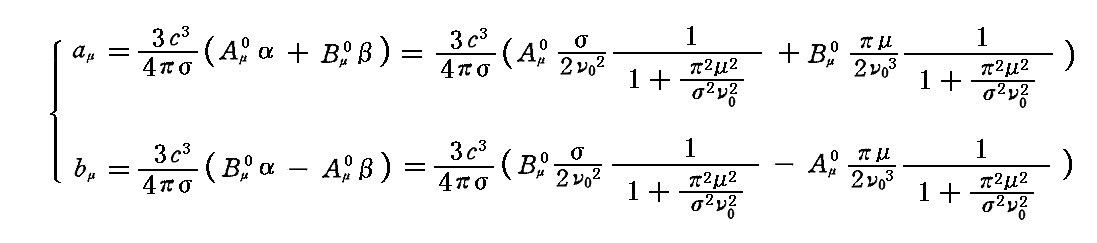
となる。これを代入すると
　
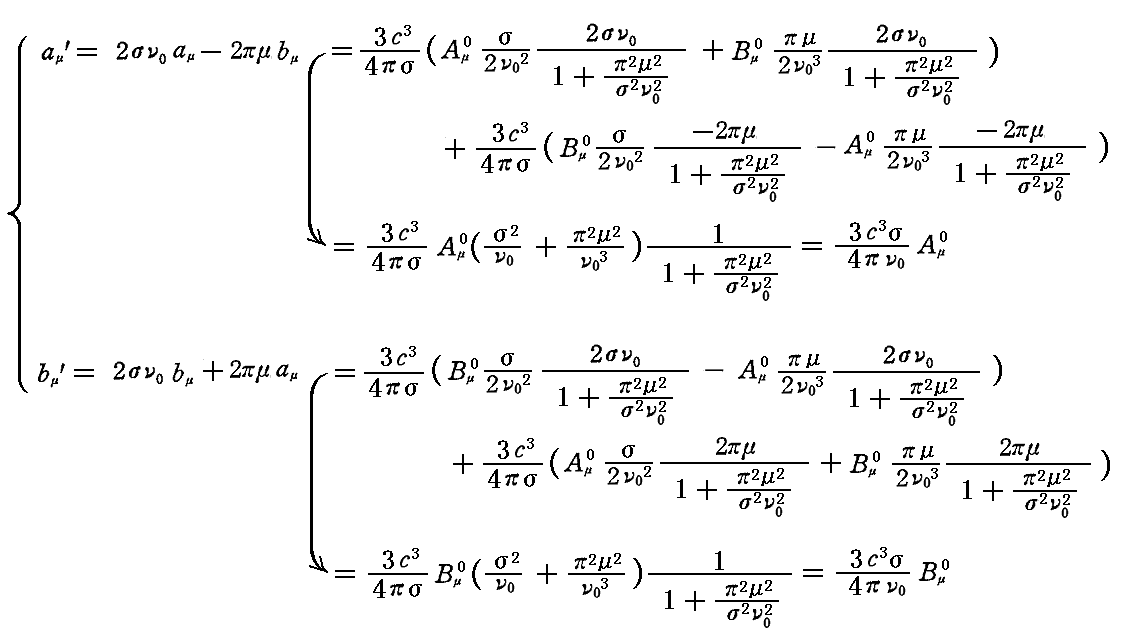
となる。したがって、ｄｔ時間に振動子によって吸収されるエネルギーは

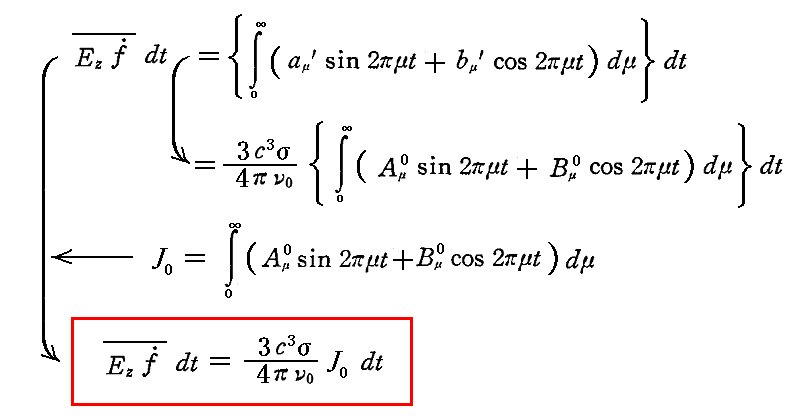
となる。すなわち

　ある［時間要素ｄｔ内に振動子によって吸収されるエネルギー］は、［励起振動に含まれるその固有周期の強度Ｊ₀］、［その対数減衰度σ］、［光速度の３乗ｃ³］に比例し、［振動数ν₀］に反比例する。

　ここで求めた吸収エネルギーの値を２．（３）３．のエネルギー方程式に代入すると

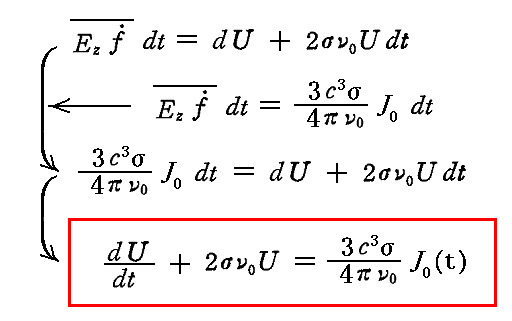
が得られる。
　この非同次一階線形微分方程式は、振動子の固有振動数ν₀に対応する励起振動の強度Ｊ₀が時間の関数として与えられるとき、振動子のエネルギーＵの計算に用いることができる。
　関数Ｕ（ｔ）およびＪ₀（ｔ）はもはやFourier積分によって表される必要はないから、今後２．（２）１．で導入した問題にする時間間隔についての制限をとりはらうことができる。

４．基礎方程式の解（原論文3．§10、著書10．§182）

　上記の非同次一階線形微分方程式の一般解は同次微分方程式

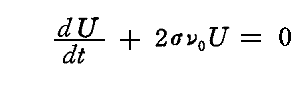
の解に定数変化法を適用することで求めることができる。同次微分方程式の解は

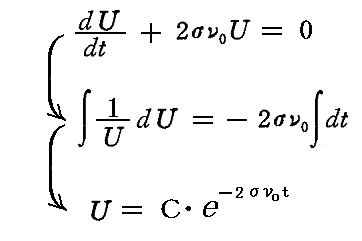
である。
　このとき、Ｃは定数であるが、これをｔの関数としたとき非同次微分方程式の特解が得られるか試してみる。

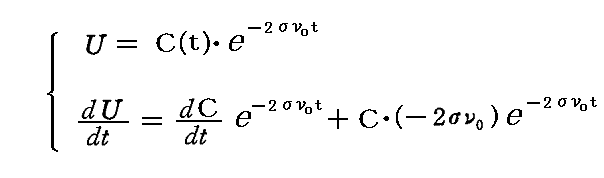
であるから、これらを前記の非同次微分方程式に代入すると

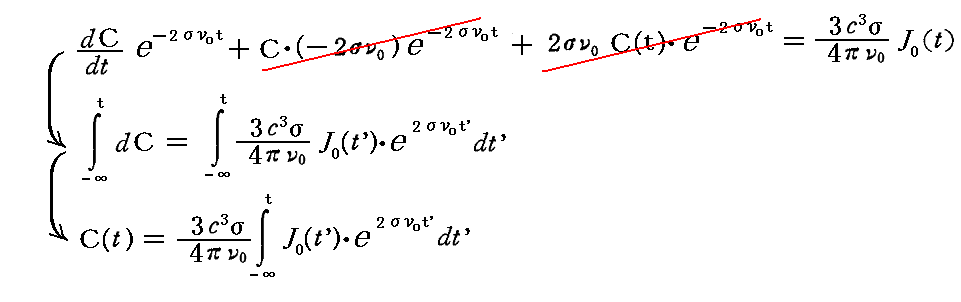
が得られる。
　これを前記の解に適用すると、非同次一階線形微分方程式の一般解は

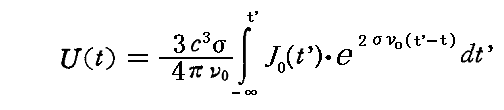
となる。
　ここでさらにＪ₀が時間に依存せず一定のときにはｔ’に関する積分は簡単に実行できて

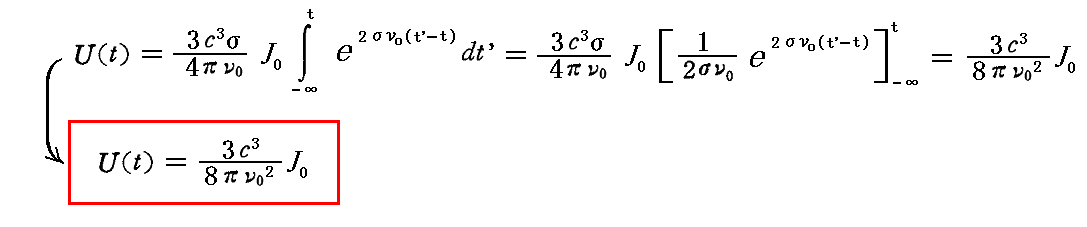
が得られる。

　一定の照射の場合、［振動子のエネルギーＵ］は［励起振動に含まれる振動子の振動数に一致する部分の強度Ｊ₀］と、［光速度の３乗ｃ³］に比例し、［振動数の２乗ν²］に反比例する。このとき［減衰係数σ］には依存しなくなることに注意。

　ここまでの議論で［振動子のエネルギー］と［励起振動の強度］との関係を確立することができた。つぎに成すべき事は、［励起振動の強度］と［周囲の場に満たされているエネルギー輻射］との関係を導くことである。

３．エネルギーの保存（原論文3．§11〜16、著書10．§183〜186）

　この章から、振動子を取り囲む電磁場における過程の考察に移るのですが、これから先の議論では第２章で導いた結論を至るところで用いる。そのとき輻射場のすべての場所、すべての時間に対して２．（４）２．で導入した“自然輻射の仮定”が満たされているとする。したがって、今後は振幅や位相によって計算する必要はなく、その代わりに強度、エネルギーといった［２．（２）３．の意味で］“ゆるやかに変化する”量だけで計算すればよい。
　以下で用いる空間要素や時間要素の意味もまたこの意味で理解すべきである。つまり、これらの要素は、考察する空間や時間の大きさに対して十分小さく、しかしそれでもなお考察する波長や振動周期に比べれば大きいような量と考えねばならない。
　今後、考察している空間を囲む容器壁の曲率は考察の対象としているすべての波長よりも大きく、完全に反射する静止した壁でできているとする。そのため今後は壁における屈折の現象は無視でき、壁は直線的に進行する輻射でくまなく照らされているとする。

（１）振動子のエネルギーと輻射強度（原論文3．§11〜13、著書10．§183）

１．一定方向と振動数と偏光を持つエネルギー輻射の強度と励起振動の強度の関係（原論文3．§11、著書10．§183）

　真空中の一点における電磁場のエネルギーの空間密度はMaxwellの電磁気学によると

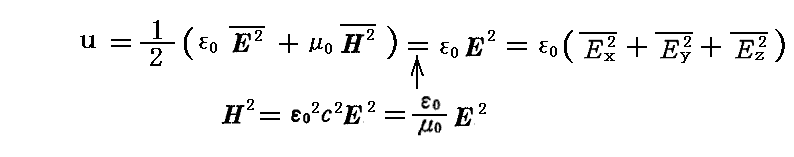
となります。ここで、ここで、Ｅ_x²、Ｅ_y²、Ｅ_z²に上横棒を付けた量は電磁場の各成分の二乗の時間的な平均値であり、ＥやＨそのものの時間的な変化に比べて時間的に“ゆるやかに変化する”量と考えることができる。

　点Ｏに前章で考察した共鳴子が１個存在すると仮定し、その軸をｚ軸に取る。そのとき共鳴子を励起する輻射の振動の強さは

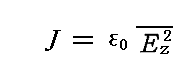
です。
　以下でこの値を算出することにしよう。この目的のためには共鳴子の位置Ｏを通る単色の輻射線の“偏光”にも考慮しなければならない。以下の議論は別稿「偏光とは何か(光の強度と偏光)」６．(１)の図と説明を参照しながらお読み下さい。
　そこの図の(ｒ，π−θ，φ＋π)の位置にある面積要素ｄσ’から来て、(θ，φ)方向に点Ｏを通過する輻射線に着目する。

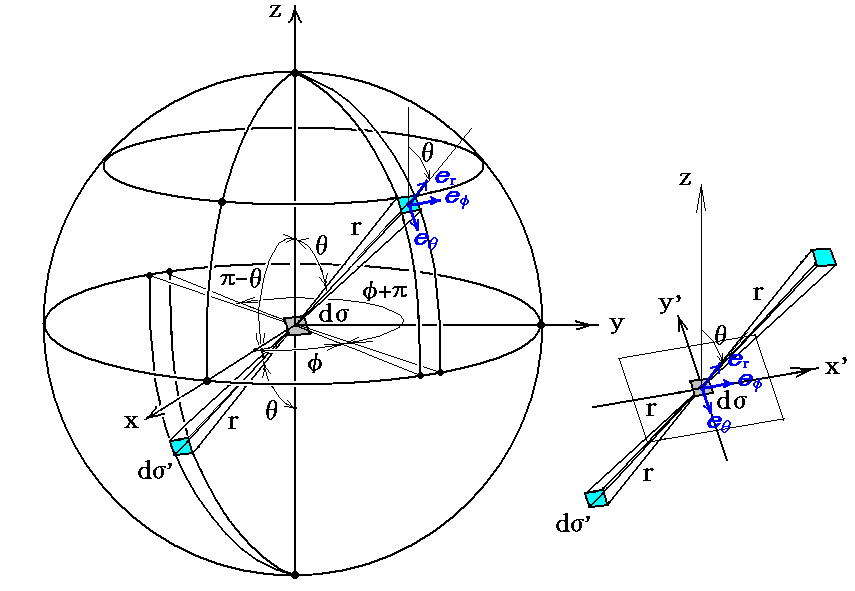
　この輻射線の強度は一連の単色輻射線に分かれる。各振動数に属する輻射線の強度は、楕円偏光の主強度ＲとＲ’を用いると下記の様に表される。ただし、ここでは［主値Ｒ’に属する偏光面］が［輻射線方向とｚ軸（振動子の軸）を通る平面］となす角をωとしている。

　下図の楕円偏光を表す面は、上図の光線の進行方向に垂直な二つのベクトルｅ_φとｅ_θが構成する平面に平行でしかも原点をとおる平面内にあるとする。

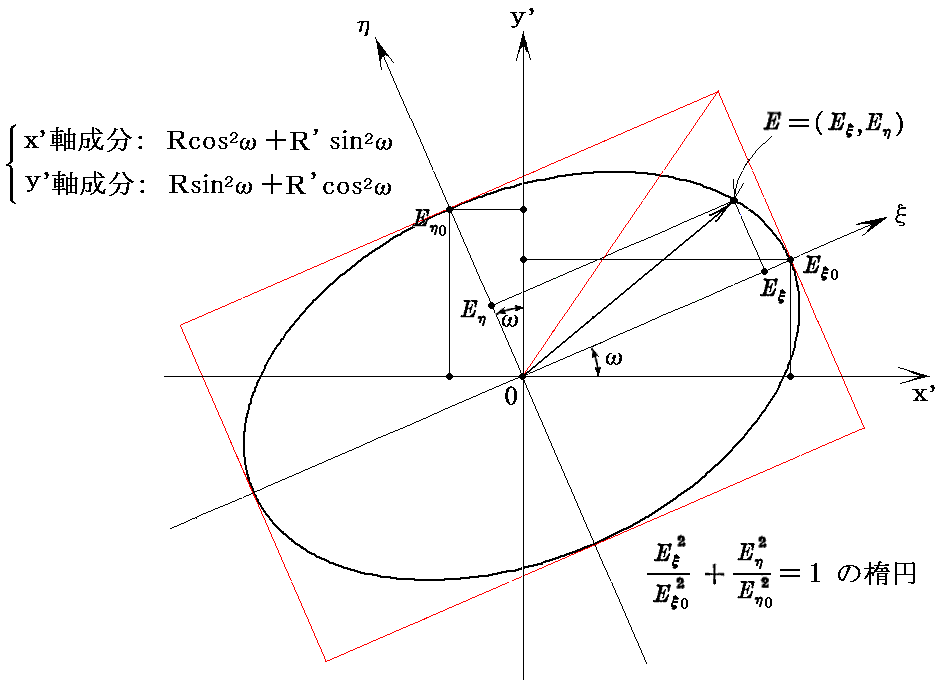
　上記の楕円偏光を示す図のｘ’軸を前図のｅ_φ方向、ｙ’軸を−ｅ_θ方向にに取ると、前記の球面座標図のｚ軸成分のみが共鳴子を励起する輻射となるので上記楕円偏光のｙ’軸成分(Ｒｓｉｎ²ω＋Ｒ’ｃｏｓ²ω)のみが残る。

［補足説明１］
　プランクはＨベルトルの方向で偏光面を定義していますが、ここではＥベクトルの方向を偏光面としている。
　またここで採用している楕円偏光を表す図（上図参照）は、古典光学で採用されている向かってくる光線を見て描かれている図であることに注意されたし。

　ポインティングの定理に従えば、［真空中の直線偏光した輻射線の強さ］は［電場の二乗平均］したものをｃ･ε₀倍したものに等しい。したがってここで考察している輻射線の電場の二乗平均は

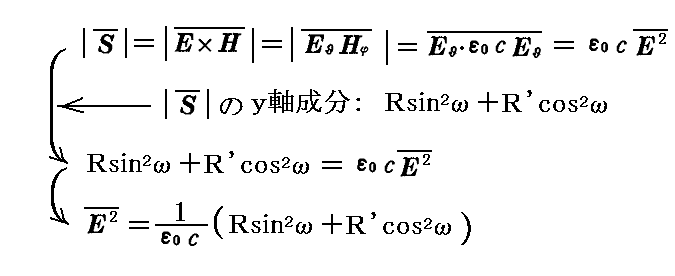
となり、励起振動の強度は、この球座標に於けるｚ軸方向の成分の二乗平均である。ところで振動子の位置に於ける電場の方向とｚ軸の成す方向は角（π／2−θ）をなす。そのため電場のｚ軸に沿った方向の成分は輻射線に垂直出会った電場の成分のcos（π／2−θ）＝sinθ倍したものになるので、二乗平均であることを考慮しすると振動子を励起する輻射の強度は

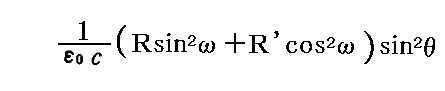
となる。
　振動数および立体角のすべてについて積分すれば、求めるべき励起振動の強度が得られる。すなわち

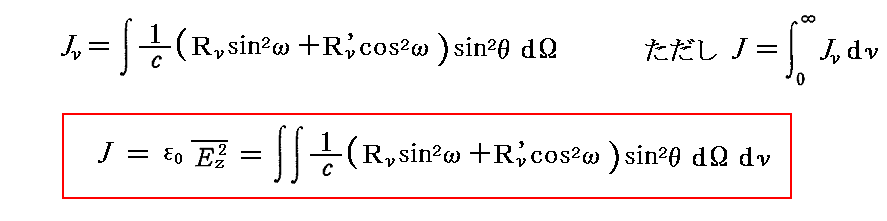
となる。こここまでのＲ_ν、Ｒ_ν’は一般に方向（θ，φ）や時間 ｔ の関数です。

　ここで、すべての輻射線が偏光しておらず、また輻射線の強さがすべての方向で同一（等方的）ならば、Ｒ_ν＝Ｒ_ν’となり、Ｒ_νをｄΩに関する積分の外に出せるので

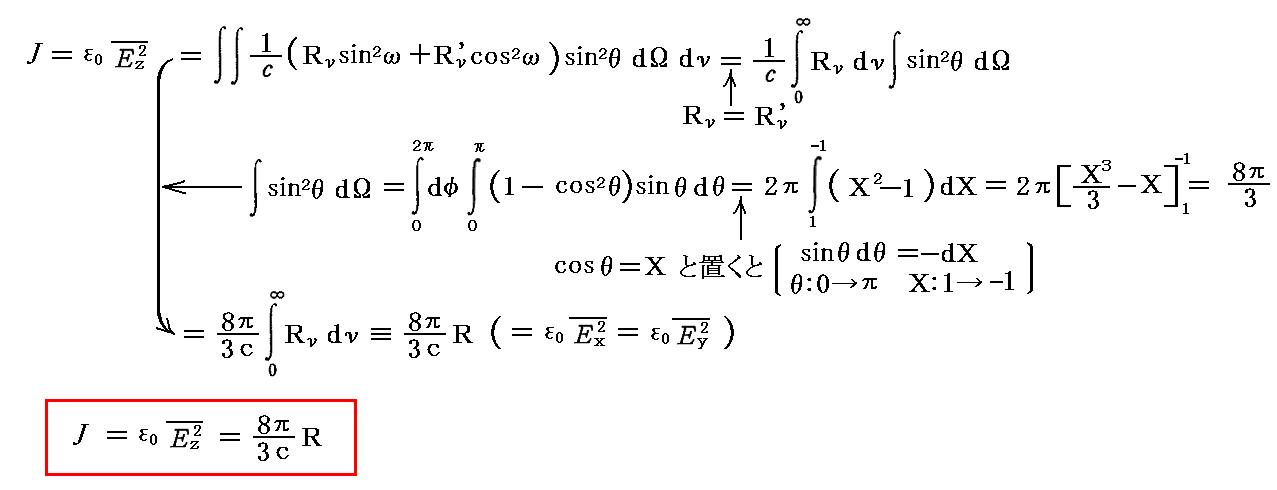
となる。ここのＲは時間のみの関数です。

［補足説明２］
　ここでＪとＲの違いに注意して下さい。この違いを理解しないとここの議論の意味が解らなくなります。
　Ｊはあらゆる方向から振動子に当たる輻射光線が、いま注目している一つの一次元振動子の振動に影響をおよぼす輻射強度のことです。
　一方、Ｒはその輻射場が等方的な場合に任意の方向の単位立体角を通過する輻射線の強度です。等方的なのだからどれか一つの方向について代表させて測定すればよいわけです。
　
　そのときある振動数についての強度Ｊ_νに寄与するＲ_νの効果はその輻射線の方向によって異なるのですが、輻射場が等方的な場合Ｒ_νは方向によらず一定なので、あらゆる方向に進む輻射線のすべての効果を加え合わせるｄΩに関する積分の外に出せます。そのため 当方的な輻射場の場合Ｊ_νはある任意の単位立体角の方向に進む輻射線の直線偏光した光の強度Ｒ_νで表せることになる。
　
　そのとき振動方向がｚ軸に一致する振動子に対する励起振動強度Ｊ_νに寄与するＲ_νの方向に依存する効果はsin²θについてのｄΩ方向積分の中で考慮されていることに注意して下さい。方向の違いによる影響の積分値が係数8π／3です。

２．輻射のエネルギー密度（原論文3．§12、著書10．§183）

　これを、３．（１）１．のエネルギー密度の表現式に代入すると

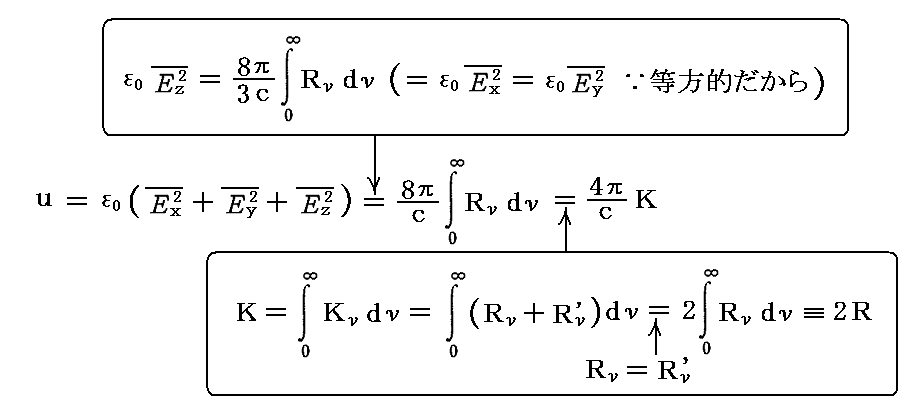
が得られる。
　これは、別稿「キルヒホッフの法則（熱的放射平衡における）」３．（２） や 「偏光とは何か（光の強度と偏光）」６．（２）２． で証明した

等方的な輻射で満たされている空間のエネルギー密度ｕは、輻射強度Ｋと次の関係にある。

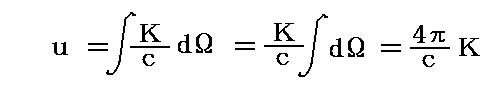
を、もう少し立ち入った計算で確認したことになる。

３．１個の振動子を励起する振動の強度（原論文3．§13、著書10．§183）

　振動子のエネルギーＵと励起振動の強度Ｊは、２．（４）３．で導いた方程式

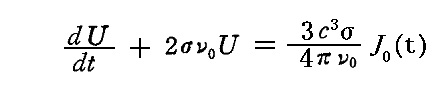
によって関係づけられていた。
　上で得たＪ_νとＲ_ν関係式

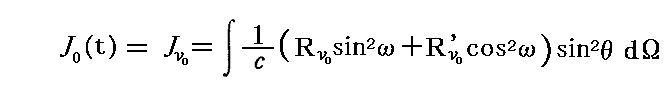
を用いて、この方程式のＪ₀（ｔ）＝Ｊ_ν（ｔ）をＲ_ν（θ，φ，ｔ）、Ｒ_ν’（θ，φ，ｔ）に置き換えることができる。そうすると、あらゆる時刻に振動子に当たるすべての輻射線の強度と偏光が知られていれば、任意の時刻の振動子のエネルギーを計算することが可能になる。
　今後は一般的に固有振動数νの任意の振動子について考えることにするので、添え字0 を省略して記述することにする。

　特に偏光していない、すべての方向に一様な輻射に対しては、Ｒ_ν＝Ｒ_ν’となり、Ｒ_νをｄΩに関する積分の外に出せるので

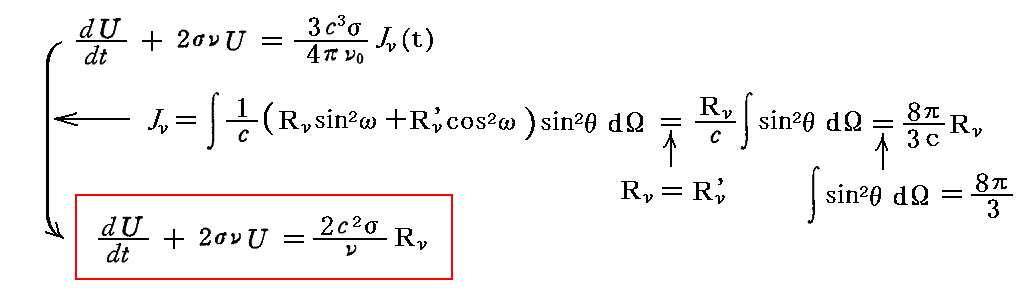
を、２．（４）３．と同様な方法で解けばよいのです。ここでのＲ_νは空間的には等方的だが、まだ時間の関数Ｒ_ν（ｔ）であることに注意して下さい。

　偏光していない、すべての方向に一様（等方的)な輻射の条件に付け加えて、さらに輻射が時間に依存しない“定常状態”であるならばＵもＲ_νも時間に依存しないと考えてよいので、ｄＵ／ｄｔ＝0を考慮すると

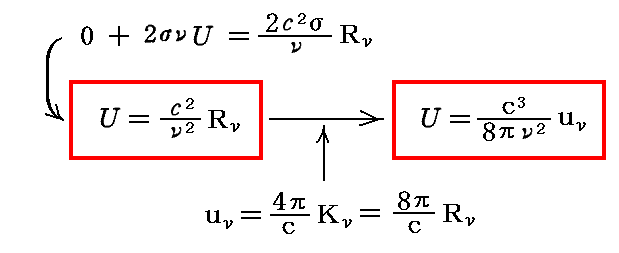
となる。
　ここで、　Ｕは固有振動数がνのただ一つの振動子（共鳴子）のエネルギーの平均値であり、　Ｒ_νは単色（振動数νを中心とした単位の振動数幅に含まれる）で直線偏光した単位立体角の方向へ進行する輻射強度（輝度）を表す。　また、　ｕ_νは輻射場の中の振動数νの輻射のエネルギー密度です。
　
　これは極めて重要な結論です。これは、定常的な輻射状態が実現されている場合には［固有振動数がνの振動子のエネルギーＵ］は、［振動数νの輻射の強度Ｒ_ν］あるいは［振動数νの輻射のエネルギー密度ｕ_ν］と密接に関係しており、それらの値により一意的に決まることを示している。
　そのとき、、振動子に対して用いた特殊なモデルに固有な量 ｅ や ｍ や減衰係数σ などは消去されており、また定数ε₀ も落ちていることに注意されたし。つまり、熱平衡状態にあるときには固有振動数ν 以外の性質には関係せずこの関係は一般的に成り立つのです。
　
　そのため、プランクは熱輻射論を進めるに当たって、前者Ｕを後者ｕ_νあるいはＲ_νの代わりに用いることができた。

［補足説明１］
　ここまでの１章〜３章（１）で説明した内容が、プランクが解説文12．で

　“・・・このかなりにわたる一連の研究は、それぞれが現今の諸観測、とりわけ、V・ビェルクネスの減衰測定との比較によって吟味され、またそのことによって確証された［Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 20. Februar 1896； Ann. d. Physik, Bd. 60, p577, 1897 に再録］のだが、その成果は、一定の固有周期をもった共振子のエネルギーと、周囲の場にあってそれに対応するスペクトル範囲のエネルギー輻射との、定常のエネルギー交換における一般的な関係を定めた［Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 18. Mai 1899, p455； Ann. d. Physik, (4)1, p69〜122, 1900 に再録(古典論文叢書10)、これはSitzungsber. Berl. Akad. Wiss. に発表した一連の５編の論文1897(2/4、7/8、12/16)、1898(7/7)、1899(5/18)の最後のもので総まとめの論文です］ことであった。
　その際、明らかになったのば、この関係が共振子の性質にまったく依存せず、とりわけ、その減衰定数にも依存しないという、まことに注目すべき結果であるが、これは私にとって非常に喜ばしい、好都合な事情であった。
　なぜなら、そのことによって、輻射のエネルギーの代りに共振子のエネルギーをとることができ、こうしてまた多くの自由度からなる錯綜した系の代りに、唯一の自由度をもつ単純な系を当てうるということで、問題全体が簡単になったからである。・・・”

と言っているものです。

［補足説明２］
　プランク自身も２章〜３章（１)の議論はかなり込み入っていて解りにくいと感じていたようです。そのため後の論文
「正常輻射場における線形共鳴子の振動法則の簡単化された導出」, Physikalische Zeitschrift 2, p530〜534, 1901年
でもっと簡単な導出法を報告しています。それが著書10．の§116〜123で説明されているものです。
　また、これがゾンマーフェルトの文献15．§20．D．、ファインマンの文献17．§16-2、16-3、太田浩一「電磁気学の基礎�U」の§14.7等々・・・に引用されているものです。
　
　この簡単化された導出法を解りやすくまとめ直したものを別稿の［付録１］で紹介しておりますので、この稿の説明と比較してみて下さい。“黒い輻射”に関して思い切った仮定をすることで論理展開は見通しが良くなって理解しやすくなっています。ただし、その中で設定されている等方性と独立性の仮定自体が解りやすくなっているわけではありません。

［補足説明３］
　ここまでの成果を得る以前に、プランクは線型振動子から［放出される輻射］と［吸収される輻射］に付いての微分方程式には時間的な非対称性があり、これを積分することにより輻射が不可逆的に平衡状態へ近づいていくことが導けるのではないかと考えていました。つまり、１章の最後で求めた微分方程式に於いて、ｆ の微分を ｔ についてではなくその代わりに −ｔ に付いて行うならば、減衰項の符号が変わり振動過程は逆方向には起こらないとして非可逆性が導けるのではないかと考えていたのです。
　当初、その方針で研究を進めていたのですが、それは結局旨くいきませんでした。プランクは、その当たりの事情を解説文12．で

　“・・・もちろん、この成果の意味するところは、今やまったく見当もつかない高さで、いっそうけわしくそびえたつことになった本来の課題に着手すべく、ほんの準備的な一歩を印したものにすぎない。
　これを征服しようとする最初の試みは失敗に帰した。なぜなら、私がもともとひそかに期待していたのは、共振子から放出される輻射が何らかの特徴において吸収される輻射とは区別され、そのことからある微分方程式が立てられて、これを積分すれば定常の輻射の性質をきめる特殊な条件が得られるだろう、ということであったが、これは見事に裏切られたのである。
　共振子は、自ら放出するのと同じ輻射にだけ反応して、近接するスペクトル範囲に対しては少しも感応しなかった。
　そのうえ、共振子が、一方的な、それゆえ不可逆の作用を、周囲の輻射の場のエネルギーに及ぼしうるだろうとする私の臆測は、ルドヴィヒ・ボルツマンの激しい反駁をひき起す［L.Boltzmann, Sitz.-Ber. d. PreuB. Akad. d. Wiss. vom 3. Ma¨rz 1898, p182］ことになり、彼は自分のより豊富な経騒をもって、この問題に関し次のことを証明してみせた。
　すなわち、古典力学の法則によれば、私の考察した事象のすべてはまさに反対の方向にも生じうるもので、つまり、共振子からいったん放出された球面波は、逆に外から内へと、絶えず縮小してゆく同心の球面となって共振子にまで収縮しつづけ、それによってふたたび吸収され、そのことによって他方また、以前に吸収したエネルギーを、それがやってきた同じ方向へと、共振子をしてふたたび空間内に送り出させるというのである。・・・”

と記しています。
　つまり純粋に力学的・電磁気学的な考察だけからは時間軸に関して完全に対称的な、すなわち可逆的な結論しか出てこず不可逆的に平衡へ近づいていく過程を導き出すことができなかったのです。
　それは、全振動過程には振動子自身の振動ばかりではなくそれを励起する１次波も属しており、過程の反転について言うときには振動子ばかりではなくて外場も反転しなければならなかったからです。この当たりは著書10．の§167〜§174で詳しく説明されています。この中には非同次波動方程式の解に関するとても興味深い考察が含まれているのですが、ここでの紹介は省略します。
　いずれにしても、上記の最初の試みに失敗したプランクは、解説文12．で

“・・・かくして私は、問題を一度反対側から、つまり、そうでなくても最初からそのほうが確実な基盤だと感じていた、熱力学から手がけてみるほかはなかった。共振子の温度ではなくて、エントロピーをそのエネルギーと関係させよう、しかも、エントロピーそのものをではなく、エントロピーのエネルギーに関する第二次微係数を関係させよう、なぜなら、これこそが共振子と輻射の間のエネルギー交換の不可逆性に対して、直接の物理的な意味をもつのだからと、ためらわずにすぐ思いついたことによって、事実、ここで熱理論の第二主法則についての私の初期の研究が役立つことになった。
　それにもかかわらず、私はその頃まだあまりにも現象論的な傾向にあり、エントロピーと確率の関連をつきつめて問うことができなかったので、当座はただ、現にある経験の成果だけを頼りにしているありさまであった。･･･”

と言っている考察に進みます。それが原論文3．の後半部§14〜19および著書10．の§184〜190に記載されているものです。以下でそれを説明します。

（２）吸収エネルギーと放出エネルギー（原論文3．§14、著書10．§184）

　ここでは、偏光していない、すべての方向に一様（等方的)な輻射の条件に付け加えて、さらに輻射が時間に依存しない“定常状態”である場合を考察する。

１．吸収エネルギー

　時間ｄｔの間に振動子によって吸収される全エネルギーは ２．（４）３． と ３．（１）１． で得られた結論より

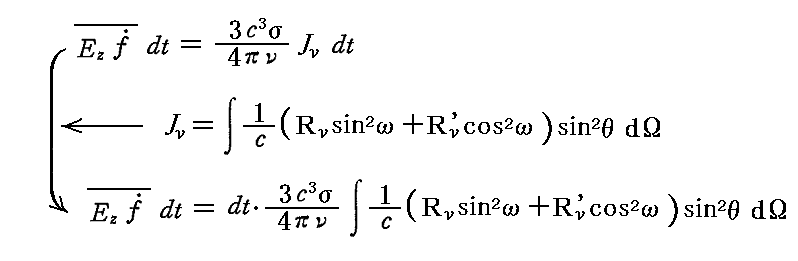
となる。
　したがって、一つの振動子に対して（θ，φ）方向に当たる輻射からは、ｄｔ時間にエネルギー量

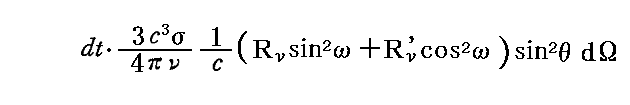
が吸収されることになる。
　ここで、［振動子に対して（θ，φ）方向に当たる輻射の強度］は、その輻射が吸収されうる［すなわち振動子に対応する振動数と偏光を持つ］ものである限り

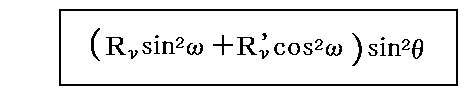
で与えられる。
　そのため次の定理が得られる。

　振動子によってｄｔ時間に吸収されるエネルギーの絶対量は、ある方向(θ，φ）に振動子に当たる吸収されうる輻射の強度(輝度)に

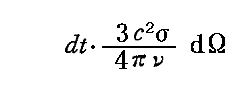
を掛け、それをすべての方向(θ，φ）について積分すると得られる。
　ここで因子（3ｃ²σ／4πν₀）は振動子によって遮られる輻射線ビームの、振動子の位置でのビームの［吸収断面積］とその［スペクトル幅］との積を与えるものである。

２．放出エネルギー

　振動子によってｄｔ時間にあらゆる方向に放出されるエネルギーは２．（３）２．で得られた結論より

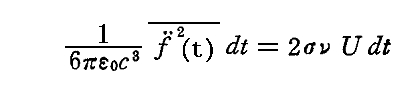
となる。
　ところで、１．（２）で説明したように、もともと

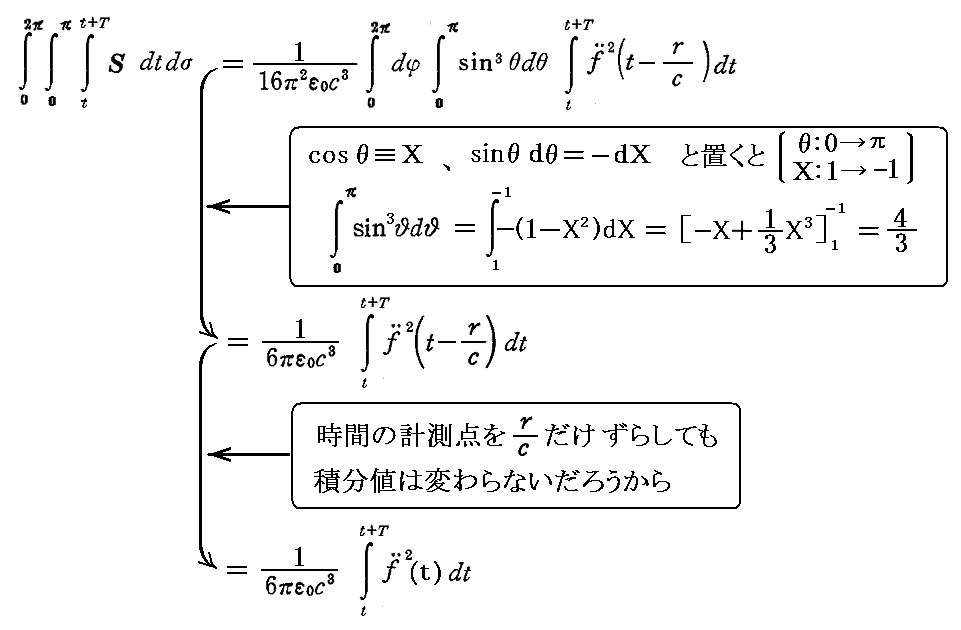
の関係があるのだから

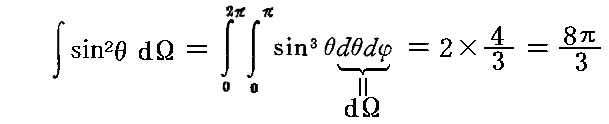
であることを考慮すると上記の式は

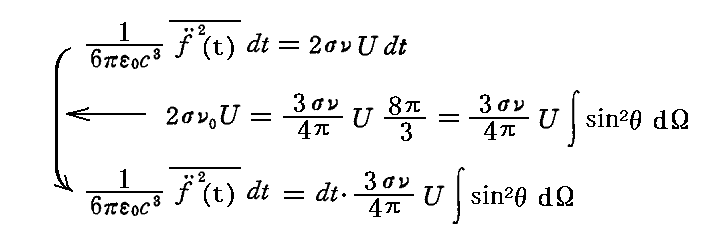
と書き直せる。
　したがって振動子によってｄｔ時間に(θ，φ）方向の単位立体角に放出されるエネルギーは

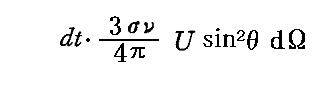
となる。これを

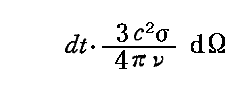
で割れば［同じ（θ，φ）方向に放射される輻射の強度（輝度）］

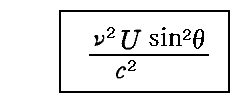
が得られる。

３．定常的輻射状態

　“等方的・定常的”輻射状態においては、前節の終わりに示したように

であるから、これを用いると

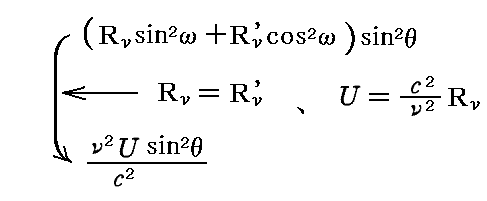
となる。つまり以下のことが確認できる。

“定常的”輻射状態においては、ある任意の方向から振動子に当たる吸収されうる輻射の強度（輝度）は、同じ方向に振動子によって放出される輻射の強度（輝度）に等しい。

　この結論は重要です。なぜなら、振動子に吸収されるエネルギーは入射する輻射のある割合が振動子に吸収されて残りが同じ方向に通過して行くのに対して、振動子から放出されるエネルギーはｓｉｎ²θの項が掛かっていますが、本来あらゆる方向に放射されます。それにも関わらず、“すべての方向から振動子に対して入射する輻射の効果を考慮すると、一つの方向に関して吸収される輻射の強度と同じ方向に放射される輻射の強度が等しくなる”と言っているのですから。

（３）共鳴子を通り抜ける輻射線の強さと偏光（原論文3．§15　、著書10．§185）

　以下の推論の準備として、振動子を通り抜ける輻射線ビームの性質をさらに詳しく考察する。あらゆる方向から輻射線ビームが座標原点Ｏに置いた振動子に当たるものとする。いま振動子に当たる輻射線の内、極座標（π−θ，π＋φ）をもった面要素から原点に向かって（θ，φ）方向にやってくる、振動子に頂点を持つ要素円錐ｄΩ内のものを再び考察する。　
　それらはさらに単色成分に分解されるものと考えられる。そしてそれらの成分のうち振動子の振動数νに対応するもののみに注目すればよい。なぜなら、それ以外のすべての輻射線は、振動子に影響を及ぼさずに、また振動子によって影響を受けずにただ通り過ぎるだけだからです。振動数νの単色輻射線の強度（輝度）は

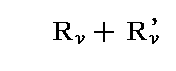
です。このときＲとＲ’は主強度を表す。この輻射線はその主偏光面の方向［ ３．（１）１．で説明したｘ’、ｙ’軸方向 ］にしたがって二つの成分

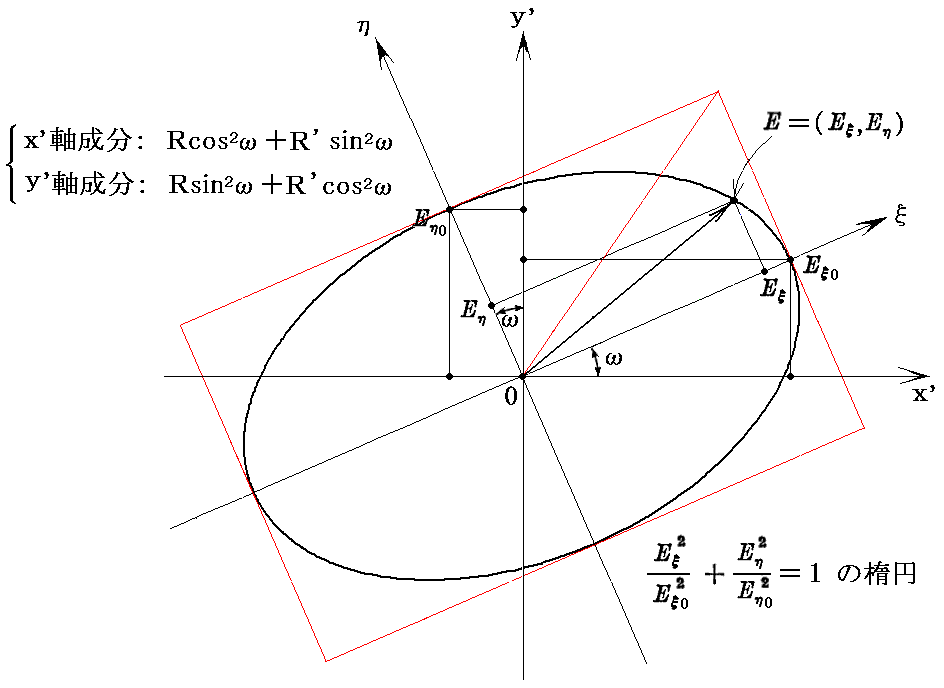
に分解される。

１．ｘ’軸成分

　ｘ’軸方向の成分

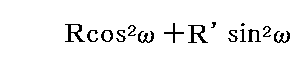
は、まさしく振動子を通過し、何ら変化せずに他方に再び出ていく。したがってそれは、振動子から開口ｄΩ内の（θ，φ）方向に出ていく直線偏光した輻射線を与える。そしてこの輻射線の偏光面は振動子の軸［ｚ軸］に垂直で強度は

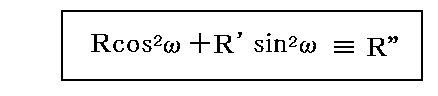
となる。

２．ｙ’軸成分

　ｙ’軸成分

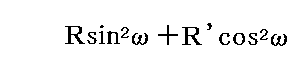
は、さらに２つの部分

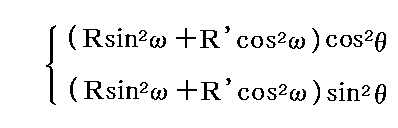
に分解される。
　この内の第１の部分は振動子の軸［ｚ軸］に垂直な成分なので、変化を受けずに振動子をとおりすぎる。
　一方、第２の部分は、３．（２）１．で説明した様に、振動子の軸に平行な成分なので吸収が起こる。そして ３．（２）２． と ３（２）３． で証明したように、吸収されるものの代わりに輻射の中に放出輻射線の強度

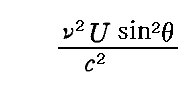
が現れる。
　第１の変化を受けない部分と、この放射輻射線の強度の和が、振動子の開口角ｄΩ内の（θ，φ）方向に出ていくｙ’軸方向に偏光した輻射線の全強度を与える。それを

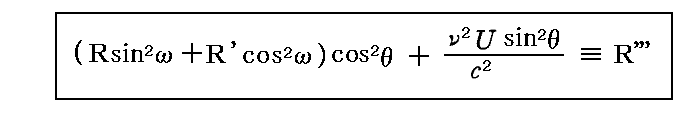
と置くことにする。

３．振動子を通り過ぎる輻射線の強度と偏光

　結局、振動子を通り過ぎ、ｄΩ内に（θ，φ）方向に振動子から出ていく輻射線は互いに垂直な二つの偏光成分で表される。二つの偏光面の一方は振動子に垂直で、もう一方は振動子の軸［ｚ軸］を通る面内にある。その主強度はＲ''およびＲ'''という値を取る。

（４）エネルギーの保存（原論文3．§16、著書10．§186）

１．系の全エネルギーＵ_t

　輻射で満たされている真空空間に、ある数の共鳴子が存在する系を考える。その系の全エネルギーＵ_tは

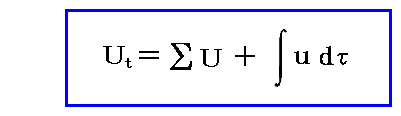
と表される。
　ここで Ｕ はここの共鳴子１個のエネルギーを表し、Σは共鳴子全体に付いての和を表す。
　また ｕ は真空の空間要素ｄτ中の輻射エネルギー密度を表す。共鳴子は無に等しいほどの小さな空間体積を占めるにすぎないので、輻射エネルギー密度の積分は容器の全空間にわたって行うと考えればよい。

　場の中に振動子が一つも存在しないとき、無限に多くの要素輻射線ビームは、直進するときも場の境界面で反射されるときも、それぞれの強度とエネルギーを変えない。
　それに対して、場の中に振動子が存在するときには、どの振動子も、それに当たる輻射線に変化を引き起こす。上に考察した振動子がｄｔ時間にそのまわりの場に引き起こす全エネルギー変化を計算しよう。
　その際、振動子の振動数νに対応する単色の輻射線のみを考慮すればよい。それ以外は振動子によって全く変化を受けないからである。そのため以下の議論ではＲに付けるべき添え字νを省略するが、Ｒ_νの意味であることを忘れないで下さい。

２．場に起こるエネルギー変化

　（θ，φ）方向に要素円錐ｄΩ内に、何らかの仕方で偏光し主強度ＲおよびＲ’の和で与えられる強度をもつ輻射線ビームが振動子に当たるとする。この輻射線ビームは３．（２）１．で得られた定理にしたがった断面積を乗じた

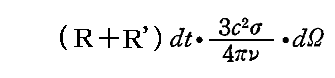
だけのエネルギーをｄｔ時間に振動子に与える。そのため入射線の側でこのエネルギー量が場から奪われる。
　それに対して他方の側で同じ（θ，φ）方向に、一定の仕方で偏光し主強度Ｒ''およびＲ'''の和によって与えられる強度をもつ輻射線ビームが振動子から出ていく。これによって、まわりの場に

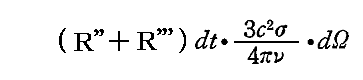
だけのエネルギーがｄｔ時間に供給される。
　したがって全体としてｄｔ時間に生ずる振動子のまわりの場のエネルギー変化は、すぐ上の式からその上の式を引き、ｄΩについて積分することにより得られる。すなわち

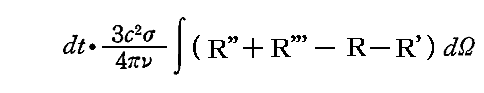
となる。

３．振動子のエネルギー変化

　同じｄｔ時間に生じる振動子のエネルギー変化は

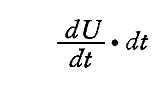
である。

４．エネルギー保存則

　振動子と場の系に対して外部からエネルギーの出入りが無ければ、エネルギー保存則により場と振動子に起こるエネルギー変化は互いに打ち消しあってゼロとなる。すなわち

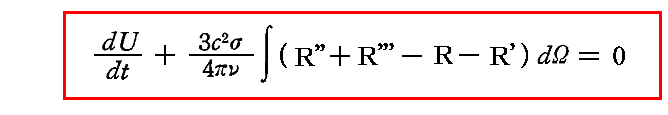
でなければならない。
　これに対してすでに求めた関係式を適用すると


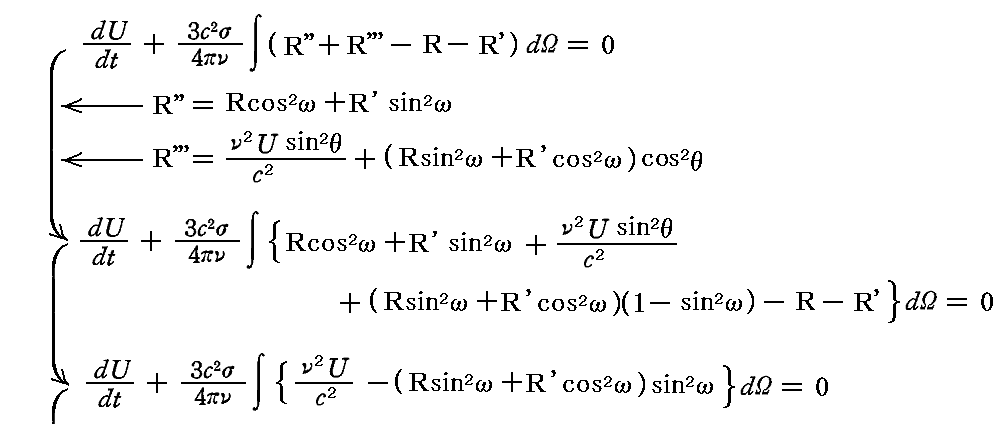
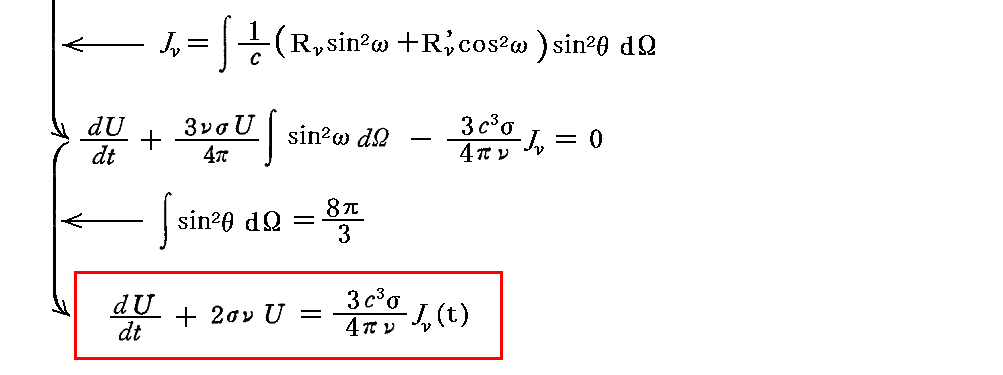
となり、２．（４）３．で求めたエネルギーの保存を表す非同次一階線形微分方程式が再び得られる。

４．エントロピーの増大（原論文3．§17〜19、著書10．§98〜99・§124〜127・§187〜189）

　ここからプランクはエントロピーの考察に入ります。彼は振動子などの物体に対して定義された熱力学的なエントロピーと同等なものとして輻射場にもエントロピーが定義されるとして電磁的エントロピーを導入します。
　振動子のエントロピーと電磁場のエントロピーをあわせて考察することにより、ここで対象としている輻射現象に対してもエントロピー増大の原理が証明できるのではないかと考えます。
　そして、振動子と輻射場をあわせた全エントロピーが最大値を取った状態こそ、系が実現する最終的な定常状態であり、その状況の輻射場を記述する法則こそ黒体輻射のエネルギー分布を与えるものであろうと予測します。

（１）輻射場のエントロピー（原論文3．§17、著書10．§98〜99）

　輻射場のエントロピーについては、すでに別稿「ウィーンの変位則」６．（５）で説明しましたが、大事な所なのでもう一度ここで復習します。

１．偏光した単色輻射のエントロピー

　熱力学第二法則から、輻射線ビームも一定のエントロピーを持つことが結論される。なぜなら放出という行為によって物体の熱は輻射熱に変わるのだが、そのとき放出物体のエントロピーは熱の放出に伴って減少する。全エントロピー増大の原理によって、その補償として別の形のエントロピーがどこかに生じなければならない。それは放射された輻射のエネルギーの中以外には考えられない。従って、直線偏光した個々の単色輻射線ビームはそれぞれ一定のエントロピーを持ってビームとともに空間に伝播し広がる。それはエネルギーの輻射と同様に単位時間に単位面積を通過するエントロピーの量として測られる。つまり各輻射線ビームはエネルギーと共にエントロピーも持ち運ぶのである。そのエントロピー量は輻射ビームのエネルギーと振動数のみに依存するはずです。
　そのとき、別稿「キルヒホフの法則（熱的放射平衡における）」３．（１）でした輻射のエネルギー流について説明と全く同様な事柄が輻射のエントロピー流についても成り立つ。
　そこでの説明のエネルギーをエントロピーに置き換え、単位面積を単位時間に単位立体角の方向へ通過していく輻射のエネルギー流である強度（輝度）Ｋに相当するものとして、単位面積を単位時間に単位立体角の方向へ通過していく輻射のエントロピー流の強度（輝度）［今後はエネルギー流との混同を避けるために比強度と呼ぶ］Ｍを考えればよい。

［補足説明１］
　プランクの論文や著書では、［エントロピー比強度］と、その［偏光した単色成分］を、Ｌの［ラテン文字］と［ドイツ文字（フラクトゥール、亀の甲文字）］を使い分けて書体を変えることで表現しています。
　しかし、インターネット上の文章で書体を使い分けることは難しいので本稿では文字そのものを変える事にする。本稿では［偏光した単色成分］を表すのに［ラテン文字］Ｌを用いているので、［エントロピー比強度］を表すのに［ラテン文字］Ｍを用いることにします。プランクの著書と比較されるときは注意して下さい。

　空洞内部にある輻射を考える。空洞内部に任意の面積要素ｄσを考え、それを時間δｔ内に立体角ｄΩの方向に通過する輻射のエントロピーを求める。ここで単位面積を単位時間に面に垂直な方向へ通過していく輻射のエントロピー流をＭとする。Ｍの事をここでは“強度（輝度）”との混同を避けるため改め“比強度”と呼ぶことにしている。


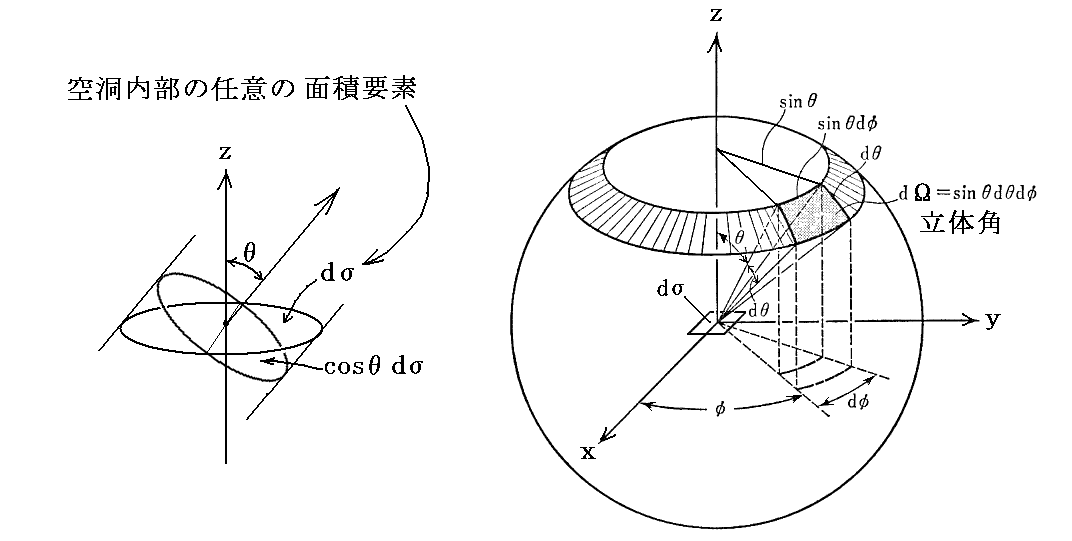
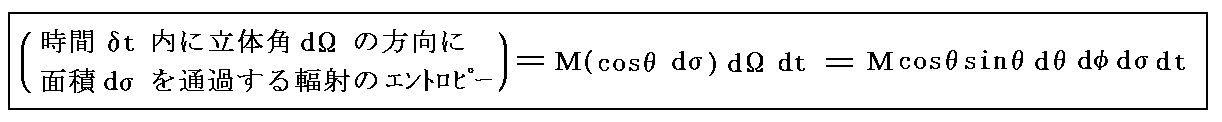
　一般にＭは場所と時間と方向に依存するが、ここでの議論のように、Ｍはすべての方向について一様と見なして良い場合には、ｄσを通って一方の立体角２πの半球領域に向かう全輻射エントロピーはφについて0→2π、θについて0→π／2まで積分して

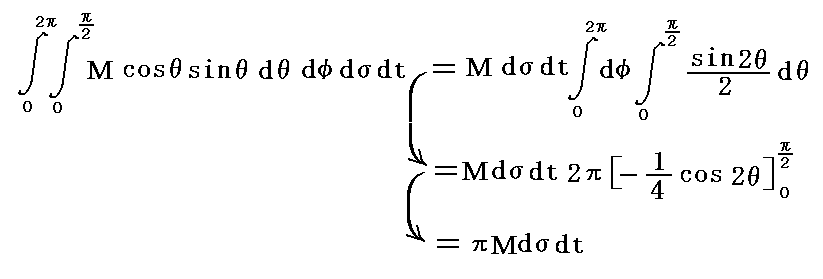
となる。

　ここで単色（νを中心とした単位の振動数幅に含まれる）で偏光面が片寄った、単位立体角の方向へ進行する輻射エントロピーの“比強度”を定義しよう。電磁波は横波だから、必ずある一つの偏光面に沿った振動で伝播する。そのとき輻射の強度は振幅（電場と磁場）Ａの二乗に比例する。その振幅Ａを二つの直線偏光成分に分け、それぞれの振動成分をＡ_xνとＡ_yν’とすると、ピタゴラスの定理よりＡ²＝Ａ_xν²＋Ａ_ｙν²となる。だから光線は二つの偏光面で振動する波が混じったものであると考えることができる。その為、それぞれの振動面（Ａ_xνかまたはＡ_yν）に対する直線偏光した単色エントロピーの比強度をそれぞれＬ_νおよびＬ_ν’とすると、すべての振動数のエントロピー輻射の比強度Ｍは

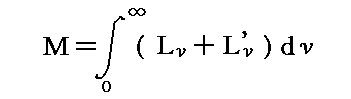
と表される。
　このときＬ_νおよびＬ_ν’は直線偏光した振動数νのエントロピー輻射の比強度で、それぞれ輻射エネルギーの偏った輝度Ｒ_νおよびＲ_ν’の値によって決められる。直線偏光した振動数ν〜ν＋ｄνの単色輻射に対するエントロピー比強度についてＭと同様に

が成り立つ。ここでＬ_νは単色（振動数νを中心とした単位の振動数幅に含まれる）で直線偏光した単位面積を単位時間に面に垂直な方向へ進行する輻射エントロピーの“比強度”を表す。
　偏光していない輻射線についてはＬ_ν＝Ｌ_ν’であるから、

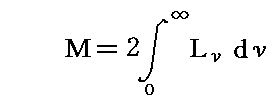
の関係が成り立つ。前に掛かっている数因子２はＭが偏光していない事を表すために掛かっている。
　以前、Ｋ_νはＫの単色成分とし、Ｒ_νでもってＫの単色かつ直線偏光成分を表すことにした。ここでのＬ_νはＭの単色かつ直線偏光した成分である事に注意。偏光していないＭの単色成分はＭ_νで表すことにする。
　このように偏光していない光線を偏光した光線によって表すと係数２が乗ぜられるが、それは電磁波が横波なので二つの偏りを持つことができることによる。実際偏光していない輻射線をニコルプリズムなどを通して直線偏光成分だけにすると、そのエネルギー強度は１／２倍になることが確かめられるが、エントロピーについても同様に考えることができる。そのため直線偏光したエントロピー比強度Ｌ_νを用いると前記の結論は

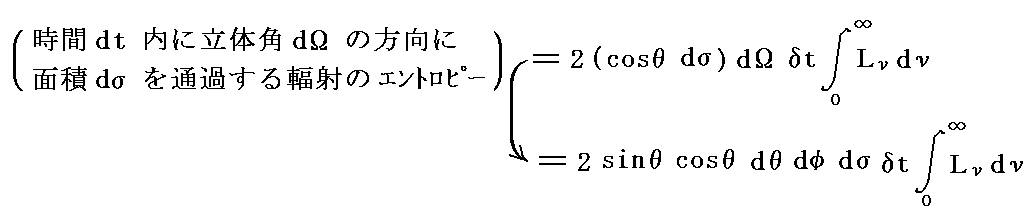
となる。

２．輻射エントロピーの空間密度　　

　輻射に満たされた空間の一点に於けるエントロピー密度ｓは空間的なエネルギー密度ｕと同様に、この点で交わるすべての輻射線を考察することで決定される。
　別稿「キルヒホフの法則（熱的放射平衡における）」３．（２）で示したように、あらゆる方向に一様な輻射場では進行するエネルギー輻射の強度Ｋから輻射エネルギーの空間密度ｕが得られた。
　全く同様に、進行するエントロピー輻射の比強度Ｍから“輻射エントロピーの空間密度”ｓが得られる。そこのエネルギー密度ｕをエントロピー密度ｓで、輻射強度（輝度）Ｋを比強度Ｍで、直線偏光した単色輻射強度（輝度）Ｒ_νを直線偏光した単色比強度Ｌ_νで置き換えればよい。すなわち

　あらゆる方向に一様な輻射場の単位体積当たりのエントロピー密度ｓは

で表される。ただしｃは光速度、Ｍは密度測定点での“エントロピーの輻射比強度”です。
　エントロピー密度ｓをスペクトル分解して

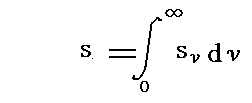
によって“振動数ν〜ν＋ｄνの間のエントロピー密度”ｓ_νを定義すれば、

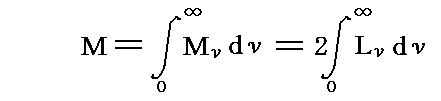
の関係を用いて

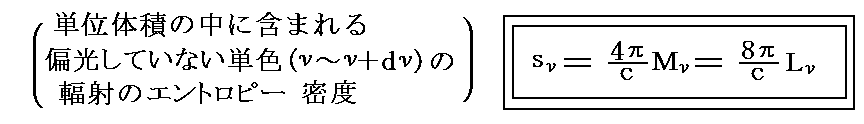
が得られる。

（２）系のエントロピー（原論文3．§17〜18、著書10．§187）

１．系の全エントロピーＳ_t

　３．（４）１．に於いて全エネルギーＵ_tを定義したのと同様に、ある瞬間の状態によって定まる系の状態量である全エントロピーＳ_tを

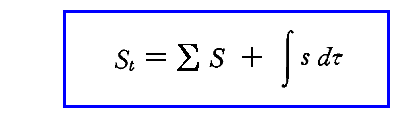
で定義する。
　ここでＳは個々の振動子のエントロピーであり、和Σは全振動子について行う。またｓは前節で定義した場の一点におけるエントロピー密度であり、積分は輻射が満たされている場の空間要素ｄτのすべてにわたって行うものとする。

　場の中に共鳴子がまったく存在しないときには、無限に多くの輻射線が直線的に進行し、克つ完全反射すると仮定した境界面で反射されている。そのとき、各輻射線の強さとエントロピーは不変のままに保たれるであろう。したがって系のエントロピー変化は生じない。
　これに反して、場の中に振動子が存在する場合には、一般に、それに当たる輻射線束のエントロピー変化を引き起こすであろう。その場合、振動子の固有振動数νに対応するような単色の輻射線だけを考慮すればよい。残りの輻射線は振動子によってなんの変化も受けないからである。そのため以下の議論ではＬに付けるべき添え字_νを省略するが、Ｌ_νの意味であることを忘れないで下さい。

２．振動子が存在する場合に輻射場のエントロピーに生じる変化

　振動子が（θ，φ）の方向に進む要素円錐ｄΩ内の何らかの偏光状態を持つ輻射線束によって照射されたとする。その輻射はエネルギーの強さの主値ＲとＲ’をもち、エントロピーの比強度（Ｌ＋Ｌ’）を持つ。
　この輻射線ビームは３．（２）１．で得られた定理にしたがった断面積を乗じた

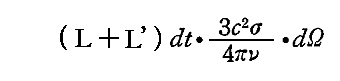
だけのエントロピーをｄｔ時間に振動子に与える。それにより、輻射線が入射した側で同量のエントロピーが輻射場から奪い取られる。
　このとき３．（２）２．で説明したように、他方の側で振動子から同じ（θ，φ）方向に、一定の仕方で偏光し主強度Ｒ''およびＲ'''の和によって与えられる強度をもつ輻射線ビームが振動子から出ていく。したがってそのエントロピー輻射は対応する比強度Ｌ''＋Ｌ'''を持つ。これによって、周囲の場には時間ｄｔ内に

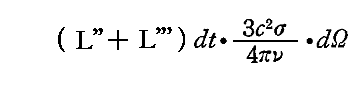
だけのエントロピーが供給される。
　したがって、全体として、振動子を取り囲んでいる場の時間ｄｔ内に生じるエントロピー変化は、すぐ上の式からその上の式を引き、ｄΩについて積分することにより得られる。すなわち

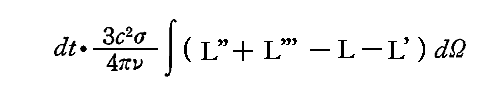
となる。

（３）ウィーンの変位則の改良（著書10．§124〜127）

　プランクは、熱輻射論を展開するとき、ウィーンの変位則を最も重要な成果として、大事なところで繰り返し利用します。そのためプランクは“ウィーンの変位則”をもっと根源的な形に改良します。

１．振動子と輻射場からなる系の断熱変化

　これまで考えてきた系、すなわち、完全に乱反射する壁によって囲まれた一様な輻射場でみたされた真空と、その中にある静止した振動子とからなる系を取り上げる。
　この系を無限にゆっくりと可逆的・断熱的に圧縮する。そのとき、断熱変化故に熱力学第二法則に従って系の全エントロピーは不変である。それに対して各振動数の輻射強度Ｒ_νは圧縮によって変化し、その輻射のエネルギー密度も変化する。そのとき、振動子のエネルギーＵも変化する。なぜなら、定常状態では３．（１）３．で証明した

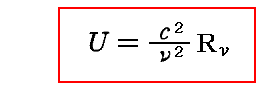
の関係式が成り立つので、振動子のエネルギーＵも単色輻射の強度Ｒ_νの変化に応じて変化するからである。
　したがって振動子は圧縮によって生じた輻射エネルギーの増大分の一部を吸収し、それだけのエネルギーを真空中の自由な熱輻射から取り上げるだろう。
　解りやすくするために、無限小の圧縮過程を２つの過程に分けて考える。第１期には圧縮がおこり、その際輻射は振動子が全く存在していないかのように振る舞う。そして第２期に振動子はそれを励起する輻射から第１期の過程によって乱された前記の関係が再び成り立つだけのエネルギーを吸収する。第１期では真空中の熱輻射のエントロピーはそれ自体一定であり続けるが、第２期では熱輻射のエントロピーは、熱を振動子に引き渡すことによって変化する。
　このとき熱輻射のエントロピーは熱（エネルギー）を振動子に引き渡すことによって変化するが、熱力学第二法則により系全体のエントロピーは不変でなければならないので、自由な熱輻射ばかりでなく振動子にもあるエントロピーが属しており、振動子のエントロピー変化はちょうど熱輻射のエントロピー変化を打ち消す様になっていなければならない。そして、共鳴子の熱力学的状態はエネルギーＵのみに依存するから、“振動子のエントロピーＳ”も“振動子のエネルギーＵ”によって決まるであろう。

２．振動子のエントロピーと輻射エントロピーの空間密度との関係

　系の全エントロピーは“振動子のエントロピーＳ”と、次式で表される“輻射場のエントロピー”

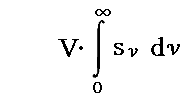
からなる。ここでＶは一様な輻射でみたされた真空の体積である。
　熱力学第二法則により、定常状態は系の全エントロピーが最大値を取る状態であると言える。それはまさしく、いま求めようとしている黒体輻射のエネルギースペクトル分布で容器が満たされた状態である。そのとき全エントロピーは極値を取るのでエントロピー変化を表す変分はゼロとならなければならない。つまり

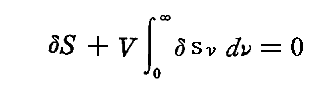
となる。これは

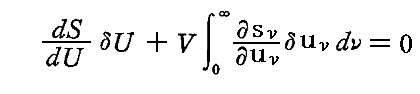
と表すこともできる。
　変分δが満たさなければいけない唯一の条件は、系の全エネルギーが変化しないということである。すなわち

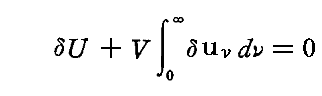
が成り立つことである。
　固有振動数νの振動子は振動数νのまわりの幅Δνの狭いスペクトル領域とのみ相互作用するとして良いので、上記の２式は下記の様に簡単化できる。ここでΔνはνに比べて小さいということ以外は任意に取れる。

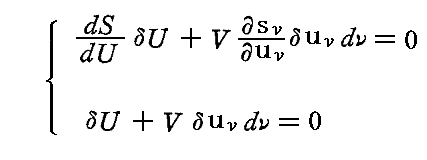
となる。
　この両式から

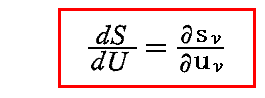
が得られる。
　これはとても重要な関係式です。すなわち系が定常状態（そのとき輻射は黒体輻射の分布）にあるとき、“振動子のエントロピー”の“振動子のエネルギー”への依存性は、“輻射エントロピー密度”の“輻射エネルギー密度”への依存性と等しい事を示している。

　ここで “振動子のエネルギーＵ” と “輻射のエネルギー密度ｕ_ν” との間には３．（１）３．で証明した関係式があるので、それをもちいると

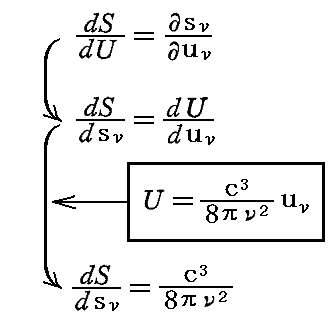
と書くことができる。これを積分して、物理的に意味のない積分定数を省くと

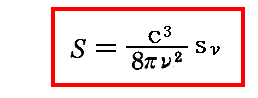
が得られる。これは系が定常状態（黒体輻射）にあるとき、［振動子のエントロピーＳ］と［振動数νの単色輻射のエントロピー空間密度ｓ_ν］との間に成り立つ関係式である。
　さらに４．（１）２．で証明した輻射エントロピー密度ｓ_νと偏光した単色輻射の比強度Ｌ_νの間に成り立つ関係式を用いると

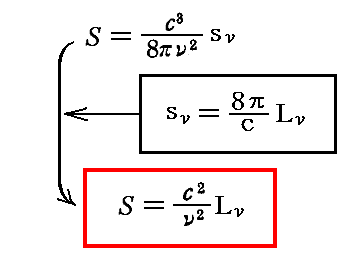
となる。これは、系が定常状態にあるとき、［振動子のエントロピーＳ］と［振動数νの単色の直線偏光した輻射エントロピーの比強度Ｌ_ν］との間に成り立つ関係を示している。

３．振動子の温度

　別稿「ウィーンの変位則」６．（２）で説明したように、輻射場のエントロピー密度とエネルギー密度から輻射場の温度が定義されて

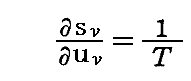
の関係がある。

　これを前節で求めた式に適用すると

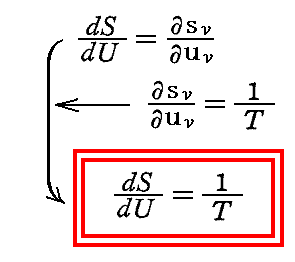
となる。ここでＴは振動子を励起する輻射の温度です。量ｄＳ／ｄＵは振動子のエネルギーとその性質のみに依存する。一般にこの量の逆数を振動子の温度と定義すれば、次の定理が成り立つ。
「輻射の定常状態において、振動子の温度はそれを励起する単色輻射の温度に等しい。」
　上記の関係式は熱力学第二法則そのものだと言ってよいものですが、今後繰り返し用いることになるでしょう。なお、この式の意味については別稿「絶対温度とは何か（積分因子とは何か）」を御覧下さい。

４．ウィーンの変位則の振動子エントロピーによる表現

　振動子エントロピーＳの振動子エネルギーＵへの依存性は、別稿「ウィーンの変位則」６．（５）３．で証明した（１３）式 に、この稿の ３．（１）３． と ４．（３）２． で得られた定常的な平衡状態にある振動子と輻射線の間に成り立つ関係式を適用すれば得られる。すなわち

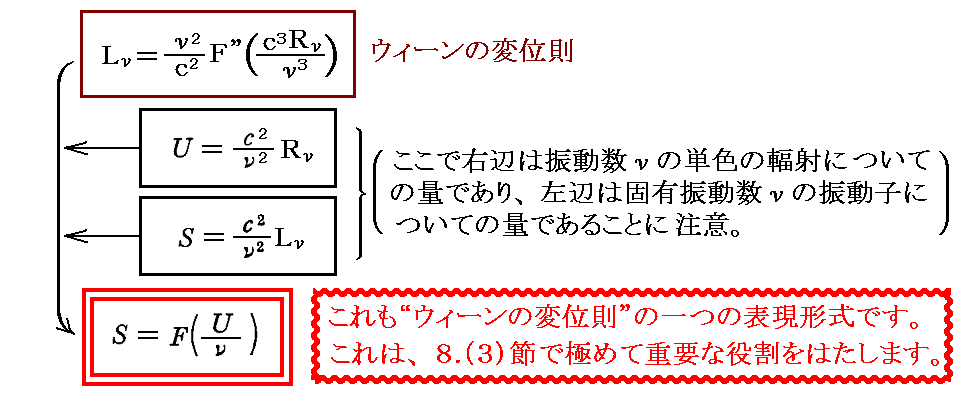
となる。
　関数Ｆは変数Ｕ／νと普遍定数のみを含み、振動子の性質に関わる定数は一切含まないことに注意。この中には光速度ｃは含まれず、また振動数νも一乗の形で現れるだけなので、これは、これまでに“ウィーンの変位則”として確立した形式のなかで最も簡単なものです。この変位則は固有振動数νの振動子についてのものである事に注意して下さい。つまり“1個の振動子が持つエントロピーは、そのものが持つエネルギーを固有振動数νで割った変数（Ｕ／ν）の関数である”と言っているのです。
　
　この普遍関数Ｆの解析的表現を見つける事ができれば、別稿「ウィーンの変位則」６．（５）３．で説明したように黒体輻射のエネルギースペクトル分布は直ちに求めることができる。そのため、このＦの具体的な形を探し当てることが今後の最大の目標となる。今後の証明過程でこの形のウィーンの変位則を繰り返し用いることになるでしょう。特に８．（３）に於いて重要な役割を果たします。

［補足説明１］
　プランクは、原論文4．の中のｐ733で“W. Wienの熱力学的な考察により、必然的にｆ(ν)とφ(ν)はともにνに比例するという結論に導くわけである。”と言って1/αと1/βがνに比例することを導いていますので、ここで説明した振動子エントロピーＳの関数としてのウィーンの変位則の表現形式を、原論文4．を書いた時点で見つけていたと思われる。そして、この形がハッキリ記述されているのは原論文5．のp204脚注の中です。そのため、以下で説明する原論文3．を書いた段階でこの形を見つけていたのかどうかは、明らかではありません。
　
　また、振動子に絶対温度を導入する手順も、上に述べた別稿「ウィーンの変位則」６．（２）の結論を利用して４．（３）３．の関係式を導くやり方と違って、原論文3．§19、§20ではとても回りくどいやり方をしています。別稿「ウィーンの変位則」６．（２）で説明した内容は著書10．から引用したもので、彼が後からまとめなおしたものです。
　プランクが原論文3．を書いた段階で、この当たりを明確に認識していたかどうかは疑問ですが、そこで展開されている内容は同じことなので、以下では上記の結論を用いて説明します。　

［補足説明２］
　上記の振動子エントロピーＳによるウィーンの変位則の表現形式の導出法は、著書10．§127の中で展開されているものです。この著書（1906年）は輻射場のエントロピーについての考察を深化させた後のものです。
　本稿の８章で説明するように、原論文7．§6〜9（1901年）の中では、ここで説明したやり方よりもより根源的で素朴な方法で求めています。それは別稿「ウィーンの変位則」５．（１）で説明した最初の形のウィーンの変位則（輻射についての）を変形して求めるものです。８．（２）で説明しておりますので参照されて下さい。

（４）エントロピーの解析的表現（原論文3．§17、著書10．§187〜189）

ここで、プランクは最も困難な課題である振動子エントロピーＳ＝Ｆ（Ｕ／ν）の解析的表現に関する考察に入ります。

１．振動子のエントロピー

　　プランクは［固有振動数νの１個の振動子のエントロピーＳ］を次式で定義します。

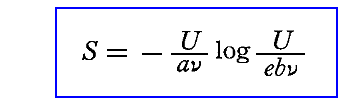
　ここでＵは１個の振動子の持つエネルギーで、νは振動子の固有振動数です。この中のａとｂは二つの正の普遍定数をあらわします。またｅは自然対数の底で、外形的な好都合さのために入れられているものです。

［補足説明１］
　上記のエントロピーの表現式は低温・短波長領域の輻射線と平衡関係にある振動数の振動子のエントロピー表現として近似的にのみ成り立つもので、真に正しい表現形式ではないことが後に解ります。
　その当たりは７．章以後で説明することとして、ここではとりあえず原論文3．が書かれた時点のプランクの説明を紹介することにします。

［補足説明２］
　この形は原論文3．§17の中で突然定義されており、プランクはなぜこの形で定義したのかを説明していません。いろいろな状況から推測すると、おそらく以下に述べる三つの理由からこの形にしたのだと思います。
　
【一番目の理由】
　４．（３）４．で導いた振動子エントロピーによる表現形式のウィーンの変位則が

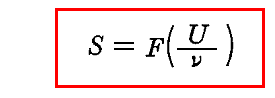
の形をしていることです。変数（Ｕ／ν）の関数としてできるだけ簡単なものを探してこのようにしたのでしょう。ただし、正直な所４．(３)４．［補足説明１］で説明したように原論文3．の段階でこの形を認識していたのかどうかは解りません。
　
【二番目の理由】
　後ほど５．（１）で説明しますが、このエントロピー表現形式をＵで微分したものに、４．（３）３．の振動子の絶対温度の定義

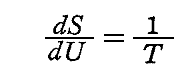
を適用して、式変形を進めて輻射の強度に変換すると、当時の実験・観測結果をほぼ旨く説明していた“ウィーンの輻射公式”（変位則ではない）が得られる事です。
　ウィーンの輻射公式は Willy Wien が「黒体の放射スペクトルにおけるエネルギー分布について」
“Uber die Energievertheilung im Emissionsspectrum eines schwarzen Ko¨rpers” ,Wiedemann Annalen 58, p662〜669, 1896年
で導いた黒体輻射のエネルギースペクトル分布を与える公式で

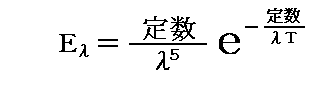
の形をしています。
　これは別稿「ウィーンの変位則」５．（２）２．で導かれたウィーンの変位則の波長λを用いた表現形式

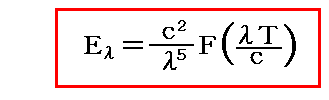
において、未知であった黒体輻射のエネルギースペクトル分布関数Ｆ（λＴ／ｃ）の具体的な形を与えるものです。この公式が与える関数形は、1897年にPaschenが実験的に得た結論によって検証されていました。
　ウィーンの輻射公式は確かに実験・観測結果を旨く説明できるのですが、その導出の過程で用いられている仮定は気体分子運動論を用いたかなり恣意的なものです。その当たりの事情は多くの解説書で説明されていますが、そこで展開されている理論は、当時の物理学者にとって、とうてい受け入れられるものではなかった。実際、プランクもウィーンの論理には全く納得していません。
　しかし、とにかくその公式は実験・観測結果を旨く説明したので、プランクはウィーンの輻射公式をＵ＝（ｃ²／ν²）Ｒ_νにより振動子のエネルギー公式に直してからＴについて解いて、さらにｄＳ／ｄＵ＝1／Ｔを適用して上記の関数形を得たのだと思います。
　
【三番目の理由】
　エントロピーがこの形であれば、系の全エントロピーは不可逆的に増大して平衡状態へ近づいていく事が証明できた［４．（５）１．参照］からでしょう。おそらく、これが最も大きな理由だと思います。
　実は、全エントロピーの増大性が証明できるもっと違った形もあるのですが、それに付いては別稿の［付録２］で説明します。

２．輻射線のエントロピー

　上記の表現に３．（１）３．と４．（３）２．で得られた結論を適用すると、［一つの単色の直線偏光した輻射線のエントロピーの比強度Ｌ］を定義することができる。すなわち

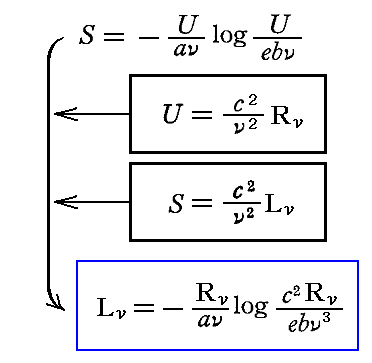
となる。

（５）系の全エントロピーＳ_t増大の証明（原論文3．§18〜19）

　ここで、再び４．（２）１．で導入した系の全エントロピー表現式に立ち帰る。この式に ４．（２）２．のＬに付いての結論 と 前節のＳの定義式 を適用すると、系の全エントロピーＳ_tが不可逆的に増大することが証明できる。

１．全エントロピーＳ_tの増大（原論文3．§18）

　４．（２）２．で求めたように、［１個の振動子を取り囲んでいる輻射場の時間ｄｔ内に生じるエントロピー変化］は

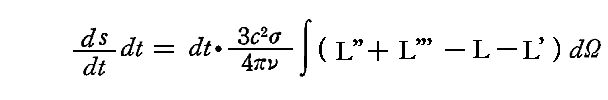
となる。
　一方、前節の定義から［同じ時間ｄｔ内に生じる振動子のエントロピー変化］は

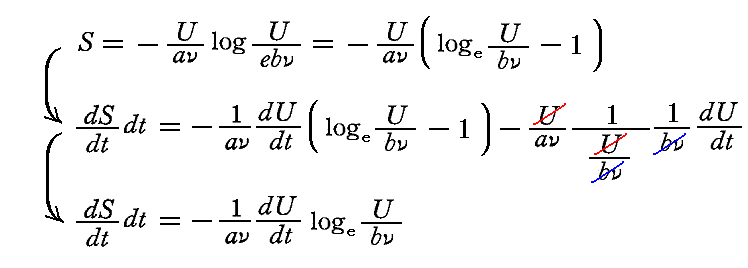
となる。
　これら二式を系全体のエントロピー関係式に代入する。そのとき、ｄτに関する積分は系内に存在する個々の振動子のまわりの輻射場に生じるエントロピー変化を全振動子について足しあわせた和Σに置き換えることができる。


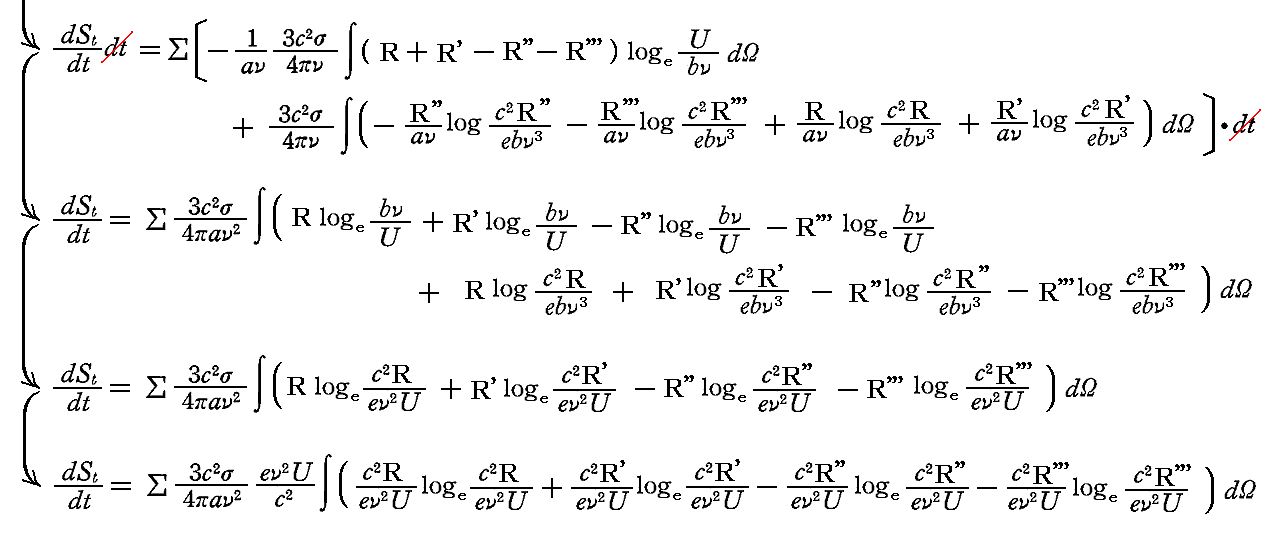
となる。ここで

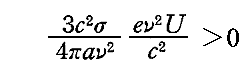
だから、ｄＳ_t／ｄｔ＞0となることを証明するためには、（　）の中の表式が常に正となる事を証明すればよい。
　ここで

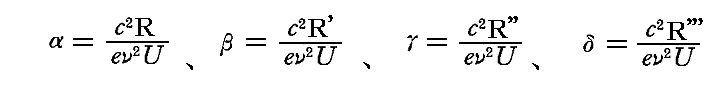
と置くことにすると、（　　）内の部分は

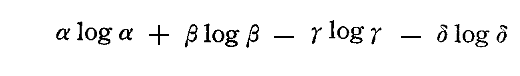
と表されるので、これが常に正になることを証明すればよい。
　正の量であるＲ、Ｒ’、Ｕ、θ、ωのすべての値に対して、Ｒ''とＲ'''は

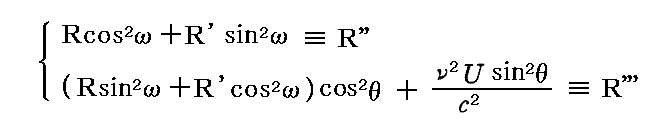
で与えられるので、Ｒ''もＲ'''も正の値になる。そのめたα、β、γ、δはいずれも正の値になる。
　まず最初に

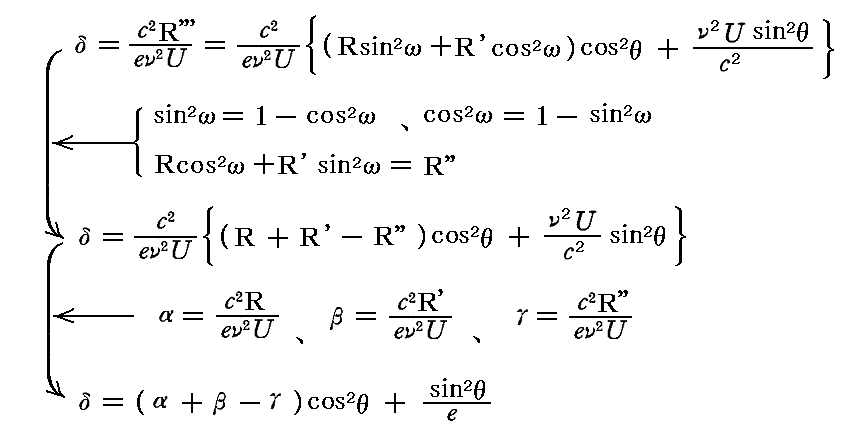
となることが言える。
　ここで

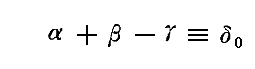
と置くと

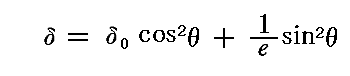
となるが、この関数のグラフは

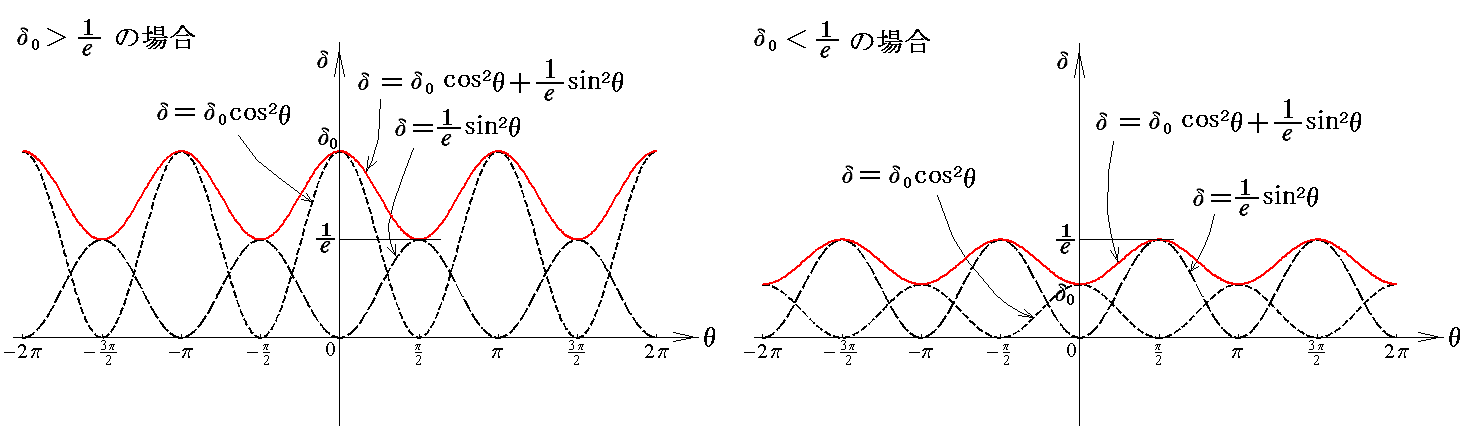
となる。このグラフから明らかなように、δは必ずδ₀と１／ｅの間にある。
　ところでｙ＝−δ･log_eδの関数のグラフは

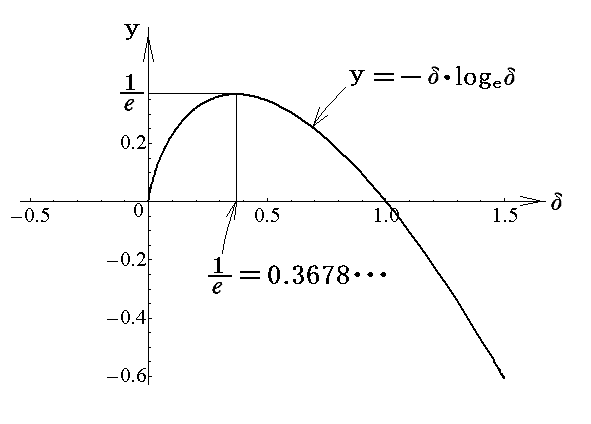
の様になるので、−δ･log_eδの値は極大値１／ｅと−δ₀･log_eδ₀の間に存在する。つまり −δ･log_eδ＞−δ₀･log_eδ₀ が常に成り立つ。
　そのため前述の式は

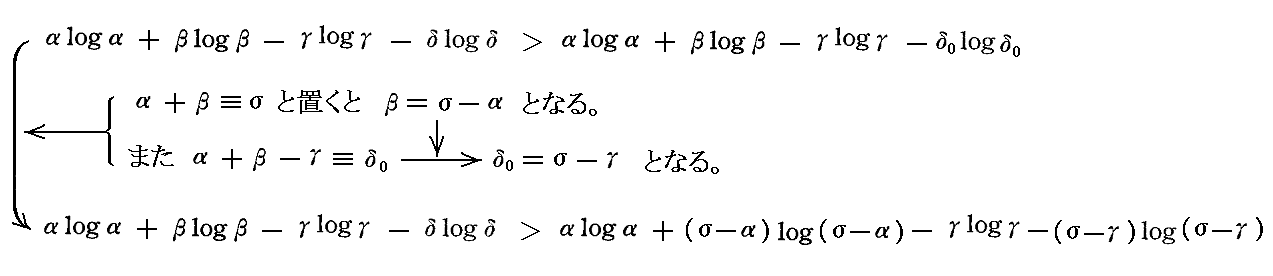
となる。この式の右辺が正であることが証明できればよいことになる。
　ここでσを任意の定数としたとき

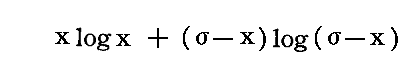
なる関数は、ｘ＝σ／2で唯一の極小値を取る。それは幾つかのσの値に対して上述の関数のグラフを描いてみれば直ちに了解できる。

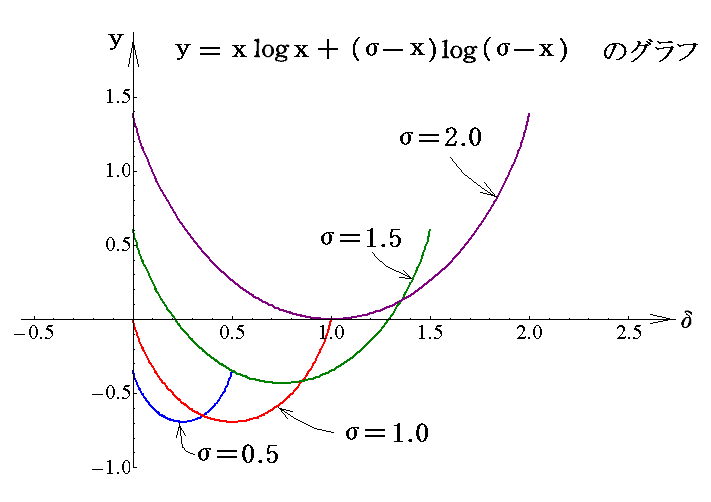
したがってｘがσ／2よりも大きいか、小さいかにかかわらず、ｘ→σ／2にしたがって極小値に近づく。
　このときＲ''の定義式から明らかなようにＲ''はＲとＲ’の間にある。したがってγもαとβ＝σ−αの間にある。そのためγはαとβの算術平均（α＋β）／2＝σ／2に対して、αやβよりもより近いところにある。そのため

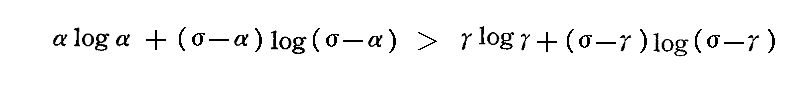
となる。したがって常に

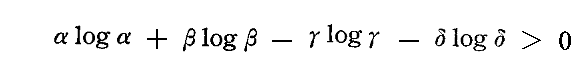
が成り立つので、

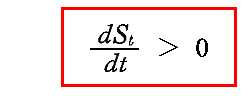
が証明できたことになる。

［補足説明１］
　４．（４）１．で定義した振動子のエントロピー表現式は、そこの［補足説明1］で注意したように真に正しいものではありません。後ほど７．章以降で導きますが正しい形は

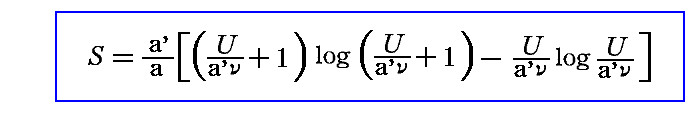
です。
　そのためプランクはこの真に正しいエントロピー表現式が得られた後に、全エントロピーの増大法則を証明し直しています。これが原論文9．あるいは著書10．§187で報告されているものです。時間的には後から書かれたものですが、ここと関連したとても重要な証明ですから別稿［付録２］で説明しておりますので御覧になられて下さい。

２．定常的な状態の条件（原論文3．§19）

　全エントロピーの絶対的な極大に対応する系の状態は、定常的な状態と呼ばれるべきである。定常的な状態に対する必要条件は、まず全エントロピーＳ_tが時間と共に変化しない事です。つまり前節の不等式を等式に変える条件です。それは、すべての位置、すべての方向について

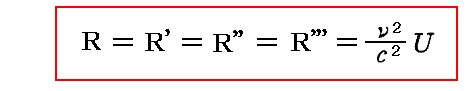
が満たされる事です。つまり輻射場全体において、それぞれの振動数のすべての輻射線が偏光しておらず、等しい強さを持つことです。

　系の全エントロピーが極大である条件としてさらに言えることは、すべての無限に小さな系の変化に対して、全エントロピーＳ_t の変化がゼロであることです。
　それは、次のように表すことができる。振動数ν₁の振動子の無限小のエネルギーが、振動数ν₂のもう一つの振動子に移され、しかしその他の振動子は不変に保たれる変化を考える。そのとき、全エントロピーＳtが極値を取っているのであるから

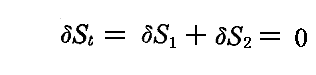
が成り立つ。
　ここでそれぞれの振動子に対して４．（４）１．で導入した［振動子エントロピーの定義式］と［エネルギー保存則］を用いると

がいえる。
　このとき選び出す振動子は任意であるから、この“一定値”は系中に存在するどの振動子に対しても同一の値でなければならない。この一定値を１／Ｔとおくことにすると、

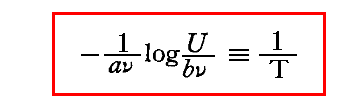
となり、全系が定常的な状態のとき、その中のあらゆる振動子のエネルギー状態はただ一つの変数Ｔに依存することになる。
　このとき

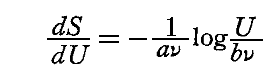
であることを考慮すると、この Ｔ こそ４．（３）３．で導入した振動子の絶対温度に他ならない。

［補足説明１］
　上記のエントロピー表現式は正しいものではありません。８．（３）で説明するように真に正しいエントロピー表現式は

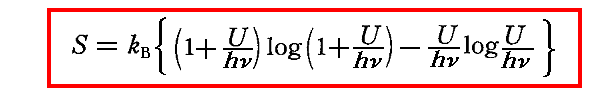
です。
　これを用いると上記の結論は

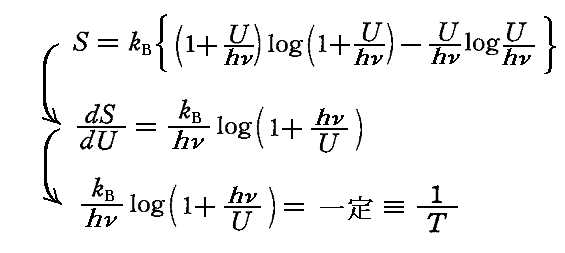
と、置き換えられなければ成りません。

［補足説明２］
　上記の議論を８．（１）の統計的エントロピー表現式で行うとどうなるかが、［付録４］に示されていますので参照されて下さい。

５．熱力学的考察（原論文3．§19〜26）

　前節までに論じた熱輻射と振動子の電磁的な性質を承認できれば、定常的な輻射状態を熱力学原理から導き出す事ができる。
　
　キルヒホッフやウィーンが得た重要な結論を導くのに使われた定理は“一様な温度の物体で取り囲まれた真空中の熱輻射はその物体壁の性質には無関係な唯一の変数である絶対温度により完全に決定される”でしたが、ここでの様に完全に反射する壁に取り囲まれた容器内の振動子と輻射の平衡においても上記の定理が成り立つであろう。
　この場合も、容器内に置かれた振動子の性質には依存しないはずであり、真空容器内で実現される輻射場の定常状態こそ黒体輻射である。
　
　そのとき熱力学第二法則は系の全エントロピーが極大の場合実現される輻射状態が系の定常状態であることを保証している。そして、系に無限小の熱ｄＵが与えられたとき、それによって引き起こされる無限小のエントロピー変化ｄＳとの関係で絶対温度Ｔが定まることを保証している。すなわち

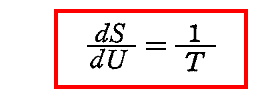
である。
　この熱力学原理を用いればただちに黒体輻射のエネルギー分布則が導き出される。

（１）エネルギー分布則の導出（原論文3．§19）

１．振動子のエネルギー分布とエントロピー分布

　前節の最後の結論より、定常状態における、振動数νを持った一個の振動子のエネルギーは

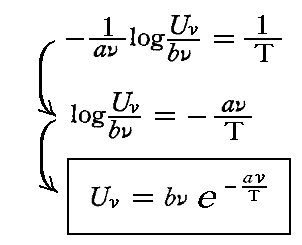
となる。

　上記の結論を、４．（４）１．で定義したエントロピーの表現式に代入すると

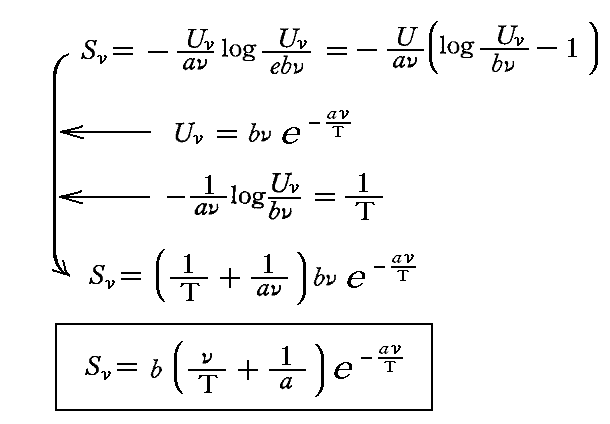
が得られる。

２．輻射場の温度の定義（原論文3．§21）

　熱力学的に振動子と平衡にある輻射場の温度は当然振動子の持つ温度と同じものであり、その絶対温度は、輻射場が熱力学的に平衡に保たれている場合に輻射場に与えられる無限に小さな熱量とそれによって引き起こされるエントロピー変化との比によって与えられる。
　そのとき、３．（１）３．で証明したように、定常状態にある振動子と輻射場の間には

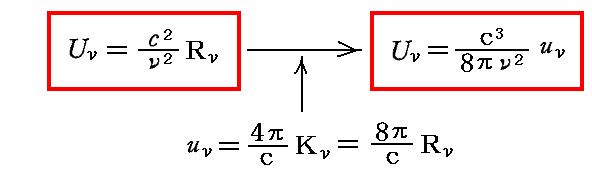
の関係式がある。ここでＵ_νは固有振動数νの１個の振動子が持つエネルギーであり、Ｒ_νは単色で直線偏光したある方向へ向かう輻射強度（輝度）であり、ｕ_νは輻射場中の任意の点における振動数νの輻射のエネルギー密度です。

　この関係式を４．（５）２．の振動子のエネルギーと絶対温度との関係に適用すると

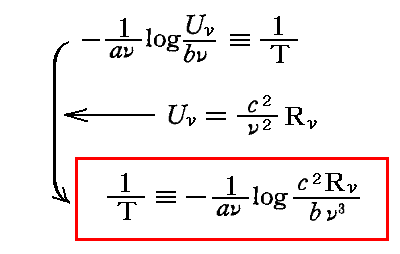
で輻射場の絶対温度が定義されることになる。つまり、上式の右辺は振動数ν、強さＲ_νの単色輻射線の温度の逆数を与える。

　以上は定常的な場合の話であったが、非定常な場合でも個々の直線偏光した単色輻射線に対して上記の温度を定義できるとしても良いであろう。つまり、輻射線のエネルギー分布が黒体輻射の分布とは異なっている場合でも、輻射線はそれが分裂したり吸収されたりすることが無ければ、たとえ完全反射する壁で反射を繰り返しても、その強さとともに自分の性質を不変のまま保持して進行している。そのため、温度もそれらの個々の輻射線に付随して不変のまま進行していると考えられるからである。

３．輻射線のエネルギー分布（原論文3．§19）

　上記の輻射場の温度の定義を用いるか、あるいは前述の振動子についての結論を輻射場についてのものに変換することで、輻射場のエネルギー分布が求まる。
　まず、直線偏光した一つの単色（つまり振動数がν）の輻射線の強さＲ_νは

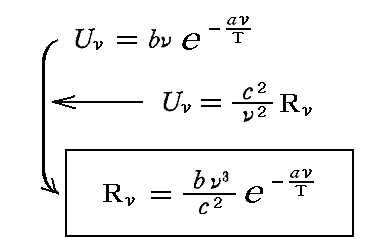
となる。
　さらにある方向に向かう全エネルギー輻射の強さＫは

となり絶対温度の4乗に比例する。これはシュテファン・ボルツマンの法則に他なりません。
　さらに個々の振動数のエネルギー密度ｕ_νは

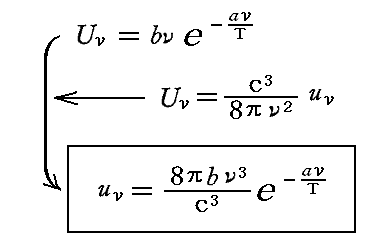
となる。
　さらに輻射場の任意の点に於けるエネルギー密度ｕは

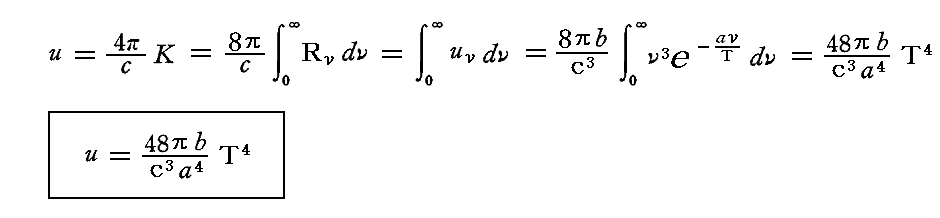
となる。　

４．輻射線のエントロピー分布（原論文3．§19）

　ここで前記の結論を４．（４）２．で定義した［輻射場のエントロピーの表現式］に代入すると、ある方向へ向かう振動数νの偏光したエントロピー輻射の比強度Ｌ_νがえられる。すなわち

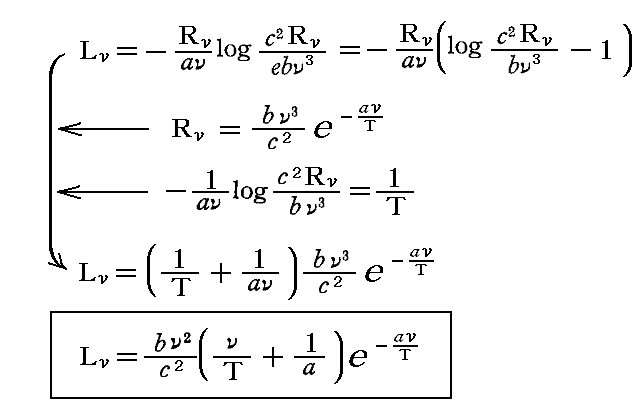
となる。
　ある方向へ向かう全エントロピー輻射の比強度Ｍは

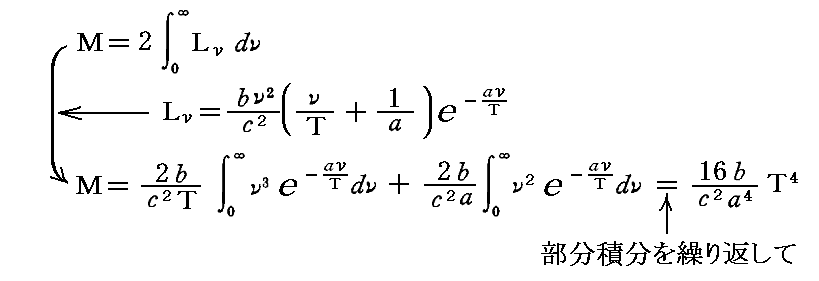
となる。
　さらに個々の振動数のエントロピー密度ｓ_νは

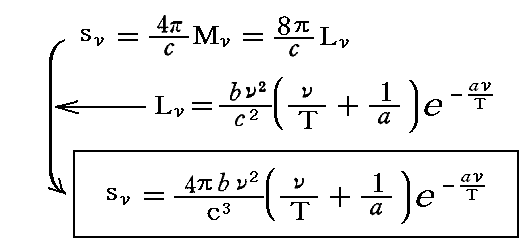
となる。
　さらに輻射場の空間的なエントロピー密度ｓは

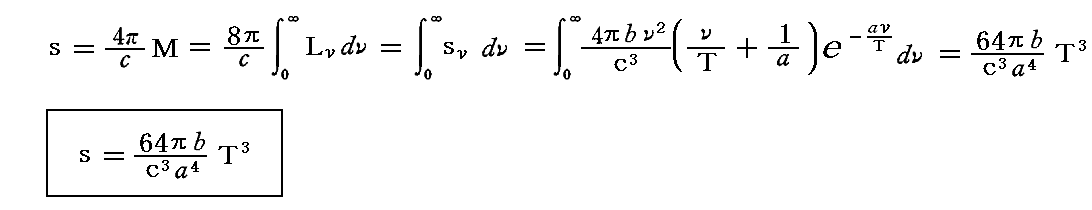
となる。

５．ウィーンの分布則（原論文3．§23）

　定常的な輻射のスペクトル分布則は、普通振動数νにではなく、波長λに関連づけられている。そのため５．（１）３．で得られた輻射のエネルギー分布則を、ある方向に向かう波長λとλ＋ｄλの間に存在する偏光した輻射強度Ｅ_λｄλで表してみる。
　プランクは原論文3．では偏光していないものをＥ_λとしているのですが、ここでは偏光しているものをＥ_λと置くことにする。これは著書10．で採用している定義ですが、等方的な輻射の場合には原論文3．での定義のちょうど1／2倍となります。
　別稿「ウィーンの変位則」５．（２）２．で説明したように、真空中の光速度をｃ、波長をλとすると

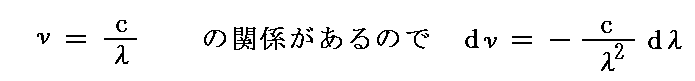
となる。
　そのため

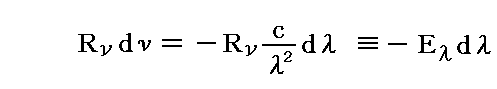
とおける。ここでＥ_λは直線偏光した波長がλを中心とした単位波長幅に含まれる輻射の輝度を表す。
　ここで積分範囲はν：0→∞からλ：∞→0となることを考慮すると

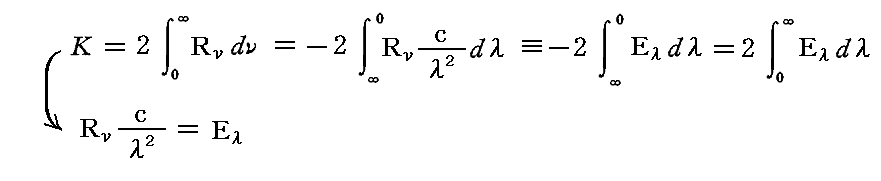
となる。
　これを前記の式に適用すると

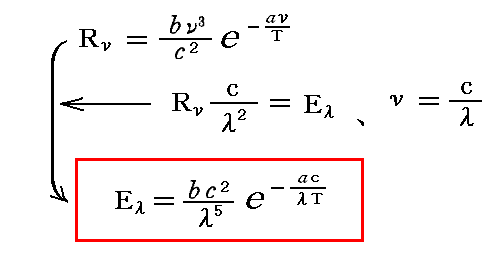
が得られる。
　これは、まさに1896年にW. Wienによって提案されたエネルギー分布則です。
　プランクは、この分布則の近似的な妥当性は
F.Paschen, Wied. Ann. 60. p662, 1897年：Sitzungsber. d. k. Akad. Wissensch. zu Berlin p405〜420, p893, 1899年
F.Paschen & H.Wanner, Sitzungsber. d. k. Akad. d. Wissensch. zu Berlin, p5〜11, 1899年
(Sitzungsberichte der Koniglich Preuβischen Akademie der Wissenschaften zu Berlin　は次のURLからダウンロード可　　http://bibliothek.bbaw.de/bibliothek/digital/index.html　)
O.Lummer & E.Pringsheim, Verhandl. d. Deutsch. Physikal. Gesellsch., 1, p23〜41, p215〜235, 1899年
H. Rubens,“Ueber　die Reststrahlen des Flussspathes”, Wied. Ann., 69, p576〜588, 1899年
等々の実験・観測結果から裏付けられていると説明している。（ただし、最後の二つの中にはすでにWienの法則からのずれが見いだされる。）
　さらに引き続いてプランクは、ウィーンは上記の式を単位体積中に存在する輻射中心の数とそれらの運動の速度に関するある仮定に基づいて求めたのだが、ここで用いた方法は、それとは全く別のものであることを強調している。

［補足説明１］
　４〜５章で紹介した内容は、プランクが解説文13．で

“・・・この過程の不可逆性からして、時間と共にその値が増大する状態函数を容易に示すことができ、それをエントロピーと解釈できるわけである。系全体のエントロピーは、すべての振動子のエントロピーと空洞輻射のエントロピーとの総和になる。一つの振動子のエントロピーを私は、

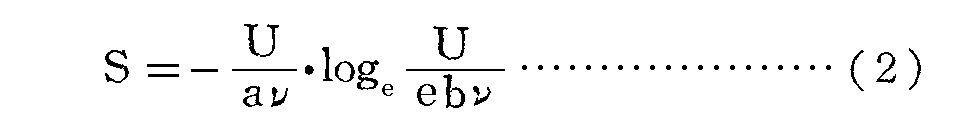
とした［前掲論文(古典論文叢書10)の式(41)］が、ここでａとｂは普遍定数であり、自然対数の底ｅを因数としてｂに付加してあるのは、単に便宜上のことにすぎない。
　また、空洞輻射のエントロピーの表現は、すべての輻射がそのエネルギーとともに、対応するエントロピーを伴うという仮定から類推により導かれたので、空間のエネルギー密度と類比的に空間のエントロピー密度が定められる。
　これらを確定した上で私は、振動子および空洞輻射の初期状態を任意に選んでも、系全体のエントロピーは時間とともに増大することを証明したが、その終りの定常状態である熱力学的な平衡状態は(その時エントロピーが最大になるのだが)、そのすべての部分において唯一つのパラメーターに、すなわち

なる関係で与えられ、熱力学的には絶対温度を表わすＴのみに依存している。
　これに式（２）のＳの値を代入し、式（１）の関係を当てはめれば、振動数νの輻射強度

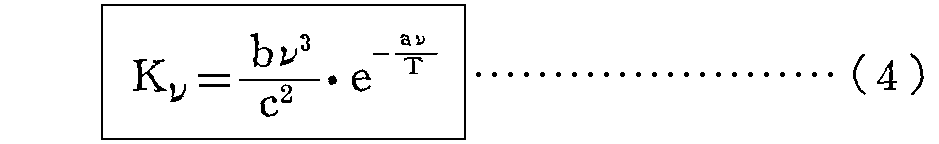
が得られる。［この計算はこちらを参照］
　これはすでに1896年、W・ウィーンによって立てられていた定常エネルギーの分布法則(古典論文叢書６)であり、当時(1899年5月)の測定によって本質的には実証されていたものである。ここまでは、万事が満足にうまく運ぶかと思われた。・・・”

と言っている部分です。ただし、解説文13．でＫ_νと言っている量は、本稿のＲ_νに相当することに注意して下さい。

（２）観測値による定数の決定（原論文3．§25〜26）

１．クールバウムとパッシェンの測定値（原論文3．§25）

　つぎに、プランクは公式中の普遍定数ａとｂを、当時得られている測定値から計算します。

　彼は、F.Kurlbaum の測定値［Wied. Ann. 65, p746, 1898年］を用いて、まずｂ／ａ⁴を求めた。Kurlbaum は100℃＝373Ｋの黒体の放射強度Ｓ₃₇₃と0℃＝273Ｋの黒体の放射強度Ｓ₂₇₃の差が
”
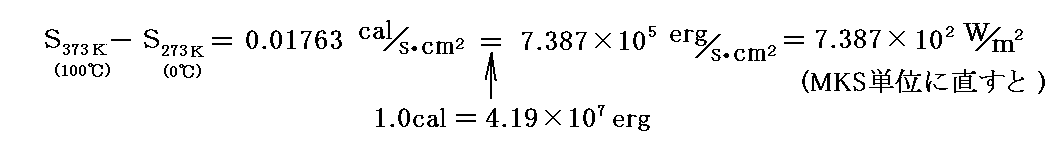となることを測定した。
　この“放射強度”Ｓは絶対温度ＴＫ（ケルビン）に保たれた黒体の単位面積から１秒間に真空中に放出される全エネルギーのことで、別稿「シュテファン・ボルツマンの法則」２．（３）で説明したものです。

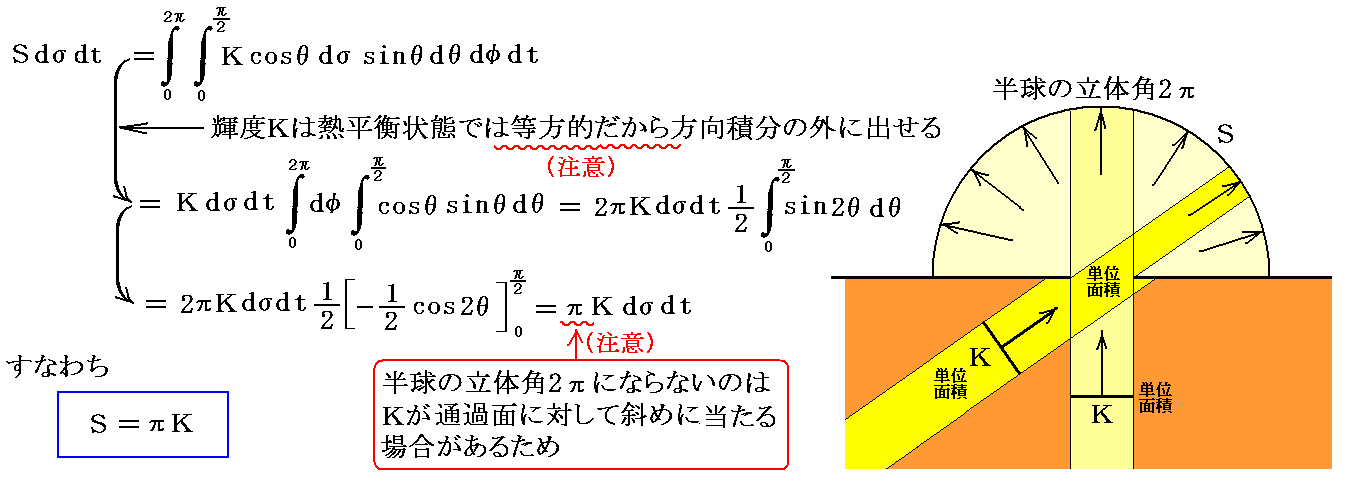
のことです。エントロピーＳやポインティングベクトルＳと同じ記号を用いていますが、これらと混同しないで下さい。
　ここで

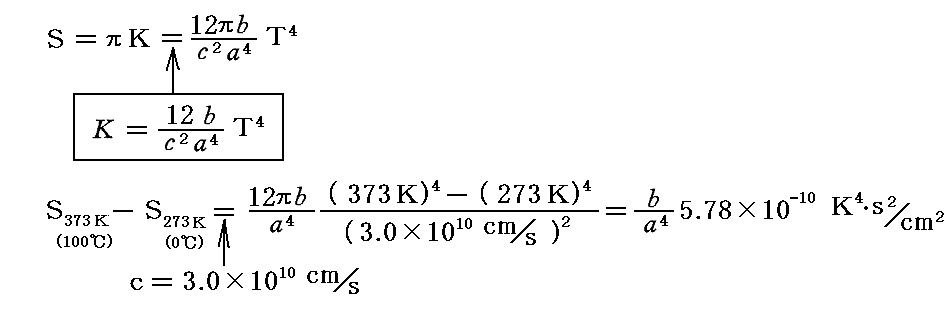
となりますので、前記の測定値と比較すると

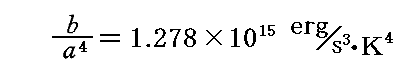
が得られる。

　一方、F.Paschen　は[Sitzungsber. d. k. Akad. d. Wissensch. zu Berlin, p419, 1899年]　で、Wienの公式の指数の定数ａｃの値として

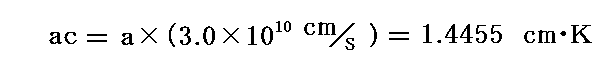
を報告している。

　これら二つの式を連立させて解けば

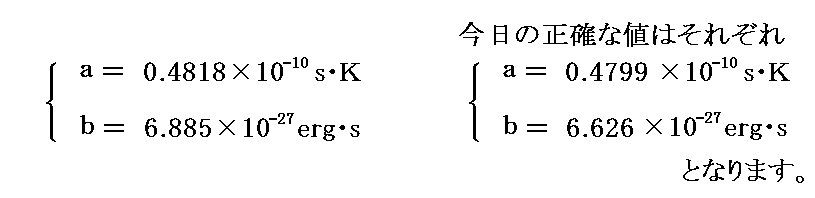
が得られる。
　ここで、ｂは後に［プランク定数ｈ］と呼ばれるものです。またａは［プランク定数ｈ］÷［ボルツマン定数ｋ_B］そのものです。つまり、プランクはこの段階で［プランク定数ｈ］と［ボルツマン定数ｋ_B］を得ていたことになる。

［補足説明１］
　この段階でこれらの定数の値が求まるのは不思議に思われるかも知れませんが、ウィーンの輻射分布公式は、後に発見される真に正しいプランクの輻射分布公式の短波長、低温側での近似形だったのですから、それもむべなるかなです。実際、後で説明するプランクの輻射法則において指数のν／Ｔ（または１／λＴ）が大きな領域では、ほぼ正確にウィーンの分布則に一致します。
　熱輻射の測定は、最初に高振動数（短波長）、低温側で可能になります。それは当初、黒体壁を実現するセラミックを作る技術が未熟なため千度以上の高温状態を実現することが難しかったからです。そのため1897年のPaschenの論文を御覧になれば解るように、当初の測定は主に温度が常温〜1000℃程度で行われていました。［この当たりは参考文献14．の天野氏の説明を参照されて下さい。］
　この温度範囲では、横軸をλで表したプランクの分布則のグラフを御覧になれば解るように波長が短い領域での放射エネルギー密度は大きくなります。そして正確な波長の測定が可能であった。しかし、低振動数（長波長）の赤外線領域では放射エネルギー密度が弱くなる上に、赤外領域での正確な波長の測定が難しかった。
　
　長波長側の正確な測定を行うには、もっとエネルギー密度が大きくなる1300℃〜1600℃程度以上の高温状態が実現され、しかも正確な波長の測定が可能になることが必要だった。ウィーンの分布則が観測値と合わなくなるのはまさにこの高温・長波長の領域ですから最初はその不一致性が解らなかったのです。
　
　そのとき、黒体の温度が1000℃以下の場合、λ＝0〜5×10^-6ｍの領域でウィーンの分布公式はほぼ正確に観測値に一致します。そのため、当初行われた短波長・低温領域での測定から得られたａやｂの値は、思いのほか正確な値だったのです。
［８．（５）［補足説明４］参照］

２．プランクの“自然単位”（原論文3．§26、著書10．§159）

　現在人類が用いている単位系は、われわれの世俗的な文化の要請から選択され定義されてきた。すなわち、長さや時間の単位は、我々の惑星の大きさや、その運動から導かれている。また、質量や温度の単位は水の密度や水の相変化を基準点として導かれている。つまり、地球表面で最も重要な液体である水を、我々を取りまく大気の平均的な圧力のもとで取り扱うことで定められた。
　具体的に説明すると、長さの単位１ｍは地球の極から赤道までの子午線長の１／１０００００００倍を１ｍと決めた。また時間の単位の１秒は、地球の自転周期の１／（24×60×60）倍を１秒とした。質量の単位１ｋｇは最大密度における一辺10ｃｍの立方体（つまり１リットル）の水の質量であり、温度の単位１℃は一気圧のもとでの水の凝固点と沸点を百等分したものである。その後、より正確な定義するためにその基準は繰り返し変更されて、現在は別稿で説明したように定められている。基準は変わったが我々の世俗的な文化に関係していることは変わらない。
　つまり、いくら厳密な定義が可能になったとしても、これらの定義には避けがたい任意性がある。質量の単位として選ばれ白金合金の固まりである質量原器はもちろんであるが、時間の単位の基準のセシウム原子にしても沢山の化学元素の中からこれを選ぶ必然性などどこにも無いのである。
　そのため、異なった時代や、異なった惑星系の生物に取ってこのような特殊な条件の下で定められた単位は、その意味を失ってしまうであろう。

　プランクは、上記の様な現時点の人類の特殊な事情に依存するような単位系ではなくて、時間的、場所的（他の惑星系に存在する知的生命体も含めて）に普遍的な意味をもつ単位系をを提唱している。それが自然単位の概念です。
　彼は、ここで導いた輻射のエントロピーの表現式

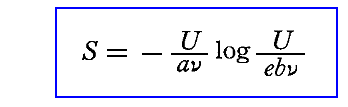
の中に現れた二つの定数 ａ と ｂ を用いて、長さ、質量、時間および温度の単位を決めればよいと言うのです。この単位は特殊な物体や物質の性質に関係なく、その意味をすべての時代、すべての脱世間的、脱人間的な文化に対して保持する。したがってこれは“自然単位”と呼んでも良いであろうと言うのです。

　長さ、質量、時間および温度の４つの単位を確定するための手段は、上に述べた２つの定数 ａ と ｂ の他に、真空中の光速度の大きさ ｃ と、重力定数の大きさ Ｇ によって与えられる。これら４つの定数の数値を、現在の単位であるセンチメートル、グラム、秒、摂氏温度で表せばつぎのようになる。

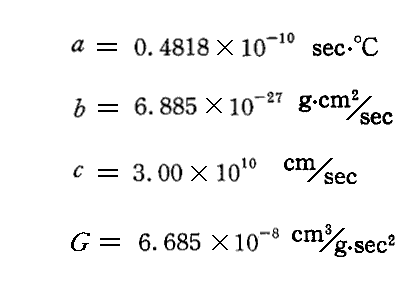
　“自然単位”とは、ここに上げた４つの定数をすべて１（ａ＝1、ｂ＝1、ｃ＝1、Ｇ＝1）としたものに他なりません。そうすれば、現在使われている各次元の量を測るときの単位はそれぞれ

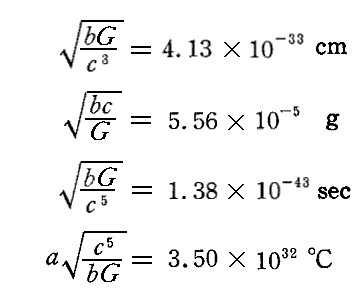
となる。
　これらの大きさは、［重力の法則］、［真空中の光の伝播の法則］、［熱理論の二つの法則］が正しい限り、その自然の意味を失わない。したがってどんなに異なった考え方で、どんなに異なった方法で、どんな知的生命体が測定しても常に同じ数値になるはずです。もちろん同じ１０進数を採用しての話しですが。　

［補足説明１］
　後に記した著書10．§159では、プランクはｂ［プランク定数ｈ］はそのままにして、ａ を ｂ／ａ＝プランク定数ｈ／ａ＝ｋ_B［ボルツマン定数］ に置き換えています。考え方は全く同じですが、ａ を ｋ_Ｂ に置き換えた場合には下記の様になります。
　現在の単位系で、それらの量は

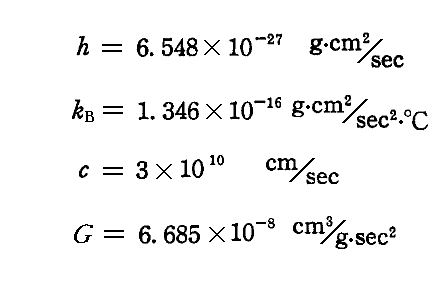
となります。
　そのとき、cmをｈ、ｋ_B、ｃ、Ｇで表す事を考える。

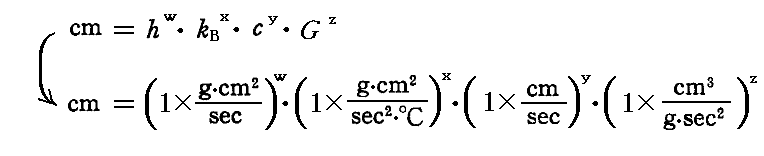
であるから、以下の連立方程式を解いて指数ｗ，ｘ，ｙ，ｚを決定すればよい。

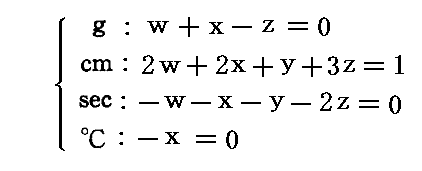
この連立方程式の解は

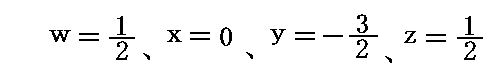
となるので

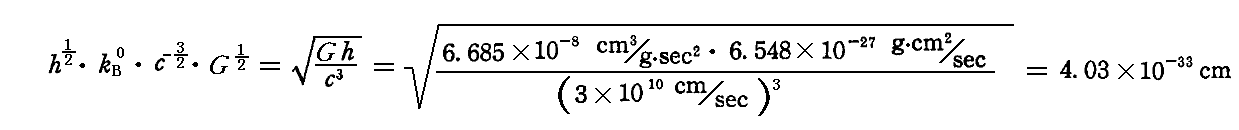
となる。ｇ、ｓｅｃ、℃も全く同様に考えればよい。
　結局、ｈ＝1、ｋ_B＝1、ｃ＝1、Ｇ＝1とした“自然単位”では、

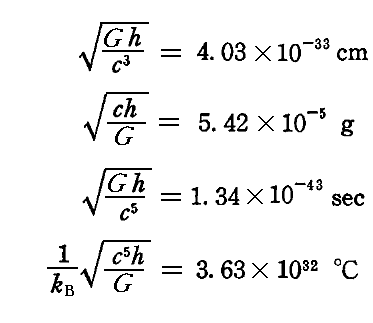
の値が、それぞれ長さ、質量、時間、温度を測るときの単位となります。
　これは前出の値と微妙に違っていますが、それは1906年の段階で得られたｈとｋ_Bのより新しい測定値を用いたためで、本来は ａ を ｋ_Ｂ に置き換えても変わりません。

［補足説明２］
　プランクの自然単位系とは、根本的な物理法則（その多くは左辺と右辺で異なる次元の物理量を結びつけている。）の比例係数を１と置くことによって構成する。
　多くの物理法則は普通、左辺と右辺で異なる物理量（つまり左辺の次元と右辺の次元が異なる）を結びつけており、その両辺を結び付ける時に掛かる定数は左右の異なる物理量（次元）を関係付ける換算定数となる。
　そういった換算定数を含む幾つかの独立の物理法則を用いれば、物理で用いられる物理量の測定単位を人間世界の任意性にもとずく事情に患わされることなく定める事ができます。
　
　最も有名な“プランクの自然単位”はもともと、
　　・ニュートンの万有引力の法則　Ｆ＝Ｇ･ｍ₁･ｍ₂／ｒ²の比例定数Ｇ（万有引力定数）
　　・プランクのエネルギー量子公式　Ｅ＝ｈν＝（ｈ／2π）･ωの比例定数ｈ（プランク定数）
　　・アインシュタインの質量エネルギー公式　Ｅ＝ｃ²ｍの比例定数ｃ²あるいはｃ（光速度）
　　・ボルツマンの法則（熱の運動エネルギー表現）　Ｅ＝1／2･ｋ_BＴの比例定数ｋ_B（ボルツマン定数）
の４つを１と置いて定められたものでした。
　
　しかし、今日の“プランクの自然単位”はプランク定数ｈそのものではなくて、それを2πで割った（ｈ／2π）が用いられている。さらにまた、Ｇ、（ｈ／2π）、ｃ、ｋ_Bの４個に加えて、さらに
　　・クーロンの法則　Ｆ＝（1／4πε₀）ｑ₁･ｑ₂／ｒ²の比例定数（１／4πε₀）［Ｑ^-2ＭＬ³Ｔ^-2］
　　　（但しε₀は真空の誘電率であり、これは有理化単位系での公式形です）
を付け加えた５個の換算定数を１に定めることによってプランクの自然単位系を構成している。これを付け加えることで電気量の測定単位を定めることができるからです。
　これらを用いると［補足説明１］の換算定数一覧は

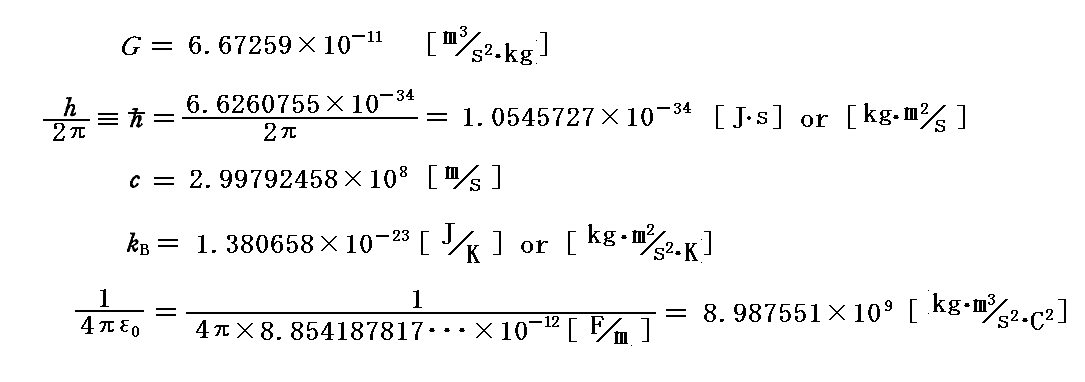
となる。但し、数値は今日の値を用い、単位系はＳＩ有理化単位系にしてある。
　［補足説明１］と同様にして、Ｇ＝1、（ｈ／2π）＝1、ｃ＝1、ｋ_B＝1、（1／4πε₀）＝1とした“自然単位”では、

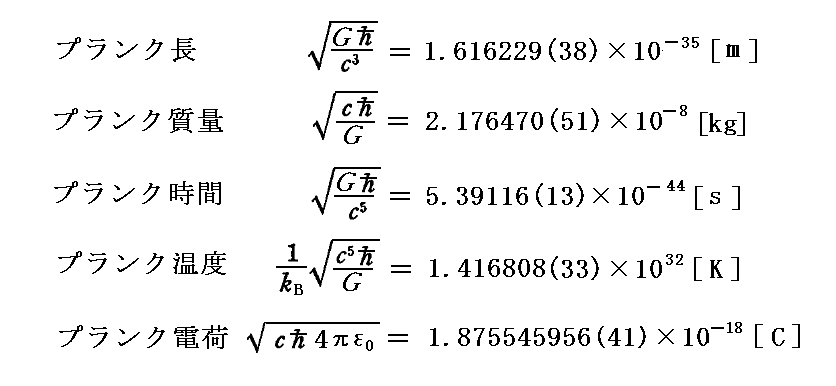
の値が、それぞれの物理量（長さ、質量、時間、温度、電気量）を測るときの単位となります。
　これらの値に、自然の秘密を解き明かす何らなのメッセージが込められているのかもしれないと検討を重ねる科学者もいます。しかしそのとき、これらの値には2πや4πの取り扱いに伴う任意性がある事を忘れないでください。その任意性に伴いぞぞれの単位となる量のオーダーはほぼ適切かもしれないが数値そのものには恣意性があります。［詳細はWikipediaの記事など参照］
　
　プランク長やプランク時間はあまりにも小さすぎ、ブランク温度はあまりにも大きすぎる。プランク質量とプランク電荷のみが我々に身近な範囲のオーダーに収まっている。実際にそういった単位としての塊に何らかの意味があるのか、その真意は不明です。
　
　スティーヴン・ワインバーグは彼の著書「科学の発見」文藝春秋（2016年刊）のp342で
　“同じ距離にある二つの電子間反発力と同じ強さの重力をもつために粒子が持っていなければならない質量（これは上記の“プランク質量”とほぼ同じオーダーの値になる、また単位電荷は上記の“プランク電荷”とオーダー的に近い）を基準にすることによって、重力及びその他のまだ発見されていない力を標準モデルの諸々の力と統一できるのではないかと考えられている。だが、人類の経済的資源のすべてが物理学者の自由裁量にまかされたとしても、そんな巨大な質量を持つ粒子を実験室内で創造することはできないだろう。”
と述べています。

６．振動子エントロピーの一般的な導出（原論文4．、著書10．§188〜189）

　プランクは、一応前節までの議論で、まがいなりにも実験結果を説明できるエネルギー分布則を導いたのですが、４．（４）１．で仮定した振動子のエントロピー表現形式は、いかにも唐突に導入された観を免れないと思っていたようです。
　そのため、彼はこの式をより一般的に導けないものかと考察を進め、原論文4．で報告しています。これは前節の理論の正当性をさらに補強するものですからここで説明します。

［補足説明１］
　実際の所、プランクが原論文4．（この６．章の内容）を執筆する以前の原論文3．を校正・出版する段階で、すでに
O. Lummer & E. Prigsheim, Verhandl. d. Deutsche. Physikal. Gesellsch., 1, p215, 1899
の測定や、少し遅れたＦ・パーシェンの測定によって、ウィーンの分布法則の検証をより長い波長へ広げるとそこに若干のずれが認められることが解っていました。
　そのずれは測定が精密になるにつれて、ウィーンの分布公式の正当性を真剣に疑わねばならぬほどはっきりしてきたのです。実際この段階で、M.Thieserなどが、観測事実と良く合う新しい分布公式を提案していました。
　そのため、プランクは“ウィーンの分布公式が変更されなければならなくなり、４．（４）１．で仮定した振動子のエントロピーの表現式を、より適切な表現に置き換えなければならなくなったときでも、彼の理論がその変更に耐えうるように、より根源的な原理から振動子エントロピーの表現式を導こう。”と考えたのです。

（１）理論の物理的基礎（原論文4．§1〜2）

　プランクは原論文4．の§1と§2で、彼が得たそれまでの成果と、彼の理論の物理的根拠を概観しています。これは、もってまわった言い回しのとても難解な文章ですが、彼の考え方を知る上でとても興味深い部分ですから、その内容を以下に箇条書で要約しておきます。

1. 　当時、輻射線そのものの温度について言うべきではなく、輻射線を放出する物体の温度についてのみ言うべきであるという見解の物理学者がいました。
   　それに対してプランクは、太陽を例に出して、太陽が黒体表面の様に輻射を放出し、輻射が途中でエネルギーを失わずに進むときに、太陽の物体としての温度は太陽の輻射線の温度以外の何者でもないだろう。もし輻射の温度を考えなくて、地球で感じる太陽光線の輻射熱の性質を論じるようとすると、太陽と地球の間での輻射の性質について非常に煩雑な手続きが必要になるであろう。そのように物体と輻射を断絶的に考えるよりも、単色の太陽輻射線のそれぞれに特有の温度を付与した方がはるかに有効であると説明しています。
2. 　プランクの理論はキルヒホッフの定理「まわりを反射壁で取り囲まれている真空空間の中に任意の物体が存在して、時間が経って定常状態が実現された場合、その状態は唯一の変数である温度によって完全に決定され、その中に配置した物体の数、形状、性質、配置などには関係しない。」を拠り所にしているのですが、彼が仮定したように、輻射による減衰はわずかでその大きさに比較して大きな波長の輻射線を放出する静止した線形振動子を十分大きな距離隔てて配置しておきさえすれば、彼が言う“自然輻射”の仮定をおくだけでキルヒホッフの定理が実現する状態になることが証明できる。そしてこの自然輻射の仮定こそ熱力学第二法則からの不可避的な要請であると彼は言っています。
3. 　分子運動論的な熱理論の立場からいくと、プランクの導入した振動子も当然熱運動によって動いているべきなのだから、振動子が静止していると仮定したことは適切ではないのではないかと言う疑念が生じる。
   　しかし、分子の速度が、その温度への依存性によって熱輻射に介入してくるのは間接的なものにすぎない。なぜなら温度は平均速度ではなくて平均運動エネルギーと関係づけられている。だから振動子の振動エネルギーの中で振動子の運動の効果は考慮されているのであるとプランクは説明します。
4. 　気体分子運動論に於ける非可逆性は、非常に多数個の分子のランダムな運動に関係していた。これに対して、プランクが論じたように、たった１個の振動子について、輻射過程の非可逆性や輻射エントロピーの概念を論じることができるのだろうかと言う疑念に対して、プランクは次のように答えています。
   　気体分子運動論における非可逆性は無数の分子の位置と速度の不規則性によっていたが、輻射場の議論の非可逆性は、輻射の中に存在する無数の振動数や位相や強さの不規則性にある。だから１個の振動子の定常的な振動といえども、実質はほとんど等しい周期と一定の振幅及び位相を持つ非常に多くの小さな固有振動の重ね合わせであり、位相が不規則に変化する沢山の振動から成り立っている。したがって、たとえ１個の振動子であっても、その無秩序さ（すなわち振動子のエントロピーや温度）について語ることができる。
5. 　上記の無秩序が熱輻射線に存在することが、ウィーンのエネルギー分布則が示しているように、“一定の色の輻射の強さ（つまり波長を固定したときの輻射強度）が温度の増大と共に限りなく増大するのではなくて、一つの有限な極値に近づいていく”というようなことが生じる原因であろう。

［補足説明１］
　上記の1〜4．までの項目については、確かにプランクの言うとおりかもしれないのですが、5．の推測についてはプランクは間違っています。
　項目5．でプランクが言っているのは以下のことです。
　ウィーン分布公式

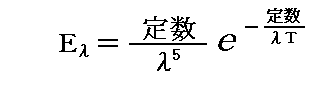
において、λを固定してＥ_λの温度による変化に着目します。そうすると

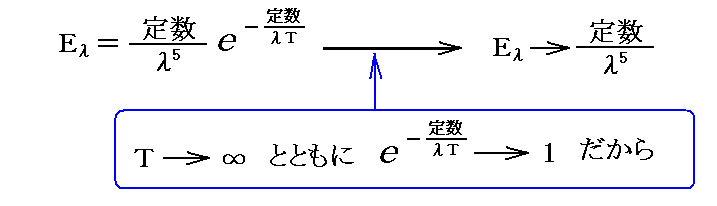
となり、温度を無限大にしてもある極値に近づいてそこで止まってしまい、決して無限大まで増大することはありません。そのことを言っているのです。
　この事実はウィーン自身も、彼の分布公式を発表した1896年の論文の（p668の）最後で注意していることですが、この時点（1900年3月）のプランクはこの事実こそ熱輻射の性質を特徴づけるものだと考えていたようです。
　
　実は、これはレーリーが彼の輻射分布則を提案した1900年6月の論文の最初のページで、ウィーンの分布公式が物理的に考えて正しくないと批判している所です。つまり“温度を無限大にすれば、それに応じて熱輻射の強度Ｅ_λも無限に増大すべきで、そうなっていないのはおかしい。”と言っているのです。［この論文は「物理学古典論文叢書１　熱輻射と量子」、あるいは参考文献１４．のデジタルライブラリーの中に翻訳掲載されています。］
　この点でレーリーが正しく、プランクは間違っていました。まさに長波長・高温領域でウィーンの分布則と観測値に食い違いが生じていたのですから。
　
　この当たりは、参考文献14．の第3章１３．や参考文献21．の§8.2.4と§8.3.4で解りやすく説明されていますので参照されて下さい。また８．（５）［法則説明４］のグラフを御覧下さい。

［補足説明２］
　前記項目5．についてはプランクは間違っていたのですが、長波長・高温領域に於けるウィーンの分布公式の特徴をレーリーと同じようにプランクもハッキリ認識していたことは重要です。
　
　それだからこそ、1900年10月の段階で長波長・高温領域のより正確な観測データが得られたとき、直ちに正しいエントロピー表現式を見つけることができた（原論文5．）のだと思います。項目5．の推論において間違っていたのはエントロピーを用いた考え方ではなくて、原論文3．で仮定したエントロピーの表現形式の方だったのですから。

（２）輻射場の中にある１個の振動子（原論文4．§3）

　ここでの議論を展開する準備として、３．〜４．章の結論を復習しておきます。

１．エネルギー保存

　３．（４）４．で証明したように、振動数νの１個の振動子に対するエネルギー保存則は

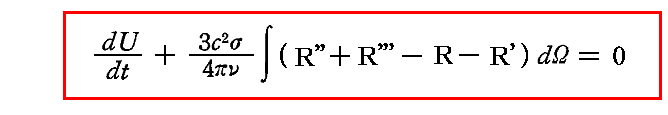
となる。
　ここでＵは振動子のエネルギー、ｔ は時間、ｃ は真空中の光の伝播速度、σ は振動子の振動振幅の対数的減少率［１．（３）参照］、ｄΩ はその先端が振動子にある円錐の無限に小さな開き角である。また、Ｒ と Ｒ’は、二つの互いに直角に偏光した、円錐ないで一方の向きから振動子にあたる振動数νの輻射線束の強さ。Ｒ'' と Ｒ''' は同一方向で逆向きに共鳴子から出てくる輻射線の強さ。つまり、振動子により輻射のエネルギーの一部が吸収された残りの通過光の強さである。
　Ｒ''とＲ''' は３．（３）で証明したように

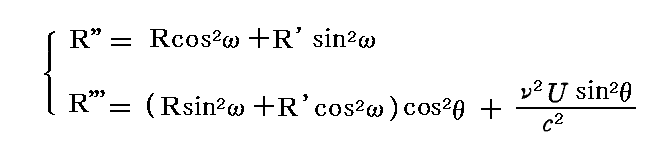
で与えられる。
　この場合のθ は輻射線の方向と振動子の軸の間の角度を、ω はＲ’の偏光面と輻射線及び振動子の軸を通る平面との間の角度を表している。Ｒ''の偏光面は振動子の軸［ｚ軸］に垂直であり、Ｒ'''の偏光面は振動子の軸を通る。

２．エントロピーの増大

　Ｓ を振動子のエントロピーと呼び、Ｌ をある時間に、ある方向に伝播する振動数νを持つエントロピー輻射の比強度と呼ぶことにする。［４．（１）１．で注意したように、この稿ではエントロピー輻射については強度と呼ばずに比強度と呼ぶことにしている］

　ＳはＵとνとのある関数になる。４．（４）１．ではＳの形を天下り的に定義して用いたのだが、ここではその表現式の正当性をより一般的考察から求めたいので、４．（３）４．で証明した様にＵとνのある関数になることだけ解っているとする。

　Ｌは、別稿「ウィーンの変位則」６．（５）３．で証明した（１３）式のように、Ｒとνとのある関数になる。そのときエントロピー輻射Ｌ、Ｌ’、Ｌ''、Ｌ'''の偏光面の方向をＲ、Ｒ’、Ｒ''、Ｒ'''と同じ意味とし、またＬの比強度をＲの強度に対応させるとすると、ここで考察している振動子を取り囲んでいる輻射場の時間ｄｔないに生じるエントロピー変化は、４．（２）２．で求めたように

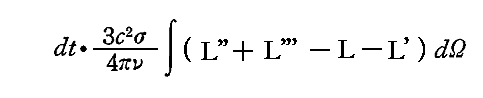
となる。
　このとき同じｄｔ時間に生じる振動子のエントロピー変化をｄＳとすれば、共鳴子と輻射場の中に生じる系全体のエントロピーＳ_tの変化は

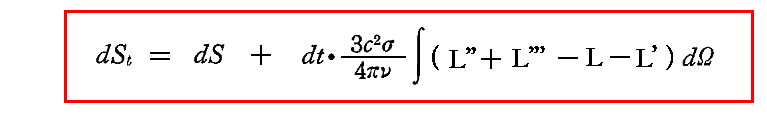
となる。これは前記のエネルギーについての式と全く類似したものになっている。

（３）特別な場合への応用（原論文4．§4〜5）

　ここでプランクは前節の結論を、“振動子のおかれている場は定常的輻射状態にあるが、振動子の振動エネルギーは初め全く任意である”特別な場合に当てはめて、さらに何か言えないか考察を進めます。

１．定常的な輻射場（原論文4．§4）

　ここで、“振動子のおかれている場は定常的輻射状態にあり、振動子の振動エネルギーは初め全く任意である場合”を考えるのですが、これに対する条件は、振動子に当たる輻射が偏光しておらず、すべての方向に対して一定であることです。つまり

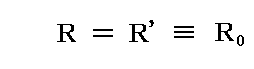
で、これが時間的にも、輻射の方向にも依存しないことです。
　これを用いると前節のエネルギー保存則は


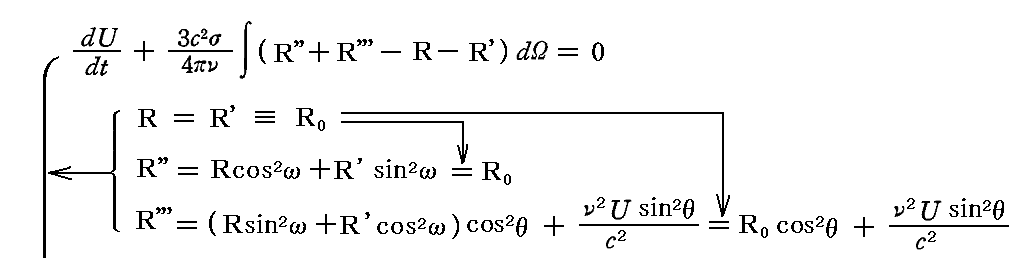
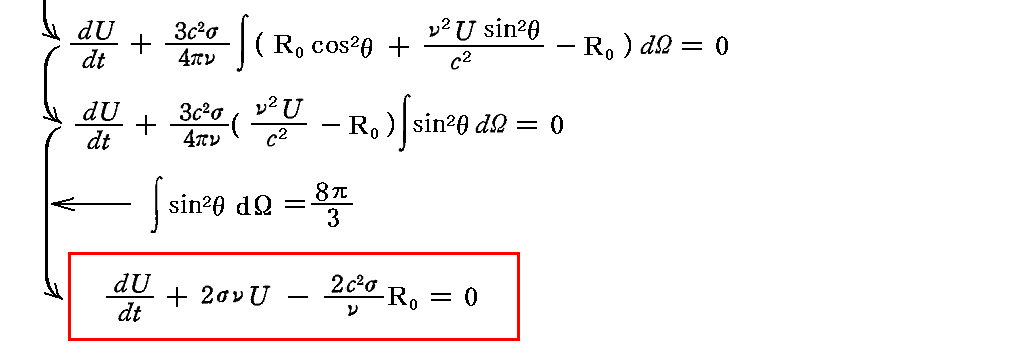
となる。

　Ｒ＝Ｒ’＝Ｒ''が成り立つので、エントロピー輻射Ｌに対しても

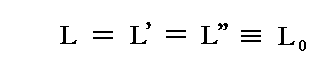
が成り立つと考えられる。そのため前節の全エントロピーの変化は

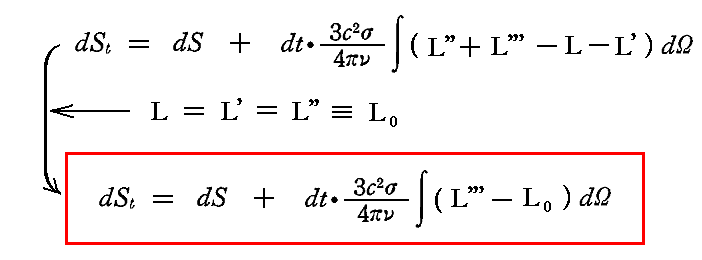
となる。ここでＬ'''は

２．系全体が定常的なときのエントロピー（原論文4．§4）

　ここで、振動子を取り囲んでいる輻射場だけではなく、系全体が定常的な輻射の状態にある場合には

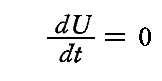
だから振動子のエネルギーＵは

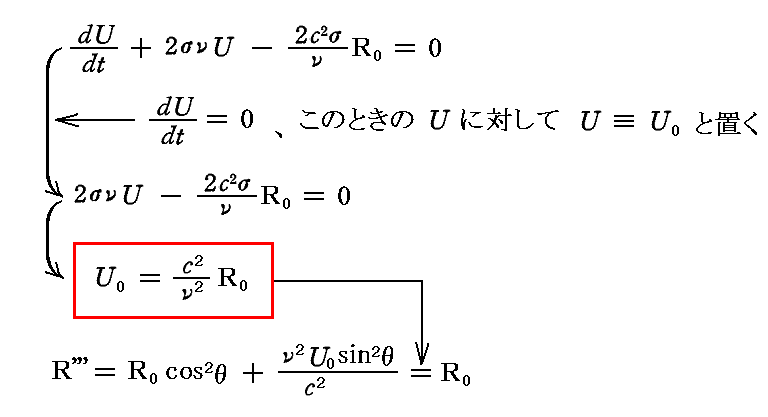
となる。ここでＲ'''＝Ｒ₀も言えるので、Ｌ＝Ｌ’＝Ｌ''＝Ｌ'''＝Ｌ₀が言えることになり、系のあらゆる部分でエネルギーもエントロピーも時間に依存しないことになる。したがって我々は、Ｕ₀を振動子のエネルギーの“定常値”と呼ぶことにする。かくしてＵは時間と共に漸近的にＵ₀に近づいてゆくはずである。

　ここで、振動子のエネルギーが“定常値”Ｕ₀からほんの少しΔＵだけズレた値を持っていたとする。すなわち

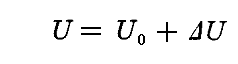
の小さな量ΔＵを、振動子エネルギーの“定常値”Ｕ₀に関する“（正または負の）余剰”と呼ぶことにすれば、これは振動子の定常状態からのズレの大きさと方向に対する尺度を与える。このとき


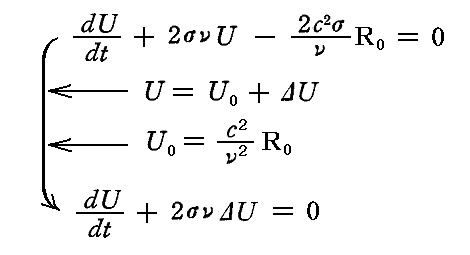
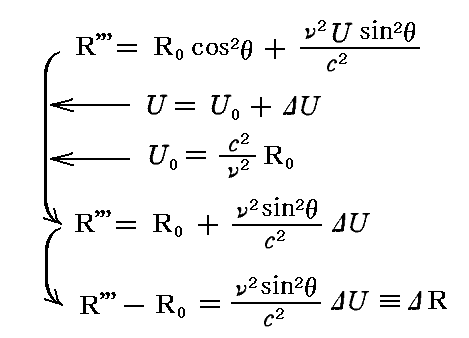
と置くことができる。
　そのため、Ｌ'''をTaylor級数に展開して、ΔＵの高次の項を無視すると

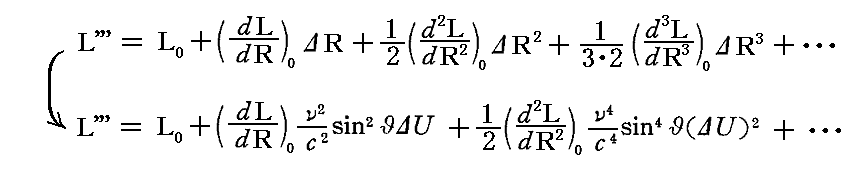
となる。
　これを前記の式に代入すると


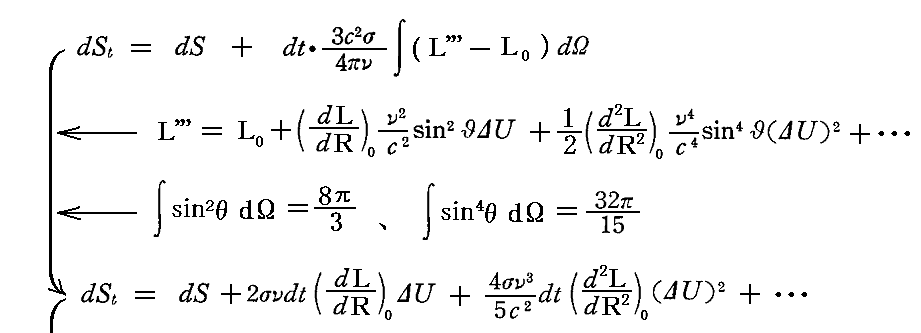
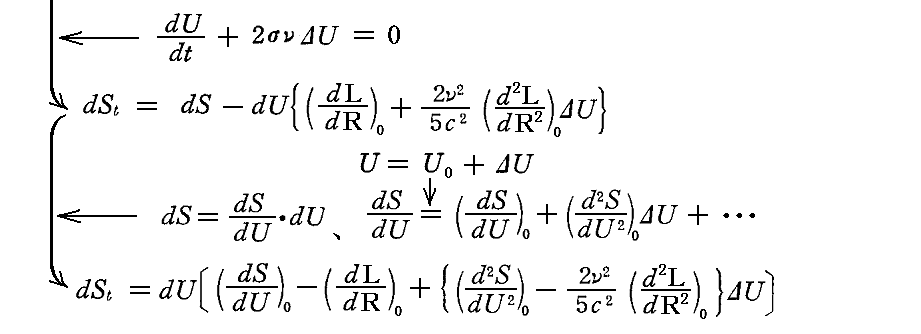
となる。この式は定常的な輻射場に対応するエネルギーUよりΔＵだけ大きいエネルギーを持った一つの振動子が、輻射場からｄＵのエネルギーを受け取った時に生ずるエントロピーの変化を表す。

３．エントロピーに不可欠の性質（原論文4．§5）

　前節の最後の式に於いて、熱力学第二法則が真であるならば、右辺は常に正かゼロで無ければならない。ここでｄＵは正あるいは負で、しかもΔＵは任意に小さいとできるので、右辺が常に正またはゼロであるためには

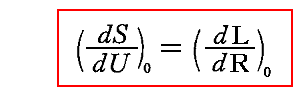
でなければならない。ここで

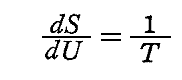
であったことを思い出すと、上式はまさに、個々の輻射線の絶対温度が

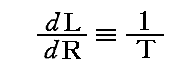
で定義され、個々の輻射線の温度と振動子の温度が等しくなっていることを意味する。
　前記の式を積分、あるいは微分すると

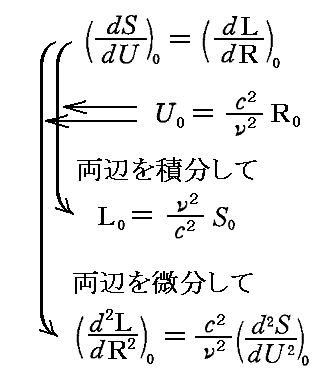
となる。ここで、積分定数は物理的に意味を持たないので省略してある。
　これらの関係式を、前節の最後の式に適用すれば

となる。ここで添え字の0は、今は余計なものとして省かれている。これは、定常的な輻射場のなかにある１個の共鳴子が、その定常値に関する小さな余剰ΔＵを含むエネルギーＵを持っていて、エネルギー変化ｄＵを蒙るときに、自然に生じるエントロピーの増大を表す。
　ところですでに求めた

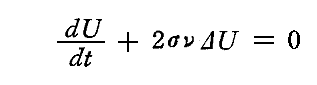
の関係式より、ｄＵとΔＵは必ず反対の符号をもっていなければならないから、ｄＵ×ΔＵ＜0 となるので、最後の項が負でなければならない。そのため

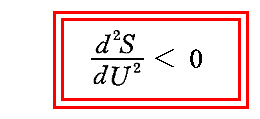
がえられる。これは、平衡状態に於ける振動子のエントロピーが極大値をとっていることを裏付けるために不可欠の条件が導き出されただけなのですが、ちゃんとそれが導けたと言うことはこれまでの振動子、輻射場、系全体に対して定義してきたエントロピーの概念が適切なものであったことを証明していると言える。
　このとき

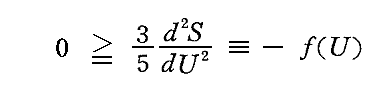
と置けばｆ（Ｕ）は必ず正の関数となる。すなわち

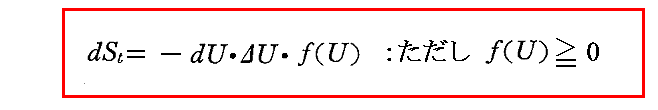
となるが、このエントロピー関数ｆ（Ｕ）は振動子のエネルギー以外に、振動子の振動数νに依存するが、対数的減少率σには依存しない。それは、以前求めた

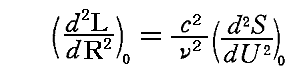
の左辺にσが含まれてはいないことから解る。

（４）エントロピー関数の導出（原論文4．§6）

　ここで考察している特別な場合の考察からも、彼が行っているエントロピーを用いた考察の正当性が裏付けられ、エントロピー関数の満たすべき性質についてさらに幾つかの重要な事が得られた。
　しかし、エンロピー関数ｆ（Ｕ）の形が決定できなければ、先に進むことはできません。つまり、それは４．（４）１．で振動子のエントロピー関数を天下り的に与えないと先へ進めなかったのと同じ状況です。
　真に正しいｆ（Ｕ）の関数形を見つける方法を知らなかったこの段階のプランクは、仕方なしに次に述べるかなり恣意的な方法でこの関数を見つけようとします。

　プランクは原論文4．§6で１個の振動子ではなくて、ｎ個の振動子の集まりを考えます。そして“全体のエントロピーの増加は全エネルギーＵ_nに依存するだけで個々のＵやその個数ｎには依存しない。”という仮定を立てて考察を進めます。彼は、前節の最後に得られた式をｎ個の振動子を含む場合に拡張して、この仮定を適用することで一つの関数方程式を導きます。そして、その関数方程式を解いて ｆ（Ｕ）＝定数／Ｕ を導きます。［ただし、この証明の論法は間違っていることが後で解ります。］

　ｆ（Ｕ）＝定数／Ｕ が成り立つと

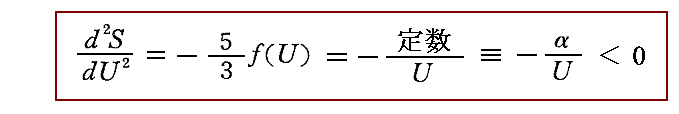
となります。ここで正の定数αは振動数νに依存する可能性があります。
　これを二回積分すれば

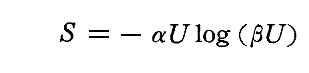
が得られます。ここで、νに依存する第二の正の定数であるβを導入する必要がありますが、これ以外の付加的な積分定数は、物理的な意味を持たないので省略できます。
　プランクは、この式を、一般的な議論から導かれる故に、彼が最も信頼していたウィーンの変位則（ただし振動子エントロピーについてのもの）

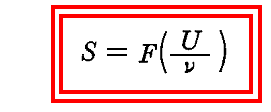
と比較して定数のν依存性を決めます。つまりウィーンの変位則が正しければ

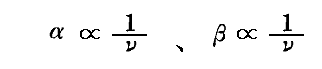
でなければなら。そのため

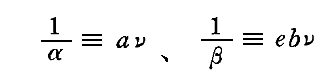
とおかなければならないことが解ります。ここで１／βの比例定数を ｂ ではなく ｅ×ｂ と置いたのは単なる計算の便利のためです。
　このように置くと、振動子のエントロピーの表現式として

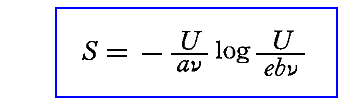
が導けます。まさに、これは４．（４）１．で天下り的に仮定したものと同じです。
　これに、熱力学第二法則

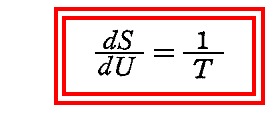
を適用し、さらに振動子のエネルギーと輻射強度の関係式

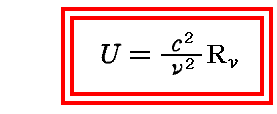
を用いて、振動子のエネルギー分布から輻射場の分布に変換すればウィーンの輻射分布公式が導けるのは５．（１）でに説明したとおりです。

　ここの一連の考察の中に、プランクが後に繰り返し使うことになる手法のすべてが現れています。つまりこの段階で考察に必要なすべての鍵を取得できたことになる。後は正しいエントロピーの表現形式を得る事だけだったのです。

　以上の考察により、プランクはエントロピーを用いた彼のやり方に、自信を深めます。さらに、このとき

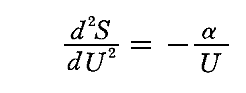
が非常に単純な形になったことから、彼はこのエントロピーＳのＵに関する二次微分係数（二次導関数）の重要性に着目します。そして、この二次微分係数の表現形式の中に本質があるに違いないと確信します。後に、これが彼を内挿式の発見に導くことになった確信です。

［補足説明１］
　ここでプランクが ｆ（Ｕ）＝定数／Ｕ を導いた証明の過程を説明しなかったのは、結局その証明は間違っていたからです。彼がそこで行った仮定“全体のエントロピーの増加は全エネルギーＵ_nに依存するだけで個々のＵやその個数ｎには依存しない。”が正しくなかったのです。そのため、それから得られた結果も正しくないので証明の説明は省略しました。
　ただし、彼がｄ²Ｓ／ｄＵ²の重要性に気付いたことは大切ですので、その部分を中心に原論文4．の内容を紹介しました。

［補足説明２］
　プランクは真に正しいエントロピー表現式が得られた後に、その正しい形を用いて、ここでの考察をもう一度やり直しています。それが著書10．§189で報告されているものです。
　そこで、“全体のエントロピーの増加はｎ個の振動子の全エネルギーｎＵ＝Ｕ_nに依存するだけで個々のＵやその個数ｎには依存しない。”と仮定したことが間違いだったことを確認しています。実は、ｎ個の振動子を含む系全体のエントロピーの変化は全振動子のエネルギーＵ_nやその変分ΔＵ_nやｄＵ_nに依存するばかりでなく個数ｎにも顕わに依存していたのです。
　また、次章で説明する内挿式を導いた原論文5．のｐ203で、上記の原論文4．で ｆ（Ｕ）＝定数／Ｕ を導いた証明が間違っていた可能性がある事を認めています。

［補足説明３］
　この章で紹介した内容は、プランクが解説文13．で

“・・・エントロピーの性質を徹底的に明らかにするために、私はまず関係式（２）を用いないでまったく一般的に、定常の輻射場の中にあって、その輻射場に対応するエネルギーＵよりΔＵだけ大きいエネルギーを持った一つの振動子が、輻射場からｄＵのエネルギーを受け取った時に生ずるエントロピーの変化を計算してみた。
　この変化は

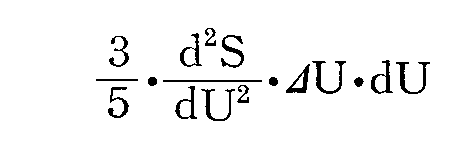
となった［Ann. Physik, (4)1, p730 (1900)(古典論文叢書11)］。
　熱力学の第二法則によってこれが常に正であり、また自然界において実際に生ずる変化では、ｄＵとΔＵとの符号がとにかく逆であることから、必然的に

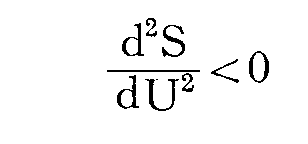
となる。
　実際、ウィーンの分布法則が導かれるエントロピーの表現式（２）によっても

が得られるのである。
　この関係が非常に単純なので、私はそれを適当な直観的考察から直接に導いてみようと考えた。そのような考察をやってみたものの、こうして私は別の面からふたたび関係（２）に、従ってまたウィーンの分布法則に到達した。
　この考察は、ある程度まで説得力があるにしても、否みがたいものとは言えないので、ここではそれを紹介することを控えておく。またそれが実際に適合しないことは、ウィーンの分布法則が測定によれば、一般的には成り立たないという事実からも明らかである。こうして式（２）を改善しようとする試みはゆき詰ってしまい、私はそれを究極的に放棄しようとしていた。・・・”

と言っている部分です。

７．内挿公式の発見（原論文5．）

　1900年10月にプランクは［共鳴子のエントロピーのエネルギーに付いての二階微分係数についての内挿式］と［ウィーンの変位則］から導かれる式を［熱力学第二法則］と結びつけることにより今日“プランクの熱輻射公式”と言われるものを導きます。
　
　内挿式の導出過程については、Sommerfeld文献15．§20や、文献18．、19．等々・・を含めて多くの本で説明されています。また、参考文献14．の国立国会図書館のデジタルライブラリーの中に原論文5．の翻訳があります。これはとても短い報告なのでぜひ原典を読まれて下さい。

　その内容は、プランクが解説文13．で

　“・・・こうして式（２）を改善しようとする試みはゆき詰ってしまい、私はそれを究極的に放棄しようとしていた。
　そのとき、こういった状態にあって、決定的な転回をもたらすべき出来事が起った。それは、1900年10月19日に開かれたドイツ物理学会で、F・クールバウムがH・ルーベンスと共におこなった、非常に長い波長部分に対するエネルギー測定の結果が報告されたことである。その報告の一部として、黒体の輻射強度は高温になればなるほど、ますますよく温度Ｔに比例するということが明らかにされたが、これは輻射強度を常に有限ならしめるウィーンの分布法則（４）とは、かなりあい容れない事実だった。
　学会の数日前［10月7日のこと］に私はこの結果を口頭で知らされたので、それからの結論を学会が開かれるまでに私なりの仕方で引き出して、振動子のエントロピーを計算してみるだけの時間的余裕があった。
　もし高温Ｔにおいては輻射強度Ｋ_νが温度Ｔに比例するとすれば、式（１）より振動子のエネルギーも温度Ｔに比例して

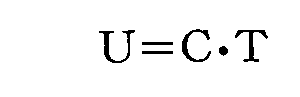
となり、これを式（３）に入れて積分すると

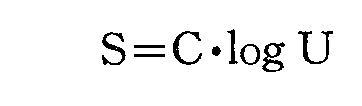
が得られ、従って

となる。［この計算はこちらを参照］
この関係は従って、Ｕの大きな値に対しては、Ｕの小さな値に当てはまる関係式（５）

にとって代るものである。
　
　そこで、Ｕの小さな値で正しい式（５）とＵが大きな値で正しい式（６）を極限として含む一般的な関係を求めれば、最も簡単なものとして

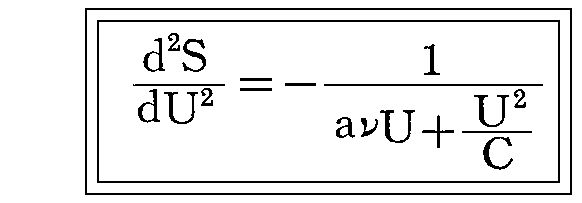
が得られ、積分すると

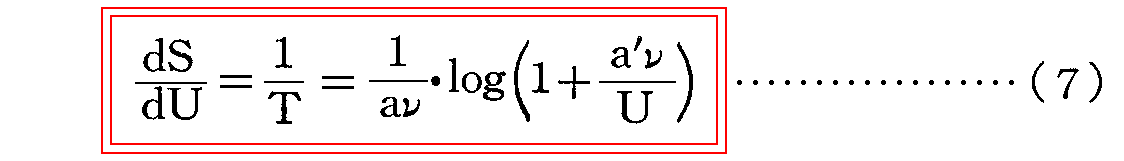
となるが、ここでは簡単のため、定数aＣ＝a'　と置いてある。［この計算はこちらを参照］
　
　（７）式は、Ｕ＝の形に直して式（１）のＵに代入すればＫ_νについてのエネルギー分布法則を与える式になるのだが、上述の物理学会でのクールバウムの講演に続く活発な討論の途中で、私はこの式を波長に換算した形で提出し、検討を加えるよう申し出たのである。［この報告が　Sitzungsber. Deutsche Phys. Ges. 2, p202〜204 (1900)(古典論文叢書12)］
　
　翌朝同僚のルーベンスが訪ねてきて、学会が終った夜、私の式を自分の観測データと詳しく比較した結果、すべての波長で十分に両者は合致することが判った、と述べた。
　ルンマーとプリングスハイムも、最初は測定値との不一致を確かめたと信じていた［M. v. Laue, Naturwiss. 29, 137 (1941)］が、間もなく（プリングスハイムが口頭で伝えてくれたところでは）、それが計算の間違いによるとはっきり判ったので、反論をとり下げた。
　それ以後の測定では、実験方法が精密になればなるほど正確に、式（７）が繰り返し実証されることになったのである［H. Rubens und G. Michel, Physik Z. 22, p569 (1921)］。・・・”

と言っている部分です。この説明で尽くされていますが、以下で幾つかの補足をします。

［補足説明１］
　解説文13．でプランクが“黒体の輻射強度は高温になればなるほど、ますますよく温度Ｔに比例するということが明らかにされたが、これは輻射強度を常に有限ならしめるウィーンの分布法則（４）とは、あい容れない事実だった。”と言っている部分が、６．（１）［補足説明１］で説明した事柄です。プランクは、この事実をエントロピーＳのＵに関する二次微分係数（二次導関数）で解釈すると（６）式になると言っているのです。
　
　上記（６）式は以下のようにして導かれます。ただし、解説文13．でＫ_νと言っている量は、この稿のＲ_νに相当することに注意して下さい。

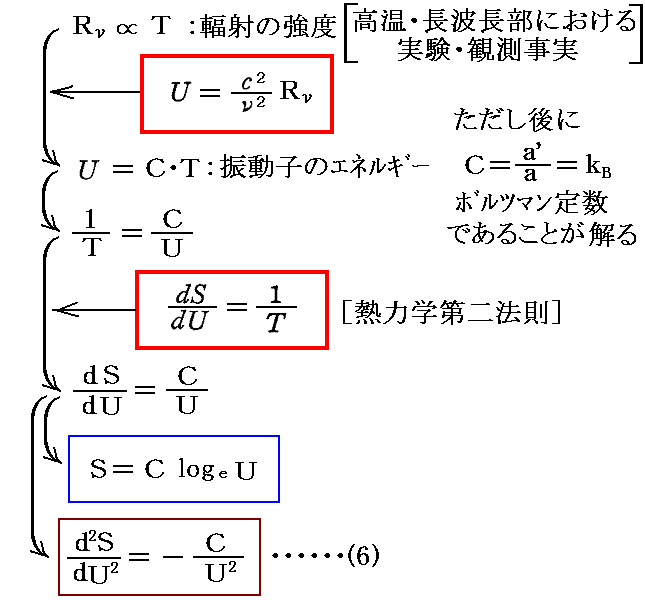
プランクは高温部でのこの形と、低温部で正しい（５）式の形をつなぎ合わせた式を考えます。それは実験事実をきわめて旨く説明する分布公式を導いた。
H. Rubens, “Ueber　die Reststrahlen des Flussspathes”, Wied. Ann. 69, p576〜588, 1899年
O. Lummer und E. Pringsheim,“U¨ber die Srtahlung des schwarzen Ko¨rper fu¨r lange Wellen”, Verhandlungen der Deutschen Physikalischen Gessellschaft 2, p163〜180, 1900年
H. Rubens und F. Kurlbaum, “U¨ber die Emission langwelliger Wa¨rmestrahlen durch deb schwarzen Ko¨rper bei verschiedenen Temperaturen”, Situngsber, d. k. preuss. Akad. d. Wissensch. vom 25, p929〜941 Oktober 1900年
H. Rubens und F. Kurlbaum, “Anwendung der Methode der Reststrahlen zur Pru¨fung des Strahlungsgegesetzes”, Drudes Ann. 4, p649〜666, 1901年
O. Lummer und E. Pringsheim, “Kritisches zur schwarzen Strahlung”, Drudes Ann. 6, p192〜210, 1901年
また８．（５）［補足説明４］のグラフを参照されたし。
(Sitzungsberichte der Koniglich Preuβischen Akademie der Wissenschaften zu Berlin　は次のURLからダウンロード可　　http://bibliothek.bbaw.de/bibliothek/digital/index.html　)

［補足説明２］
　上記解説文13．の（５）式と（６）式を極限として含む内挿式として、原論文5．に書かれているのは上記解説文13．中に書かれている形と違って

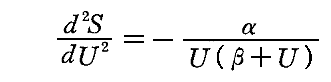
の形です。より一般的に許される形として、定数αとβを用いて書かれています。
　このとき、この式だけからではαとβが何を意味するのか解りません。そのためプランクはこれを積分して得られる

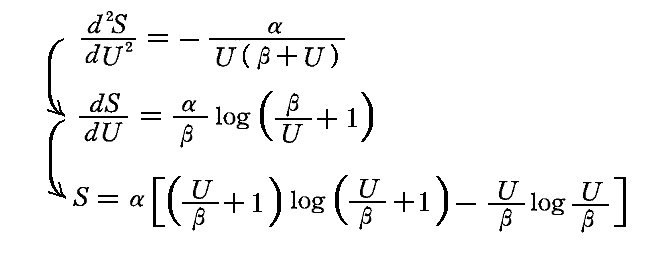
を、彼が最も信頼している“ウィーン変位則”（ただし振動子エントロピーについてのもの）

と比較することで、αとβを振動数νに結びつけます。すなわち

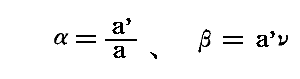
でなければならいとして、α→ａ’／ａ と β→ａ’ν に変換します。
　αをわざわざａ’／ａと置いたのは（７）式が簡単な形になるようにするためで深い意味は有りません。一方、β→ａ’νと置かねばならないことは本質的です。
　こう置くとｄＳ／ｄＵが解説文13．の（７）式

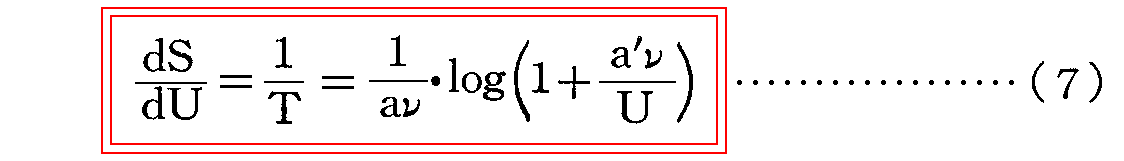
の形になります。
　また上記の振動子のエントロピー表現式は

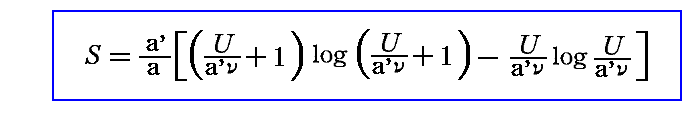
となります。
　ちなみにａ’／ａ＝Ｃと ａ は後に

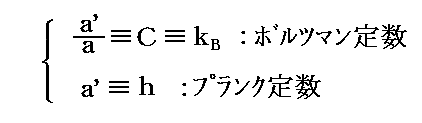
と呼ばれることになります。

［補足説明３］　
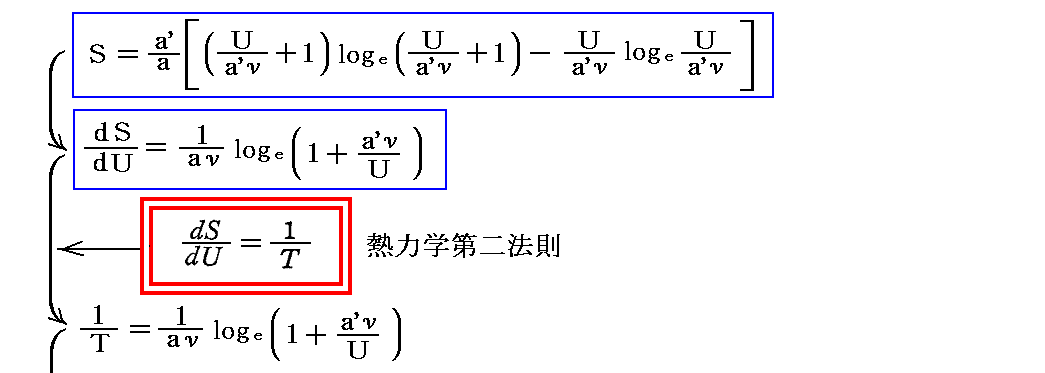
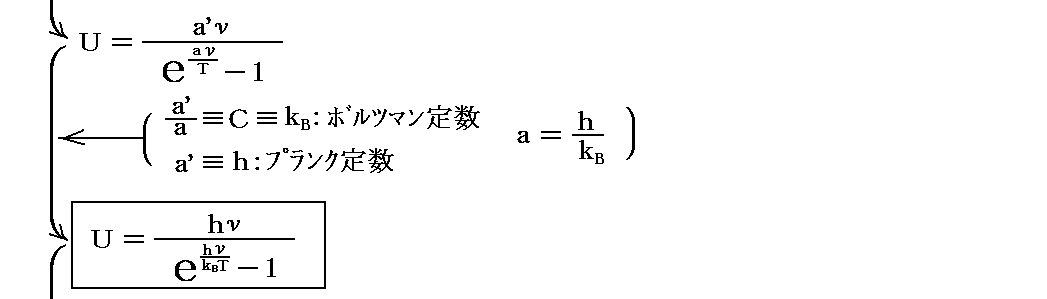
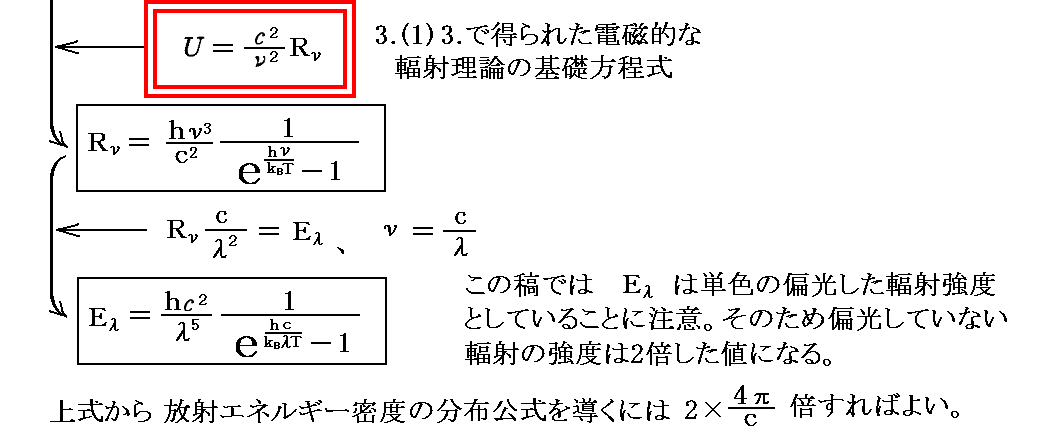
　前記の振動子のエントロピー表現式が得られると、直ちにプランクの黒体輻射の分布公式が導き出せます。ただし、解説文13．でＫ_νと言っている量は本稿のＲ_νに相当しますので、それに置き換えます。

［補足説明４］　
　この段階で、正しい黒体輻射の分布公式が導き出せたことになるのですが、まだ“エネルギー量子ε＝ｈν”の概念は出てきていません。
　上記の振動子エントロピーの表現式を統計力学的に解釈して始めて発見されるものです。それが次章８．の内容です。

８．内挿公式の統計力学的解釈（原論文6．、原論文7．§1〜10、著書10．128〜154）

　前章で説明したようにプランクが見つけた振動子のエントロピーの表現式は実験事実を極めて旨く説明しました。これを受けてプランクは、解説文13．で下記のように述べている考察に進みます。

　“・・・黒体輻射のスペクトル上のエネルギー分布法則の問題は、これで究極的に解決したと見なしてもよいであろう。だがここに、この法則の物理的意味を適切に基礎づけるという理論的に非常に重要で、これまでとは比較にならぬほど困難な課題が残された。
　問題は、式（７）から積分によって得られる振動子のエントロピーの表現を理論的に導出することなのだが、その表現は

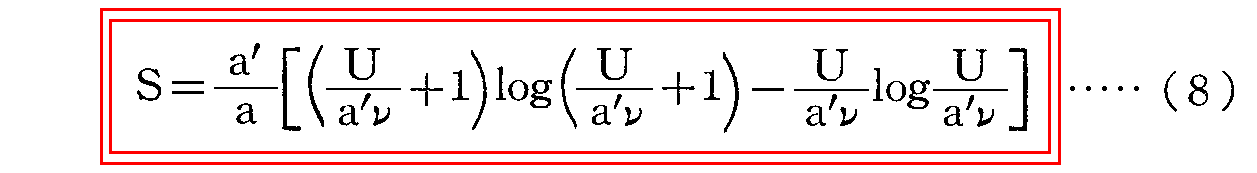
の形に書かれる。
　この表現に物理的意味を与えうるためには、電気力学の領域をはみ出した、エントロピーの本質に関するまったく新しい考察が必要であった。・・・”

　この部分は、プランクがどうやって Ｓ＝ｋ_Blog_eＷ に気付いたのかを明らかにすることが最も重要です。ところが、プランクは、源論文6．と7．の中ではそのことについて詳しいことは何も述べていません。ボルツマンの得た結論を利用したと言っているだけで、後はＷの統計的な計算法とこの式を用いた議論を展開しているだけです。
　なぜ Ｓ＝ｋ_Blog_eＷ なのかが最も難しい所ですが、それをするにはボルツマンの統計力学に深く立ち入らないといけません。いつか機会があればその当たりの説明に挑戦したいのですが、残念ながら今の私がその当たりを良く理解しているわけではないので、ここではやりません。
　
　以下の説明は、この関係式を認めることができて、Ｗを求める統計的計算法に納得できたとしての議論です。そこさえ納得できれば、ここは論理的に難しいところはありません。実際、プランクが Ｓ＝ｋ_Blog_eＷ の関係式に気付いた後の理論については多くの参考書、教科書で解説されていますが、そんなに難しくはありません。
　参考文献14．の国立国会図書館のデジタルライブラリーの中に 原論文6． と 原論文7． の翻訳があります。これらは、比較的短く理解しやすい論文なのでぜひ原典に当たられて下さい。　

（１）共鳴子のエントロピーをそのエネルギーの関数として表す
　　　　　（原論文6．、原論文7．§1〜5、、著書10．§146〜148）

　ここはPlanckの考察の本質をなすところですが、非常に解りにくい。ここのやり方は、統計力学的に言うとミクロカノニカル分布を用いるやり方と言えるのですが、その当たりについては、江沢文献「統計力学へのアインシュシタインの寄与」p121〜122　と　p124〜125を参照されて下さい。
　そこで説明されている様に、Einsteinは1906年に展開した光量子論第2論文の中で【光量子仮説】と【カノニカル分布の手法】を用いて熱輻射法則を導きます。この論文は、彼の光量子論第1論文に続くもので、熱輻射公式の求め方として、超有名な論文ですが、このやり方の詳細については別稿「統計力学の基本的な応用例」3．（1）1．［補足説明２］も参照して下さい。

１．同一の固有振動数を持つＮ個の振動子の系のエントロピー

　エントロピーは無秩序性を前提としている。
　その無秩序性は、振動子の単色的な振動の場合に、それが永続する定常的な輻射場の中にあるときでも、振動の時間よりも大きいが測定時間よりも短い時間間隔で、単色的振動子が輻射場を通じて他の同じ固有振動数の単色的振動子と、その振動の振幅と位相を無秩序に交換している不規則さに由来するであろう。［これがプランクが“自然輻射の仮定”と呼んで理論の拠り所としているものです。］
　そのとき、定常的な振動をする単色的な振動子の個々のエネルギーは時間的には変動するが、個々の振動子エネルギーは時間的な平均値であると考えるべきである。
　さらに同じ性質（つまり同じ固有振動数）を持った多数の振動子が、定常的な輻射場の中にあって、輻射場を通じて互いに影響するだけで振動子どうしが直接影響を与えないほど互いに十分離れている場合、その単色の個々の振動子のエネルギーは同じ固有振動数を持つ多数の振動子が同一時刻において持つ様々なエネルギー平均値と考えるべきである。
　今後、個々の振動子の平均エネルギーＵはこの意味で用いられる。

　今、【固有振動数νが等しいＮ個の振動子からなる系】を考える。そのときＮ個の振動子の全エネルギーは

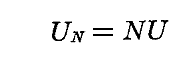
となる。Ｕは一つの振動子が持つ上記の意味で平均化されたエネルギーで、すべての振動子は平均的に同じエネルギーを持っていると考えて良いであろう。
　また、同じ系の全エントロピーは

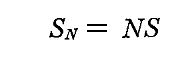
となる。Ｓは個々の振動子の平均エントロピーを表している。また全エントロピーＳ_Nは、全エネルギーＵ_Nを個々の共鳴子に配分することによる無秩序性に基づいている。
　　そのとき、１個の振動子のエントロピーＳは多数の振動子に同時にエネルギーを配分する配分の仕方によってきめられる。それはボルツマン氏が明らかにした熱力学の第二法則の確率論的考察を輻射の電磁理論に導入することで達成されるであろう。

　ボルツマンの統計力学の原理に従って、系のエントロピーＳ_Nを、Ｎ個の振動子が全体としてエネルギーＵ_Nを持つことに対する確率Ｗの対数に比例すると置く。すなわち

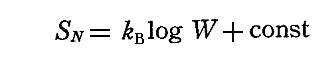
と置くことにする。

　このように置けるであろうと言う根拠は、今まで議論してきた輻射の電磁理論の中には存在しないのだが、プランクはボルツマンによって展開された運動学的気体論の成果を拠り所としてこのように置くことにしたと言っている。［この仮説が一番重要なのですが、本稿では深く立ち入らない。］

２．分配総数Ｗの導出

　Ｎ個の振動子が全体として振動エネルギーＵ_Nを持つ分配数Ｗを求めよう。
　そのためには、Ｕ_Nを連続的な値であると考えるのでは無しに、離散的な整数個の有限な比として部分からなる量と考える事が必要である。そうしないと実質的な確率を計算することは不可能である。その様な１つの部分をエネルギー要素εと呼ぶことにする。
　そうするとＵ_Nは

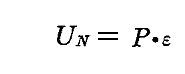
と表される。
　ここでＰはＮよりも十分大きな整数であるが、εの値はきめないでおく。この段階では単に分配の数を有限にするために仮の要素を考えるだけであり、最終的な結論においてε→0とするつもりである。

　今、Ｐ個のエネルギー要素εをＮ個の振動子に配分する場合、その分配のやり方の数は次の様にして計算すればよい。例として 【Ｎ＝10個の振動子】 に、 【Ｐ＝100個のエネルギー要素】 を配る場合、一つの配り方は例えば次のような数の並びで表される。

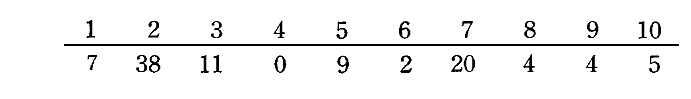
上段の数字は10個の振動子を表しており、下段の数字は上段の振動子に振り振られたエネルギー要素の数を表している。これは100個の粒を10個の箱に分配するやり方の数であり、100個の粒を１列に並べたときに10−1＝9個の仕切りを入れて分ける分け方の数と同じである。
　つまり、Ｐ個の粒の並びの間にＮ−1個のの仕切りを入れる入れ方の数である。それはＰ＋Ｎ−１個の球があり、その内のＰ個は同じもの、Ｎ−１個は他種類の同じものであるとき、それらＰ＋Ｎ−1個の球を一列に並べる並べ方の総数です。
　この数は高校数学の順列組み合わせで習うように、粒と仕切りがすべて異なっているとして一列に並べる並べ方の総数（Ｐ＋Ｎ−1）！を、粒だけ、あるいは仕切りだけ、をそれぞれ入れ替える並べ方の数で割ってやればよい。つまり

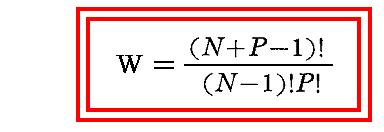
となる。ここでもう一度注意しますが、Ｎは、輻射と振動子の集合からなる系の中に含まれる、固有振動数がνの振動子の数です。またＰは、このＮ個の振動子に分配されるエネルギー要素εの数です。
　このとき、ＰやＮは非常に大きな数なので

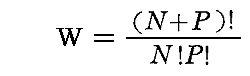
とすることができる。さらにStirlingの公式により　Ｎ！≒Ｎ^N　が言えるので

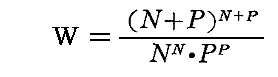
となる。

３．分配（Complexion）に対する仮説

　これから先の計算の基礎になる仮説は次のようなものです。

　固有振動数νのＮ個の振動子が全体として振動エネルギーＵ_Nをもつための確率は、エネルギーＵ_NをＮ個の振動子に配分する場合に可能な分配数（Complexionの総数）Ｗに比例する。
　これは言葉を変えれば、ある一つの分配（Complexion）は、他の分配（Complexion）と等しい確率で生じると言うことです。

　この仮説が妥当かどうかは、経験によって確かめる他ない。経験によりこの仮説の妥当性が確認できれば振動子のエントロピーは、付加定数（今後ｋ_Bと書く）を適当にきめることにより、次のようになる。


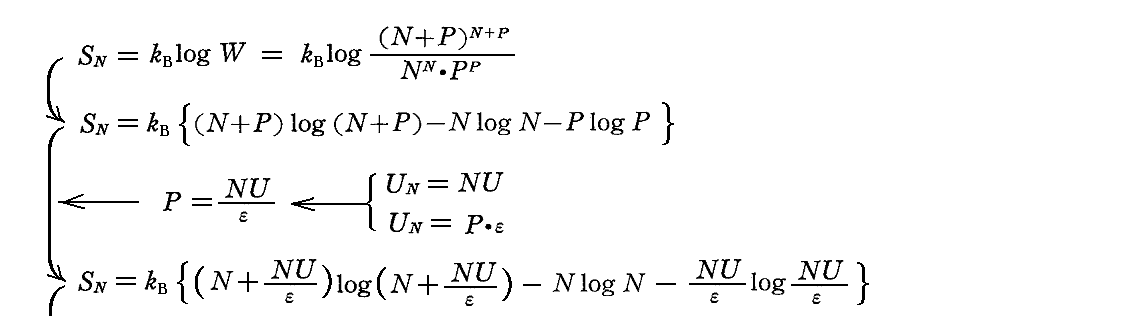
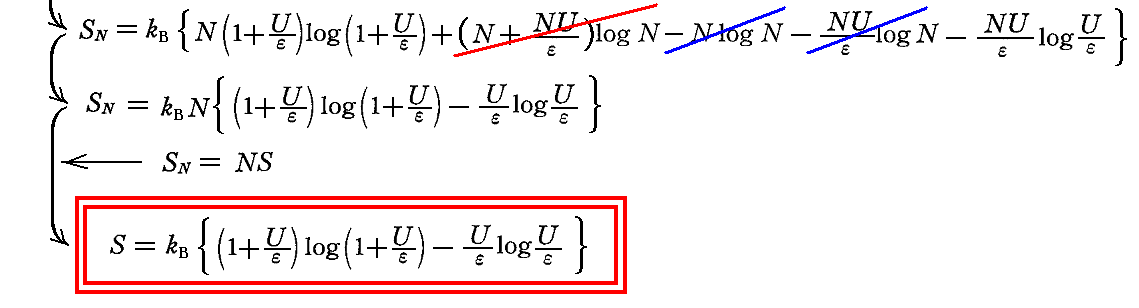
このようにして、固有振動数νの１個の振動子がもつ（平均的）エントロピーＳを、それが持つ（平均的）エネルギーＵの関数として表すことができた。

４．全体系に対する考察

　【様々な固有振動数を持つ振動子系と輻射場からなる全体系】についても同様に考えればよい。
　今、固有振動数νの振動子がＮ個ありそれ全体が持つエネルギーをＥ、
　　　固有振動数ν'の振動子がＮ'個ありそれ全体が持つエネルギーをＥ'、
　　　固有振動数ν''の振動子がＮ''個ありそれ全体が持つエネルギーをＥ''、
　　　等々・・・・
とする。
　それらすべての振動子の持つエネルギーをＥ₀とすると

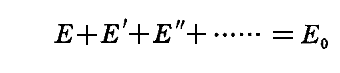
となる。
　振動子系の持つエネルギーの和 Ｅ₀ は、当然のことであるが全体系のエネルギー Ｅ_ｔ よりも小さくなければならない。そのとき Ｅ_ｔ−Ｅ₀≡Ｅ_rad が空間を満たしている輻射場の持つエネルギーとなる。
　この系に対して、それぞれのエネルギー分配を任意に行えば、Ｅ、Ｅ'、Ｅ''、・・・・のそれぞれに対して前記と同じ分配数（Complexionの総数）が得られる。このとき次のことに注意して欲しい。すなわち、分配数（Complexionの総数）を計算するときに仮定したエネルギー要素εに関しては、固有振動数が異なる系に関しては互いに異なったものを仮定してもかまわないだろうから、それぞれをε、ε'、ε''、・・・としている。

　こうして得られるすべての分配数（Complexionの総数）を掛け合わせて Ｗ×Ｗ'×Ｗ''×･・・・≡Ｗ₀ とすればすべての振動子へのエネルギー分配の可能な分配数（Complexionの総数）Ｗ₀が得られる。

　このとき、

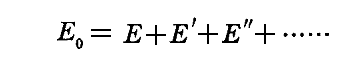
を一定に保つ可能なエネルギー分配のなかには、可能な分配数（Complexionの総数）Ｗ₀が他のどんな分配の場合よりも大きくなるような唯一のＥ、Ｅ'、Ｅ''、・・・・の分配がある。

　この分配に対して、ＥをＮで割り、Ｅ'をＮ'で割り、Ｅ''をＮ''で割り、以下同様・・・・にすることで、それぞれの固有振動数の振動子１個当たりの平均的なエネルギー値Ｕ_ν、Ｕ_ν'、Ｕ_ν''、・・・が得られる。
　これが得られれば、３．（１）３．で証明した関係式

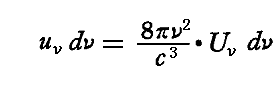
を用いて輻射場のエネルギー密度に変換できるので、各振動数の単色輻射に対するエネルギー密度が得られる。そのようにして得られた輻射エネルギー密度の振動数に対する分布法則こそ、振動子系群が全エネルギーＥ₀、輻射場が全エネルギーＥ_rad を持つときに実現される“黒体輻射の分布法則”です。
　このときＥ₀の値を、与えられた全エネルギーＥ_ｔに対してどの様な割合にしたらよいかも直ちに計算できます。それはまず、上記の手順によって求まる単色の輻射エネルギー密度を全体積、全振動数領域にわたって積分して輻射の全エネルギーＥ_radを求める。このようにして定まる二種の全エネルギーの和 Ｅ₀＋Ｅ_rad が Ｅ_ｔ を越えるようならばＥ₀の値を小さくし、Ｅ_ｔよりも少なければＥ₀の値を大きくして、Ｅ₀＋Ｅ_rad＝Ｅ_ｔとなるようにＥ₀の値を調整すれば良いのです。

　この一連の手続きを実行するのは非常に煩雑であるようにみえるが、次の事情を鑑みれば８．（１）１．〜３．で行った、ただ一つの固有振動数の振動子系についての考察をすれば十分なことが解る。
　それは、熱力学第二法則より振動子の全体系の温度Ｔは

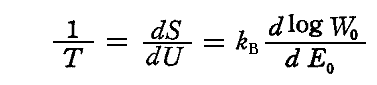
で表現されるが、これは個々の振動数ν、ν'、ν''、・・・・の系についても言えることで、平衡状態において常に

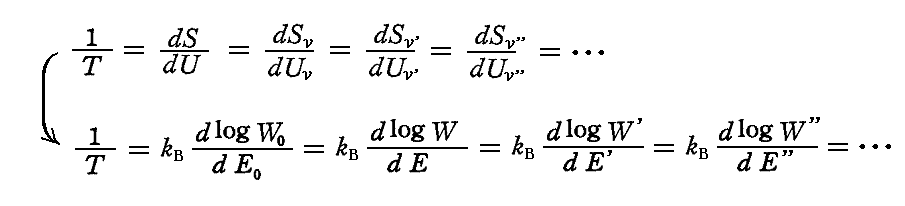
が成り立っているからです。この事に関して下記の［補足説明３］と［付録４］を御覧下さい。
　
　そのため、固有振動数の異なる系間のエネルギーＥ、Ｅ'、Ｅ''、・・・・の分配に関しては、すべての系が“同じ温度でなければならない”ことを通じて自動的に調整されているのです。
　そのとき固有振動数ν、ν'、ν''、・・・・の各系を構成する振動子の数Ｎ、Ｎ'、Ｎ''、・・・・は全く任意で良い。
　さらに固有振動数ν、ν'、ν''、・・・・の各系に於けるエネルギー要素ε、ε'、ε''、・・・の設定についても全く任意で良いことに注意して下さい（実際、後で解るようにε＝ｈν、ε'＝ｈν’、ε''＝ｈν''、・・・だったのですからこのことは重要です）。
　
　結局、ただ一つの固有振動数の振動子系について考察すれば十分なのです。
　これはとても重要なことなので、８．（３）［補足説明５］や８．（４）［補足説明１］でもう一度注意を促します。

［補足説明１］
　この節の内容が、プランクが解説文12．で

　“・・・しかしながら、たとえこの輻射公式が絶対に正確だと保証されるにしても、それはただうまくあたった内挿式だという意味で、あくまでもまったく制限された価値をもつにすぎないだろう。従って私は、この式を立てたその日から、それにほんとうの物理学的な意義を付与するという課題に没頭したのであり、そしてこの問題は、私をおのずからエントロピーと確率の関係についての考察に、こうしてまた、ボルツマンの思考過程へと導くことになった。私の生涯で最も緊張した研究作業の数週間がたって、ついに暗闇はしらじらと明け、新しい、思いもかけなかった遠景が姿を見せはじめた。・・・”

と言っている部分です。

［補足説明２］
　この節の４．全体系に対する考察の最後の部分で、固有振動数が異なる系間のエネルギー分布は温度が等しい事を通じて互いに自動調整されると述べましたが、それがどの様な電気力学的な方法に基づいて達成されるのかをプランクは説明していません。彼は、全固有振動数系を含む全体系についてのエネルギーの分配確率の最大化によってあたかも達成されるような言い方で誤魔化しています。原論文6．を読まれたらお解りのように、この部分は彼の説明の中で最も歯切れの悪いところです。
　もちろん、４．（５）２．で説明した考察を、新しいエントロピー表現式でやり直せば、全体系のエントロピーが極大値を取っている場合、振動数が異なる振動子系の温度が互いに等しくなければならいなことは言えます（［付録４］も参照）。しかし、どの様な方法で固有振動数が異なる振動子系間のエネルギー移動が起こり、等温になるように調整されるのかは説明されていません。
　彼の理論は、同じ固有振動を持つ振動子は同じ振動数の輻射との相互作用を通じて互いに作用し合い、同じ振動数を持つすべての輻射線の強度と偏光の大きさと方向が互いに一様になってエントロピーが最大の定常状態が実現されることを電気力学的方法で証明しているだけです。
　
　実際、プランクは著書10．§190で、彼の理論は振動数が異なる振動子間のエネルギー移動に関して何の説明も与えることができていない事を認めています。この理論の基礎となっている振動子は、その固有振動数に対応する輻射線のみと相互作用して、他の振動数の輻射線とは相互作用しないからです。つまり、輻射エネルギーを放出・吸収する以外の作用を仮定しないと振動子は、その固有振動数が異なる振動子とエネルギーの交換ができないのです。
　そのため、プランクは異なった固有振動数の振動子間のエネルギー交換が起こるには、振動子が互いに衝突して、振動子と輻射線の相互作用とは全く異なった形の相互作用が存在する事を仮定しなければならないだろうと言っています。それが有れば、異なる振動子間のエネルギー移動が可能になる。そのためには自然界に存在する振動子の構造がさらに詳細に解明されなければならいし、その解明によって作用量子ｈの意味がさらに明らかになるだろうと述べています。
　これは有る意味、当時すでに明らかになっていた気体や固体の比熱が低温部において示す理論と観測の不一致を量子論によって説明できることを予言するような言い方です。

［補足説明３］
　全固有振動数系を含む全体系についてのエネルギーの分配確率が最大値をとる場合に成り立つ事、すなわち［異なる振動数の振動子系の温度が等しくなること］についてプランクは詳しく説明してくれていませんが、江沢先生が参考文献２１．ｐ246〜248で、とても解りやすく説明して下さっています。その内容をそのまま［付録４］として引用しておきますので御覧下さい。
　これはプランクが４．（５）２．で説明している事柄を分配数Ｗの議論に焼き直したものです。Ｓ＝ｋ_B･log_eＷに注意されて、その部分と比較しながらお読み下さい。

（２）ウィーンの変位則を導入（原論文7．§6〜9、著書10．§127）

　プランクは、熱輻射の理論を確実に根拠づけている基礎の中で最も価値あるものと評価している“黒体輻射についてのウィーンの変位則”を、ここで議論している振動子のエントロピーに関係したものに変形します。

　それは４．（３）４．ですでに導いたものですが、原論文7．では別稿「ウィーンの変位則」５．（１）で求めた最初の形からより素朴なやり方で求めています。ここではそこの手順を紹介します。


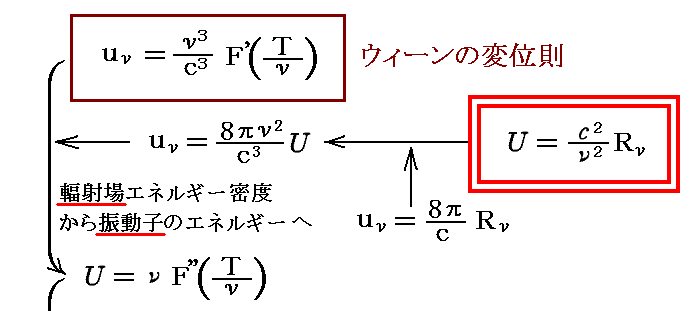
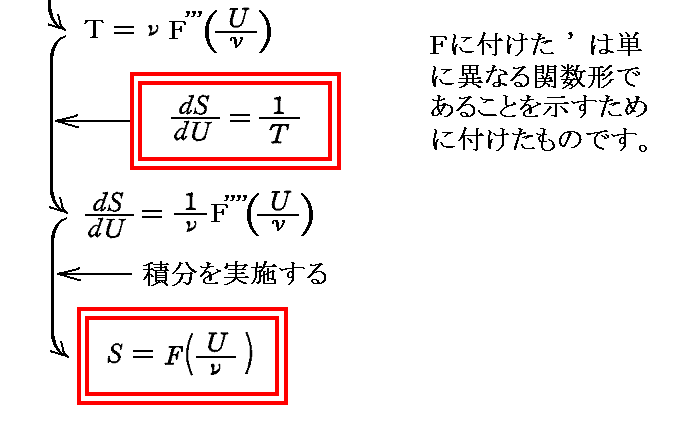
　このＳは固有振動数νの１個の振動子のエントロピーであることを忘れないで下さい。

（３）エネルギー要素の解釈（原論文7．§10、著書10．§148〜149）

　プランクは、前々節と前節で得た二つの結論を用いて最終的な考察に進みます。

　８．（１）節で導いた［統計的に求めた振動子のエントロピー表現式］

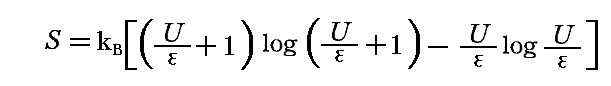
と、８．（２）節で説明した［ウィーンの変位則］

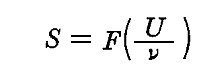
を比較すると、直ちに“エネルギー要素εは振動数νに比例しなければならず、そのときの比例定数は普遍定数でなければならない”ことがわかる。
　すなわち

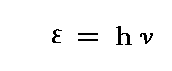
であり、かってにε→0とすることはできないことを表している。
　これは、エントロピーの統計力学的解釈【このことに付いては8．（1）2．を復習されたし】から解るように、“振動子の持つエネルギー値がε＝ｈνの整数倍の飛び飛びの値しか取ることはできない”ことを表している。もちろんこのνは振動子の固有振動数です。
　
　この“普遍定数”ｈこそ、プランクが発見した有名な“プランク定数” ｈ であり、関係式“ε＝ｈν”こそ、エネルギー量子を表す “魔法の公式” です。

［補足説明１］
　プランクがエネルギー要素εを考えたのは、エントロピーを導くために必要なエネルギー分配の“場合の数”を数えるためには振動子の取り得るエネルギーの値が離散的でないと無限大になってしまうからです。当初の彼のもくろみは、その様に有限なエネルギー要素εを仮定して得たエントロピー表現に於いて、最終的にε→0（あるいは比例定数ｈ→0）として連続的なエネルギー分布にすれば良いというものだったのでしょう。
　
　ところが最終的に得られたエントロピー表現式のなかのエネルギー要素εは必ず（Ｕ／ε）のように組み合わせられた変数の中にしか出てこなかったのです。そのため“かってにε→0（あるいは比例定数ｈ→0）とすることはできない”のです。その様なことをするとエントロピーが（Ｕ／ε）の関数であることにならない。もし、かってにｈを小さくしたり大きくしたりすることができるのならＵ／εが定まらず、状態量であるべきエントロピーＳが確定しないことになります。
　
　すなわち、ε＝ｈνの比例定数ｈはある確定した値の“普遍定数”でなければならないのです。

［補足説明２］
　［エントロピーのエネルギー二次微分係数の内挿式から得られたエントロピー表現式］

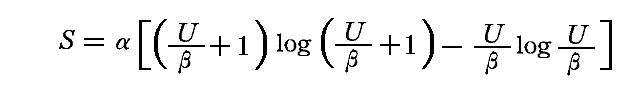
と［ウィーンの変位則（プランクが改良したＳ＝Ｆ（Ｕ／ν））］を比較すると、解説文13．の（８）式

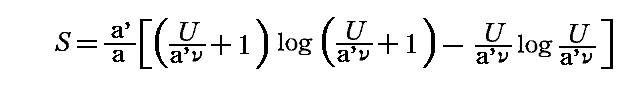
が得られて確かにβ＝ｈνは導けます。しかし、この比較から解るのはβがエネルギーの次元を持つ量である事だけで、βが統計的に分配される離散的な量であるエネルギー要素εであるとは決して解らないことに注意して下さい。
　
　だから、
［統計的に求めた振動子のエントロピー表現式（解説文13．の（１２）式）］

と
［ウィーンの変位則（プランクが改良したＳ＝Ｆ（Ｕ／ν））］
を比較して初めて“エネルギー量子の概念”が出てくるのです。またこの式と比較して初めて、ａ’／ａがボルツマン定数であることが解るのです。
　
　世にある解説書は、ここのところの説明が実に不明瞭です。そのためここで、エネルギー量子（ｈが普遍定数であることと同義）とボルツマン定数ｋ_Bは“振動子についての統計的（確率的）エントロピー表現式”を“振動子のエントロピーについてのウィーンの変位則”で解釈することから出てきたことを特に強調しておきます。
　
　
　なぜウィーンの変位則からエネルギー量子の考え方が導き出されるのか非常に不思議ですが、ウィーンの変位則は輻射のエネルギー分布に極大値を取る波長領域があることと関係しており、それは短波長（高振動数）領域のエネルギー分布密度が零に近づくことから生じている。
　そのとき、エネルギー分布に極大値が生じるのはエネルギーが量子化されているためだったのですから、ウィーンの変位則の中にエネルギー量子発見の鍵が隠されていたのもむべなるかなです。
　そのように考えればウィーンの変異則を導き出す過程の中にエネルギー量子発見に繋がる鍵が隠されていることになります。それが「断熱不変量の定理」だったわけです。

［補足説明３］
　解説文13．の�Vでは、エントロピー内挿式から得られたエントロピー表現式［解説文13．の（８）式］と、ボルツマン流の統計的手法で導いた振動子のエントロピー表現式［解説文13．の（１２）式］を比較して作用量子を導いたように説明しています。確かにやることは同じなのですが、プランクに取ってエントロピー内挿式は単なる実験観測値を旨く説明する実験式の意味しか無かったのですから、実際の展開は（８）式を用いて導いたのではありません。
　
　1901年の原論文7．では、実験式である内挿式［解説文13．の（８）式］ではなく、上記の様に［統計的に求めた振動子のエントロピー表現式（解説文13．の（１２）式）］を、彼が最も信頼していた［ウィーンの変位則（プランクが改良したＳ＝Ｆ（Ｕ／ν））］と比較することでエネルギー要素の表現式ε＝ｈνを導いています。
　ローレンツが、“このやり方のほうがより厳密である”と言ったものです。

［補足説明４］
　プランクの理論を振り返えれば解るように、エネルギーが量子化されて飛び飛びの値しか取れないのは“振動子のエネルギーについて”であって、輻射のエネルギーについてではないことに注意してください。
　
　プランクの理論では輻射の取るエネルギーが量子化されているかどうかは解りません。つまり輻射場においてもエネルギー量子ε＝ｈνが成り立つのか？あるいは成り立たないのか？は全く明らかではありまん。
　この時点のプランクに取って輻射は連続的なマクスウェルの電磁波なのですから、波のエネルギーを量子化するなど思いもよらないことでした。
　実際、輻射のエネルギーがどうなっているのかは、プランクを初めとして多くの物理学者を悩ました大問題でした。そこにアインシュタインの光量子仮説（1905年）という革命的な考え方が出てくるのです。

［補足説明５］
　ここで導かれたエントロピーＳの表現式は、あくまで１個の振動子の持つエントロピーであり、その中のＵは、その１個の振動子の持つ平均エネルギーです。またνは、その振動子の固有振動数です。
　そのとき固有振動数νが同じ振動子についてはすべて同じエントロピーや平均エネルギーを持ちますが、他の固有振動数の振動子のエントロピーやエネルギーとはどの様な関係になるだろうか？
　
　それは8．（1）4．で説明した様に、ｄＳ／ｄＵ＝１／Ｔを通じて関係づけられています。つまり“どの振動子の温度も等しくなければならないことを通じて、ｄＳ／ｄＵはどの振動子のｄＳ_ν／ｄＵ_νについても等しい値になるようにＳ_νとＵ_νが定まっている”と言うことです。
　すなわち“１／Ｔ＝ｄＳ_ν／ｄＵ_ν＝（ｋ_B／ｈν）log（１＋Ｕ／ｈν）は、固有振動数が違っても同じ値を持つ”のです。そのため以下のような事情が生じます。

1. 　εはかってに大きくしたり小さくしたりすることはできないと言いましたがそれはｈの値をかってに変えることはできないと言う意味に於いてであって、ε＝ｈνですからν（振動子の固有振動数）を通じて大きくなったり小さくなったりします。そのときνの変化に応じてＵ／ｈνの値が第一項目中の（１＋Ｕ／ｈν）の１に対して大きくもなり、小さくもなります。
   　そのため第二項目の−（Ｕ／ｈν）log（Ｕ／ｈν）との兼ね合いで、１／Ｔ＝ｄＳ_ν／ｄＵ_ν＝（ｋ_B／ｈν）log（１＋ｈν／Ｕ）の値が異なる固有振動数の振動子のものと同じ値（つまり同じ温度）を持つためには、νの違いに応じて１個の振動子がもつ平均エネルギーＵが変化しなければならない。
2. 　振動子が保持し得る“エネルギー量子”εは比例定数ｈとそれぞれの振動子の固有振動数νの積です。そのため“固有振動数の大きな振動子については、その振動子がとりえる“エネルギー量子”ε＝ｈνの固まりはνとともに大きくなる。それは各固有振動数の振動子にエネルギーが配分される確率はνが大きくなるにつれて小さくなることを意味します。なぜならやりとりするエネルギーの固まりが大きいため分配の場合の数がすくなくなるからです。そのため固有振動数νが大きな振動子の１個当たりの平均的なエネルギー値Ｕはνの増大と共にゼロに近づいていきます。”
   　それは、第一項目の（１＋Ｕ／ｈν）log（１＋Ｕ／ｈν）と第二項目の−（Ｕ／ｈν）log（Ｕ／ｈν）との兼ね合いがあるため、１／Ｔ＝ｄＳ_ν／ｄＵ_ν＝（ｋ_B／ｈν）log（１＋ｈν／Ｕ）の値が異なる固有振動数の振動子のものと同じ値を持つためにはν→∞と共にＵ→0とならねばならないと言うことです。
   　そのとき、任意の振動数を持つ輻射の単位振動数幅当たりのエネルギー密度は、同じ固有振動数の振動子が持つエネルギーにリンクしていたので、当然のことですが輻射の単位振動数幅当たりのエネルギー密度もν→∞と共にゼロに近づきます。
   　これが輻射分布則公式における短波長側の単位振動数幅当たりのエネルギー密度が零に近づくメカニズムです。
3. 　固有振動数νが小さな振動子の１個当たりの平均エネルギーＵも振動数νの減少（波長λの増大）と共に変化します。なぜなら、ε＝ｈνに於いてν→0とともにε→0となるため、一項目目（１＋Ｕ／ｈν）log（１＋Ｕ／ｈν）と二項目目（Ｕ／ｈν）log（Ｕ／ｈν）の兼ね合いで、固有振動数が異なる振動子においても同じ１／Ｔ＝ｄＳ_ν／ｄＵ_ν＝（ｋ_B／ｈν）log（１＋ｈν／Ｕ）の値を持つためにはνの違いに応じてＵが変化しなければならないからです。実際、ν→0とともにＵ→ｋ_BＴとなっていきます。
   　 　そのとき、任意の振動数の単色輻射の単位振動数幅当たりのエネルギー密度は、同じ固有振動数の振動子が持つエネルギーにリンクしていたので、当然のことですが輻射の単位振動数幅当たりのエネルギー密度もν→0と共にｋ_BＴに比例する値に近づきます。
   　これが輻射分布則公式における低振動数（長波長）側の単位振動数幅当たりの輻射エネルギー密度が零に近づくメカニズムです。ｋ_BＴではなくてゼロに近づくのは輻射の式ではｋ_BＴの前にν²が掛かっているからです［８．（５）［補足説明２］参照］。

　このように考えれば、“振動数に比例する”エネルギー量子の概念が、分布則のメカニズムに本質的な役割を果たしていることが解る。

［補足説明６］
　プランクは1906年に出版した著書10．§150で、振動子エネルギーの位相空間に於ける楕円形の面積要素が互いに等しくなるように分けて、それらに等確率性を適用してエネルギー要素を導入しています。そうすれば“ウィーンの変位則”を引き合いに出さなくても、ε＝ｈνが導ける事を説明しています。
　
　これは後に注目されることになる“断熱不変量の定理”を用いたエネルギーの量子化に繋がる着想です。これは朝永先生の参考文献16．§8で説明されている論法そのままでして、とても興味深いものです。
　実際、“ウィーンの変位則”をもっと一般的な“断熱不変量の定理”に焼き直すことにより、様々なエネルギーを量子化する一般的なやり方が発見されるのですから、この着想は重要です。

（４）固有振動数νの１個の振動子が持つエネルギー（原論文6．、原論文7．§10、著書10．§152〜154）

　固有振動数νの１個の振動子のエントロピー表現式が確定すると、その振動子が持つエネルギーは直ちに求まる。これは７．［補足説明３］で説明した内容ですが、大事なところなので繰り返しておきます。すでに述べたように ａ’→ｈ 、 ａ’／ａ→ｋ_B と置くことにしたので

となります。

［補足説明１］
　定常的な平衡状態では、どの振動子の温度Ｔも等しくなる。前節の［補足説明５］で説明したように、この温度が等しいと言うことを通じて他の固有振動ν’を持つ１個の振動子の平均エネルギーも定まります。それは上記の式のνを単にν’に変えればよいのです。
　
　それ故に“上記の式は“固有振動数を変数とした”振動子のエネルギー分布則を表している”と言っても良い。

［補足説明２］
　固有振動νの振動子が、今考えている輻射場との平衡を考えている系の真空の箱の中に何個あるかは全く任意です。
　そのため固有振動数νの振動子の数がＮ_νであるとすると、その全体が持つエネルギーはＮ_ν・Ｕ（ν，Ｔ）となります。つまり、数Ｎ_νに応じて変化します。
　それをすべてのνについて加え合わせたものが振動子全体が持つエネルギーとなります。これが8．（1）4．で説明した

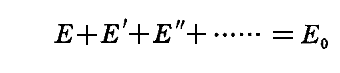
に他なりません。

［補足説明３］
　ここで【ν／Ｔが小さなとき】、すなわち固有振動数νが小さい振動子の絶対温度Ｔが高いときのエネルギー値を考えると

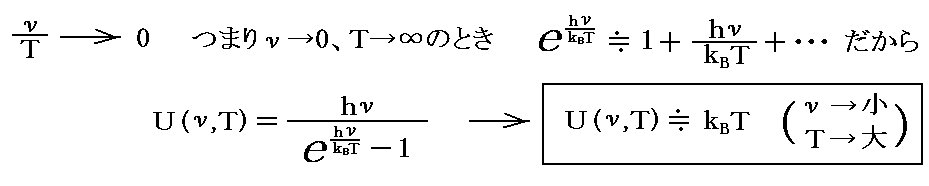
となる。
　これは、まさしくボルツマン統計力学における“エネルギー等分配則”にしたがって各振動子には固有振動数の違いにかかわらずすべての振動子にエネルギーが等分配されることを示している。
　このとき（1/2）ｋ_BＴではなくてｋ_BＴとなるのは、ポテンシャルエネルギーも含むからである。このことについては、別稿「調和振動子」２．（３）などを参照。
　このとき振動子の固有振動数νなどの振動子の性質には全く依存しなくなることに注意。
　
　
　一方、【ν／Ｔが大きなとき】、すなわち固有振動数νが大きい振動子の絶対温度Ｔが低いときのエネルギー値を考えると

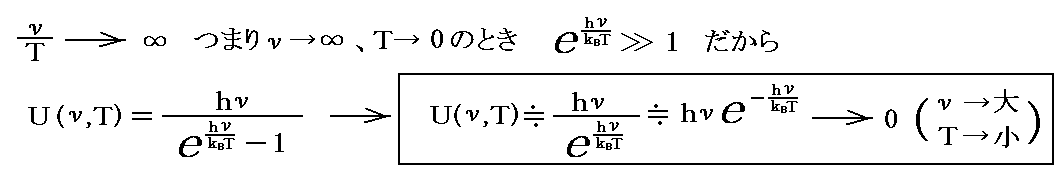
となる。
　つまり、温度が低くなると振動数νが大きな振動子には、同じ温度であっても、エネルギーが分配されなくなる。これは、固有振動数νが高い振動子が持つエネルギー量子ε＝ｈνの大きさが大きくなるため、エネルギーをもらって保持することが困難になる（“縮退”する）ことを意味している。

［補足説明４］
　エントロピー表現式において【ν／Ｔが小さなとき】

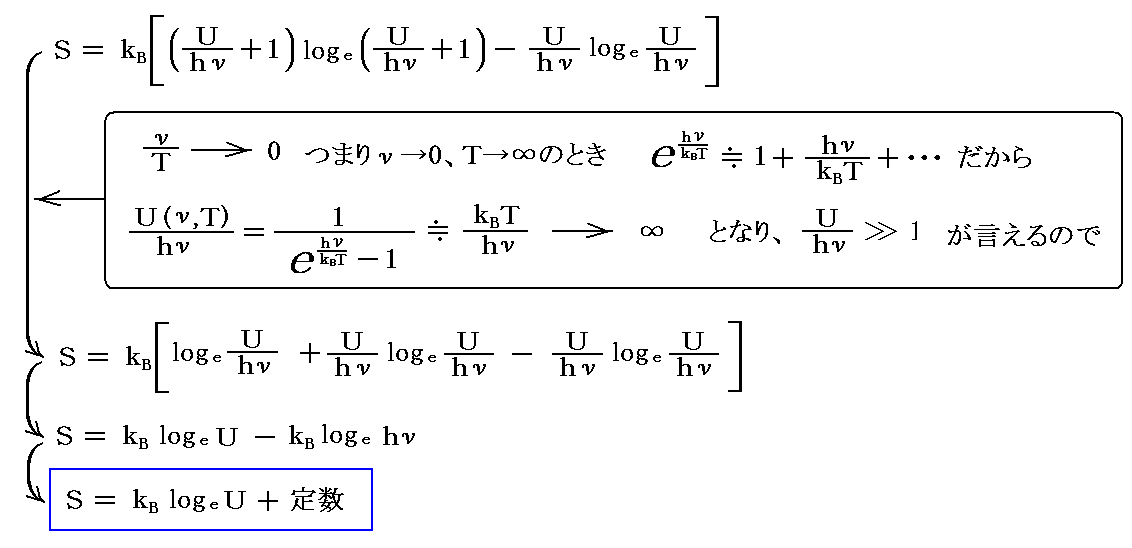
となります。
　これは、７章で説明した低振動数の高温部における振動子のエントロピー表現式に一致します。そこでの定数Ｃはボルツマン定数ｋ_Bであったことを思い出して下さい。そして、これは低振動数の高温部の輻射場について正しい“レーリーの輻射分布公式”を与えたものです。
　
　
　一方、【ν／Ｔが大きなとき】

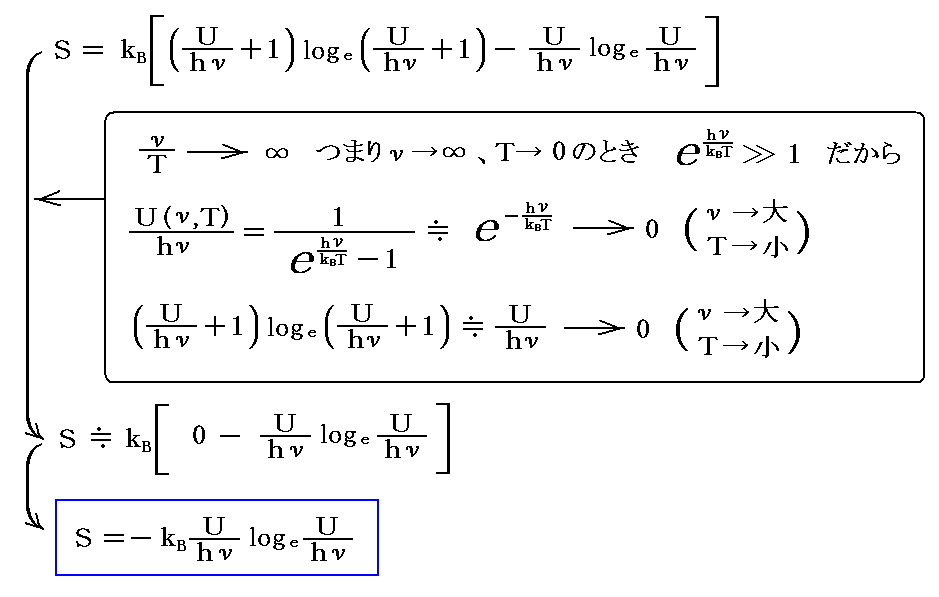
となります。
　これは４．（４）１．で振動子のエントロピー表現式として仮定したもので、振動数が大きくて温度が低いときの輻射場について正しい“ウィーンの輻射分布公式”を与えたものです。

（５）輻射場のエネルギー分布（原論文7．§10、著書10．§152〜154）

　【振動子のエネルギー分布則】が解れば、３．（１）３．の成果を用いて、直ちに【輻射のエネルギー分布則】が求まる。ここも７．［補足説明３］で説明した内容ですが、大事なところなので繰り返しておきます。

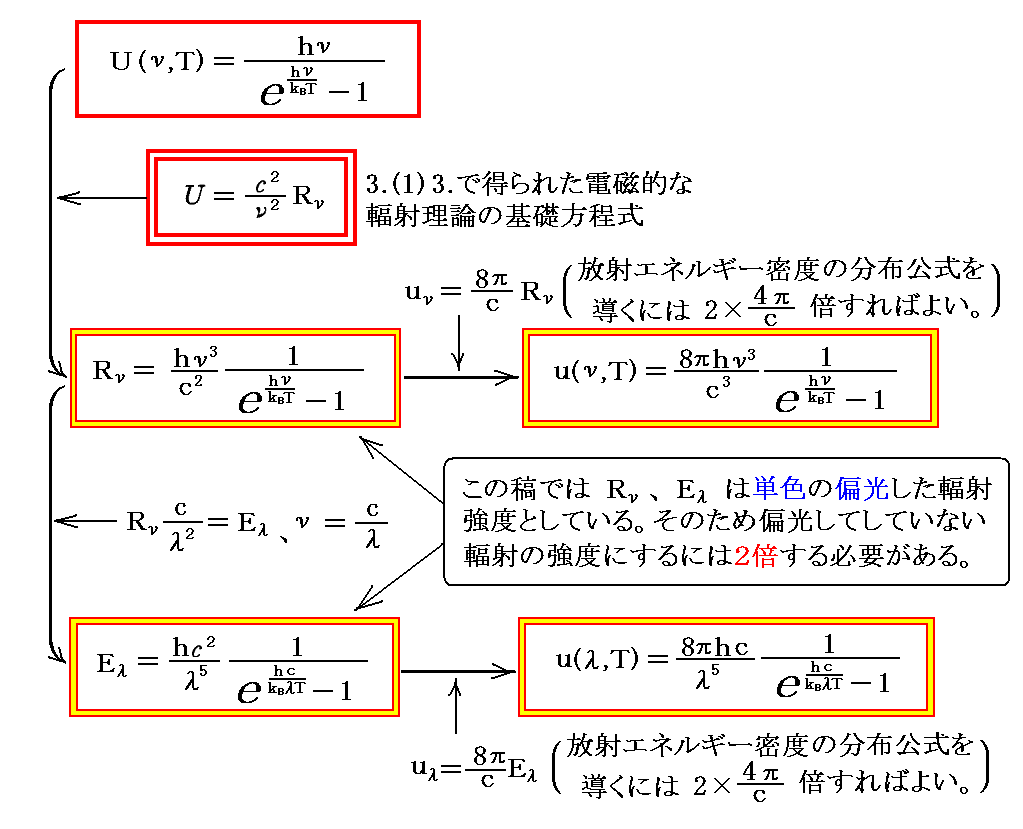
　これらはいずれも“プランクの熱輻射公式”と言われる。いずれの式も単位振動数幅（あるいは単位波長幅）当たりの輻射強度あるいは輻射エネルギー密度の、振動数（あるいは波長）に関する分布関数です。　

［補足説明１］
　ここで特に注意して欲しいことは、前節で導いたＵ（ν，Ｔ）は固有振動数νの“１個の振動子”の持つエネルギーの平均値であり、それのνに関する分布則は、それぞれの振動数を持つ１個の振動数のエネルギー値を表している。
　だからある特定の固有振動数の振動子系全体が持つエネルギーは、その固有振動数を持つ振動子が、その輻射空間の中に何個含まれているかによって異なります。
　
　これに対して本節で導いたｕ（ν，Ｔ）は振動数νの単色輻射の“単位体積当たりの”エネルギー密度を表しています。
　そのとき、その輻射と平衡関係にある同じ固有振動数を持つ振動子が何個存在しようとその数には全く無関係であることに注意して下さい。輻射場が持つ振動数νの単色輻射の全エネルギーはその輻射が占めている空間の体積に関係するだけです。ただしｕ（ν，Ｔ）は単位体積当たりのエネルギー密度ですから、その空間体積の広さには関係しないと言うことです。

［補足説明２］
　輻射公式において【ν／Ｔが小さなとき】、すなわち【絶対温度Ｔが高】く、光の【振動数が低い（長波長）】ときの輻射場の強度分布とエネルギー分布 は

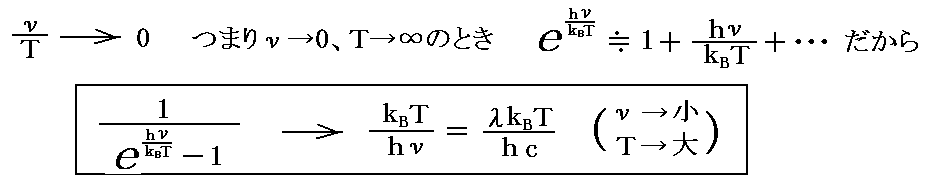
となるので

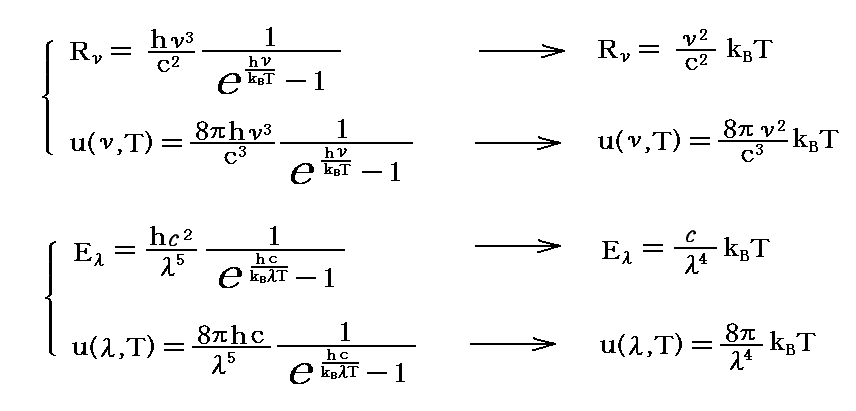
となる。
　これはまさしく、高温・長波長の部分で成り立つ“レーリーの輻射分布公式”です。
　
　このとき、前節［補足説明３］で注意したように、振動子の場合であれば、ｋ_BＴの意味をボルツマン統計力学における等分配則で解釈できるのですが、ここの輻射場に於けるｋ_BＴが何を意味するのかは全く明らかではありません。
　レーリーは1900年6月の論文で、ｋ_BＴの前に掛かっている係数の意味を輻射場に於ける定常波モードの単位振動数幅（あるいは単位波長幅）当たりのモードの数と解釈して、それに等分配則で割り振られるエネルギー値ｋ_BＴを乗じて分布則を導きました。しかし、その様な解釈は理解に苦しむもので、当時のプランクがレーリーの論文を知っていたとしてもとうてい納得できるものでなかったでしょう。（ちなみに、プランクがレーリーの論文を知ったのは1900年10月7日の様です。）
　
　
　一方【ν／Ｔが大きなとき】、すなわち【絶対温度が低】く、光の【振動数が高い（短波長）】ときの輻射場の強度分布とエネルギー分布は

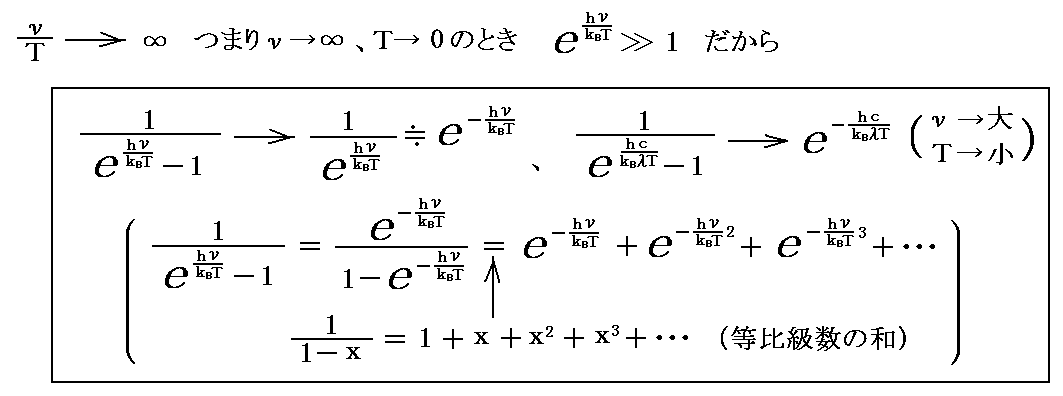
となるので

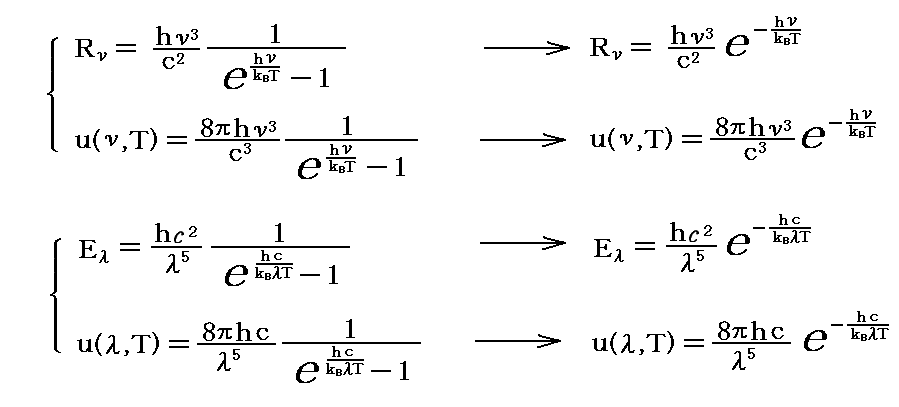
となる。
　これはまさしく、低温・短波長の部分で正しかった“ウィーンの輻射分布公式”です。

［補足説明３］
　上記のν／Ｔについて両極端に極限移行したときの分布公式についての補足です。
　
　多くの教科書では【レーリーの輻射分布公式】はレーリーとジーンズが採用した手法で説明されています。すなわち輻射が存在する空洞内に於ける電磁波の定常波のモードを考えて、その各振動モードが輻射の取り得る自由度そのものであるとします。
　そして「輻射の自由度（つまり定常波振動モードの一つ一つ）にボルツマンの等分配則を適用」して輻射分布公式を導きます。
　プランクは、1906年の著書10．§165、166でレーリーの理論を吟味していますが、プランク自身このやり方には決して納得していませんし、私自身も納得できるものではありません。
　
　
　また【ウィーンの輻射分布公式】についてですが、ウィーンは容器の中に気体分子と電磁波が閉じこめられており、その中の気体分子が黒体として電磁波を吸収・放出していると仮定した。
　そして「気体分子が放出する電磁波の波長と強度はその分子が持つ速度で決まる」と言うかなり恣意的な仮定をして、気体分子の速度分布から黒体輻射のエネルギー分布を導いた。
　しかし、ウィーンが行った仮定はかなり疑わしいもので、レーリーやプランクを含めて多くの物理学者が納得できるものではなかったのは確かです。
　
　それに対して、【プランクの輻射分布公式】は、“自然輻射の仮定”という解りにくいものを含んでいますがはるかに納得できるやり方によって導かれたものです。そしてプランクの法則はν／Ｔが大きな場合も、小さな場合にも観測事実を正しく説明する分布公式を与えた。
　そのとき、この特異な分布則を導き出す原理が「振動数に比例するエネルギー量子の概念」だったのです。

［補足説明４］
<輻射エネルギー密度の波長分布>

　
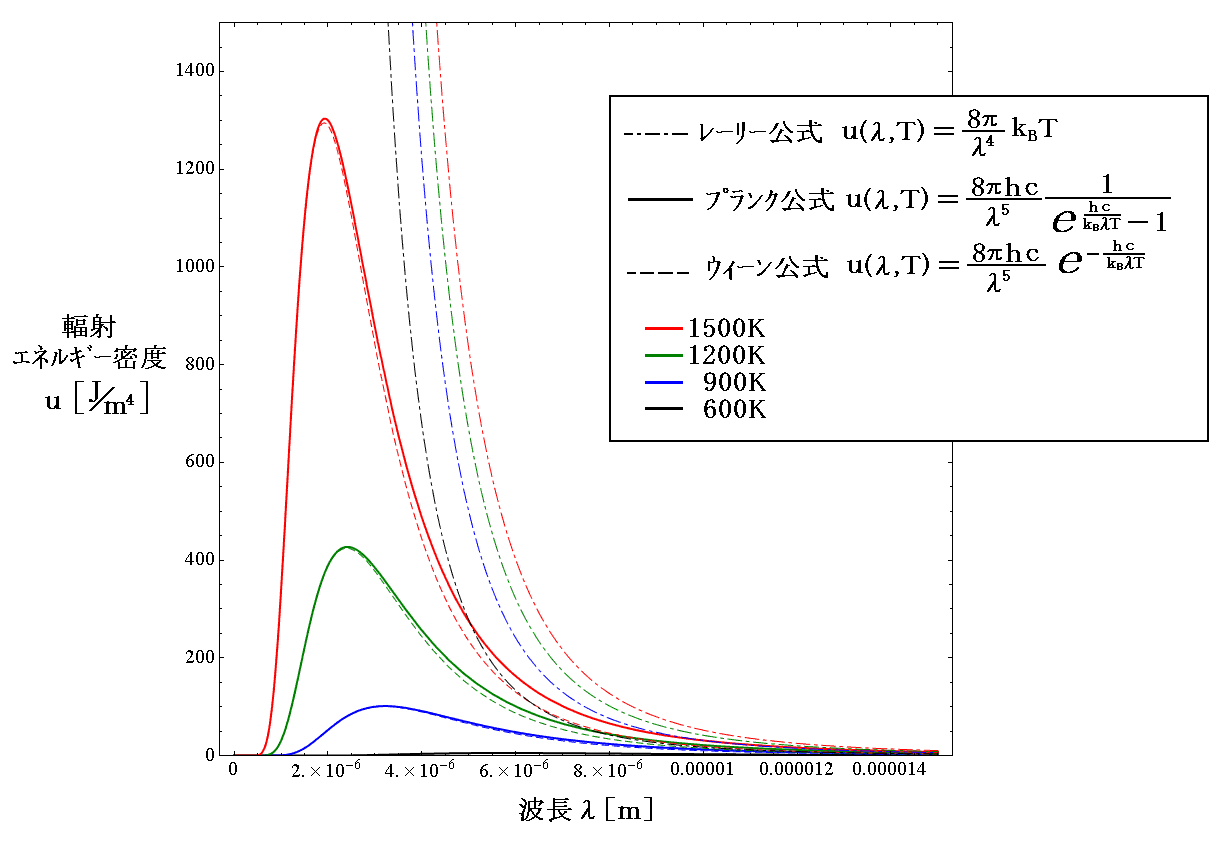
<輻射エネルギー密度の波長分布>
　クールバウムとルーベンスがウィーン公式と観測値のズレを明らかにしたλ＝2.4×10^-5〜5.1×10^-5ｍの波長領域を示す。

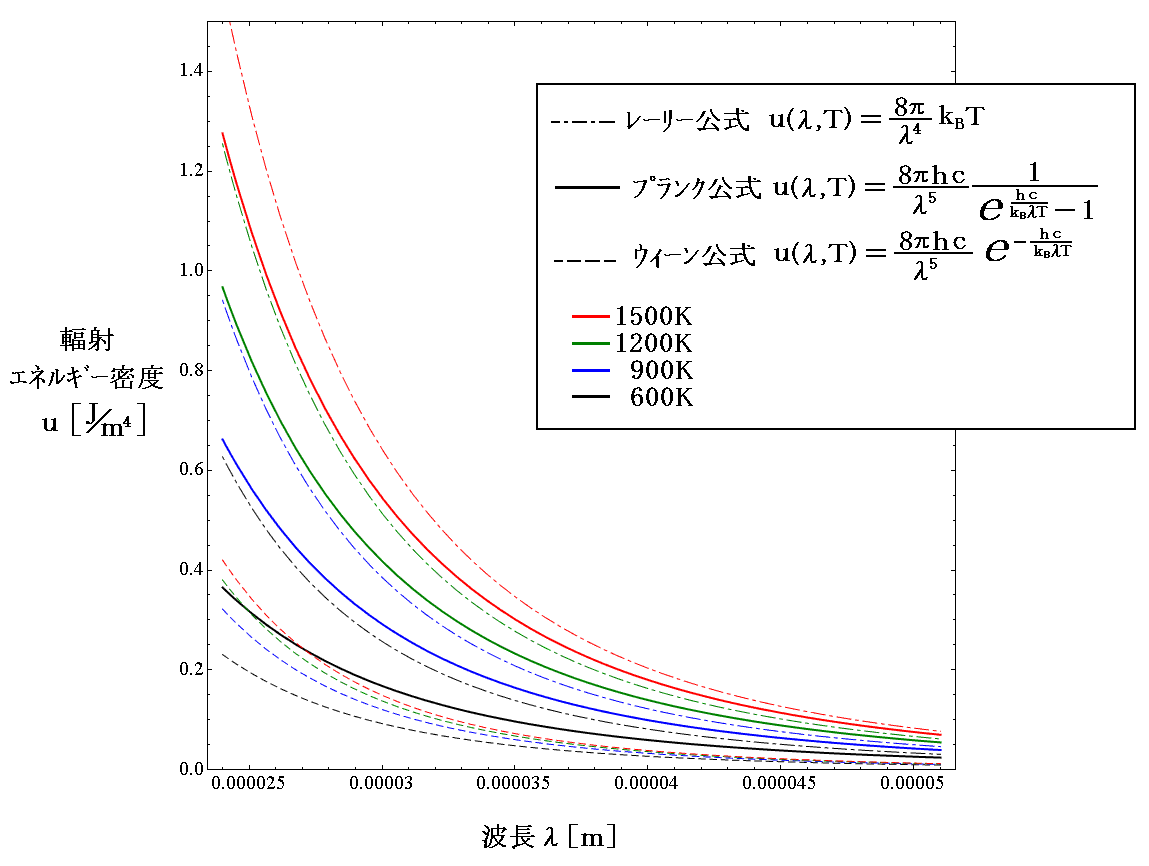
　プランク公式やレーリー公式ではエネルギー密度は絶対温度Ｔに比例して増大する。そして温度が高くなるほどレーリー公式とプランク公式の一致性は良くなる。一方ウィーン公式では温度が増大しても、プランク公式との差はほとんど変化しなくなることが解る。

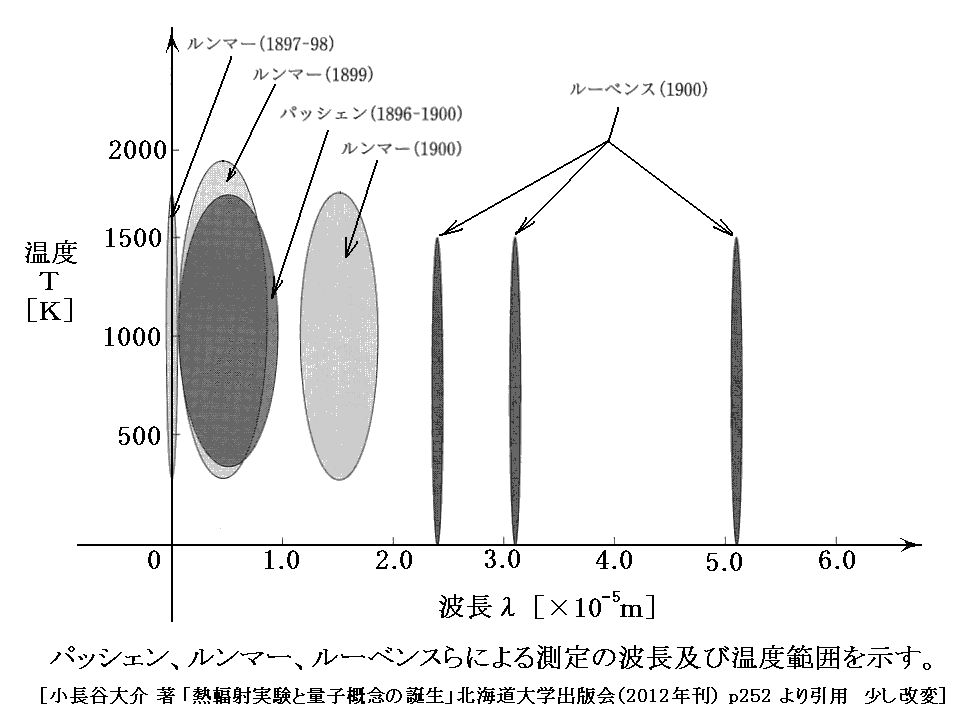
　ルーベンス（1900年）の測定は、波長を固定して、黒体炉内の温度を変えて、炉内輻射場のエネルギー密度が絶対温度Ｔのどの様な関数になるかを測定した。そうして、当時提案されていた様々な熱輻射公式と比較したのです。その当たりを説明したA．Pais著「神は老獪にして・・・」p485〜489を別ページで引用。

［補足説明５］
<輻射エネルギー密度の振動数分布>

　
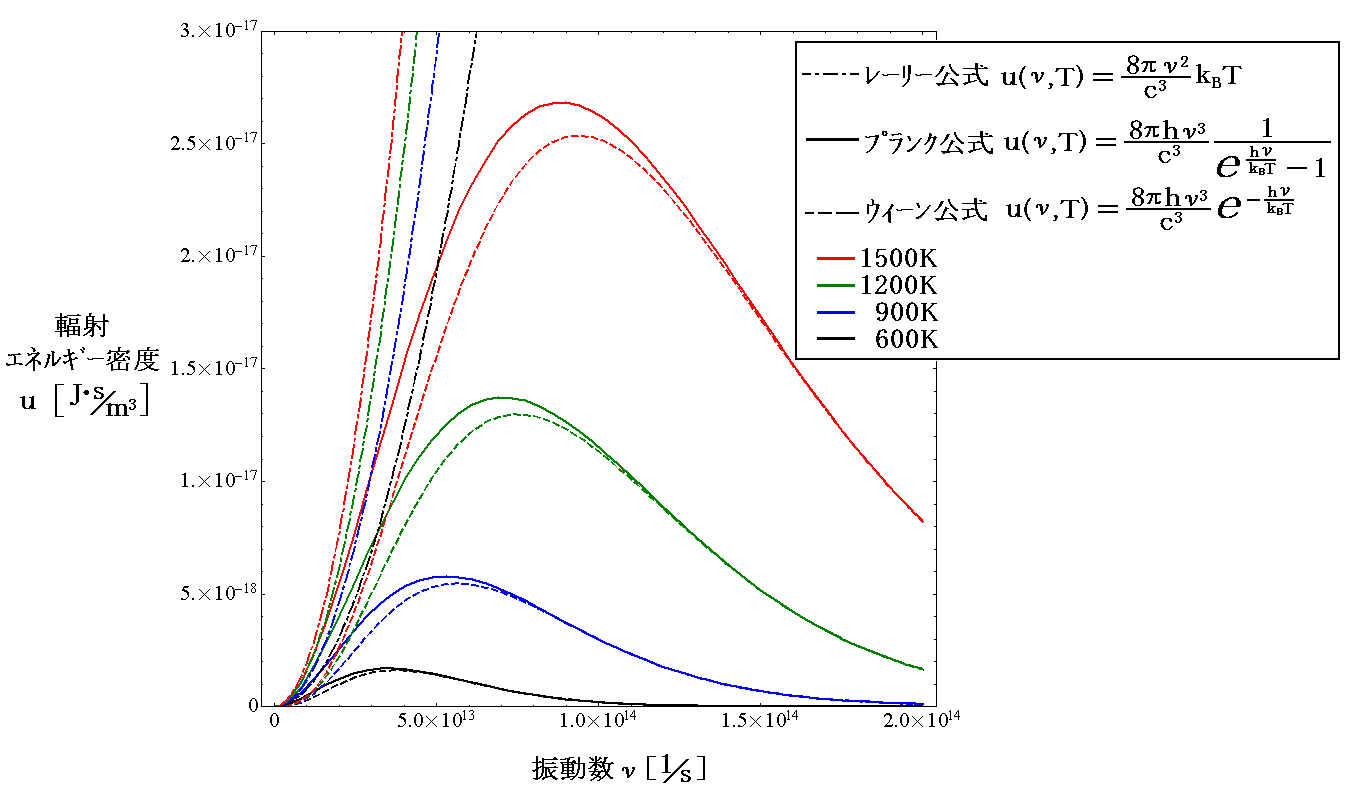
<輻射エネルギー密度の振動数分布>
　クールバウムとルーベンスがウィーン公式と観測値のズレを明らかにしたλ＝2.4×10^-5〜5.1×10^-5ｍに相当する振動数領域を示す。

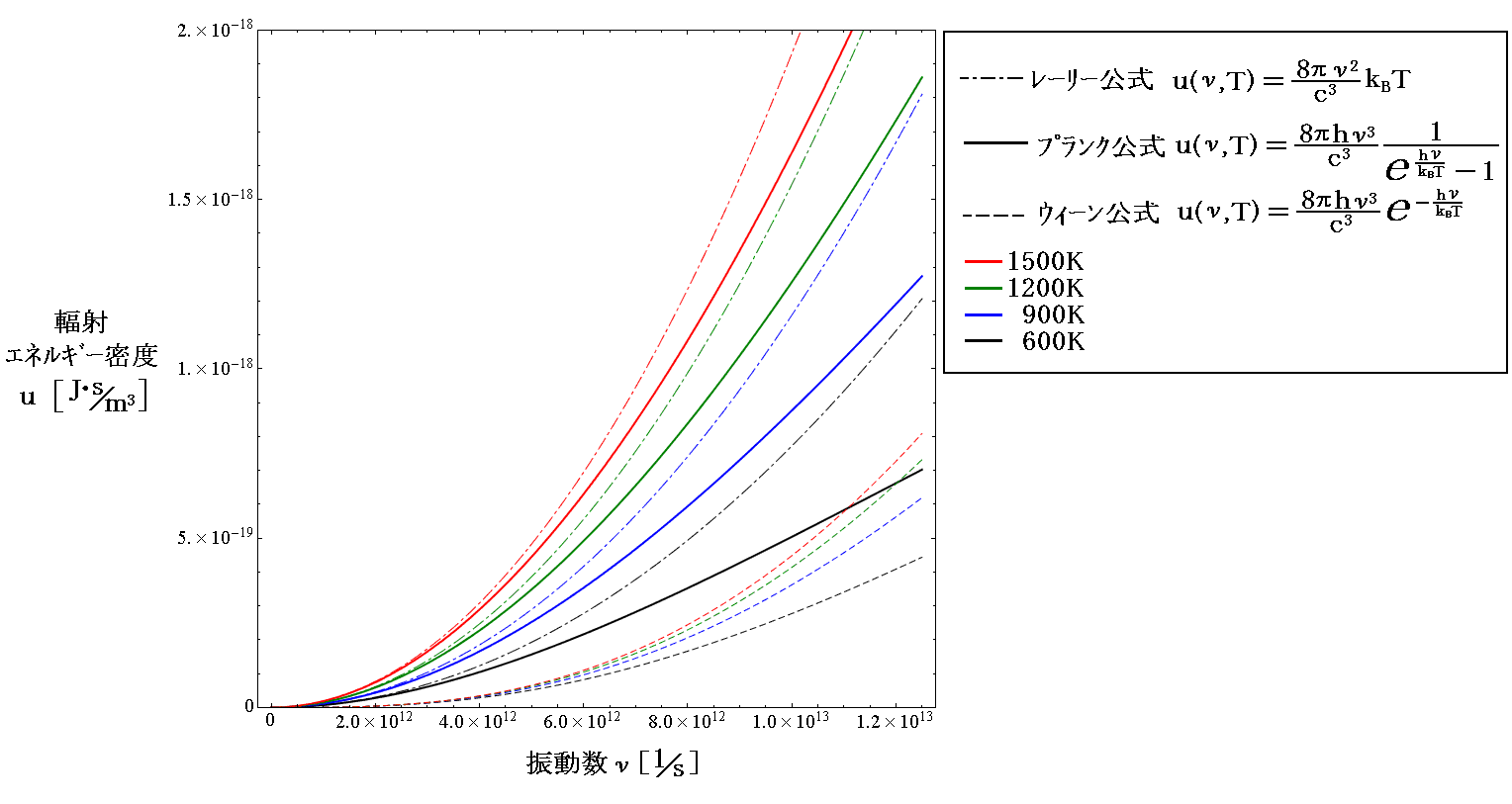
９．実験との比較（原論文3．§25、原論文6．、原論文7．§11〜12、原論文8．、著書10．§138〜144･§155〜158）

　著書10．§138〜144で、プランクは［力学的熱理論の確率的考察（今から説明する）］を［電気学的熱理論に於ける確率的考察（前節まで説明したもの）］と対比させることで、普遍定数ｋ_Bの意味を説明しています。
　彼の理論を検証する手がかりは当時少なかったのですが、これから得られるｋ_B＝［気体定数］／［アボガドロ数］の関係式に輻射分布の実験・観測結果から（普遍定数ｈと共に）得られる普遍定数k_Bの値を代入して、　“アボガドロ数Ｎ_A”と“電気素量ｅ”の値を求めることができます。この値こそが彼に自分の理論の正当性を確信させたものです。
　これはまた、彼が　Ｓ＝ｋ_B･log_eＷ　に思い至った事情を推測する手がかりになる興味深い記述ですので、この内容を紹介することからこの章を始めます。

（１）単原子理想気体のエントロピー（著書10．§138〜144）

　ここは、下記のボルツマン論文の内容をほぼそのまま単原子理想気体に適用したものです。
L. Boltzmann, “U¨ber die Beziehung zwischen dem zweiten Hauptsatze der Mechanischen Wa¨rmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sa¨tzen u¨ber das Wa¨armegleichgewicht（熱力学の第2法則と熱平衡についての諸定理に関する確率論の計算との間の関係について）”, Wiener Berichte 76, p373〜435, 1877年［「物理学古典論文叢書6　統計力学」（東海大学出版会）の第3論文］
　ただし、この中でボルツマン自身が Ｓ＝ｋ_Blog_eＷ の形を明確に認識していたわけではありません。これはあくまでプランクが1900年の段階で提起した表現形式です。

１．分布関数の実現確率

　ｋ_Bの意味を明らかにする目的には特に単純な系について考察すれば十分です。そのためＮ個の同一種類の“単原子分子からなる理想気体”を考える。ここで空間座標（ｘ，ｙ，ｚ）と速度成分座標（ξ，η，ζ）からなる６次元の位相空間を考える。その中の要素領域

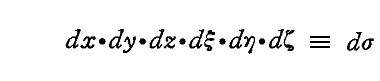
について、その状態要素ｄσ中に見いだされる分子の数を

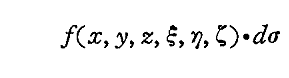
とおく。今後すべての要素領域ｄσはすべて同じ大きさであるとする。
　ｆ（ｘ，ｙ，ｚ，ξ，η，ζ）の最も実現する確率が高いものが、平衡状態における気体の状態を一義的にあらわす分布関数であるといえる。 ｆ はすべての領域で連続で微分可能であると仮定する。またこのすべての要素領域についての積分

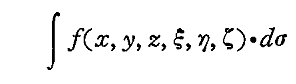
は系内に含まれる気体分子の全数とならねばならない。

　ここで重要なのは任意に与えられた空間・速度分布ｆ（ｘ，ｙ，ｚ，ξ，η，ζ）が実現する確率を求めることである。その確率の計算法が解れば、確率の最も大きくなる分布関数を探して、平衡状態において熱力学的に実現されている状態を決定することができる。
　この確率の計算法を考えるために、例えば 【10個の分子】 と 【7個の要素領域】 を考察する。この7個の要素領域とは、先ほどの　ｄｘｄｙｄｚｄξｄηｄζ≡ｄσ　の要素領域が7個あると言うこと。
　このとき一つの分布状態は次の様な数の並びによって表される。

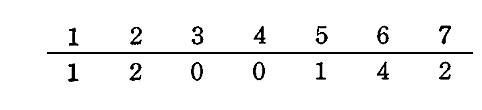
これは

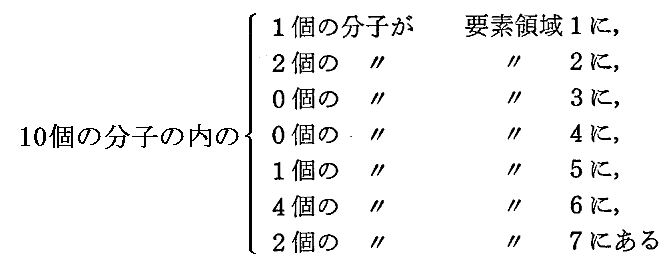
と言うことを表している。
　このとき、10個の分子に1〜10の番号を付けて、上記の並びを

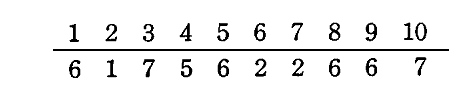
の様に表すこともできる。これは

を意味している。
　この配置の実現確率Ｗ（または上記配列の可能な数）を求めるには、全分子数が与えられている条件の下で可能な重複を許す順列の数に等しい。上記の例では

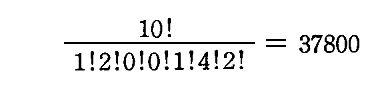
となる。ここで分子は全分子数の階乗であり、分母は各要素領域にある分子数の階乗を、7個すべての要素領域について求めて、その積を取ったものです。
　従って一般的な、与えられた空間・速度分布の実現される確率として

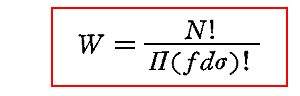
が得られる。こごて記号Πはすべての要素領域ｄσに於ける分子数（ｆ・ｄσ）の階乗の積を表す。　

２．一つの定まった状態にある気体のエントロピー

　ボルツマンの統計力学から導かれるエントロピーの表現式 Ｓ＝ｋ_Blog_eＷ ［これが一番重要なのですが、この稿ではこの仮説に関して深く立ち入らない。］に従って

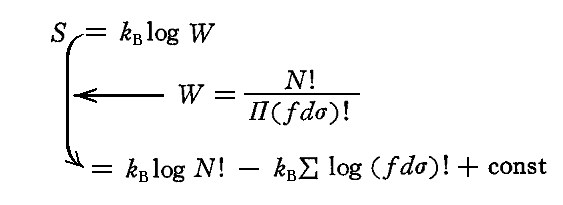
となる。和Σはすべての要素領域ｄσにわたって取られる。

［補足説明１］
　ここで、要素領域ｄσに含まれる分子数（ｆ･ｄσ）は大きな数であるから、その階乗にはスターリング（Stirling）の公式が適用できる。それは大きな数ｎに対して

と近似できることでした。
　スターリングの公式の証明はこちらの別稿あるいはこちらのページをご覧下さい。

　上記公式のｎを（ｆ･ｄσ）に置き換えたものを上式に適用すると

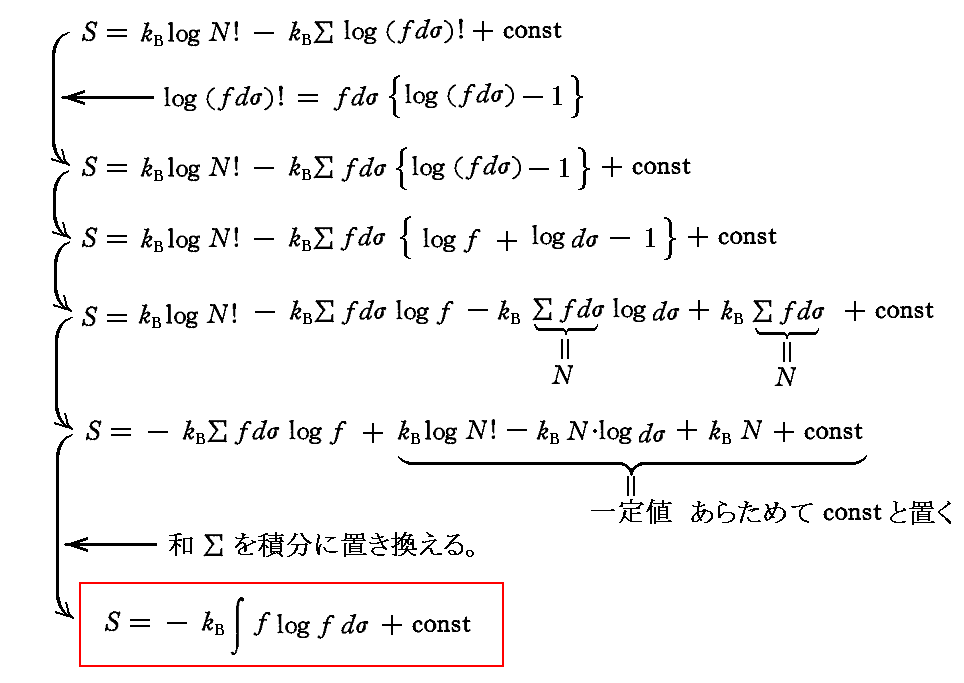
となる。
　これは、気体分子の任意の与えられた空間・速度分布の気体状態に対する、“単原子理想気体の持つエントロピー表現式です。

　これは、４．（４）１．で仮定した振動子のエントロピー表現式

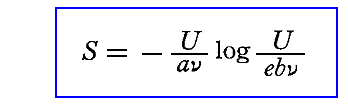
や、７．章で求めた内挿式としての振動子エントロピー表現式

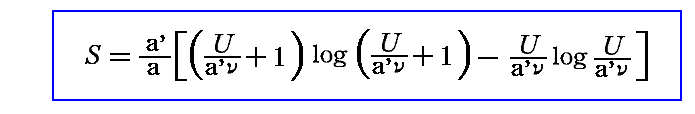
と、非常によく似た形をしている。
　そのため、プランクはこの類似性から“振動子エントロピーの解釈”にボルツマン統計力学の“エントロピーの確率表現”を用いることを思いついたのではないかと推察されている。

３．分布関数の導出

　平衡状態に於ける気体のエントロピーは、【体積Ｖが一定】、【全分子数が一定】、【全エネルギーＵが一定】の条件の下でエントロピーＳが最大値を取る条件から求めることができる。
　【気体の全体積】 は

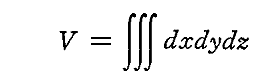
で与えられる。
　【気体の全分子数】 は

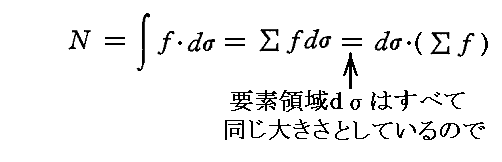
で与えられる。
　また、【気体の全エネルギー】 は、分子の質量をｍとすると

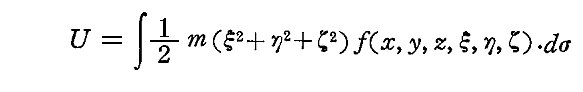
で与えられる。
　これらの式より、【全分子数が一定の条件】 は

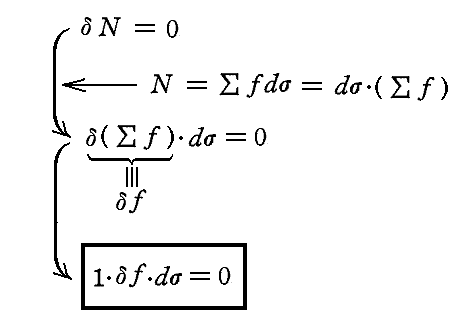
で与えられる。
　また【全エネルギーが一定の条件】は

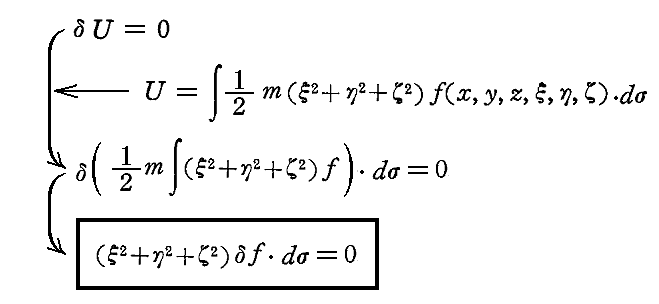
となる。

［補足説明１］
　上記の式変形の最後の部分で、(1/2)ｍの項を省略していますが、ラグランジュの未定乗数法を用いるときには、こういった定数部分は取り除いておいてもかまいません。
　後で未定乗数を決定するときに、省略した事項は調整されて旨く復活されます。このことについては、9．(1)5．をご覧になれば了解できます。

　平衡状態において、気体のエントロピーＳが満たすべき条件は、Ｖ、Ｕ、Ｎが一定値として与えられた条件の下で

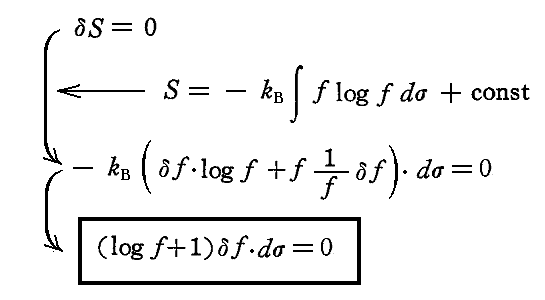
となることです。

［補足説明２］
　Ｖ、Ｕ、Ｎが満足すべき条件式の下で、上記の式を満たす関数ｆ（ｘ，ｙ，ｚ，ξ，η，ζ）を求めるには、変分法に於ける“ラグランジュの未定乗数法”という数学テクニックが使われます。詳細は別稿「多変数関数の極値とラグランジュの未定乗数法」をご覧ください。
　
　特に、そこで引用している別稿「統計力学におけるラグランジュの未定乗数法」４．と比較検討される事を勧めます。ここでブランクが用いているエントロピー関数Ｓは、上記別稿の(5.61)式に他なりません。ただし、そこでは定数ｋ_Bは乗じられていませんが。

　ここで、多変数関数の極値問題を解くラグランジュの未定乗数法を適用する。そうすると、λとβを二つの未定定数として

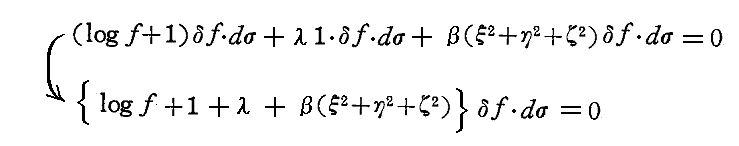
が成り立ちます。
　ここで、任意の　δｆ・ｄσ　に対して上式が常に成り立つためには｛ ｝内がすべて　0　であることが必要ですから以下が成り立つ。

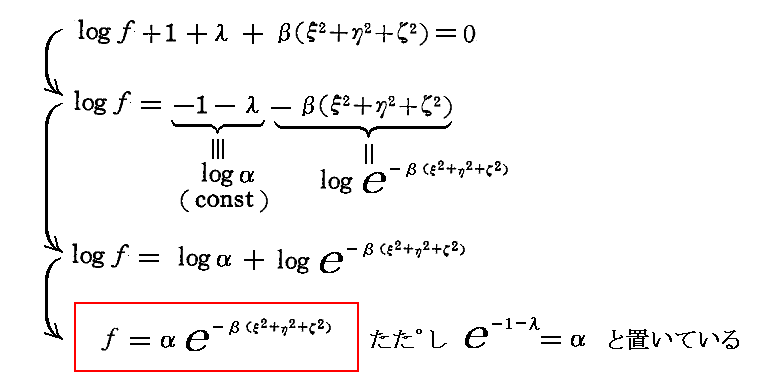
となります。
　この式から明らかになることは、平衡状態では分子の空間的な分布は一様になり座標（ｘ，ｙ，ｚ）に依存しなくなることです。このことに付いては別稿「統計力学におけるラグランジュの未定乗数法」４．も参照されたし。また関数ｆ（ｘ，ｙ，ｚ，ξ，η，ζ）は“Maxwellの速度分布”と言われるものになります。

４．常数αとβの決定とエントロピーＳの表現式

　定数αとβは、Ｎ、Ｖ、Ｕの値から求められます。前記のｆ（ｘ，ｙ，ｚ，ξ，η，ζ）の表現式をそれぞれの式に代入すると


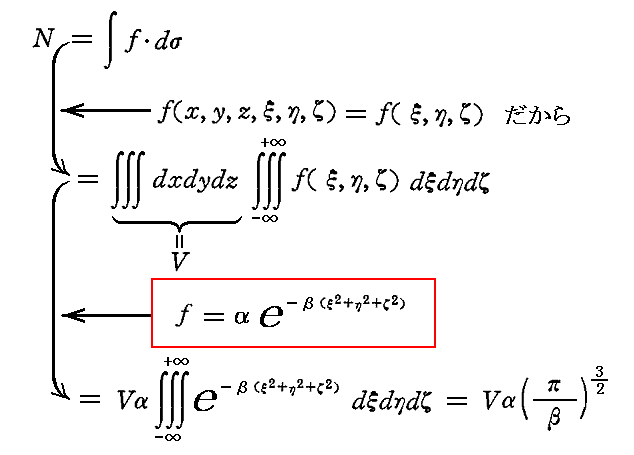
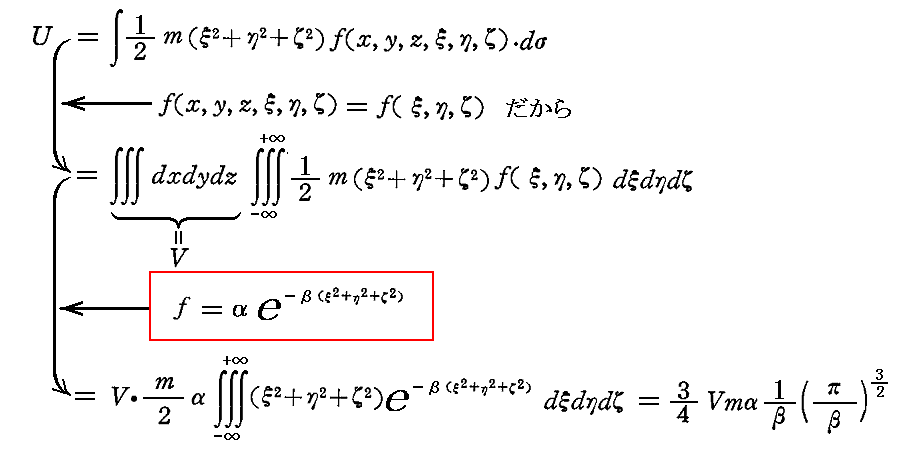
となります。式変形の最後の積分計算については、別稿の積分公式を御覧下さい。
　これらの式をαとβについて解くと

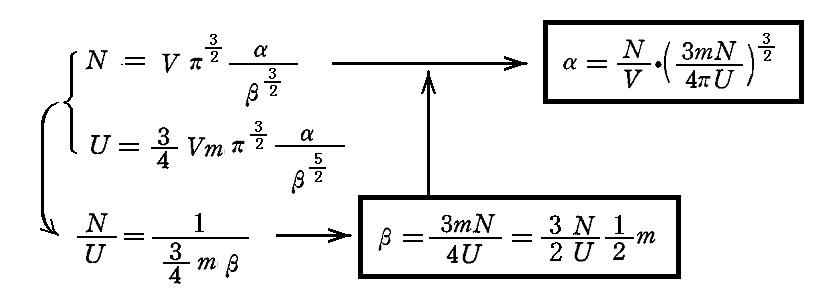
が得られるので関数ｆ（ｘ，ｙ，ｚ，ξ，η，ζ）として、最終的に

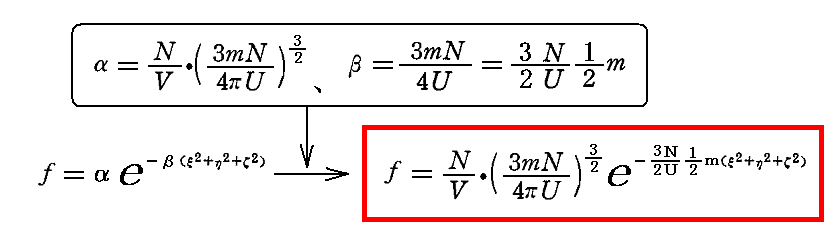
が得られます。これが、エントロピーＳが極大値を取る時に実現される各要素領域ｄσに於ける分子数（ｆ・ｄσ）の値です。
　これを前出のエントロピー表現式に代入すると、平衡状態で実現されるエントロﾋﾟーが極値を取ったときの値が得られる。



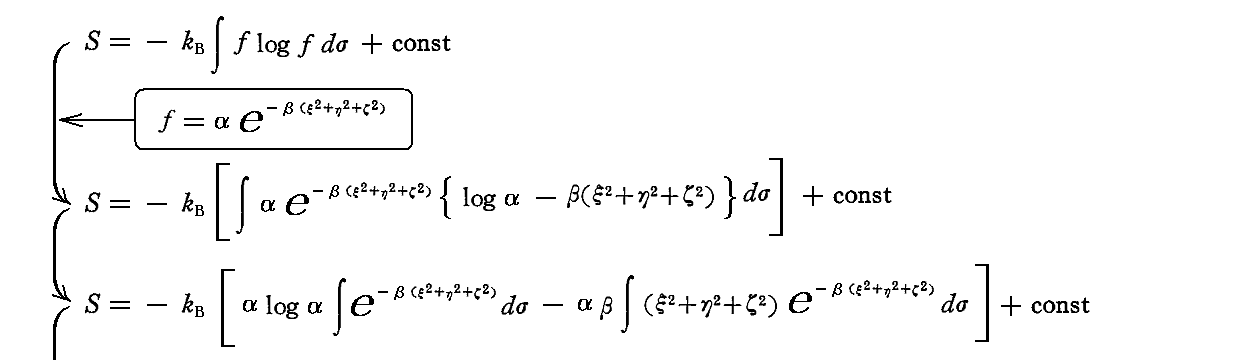
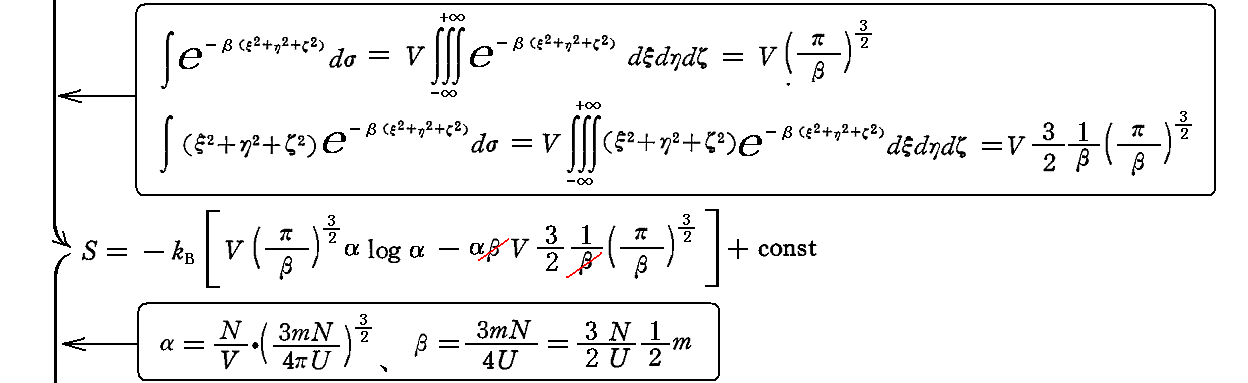
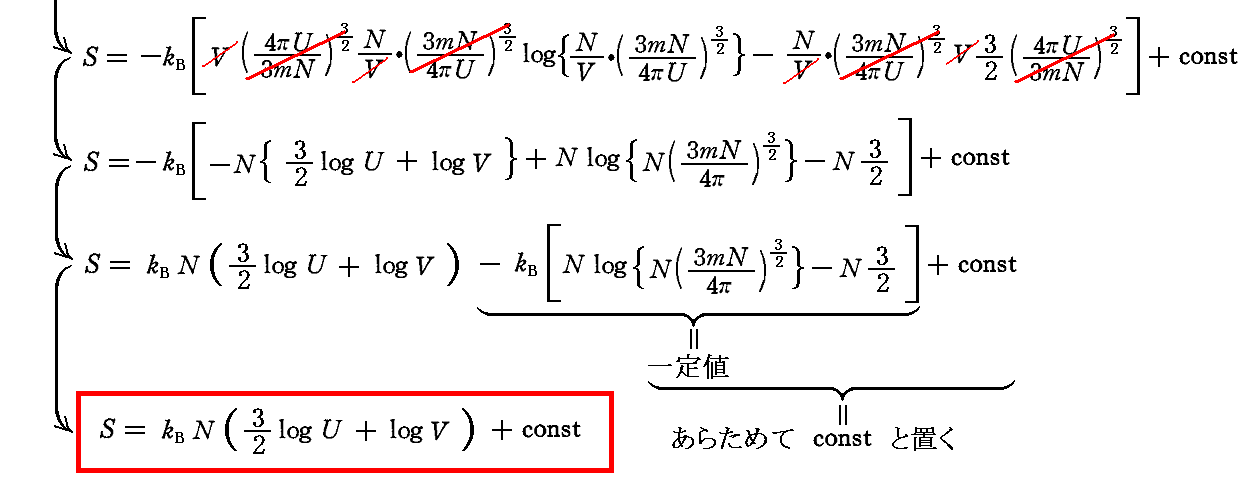
となります。これは事項で利用します。　

５．熱力学関係式との対比

　ここで求めたエントロピーの表現形式は、最初に仮定したエントロピーと確率との関係式のみに基づいている。この中には、どこにも気体論の法則は用いられていない。したがって、このエントロピー表現式から得られる結論が、単原子理想気体の熱力学的振る舞い（状態方程式、比熱、等々・・・）とどの様に対応するのかを調べることは重要です。

　熱力学に於けるエントロピーの定義式（熱力学第二法則）

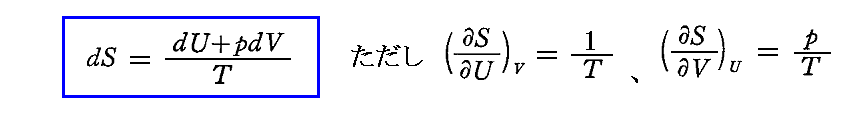
［この式の意味については別稿「絶対温度とは何か（積分因子とは何か）」を参照］から、直ちに以下の関係式が導かれる。

　まず、上記式の第一項より

これは、まさしく古典的統計力学に於ける“エネルギー等分配則”を表している。
　
　また、この関係式から、先に導入した未定定数βが絶対温度Ｔの逆数に比例する量

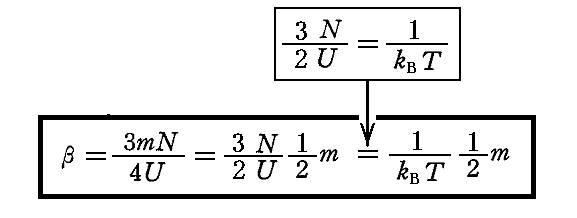
であることが解る。普通の教科書と違って、上記の表現には(1/2)ｍの余分な項が掛かっていますが、これは9．(1)3．［補足説明１］で説明した事情が有るからです。
　いずれにしても、ここの手順が未定定数βを絶対温度Ｔと関係付ける方法です。普通の教科書では、例えば別稿「統計力学におけるラグランジュの未定乗数法」5．［補足説明4］の(5.91)式などを使いますが、プランクのやり方の方がはるかに優れている。
　
　これから、前述の分配関数は

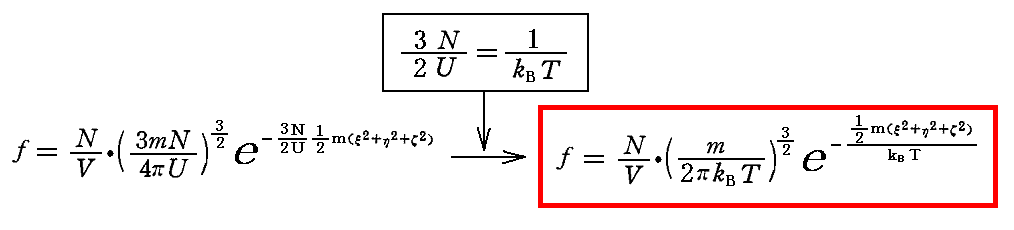
となり、係数の確定した、温度Ｔの関数としての“Ｍaxwellの速度分布則”が得られる。

　さらに、第二項より

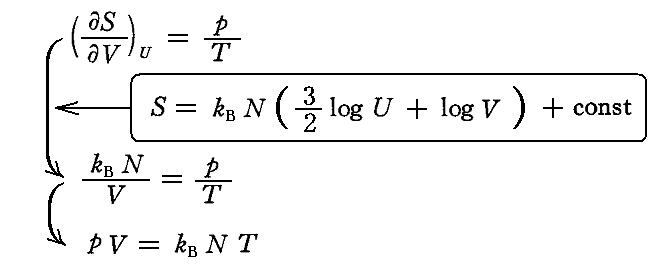
がえられるが、これを理想気体で成り立つ“ボイル・ゲーリュサック・アボガドロの法則”

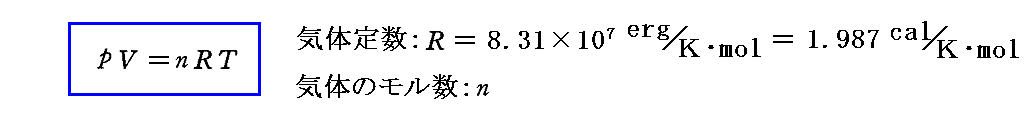
と比較すると

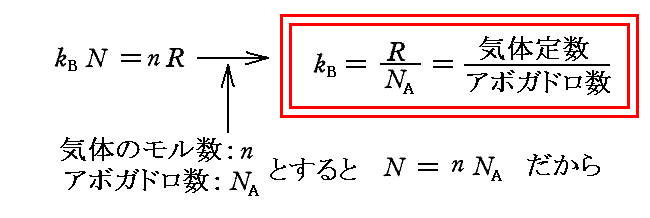
であることが導かれる。この関係式は９．（４）１．でボルツマン定数ｋ_Bからアボガドロ数Ｎ_Aを求めるときに使いますが、この関係式が求めたいので９．(１)式の議論をしたのです。

［補足説明１］
　ラグランジュの未定乗数法を含めて、この節の内容は、最近の本では例えば戸田盛和著「物理学入門コース７　熱・統計力学」岩波書店（1983年刊）の第5章などに解りやすく説明されています。ここのプランクの説明と比較してみて下さい。議論の仕方は微妙に違いますが同じことです。
　
　ただし、この当たりの説明でいつも思うのですが、最近の教科書における温度やボルツマン定数の導入は実に曖昧で解りにくいです。本来、絶対温度Ｔは熱力学的にしか導入・定義できないのですから、ここで説明したプランクのやり方がはるかに明快で解りやすい。まさに王道に沿った議論です。

（２）シュテファン・ボルツマンの法則とウィーンの変位則の導出（原論文7．§11〜12、著書10．§155〜156）

１．シュテファン・ボルツマンの法則（原論文7．§11、著書10．§155）

　“プランクの熱輻射公式”から“シュテファン・ボルツマンの法則”が直ちに導けます。上記のエネルギー密度関数ｕ（ν，Ｔ）を振動数νに関して0〜∞まで積分すれば、黒体輻射平衡にある輻射場の単位体積当たりのエネルギー密度が求まる。



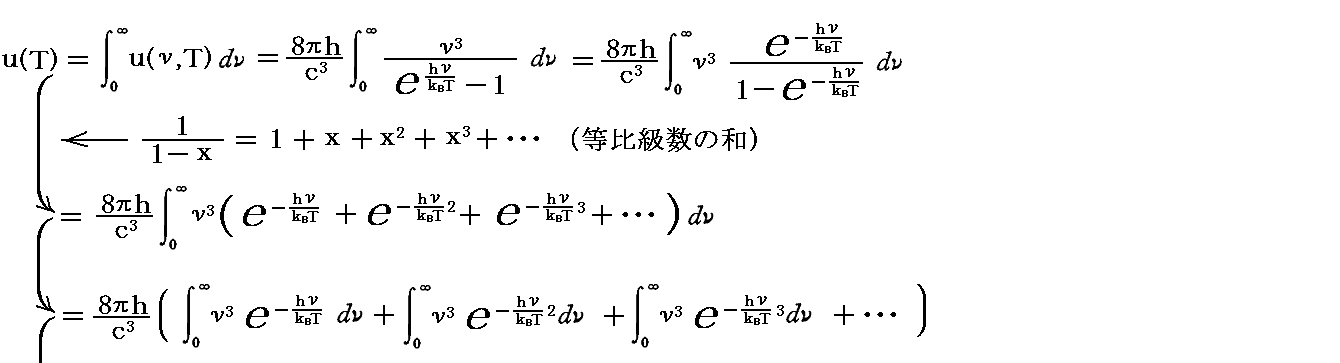
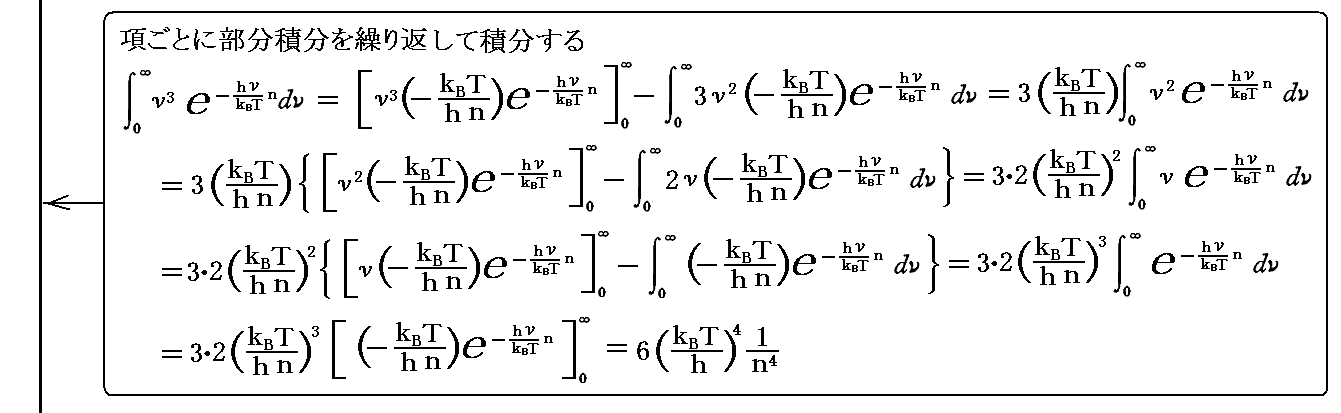
　この結論を別稿「シュテファン・ボルツマンの法則」２．（２）２．の“輻射場のエネルギー密度”についての表現式

や、別稿「シュテファン・ボルツマンの法則」２．（３）の温度Ｔの黒体の面要素ｄσからｄｔ時間に真空の半空間のあらゆる方向に放射される“全放射エネルギーＳ”についての表現式

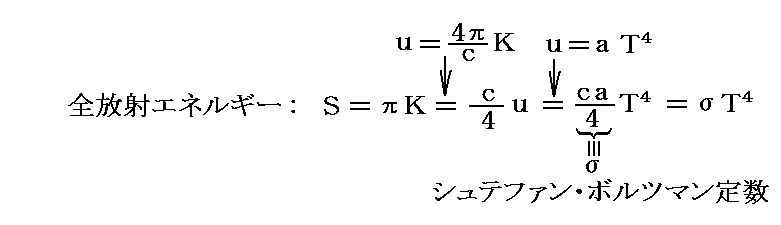
と比較すると、それぞれの定数は

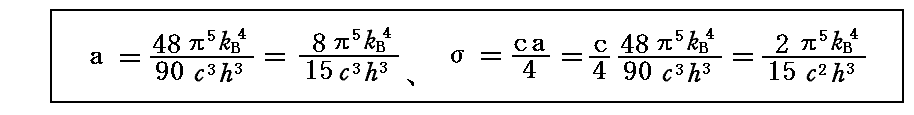
となります。
　別稿「シュテファン・ボルツマンの法則」２．（３）では定数の意味は明らかではありませんでしたが、ここでより根源的な普遍定数ｋ_B、ｈ、ｃに関係づけられた事になります。そのため輻射場のエネルギー密度ｕや、全放射エネルギーＳが観測できれば、それらのデータにより普遍定数ｋ_Bとｈを決定することができる。

２．ウィーンの変位則（原論文7．§12、著書10．§156）

　同様に“プランクの熱輻射公式”を波長で微分した導関数がゼロである条件から、“ウィーンの変位則”が直ちに導かれる。ウィーンの変位則は最大強度あるいは最大エネルギー密度を与える波長が温度に逆比例して変化するというものでしたが、それが成り立つ事を確かめるためには、分布曲線が最大値を取る波長（λ_maxと置く）を絶対温度Ｔの関数として求めて見ればよい。
　すなわち

のいずれかを用いればよい。例えば左の式を用いると


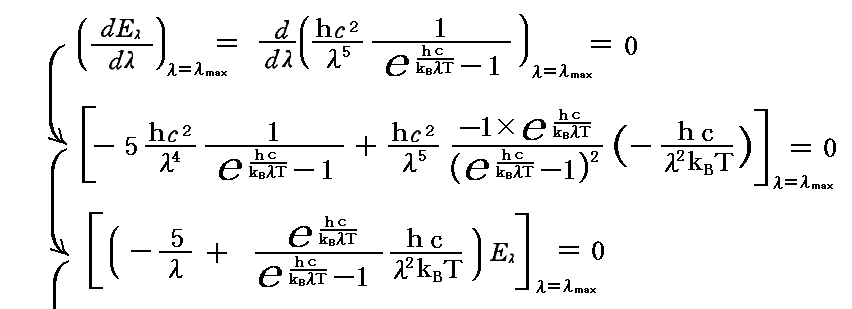
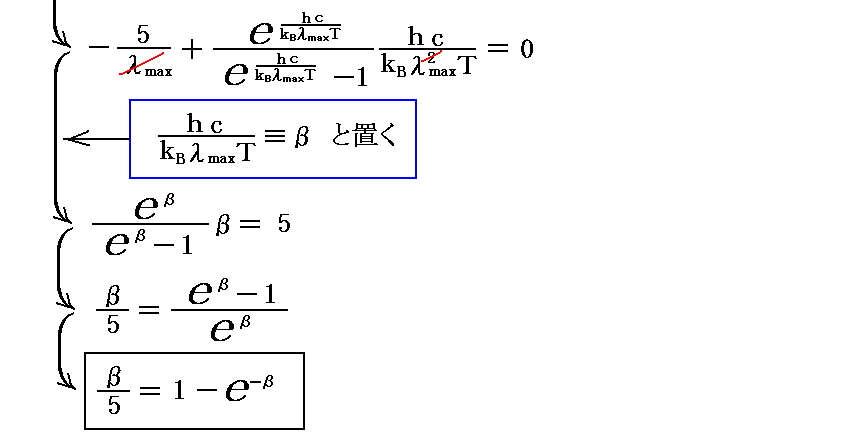
のような超越方程式が得られる。この左辺と右辺のグラフを描いてみると

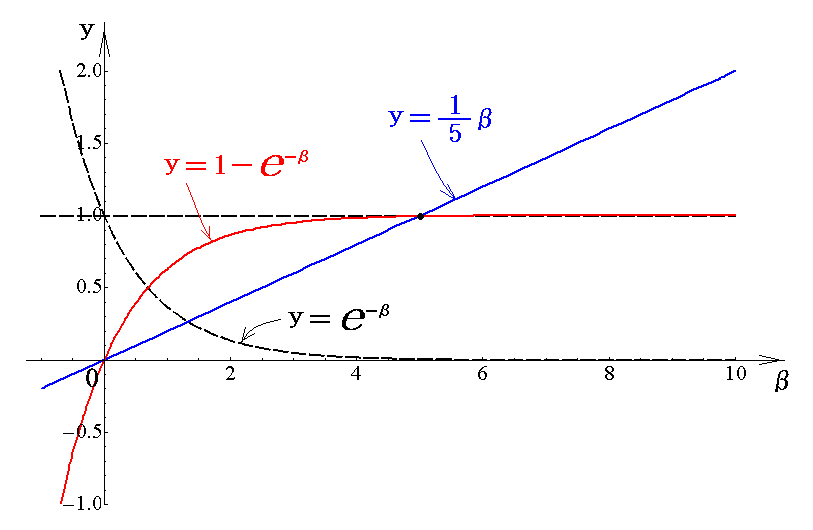
の様になるので、解βは5に近い値であることが解る。これを求めるには数値計算で解けばよい。簡単に行うには例えばこのようにすればよい。いずれにしても β＝4.9651・・・ が求まる。
　つまり上記の超越方程式はただ１つの確定した解を持つ。その為

となり、別稿「ウィーンの変位則」５．（２）２．で求めた式が成り立っていることが解る。
　この式によって、それまでその意味が明らかではなかった、定数ｂが根源的な普遍定数ｋ_B、ｈ、ｃに関係づけられたことになる。そのため、右辺の定数 ｂ を観測から求めれば、その値から普遍定数ｋ_Bとｈを決定することができる。

（３）ボルツマン定数ｋ_Bとプランク定数ｈの決定（原論文7．§11〜12、著書10．§157）

　プランクは、原論文3．６．７．の最後で、実験・観測値との比較から普遍定数 ｋ_B と ｈ の値を導きます。

　原論文7．で、プランクはシュテファン・ボルツマン定数σの観測値として F.Kurlbaum の測定値［Wied. Ann. 65, p746, 1898年］を用いている。Kurlbaum は100℃＝373Ｋの黒体放射強度Ｓ₃₇₃と0℃＝273Ｋの黒体放射強度Ｓ₂₇₃の差が7.31×10²Ｗ／ｍ²であることを測定した。これから

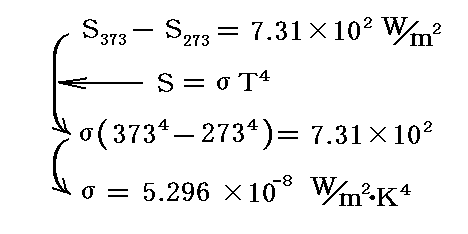
となる。この値を用いると前節の比例定数ａは

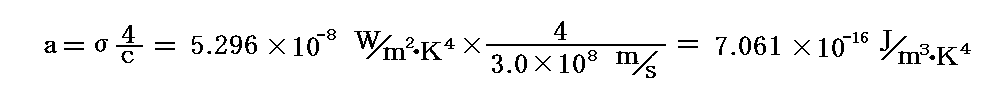
となる。そのため

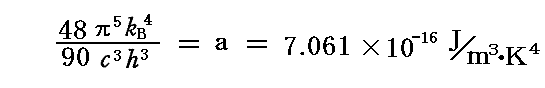
となる。

　一方、ウィーンの変位則の定数ｂについてはO. Lummer と E. Pringsheim の測定値［Verhandle. der Deutschen Physikal, Gesellsch., 2, p176, 1900年］を用いている。観測値は ｂ＝2.940×10^-3ｍ・Ｋ であったので

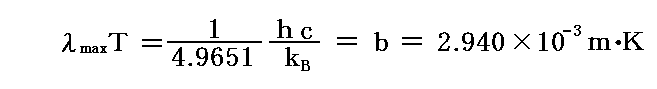
となる。

　当時、光速度はかなり正確に測定できていたから、結局

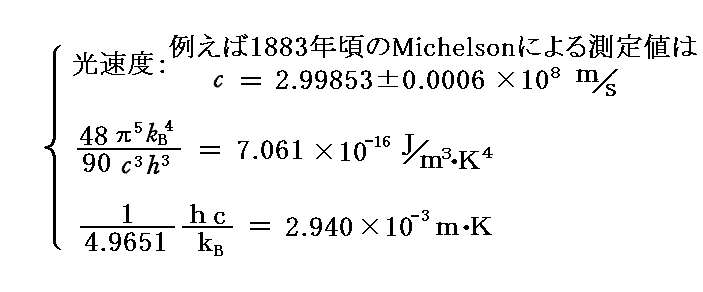
の三式を連立させて解けば普遍定数 ｋ_B と ｈ を決定することができる。
　その様にしてプランクが得た値は

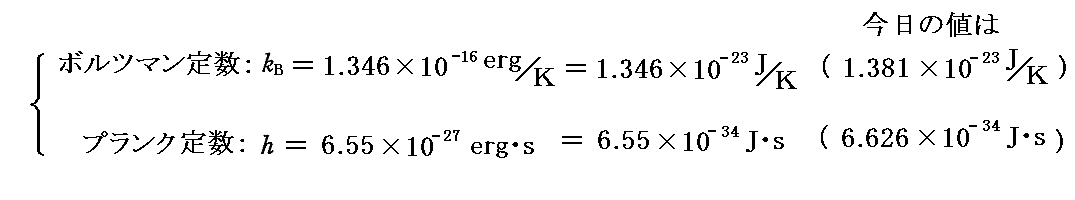
です。これは５．（２）１．で説明した原論文3．ですでに得ている値に一致する。

（４）アボガドロ数Ｎ_Aと電気素量ｅの決定（原論文6．、原論文８．著書10．§158）

　プランクは原論文6．の最後で、５．（２）１．で説明した原論文3．ですでに求めていた普遍定数ａとｂからボルツマン定数ｋ_B＝ｂ／ａを求めて、“アボガドロ数Ｎ_A”と“電気素量ｅ”の値を導いて見せます。
　別稿「アボガドロ数の測定法」１．と６．でも注意しましたように、これらの値は精度に於いて他の測定法に約10年先行しており、偉大な功績です。
　この当たりについては、別稿「Perrinのソルヴェイ会議報告」�\．も参照されて下さい。

１．アボガドロ数Ｎ_A

　９．（１）で説明したように、平衡状態にある単原子理想気体の状態方程式に、ボルツマン統計力学のエントロピー確率表現式を適用すると

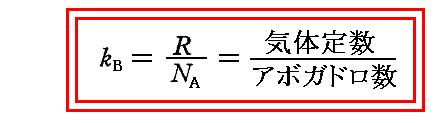
が導かれます。
　気体定数Ｒは当時かなり正確に測定できていましたので、その測定値と前節で求めたボルツマン定数ｋ_Bの値から直ちにアボガドロ数Ｎ_Aが求まる。

２．電気素量ｅ

　別稿「アボガドロ数の測定法」２．（１）で説明したように、電気分解に於ける［ファラデー定数Ｆ］と［電気素量ｅ］と［アボガドロ数Ｎ_A］の間には

の関係がある。
　ファラデー定数Ｆは当時かなり正確に測定できていましたので、その測定値と上で求めたアボガドロ数Ｎ_Aの値から直ちに電気素量ｅの値が求まる。

［補足説明１］
　この章の内容は、プランクが解説文13．で

　“・・・　この理論の実験的な検討については、当時はまだ非常に限られたことしかできなかったが、それというのも、そのためにとり扱えたのが定数ｋだけであって、しかもその値はたかだかオーダーがある程度知られていたにすぎなかったからである。ｋはボルツマンによれば、いわゆる絶対気体定数を意味する［L. Bo1tzmann, Situngsber. Wien. Akad. Wiss. (II) 76, p428 (1877)］のだが、いまのそれは、その場合の様にグラム分子における

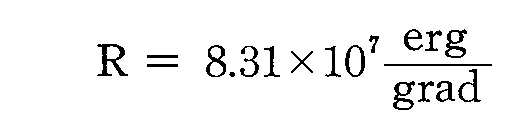
にではなく、現実の分子に関するものである。従って

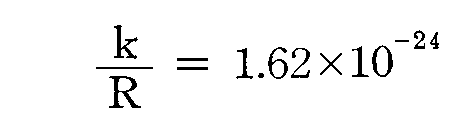
という比は、一グラム分子の質量を現実の分子の質量に換算する換算因子であって、ローシュミット数Ｌの逆数に等しい。ここから私はまた、一価の一グラムイオンの電気量(静電単位での)2.895×10¹⁴に、この換算因子を乗じて電気的要素量子の値を4.69×10^-10ｅｓｕと算定したが、F・リヒャルツ［F. Richarz, Wied. Ann. 52, p397, 1894］は1.29×10^-10を、 J・J・トムスン[J. J. Thomson, Phil. Mag. (5) 46, p528, 1898]は6.5×10^-10を見いだしていた。電気的要素量子のそれ以上の測定は当時まだおこなわれていなかった。
　以上の結果で私はある程度満足できたが、多くの物理学者の目には事情は当然別様に映った。熱輻射の測定から電気的要素量子を算定するといったことは、時として真面目に受取られさえしなかった。だが私はこのような疑惑によって、私の定数ｋに対する自信を失うようなことはなかった。もっとも、それに対する完全な確信をはじめて得たのは、Ｅ・ラザフォードとＨ・ガイガーがアルファ粒子の計算から、電気的要素量子の4.65×10^-10という値に達した［E.Rutherford and H.Geiger, Proc.Roy.Soc.London(A), 81, p162〜173 (1908)］と知った時である。その後測定の方法が精密になって、この値は周知のごとく少しだけ大きくなった。
　これに比べて、最初はまったく宙に浮いていた、第二の定数ｈの値を吟味するという課題は、はるかに期待がもてぬもののように思われた。それゆえ、J・フランクとG・ヘルツが、電子の衝突によるスペクトル線の励起に関する実験で、これを測定するのにそれ以上直接的であることを望みえないほどの方法を見いだしたことは、私には大きな驚きであり、かっ喜びでもあった。これによつて作用量子の実在に関する最後の疑いもまた消え去ったのである。・・・”

と言っている部分です。また解説文12．の１．（４）で説明している部分です。

［補足説明２］
　この稿で説明したプランクの理論には、正直なところ、私自身良く解らない所や納得できない所、またこの推論は本当に正しいのだろうかと思う所もあります。未知の領域を切り開いていく物理学の理論とは本来そのようなものかも知れません。その様なものだけれども以下のことは確実に言える。
　すなわち、彼が提出した輻射法則は実験観測値と極めて良く一致した。実際、今日のより正確な多方面にわたる観測からも、その一致性は極めて高いことが解っています。一致したからこそ、次に述べるように正確なアボガドロ数や電気素量の値を求めることができた。そして、輻射場の性質を温度の概念と結びつけて説明できたことも重要です。
　また、この章で説明したように、この輻射法則と実測値を比較することで求められたボルツマン定数ｋ_Bとプランク定数ｈは、極めて正確なアボガドロ数Ｎ_Aや電気素量ｅの値を与えた。1900年当時までに測定されていたアボカド数Ｎ_Aや電気素量ｅの値はたかだかその位（10の指数）が確認できる程度だったのに、プランクの得たＮ_Aやｅの値は（今日の値と比較しても）誤差数パーセント以下という驚くべき精度だったのです。
　このことこそが作用量子ｈとボルツマン定数ｋ_Bが絡むこの理論展開の正しさを保障しているし、自然界に存在する特異なメカニズムの存在を示している。解説文12．や13．を読むとプランクの言いたいこともまさにこの点にあることが解ります。
　
　世にある解説書の中にはプランク自身はエネルギー要素の意味をつかみ切れていなかったとか、彼の理論にはいろいろな欠点があると指摘しているものもあります。しかし、原論文3．や6．の最後の部分を読めばプランクはｈとｋ_Bの重要性をハッキリと把握しており、その意味を正確に理解していたことが解ります。これは正にプランクが最初です。
　
　実際、プランクは原論文3．§26や、文献10．§159で、これら二つの定数（ｋ_Bとｈ）に光速ｃと万有引力定数Ｇを加えた４つですべての物理量を表現・測定できるとして“自然単位”の概念を提唱している［５．（２）２．参照］。つまり、この４個の量の値を１として、それ以外の量を表現すれば、［重力の法則］、［真空中の光の伝播の法則］、［熱力学の二つの法則］が正しい限り、宇宙の任意の知的生命体が任意の場所で、どの様に異なった方法で測っても、あらゆる物理量(質量、長さ、時間、温度、・・・）が同一の値を持つことになるであろうと言っています。この事からも、プランクが当初よりｋ_Bとｈは極めて根源的な普遍定数であると認識していたことは明らかです。
　それ故に、プランクの発見は量子理論の嚆矢として高く評価されるべきものだと思います。

１０．まとめ

　後にプランクの輻射法則の別証明が様々提案されます。プランク自身もいろいろな別証明を示しています。それらは、それぞれ特徴はあるのですが、プランクの輻射法則がなぜ絶対温度に関係するのかを最も明確に示してくれているのは、この稿で説明したプランクが最初に用いたやり方です。他の方法ではその点が実に曖昧で絶対温度との関連性の見通しが良くありません。
　エントロピーこそ積分因子である絶対温度Ｔを正確に説明するものですから、このエントロピーを用いるアプローチこそ、輻射公式の絶対温度との関連性を一番明確に理解させてくれます。また、それだからこそ作用量子ｈを発見できたのではないでしょうか。この点に於いてこの最初の証明法はもっと評価されてしかるべきです。
　Planckが文献13．「作用量子発見の歴史によてせ」を記したのは彼の晩年の1943年です。量子論が発展して20年以上経ったこの時期に、彼が何故この文章を残したのか考えて見て下さい。
　彼にとってエントロピーを用いるこの証明法こそが、最も本質的で重要な証明だったのだという確信が、時代を経るにつれてますますハッキリしてきたからです。
　
　
　実際のところ
　ゾンマーフェルドは「理論物理学講座�X　熱力学および統計力学」の序文で次のように述べている。
　“・・・プランクは、この概念（エントロピー）が一般に通用するものであるという確信を、つとにその博士論文の中でのべているが、この確信がプランクを1900年の彼の輻射則や量子論へ導いたのである。・・・”
　
　またエミリオ・セグレは彼の著書「Ｘ線からクォークまで」みすず書房（1982年刊）の第4章で次のエピソードを紹介している。
“・・・1931年のことであるが、アメリカの物理学者のR. W. ウッドがプランクに、いったいどうやって量子論のような信じがたいものを作り出したのかと尋ねると、プランクはこう答えた。「それはいわば絶望的な行為だった。6年間というもの、私は黒体の理論と取っ組み合っていた。この問題が本質的なものだということはわかっていたし、答えもわかっていた。そこで私は何を犠牲にしてでもその理論的な説明を見つけ出さなければならなかったのだ。ただし、神聖犯すべからざる熱力学の二つの法則だけはそのままにしてね。（Planck letter to R.W.Wood、7 October 1931, American Institute of Physics Archives, New York）」・・・”［Armin Hermann, The Genesis of Quantum Theory(MIT Press,1971),p23］
　熱力学の二つの法則は量子論の世界でも正しいものだったのですから、プランクの確信はまさに本物だったわけです。
　
　またプランク自身も解説文13． のなかで次のように述べている。
　“・・・この問題にとり組むようになったとき、以前には好ましくないと感じられていた外的状況、すなわち私の切り拓いた方向に対して専門仲間が関心を持ってくれないということが、今やまさしく私の仕事を楽にする事情として、むしろ好都合になるように運命ははからった。というのは当時、実験の面からも理論の面からも、正常スペクトルのエネルギー分布の問題には多くの優れた物理学者がとり組んでいたが、彼らはすべて輻射強度Ｋ_νを温度Ｔの函数として表現しようという方面でのみ研究していたのに対して、私はエントロピーＳがエネルギーＵに依存している点に、より深い関連を推定していた。エントロピー概念の意義が当時はまだ正当な評価を受けておらず、私の方法には誰も注意を払わなかったので、私は十分な時間をかけて徹底的に計算をやってみることができ、どの方面からも邪魔されはしないか、追い越されはしないかと心配する必要はなかったのである。・・・”
　これが文献3．と4．で報告されているもので、彼が真に正しい輻射公式を見いだすことを可能にした最も重要な考察です。重要な所なのに難解なので、ここを詳しく紹介している解説書はほとんどありません。原論文を読むしかありません。
　
　また、プランクは同じ解説文13．の別な所で
　“・・・だが他によい方策もなかったので、私はボルツマンの方法を用い、任意の物理系の任意の状態に対してまったく一般的に　Ｓ＝ｋ_B･log_eＷ　という式を立てた。ここでWは、状態のしかるべく算定された確率を表わしている。この関係が実際に普遍的な意味をもつとすれば、エントロピーが加算量であるのに対して確率は乗算量であるのだから、定数ｋ_Bはその単位にだけは依存するにしても、普遍定数でなければならない。それはしばしば、ボルツマンの定数と俗称されているが、ボルツマンがこの定数を導入したのでもなく、また私の知る限り、彼はその値を求めることにも思い及ばなかったということは、注意しておく必要がある。もしそれをやっていたのなら、彼は現実の原子の数を問題にせねばならなかったであろうが、この問題は同僚のJ・ローシュミットにまったく委ねてしまって、彼自身が自分の計算をする時いつも念頭においていたのは、運動論的気体理論が力学的な体裁をとりうるかどうかということだけであった。それゆえ彼はグラム原子のレベルで満足していたのである。文字ｋ_Bは非常に徐々に一般の間に浸透していったのであって、それが導入されて数年後でも、なおそれの代りに、一グラム原子に相応する原子数であるローシュミット数Ｌで計算するのが普通のことであった。・・・”
と述べている。
　ここが、彼が正しい輻射法則を量子論的に解釈することを可能にした方法で、もう一つの重要な考察です。こちらは多くの解説書で説明されています。
　
　この事に関係して、ゾンマーフェルトは「理論物理学講座�X　熱力学および統計力学」講談社（1969年刊）§29で次のように述べている。
　“・・・ボツルマン自身は一度もこのような形［つまりＳ＝ｋ_Blog_eＷ］で公式を書いたことはなかったのだが、それはたいしたことではない。最初にこの式を書いたのはプランクである。また定数ｋ_Bを入れたのもボルツマンではなくプランクである。ボルツマンは単にＳと状態確率の対数とが比例することを述べただけである。・・・”
　つまり、今日知られているエントロピーの統計力学的な解釈に基づく表現形式 Ｓ＝ｋ_Bｌｏｇ_eＷ を初めて与え、定数ｋ_Bを入れたのはプランクです。今日の量子統計力学理論の大半がこの関係式に基づいているのですから、プランクの考察がいかに先見性に満ちていたかが解ります。
　
　プランクの論文の至る所に出てきて、証明の中核をなすのが

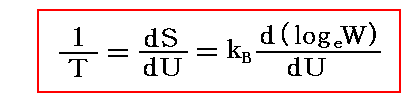
の関係式です。これは別稿「反応熱と熱化学方程式」８．で注意を促しましたが、熱力学におけるエントロピーの定義式（つまり熱力学第二法則）　ｄＳ＝ｄＱ／Ｔ　中の熱の移動量ｄＱをエネルギーの変化量ｄＵに変え、エントロピーＳに前記の統計力学的な状態数Ｗを適用したものです。これは今日の熱・統計力学で最も重要な関係式ですが、当時この式の重要性を最も深く理解していたのはプランクだと思います。
　実は、系のエネルギーがＵのとき、系がその状態を取る確率を表す分配関数ｆ（Ｕ）は位相空間に於ける状態数Ｗ（Ｕ）と ｆ（Ｕ）＝1／Ｗ（Ｕ） の関係にあります。この関係式を用いて上式を積分すると

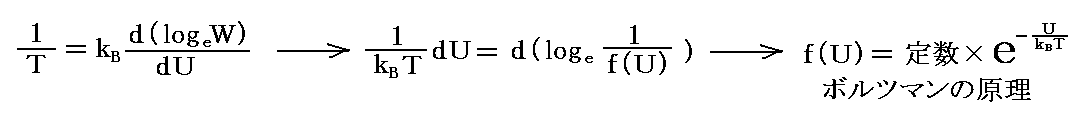
となり、ボルツマンの原理となります。これこそ熱理論［つまり温度（エントロピー）と熱量の理論］と力学理論［つまりエネルギーと仕事の理論］を結びつける［つまり温度とエネルギーを結びつける］最重要な関係式ですが、これを一番最初に認識して導入したのはボルツマンです。
　だから前に記した式の

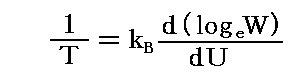
の部分はボルツマンの原理そのものです。この表裏一体関係を正しく認識していたプランクだからこそ、これを熱力学の第二法則と比較することによって

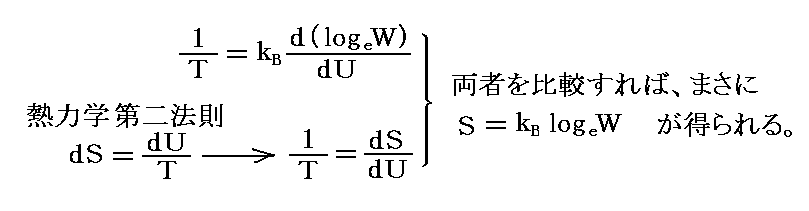
のように Ｓ＝ｋ_Bｌｏｇ_eＷ の関係式を提起できたのでしょう。確かに、この形はプランクが文献10．の§134で述べているエントロピーが満たすべき形を満足している。
　
　実際のところ、我々がこの式Ｓ＝ｋ_Bｌｏｇ_eＷを始めて学ぶとき最も理解に苦しむ所は“本来連続的な量であるはずのエントロピーＳが単なる自然数の集合である状態数Ｗと単純に結びつけられるところ”です。
　このとき、高林先生が文献２０．のｐ26で、いみじくも指摘されているように
　“・・・さて、エネルギーがε＝ｈνによって「量子化」されたが、そのことによってＷは実際に数えられるもの「自然数」となり、エントロピーもその対数の意味で「量子化」され、それはもはや付加定数をともなわない絶対的な量となったわけで、この点も重要である。・・・」
ということに気付けば、量子化されて初めてエントロピーが単なる自然数Ｗに関係づけられ、克つ定数ｋ_Bが確定した意味をもつことになったことが理解できます。つまり、ボルツマン定数ｋ_Bは、新しい物理量である温度（これはエントロピーと共に導入された）を、それまでの長さ・時間・質量で定められた様々な物理量と結びつける根源的な換算定数となる。温度はエントロピーと共に導入されたのだから、エントロピーとそれらの古い物理量を結びつける換算定数と言っても良い。
　
　事実これらの関係式は量子論に於いても正しいものです。高林先生が文献２０．のｐ26に書かれているように
　“・・・量子的不連続性が空洞輻射のなめらかな連続スベクトル分布［原子の線スペクトルではなく！］に関する一見複雑な統計力学的分析から初めて観測されたということは、一見不思議に見えるが、よく考えてみるとそうでないことをここで注意しておきたい。
　第一に、まだ原子の構造がわかっていないような時期にあって、この空洞輻射の問題は原子模型の特性によらないような、純粋で絶対的な［結局は輻射場自体の性質を反映するような］問題であり、輻射場の問題を原子構造の問題から分離することを可能にする問題であったということである。
　第二に「量子」というような新しい運動学にかかわる概念に達するためには、純粋の力学的問題の追及よりも、実際にプランクがとったように熱輻射というような問題について「熱力学」と「ボルツマンの原理」のような普遍的原理［たとえそれの力学的基礎が変革されたとしても、それ自身としては護持されるような］に対する強い信念をもって進むほうがより有効であったということである。・・・”
　それだからこそ、プランクがエネルギー量子を発見することができたのだと思います。
　
　
　輻射公式になぜ絶対温度Ｔとボルツマン定数ｋ_Bが絡むのか？が説明されないと熱輻射論は絶対に理解できない。絶対温度Ｔは熱力学でしか導入できないし、エントロピーと密接に関係（もちろんｋ_Bも）している。だからプランクが行った絶対温度とエントロピーから入る考察は“王道”だった。
　
　王道であるが、絶対温度とエントロピーの概念はとても難しく大家と言われる人でもそれを正しく理解できていたのか疑わしい。プランクは、最晩年に記した「過ぎし日々への個人的回想（Die Naturwissenschaften, Heft 8 v.30, Oktober 1946年）」の中でキルヒホッフやアーレニウスといった大家でさえもエントロピー概念を正しく理解していなかったことを嘆いている。
　当時エントロピー概念を正しく理解していた科学者は少ない。おそらく、その中で最も深く・正しく理解していたプランクだからこそ　Ｓ＝ｋ_B・log_eＷ　の形を書き表せたし、１／Ｔ＝Δ（k_Bｌog_eＷ）／ΔＵ　の関係式を認識できたのだろう。さらに、そのようにして　ボルツマン定数ｋ_B　を認識できたプランクだからこそ　プランク定数ｈ　を発見できたのだろう。
　プランクのたどったこの王道はとても難解だから世の一般の教科書は避けているのですが、もっと紹介されても良いものだと思います。
　
　さて、ここで最後のまとめですが、高林先生が文献２０．のｐ27に書かれている内容の引用です。
プランクの熱輻射分布公式（エネルギー密度に関して）は

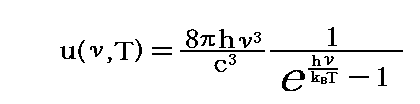
の形をしている。この中の三つの普遍定数ｃ、ｈ、ｋ_Bを含む事は、それが［輻射場］の［量子論］的［熱統計］理論である事を象徴的に表している。このように波動場の量子力学に繋がるものが、量子論の最初に現れたことは驚くべき事である。これ以後、プランク自身を初めアインシュタインなどの人々によってこの公式の意味が繰り返し繰り返し問い直され、量子論の進展に何度も新たな示唆を与えることになる。
　そして、量子論の以後の全展開はプランクの“魔術的な公式”

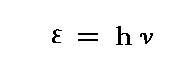
から流れ出したと言っても良い。この大発見は、本人の思い及ばなかった遠大な展望を持っていた。

１１．参考文献

　プランクは共鳴子の集合と輻射場の間を行ったり帰ったりしながら彼の論理を展開します。
　彼にとってレーリーのような輻射場そのものの自由度を考えて、それに等分配則でｋ_BＴを割り当てるような解釈［これは1900年6月に出てくる］はとうてい納得できるものではなかったでしょう。実際の所、我々がレーリーの理論を初めて学ぶとき最も面食らうのは電磁波の定常波の一つ一つに統計力学の等分配則によってエネルギーｋ_BＴを割り当てるという考え方です。確かにその考え方が、長波長・高温領域におけるエネルギー分布を旨く説明するのですが、プランクがたとえ知っていた（プランクがレーリーの理論を知ったのは1900年10月7日）としても納得できるものではありません。ファインマンは文献17．§16-2で輻射場と熱平衡にある調和振動子（共鳴子）に等分配則でｋＴを割り当ててレーリー・ジーンズの分布則を説明していますが、これはプランクがエントロピーについての内挿式の高温・長波長領域での表現式を導くために、共鳴子にエネルギーＵ＝Ｃ・Ｔを割り当てたことと同じです。この比例定数Ｃこそ、後にボルツマン定数ｋ_Bに置き換えられるものです。
　また低温・短波長領域におけるエネルギー分布の減衰曲線をかなり旨く説明するウィーンの分布則についても、そこに用いられている気体分子運動論的な仮定はとうていプランクが納得できるものではないのは明らかです。
　プランクには、初期状態に於いて任意の分布をしている輻射場を最終的に黒体（空洞）輻射のエネルギー分布に導くのは黒体（共鳴子）と輻射の相互作用であろうという考え方がありました。そのため、それらの相互作用の中にこそ黒体輻射のエネルギー分布を説明する鍵があると考えたのですから、最後まで共鳴子を使って論じるやり方を捨てきれなかったのでしょう。

　プランクが輻射公式を証明してしばらく経った1920年の段階では、電子を含む物質はｈνの固まりの状態でエネルギーを光りとやりとりすると言う考え方は確立していました（別稿「Einsteinの光量子論（905年）」§8［補足説明3］を参照）。しかし、当時においても、固まりとして物質とやりとりされるエネルギーｈνを、光そのものがどんな形で保持しているのかは全く明らかではありません。これは1920年の解説文12．の最後の所でプランク自身が述懐しているところです。
　ｈνが光のエネルギーだと言っても、当時波であると考えられていた光［これはヤングやフレネルによって比較的近年（1820年ころ）に取り上げられた考え方］の取り得る状態というものが何か解らないと、それがなぜプランクの輻射法則のような数の分布になるのか全く明らかにはなりません。また、光を粒子（光子）と捉える考え方［粒子説はアインシュタインが初めて唱えたのではなくて、ニュートン以来の長い歴史があります］では、レーリーのような定常波の存在数で取り得る状態を数えてｈνを与えることはできないのも明らかです。
　最初から光を波として習う我々は、アインシュタインの光量子仮説は革命的であると教えられますが、“光は粒子である”とする考え方自体はもともと古くからありました。そして、かっては主流でした。実際１８世紀の物理学者・天文学者の多くは光は粒子だと考えていた。そう考えた方が何光年もの彼方の星々からやってくる光が我々の所に届くわけを理解しやすい。波では薄まってしまって本当に地球まで届くのか疑問です。
　しかし、１９世紀後半に確立したマックスウェルの電磁気学による光の波としての説明がとても旨く成功して、光はほぼ波であろうとの認識が確立したのが１９世紀末の状況でした。実際、光が電磁波の一種であると言うことが明らかになったことはどんなに強調してもしすぎることが無いくらいの大発見であり、大成功を収めた理論だったのです。
　そのため、当時の物理学者にとって、ほんの数十年前まで光が粒子なのか波動なのかは論争の的で最大の謎だったことは周知の事実です。プランクも光が絡む現象を深く考えたときに粒子的な考え方と波動的な考え方の齟齬に苦しんだと思いますが、マックスウェルの電磁気学の成功を良く理解していたプランクが、今更光の粒子説に後戻りできるはずは無かったのも確かです。プランクが原論文1．や2．で拠り所としたヘルツの理論などは、まさに当時の最新鋭の理論だったわけですから。
　結局、光は粒子でもなく波でもないのですから、プランクのように光と相互作用する振動子のエントロピーとエネルギーを使って考えるしか無かったのでしょう。　

<プランクの原論文>
　Annalen der Physik は　http://de.wikisource.org/wiki/Annalen_der_Physik　に行けば一部を除いてほとんどを無料でダウンロードできます。またそこにないものは、 http://onlinelibrary.wiley.com/journal/10.1002/(ISSN)1521-3889/issues から有料でダウンロードできます。
　ちなみに、Wied. Ann. とはG. H. Wiedemann が編集長だった時代（1877〜1899年）の Annalen der Physik und Chemieです。また、Drudes Ann. とはP. K. L. Drudeが編集長だった時代（1900〜1906年）の Annalen der Physik のことです。
　文献題目後の括弧（§No．〜No.）は著書10．の該当する節No.です。

1. M. Planck,“Absorption und Emission electrischer Wellen durch Resonanz”, Sitzungsber. Berl. Akad. Wiss. vom 21. 3. 1895；
   Wied. Ann., vol.293, 57, p1〜14, 1896年 に再録
   「共振による電波の吸収および放出」（§112〜115）
   　この内容はＨ．ヘルツの偉大な研究「Maxwell理論による電気的振動の力」Wiede. Ann. 36, p1〜22, 1889年（D. E. Jones による英語訳論文はこちらを参照）に基づいている。
2. M. Planck,“Ueber electrische Schwingungen, welche durch Resonanz erregt und durch Strahlung geda¨mpft werden”, Sitzungsber. Berl. Akad. Wiss. vom 20. 2. 1896；
   Wied. Ann., vol.296, 60, p577〜599, 1897年 に再録
   「共振により励起され輻射により減衰させられる電気振動について」（§104〜115）
3. 物理学史研究刊行会編「物理学古典論文叢書１　熱輻射と量子」東海大学出版会（1970年刊）
   10.「非可逆的な輻射現象について」邦訳版の引用（§128〜132、§175〜187、§159）
   M. Planck,“Ueber irreversible Strahlungsvorga¨nge”, Sitzunsber. Berl. Akad. Wiss. vom 18. 5. 1899年；
   Annalen der Physik, vol.306, (4).1, p69〜122, 1900年 に再録
   　これはSitzungsber. Berl. Akad. Wiss. に発表した一連の同じ題目“Ueber irreversible Strahlungsvorga¨nge”の５編の論文1897年(2/4、7/8、12/16)、1898年(7/7)、1899年(5/18)の最後のもので、それらの総まとめの論文です。プランクの考え方をたどる上で最も重要な論文ですが、かなり難解です。
4. 物理学史研究刊行会編「物理学古典論文叢書１　熱輻射と量子」東海大学出版会（1970年刊）
   11.「輻射熱のエントロピーと温度」邦訳版の引用（§101、§188〜190、§162）
   M. Planck,“Entropie und Temperatur Strahlender Wa¨rme”, Annalen der Physik, vol.306, (4).1, p719〜737, 1900年
   文献３．で導入したエントロピー表現式を熱力学的考察からできるだけ一般的に導こうとしたものです。これも重要な論文です。
5. 物理学史研究刊行会編「物理学古典論文叢書１　熱輻射と量子」東海大学出版会（1970年刊）
   12.「Wienのスペクトル式の一つの改良について」邦訳版の引用（§189）
   M. Planck,“U¨ber eine Verbesserung der Wien'schen Spectralgleichung”, Verhandlungen der Deutchen Physicalischen Gesellschaft, 2, p202〜204, 1900年
   　10月19日の講演記録で、エントロピーの表現の内挿式として正しい輻射法則が導びけることを報告したものです。
6. 物理学史研究刊行会編「物理学古典論文叢書１　熱輻射と量子」東海大学出版会（1970年刊）
   13.「正常スペクトルにおけるエネルギー分布の法則の理論」邦訳版の引用（§146〜152、§158）
   M. Planck,“Zur Theorie des Gesetzes der Energieverteilung im Normalspectrum”, Verhandlungen der Deutchen Physicalischen Gesellschaft, 2, p237〜245, 1900年
   　12月14日の講演記録で内挿式の物理的意味を説明しています。ここで初めてエネルギー量子が導入されます。
7. 物理学史研究刊行会編「物理学古典論文叢書１　熱輻射と量子」東海大学出版会（1970年刊）
   14.「正常スペクトル中のエネルギー分布の法則について」邦訳版の引用（§145〜157）
   M. Planck,“Ueber das Gesetz der Energieverteilung im Normalspectrum”, Annalen der Physik, vol.309, (4)4, p553〜563, 1901年
   　最終的に論文の形で発表したものです。共鳴子のエントロピーの表現式をウィーンの変位則と比較することでエネルギー量子ε＝ｈνを導き出した一番有名な論文です。
8. M. Planck, “Ueber die Elementarquanta der Materie und der Elektricita¨t”, Annalen der Physik, vol.309, (4)4, p564〜566, 1901年
   「物質と電気の要素量子について」（§158）
   　原論文6．と７．の物理定数の部分だけを抜き出して、まとめて説明したものです。
9. M. Planck, “Ueber irreversible Strahlungsvorga¨nge (Nachtrag)”, Annalen der Physik, vol.311, (4)6, p818〜831, 1901年
   「非可逆的輻射過程について（補足）」（§187）
   　この論文は、文献３．や４．で証明した全エントロピーが散乱過程の結果として常に増加するという考察を、文献７．や８．で得た正しいエントロピー表現式を用いてやり直したものです。［付録２．参照］

<プランクの著書>

10. マックス・プランク著「熱輻射論（1906年初版本）」（物理科学の古典7）東海大学出版会（1975年刊）
    Vorlesungen u¨ber die Theorie der Wa¨rmestrahlung, Leipzig, Johann Ambrosius Barth,(初版は1906年刊）
    　これは熱輻射論の参考書として一番に挙げられる有名な本です。プランクらしい几帳面で丁寧な説明ですが、かなり込み入っています。原論文と比較しながら（「原論文題目」の後に、この本の対応する節§〜を表示）一歩一歩たどる必要があります。
    　巻末の解説（p210〜216）で訳者の西尾氏がプランクのたどった考察の跡を概説されていますが、参考文献18．19．とほぼ同じ内容です。
    ［2021年10月追記］
    　この訳本は長い間絶版状態でしたが、「熱輻射論講義」(岩波文庫)として最近（2021年6月）再版されています。是非ご覧になることを勧めます。ｱｲﾝｼｭﾀｲﾝの特殊相対性理論（1905年）原論文と並んで、一度は読んで見るべき本だと思います。
11. マックス・プランク著、寺沢寛一、小谷正雄訳　理論物理学汎論第五巻「理論熱学」裳華房(1932年刊)
    Einfu¨hrung in die Theoretische Physik �X “Einfu¨hrung in die Theorie der Warme”（1930年刊）
    　第四篇「原子観　量子論」が関係するところですが、より一般的な議論の中で説明されており明快ですが、文献10．を読んでおかないと、これだけから理解するのはかなり難しいと思います。

<プランクの解説文>

12. マックス・プランク（河井徳治訳）「現代物理学の思想（上）」−講演と回想−　法律文化社（1971年刊）p169〜187
    ノーベル賞講演「量子理論の起源と今日までの発展」（1920年6月2日）
    　これは有名な講演の原稿で熟読する価値があります。
13. マックス・プランク著（浜田貞時訳）「現代物理学の思想（上）」−講演と回想−　法律文化社（1971年刊）p19〜35
    マックス・プランク著「作用量子発見の歴史によせて」（1943年）
    M. Plank, “Zur Geschichte der Auffindung des Wirkungsquantums”, Naturwissenchaften, 31, 153, 1943年
    　これは、後世のために当事者本人が作用量子発見の過程を書き残してくれたもので、晩年に雑誌「自然科学」に寄稿した文章です。これも熟読する価値があります。

<その他の参考文献>

14. 天野清 著 「熱輻射論と量子論の起源」大日本出版（1943年刊）
    　日本人による熱輻射論の解説書として有名な文献です。これは国立国会図書館の近代デジタルライブラリーのURL［ http://kindai.da.ndl.go.jp/info:ndljp/pid/1063572 ］から、その全文をダウンロードして読むことができます。
    　プランクの上記文献5．6．7．もこの中で翻訳紹介されていますのでこれらの文献をお持ちでない方はこのURLを参照されて下さい。（文献3．4．5．6．7．の翻訳版を2023年1月に追加引用しましたので当HPでも見られます。）
    　本文だけならば下記ＵＲＬにｐｄｆファイルがあります。
    http://www.cam.hi-ho.ne.jp/munehiro/science/amanokiyosi/netufukusha-ryosi-kigen.pdf
    　これは多くの文献を読破した上で書かれた労作ですが、原論文とつきあわせながら読まないと、この本文だけから理解するのは難しいです。ただし、本稿を読まれた後に是非再読されて見て下さい。とても味わい深い内容です。
    　
    天野清　著「量子力学史」も下記URLからpdfファイルとしてとしてダウンロードできます。第3〜4章が関連する章です。
    http://www.cam.hi-ho.ne.jp/munehiro/science/amanokiyosi/RyoshirikigakuShi.pdf
15. アーノルド・ゾンマーフェルト著「理論物理学講座�X　熱力学および統計力学」講談社(1969年刊)§20、§33、§35
    　§20で内挿式の導入までが論じられています。この部分は文献18．や19．で紹介されているものと同じですが、この様な単純な説明ではなぜプランクがエントロピーにこだわったのかが解りません。プランクが追求したのは、非可逆的な変化により最終的な平衡状態に達した結果として黒体輻射のエネルギー分布が得られるということであり、その移行過程を明らかにするためのエントロピーだったのですから、その点が解説されないとプランクの理論は理解できません。
    　また、ゾンマーフェルトは§33、35で量子仮説により内挿式を説明しています。ただし、それは一般的な流れの中で論じているのでエネルギー量子導入の必然性はプランクの論文より解りにくい。ここはプランクの論文の方がはるかに解りやすいです。
16. 朝永振一郎著「量子力學�T［第２版］」みすず書房(1969年刊)§7〜§8
    　熱輻射論をきちんと説明した数少ない教科書の内の一つです。これは、プランクが用いたエントロピーとウィーンの変位則ではなくて（その後の量子論の発展を視野に入れて）“断熱不変量の定理”を用いて熱輻射論が展開されており、とても興味深い内容です。
    　ただし、このやり方では量子の導入はスムーズですが絶対温度との関係が今ひとつ解りにくい。絶対温度との関係はプランクのやり方のほうが遙かに明快です。
17. リチャード・ファインマン「ファインマン物理学�U　光、熱、波動」岩波書店（1968年刊）
    　この本の§16-2、16-3 に、プランクのやり方に関係した興味深い説明があります。ファインマンらしい、明快な文章です。
    　§16-3で説明されているものは、振動子へのエネルギー分配に関して分配関数についてのボルツマンの原理を用いるものです。ただし、このやり方では絶対温度との関係が間接的になり明瞭ではありません。ここでファインマンが紹介しているやり方は、デバイが報告（P.Debye, Annalen der Physik, 33, p1427〜, 1910年）したものですが、もともとEinsteinが1906年に展開した光量子論第2論文の中で【光量子仮説】と【カノニカル分布の手法】を用いて展開したものです。この論文は、彼の光量子論第1論文に続くもので、熱輻射公式の求め方として、超有名な論文です。このことに付いては江沢氏の文献「統計力学へのアインシュタインの寄与」のp124-125で説明されています。
    　それ以外の輻射法則の求め方として有名なものにアインシュタインの論文（A.Einstein, Physikalische Zeitschrift, 10, p185〜193, 1909年； Verhandlung der Deutsche Pysikailsche Gesellschaft, 18, p318〜, 1906年；Physikalische Zeitschrift, 18, p121〜, 1917年、これらは「物理学古典論文叢書２」に翻訳あり）や、ボーズの論文（S.N.Bose, Zeits. f. Phys., 26, p178〜, 1924年、これはネットからDownlordできるBoseの論文集にあり）などが在ります。
18. Edmund Whittaker著「A history of the theories of aether & electricity (Two Volumes Bound As One)」Dover
    (Volume �T:The Classical Theories､ Volume �U:The Modern Theories 1900-1926)
    　この�U巻のp78〜85にプランクのたどった手順が要領よく紹介されています。しかし、原論文に当たらないとこの文章だけから理解するのは困難です。
    　これとほぼ同じ内容が太田浩一著「電磁気学の基礎�U」シュブリンカー・ジャパン（2007年刊）のp529〜535で紹介されています。
19. 広重徹著「物理学史�U」倍風館（1979年刊）§15-2（p153〜157）
    　この解説もプランクが実際にたどった軌跡に沿っています。内容は文献18．と同じレベルで、やはりこの文章だけから理解するのは難しいです。
20. 高林武彦著「量子論の発展史」筑摩学芸文庫
    　これは1977年に中央公論社から発刊されていた名著の復刻版です。この文庫版のｐ21〜27が該当する部分です。本稿を御覧の後にその部分を読まれるとなるほどと納得できるのですが、その記述だけから理解するのは難しいです。ただし、高林先生の説明はとても味わい深いものですから是非御覧になられて下さい。
21. 江沢洋著「現代物理学」朝倉書店
    　これは、解りやすく丁寧に説明してあり、高校の物理教師に取って、ありがたい本です。この中の§8.1〜§8.3が該当するところです。特に、レーリーの理論と、プランクが採用したエントロピーの統計的計算法について解りやすい丁寧な説明がありますので御覧下さい。しかし、この稿で説明したプランクのたどった論理については、やはり省略されています。
22. フリードリッヒ・フント著「量子論の歴史」講談社（1978年刊）第２章
    　量子力学の大家による歴史書です。含蓄深い考察が色々見られますが、これから理解するのは困難です。本稿を読まれた後に御覧下さい。

<参考文献の追加>

23. 小長谷大介著「熱輻射実験と量子概念の誕生」北海道大学出版会（2012年刊）
    　これはこのページを作った後（2012.8.10）に手に入れて読んだのですが、熱輻射の実験手法と装置についてとても詳しい説明があります。実験・観測の方法はとても知りたい所だったので、ありがたい本です。
    　また、第６章でプランク理論の特徴について興味深い考察がなされていますので御覧ください。
24. Ａbraham Pais著（西尾成子、今野宏之、山口雄仁共訳）「ニールス・ボーアの時代１」みすず書房（2007年刊）
    原本は1990年刊。この第5章“自然は飛躍する（量子物理学のルーツ）”に熱輻射理論がその歴史的背景も含めて簡潔・明快に説明されています。

　プランクの“熱輻射公式”と“作用量子ｈ”は、量子力学を学ぶとき最重要なトピックスですが、彼の用いた方法を真面目にキチンと説明している教科書はほとんどありません。どの本を読んでもこの部分の説明は省略されていて、“とても知りたいところなのになぜ説明されていないのだ？”と、いつもフラストレーションが溜まる所でした。このページを作って、やっとその胸のつかえが下りた感じです。
　作って見て改めて感じるのですが、プランクが展開した論理は本当に込み入ってますね。よくもまあ、このような複雑な考察を地道に積み上げたものだと思います。
［熱輻射論関連ページを作っての独り言］