電磁場の非同次波動方程式

　ヘヴィサイド（O.Heaviside）1885年とヘルツ（H.Hertz）1890年が集大成したMaxwell方程式系から、電場及び磁場が満たす非同次波動方程式を導きます。そして、電磁ポテンシャルＡ、φの非同次波動方程式について説明します。

　単位系として非有利化Gauss単位系を用います。電磁気学の単位系については別稿「電磁気学の単位系が難しい理由」５．（４）をご覧下さい。制御
　また、相対論的な４元ベクトルや、計量テンソルの表現としては別稿３．で説明した右側の定義を用います。

１．電磁場のMaxwell方程式系

（１）非有理化単位系

　非有理化単位系で表した法則

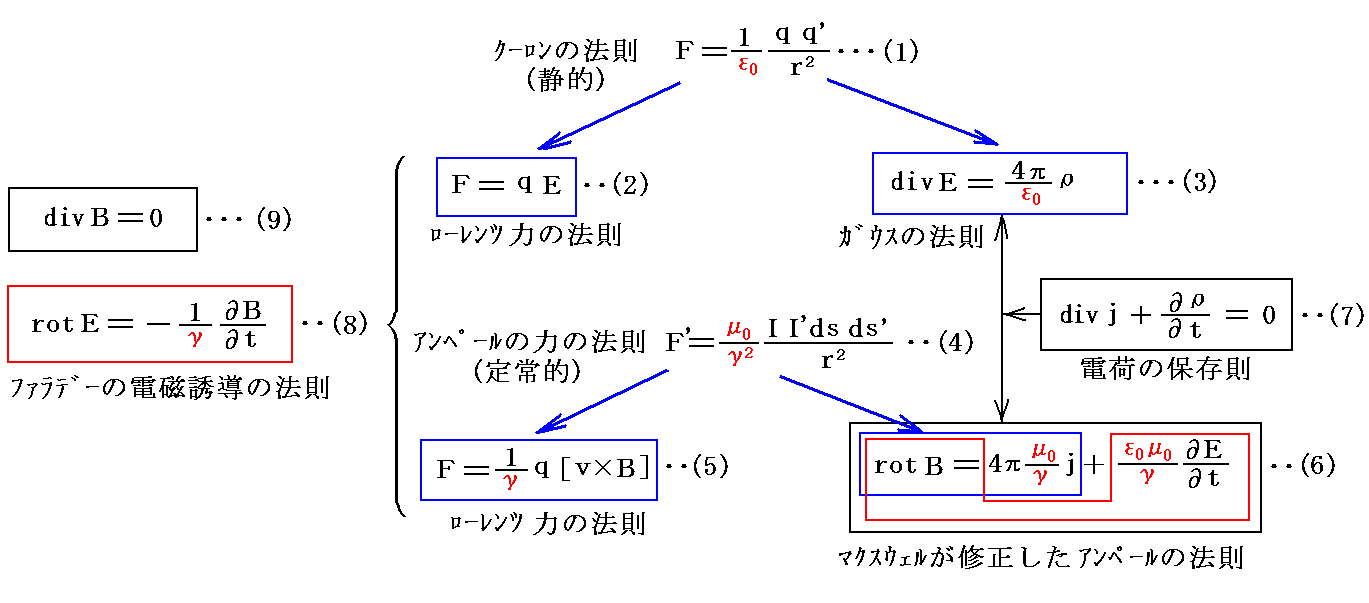
　ｑ、ｊ、Ｅ、Ｂ、ε₀、μ₀、γは、（２）（３）（５）（６）（７）（８）等の式で互いに関係づけられているから、当然何らかの制約があるはずです。式をやりくりしてみたら１．（３）で述べたように

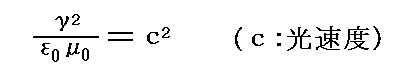
と言う関係を満たさなければならなかった。そして実験で測定してしてみると４．（１）で述べたように定数ｃは光速度だったと言うわけです。
　このとき、３個の比例定数ε₀、μ₀、γに対して条件式は１個だけだから２個は任意に取れる。そのためその２個を一番簡単な置き方にしよう。そして、どの２個を選ぶかで３通りの単位系が考えられる。
　（１）静電単位系：ε₀＝１、γ＝１、μ₀≒１／ｃ²
　（２）電磁単位系：μ₀＝１、γ＝１、ε₀≒１／ｃ²
　（３）ガウス単位系：ε₀＝１、μ₀＝１、γ≒ｃ
　もともと、静電気の研究から始まったので（１）の単位系がつくられた。しかし、電流の磁気作用が発見されてからは最も重要な応用は動電気的なものとなったので、（２）の単位系が重要になった。しかし、理論的な考察には次元の対称性から（３）も捨てがたい。
　このように三種類の単位系が並立する事になったのは、電磁気学を展開するには４個の物理量［電荷ｑ］［電流Ｉ］［電場Ｅ］［磁場Ｂ］の導入がどうしても必要だったからです。そのとき、これらの導入には最低３個の比例定数(４個でなく３個で良いのは１．（３）２．で注意したように、そこのｋ₁に１以外を与えても何の意味もないからです)が必要なのに、条件式は１個だけだからです。つまりこれらの単位系が並立する事の中に電磁気学の本質がある。

（２）有理化単位系

　今日、広範に使われている
　（４）MKSA有理化単位系：γ＝１、μ₀＝4π×10^-7［N/A²_orＨ／ｍ］、ε₀≒10⁷／（4πｃ²）［Ｆ／ｍ］
については、別稿５．（４）２．を参照されたし。

　補足しますと、オランダの H．A．Lorentz や英国の Oliver Heaviside は 有理化されたガウス単位系 を用いています。

２．電場Ｅ、磁場Ｈの波動方程式

　以下ではε₀＝１、μ₀＝１、γ≒ｃ の非有理化Gauss単位系の方程式系で論じます。そのとき、この単位系ではＢ＝Ｈですので、Ｂの代わりにＨを用います。

（１）電磁場の方程式系

１．ヘヴィサイド・ヘルツのMaxwell方程式系

　１．（１）で示したMaxwell方程式系を説明する。
　まず、最初の２つは

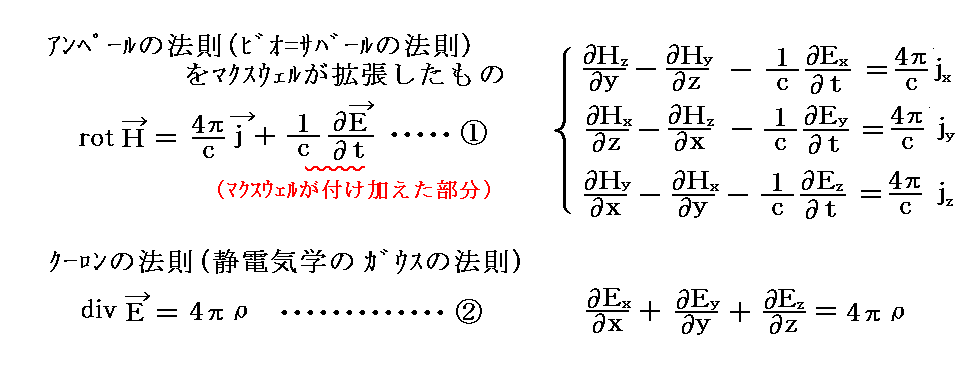
です。この２つは電荷や電流という物質が担う量と電磁場との関係を示している。これを今後�@式、�A式とする。
　次の２つは

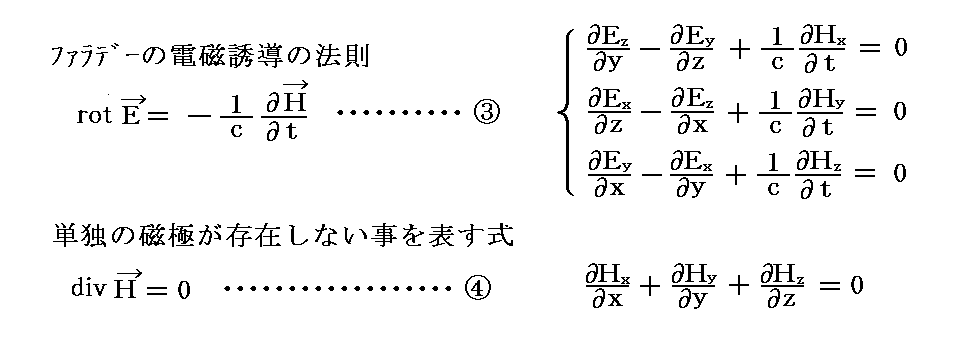
です。この２つは電場と磁場という二種類の場の間に存在する関係、あるいは電場、磁場そのものが持つ性質を表している。これを今後�B式、�C式とする。特に�C式は磁場は連続している（つまり磁力線は連続している）ことを表している。これは�A式が電気力線は必ず電荷から出発し、電荷に終わることを示しているのに対して、�C式は磁力線についてはその様な事は無く、磁力線は常に連続しており、磁力線の終端である磁荷（つまり電気力線が出入りする電荷の様なもの）が存在しないことを示している。

　以上の４式がヘヴィサイドとヘルツが整理統合したいわゆるMaxwell方程式といわれるものです。以後の議論はこの�@〜�C式から出発する

２．電荷保存則（連続の式）

　１．（１）で説明した電磁場の方程式系の中にはいわゆるMaxwell方程式�@〜�Cとは別に“電荷保存則”を表す（７）式

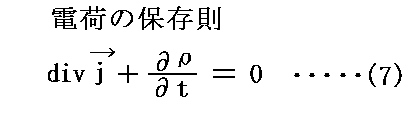
がありました。この（７）式は別稿「マクスウェルによるアンペールの法則の拡張」（２）で説明したように


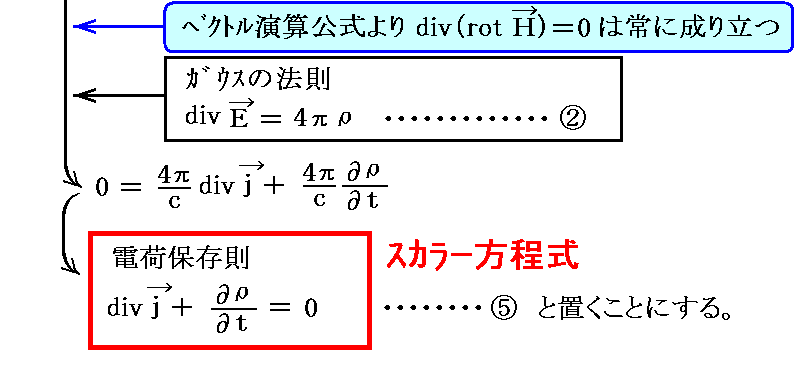
となります。このことは別稿「アインシュタインの特殊相対性理論（1905年）」３．（４）［補足説明４］でも説明しています。
　そのため、電荷保存則（連続の式）（７）はMaxwell方程式�@、�A式と極めて密接な関係にあります。つまり、“電荷保存則（連続の式）”（7）式 は ［Maxwell方程式�@、�A式］ と等価です。
　今後の使用に便利な様に、この“電荷保存則”（７）式を改めて�D式と置くことにします。

［補足説明１］
　このとき、先ほどの�@、�A式は、別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明３］で示した様に、［相対論的４元ベクトル方程式］と見なせます。この両辺の４元ｄｉｖを取ったとき、２階反変交代（反対称）テンソルの４元ｄｉｖは恒等的に0となるベクトル演算公式により、右辺も0となって“電荷保存則”は直ちに導けます。
　
　実際の計算は別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明４］で示した様に






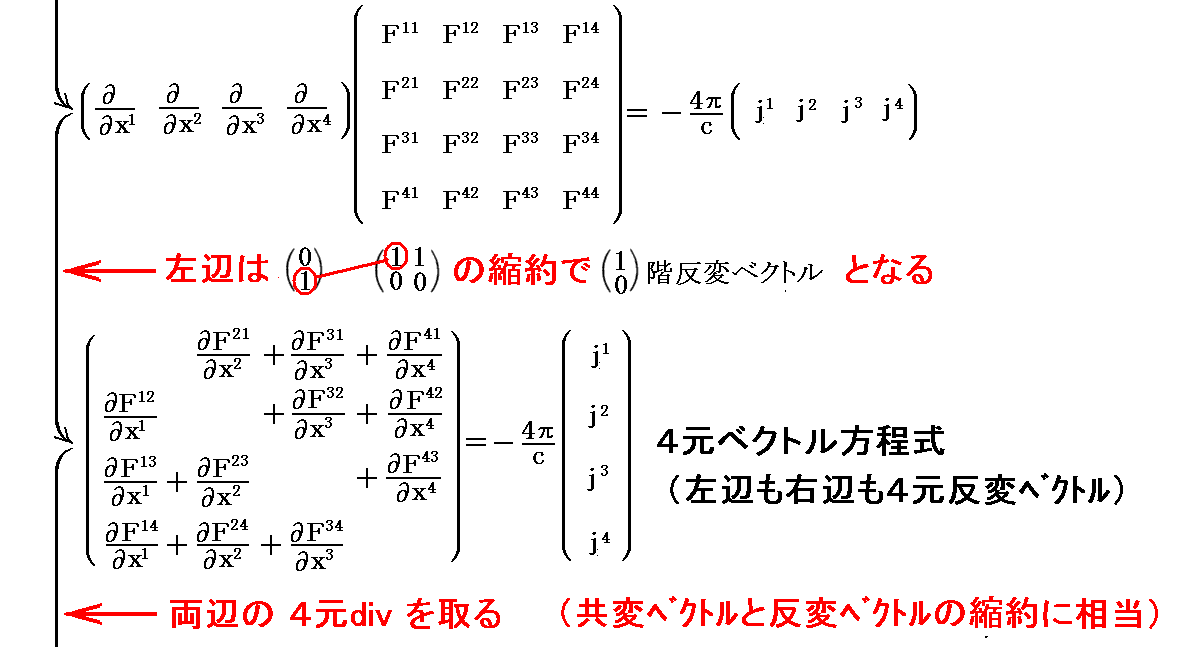
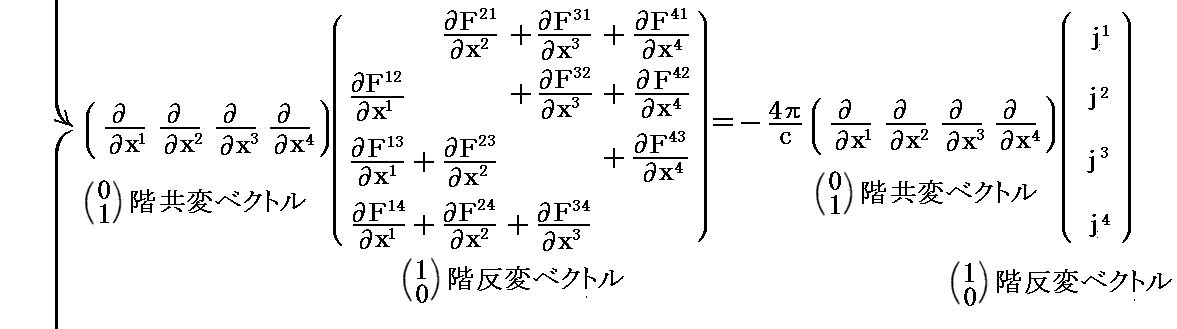
となる。
　要するに、本文中で示した、“電荷保存則（連続の式）”�D式 は ［Maxwell方程式�@、�A式］ と等価である事の証明を、相対論的な４元divで一気に行えばこうなるということです。
　さらに補足しますと、上記の式変形について３．（３）３．［補足説明２］もご覧下さい。

３．ローレンツの力の法則

　１．（１）で説明した電磁場の方程式系の中には “いわゆるMaxwell方程式系” とは別に“ローレンツの力の法則”（２）、（５）式がありました。

この2つをまとめて、今後�E式と置くことにする。
　“いわゆるMaxwell方程式”�@〜�C式 は電場、磁場間の関係と電場、磁場と物質（電荷密度、電流密度）の間の関係を与えるものですが、この中には物質（電荷密度、電流密度）に働く力と電場、磁場との関係式が抜けています。ここで取り上げる“ローレンツの力の法則”は、その抜けている関係式を与えるものです。
　我々は電磁場の存在を直接観測することはできません。我々は荷電粒子の受ける力（加速度）を通してしか電磁場を認知できないのです。従って電磁場を観測可能な物理現象に関係付けるこの“ローレンツの力の法則”は必須の法則です。

［補足説明１］
　そのとき、前項の［補足説明１］で説明した様に “電荷保存則” と “Maxwell方程式�@、�A式” は密接に関係しましたが、“ローレンツの力の法則” も “Maxwell方程式�@、�A式” と密接に関係します。
　実際、別稿「Maxwell方程式系の先見性と電磁ポテンシャル」４．（２）で説明した様にローレンツの力の法則の力を４元力表示に拡張すると、４元力の３次元表示は別項「４元速度、４元加速度と４元力」５．（３）で説明したように

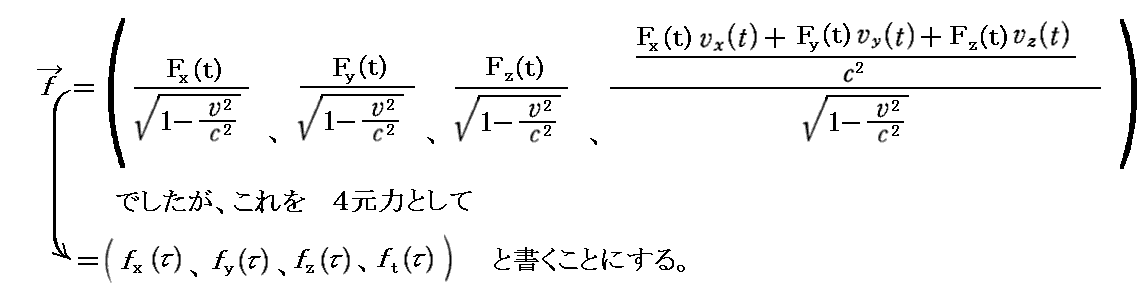
　ここで、Ｓ’系はＳ系のｘ軸に沿って速度Ｖでｘ軸の正方向へ移動しているとしてます。またその移動速度を電荷の移動速度ｖと混同しないように大文字の“Ｖ”で現しています。上記成分表示式の分母の平方根記号内のｖは座標系の移動速度ではなくて“電荷の移動速度”です。それは座標時を固有時に置き換える関係で出てきた速度なのですから。もちろん電荷の移動速度ｖは座標系の移動速度Ｖとは何の関係もありません。
　この第４成分 ｆ _t の表現を “ローレンツの力の法則” により電磁場（ＥとＨ）と４元速度ｕ による表現に置き換えると


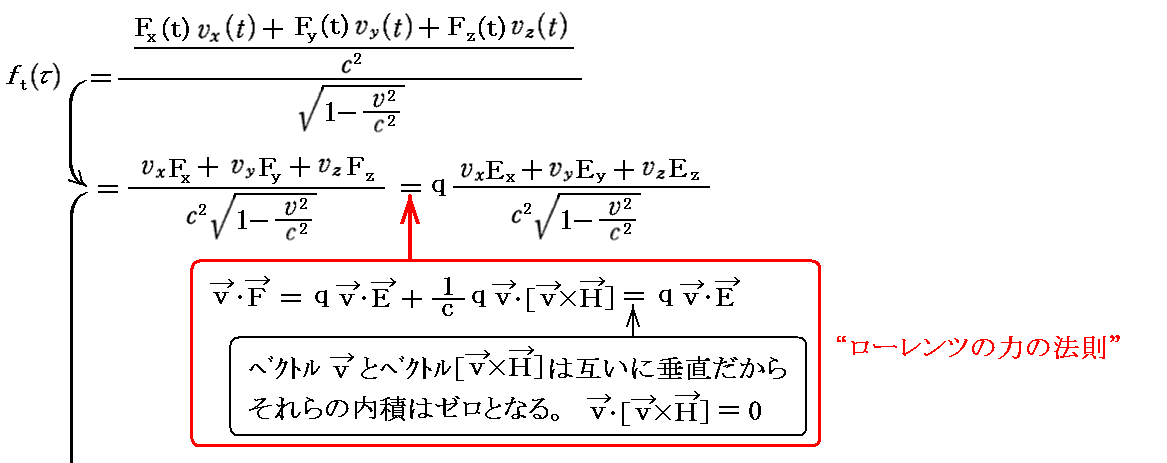
と成ります。このとき用いた４元速度の ３次元表示 と ４元表示 の関係は別稿「４元速度、４元加速度と４元力」２．（３）を復習されたし。このように、電磁場中で電荷に対して成される仕事が電場によるものしか現れないのは、磁場による力が電荷の移動方向に対してつねに垂直にしか働かないからです。
　同様にして４元力のすべての成分を書き記すと





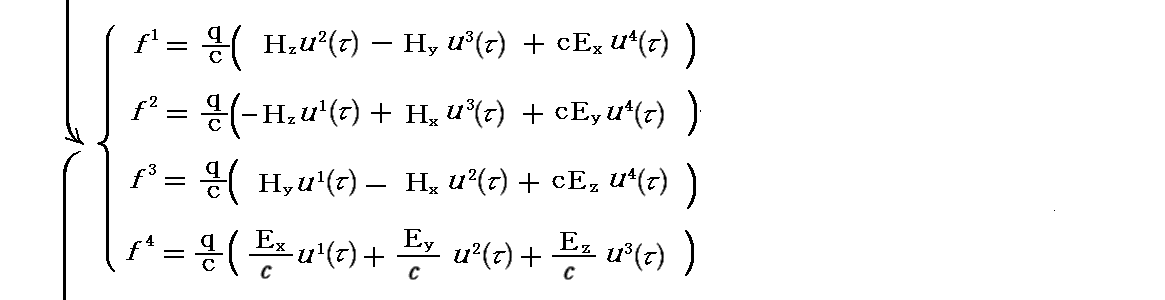
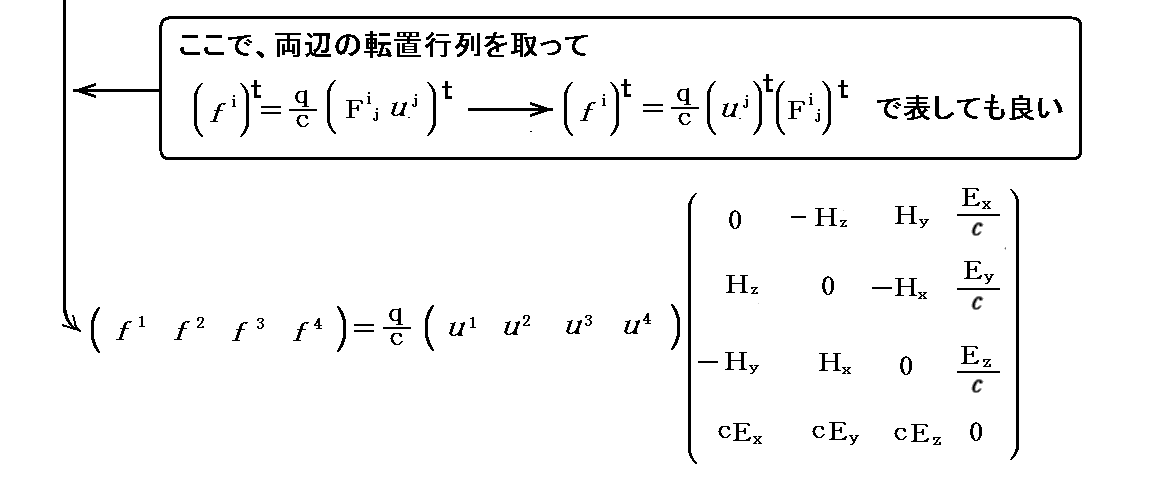
いずれにしても相対論的な“ローレンツの力の法則”は

となります。上記の式は “４元速度” と “４元力” を用いた相対論的な表現にしてある。上記の“４元電磁場テンソル”Ｆ^ｉ_ｊが２階混合テンソル

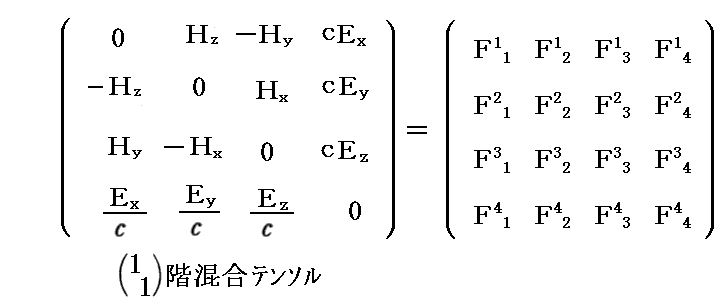
であることは別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明２］でご確認ください。
　
【 ２階反変テンソル表現 】
　補足しますと、先ほど４元速度として反変ベクトル表示を用いましたが、以下の様に共変ベクトル表示を用いることもできます。そのようにすると、電磁場テンソルは必然的に２階反変テンソルの形になります。



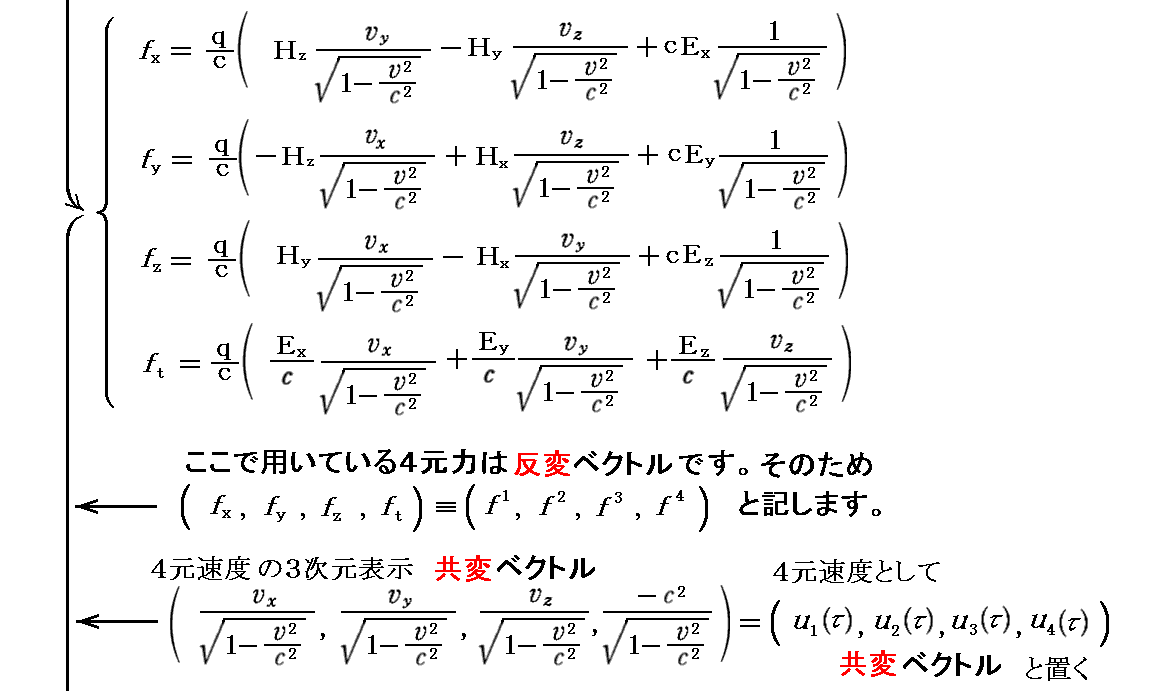
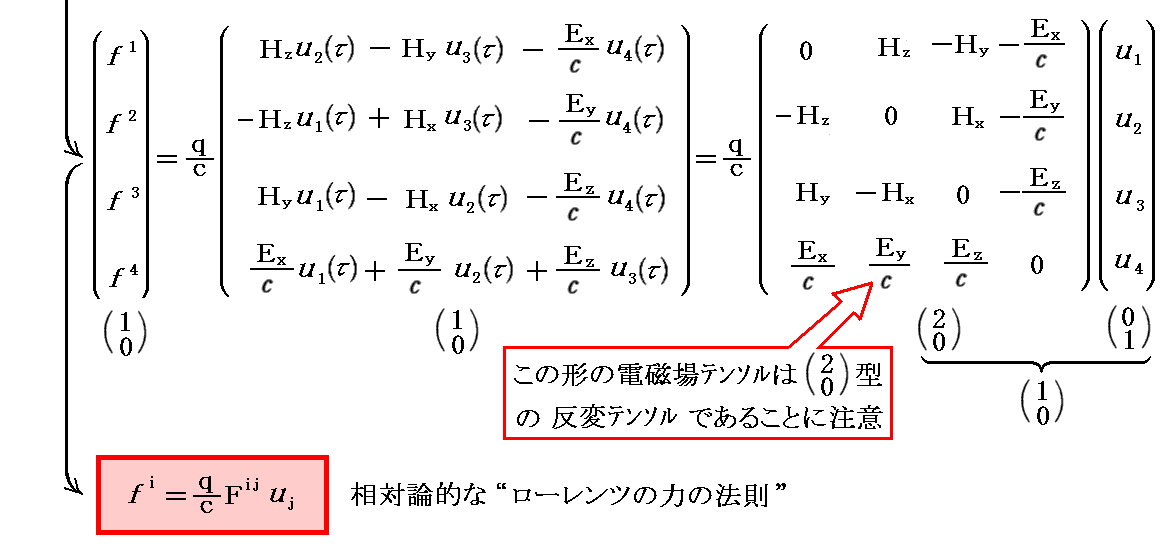
実際、上記の“４元電磁場テンソル”Ｆ^ｉｊが２階反変テンソル

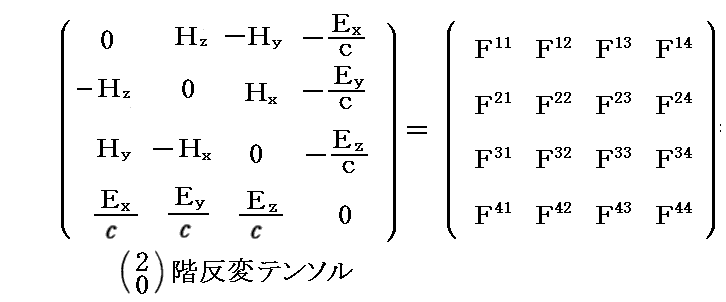
であることは別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明２］でご確認ください。
　
【 ２階共変テンソル表現 】
　さらに補足しますと、最初のローレンツの力の法則の両辺を共変ベクトル表示にすると




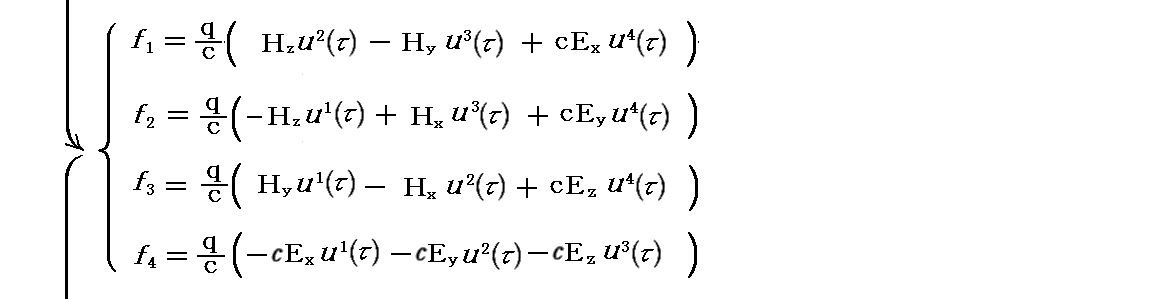
となります。つまり、右辺の４元速度ベクトルを反変表示のままにすると、電磁場テンソルは必然的に２階共変テンソルの形になります。実際、上記の電磁場テンソルが２階共変テンソル

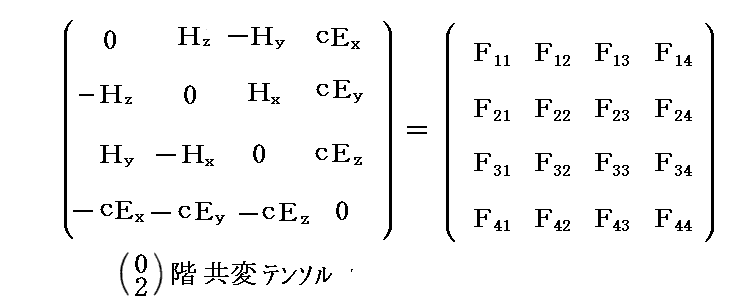
であることは別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明２］でご確認ください。
　上記式変形の途中で、４元速度ベクトルの３次元表示として共変ベクトル表示を用いると、以後の変形は以下の様になります。


つまり、右辺の速度ベクトルを共変表示にすると、電磁場テンソルは必然的に（_１^１）型２階混合テンソルの形になります。実際、上記の電磁場テンソルが（_１^１）型２階混合テンソル

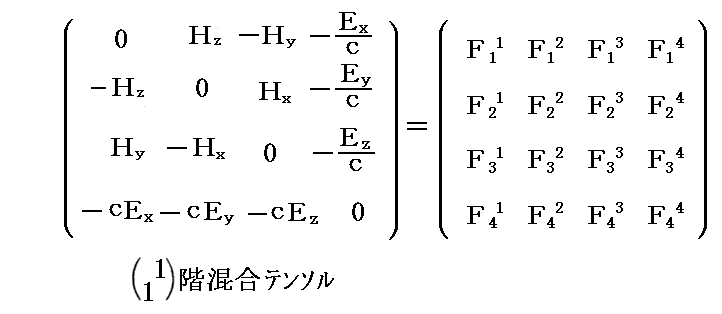
であることは別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明２］でご確認ください。
　補足しますと、ここでは“４元速度”と“電磁場テンソル”で表現しましたが、４元速度の代わりに“４元電流密度”で表す事もできます。
　
　結局、４元力と４元速度を共変ベクトル表現、反変ベクトル表現のいずれを用いるかに応じて電磁場テンソルを２階混合テンソル、２階反変テンソル、２階共変テンソルのいずれかに調整できます。これらの形については別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）［補足説明２］でご確認ください。
　ここに出てきた“反変・共変”の概念と、その間を取り持つ“計量テンソル”（［補足説明２］参照）の概念が理解できていない方は別稿「基底ベクトル・双対基底ベクトルと反変成分・共変成分（計量テンソル・クリストッフェル記号・共変微分とは何か）」 をご覧下さい。
　
　ここで、出てきた電磁場２階テンソルはいずれも、２．（１）２．［補足説明１］で説明する（2，0）型２階反変テンソルと、物理的には同じものです。そしてこのテンソルは、そこで説明した様にMaxwell方程式�@、�A式の左辺

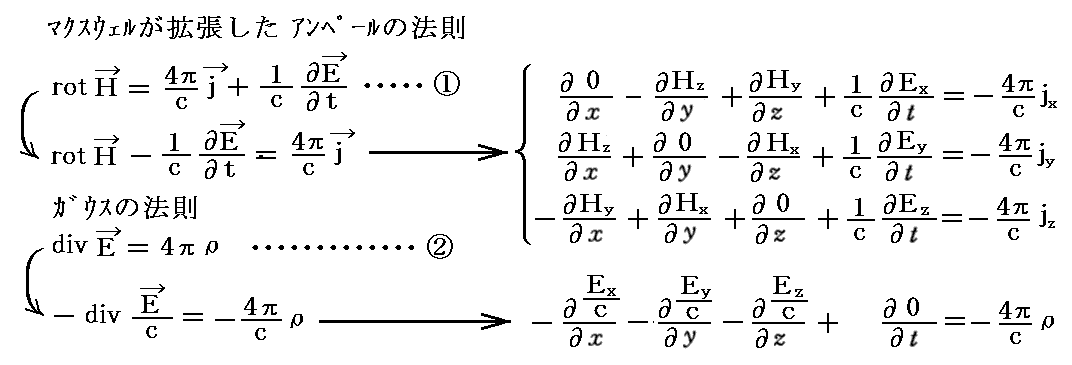
から出てくるものです。
　故に “ローレンツの力の法則”�E式 は ［Maxwell方程式�@、�A］ と、密接に関係することによって、最初に述べた“電磁場を現実の物理（力学）現象に関係付ける”ことを実現しています。

　以上は電磁場テンソルを用いた表現でしたが、第３章との関連を見越して、電磁ポテンシャルを利用した表現に変換しておきます。その事を、できるだけ多くの表示形式について説明します。
　以下の議論から解る様に、“電磁場テンソル”は“４元電磁ポテンシャルベクトル”の“４元回転演算”で得られる２階テンソルです。（“４元回転演算”については３．（１）３．［補足説明２］をご覧下さい。）
　そのとき、その特質から明らかな様に、反変テンソルや共変テンソルを構成する場合には演算としての意味を持つのですが、混合テンソルを構成する演算としては意味を持たないのでしょう。

［補足説明２］
　本稿ではGauss単位系（非有理化-磁場H）を採用し、相対論的な４元ベクトルや、計量テンソルの表現として別稿３．で説明した右側の定義を用いていることを忘れないで下さい。
　
　まず1906年3月のM．Planck論文から始めます。その論文でPlanckは相対論的に正しい運動方程式

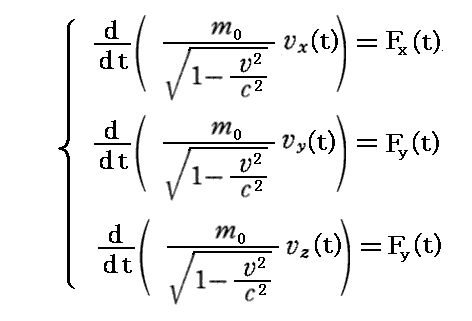
を導きます。これは３次元表示での相対論的方程式ですが、完璧に正しい式です。しかし、相対性理論ではすべての量、すべての方程式は４元化されるべきです。
　運動方程式もそうあるべきで、その４元化は以下の手順でなされる事を別稿「４元速度（４元運動量、４元電流密度）、４元加速度と４元力」５．（４）で説明しました。

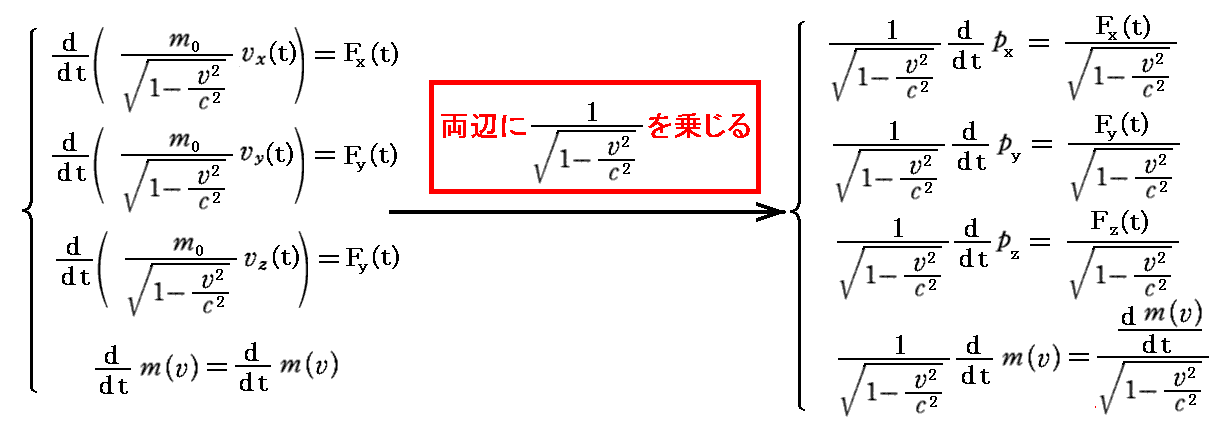
　このとき、第４成分も付け加えて４元化するためには、両辺に

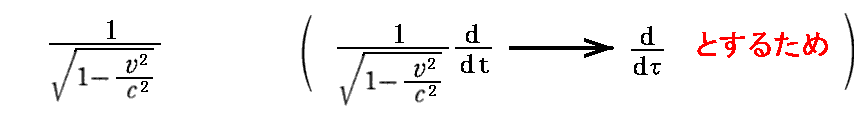
を乗じなければいけません。なぜそうしなければならないのかは前記別稿５．（４）を復習されてください。このとき上記の→右側の表現は、下記の４元ベクトル方程式表現と等価です。

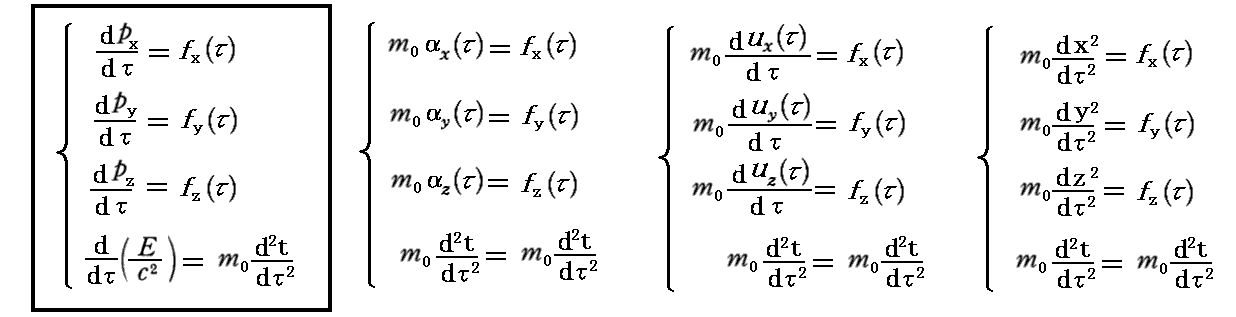
このときｍ₀は固有質量、τは固有時です。またｐ、α、ｕはそれぞれ４元運動量、４元加速度、４元速度を表します。
　ここでは別稿「電磁場中の荷電粒子の運動」との比較を考慮して上記一覧の左端の表現を用います。Gauss単位系（非有理化-磁場Ｈ）に書き換え、力の具体的形として“ローレンツの力の法則”を利用すると“４元運動方程式”は以下の様になります。ただし、そのとき

と置き換えています。
　つまり、最初は速度ベクトルとして反変ベクトル表示を用います。そうすると電磁場テンソルは必然的に（1，１）型混合テンソルとなります。そのため以後の展開は下記の様になります。




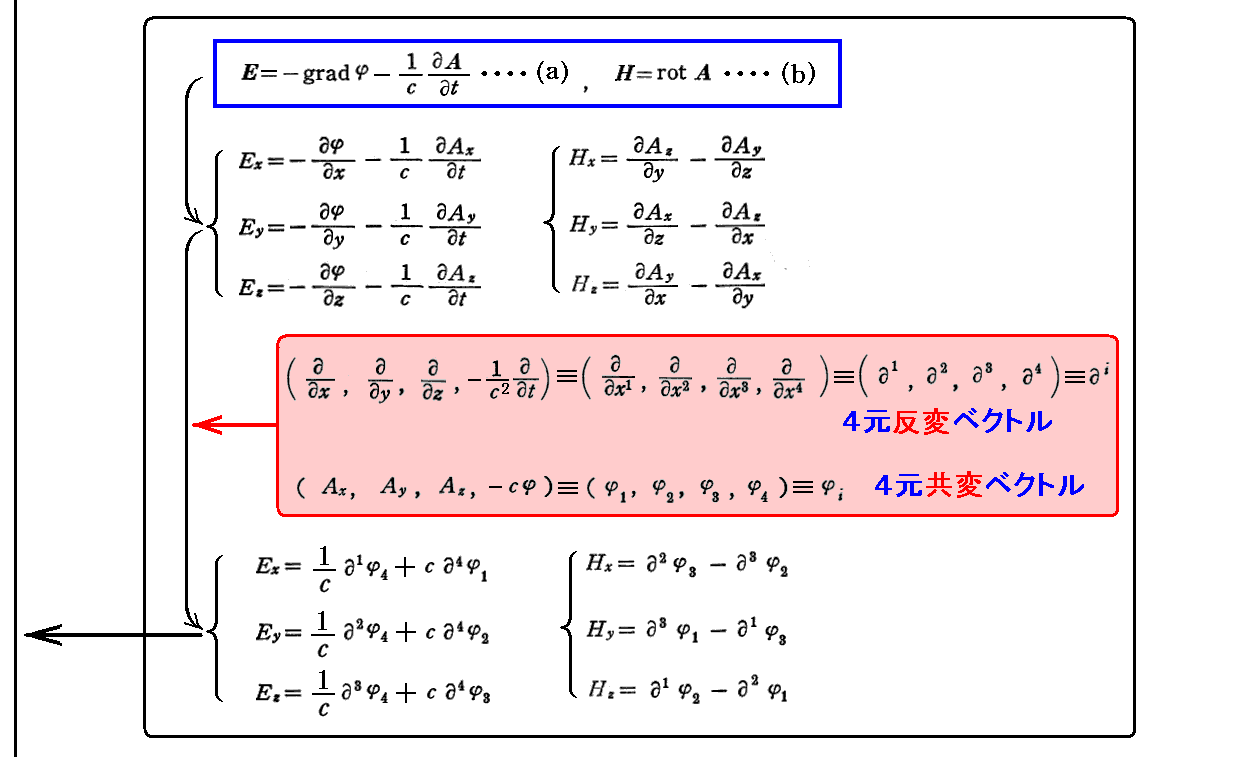
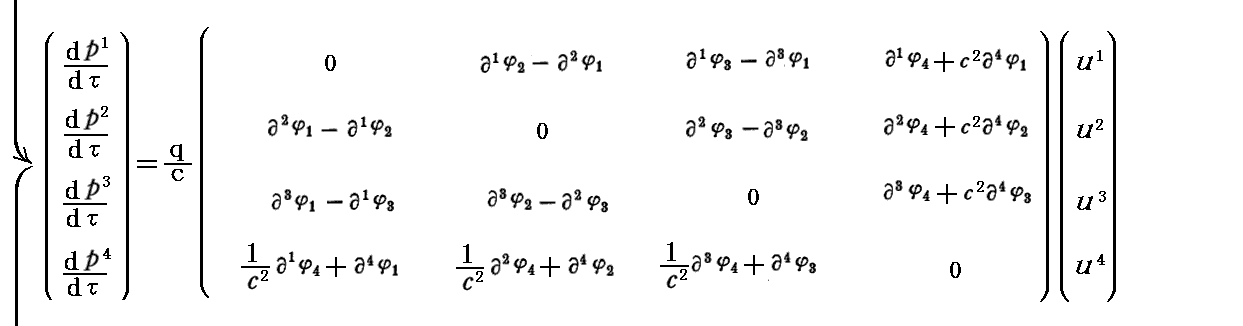
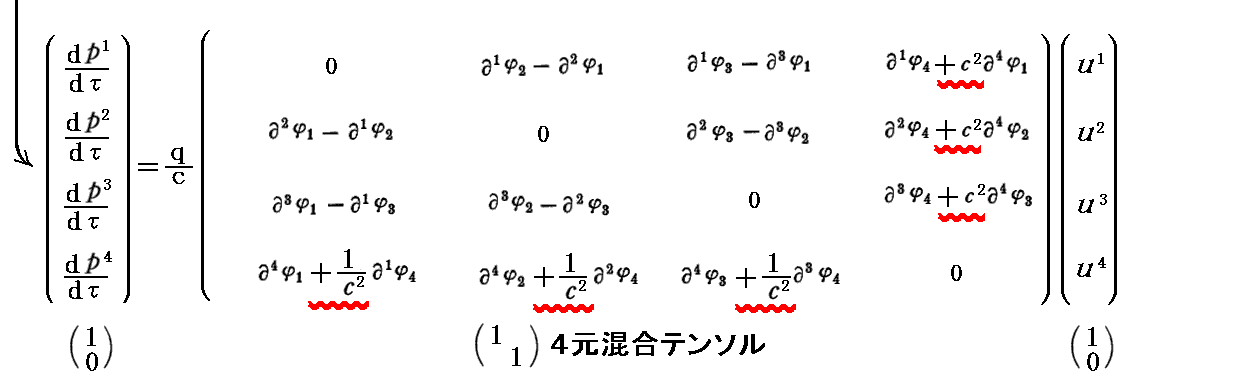
　上記で電磁場テンソルを３．（１）で導入する電磁ポテンシャルで置き換えていますが、このとき(1，1）型混合テンソルの行列表現の第4列目の表示と、第4行目の表示が、赤波線で示している様に他の（行・列）要素と揃った形にならないことに注意してください。そのため、混合テンソル形式の表示では、反対称テンソルには成りません。つまり、４元回転演算という操作が(1，1）型混合テンソルを作り出すときには、意味を持たない。
　補足しますと、“ミンコフスキー時空”の“計量テンソル”を用いて変形すると様々な表示形式の方程式に変更できます。




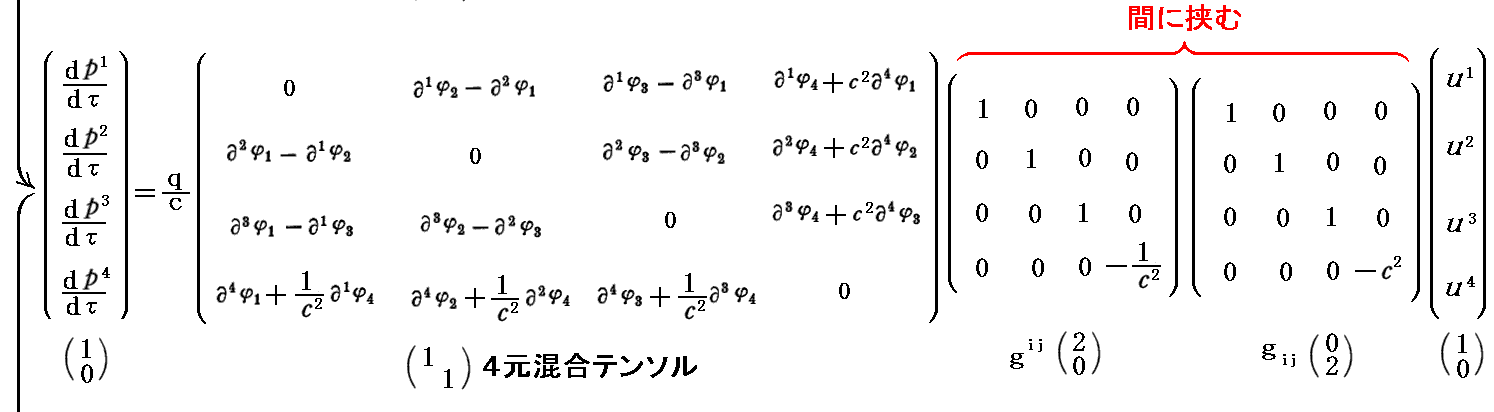
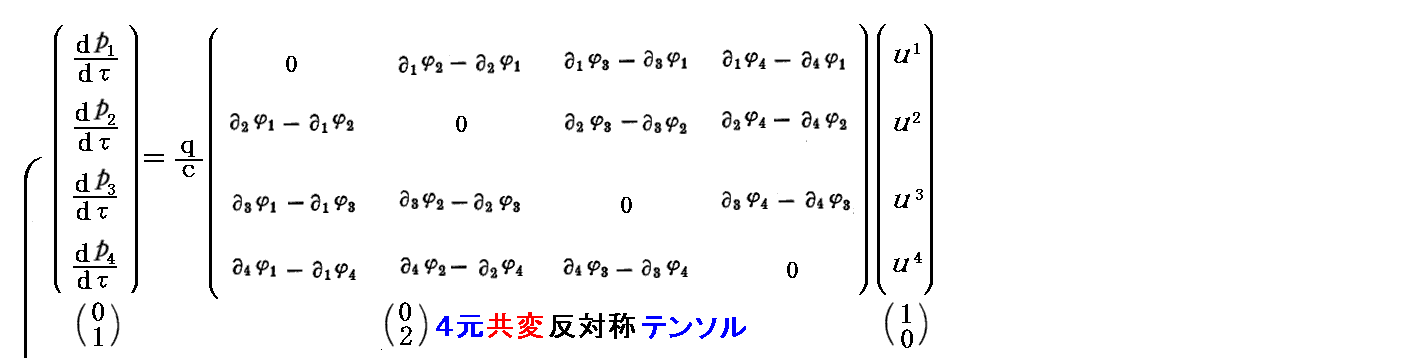
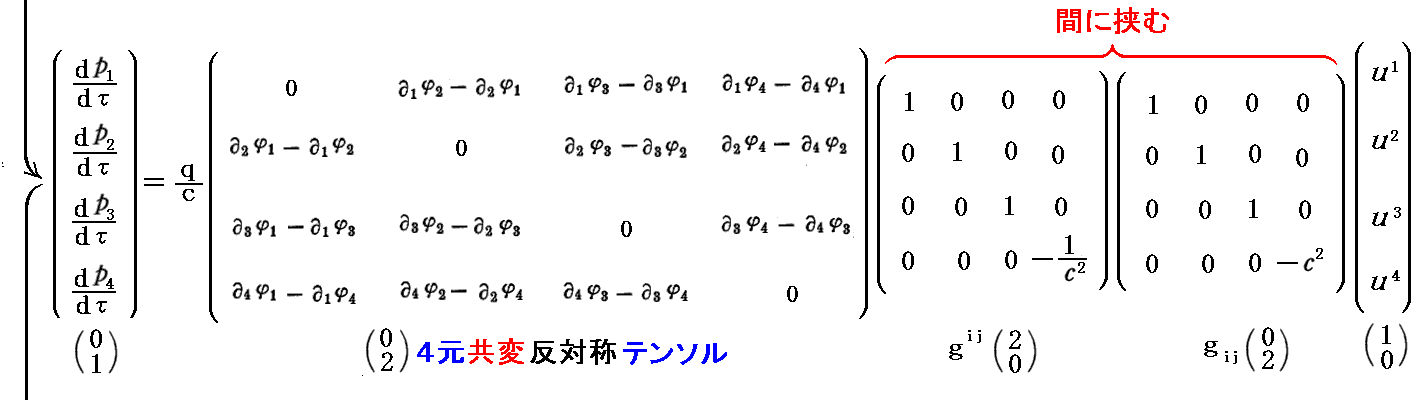
　ここで注意して欲しい事ですが、上で求めた４元反変テンソルや次で求める４元共変テンソルの第４列、第４行は他の行・列要素の表現と同じ形になっており、反対称テンソルである事が実現されています。そのため、４元回転演算という操作が意味を持ちます。




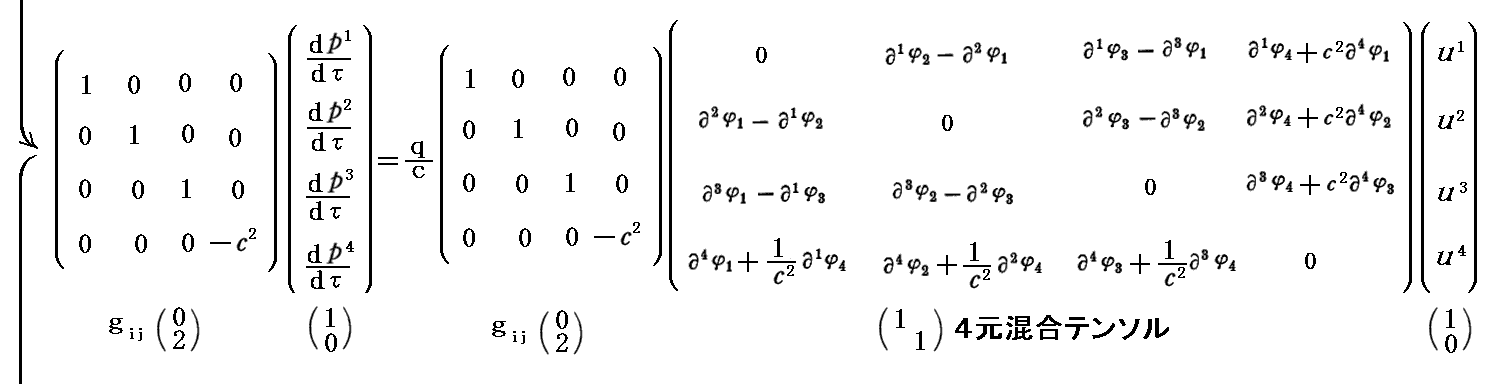
　上記の４元共変反対称テンソルは、次に述べる様に４元反変反対称テンソルの左右から共変計量テンソルを作用させても導く事ができます。




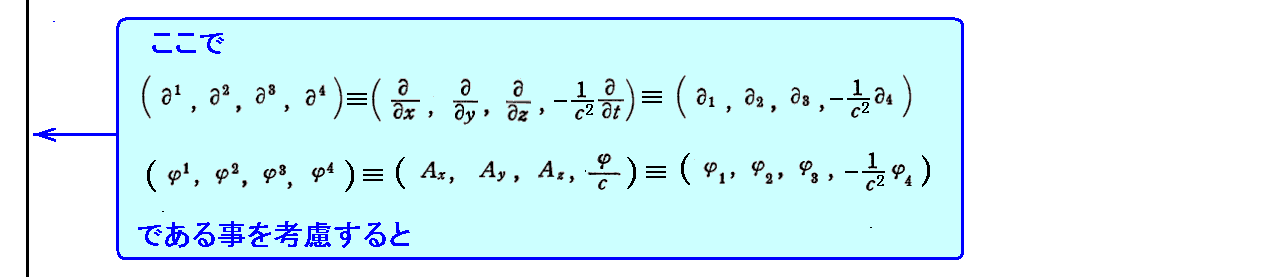
　このとき、（2，0）型や（0，2）型の電磁場テンソルの行列表現の第4列目の表示と、第4行目の表示に於いて、先ほど注意した不揃いがなくなることに注意されたし。そしていずれも反対称テンソルになります。
　
　
【 ２階反変テンソル表現 】
　上記以外に、左辺は反変ベクトル表示のままで、右辺の速度ベクトルを共変ベクトル表示にすると、先に説明したように電磁波テンソルは（2，0）型２階反変テンソル表現になります。




　
　
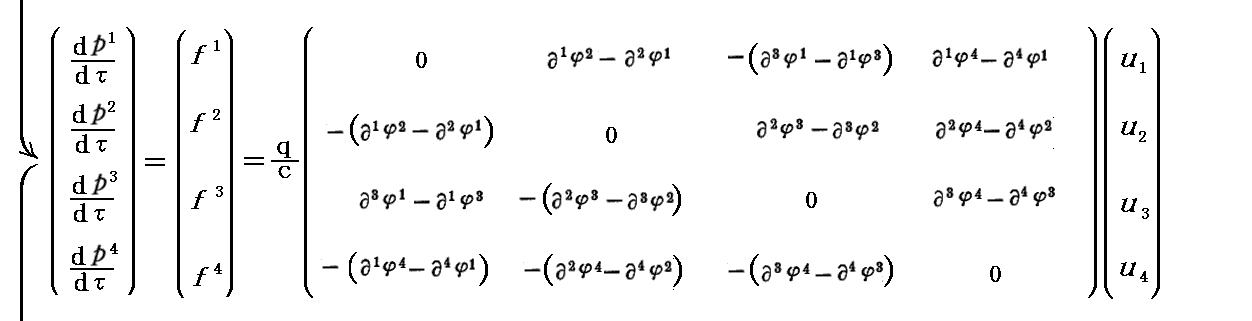
【 ２階共変テンソル表現 】
　最初の式の第４成分の両辺に−ｃ^２を乗じて、両辺を共変ベクトル表示にする。つまり

とする。こうすると先に説明したように右辺は（0，2）階共変テンソル型の電磁場テンソルと反変ベトクル表示の４元速度の積（縮約）になります。この場合を以下で説明します。




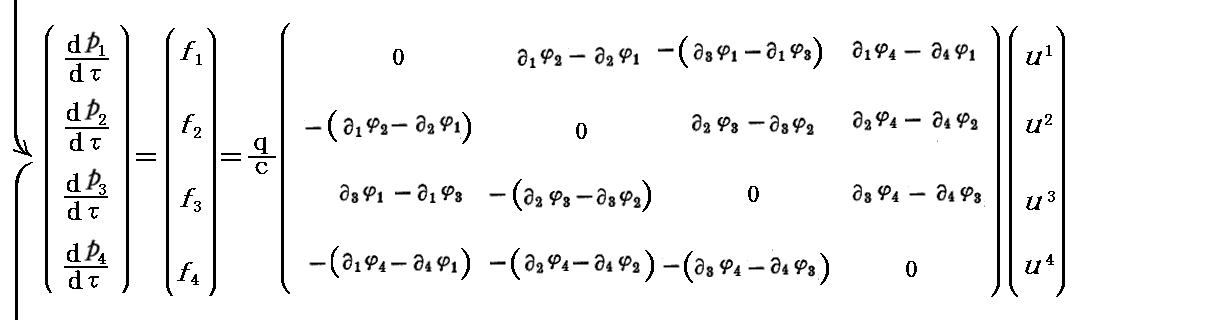
　上記の表現から出発して、ミンコフスキー時空の共変計量テンソルを作用させて変形すると様々な表示形式の方程式に変更できます。繰り返しになりますが、以前の議論と整合性が成り立っている事を確認しておきます。




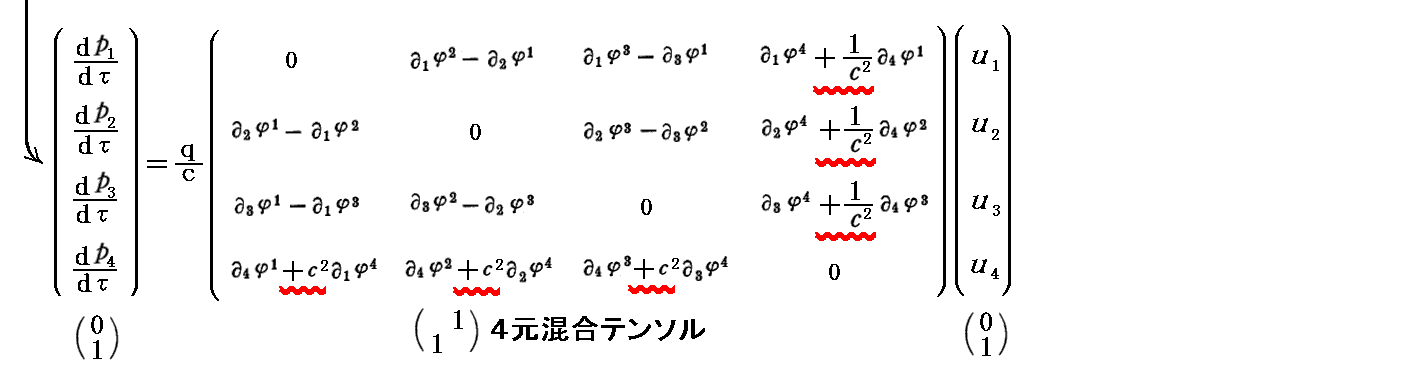
　この（_１^１）型４元混合テンソルの場合にも、先に述べた（^１_１）型４元混合テンソルの場合と同様な事情が、第４列と第４行の表示に現れていることに注意して下さい。




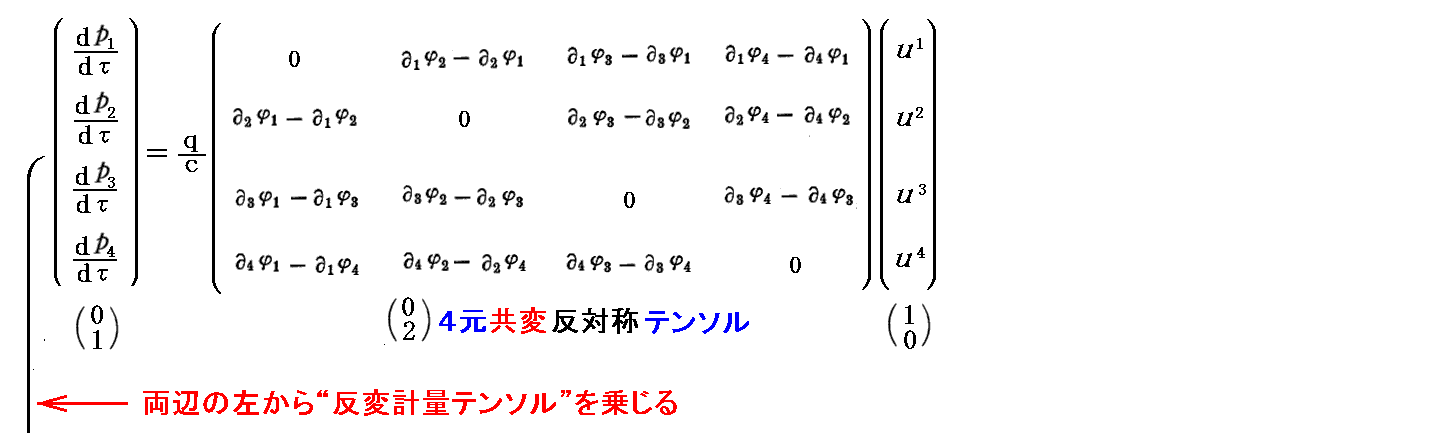
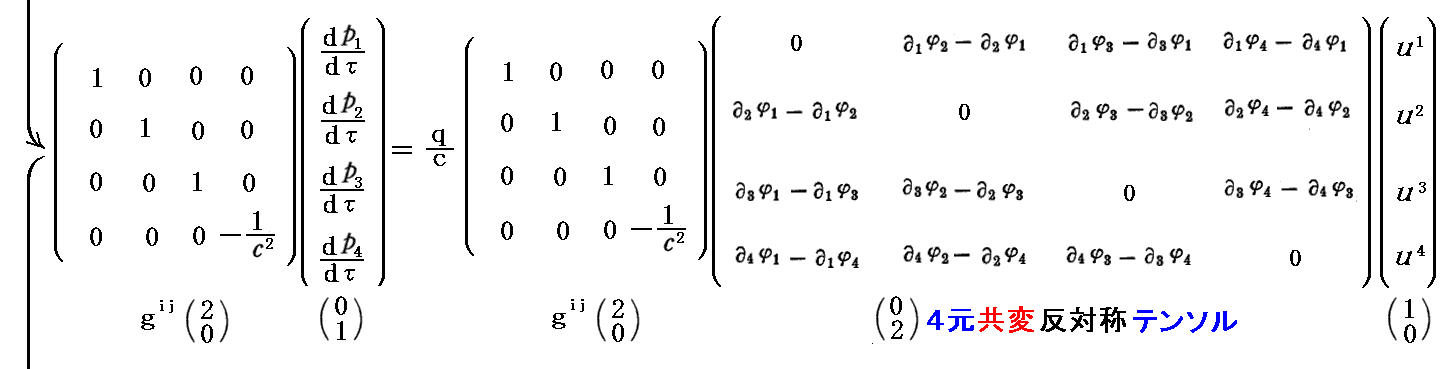
　最初の４元共変反対称テンソルの左右から反変計量テンソルを作用させるとは、４元反変反対称テンソルを導く事ができます。これは以前説明した操作の逆過程です。

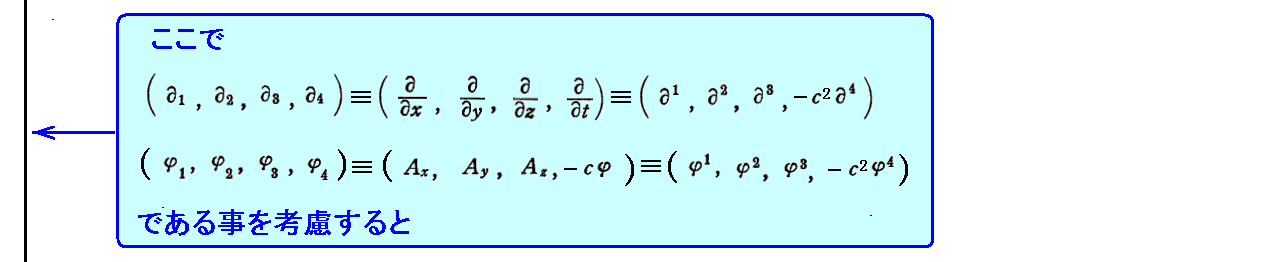
　この項の最初に述べた様に、“ローレンツの力の法則”はMaxwell方程式系を構成する法則の中で唯一の“力学的法則”です。そのためこの法則は、“変分原理”に従って正統的に導かれる“Euler-Lagrange方程式”であるはずです。その事は別稿「電磁場中の荷電粒子の運動」で説明しましたが、丁度良い機会ですので復習しておきます。
　ただし、上記別稿ではMKSA有理化単位系を用いていましたが、ここでは本稿で採用しているGauss単位系（非有理化-磁場H）で展開します。また、相対論的な４元ベクトルや、計量テンソルの表現としては別稿３．で説明した右側の定義を用います。

［補足説明３］
　要するに、荷電粒子の運動方程式を変分原理から導く事を考えるのですが、その導くべき運動方程式として［補足説明３］で様々に議論した中の1つを取り上げて、それを導く事を考える。その中の１つを選ぶのですが、導くべき方程式として

を選びます。
　これをもう少し具体的な４元電磁ポテンシャルで表すと

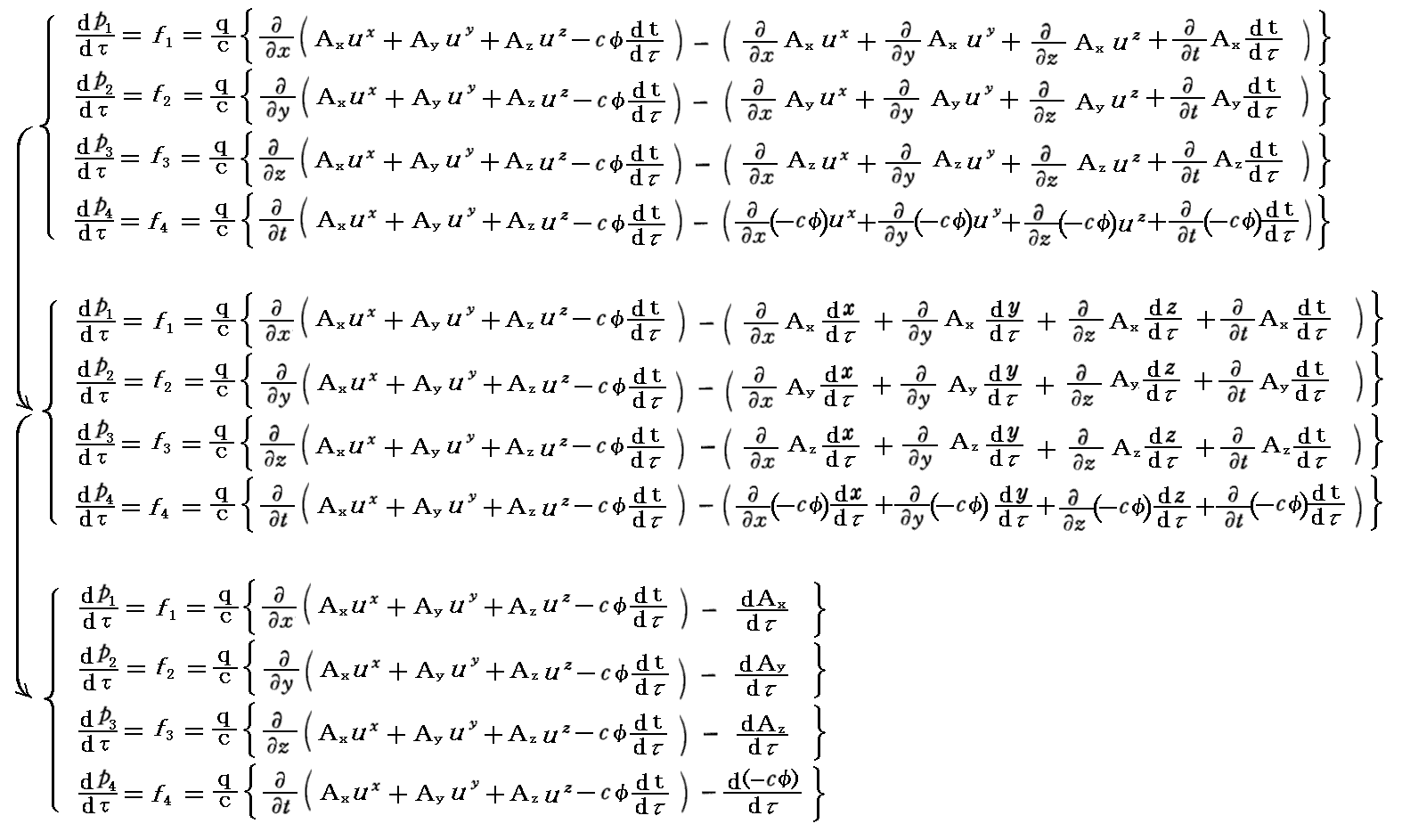
となります。
　上記の“運動方程式”が“Euler-Lagrange方程式”によって導けるためには、“Lagrangean”として

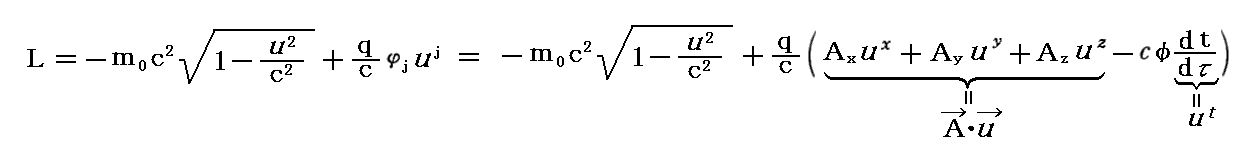
とすれば良いことが解ります。
　実際、これを“Euler-Lagrange方程式”に代入すると、以下の様に上記の“運動方程式”が導けます。

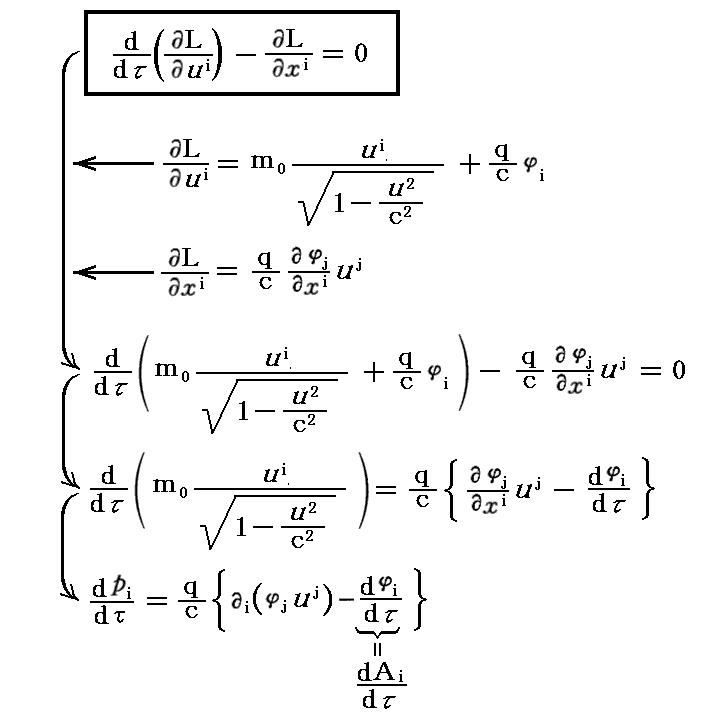
　この当たりについてはランダウ・リフシュツ「場の古典論」§16などを復習して下さい。
　また別稿「電磁場中の荷電粒子の運動」２．もご覧下さい。ただし、そこではMKSA有理化単位系を用いているため、ｃが関係するところで表現が少し異なる所があります。

（２）電磁場の非同次波動方程式

　２．（１）１．で示した式の中で�@式と�B式は、両辺に電場と磁場が同時に現れているが、この二式を組み合わせることで電場Ｅだけ、あるいは磁場Ｈだけの方程式を得ることができる。
　以下でその事を説明するが、空間微分と時間微分の演算順序を交換できることに注意してお読み下さい。

１．電場の非同次波動方程式

まず、�@、�B式から電場Ｅの波動方程式を導く。




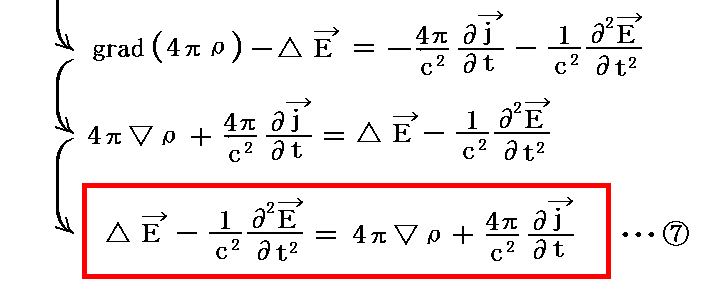
となる。これを�F式と置くことにする。上で用いたベクトル演算公式　rot（rotＥ）＝grad（divＥ）−△Ｅ　の証明はこちらを参照。

　もちろん、�@式の両辺の時間微分を取って、�B、�A式を用いても良い。このやり方でも同様な式が得られる。

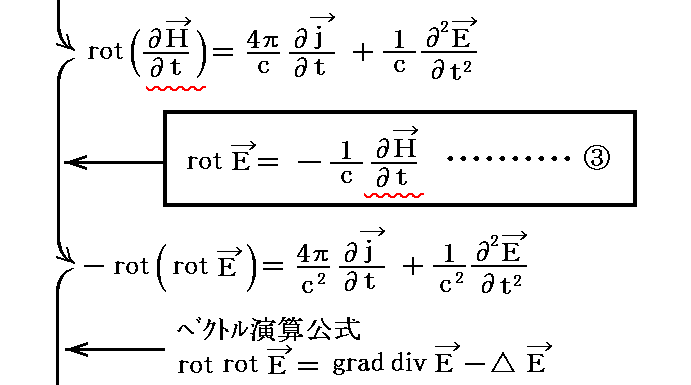
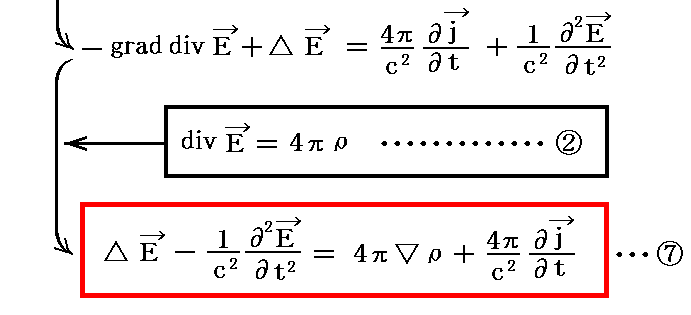
２．磁場の非同次波動方程式

　�@、�B式から磁場Ｈだけの方程式を求める。�@式の両辺のrot演算を取って�B、�C式を用いて、先ほどと同様な変形をすると



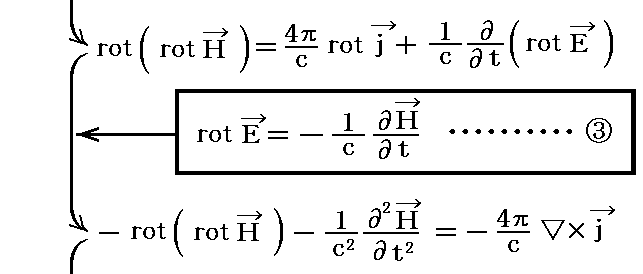
が得られる。これを�G式と置くことにする。

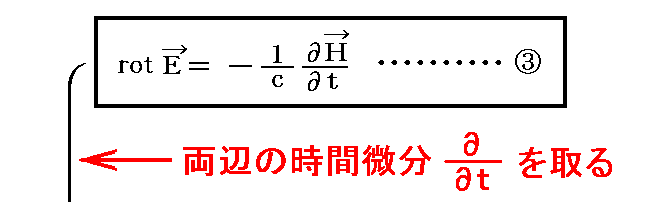
　もちろん、�B式の両辺の時間微分を取って開始してから、�@、�C式を用いても良い。このやり方でも同様な式が得られる。

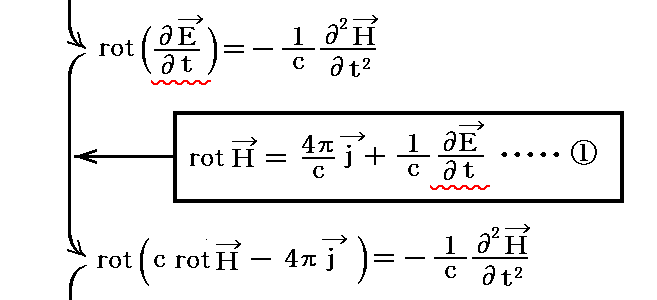
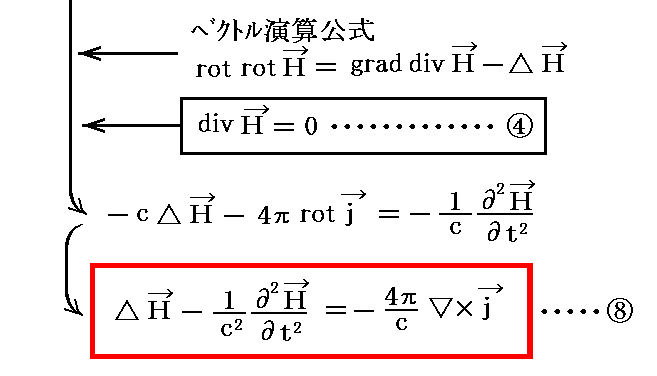
３．Maxwell方程式系と電磁場波動方程式の等価性

　ここで説明した方法で、ヘヴィサイドとヘルツが整理したMaxwell方程式系�@〜�C式から、電磁場の非同次波動方程式を最初に導いたのはオランダ人のH．A．Lorentz（1892年）のようです。このことに付いては太田文献2．のp109-02、p112-02やp210をご覧下さい。

　ここで重要なことは、電場だけ、磁場だけの方程式にするには、必ず�@式と�B式を組み合わせなければなりません。�@と�Bの両方を使用する上記の導き方からも解る様に、［Maxwell方程式系�@�B］は［電場Ｅ、磁場Ｈの非同次波動方程式�F、�G］と等価です。
　ただし、�@�Bから�F�Gを導くとき�Aと�Cを援用していますし、逆に�F�Gから�@�Bを導くとき、�Aと�Cの援用は必要です。そのため、より正確に言えば下図の様に対応した等価性であると言える。

《2.(2) まとめ》

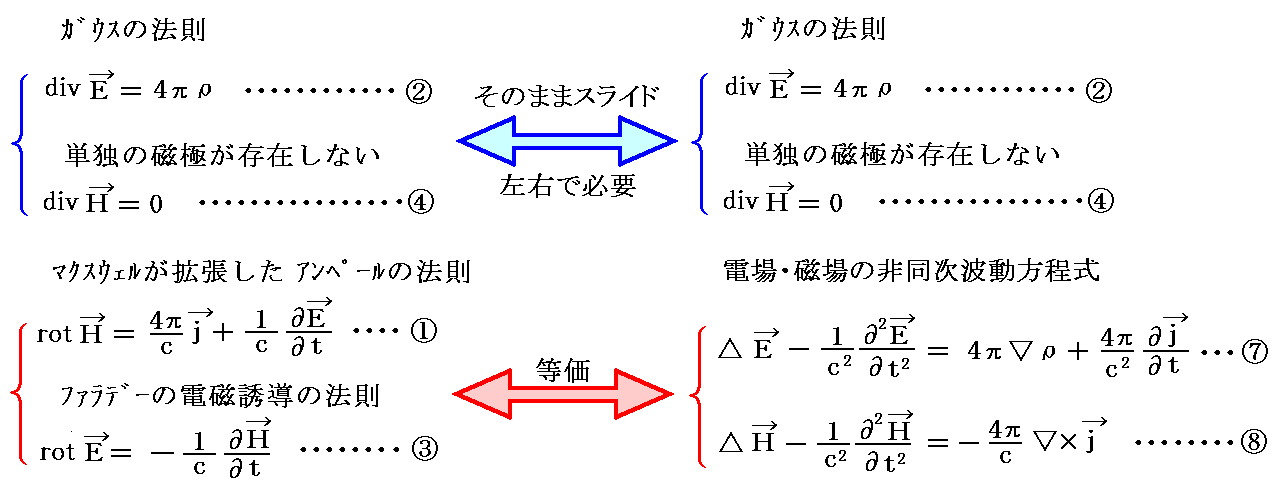
すなわち、�@�Bの方程式系を�F�Gで置き換えたとき�A�Cの方程式も必要です。
　つまり、左側の�@〜�C方程式系の代わりに、右側の�A�C�F�G方程式系を考察する事によっても［電磁場の様子］ と ［電荷密度・電流密度分布］ との関係を導く事ができるということです。

（３）Maxwell方程式系、波動方程式系と特殊相対性理論

　ここで導いた［電場Ｅ、磁場Ｈの非同次波動方程式�F、�G］の形から、これらの非同次波動方程式系が特殊相対性理論を満たす事を見通すのは難しい。
　本来、電場Ｅと磁場Ｈは相対論的には両方合わせて２階テンソル場を構成します。古典的電磁場理論で考えられていたようなベクトル場ではありません。だからベクトル量と見なしたときの電場Ｅや磁場Ｈの成分値の変換式はローレンツ変換共変の変換式であって、決してローレンツ変換そのものではありません。そのため、電場Ｅや磁場Ｈを前面に出した波動方程式形式から相対性理論を見通すのは難しい。
　そのとき、(７)、(８)式の右辺を 0 とした同次波動方程式系は、別稿「アインシュタインの特殊相対性理論（1905年）」３．（２）１．［補足説明１］の様に特殊相対性理論の中で利用されていますが、　方程式系の相対論的な構造を明らかにするためでは無くて、次節（４）で説明する様な意味で使われています。

　特殊相対性理論に対しては、むしろ元の［Maxwell方程式系�@〜�C、�Dと�E］の方が見通しが良い。
　実際１．（１）で説明した方程式系の中の（3）、（6）式や（8）、（9）式（すなわち�@〜�Cの方程式系）は別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（２）や５．（３）で説明した様に相対論的方程式の形をしています。
　さらに、１．（１）で説明した方程式系の中で、“電荷の保存則”(7)式や、“ローレンツの力の法則”(2)、(5)式は、２．（１）２．［補足説明１］や２．（１）３．［補足説明１］で説明した様に、元々相対論的方程式です。
　そういった意味で、１．（１）で説明した方程式系の方がより根源的なのかもしれません。

　補足しますと、第３章で説明します ［電磁ポテンシャルＡ、φで表した波動方程式系］ は、特殊相対性理論に適した形をしています。

（４）同次波動方程式と特殊相対性理論

　先ほど求めた非同次波動方程式の右辺を構成する電荷密度分布と電流密度分布が全空間にわたってゼロの場合、同次波動方程式に帰着します。それは電荷密度及び電流密度分布がゼロの場合のMaxwell方程式系�@〜�Cを用いることでも導かれます。このことは別稿「アインシュタインの特殊相対性理論（1905年）」３．（２）１．［補足説明１］で説明しました。
　なぜそこで説明したのかと言いますと、この波動方程式こそ何も無い真空中で存在できる電磁場の振る舞いを説明する方程式だからです。この解によって電磁場の波動である光の示す巨視的な性質が旨く説明できるからです。そのことに付いては先に挙げた別稿３．（２）１．［補足説明２］〜［補足説明７］をご覧下さい。

　もちろん相対性理論が発見される以前からMaxwell方程式から波動方程式が導かれる事は知られていましたし、波動方程式の中に現れる定数ｃが波動の伝播速度である事は知られていました。
　ところが、やがてこの定数ｃが光の速度と一致することが解ってきます。つまり定数ｃが、波動方程式の解である電磁場の波動の伝播速度であり、この定数が光の速度と一致するのであれば、光の波は電磁波そのものであると考えられる様になります。

　そういった時代に、Maxwell方程式や波動方程式がどの慣性系に於いても成り立つのか（つまり“相対性原理”が成り立つのか）が、問題になります。自然現象を表す方程式が相対性原理を満たすべきだという考え方は、アインシュタインの特殊相対性理論（1905年）の発見以前から広く考察されていたことです。もちろんそのとき、自然現象を表す方程式はある特定の空間（絶対静止空間）に於いて成り立つものであり、それとは異なった慣性系では方程式の形は変化するという考え方もありました。
　そのとき、相対性原理が正しくて、あらゆる慣性系に於いて同一方程式となるのなら、ｃは慣性系によらない定数となりますから、光速度はどんな慣性系で測定しても一定である事になります。
　あるいは、絶対静止の空間でのみで方程式が正しいのであって、それ以外の慣性系では方程式の形は変更を受け、光の速度は異なった値になるのなら、このことを確かめることにより絶対静止空間（エーテル空間）を確かめる事ができるかも知れません。
　いずれにしても、このことを確かめる観測や実験が多数行われます。中でも特に有名なのがマイケルソン・モーリーの実験です。

　そのとき、上記とは違って次の様に考える事もできます。
　すなわち、光速ｃがそれを観測する慣性系によらず、つねに一定不変な定数である事は慣性座標間のガリレイ変換や、その変換に伴う速度の変換則に矛盾します。このことがひとつの着想をうみます。
　すなわち別稿３．（２）［補足説明２］で説明した
『波動方程式が真に正しい物理法則を表しており“相対性原理”を満たしているのなら、波動方程式は二つの慣性系で同じ形になるべき（つまり光速ｃは定数であるべき）であるが、そのことから逆にガリレイ変換に変わる新しい座標変換法則（“ローレンツ変換”）を導くことが出来るかもしれない。』
という考え方です。
　実際、その考え方に従って導かれた変換こそが相対性理論の本質をつかさどる“ローレンツ変換”だったのです。それを導く具体的な方法についてはこちらを、あるいはこちらを参照されたし。
　もちろんこれは、光速度があらゆる慣性系で測って一定であるということから、それらの慣性系間の座標変換法則を導く事と同じです。そういった考え方にもとずく座標変換則の導出についてはこちらの［補足説明３］の中に記した引用先を参照して下さい。

　そういった試みのすべてを旨く説明し、すべての疑問を解決するものとして、集大成されたものがアインシュタインの展開した特殊相対性理論です。それが「アインシュタインの特殊相対性理論（1905年）」で展開されているものです。

３．電磁ポテンシャルＡ、φの波動方程式

　電磁ポテンシャルの導入は別稿「線型振動子による電磁波の放出」１．（１）や、別稿「Maxwell方程式系の先見性と電磁ポテンシャル」３．（２）ですでに説明していますが、特殊相対性理論の高い見知から今一度振り返ってみます。
　ここも非有理化Gauss単位系で展開します。さらに、“本稿特有な計量テンソル定義”と“本稿特有な４元表示”を用いています。

　今日の教科書で展開されている標準的な方法で電磁ポテンシャルＡ、φの非同次波動方程式を導きます。
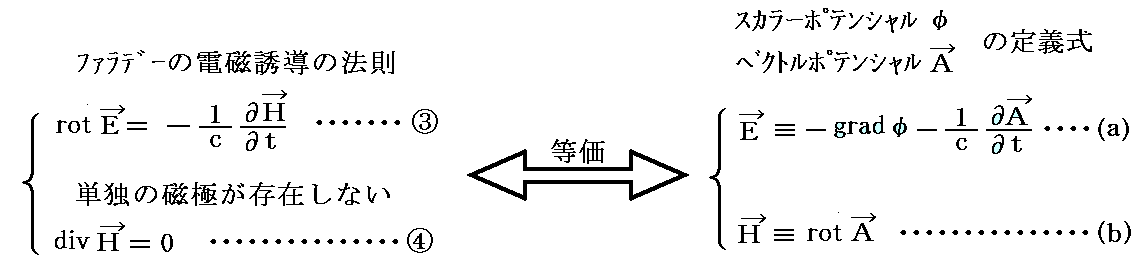
　すなわち、まず３．（１）で、Maxwell方程式（divＨ＝0とファラデーの電磁誘導の法則）からベクトルポテンシャルＡとスカラーポテンシャルφを定義・導入します。
　そして、３．（２）１〜２．で、上記の定義式を用いてMaxwell方程式（アンペールの法則）からベクトルポテンシャルＡの非同次波動方程式を、Maxwell方程式（ガウスの法則）からスカラーポテンシャルφの非同次波動方程式を導きます。
　最後の３．(２)３．で、Lorenzの条件式と、ベクトルポテンシャルＡ・スカラーポテンシャルφの定義式を、先に求めた非同次波動方程式に適用して、逆にMaxwell方程式系を導き、両者の等価性を説明します。
　
　ただし以下の事柄に注意して下さい。すなわち、歴史的な展開は上記とは逆でして、最初ノイマンは電場Eを定義するベクトルポテンシャルＡとスカラーポテンシャルφを

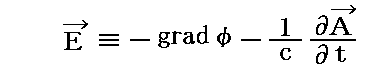
によって導入します。そして、(ｘ’，ｙ’，ｚ’)における電荷密度をρ’としたとき、φは

定義され、(ｘ’，ｙ’，ｚ’)における伝導電流をｊ’としたとき、Ａは

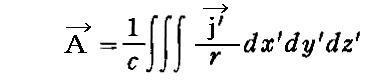
で定義されるとしました。
　その後、デンマーク人のL．Lorenz は、そのベクトルポテンシャルＡとスカラーポテンシャルφを

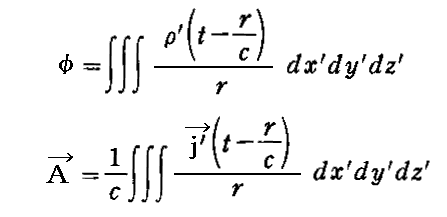
で置き換える事を提案します。つまり電荷や電流による影響は光速度ｃで伝わるとしたのです。そしてφとＡがこのように置き換えて定義されると、この定義は

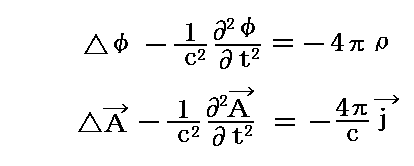
という非同次波動方程式と同等であるとした。
　さらに、Lorenzは、電荷保存の式

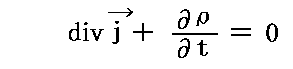
から、今日Lorenzゲージと呼ばれている条件式

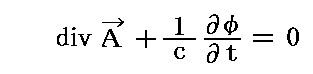
を導きます。そしてこのLorenzの条件式と、ベクトルポテンシャルＡ・スカラーポテンシャルφの定義式を、先ほどの非同次波動方程式に適用すれば、今日Maxwell方程式と呼ばれているものに相当する方程式系が導かれることを示します。
　このLorenzが行った最後の手順が、３．(２)３．で説明しているものに相当します。

（１）電磁ポテンシャルＡ、φ

１．ベクトルポテンシャルＡの定義

　２．（１）で説明した４つのMaxwell方程式の最初の２つ�@式と�A式は、左辺は電磁場だが右辺に電荷密度と電流密度を含んでおり、これは荷電物体と電磁場の相互作用を表すものでした。
　これに対して�B式と�C式は電磁場ベクトルのみを含む線形の１次方程式ですから、比較的簡単に積分して解を得ることができます。

　まず、�C式から

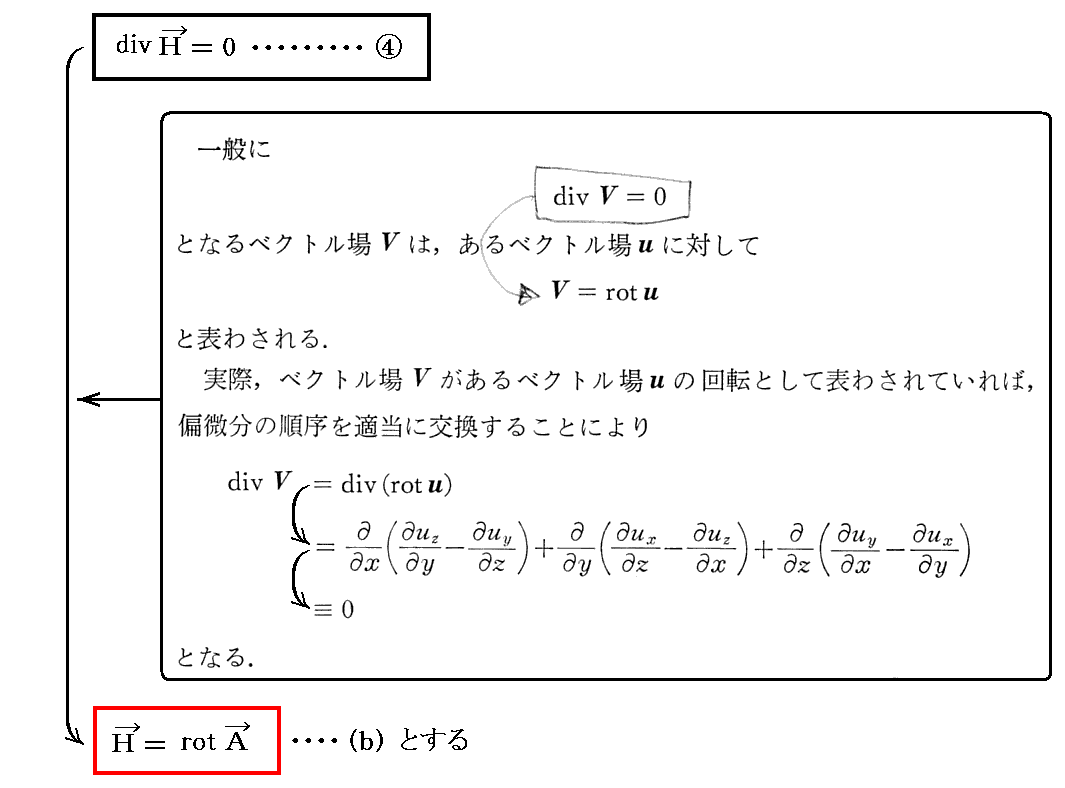
が言える。上記で用いたベクトル演算公式に付いてはこちらも参照して下さい。
　このベクトル場Ａを電磁場の“ベクトルポテンシャル”と言う。これはベクトル場Ａの定義式と見なすこともできる。つまり磁場Ｈはベクトル場Ａのrot演算から得られる。
　今後この関係式を（ｂ）とおくことにする。　

２．スカラーポテンシャルφの定義

　更に、�B式から



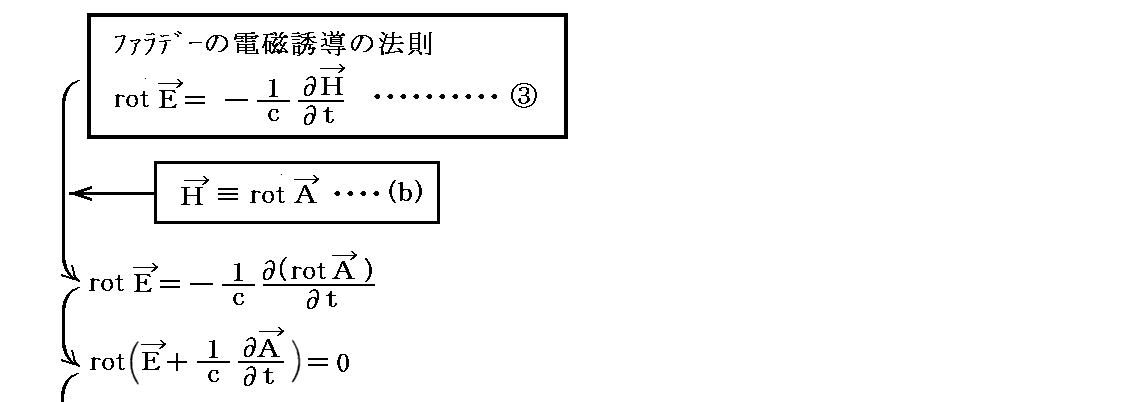
が言える。上記で用いたベクトル演算公式に付いてはこちらも参照して下さい。
　このとき導入されるスカラー場φを電磁場の“スカラーポテンシャル”と言う。これはスカラーポテンシャルφとベクトル場Ａの定義式と見なすこともできる。つまり電場Ｅは ［スカラー場φにgrad演算を施したもの］ と ［ベクトル場Ａの時間微分したもの］ の和となる。
　今後この関係式を（ａ）とおくことにする。　

３．［電磁ポテンシャルＡ、φの定義式］ は ［Maxwell方程式�B、�C式］ と等価

　このとき、逆に（ａ）、（ｂ）式から�B、�C式を導く事もできます。
まず、(ａ)(ｂ)式から�B式を導く。


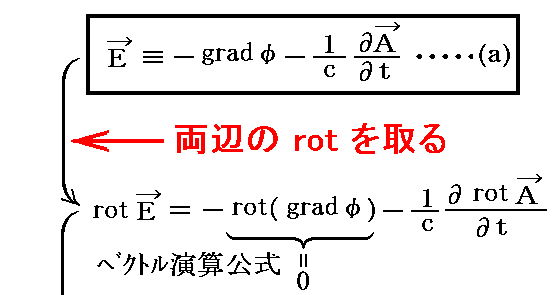
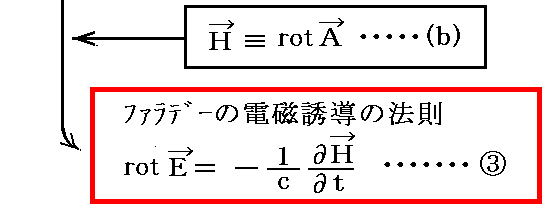
この式変形を最初に導いたのはLorenzです。

次に、(ｂ)式から�C式を導く。

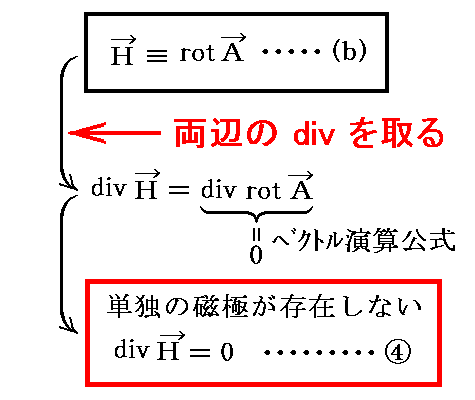
つまり、(ａ)、(ｂ)式から�B、�C式が導けるのですが、これは上記１．２．の逆変換に相当します。

　ここで述べた逆変換に相当する計算は、ある意味においてL．Lorenzがすでに行っている事です。このことについては太田文献2．ｐ112-01をご覧下さい。
　さらに補足しますと、今日電磁ポテンシャルは上記の様な手順で導入されますが、歴史的には話は逆でして最初(ａ)式が発見されます。(ａ)式はノイマンが見つけたもので、Maxwellはこれから�B式を導きました。そして、デンマーク人のLorenzは電磁ポテンシャルの波動方程式(ｄ)（ｅ）式から出発して、その波動方程式にノイマンの関係式(ａ)とLorenzのゲージ条件を適用してMaxwell方程式に相当するものを導きました。また、(ｂ)式は1846年にW．Tomsonが見つけたものです。
　この当たりはとても錯綜していまして私どもには良く解りません。Whittakerの文献の8章の解説が理解の一助になるかも知れません。

　逆変換できることから、［Maxwellの方程式�B、�C式］ と ［電磁ポテンシャルの定義式(ａ)、(ｂ)式］ はお互いに 等価 です。

［補足説明１］
　上記の等価性について補足します。
　別稿「Maxwell方程式系の先見性と電磁ポテンシャル」５．（３）で説明した様に、［Maxwell方程式�B、�C式］ は ［相対論的3階テンソル方程式］ に まとめることができました。そのところを復習すると

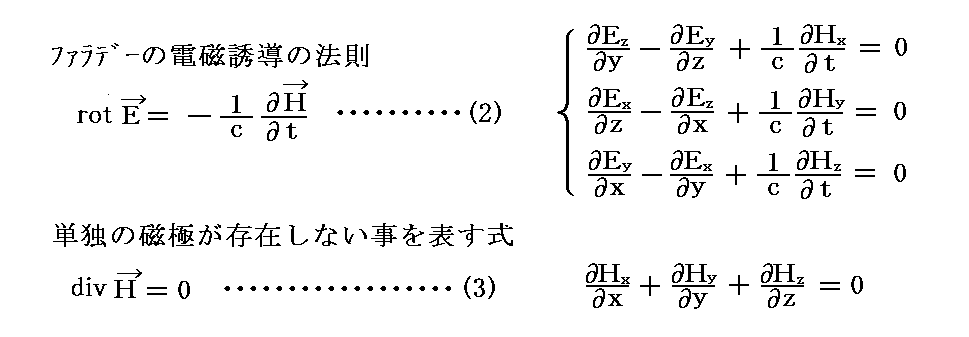
を変形していくと




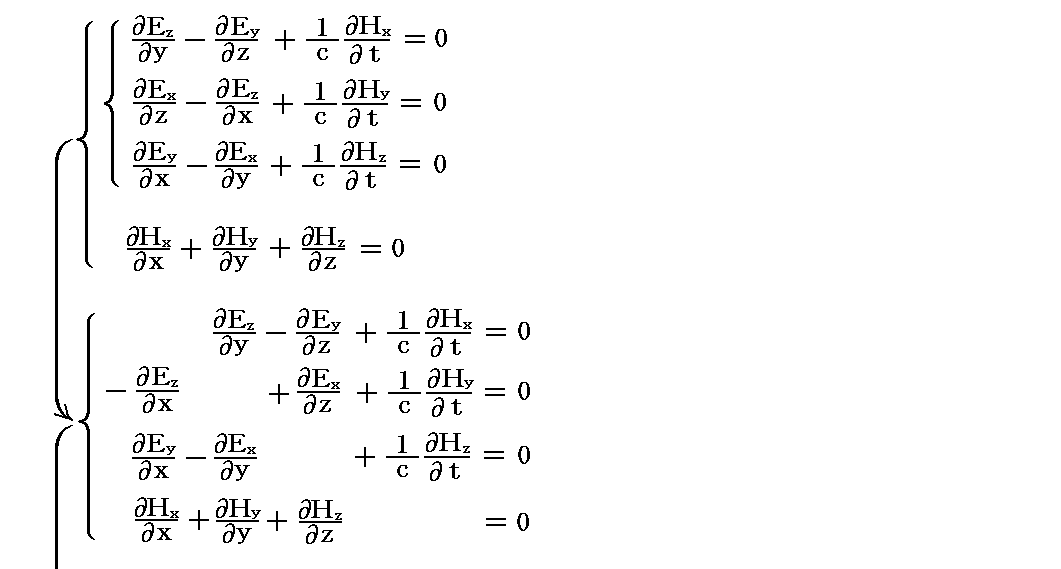
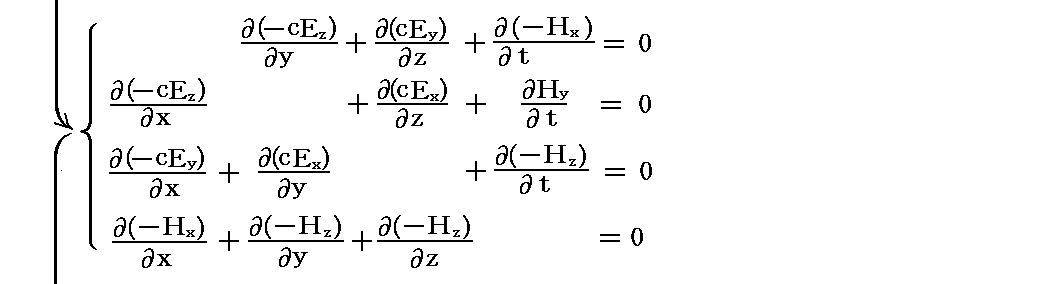
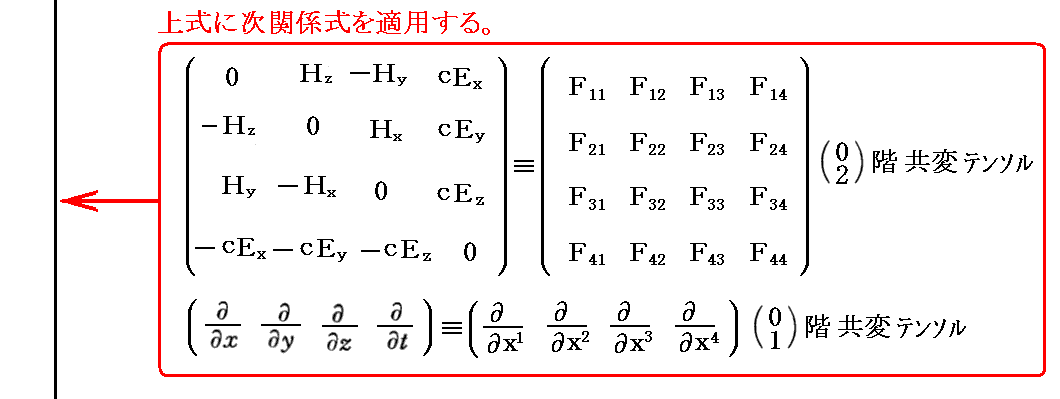
となります。この表現はとても解りにくいが、（0，１）階共変テンソル（つまり１階共変ベクトル）と（0，２）階共変テンソルの“直積”から作られる（0，３）階共変テンソルの“テンソル方程式”を表している。
　このテンソルは4×4×4＝64個の成分を持ちます。その（ｉ，ｊ，ｋ）成分が ∂_ｊＦ_ｋｉ＋∂_ｊＦ_ｉｋ＋∂_ｋＦ_ｊｉ であるということです。そして、上記のテンソル方程式は、その全ての成分が 0 であることを示している。
　このとき、テンソル方程式の形から解るように64個成分それぞれが一つのテンソル方程式の１成分ですから方程式が64個あることになります。ただし、64個の方程式の内で独立なのは4個だけです。それは（ｉ，ｊ，ｋ）として（1，2，3）（1，2，4）（1，3，4）（2，3，4）を持つものです。そうなることは別稿「ミンコフスキーの４次元世界」４．（２）２．［補足説明２］を、あるいは別稿「対称テンソルと反対称テンソルの独立成分の数」２．（２）を参照して下さい。この独立な４個が前記のMaxwell方程式の４式に相当します。
　
　そのとき、別稿「ミンコフスキーの４次元世界」４．(２)２．［補足説明３］で説明したように、［電磁ポテンシャルの定義式(ａ)、(ｂ)式］ から上記の［相対論的3階テンソル方程式］を演繹的・恒等的に導く事ができます。そこの議論を以下で復習します。ただし、上記別稿は“有理化gauss単位系”を用い、しかも“特殊な形の計量テンソル定義”でしたので、本稿の“非有理化gauss単位系”と“本稿特有な計量テンソル定義”と“本稿特有な４元表示”に書き直しています。
　まず、別稿の３．（１）［補足説明５］で述べたように４元共変ベクトルとしての電磁ポテンシャルは（Ａ_ｘ，Ａ_ｙ，Ａ_ｚ，-ｃφ）です。これを（φ₁，φ₂，φ₃，φ₄）＝φ_ｉ と置くことにします。
　そのとき別稿の３．（９）３．で説明したように、共変ベクトル場を微分したものを下記の様に組み合わせたものは４元の“回転”と呼んで交代（反対称）2階共変テンソル場となるのでした。ここで注意してほしいのですが４元微分演算は共変性のベクトルです。それを共変ベクトルに作用させるのですから、いわゆる“縮約”はできません。“直積”ならできます。ただし、ここで言う“回転”は直積ではありませんが直積操作に似ていまして、結局２階共変テンソルとなります。このことに付いては［補足説明２］をご覧下さい。
　【３次元ベクトルの３次元回転演算操作では３次元ベクトルが生じましたが、４元共変ベクトルの４元回転演算操作では２階共変テンソルになると言うことです。おそらくこちらの４元表示が“回転”演算本来の形なのでしょう】
　
　ここで取り上げている［電磁ポテンシャル定義式］(ａ)(ｂ)式は一緒になって２階共変テンソル（しかも反対称性）を構成する（別稿の４．（２）１．［補足説明３］参照）もので、まさにその例です。




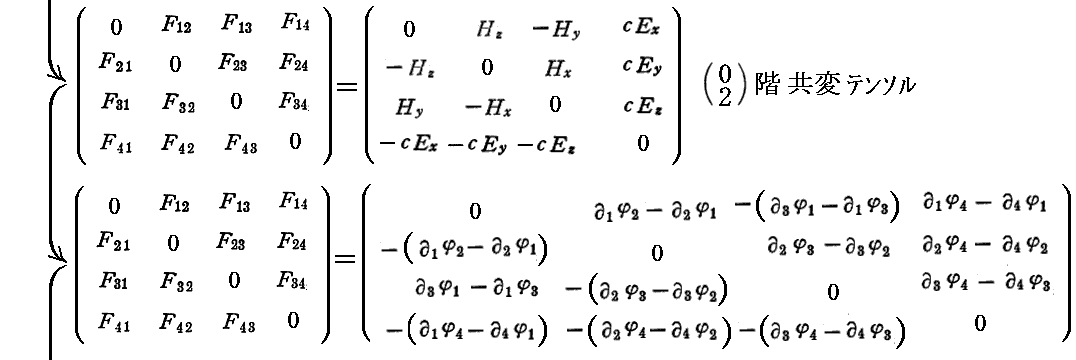
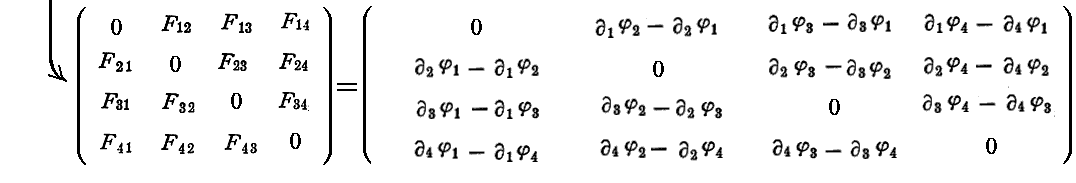
すなわち、［電磁ポテンシャルの定義式］は２階共変反対称テンソルを構成しています。
　
　この［電磁ポテンシャルの定義式］を前記の3階共変テンソル

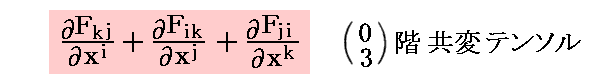
に適用してみれば、それが恒等的に0となることが解ります。実際、


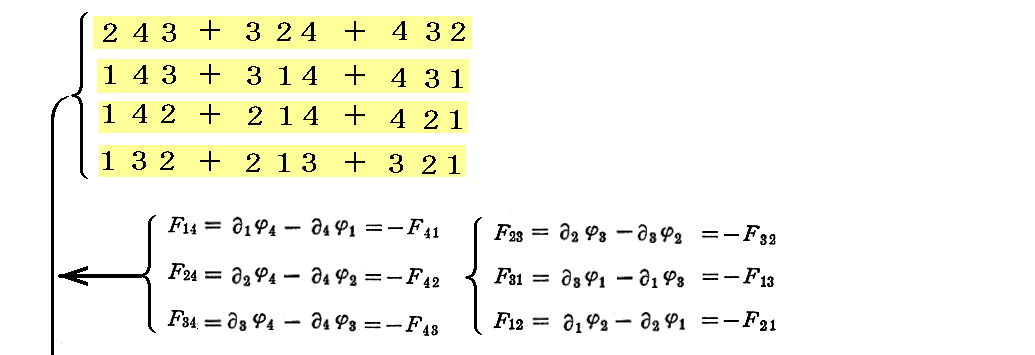
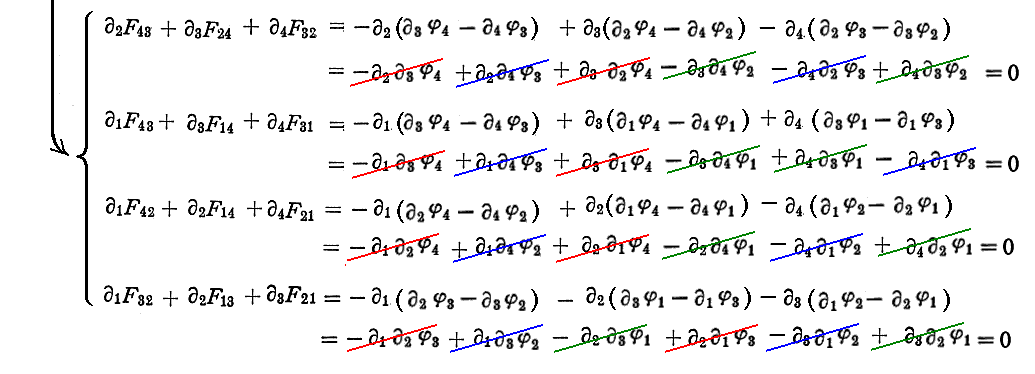
が直ちにいえる。
　さらに、この［電磁ポテンシャルの定義式］を用いると、前記の3階共変テンソルが交代（反対称）テンソルであることが証明できます。実際一つの要素について計算して見ると

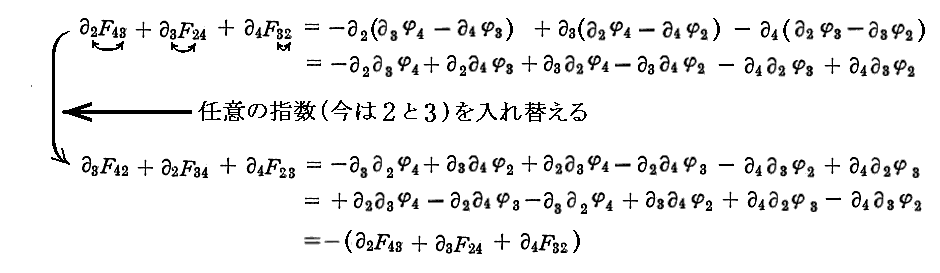
となります。他の3要素についても同様に証明できます。
　いずれにしても、このように構成された3階共変交代（反対称）テンソル方程式は、マクスウェルの方程式

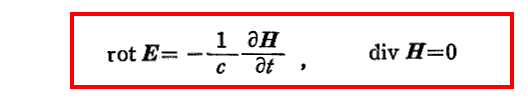
そのものを表している。
　
　この相対論的な説明からも上述の等価性が完璧である事が解ります。

［補足説明２］
　上記［補足説明１］に出てきた“４元回転演算”について補足します。これは２つの４元ベクトルの“直積”の一部を取り出したものです。２つの４元ベクトルＡとＢの“直積”からは16個の成分Ａ_ｉＢ_ｊが生じますがこれは次の様に書き表すことができます。

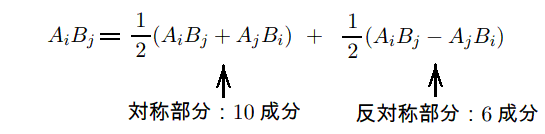
　このときＡ_ｉＢ_ｉの様に同じ成分の組み合わせは、対象部分の成分としてはカウントできますが、反対称部分の成分は消えてしまいます。またＡ_ｉＢ_ｊとＡ_ｊＢ_ｉの様に添字を入れ替えたものは対象部分の成分としては同じになり、反対称部分の成分としても符号が入れ替わるだけなので独立なものとは見なせません。だから結局、対称部分は10成分、反対称部分は6成分のみが独立となります。つまり、前記の“４元回転演算”はこの反対称部分の成分を取り出したものです。そのため４元共変テンソルとなります。実際、このようにして構成したものは４元テンソルとしての変換式に従って変換されますので、その様に見なせるということです。
　３次元ベクトルに関して同じ“直積”を作ると

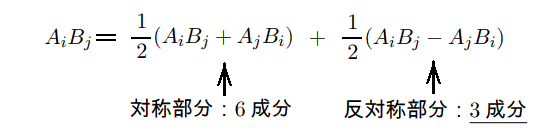
となりますが、その反対称部分は３成分となりますので、反対称部分の成分数が丁度ベクトルの次元数（３次元）と同じなので、それをベクトルと見なして慣習として

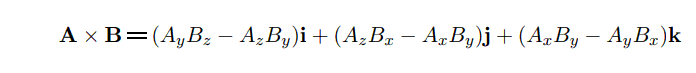
と表すことにしているだけです。本来は３元共変テンソルと見なすべきものだったのです。

（２）電磁ポテンシャルＡ、φの非同次波動方程式

　別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）で説明したように、電磁ポテンシャルＡ、φが満たす非同次波動方程式を最初に導いたのは、デンマーク人のL．Lorenzです。それは1867年のことです。
　ただし、LorenzがMaxwell方程式を認識していたわけではありませんから、下記の様にMaxwell方程式から出発して導いたわけではありません。その導き方は別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）１．で説明した手順によります。このことに付いては別稿§4.2“ローレンスの光と電流”110-02〜をご覧下さい。
　さらにそのとき、Lorenzは、本節３．(２)３．で説明する逆変換に相当する式を導いていますので、LorenzはＭaxwell方程式に相当する式に到達していたとも言えます。このことに付いては別稿§4.2“ローレンスの光と電流”111-02〜をご覧下さい。

1．ベクトルポテンシャルＡの波動方程式

　“電磁ポテンシャルの定義式”(ａ)(ｂ)式を、“Maxwellが改良したアンペールの法則”�@式に代入すると



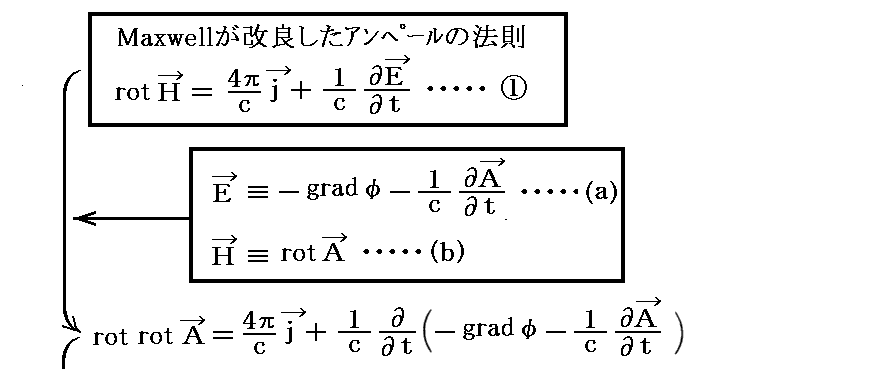
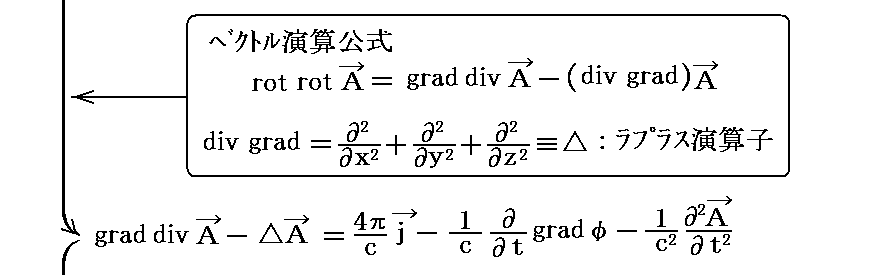
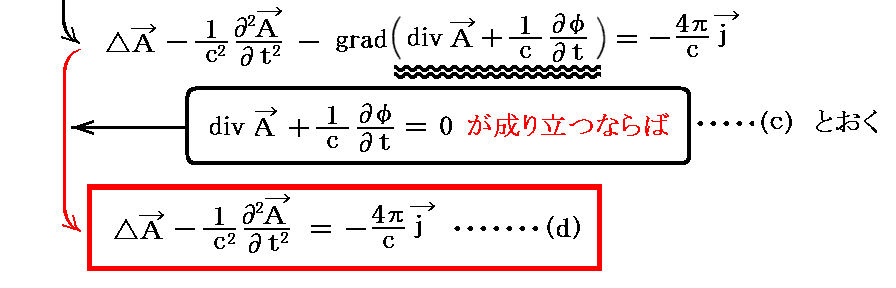
となり、ベクトルポテンシャルＡの非同次波動方程式が得られる。これを今後(ｄ)とおく。
　ここで

の関係式を用いたことに注意して下さい。以下でも繰り返し用いますが、この関係式を今後“ローレンツ（Loreinz）の条件”と呼び、(ｃ)とおくことにします。

２．スカラーポテンシャルφの波動方程式

　“電磁ポテンシャルの定義式”(ａ)式を、“ガウスの法則”�A式に代入すると


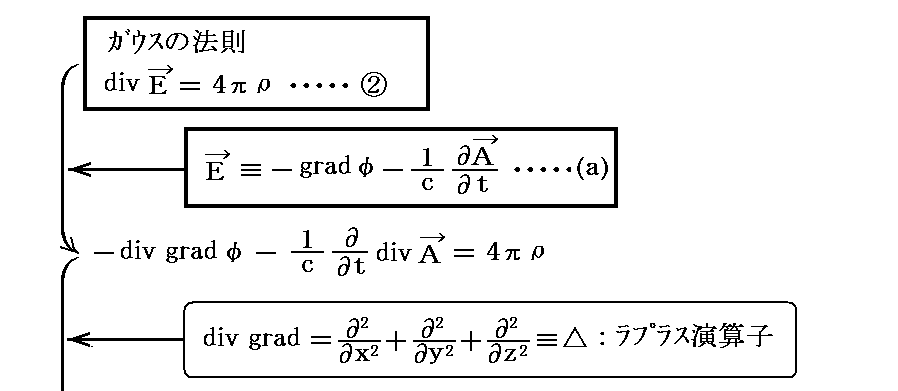
となり、スカラーポテンシャルφの非同次波動方程式が得られる。これを今後(ｅ)とおく。

［補足説明１］
　上記の電磁ポテンシャルについての非同次波動方程式（ｄ）、（ｅ）式を初めて導いたのはデンマーク人のLorenzです。
　今日の教科書では、上記の様にMaxwell方程式に電磁ポテンシャルの定義式を適用して導きますが、Lorenzがこれらの波動方程式を導いたときにはMaxwell方程式を知らなかったので、別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．(２)１．でWhittakerが説明している方法で導いたのです。
　要するに、最初に“遅延電位”と“遅延ベクトルポテンシャル”の表現式を仮定して、これが解であるためには上記の波動方程式が成り立たねばならないというやり方で証明したのです。実際の証明計算は別稿「非同次波動方程式の一般解」３．（３）や、別稿「ポアソン方程式と波動方程式」２．などをご覧下さい。

３．［Maxwell方程式系�@〜�C式］ と ［電磁ポテンシャルＡ、φの波動方程式系(ｄ)(ｅ)］ の等価性

　１．２．項の手順とは逆に(ｄ)、(ｅ)式から�@、�A式を導くことができます。これは（２）1．〜2．の逆変換に相当します。
　そのとき、Ａ、φをＥ、Ｈの方程式に変換するのですから、Ａ、φとＥ、Ｈを結ぶ ［電磁ポテンシャルＡ、φの定義式(ａ)、(ｂ)式］ の援用が必要なのは当然ですが、さらに ［ローレンツの条件(ｃ)式］ の援用も必要になります。

まず、(ｄ)式から�@式を導く。そのとき(ｂ)(ａ)式と(ｃ)式を援用します。



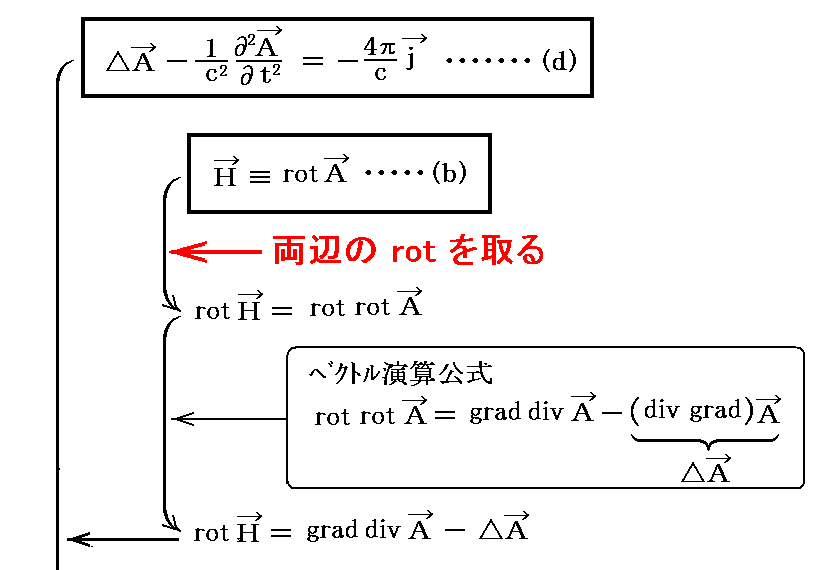
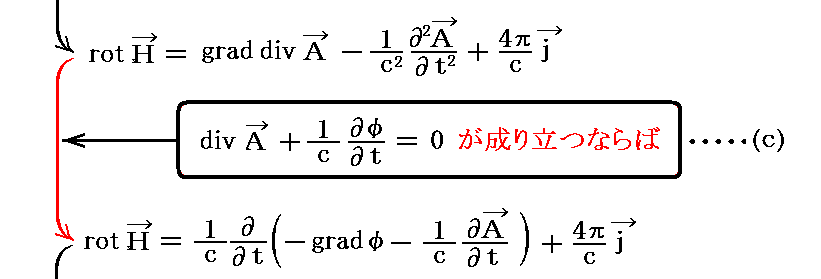
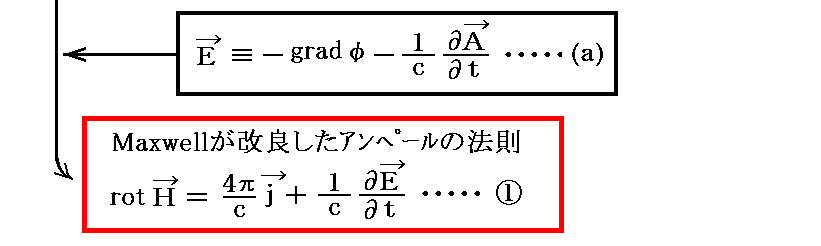
上記と同じなのですが、こちらの式変形も参照して下さい。

　上は(ｂ)式の両辺の rot を取ったものを援用しましたが、もちろん(ａ)式の両辺の 時間微分 を取ったものを援用しても良い。



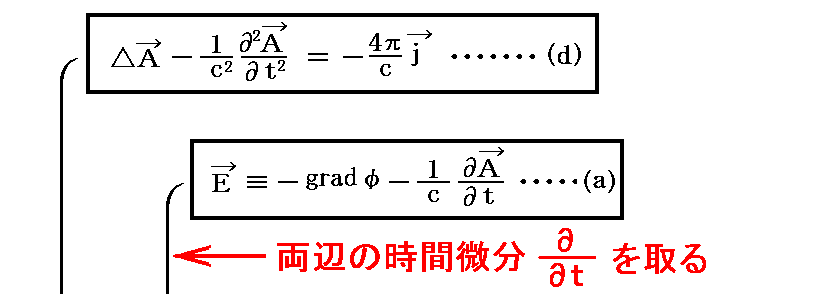
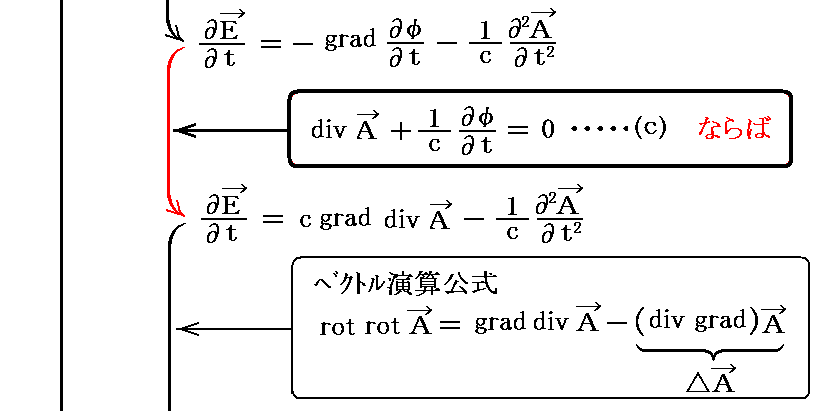
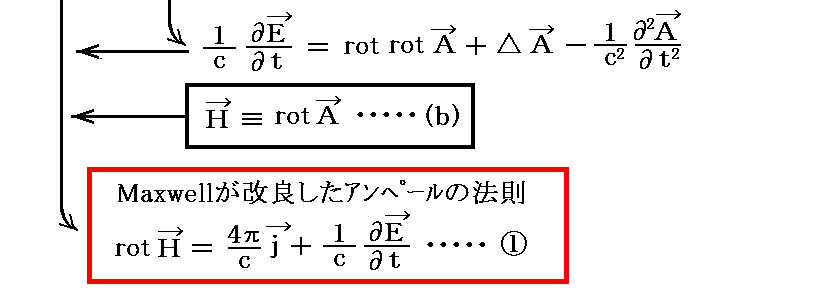
　上記と同じなのですが、こちらの式変形も参照して下さい。こちらが、Lorenzが実際に行った式変形です。

次に、(ｅ)式から�A式を導く。そのとき(ａ)式の両辺のdivを取ったものを援用する。


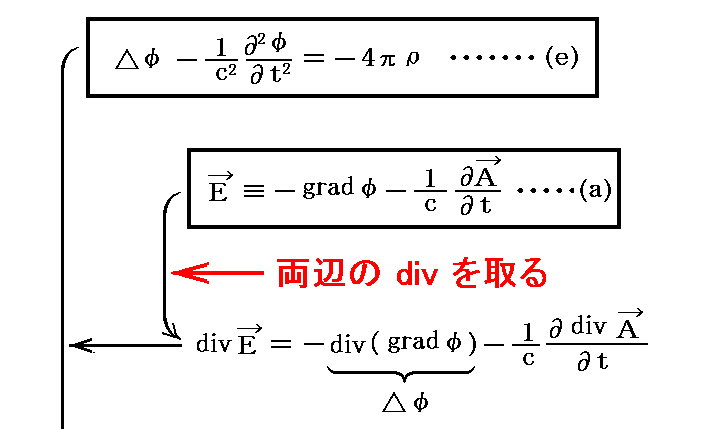
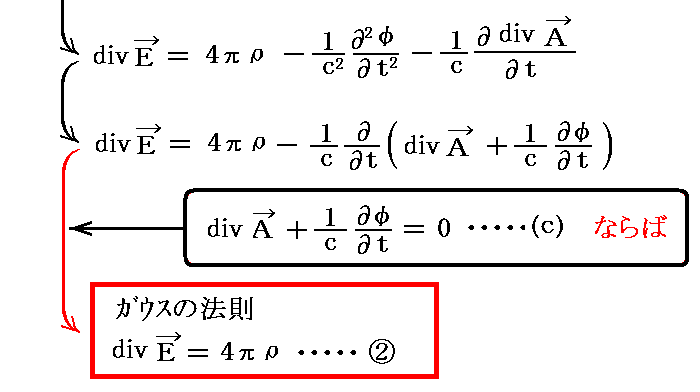
　上記と同じなのですが、こちらの式変形も参照して下さい。

　ここで述べた逆変換に相当する［電磁ポテンシャルＡ、φの波動方程式］から［Ｍaxwell方程式］を求めることは、ある意味においてL．Lorenzがすでに行っている事です。このことについては太田文献2．ｐ111-02をご覧下さい。

《3.(2) まとめ》
　以上の様に逆変換も可能ですから、 ［Ｍａxwell方程式系�@〜�C］ と ［電磁ポテンシャル方程式系(ａ)(ｂ)(ｄ)(ｅ)］ は互いに等価でして、下記の様に対応することが解ります。

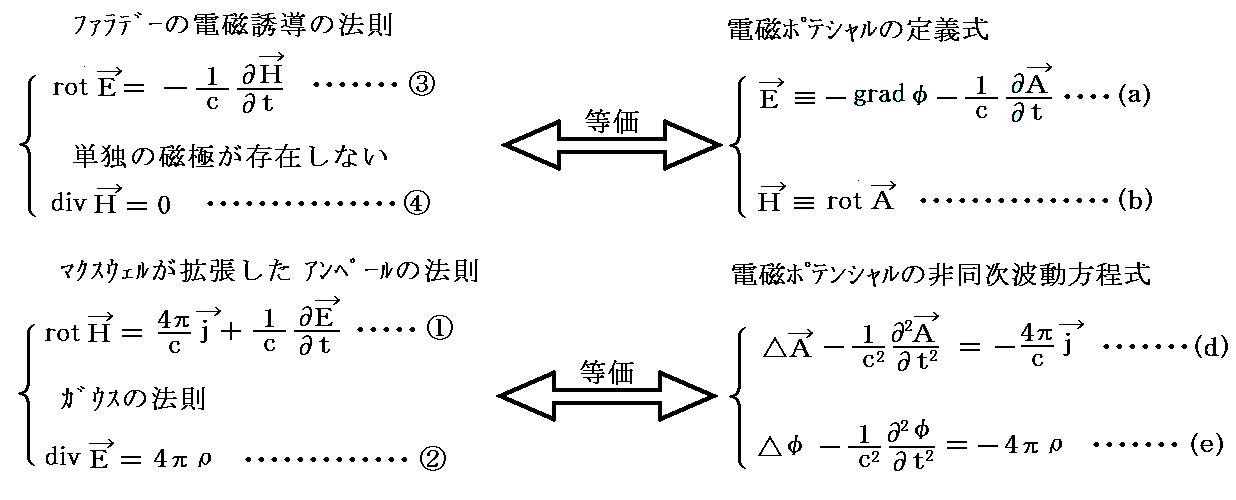
　上段の�B�Cと(ａ)(ｂ)が対応するのは、�B�Cが場そのものの関係を示しており、(ａ)(ｂ)も場Ａとφそのものの関係を（場ＥとＨとの関係を含めて）示しているからです。
　これに対して下段の�@�Aと(ｄ)(ｅ)が対応するのは、どちらも場とその場を生じる物質(電荷と電流）の関係を示しているからです。
　
　さらに補足しますと、３．（１）３．［補足説明１］で説明したように、上段の�B＋�C と (ａ)＋(ｂ) は、どちらも元々相対論的な方程式です。このことは、�B＋�Cについては別稿　「Maxwell方程式系の先見性と電磁ポテンシャル」５．（３）で、（ａ）＋（ｂ）については別稿の３．（１）で確認できます。そのとき別稿「ミンコフスキーの４次元世界」４．(２)２．［補足説明３］もご覧下さい。
　
　さらに、相対論的に見通しの良い�@＋�A方程式系が、そのまま(ｄ)＋(ｅ)方程式系に変換されますので、右側の電磁ポテンシャル非同次波動方程式系も相対論的に見通しの良い方程式です。つまり、下段の左右どちらの方程式系も相対論的な見通しが良い方程式です。そのことは、（ｄ）＋（ｅ）については別稿　「Maxwell方程式系の先見性と電磁ポテンシャル」３．（２）で、�@＋�Aについては別稿の５．（２）で確認できます。そのとき�@＋�Aに関しては２．（１）２．［補足説明１］も復習されて下さい。また、３．（３）３．［補足説明２］もご覧下さい。
　
　結局の所、次節で説明する“Lorenzの条件式”（ｃ）式に従った電荷と電流密度の分布の下で、非同次波動方程式（ｄ）、（ｅ）式を解いて電磁ポテンシャルＡとφを求める。
　次に、その様にして求められた電磁ポテンシャルＡ、φから（ａ）、（ｂ）式によって電場Ｅと磁場Ｈを求めることになります。

（３）ゲージ条件

１．Lorenzの条件式

　前節でMaxwell方程式�@�Aから電磁ポテンシャルの波動方程式(ｄ)(ｅ)を導くとき

という条件式を用いました。この条件を明示的に指摘したのは、デンマーク人のL．Lorenz（1867年）ですので、今日この条件式は“Lorenzのゲージ条件”と呼ばれています。
　
　今日の様にMaxwell方程式系に電磁ポテンシャルの定義式を適用して波動方程式を導く立場で見ると、この条件式が必要な理由は単純です。この条件を置かないと、この余分な項のために、綺麗な形の非同次波動方程式にならないからです。この余分な項が消去できれば、電磁場ポテンシャルの解を電荷密度、電流密度の遅延関数の積分として求める事ができる波動方程式が導けます。このことは３．（２）１．〜２．を復習されれば明らかです。ただし、歴史をたどれば解るように、Lorenzはこれとは全く違う方法でこの条件式を導いています。
　
　それでは、Lorenzはどの様な過程でこの条件式を導いたのかといいますと、彼は非同次波動方程式を満たす（彼が発見した）遅延電荷密度関数や遅延電流密度関数に“電荷保存則”を適用して導いたのです。
　このことに付いては太田文献2．§4.2のp110-02や、ホィティカーの解説「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）１をご覧下さい。これは別稿「線形振動子による電磁波の放出」１．（２）２．でも説明しました。
　ホィティカーの解説が最も解りやすいと思います。これを４次元相対論的に展開したものが３．（３）３．で説明するものです。

２．ゲージ条件が必要なことの今日的な説明

　Lorenzがこの条件式を設定した理由は明白ですが、その様な条件を設定できる根拠はどこにあるのでしょうか。その事に付いて、今日では次の様に説明されています。

　電場Ｅや磁場Ｈの代わりに電磁ポテンシャルφ、Ａを用いた議論では、なぜこの条件式が必要になるのか。それは、３．（１）で導いた電磁場Ｅ、Ｈと電磁ポテンシャルＡ、φを結び付ける定義式(ａ)(ｂ)では電磁ポテンシャルの決定に任意性が残るからです。別稿「Maxwell方程式系の先見性と電磁ポテンシャル」２．（３）１．［補足説明１］で説明した様にこの定義では電磁ポテンシャルには任意性が残ります。最初に電磁ポテンシャルがＡ₀とφ₀で与えられた場合、それらに gradχ や −（1／ｃ）∂χ／∂ｔ を加えた

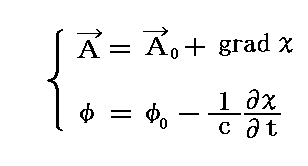
も定義式(ａ)と(ｂ)を満足します。
　そのことは上式を定義式に代入してみれば

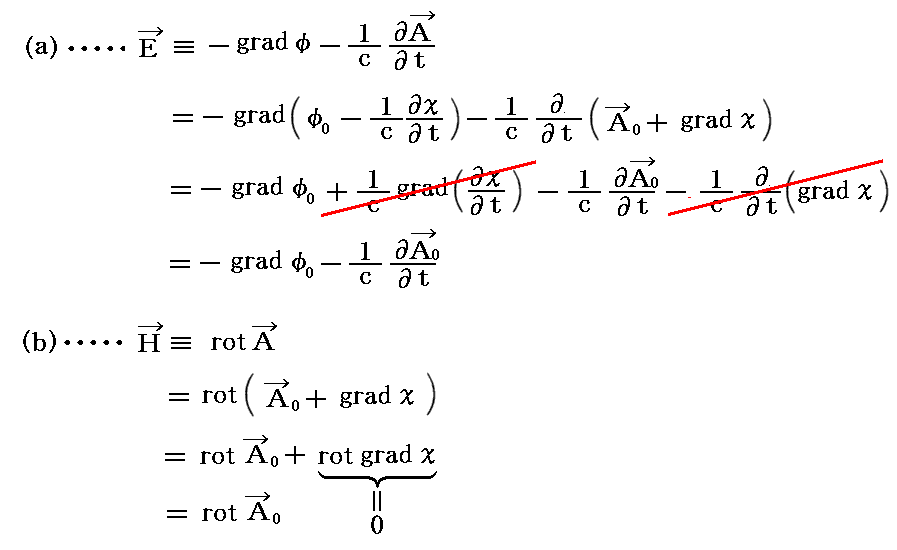
となることから解ります。
　ここでχは時間的に変化する任意のスカラー関数であってかまいませんが、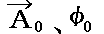の組みから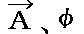の組みへ移る事を“ゲージ変換”（gage transformation）と言います。上記のことは、観測可能な量である電場Ｅや磁場Ｈはゲージ変換しても、その値を変え無い事を意味します。
　このように電磁ポテンシャルが持つ任意性を“ゲージ自由度”といいます。実際の電場Ｅや磁場Ｈを定めるＡやφを確定するには、その自由度を制限するさらなる条件が必要で、その制約条件を“ゲージ条件”と言います。
　上記の“Lorenzの条件式”は、それに相当するものだと言うのが今日的な説明です。しかしこれはいかにも付け焼き刃的なつじつま合わせの説明です。
　Lorenz条件式に対する上記の説明は、ランダウ・リフシュツ著『場の古典論』の中で説明されているものです。推測ですが、今日多くの書籍で採用されているこの説明は、おそらく『場の古典論』の記述からの受け売りなのでしょう。

３．Lorenzの条件式の物理的な意味

　“Lorenzの条件式”を

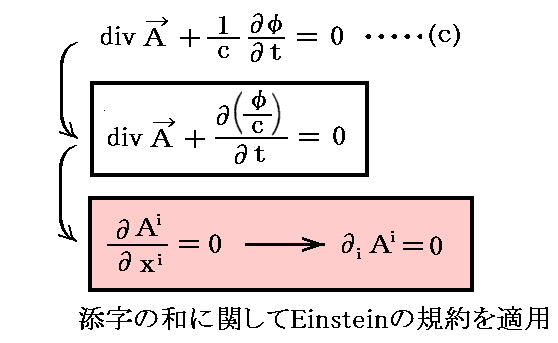
と書き直して、（Ａ^ｘ，Ａ^ｙ，Ａ^ｚ，φ／ｃ）≡（Ａ^１，Ａ^２，Ａ^３，Ａ^４）と並べて見れば、相対論的な“電荷保存則”

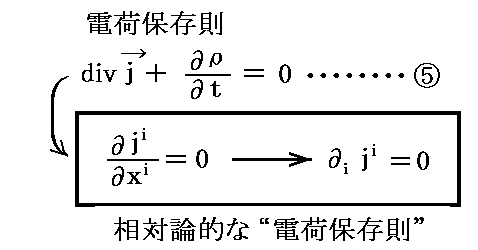
に現れる４元反変ベクトル（ｊ^ｘ，ｊ^ｙ，ｊ^ｚ，ρ）≡（ｊ^１，ｊ^２，ｊ^３，ｊ^４）と旨く対応します。どちらも相対論的な４元反変ベクトルに４元div演算（共変ベクトル）を施したら 0 となる事を示している。
　このことは別稿「Maxwell方程式系の先見性と電磁ポテンシャル」３．（１）［補足説明３］と［補足説明５］で説明しました。ならば電荷保存則とLorenzの条件式が密接に関係するのではないかと思われます。

　実際、［電磁ポテンシャル波動方程式(ｄ)、(ｅ)式］ と “電荷保存則”�D式 が成り立てば、以下の様にして“Lorenzの条件”(ｃ)式が導けます。すなわち(ｄ)、(ｅ)式を成分表示して相対論的な４元ベクトル方程式とみなして変形する。本当は、（ｊ_ｘ，ｊ_ｙ，ｊ_ｚ，ρ）と（Ａ_ｘ，Ａ_ｙ，Ａ_ｚ，φ／ｃ）はどちらも反変ベクトルですから、（ｊ^ｘ，ｊ^ｙ，ｊ^ｚ，ρ）と（Ａ^ｘ，Ａ^ｙ，Ａ^ｚ，φ／ｃ）の様に書くべきです。その辺は上記別稿を復習されて下さい。








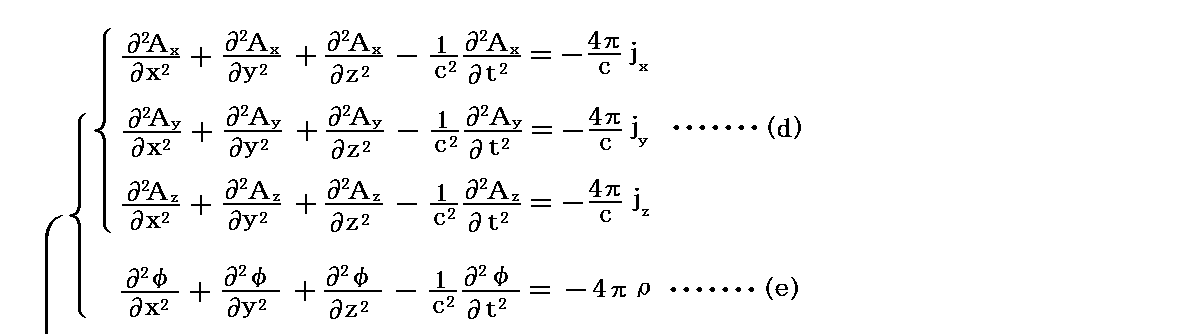
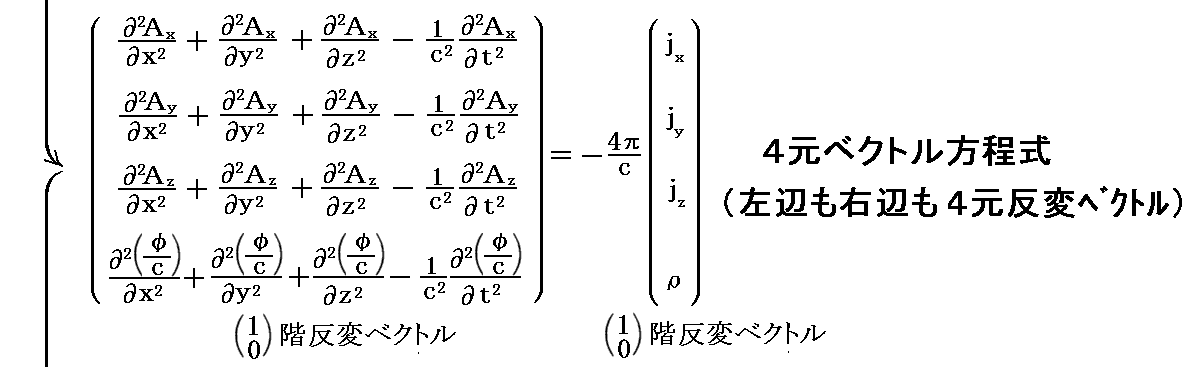
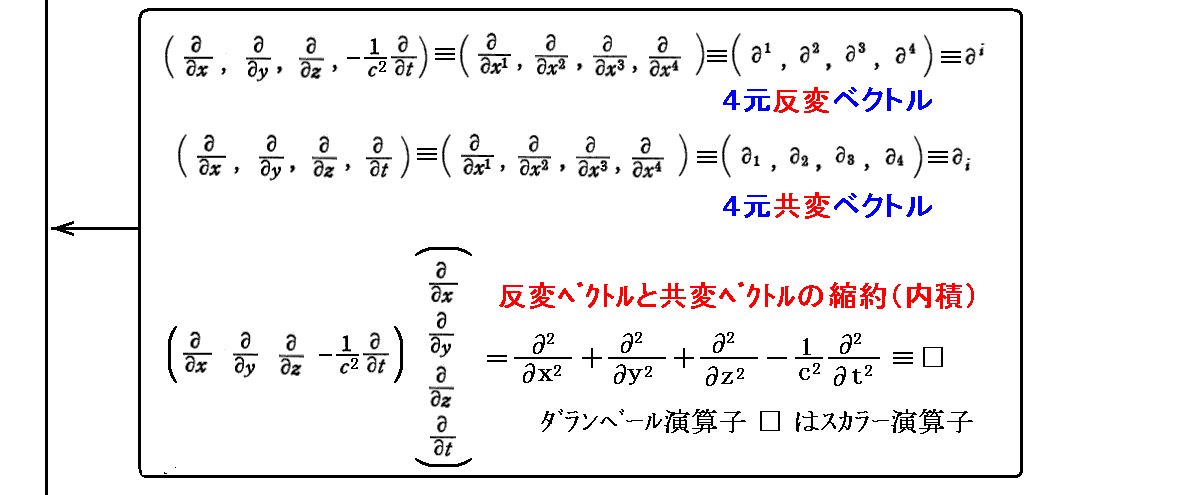
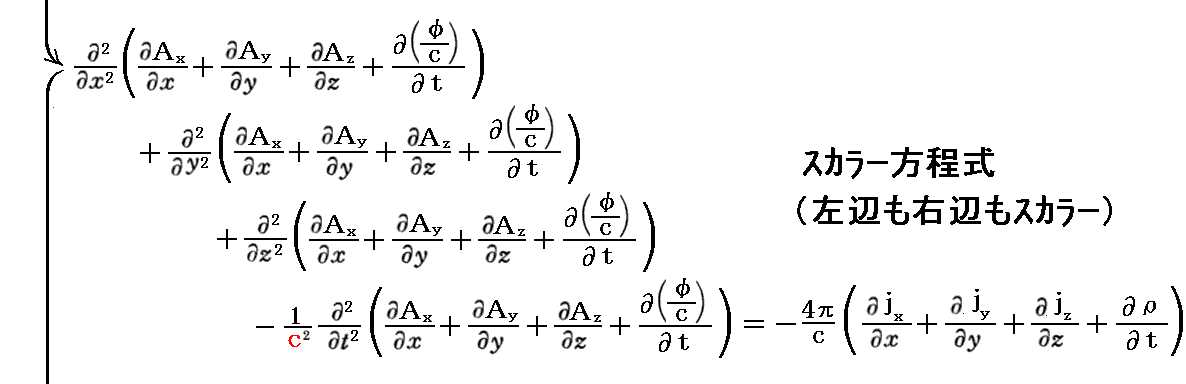
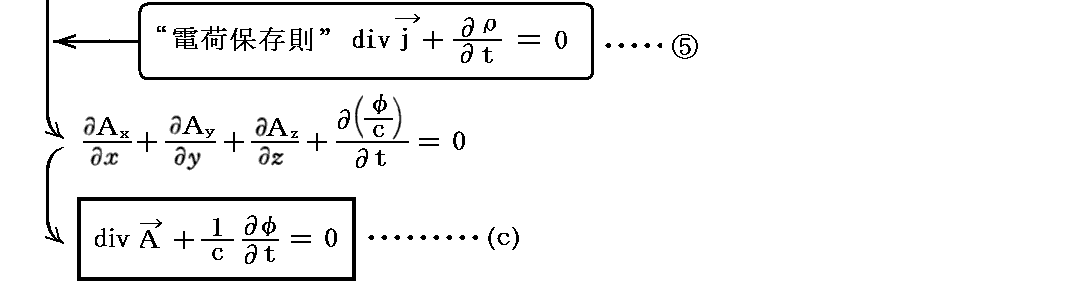
となります。

　これを３次元的・古典論的に行うと、「Maxwell方程式系の先見性と電磁ポテンシャル」２．（２）１におけるホィティカーの示した手順の脚注１）の展開になる。

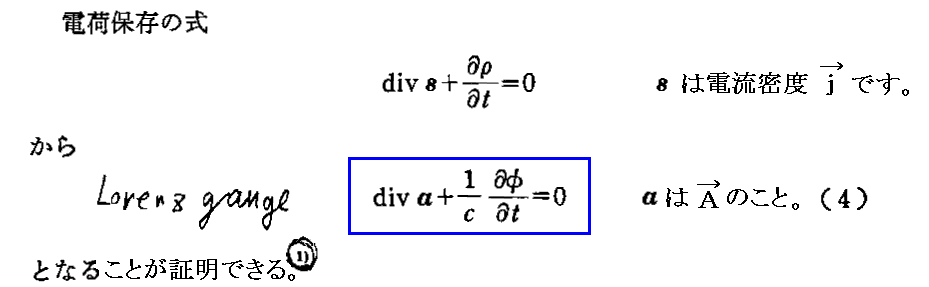
　すなわち、上記の“電荷保存式”中の電流密度ｓや電荷密度ρが遅延時間の項を含む遅延電流密度関数ｓ’（ｔ−ｒ／ｃ）であり、遅延電荷密度関数ρ’（ｔ−ｒ／ｃ）であるとすると、それらは当然ベクトルポテンシャルａとスカラーポテンシャルφの“非同次波動方程式”

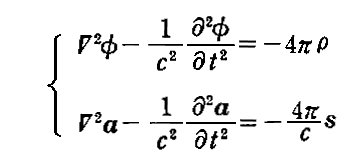
の解となりますので、

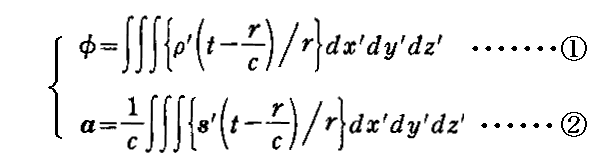
の様におけます。以下の展開ではこの2つの関係式�@�Aから出発します。

この式変形の意味は解りにくいので、別稿「線形振動子による電磁波の放出」１．（２）２．を参照されたし。

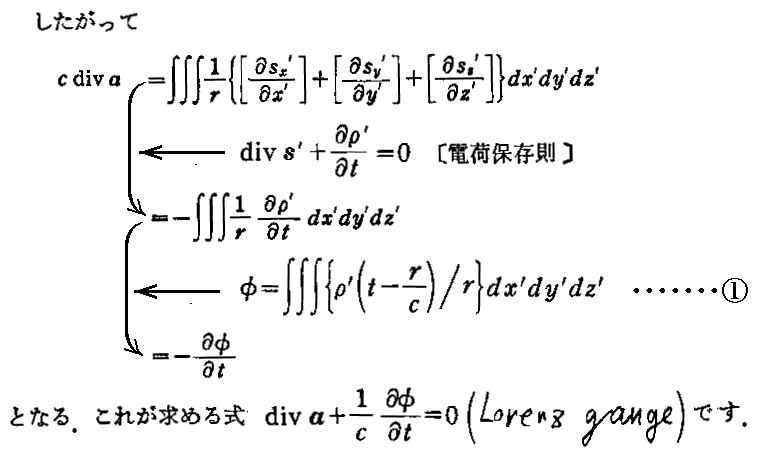
　いずれにしても、“Lorenzの条件”(ｃ)式 は 　［電磁ポテンシャル波動方程式(ｄ)、(ｅ)式］ と “電荷保存則”�D式 から必然的に導けます。だから“Lorenzの条件式”の物理的意味は電荷保存則であると言って良いでしょう。
　
　このとき、２．（１）２．［補足説明１］で注意したように“電荷保存則”�D式 は ［Maxwell方程式�@、�A式］ と等価でしたから、［Maxwell方程式�@、�A式］と［電磁ポテンシャル波動方程式(ｄ)、(ｅ)式］が等価なら、Lorenzの条件式(ｃ)式が(ｄ)、(ｅ)式の中に含まれているのは当然かも知れません。実際、(ｄ)、(ｅ)式を得るためには(ｃ)式が成り立つことが必然の条件なのですから。このことは３．（２）１．や３．（２）２．の式変形を見なおせば確認できます。。
　
　その様に見なすことができるのは、スカラーポテンシャルφやベクトルポテンシャルＡが下記［補足説明１］で説明する様なものであるとすれば φ と Ａ の関係は丁度“電荷保存則”に於ける ρ と ｊ の様な関係と見なすことができるからでしょう。］

［補足説明１］
　ここで、スカラーポテンシャルφやベクトルポテンシャルＡとは何なのかを補足します。これらの量の説明は
前野昌弘著「相対論講義録2010年度（平成23年2月4日版）」p97〜98
の解説が秀逸なので前野氏のＨＰからそのまま引用しています（別稿「カルマン渦列」２．（３）２．［補足説明３］も参照）。
　スカラーポテンシャルφをつくるものは電荷と、ベクトルポテンシャルＡを作るものは電流になります。下左図の○に＋の記号の位置に電荷が存在する。また下右図の黒矢印の位置に電流密度素片が存在するとします。本来電流は連続した回路となるのですが、その一部が取り出されていると考えて下さい。

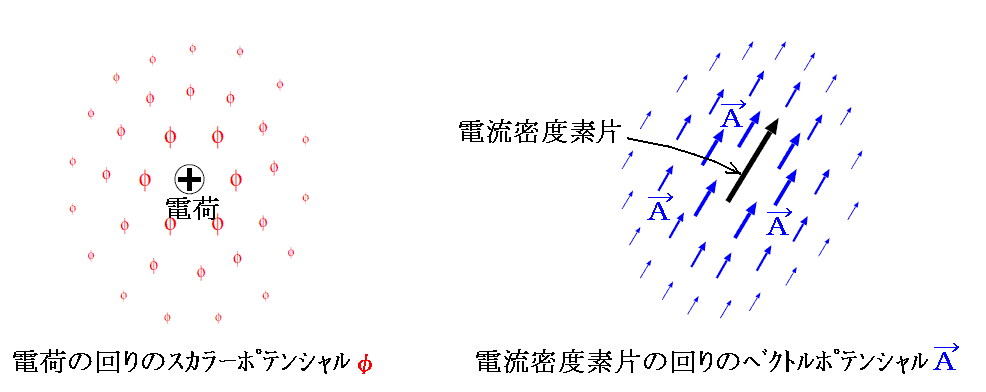
上左図の電荷の回りのφの値を決めるのが、次式

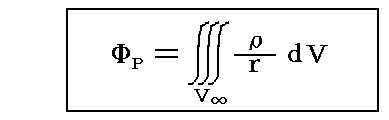
です（非有理化gauss単位系）。上左図ではφ記号の大きさでφの値の大きさが、その分布の様子とともに示されています。φの大きさは電荷からの距離に反比例して小さくなる。もちろん上式のρは電荷密度です。そして、電荷がたくさん分布している場合は、それぞれの電荷が作るスカラーポテンシャル場を重ね合わせたものになります。
　また上右図のＡベクトルの分布を決めるのが、次式

です（非有理化gauss単位系）。図の青矢印の分布でベクトルポテンシャルＡの分布の様子が示されています。ベクトルＡの方向がすべて電流密度素片の方向を向き、その大きさは電流密度素片からの距離に反比例して小さくなります。もちろん上式の（ｊ_ｘ、ｊ_y、ｊ_ｚ）は電流密度ベクトルです。もちろん電流密度素片が連続的に分布して回路を作る場合は、それぞれの電流密度素片が作るベクトルポテンシャル場を重ね合わせたものになります。
　
　スカラーポテンシャルの意味は別稿「保存力」で説明した二次元の場合のポテンシャルの山を三次元に拡大したもので尽くされています。もし電荷ｑがスカラーポテンシャル場φの中に存在するとｑφという位置エネルギーを持つことになり、場φの大きさの勾配に従った力を受けることになる。
　
　ベクトルポテンシャルの意味を、上図の電流密度素片が縦方向に無限に連なった無限直線電流の場合で説明します。無限直線電流が作るベクトルポテンシャルＡの分布は、上記の電流密度素片が作るベクトルポテンシャルを重ね合わせたものになりますから、下図の様に直線電流の回りに、直線電流の方向を向いて分布し、その大きさは距離に逆比例して小さくなります。

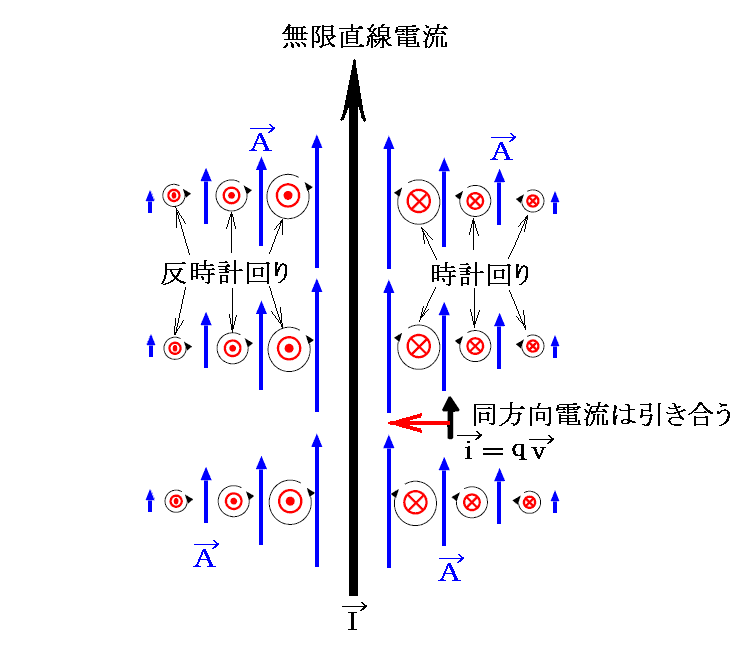
このベクトル場Ａを流れの流速を表す様なものだと見なして、別稿「カルマン渦列」２．（２）で説明したベクトル演算 rot

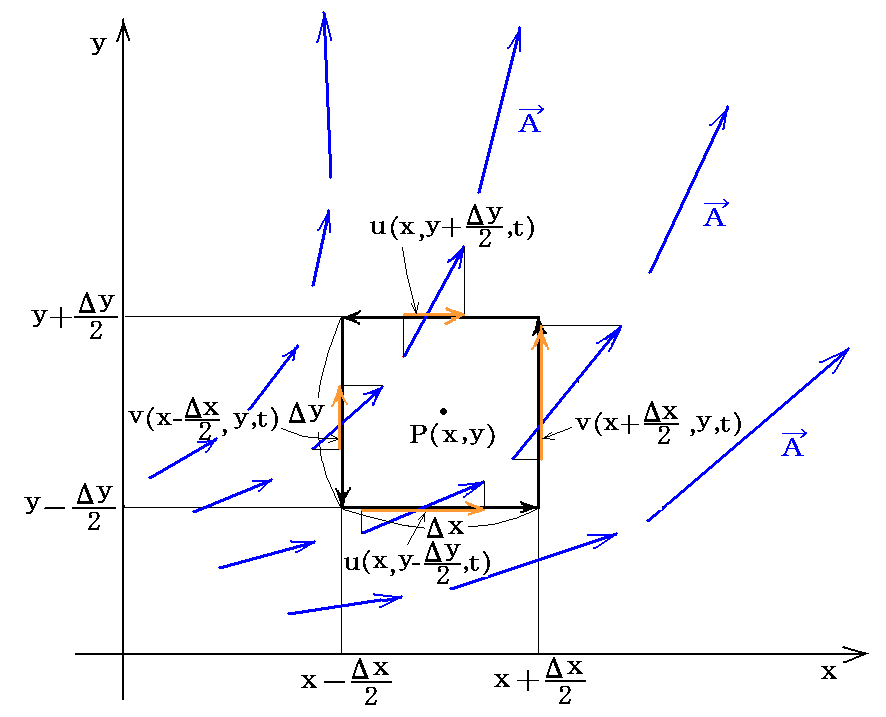
の意味を適用する。
　一つ前の図の青矢印で示した流れの場Ａは導線の左側では反時計回りの渦を、導線の右側では時計回りの渦を生み出す。実際ベクトル演算rotＡはその渦の回転を右ネジと見なしたときネジの進む方向のベクトルを意味する。この rotＡ こそ電磁気学における磁場ベクトルＨです。
　つまり磁場Ｈ＝rotＡは導線の回りに渦を巻くように存在することになる。一つ前の図の赤丸に赤点は手前向きの磁場ベクトルＨを赤丸に赤×は向こう向きの磁場ベクトルＨを表す。その○の大きさが磁場ベクトルＨの大きさを表している。
　このようなベクトルポテンシャル場の中に電流素片 ｉ＝ｑｖ を入れるとローレンツの力の法則に従った力を受けるので、電流素片 ｉ＝ｑｖ は一つ前の図中赤矢印方向の力を受けることになる。
　つまり、ベクトルポテンシャルＡと同方向の電流要素 ｉ はベクトルポテンシャルＡが増大する方向に力を受け、ベクトルポテンシャルＡと反対向きの電流要素 ｉ はベクトルポテンシャルＡが減少する方向の力を受ける。これはちょうど−電荷がスカラーポテンシャルφが増大する方向に力を受け、＋電荷がスカラーポテンシャルφが減少する方向に力を受ける事情によく似ている。
　まさに、それら分布状況がポテンシャル（位置エネルギー）を表している。

［補足説明２］
　３．（３）３．本文中の式変形に付いて補足します。
　《3.(2) まとめ》で示した様にMaxwell方程式�@�Aは電磁ポテンシャル非同次波動方程式（ｄ）（ｅ）と等価です。
　
　そのとき、�@�Aを４元ベクトル方程式に統合して両辺の４元ｄｉｖを取ったものについて２．（１）２．［補足説明１］で説明しました。そのとき左辺の４元テンソルの反対称性から左辺が 0 となる事が必然的に言えて、それから電荷保存則が導けるのでした。
　
　ここで示した操作は（ｄ）（ｅ）に付いて、それと同じ操作４元ｄｉｖを取るものです。その式変形の類似性について、是非そこと比較検討して見てください。ここでは、まず右辺の電荷保存則から左辺が 0 になる事が必然的に言えて、それから左辺の構成要素であるローレンツの条件式が成り立つ事が言える事になったのです。

４．参考文献

この稿を作るに当たって、下記文献を参考にしました。感謝！

1. 太田浩一著「マクスウェル理論の基礎（相対論と電磁気学）」東京大学出版会（2002年刊）
2. 太田浩一著「マクスウェルの渦アインシュタインの時計（現代物理学の源流）」東京大学出版会（2005年刊）
   　第4章、第7章および引用文献のリスト
3. 内山龍雄著「相対性理論」岩波書店（1977年刊）第�V章“相対論的電磁気学”
   　これは電磁気学単位系としてMKSA有理化単位系を採用し、４元ベクトルや計量テンソル表見として別稿３．で説明した左側の定義を用いています。ただし、４元電磁ポテンシャルの表現は単位系に依存しますので注意。
4. 中野董夫著「相対性理論」岩波書店（1984年刊）第8章“電磁気学”
   　これは電磁気学単位系としてMKSA有理化単位系を採用し、４元ベクトルや計量テンソル表見として別稿３．で説明した左側の定義を用いています。ただし、４元電磁ポテンシャルの表現は単位系に依存しますので注意。
5. P.G.ベルグマン著「相対性理論序説（新訂増補版）」秀潤社（1978年刊　原本は1942年刊）非有理化Gauss単位系（磁場H）
   第�X章“ｎ-次元連続体におけるベクトルとテンソル”、第�Z章“相対論的電気力学”
6. C.メラー著「相対性理論」みすず書房（1959年　原本は1951年刊）
   第�W章“相対性理論の４次元定式化：テンソル算法”、第�X章“真空中の電磁気学”
   　これは有理化したGauss単位系を用いていますので注意して下さい。