このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
波動現象に内在するメカニズムの説明です。波動方程式とは何か、伝播速度は何によって決まるか説明します。
ここでの議論には、高等学校では習わない偏微分の概念が必要になる。偏微分自体そんなに難しいものではないのでここで説明する。
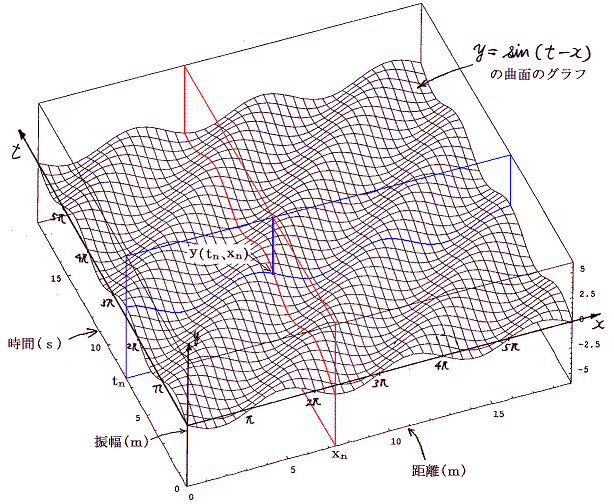
一般に2変数の関数は、その2変数をx軸、t軸(これを時間軸とする)の方向に取ると、その関数値をy軸の値として表した一つの曲面で表すことができる。下図は高校物理で出てくる波を表す関数 y=sin(t−x) をそのようにして表したものです。

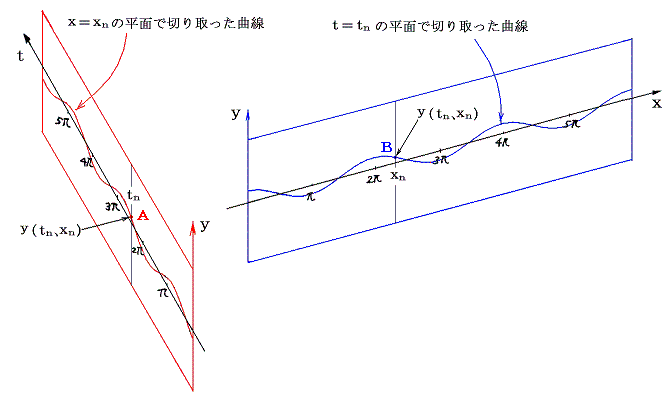
関数y(t、x)の点(tn、xn)におけるtについての偏微分係数とはx=xnの平面で切り出した曲線のt=tnにおけるt軸に沿った方向での微分係数のことです。すなわち上図のA点における曲線のt軸に対する傾きを意味する。また二階の偏微分係数とは、その傾きの変化分を意味する。
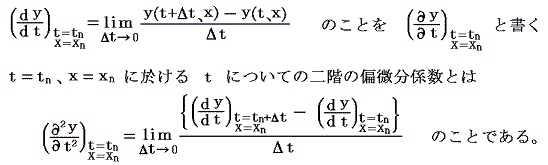
偏微分係数がt−x座標のあらゆる点で定義できる場合、一つの関数となる。これをtについての偏導関数という。
まったく同様に関数y(t、x)の点(tn、xn)におけるxについての偏微分係数とはt=tnの平面で切り出した曲線のx=xnにおけるx軸に沿った方向での微分係数のことです。すなわち上図のB点における曲線のx軸に対する傾きを意味する。また二階の偏微分係数とは、その傾きの変化分を意味する。
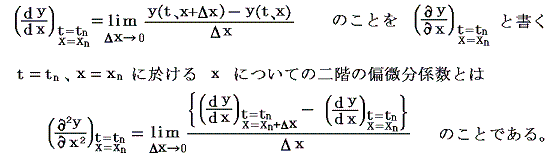
偏微分係数がt−x座標のあらゆる点で定義できる場合、一つの関数となる。これをxについての偏導関数という。
後で出てくる波動方程式は、t−x平面上の任意の点において、xについての二階偏微分係数がその点におけるtについての二階偏微分係数のある定数倍であることを意味している。その関係を満足する曲面こそが波の伝播の様子を表すものであり、その比例定数が波の伝播速度に関係する。
様々な波動現象を比較して論じると、その本質が見えてくる。
縦波の運動は「音速の理論」で述べたように、以下のモデルで説明できる。
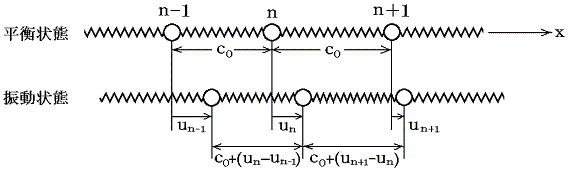
質量mの重りが多くのバネにより一直線につながれていて、平衡状態での重りの間隔はc0とする。質点の大きさは無視できc0は個々のバネの平衡状態における長さです。上図は重りが静止している平衡状態と波が生じている振動状態のある瞬間の状況を表している。
n番目の質量mに対する運動方程式(運動の第2法則)はバネについて成り立つフックの法則(バネ定数k)を利用して
![]()
の様な形に記述できる。これは媒質の変位uの速度の時間的な変化量(つまり加速度)は媒質の変位の位置的な変化の大きさの場所的な変化量(つまり変位の勾配の変化量)によることを示している。
質量のないバネと質点が交互にならんだまま、個々の質点の質量を小さくしながら数を増やし、質点間の間隔c0を0に近づける。そうすると、質量を一様にバネに沿って分布させたスリンキーのようなモデルにすることができる。そのときには集中した質量や質量のないバネは存在しない。そのかわりに、それに沿って質量が分布した一つの長いバネがある。そのとき長いバネの単位長さ当たりのバネ定数k0は個々のバネのバネ定数kを単位長さの中に存在するバネの数N0で割ったものになる。その理由は「直列と並列2.バネ定数」参照。
ここで単位長さ当たりの質量をM0を一定に保ちながら、単位長さ中に存在するバネの数N0を無限大に、また質点mの間の間隔c0を無限小のΔxに近づける場合を考える。すなわち
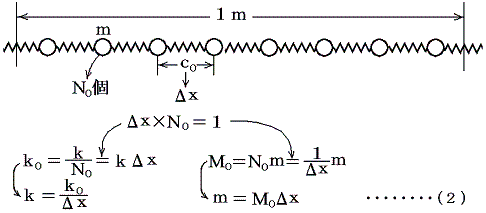
が成り立つとする。(2)式を用いると(1)式は

ここで「音速の理論」 2.音速で述べた議論を参考にすると、三次元的に広がった媒質にたいしては、バネ定数k0は体積弾性率κに、単位長さ当たりの質量M0は体積密度ρ0密に置き換えればよいことが解る。
弦を伝わる波の場合も前節とまったく同様な式が成り立つ。弦の振動は次のようなモデルで取り扱える。質量mの粒子を糸で多数つなぎ、両端を張力Tで水平に引っ張って固定する。静止状態では粒子は等間隔c0で並んでいるとする。任意の時刻tにおける、n番目の質量mの横方向の変位をun、n+1番目の質量mの変位をun+1とする。このとき変位の差un+1−unはc0に比較して十分小さいとし、糸の張力Tは振動中も変化せず一定と仮定できるものとする。
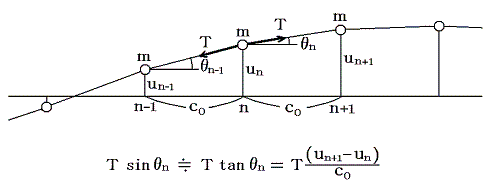
今n番目の質量mに対する運動方程式(ニュートンの運動の第2法則)を考えると
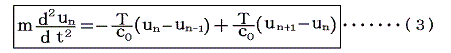
となる。これは(1)式のk0をT/c0 に置き換えた式だから、前節とまったく同様な議論ができる。すなわち単位長さ当たりの質量をM0を一定に保ちながら、単位長さ中に存在する質点の数N0を無限大に、また質点mの間の間隔c0を無限小のΔxに近づける場合を考える。すなわち
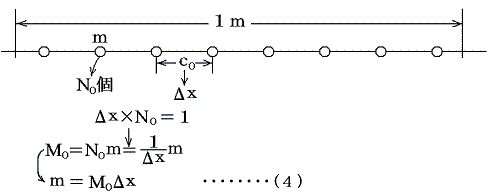
が成り立つとする。(4)式を用いると(3)式は

「交流電気回路」6.波として伝播する交流 に出てきた2本の平行導線を伝わる波(下図参照)を考える。
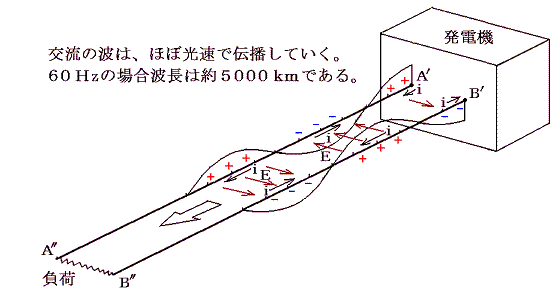
2本の平行導線は一種のコンデンサーになる。さらに、それは小さなコンデンサー(平行導線の短い部分)を並列につないだものであると見なすことができる。また、平行導線の一部分と、その平行導線を結ぶコンデンサーを一つの閉回路とみなすと、その閉回路は、それを貫く磁束密度の変化に対して一種のコイルとしての働き、つまりインダクターとしての働きをする。そのため、2本の平行導線は下図の様なモデルで説明できるだろう。そのときコンデンサーは断線しているのと同じだからインダクターは導線に沿って直列につながっているのと同じになる。ここでは簡単化のため、導線は抵抗(レジスタンス)=0の完全導体とする。
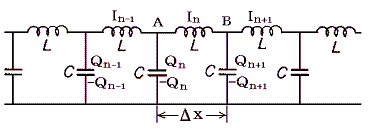
下側の導線を電位の基準0Vとすると、A点の電位はコンデンサーにたまっている電荷がQnだから(コンデンサーの公式により)VA=Qn/Cとなる。同様にB点の電位はVB=Qn+1/Cとなる。
n番目のインダクターLに生ずる起電力は自己誘導の法則により
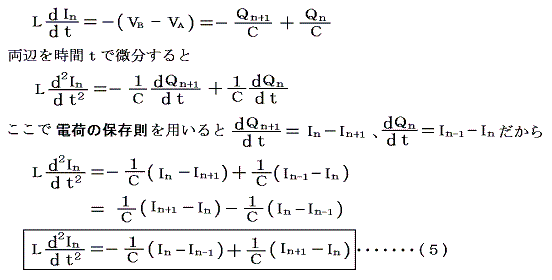
が得られる。(5)式は(1)、(3)式とまったく同じ形をしている。
コンデンサーの並列結合は各々のコンデンサーの容量の和になり(「直列と並列」3.電気容量参照)、インダクターの直列結合は個々のインダクタンスの和になる(「コンデンサーのエネルギー」の自己誘導係数の導き方参照)。そのため以下議論は前節と同様な展開ができる。すなわち単位長さ当たりのキャパシタンスC0やインダクタンスL0を一定に保ちながら、単位長さ中に存在するキヤバシターやインダクターの数N0を無限大に、その間隔Δxを無限小に近づける。すなわち
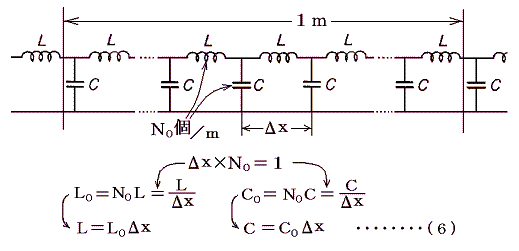
が成り立つとする。(6)式を用いると(5)式は
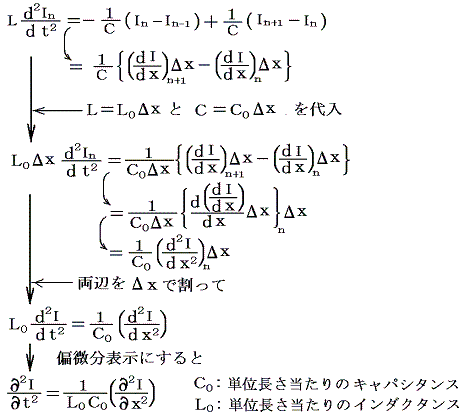
電荷の保存則を出発点とし、それを自己誘導の法則で変形して行くと電圧Vに関する同様な式
![]()
が得られる。 ただし以下ではそうしないで、VとIを対称的に論じてみよう。
インダクターにたいする自己誘導の法則は、2点間の電位差はその間に存在する回路素子を流れる電流の関数として決まるというキルヒホッフの第2法則を意味している。それに対して前記の極限操作をすると
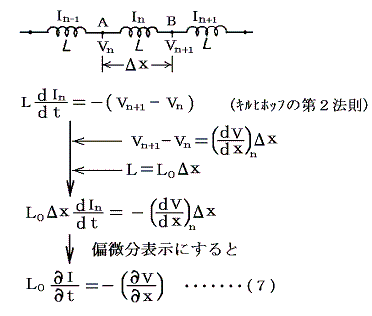
が得られる。
同様に電荷の保存則は回路の節点で成り立つキルヒホッフの第1法則を意味する。同様な極限操作により
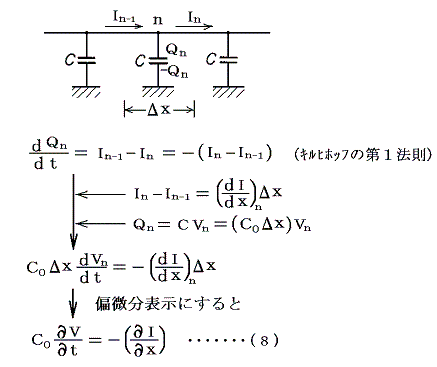
が得られる。
(7)式と(8)式はVとIに対して対称的な形をしてる。(7)式の両辺をtで偏微分したものと、(8)式の両辺をxで偏微分したものを一緒にすると
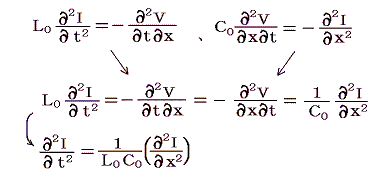
が得られる。
同様に(7)式の両辺をxで偏微分したものと、(8)式の両辺をtで偏微分したものを一緒にすると
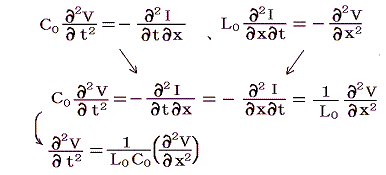
が得られる。VもIも同じ方程式を満足する。
液体の深さhに比べて波の波長が十分大きくて、液体全体が深度によらない速度で波動と供にほぼ水平に移動する波を長波という。長波については「共振(共鳴)」5.共振の例参照。今、幅b、深さhの水路を伝播する長波を考察するために、下図のように座標軸を取る。y=0が静止したときの水面であるとする。
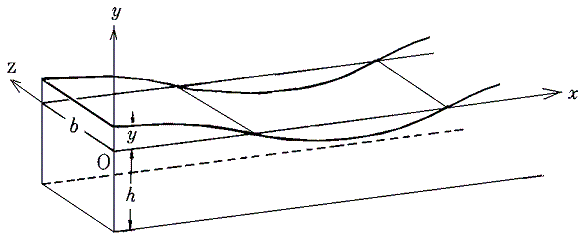
上下振動の振幅Aは波長λに比較して十分小さいと考えて良く、上下方向の速度、加速度は水平方向の速度、加速度に比較して無視することができる。今xとx+Δxの面に挟まれた厚さΔx、幅b、高さh+yの流体の塊に付いて運動方程式を考えよう。その塊が持つx方向の速度をuとする。また流体の密度(単位体積の質量)をρとする。大気圧は共通だから以下の議論では省略できる。
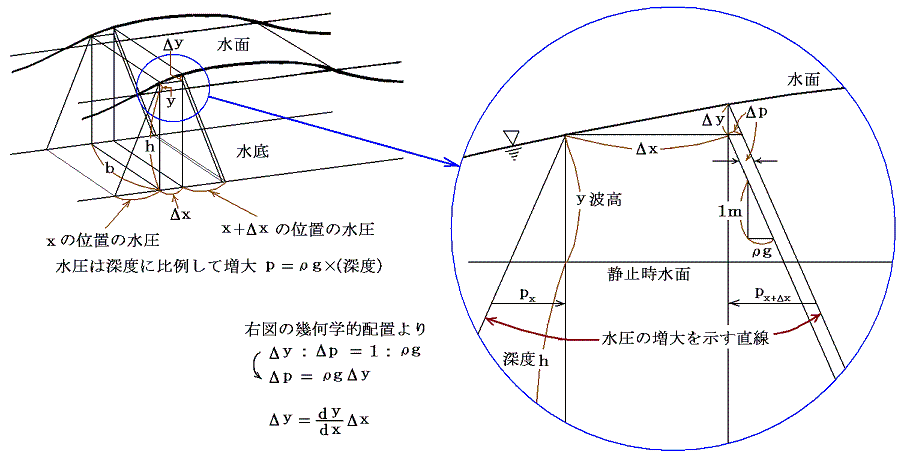
着目している流体塊の質量はρb(h+y)Δx。また流体塊のx面に働く右向きの圧力と(x+Δx)面に働く左向きの圧力の差Δpが流体塊に働くx軸方向の力だから運動の第2法則は
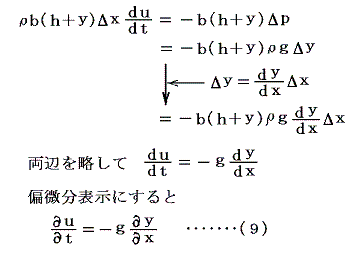
となる。
次に上記の流体塊の水面の高さの変化を考える。xとx+Δxの面を固定すると、その面を通して流入・流出する水の量がその位置の水面の高さ変動に関係する。
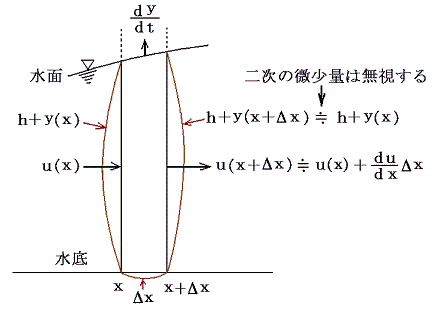
水は非圧縮生流体だからいわゆる連続の方程式がなりたつ。そのため、面積(bΔx)の水面の上下動は、xとx+Δxの位置の幅b、高さh+yの仮想平面を出入りする水量に関係する。

となる。
ここで(9)、(10)式は前節の(7)、(8)式とよく似ている。前節と同様な手順をたどることにより
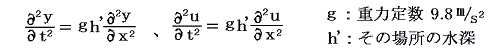
となり、y及びuについての方程式が得られる。
[補足説明1]
もちろん連続の方程式を運動の第2法則を用いて変形していく初等的なやり方でも良い。液面の上下動の加速度はxとx+Δxの面を出入りする流体速度の時間微分の差分(Δx離れた位置の)に依存し、それぞれの面の位置での流体速度の時間微分はその位置での液面の勾配に依存するから、下記の様に変形できる。
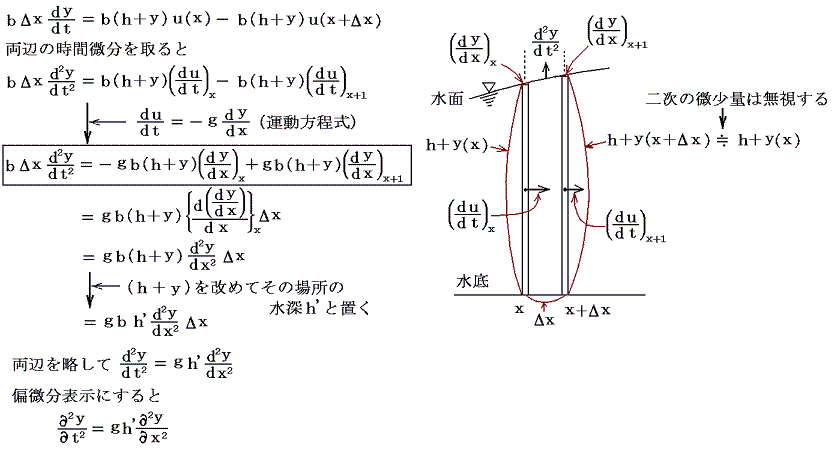
前節の考察から明らかなように様々な波動現象は(1)(3)(5)・・・式等々を出発点として、すべて同形の方程式

に到達する。この形の方程式を特に波動方程式と呼ぶ。つまり波動となって伝わる物理量 f(t、x) があり、その物理量 f の時間的な変化の二階微分は、その物理量 f の距離的な変化の二階微分に比例する。そのとき比例定数
c の平方根が次で述べるように波の伝播速度になる。
「音速の理論」のときには(1)式(波動方程式(11)式の元になった式)の解として
![]()
の形を天下り的に与えて論じたが、実はその形は何でもよいのです。(1)式にしろ、もっと一般の(11)式にしろ波を表す関数fが時間tと変位 x の一次結合 ξ=at−x の関数でありさえすれば良いのです。つまり f(ξ)=f(at−x) の形をしていれば良いのだ。なぜなら、このような合成関数のtやxについての微分は高校数学で習うように
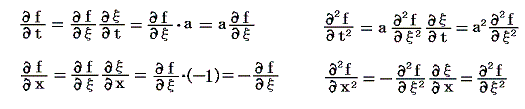
となる。ここでは偏微分記号をもちいたが、高校レベルの常微分の考え方で良い。それらを(11)式に代入すると
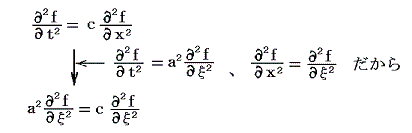
となる。つまり a2=c が成り立ちさえすれば、関数 f はどの様な形であっても必ず波動方程式(11)式を満足するのです。
考えてみればこれは当たり前です。f が ξ=at−x に対する関数であるということは、その関数 f の t の変化に関する関数形と、x の変化に関する関数形が(定数倍の違いはあるが)同じと言うことを意味している。関数形が同じなら一階微分だろうと、二階微分だろうと t に関するものと x に関するものが同じになるのは当たり前であり、波動方程式を満足するのも当たり前です。
これは、x軸(正)方向の変化がそのままt軸(負)方向にそっても起こることを意味する。そして、このことが波がその波形を保ったままで速度 a で伝播することを意味する。このことは図示してみれば明らかです。
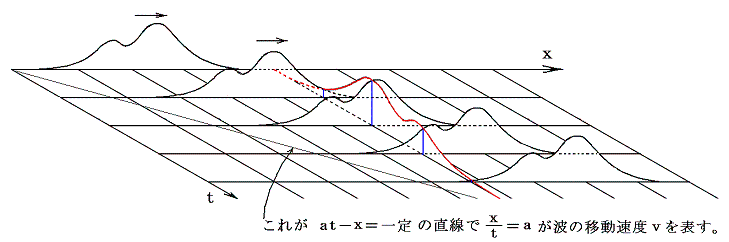
任意の波形の波をx軸方向に速度 x/t=a で動かしてやりさえすれば、x値を固定したときの時間軸 t に沿った振幅の変化がx軸方向の振幅変化と全く同じになる(定数係数の違いを除いて)ことがわかる。これこそ波動方程式が要求していた事柄です。
波動方程式 ∂2f/∂t2=c・∂2f/∂x2 の解曲線 f(x,t) の振る舞いに付いてもう少し補足します。
波動方程式の右辺の x の二階導関数 ∂2f/∂x2 は、場所 x における解曲線の曲がり具合が 上に凸であるか凹であるか を示しています。
また波動方程式の左辺の t の二階導関数 ∂2f/∂t2 は場所 x の位置において f の大きさ が時間の経過とともに増大あるいは減少する加速度を表しています。
上記の f(x,t)グラフ の場所的・時間的変化の様子を検討されれば波動方程式が表している状況を旨く反映していることがお解りだと思います。
そのとき、波動方程式では、f(x,t)グラフ が時間的に右に動いても、左に動いても上記の状況を満足することに注意して下さい。
ここで η=at+x の様に−を+にした形にしても同様に(11)式を満足する。η についても ξ についての計算とまったく同様です。更に言えばtとxの順番を入れ替えて ξ=ax−t や η=ax+t の様にしても同様に(11)式を満足する。ただしこの場合は a2=1/c となる。
本質は t と x の一次結合の関数でありさえすればその形はどの様なものでも良い所にある。一般解は f(at−x) と、線形結合の符号を入れ替えた解
g(at+x) との和で表される。
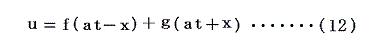
(12)式が解になることは方程式(11)に代入してみれば了解できる。そのとき必要な条件は a2=c が成り立つことです。
関数 f(ξ) や g(η) がどんな形であるかは決して微分方程式(11)式からは定めることはできない。その形は最初に与えられた波形(初期条件)と境界での反射の様子(境界条件)によって初めて定まる。そして、その最初の波形は、波動方程式を導くときに用いた条件(媒質の連続性や変位のなめらかさ、またそこで仮定した種々の微少性)を満足するものであればどの様なものでも良い。
解の形として正弦関数や余弦関数を用いる場合が多いが、その理由はそれらの和を取ることで任意の波形が表現できるからです。そのとき、それらの関数の和も波動方程式を満足する事は代入してみれば解る。また、その形で論じると波の周期や波長を明瞭に認識することができるからです。定数 a を 2π/T と 2π/λ の2つの部分に分けて表し ξ=(2π/T)t−(2π/λ)x や η=(2π/T)t+(2π/λ)x の様に置いてみると、T は周期に、λ は波長になり論じるのに便利だからです。しかし本来そのような周期的な関数である必要もない。
波動関数はx軸に沿って正負の方向に進行する波以外に定常波といわれる解も満足する。たとえば前出の f(ξ) と g(η) が同じsin関数の場合、三角関数の公式を用いると(12)式は
となるが、これは下図の様な振動を表す。このように正負の方向にすれ違う同型の波を重ね合わせると定常波ができることは、高校物理の授業で習うところです。
この場合もグラフを子細に検討すれば任意の (x、t) の位置でx軸方向の x の二階微分と t 軸方向のtの二階微分が常に同じになる(定数係数の違いを除いて)ことがわかる。つまりこの形の解も波動方程式を満足している。これはもともと(12)式と同じものであるから満足して当然です。もっと任意の波形についても定常波を考えることができる。
一般解(12)式は一つの重要な結論を含んでいる。ξ=at−x または η=at+x が一定値なら f(ξ) や g(η) が一定の値になる。例えば at−x=(一定値) {つまり x=at−(一定値)}なら、これはx−t平面上で傾き a の直線のグラフになる。変位一定の部分が、その直線のグラフに沿って移動していくことを意味する。つまり f(ξ) はその形を保ったままx軸の正の方向へ速度 a で移動する波を表す。同様に g(η) はx軸の負の方向へ速度 a で移動する波を表す。
その当たりを高校物理で良く出でくる y=sin2π(t/4−x/6)を例に取って見てみる。
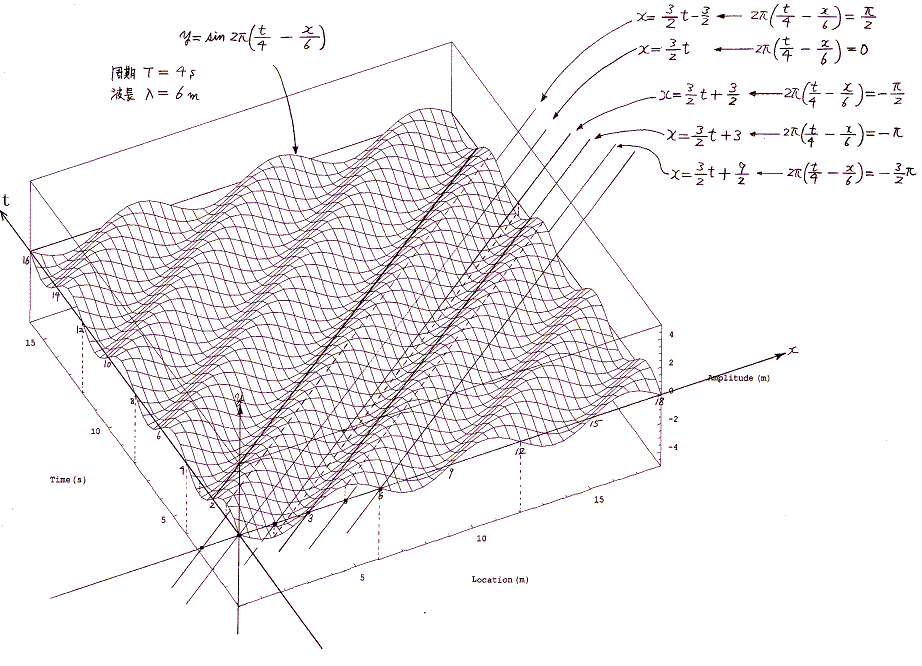
まさに、波は 3/2=1.5m/s の速さでx軸の正の方向へ伝播している。
ところで、解(12)式中のaは波動方程式(11)中のcと a2=c で結びつけられるから波動方程式(11)式の比例定数cの平方根が波の伝播速度を表している。つまり前述2.項で導かれた波動方程式の比例定数の平方根をとると
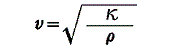
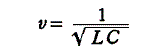
となるわけです。
[補足説明1]
上で説明した様に、波動方程式(11)式の比例定数cの平方根が波の伝播速度に関係するのですが、ここで取り上げたすべての例に於いて比例定数cは様々な物理量に関係しますが、いずれも実際に発生する波の波長や振動数(振動周期)には依存していませんでした。
しかし、現実の波動現象に置いては比例定数cは発生する波長(振動数or振動周期)に関係します。つまり、発生する波の形状が異なるとその伝播速度は少し変化します。そのため2.(2)の図で説明した様にその波の形を変えずに波が伝播する事はありません。一定の位相速度で、その波の形を変えずに伝播する事はありません。
そして、その場合に様々な波長の波を重ね合わせた波群の速度(“群速度”という)は単独な波の伝播速度(“位相速度”と呼ぶ)とは異なったものになります。つまり別稿「群速度と位相速度」で説明する“位相速度”と“群速度”が異なったものになるには、波動方程式(11)式の比例定数cが発生する波の振動周期(波長)に依存して変化する事が必要です。
ここはなかなか解りにくい所ですが、波動方程式(11)式の比例定数cが一定不変の定数であるとは、ある振動周期Tで波長λの波が発生して伝播していくとすると、振動周期をTからT+δTに変えたとき、発生伝播する波の波長はλ+δλになるのですが、このとき
が成り立つようにδTとδλは変化すると言うことです。
波を角振動数(角速度)ωと波数kによる表現にすると
が成り立つ様にδωとδkが変化しなければ成らないと言うことです。
この場合のみ位相速度速度が発生する波の振動周期(波長)に依存しないと言うことで有り、この場合のみ発生・伝播する波の形は変形すること無く伝播すると言うことです。
2本の導線は抵抗R=0の完全導体とする。前述2.(3)と3.(3)の結論から導けるように、電線を伝わる波が満足すべき波動方程式
![]()
の解で、x軸の正方向に伝播するものは
![]()
となる。f(ξ)は初期条件から決まる任意の関数。これを自己誘導の法則(7)式に代入して
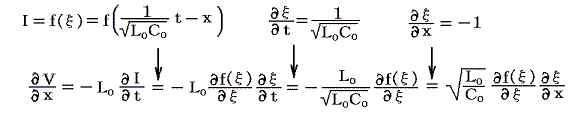
両辺をxで積分すると
![]()
が得られる。α(t)は積分定数です。この式と上記I=f(ξ)を電荷の保存則(8)式に代入して整理すると
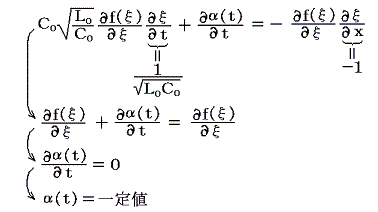
となる。つまり定数α(t)は電位の基準を与える単なる定数です。だからα=0とてさしつかえない。結局V(ξ)=V(t,x)は
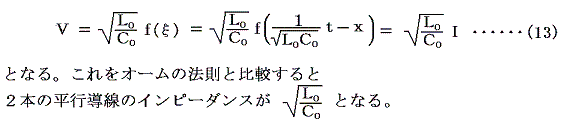
L0とC0はそれぞれ平行導線の単位長さ当たりのインダクタンスとキャパシタンスだから、電線のインピーダンスは電線の長さに無関係になる。しかもこれはIとVに位相のずれを引き起こす項目を含まない単なる抵抗を意味し波動抵抗と呼ばれる。そのため電圧と電流は同位相で伝播していく。(次図参照)
もちろん以前に説明したようにx軸の負方向に伝播する
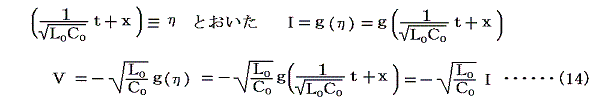
も解になる。(14)式の符号が(13)式と逆転していることに注意。さらにそれら2つの解の和 f(ξ)+g(η)も解になる。
電線のインピーダンスが ( L0/C0)1/2 ということは、その2本の導線の端を大きさが ( L0/C0)1/2 のオーム抵抗で結合すれば(電流−電圧関係に不連続が表れず)反射が起こらないことを意味する。つまり完全なインピーダンスマッチングが取れて、波はすべて端末に結合した抵抗に吸収され、最終的に熱エネルギーとなって消費される。
2本の導線がそれぞれ広い帯(幅w)となり、その間(間隔d)の空間が真空で、帯の物質が完全導体の場合を考える。このとき、縁の部分を無視すれば、中間の空間では、電界Eも磁界Hも一様になる。Eは帯の面に垂直で、Hはそれに平行です。
前述のように、その波形は初期条件・境界条件のみに依存し、どの様なものでも良かったので、ここでは正弦関数を仮定して図示する。ここで電圧の基準点を平行導線の中間部にすると二本の導線の電位は下図赤線のようになる。そのとき電流の分布は(13)(14)式から解るように、V>0の所では波の進行方向を向きその大きさはVに比例している。V<0の所では波の進行方向とは反対の方向を向きその大きさはVに比例している。また、電荷の分布は電圧の分布と同じです。
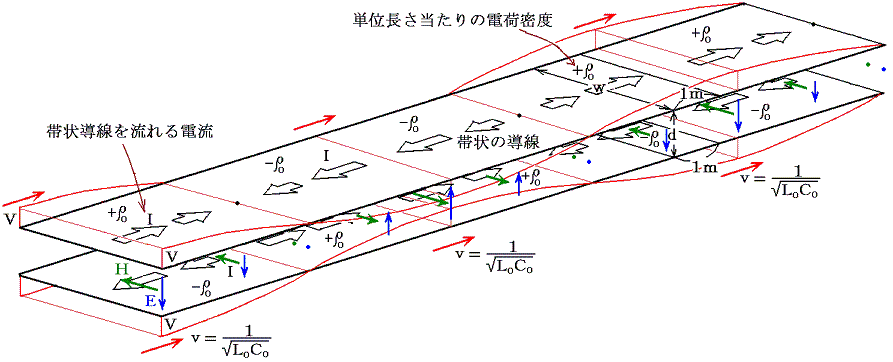
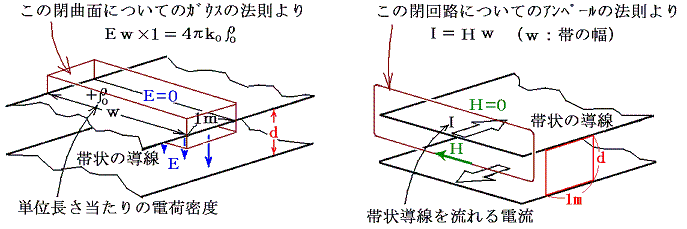

ここでε0=8.854×10-12F/m、μ0=4π×10-7N/A2(またはH/m)だから、伝播速度は1/{8.854×10-12(F/m)×4π×10-7(N/A2)}1/2=3.0×108m/sとなる。このとき[F]=[C/V]、[V]=[J/C]=[kgm2/(s2C)]、[A]=[C/s]だから、確かに速度の単位[m/s]になることに注意。
また仮にd/w=0.1としてε0、μ0を代入すると波動抵抗は38Ω程度になり、これは導線の長さに依存しない。このときも確かに抵抗の単位[V/A]=[Ω]になることに注意。
実際には平行板を丸めた円筒状の同軸ケーブルが利用される。その際の波動抵抗は内部導体と外部導体の半径比と、絶縁のために導体間に充填されている絶縁体の誘電率で決まるが、実用されてい同軸ケープルの波動抵抗は50Ω〜75Ω程度です。
長波の伝播に伴って、液体の各部分がいかなる運動をするのかを調べてみよう。2.(4)長波 で得た式
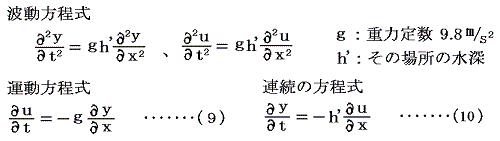
は、前項 3.(4)電線を伝わる波の補足 で用いた
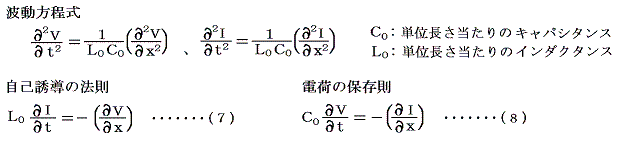
とまったく同じ形をしている。そのため、Vをyに、Iをuに、gを1/L0に、h’を1/C0に置き換えれば前項の議論がそのまま利用でき、そのときの結論が成り立つ。つまり方程式の解として
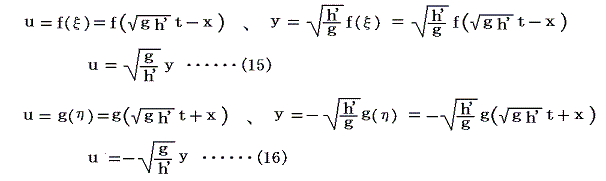
が得られる。ここでf(ξ)やg(η)は初期条件から決まるξとηの任意の関数でよい。
ここでx軸の正方向に伝播する長波では、(15)式に従ってy>0の場所(水面が上昇している)では、深さ方向に関してすべて同一の速度u>0でx軸の正方向に動き、y<0の場所(水面が下降している)ではu<0でx軸の負方向に動くことが解る。前述のように、その波形は初期条件・境界条件のみに依存し、どの様なものでも良いのだが、ここでは正弦関数を仮定して図示する。

同様にx軸の負方向に伝播する長波では、(16)式に従ってy>0の場所(水面が上昇している)では、深さ方向にすべて同一のu<0でx軸の負方向に動き、y<0の場所(水面が下降している)ではu>0でx軸の正方向に動くことが解る。
本節で説明した内容については、別稿「水の波」§32.“長い波”や、別稿「波動」53.“長波”なども参照されて下さい。