挷榓怳摦巕乮帺桼怳摦丄嫮惂怳摦丄尭悐怳摦丄嫮惂尭悐怳摦乯
丂暿峞乽塣摦偺朄懃乿俁丏乮係乯偲丄暿峞乽僄僱儖僊乕曐懚懃偺徹柧乿俀丏偱椡偺尰傟曽偺堘偄偱丄塣摦偺條巕偑曄傢傞偙偲傪娙扨偵愢柧偟傑偟偨偑丄偙偙偱偼丄椡偑堦師尦乮倶惉暘偺傒乯偱倃亖倃乮倶乯偺傛偆側埵抲娭悢偲偟偰梌偊傜傟傞応崌偺廳梫側椺偱偁傞挷榓怳摦巕偵偮偄偰愢柧偟傑偡丅
丂杮峞偺撪梕偺廳梫側墳梡偑乽慄宍怳摦巕乮揹婥憃嬌巕乯偵傛傞揹帴攇偺曻弌乿偱偡偺偱丄崌傢偣偰偛棗壓偝偄丅
侾丏椡偑埵抲娭悢倃亖倃乮倶乯偲偟偰梌偊傜傟傞応崌偺堦斒揑惈幙
丂偙偺応崌僯儏乕僩儞偺塣摦偺戞擇朄懃偼
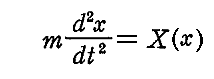
偲側傞丅
丂亂椡偺応偑埵抲娭悢偲偟偰梌偊傜傟傞応崌亃偵偼丄愊暘偵傛偭偰僄僱儖僊乕曐懚懃傪摫偔帠偑偱偒傞丅椉曈偵倓倶乛倓倲傪忔偠偰曄宍偡傞偲
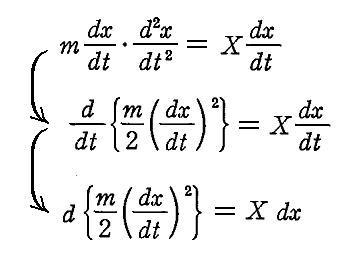
偲側傞丅
丂塃曈偺倃倓倶偼椡倃偵傛偭偰側偝傟傞巇帠偺旝彫曄暘偩偐傜丄偙傟偼乬幙揰偺塣摦僄僱儖僊乕偺曄壔偼丄椡倃偵傛偭偰側偝傟傞巇帠偵摍偟偄丅乭偙偲傪堄枴偡傞丅偨偩偟幙揰偺塣摦僄僱儖僊乕俿偼
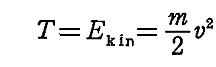
偱掕媊偟偰偄傞丅偙偙偱偝傜偵億僥儞僔儍儖僄僱儖僊乕倁傪
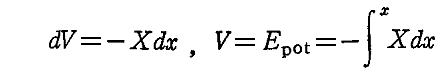
偱掕媊偡傞偲丄慜婰偺娭學幃偼愊暘偱偒偰倁偺晅壛揑側掕悢偺擟堄惈傪彍偄偰
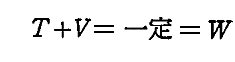
偲側傞丅倂偼慡僄僱儖僊乕偲屇偽傟傞掕悢偱丄乬僄僱儖僊乕曐懚懃乭偲偄傢傟傞娭學幃偱偁傞丅
丂僄僱儖僊乕曐懚懃偼埲壓偺傛偆側拲栚偡傋偒悢妛揑張曽傪採嫙偡傞丅偡側傢偪
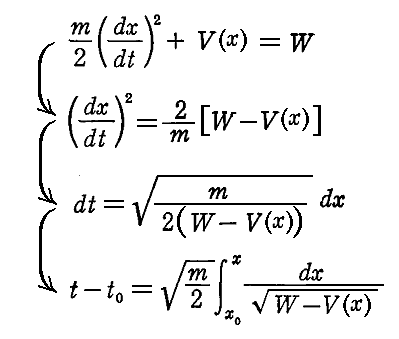
偺條偵偟偰 倲 傪 倶 偺娭悢偲偰抦傞偙偲偑偱偒傞丅
丂偁傞偄偼丄偦偺摼傜傟偨寢壥傪媡偵夝偄偰 倶 傪 倲 偺娭悢偲偟偰媮傔傞偙偲傕偱偒傞丅偙傟偼塣摦曽掱幃偺姰慡側愊暘偵側偭偰偄傞丅
乵曗懌愢柧乶
丂忋婰偺丂乬亂椡偺応偑埵抲娭悢偲偟偰梌偊傜傟傞応崌亃偵偼丄愊暘偵傛偭偰僄僱儖僊乕曐懚懃傪摫偔帠偑偱偒傞丅乭丂偺拞偺亂椡偺応偑埵抲娭悢偲偟偰梌偊傜傟傞応崌亃偵晅偄偰曗懌偟傑偡丅
丂
丂偙傟偼杮峞偺挷榓怳摦巕偺応崌偺丂俥亖亅倠倶丂偺條側宍偵偐偓傞昁梫偼柍偄偺偱偡丅
丂偡側傢偪丄丂俥亖堦掕乮椡偑応強偵埶傜側偄帠偼丄椡偑偁傞堄枴応強偺娭悢偱偁傞帠傪堄枴偡傞乯丂傗丂俥亖亅侾乛倰2丂偺條側傕偭偲堦斒揑側椡偺応偵偮偄偰傕惉傝棫偮帠偵拲堄偟偰壓偝偄丅
丂
丂峏偵偙偺偲偒丄忋婰偺椺偱偼丄丂俥亖亅grad乮1/2倠倶2乯丂傗丄俥亖亅grad乮們倧値倱倲丒倶乯丂傗丄俥亖亅grad乮亅1乛倰乯丂偺條偵丂俥亖亅grad乮兂乯丂偵傛偭偰椡傪摫偔偙偲偑偱偒傞億僥儞僔儍儖応兂乮亖1/2倠倶2丂丄亖們倧値倱倲丏倶丂丄亖亅1乛倰丂乯偑懚嵼偟傑偡偑丄傕偲傕偲偦偺條偵億僥儞僔儍儖応兂偑懚嵼偡傞椡偺応偱偁傞昁梫偼柍偄丅
丂偡側傢偪丄億僥儞僔儍儖応偱柍偔偰傕偐傑偄傑偣傫丅椡偺応偑埵抲嵗昗偵傛偭偰堦堄偵寛掕偝傟偰偄偝偊偡傟偽椙偄偺偱偡丅
丂
丂偡側傢偪丄亂俥偑埵抲嵗昗偺娭悢亃偱偁傟偽丄塣摦曽掱幃偱峫嶡偟偰偄傞暔懱偺懚嵼埵抲偵傛傞堘偄偵敽偆乬埵抲僄僱儖僊乕乭偲尵偆傕偺偑忢偵掕媊偱偒偰丄偦偺暔幙偑偦偺帪乆偵懚嵼偡傞応強偱帩偭偰偄傞乬塣摦僄僱儖僊乕乭偲偄偆傕偺偲崌傢偣偨傕偺偑丄偄偭傕堦掕抣偲側傞丅偮傑傝乬僄僱儖僊乕曐懚懃乭偲偄偆傕偺偑惉傝棫偮偺偱偡丅
丂
丂埲忋偺帠暱傪棟夝偝傟偨忋偱暿峞乽幙揰偺擇師尦塣摦乮曻暔慄丄懭墌塣摦乯乿傪暅廗偝偨偟丅
丂
俀丏挷榓怳摦巕
丂挷榓怳摦巕偲偼扨怳摦傪峴偆怳摦懱偺偙偲偱偡丅偮傑傝暅尦椡偑曄埵偺検偵斾椺偡傞怳摦懱偺憤徧偱偡丅扨怳摦偲暅尦椡偺娭學偼暿峞偱娙扨偵愢柧偟傑偟偨偑丄偙偙偱偼傕偆彮偟徻偟偔愢柧偟傑偡丅
丂怳暆偑彫偝偄応崌丄戝敿偺怳摦偑偙偺傛偆側暅尦椡偱嬤帡偱偒傞偺偱墳梡忋偲偰傕廳梫偱偡丅
乮侾乯僄僱儖僊乕曽掱幃偺愊暘
丂幙揰偵曄埵倶偵斾椺偟偰丄忢偵嵗昗尨揰曽岦偵摥偔椡偑嶌梡偡傞応崌傪峫偊傞丅
丂偡側傢偪丄亂1丏偱弎傋偨椡偺応亃偑 倠 傪斾椺掕悢偲偟偰 倃乮倶乯亖亅倠倶 偱昞偝傟傞応崌傪峫偊傞丅偙偺偲偒塣摦曽掱幃偼
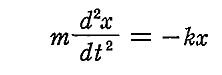
偲側傞丅
丂亂椡偑埵抲嵗昗偺娭悢亃偱偁傞偐傜慜復偺堦斒揑曽朄偵廬偭偰丄愊暘傪幚峴偟偰丄僄僱儖僊乕曐懚懃傪摫偔偙偲偑偱偒傞丅
丂挷榓懇敍椡乵倃乮倶乯亖亅倠倶乶偺応崌偺億僥儞僔儍儖僄僱儖僊乕 倁 偼
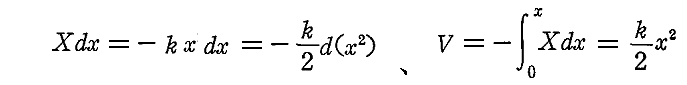
偲側傞丅偨偩偟擟堄偵庢傟傞愊暘掕悢偼倁偑尨揰偱僛儘偵側傞傛偆偵寛傔偰偄傞丅廬偭偰僄僱儖僊乕曐懚懃偼
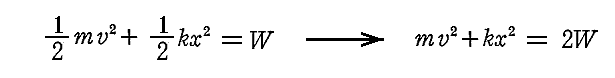
偲側傞丅弶婜忦審傪倲亖0偱倶亖倎丄倴亖倓倶乛倓倲亖0偲偡傞偲 2倂亖倠倎2 偲側傞偺偱

偲側傞丅弶婜忦審乮倲亖0偱倶亖倎丄倴亖倓倶乛倓倲亖0乯傪峫椂偡傞偲
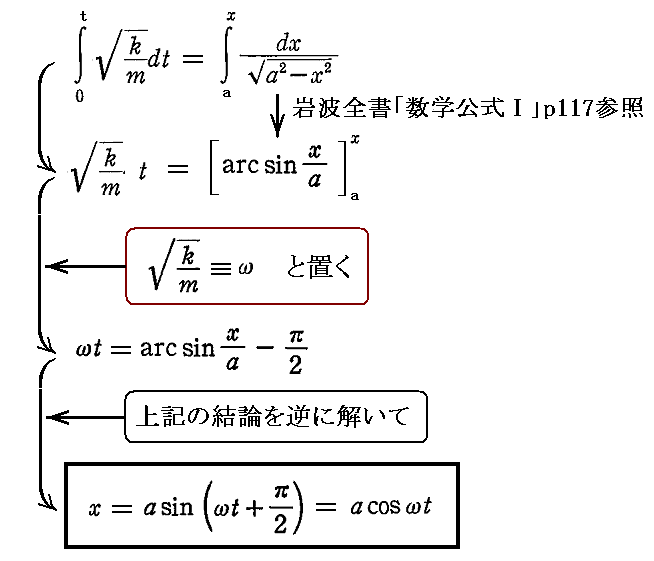
偲側傞丅偮傑傝丄僄僱儖僊乕曽掱幃傪梡偄傞偲丄椡倃偑倶偺偳偺條側娭悢偱偁偭偰傕忢偵塣摦曽掱幃偺夝傪梌偊傞丅
丂偙偙偱冎偺暔棟揑堄枴偼柧妋偱偡丅冎 偼扨埵帪娫偵夞揮偡傞妏搙傪堄枴偡傞乬妏懍搙乮妏怳摦悢乯乭偱偡丅偦傟偼乬廃婜乭冄丄乬怳摦悢乭兯偲埲壓偺傛偆偵娭學偡傞丅
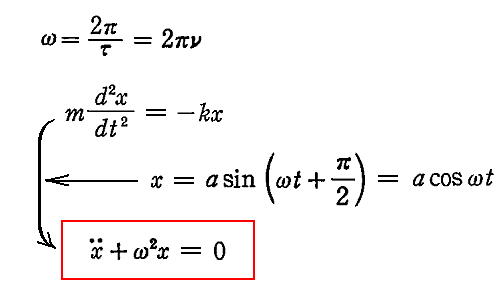
嵟屻偺宍傪尒傟偽夝傞傛偆偵丄偙傟偼倶傗倶偺帪娫旝暘偵娭偟偰乬堦師丒摨師丒曽掱幃乭偵側偭偰偄傞丅偮傑傝幃偺拞偵丂倶2丆倶3丆倶丒乮倓倶乛倓倲乯丆乮倓倶乛倓倲乯2丆乮倓2倶乛倓倲2乯2丆摍乆丒丒丒丒丒側偳偺崁偑懚嵼偟側偄偱丄偟偐傕塃曈偑0偱偁傞帠傪堄枴偡傞丅丅丂
丂
乮俀乯掕悢學悢偺摨師慄宆旝暘曽掱幃
丂椡倃偑倶偵娭偟偰慄宆偱偁傞偙偲偵拝栚偡傞偲丄慜愡偲偼堘偭偨曽朄偱夝偔偙偲傕偱偒傞丅偙偺傛偆側乬摨師丒慄宆丒旝暘曽掱幃乭乮慄宆偲偼堦師曽掱幃偱偁傞帠傪堄枴偡傞丅乯
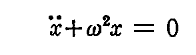
偼
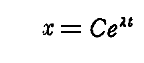
偺宍偺摿夝傪帩偮偙偲偼偨偩偪偵夝傞丅
丂偙偺偲偒兩偼丄摿夝傪旝暘曽掱幃偵戙擖偟偰摼傜傟傞 兩 偺擇師曽掱幃偺崻偲偟偰寛傔傞偙偲偑偱偒傞丅偦偺傛偆偵偟偰摼傜傟傞夝偼丄旝暘曽掱幃偺摿夝偱偁傝丄堦斒夝偼偦傟傜偺摿夝偺廳偹崌傢偣偱摼傜傟傞丅偡側傢偪
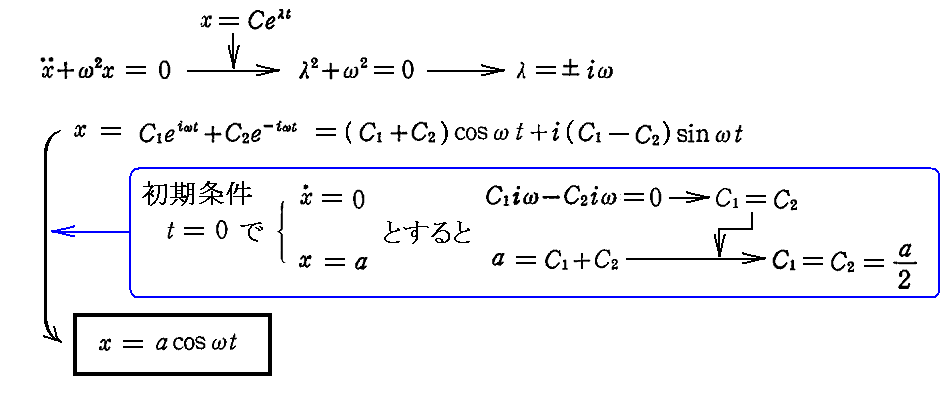
偲側傞丅掕悢俠1丄俠2偼丄弶婜忦審偐傜寛傑傞偙偲偵拲堄丅
丂偙偺傛偆側娙扨側夝朄偑壜擻側偺偼丄挷榓怳摦椡倃乮倶乯亖亅倠倶偑丄嵗昗偵娭偟偰慄宆偱偁偭偨偨傔偵丄怳摦偑偨偩堦屄偺掕悢冎偱昞偣偨偐傜偱偡丅椡偑旕挷榓宆乮旕慄宆乯偺応崌偵偼慜愡偺僄僱儖僊乕愊暘偺曽朄傪梡偄側偗傟偽側傜側偄丅
丂
乮俁乯曗懌愢柧
丂埲忋偺條偵偟偰摼傜傟偨夝
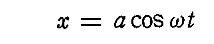
偑丄僄僱儖僊乕曐懚懃傪枮偨偟偰偄傞偺傪妋擣偟傑偡丅偙傟傪僄僱儖僊乕曐懚懃昞尰幃偺嵍曈偵戙擖偡傞偲
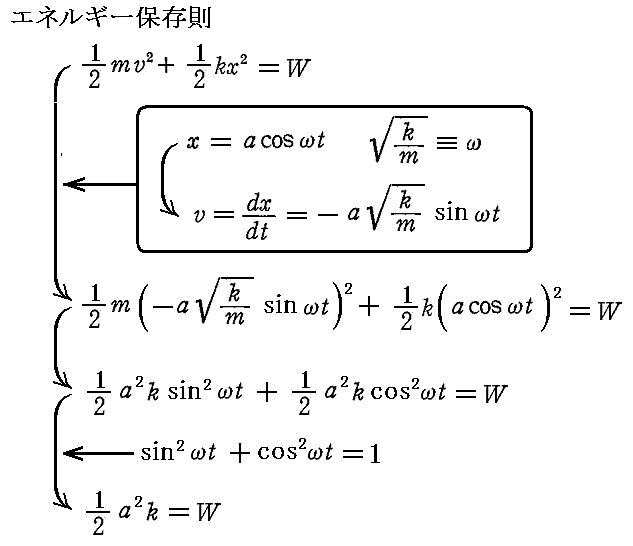
偲側傝丄妋偐偵塃曈偺僄僱儖僊乕抣倂亖倎2倠乛2偵堦抳偟傑偡丅
丂強偱丄擟堄偺帪崗偺塣摦僄僱儖僊乕俲偺昞尰幃偐傜丄1廃婜娫冄偱偺乻暯嬒塣摦僄僱儖僊乕乼傪媮傔傞偲
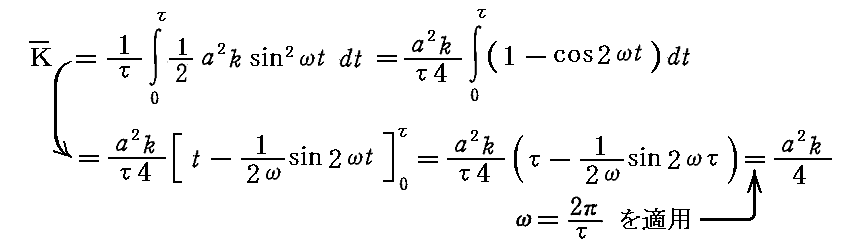
偲側傝傑偡丅偙偙偱丂倠亖倣冎2丂偱偁傝丄倎亖嵟戝怳暆丂偱偁傞帠傪朰傟側偄偱壓偝偄丅
丂峏偵丄擟堄偺帪崗偺埵抲僄僱儖僊乕倀偺昞尰幃傪梡偄偰1廃婜娫冄偱偺乻暯嬒埵抲僄僱儖僊乕乼傪媮傔傞偲
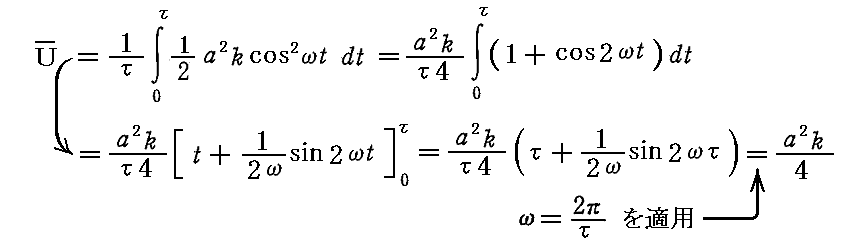
偲側傝傑偡丅
丂偡側傢偪丄扨怳摦懱乮挷榓怳摦懱乯偺堦廃婜娫冄偺乻暯嬒塣摦僄僱儖僊乕乼偲乻暯嬒埵抲僄僱儖僊乕乼偲偼摍偟偄丅
丂傑偨丄偦偺抣偼乮擟堄偺帪崗偵懳偟偰堦掕偲側傞乯慡僄僱儖僊乕抣倂亖倎2倠乛2 偺 1乛2 偲側傞丅
丂扨怳摦巕乮挷榓怳摦巕乯偵懳偟偰惉傝棫偮忋婰偺寢榑偼丄偲偰傕廳梫偱丄條乆側強偱棙梡偝傟傑偡丅
丂
俁丏嫮惂怳摦
乮侾乯旕摨師慄宆旝暘曽掱幃
丂偙偙偱偼嫮惂怳摦椡偑們sin冎倲偱梌偊傜傟傞
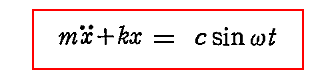
偺宍偺嫮惂丒旕尭悐怳摦偺旝暘曽掱幃傪峫嶡偡傞丅偙偙偱 冎 偼嫮惂怳摦偺妏懍搙乮妏怳摦悢乯丄們 偼嫮惂怳摦椡偺怳暆偱偁傞丅偙偙偱傕暅尦椡偼丄彫怳摦偺応崌偵嬤帡揑偵嫋偝傟傞倶偵娭偡傞慄宆壔傪峴偭偰 亅倠倶 偲偟偰偄傞丅偮傑傝 倶2 傗 倶3 側偳偺崅師偺崁偼柍帇偱偒傞応崌傪峫偊偰偄傞丅
丂塃曈傪壛偊偨偙偲偵傛傝丄旝暘曽掱幃偼傕偼傗摨師偱偼側偔側傞偑丄偙偺宍偺旝暘曽掱幃偺夝偼旕摨師慄宆旝暘曽掱幃偺摿夝偲丄塃曈傪僛儘偲抲偄偨摨師旝暘曽掱幃偺堦斒夝偺榓偱昞偝傟傞丅
丂旕摨師慄宆旝暘曽掱幃偺摿夝偼
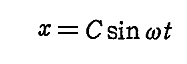
偱梌偊傜傟傞丅偙偺偲偒偺掕悢俠偼丄偙偺夝傪旝暘曽掱幃偵戙擖偡傟偽寛掕偱偒傞丅偡側傢偪
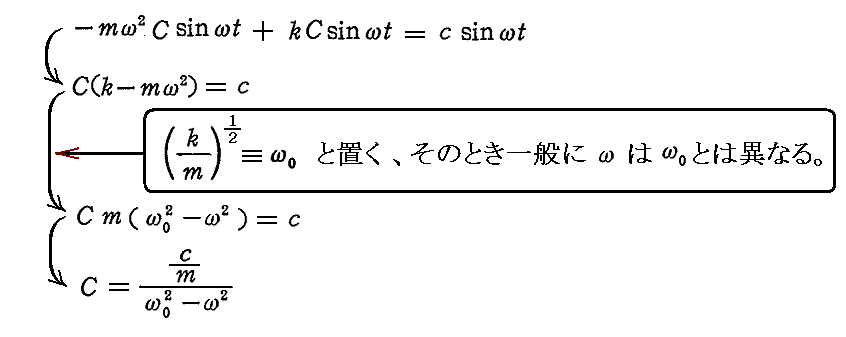
偲側傞丅
丂屘偵夝偼丄偦偺摿夝偲乮愭傎偳媮傔偨乯摨帪旝暘曽掱幃偺堦斒夝偲偺榓偱偁傞
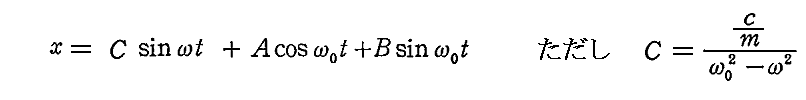
偲側傞丅
乮俀乯旕摨師慄宆旝暘曽掱幃偺摿夝偺堄枴
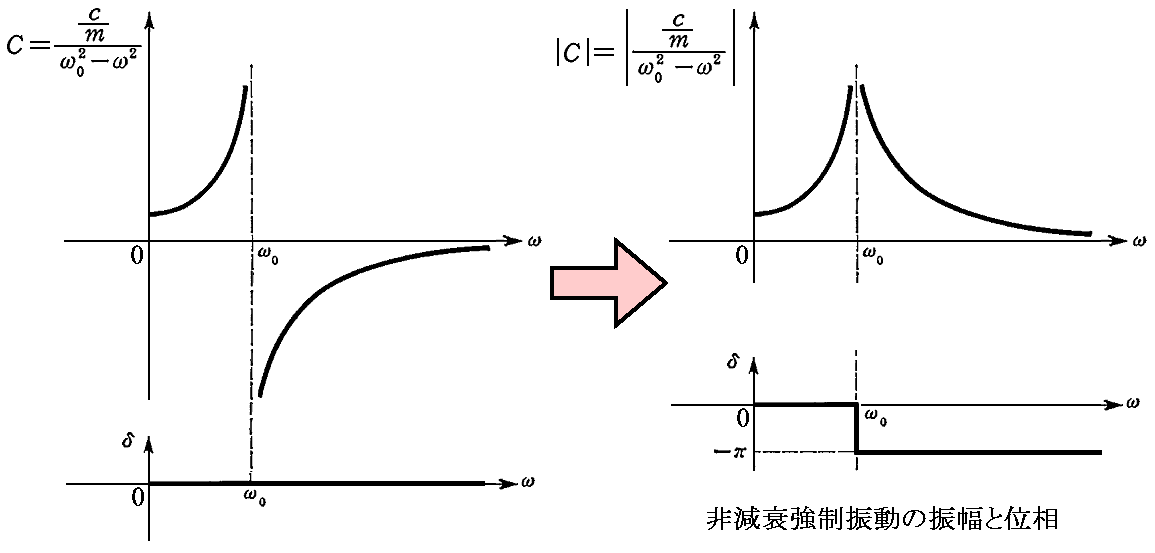
丂摿夝偺怳暆俠偼丄冎偑憹戝偟偰冎仺冎0偵嬤偯偔偲嫟偵柍尷戝偵側傞丅冎偑冎0傪挻偊傞偲俠偼惓偺柍尷戝偐傜晧偺柍尷戝偵旘傃堏傝冎仺亣偲偲傕偵0偵廂懇偡傞丅
丂偨偩偟丄怳暆偼杮棃惓偲峫偊傞傋偒偱偁傞偺偱乥俠乥偱掕媊偟偰丄晞崋偺曄壔偼sin冎倲偺埵憡偵晧傢偣傞傋偒偱偁傞丅偮傑傝冎亖冎0偱兟亖亇兾偺曄壔偑偁傞偲偟偨曽偑傛偄丅偙偺偲偒冎偑冎0傪挻偊傞偲偒埵憡偺曄壔偑兟亖亄兾偲兟亖亅兾偺偳偪傜偱偁傞偐偑栤戣偵側傞偑丄嫮惂丒旕尭悐怳摦傪俆丏復偱愢柧偡傞嫮惂丒尭悐怳摦偺嬌尷偺応崌偲峫偊傞偲丄兟亖亅兾傪偲傞傋偒偱偁傞偙偲偑夝傞丅壓恾偼偦偺摉偨傝偺條巕傪恾帵偟偨傕偺偱偁傞丅
廬偭偰摿夝偼
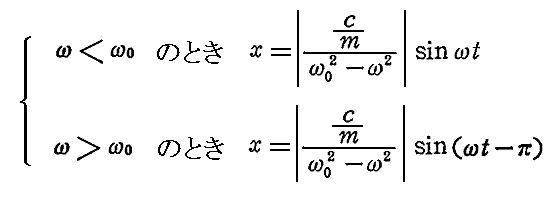
偲側傞丅
丂冎亖冎0偱丄怳暆偑柍尷戝偵側傞偺偼丄帺桼怳摦偲嫮惂怳摦偺娫偺嫟柭偺尰徾偱偁傞丅偮傑傝丄怳摦宯偺屌桳怳摦悢冎0乛2兾偵丄嫮惂怳摦椡偺怳摦悢冎乛2兾偑嬤偯偔偵偮傟偰怳暆偑偍偍偒偔側偭偰偔傞丅
丂偨偩偟偙偙偱丄慄宆偺怳摦偺旝暘曽掱幃偼丄杮棃柍尷彫怳摦偺応崌偵偺傒惓偟偄嬤帡揑側傕偺偱偁傞偐傜丄柍尷戝偺怳暆偑尰傟傞椞堟偼丄晄揔愗側奜憓偱偁傞偙偲傪拲堄偟偰偍偐側偗傟偽側傜側偄丅
乮俁乯旕摨師慄宆旝暘曽掱幃偺堦斒夝
丂偙偙偱堦斒夝偵婣偭偰丄偦偺惈幙傪挷傋偰傒傞丅堦斒夝偺掕悢 俙 偲 俛 偼弶婜忦審偵傛偭偰寛傑傞丅偦偺偨傔

偲側傞丅
丂偙偙偱擇偮偺怳摦悢 冎偲 冎0 偑廫暘嬤愙偟偨嫟柭偵嬤偄摿暿側応崌傪挷傋偰傒傞丅

偲側傞丅偙偺僞僀僾偺怳摦偼丄傕偼傗帺桼怳摦偺傛偆側廃婜惈傪帵偝側偄丅嶰妏娭悢偺奜偵妡偐偭偰偄傞 倲 偺偨傔偵怳暆偼帪娫偲嫟偵憹戝偟偰壓恾偺條偵柍尷戝偵敪嶶偡傞丅
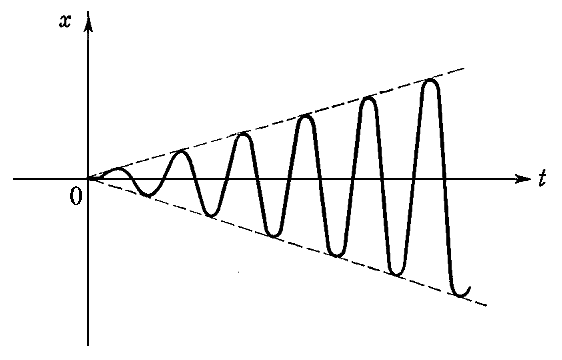
丂偨偩偟丄怳暆偑戝偒偔側傞偲丄慄宆側岦怱椡偺壖掕偑惉傝棫偨側偔側傞偺偱丄晛捠柍尷戝怳暆偼幚尰偟側偄丅
丂
係丏尭悐怳摦
乮侾乯摨師慄宆旝暘曽掱幃
丂偙偙偱偼丄尭悐傪堷偒婲偙偡崁偲偟偰懍搙偵斾椺偟丄懍搙儀僋僩儖偲斀懳岦偒偺椡偑摥偔偲壖掕偡傞丅偦偺応崌偺旝暘曽掱幃偼
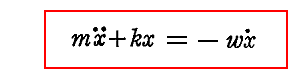
偲側傝傑偡丅偙傟偼嬻婥拞偱怳摦偡傞怳摦巕偺怳暆偑嬻婥掞峈傪庴偗側偑傜尭悐偟偰偄偔応崌側偳偑摉偰偼傑傝傑偡丅
丂偙傟偼摨師慄宆旝暘曽掱幃偱偡丅偙偙偱

偺抲偒姺偊傪偡傞偲
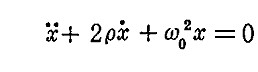
偲側傞丅偙偺曽掱幃偼俀復乮俀乯愡偱帵偟偨曽朄偱夝偔偙偲偑偱偒傞丅
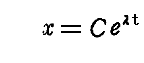
偲偍偒丄旝暘曽掱幃偵戙擖偡傞偲丄兩傪寛傔傞俀師曽掱幃偑摼傜傟傞偺偱

偲側傞丅
乮俀乯夝偺條巕
丂慜愡偱壖掕偟偨弶婜忦審帪偺夝傪恾帵偡傞丅夝偺條巕偼兿偑冎0傛傝傕戝偒偄偐彫偝偄偐偵傛偭偰堎側傞丅
侾丏兿亙冎0偺応崌
丂偙偺応崌
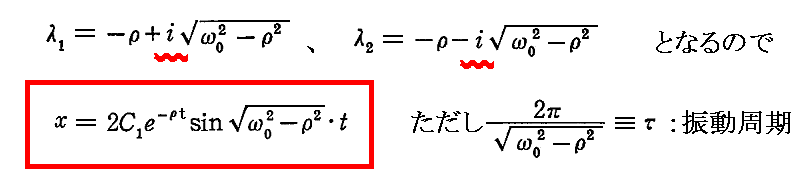
偲側傞丅
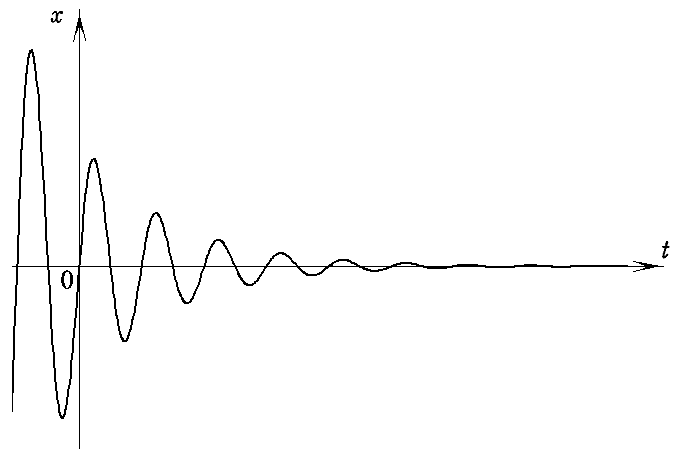
丂偙偺応崌偵偼尭悐崁倕亅兿倲丂偑妡偐偭偰偄傞偨傔偵怳暆偑巜悢娭悢揑偵尭彮偟側偑傜怳摦偡傞偙偲傪帵偟偰偄傞丅兿偑彫偝偄応崌偵偼俀丏復偱愢柧偟偨旕尭悐怳摦偺応崌偲傎偲傫偳曄傢傜側偔側傞丅
俀丏兿亜冎0偺応崌
丂偙偺応崌偵偼兩1丄兩2偑幚悢偱
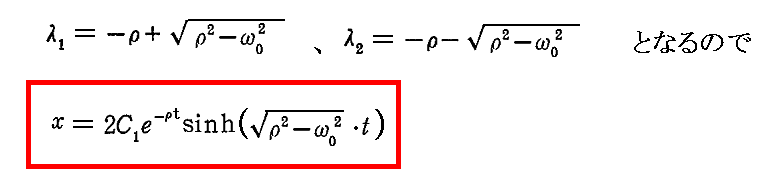
偲側傞丅
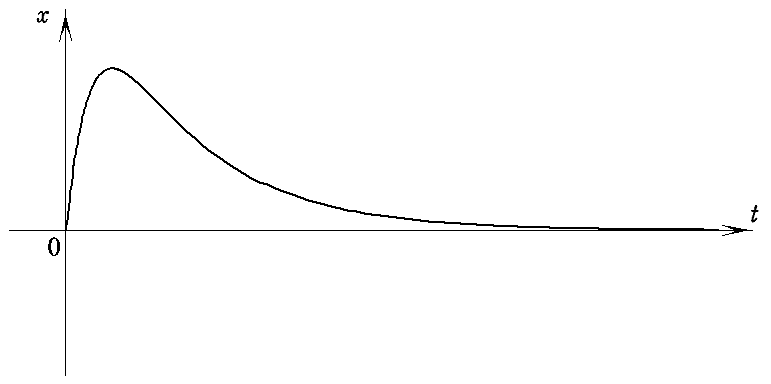
丂偙偺応崌偵偼侾夞偩偗怳暆偑怳傟偨屻偵丄怳摦傪孞傝曉偡偙偲側偔尭悐偡傞偙偲傪帵偟偰偄傞丅
丂
俆丏嫮惂丒尭悐怳摦
乮侾乯旕摨師慄宆旝暘曽掱幃
丂嵟屻偵嫮惂椡偲尭悐椡偺椉曽偑摥偔応崌傪峫偊傞丅偙偺応崌傕慜愡偲摨偠抲偒姺偊傪偡傞偲旝暘曽掱幃偼

偲側傞丅
丂偙傟偼旕摨師慄宆旝暘曽掱幃偱偁傞偑丄偙偺夝偼丄偙偺旕摨師曽掱幃偺摿夝偲塃曈偑僛儘偺摨師慄宆旝暘曽掱幃偺堦斒夝偲偺榓偵側傞丅
丂摨師慄宆旝暘曽掱幃偼慜愡偱媮傔偨尭悐怳摦偺応崌偲慡偔摨偠偱偁傞偐傜偦偺夝偑棙梡偱偒傞丅偟偐偟丄夝偺偙偺晹暘偼帪娫偲嫟偵巜悢娭悢揑偵尭悐偟偰峴偔丅偦偺偨傔廫暘挿偄帪娫偑宱偭偨屻偵偼旕摨師旝暘曽掱幃偺摿夝偺傒偑巆傞偺偱摿夝偺惈幙傪挷傋傟偽傛偄丅
乮俀乯旕摨師慄宆旝暘曽掱幃偺摿夝
丂旕摨師旝暘曽掱幃偺摿夝偲偟偰
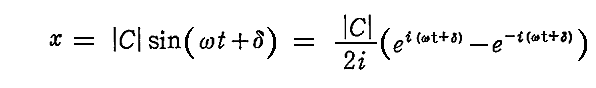
偺宍偑峫偊傜傟傞丅偙傟傪旕摨師慄宆旝暘曽掱幃偵戙擖偟偰 偺偍偺偍偺偵偐偐傞學悢傪斾妑偡傞偲
偺偍偺偍偺偵偐偐傞學悢傪斾妑偡傞偲
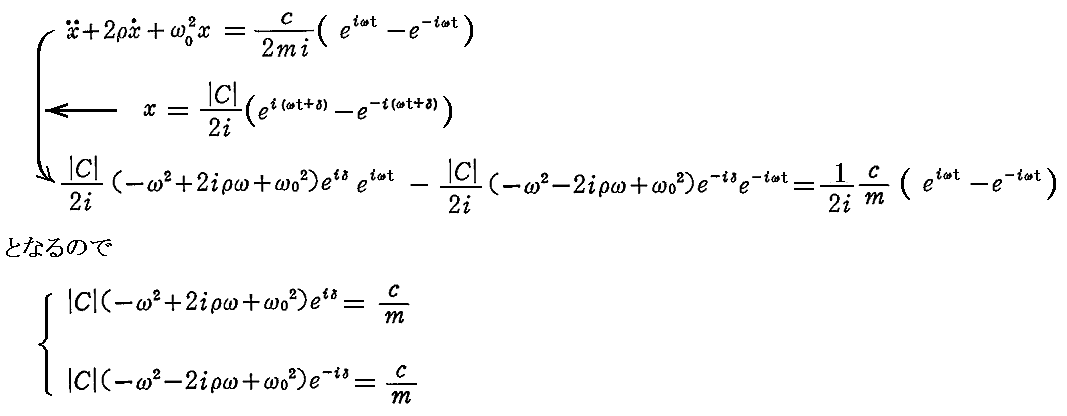
偑摼傜傟傞丅偙偺擇幃偺曈乆傪忔偠傞偐丄妱傝嶼偡傞偙偲偵傛傝
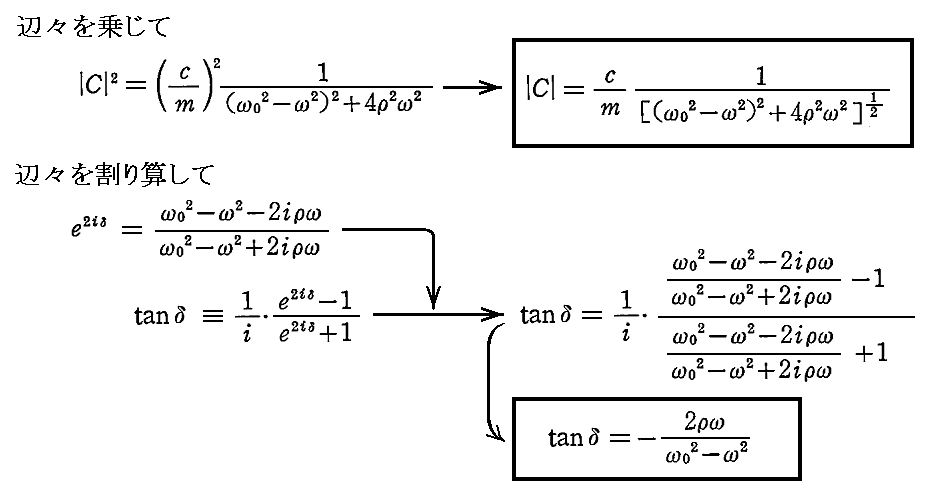
偑摼傜傟傞丅
俁丏乮俀乯偲摨條偵冎偺娭悢偲偟偰怳暆偲埵憡傪帵偡偲
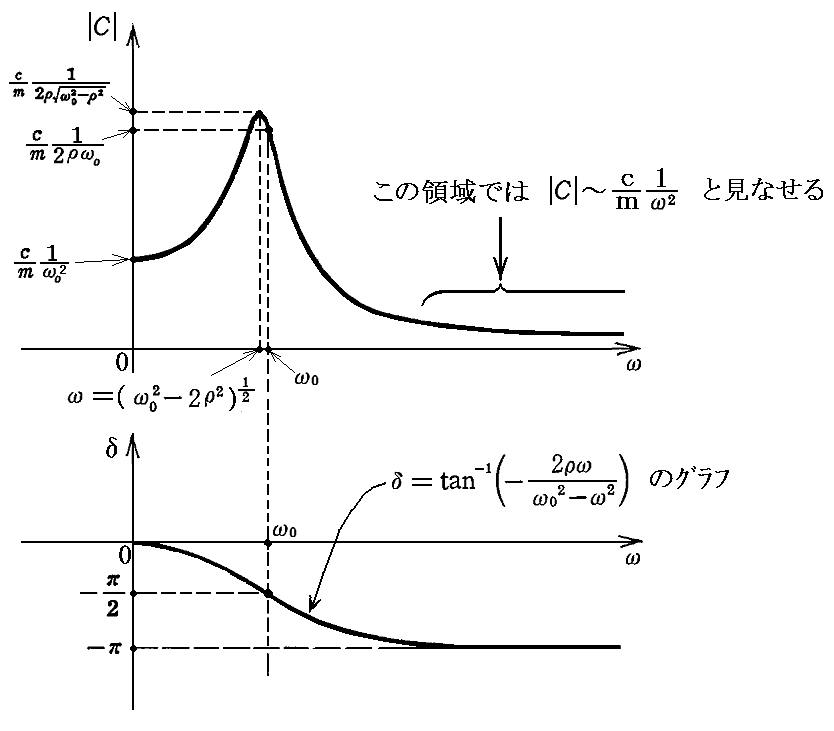
偲側傞丅偙偺偲偒奜椡偲偟偰摥偔嫮惂怳摦偺妏怳摦悢冎偺曄壔偵墳偠偰怳摦偼埲壓偺傛偆偵曄壔偡傞丅
- 冎亙冎0 偺応崌
丂嫮惂怳摦偺妏怳摦悢 冎 偑屌桳妏怳摦悢 冎0 傛傝傕偢偭偲彫偝偄応崌偵偼丄怳摦巕偼奜椡偺嫮惂椡偵抶傟傞偙偲側偔捛廬偟偰怳摦偡傞偑丄嫮惂怳摦偺妏怳摦悢 冎 偑屌桳妏怳摦悢 冎0 偵嬤偯偔偵偮傟偰怳摦巕偺埵憡偺抶傟偑惗偠偰偒偰丄偦偺抶傟偺検偼 兟仺亅兾乛2 偵嬤偯偄偰偄偔丅
丂傑偨丄媡偵 冎仺0 偺応崌丄 兟仺0 偵嬤偯偒丄怳暆偼
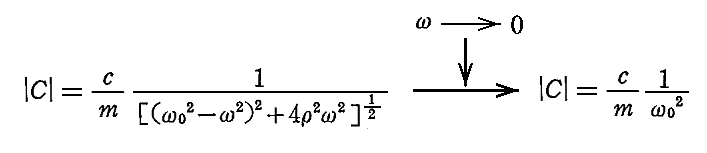
偵嬤偯偄偰峴偔丅
- 丂冎乣冎0 晅嬤
丂俁丏乮俀乯偺嫮惂怳摦偱偼怳暆偑柍尷戝偵敪嶶偟偨偑丄偙偙偱偼尭悐崁偺堊偵怳暆偼桳尷偺抣偵偲偳傑傞丅偙偺偲偒怳摦巕偺埵憡偺抶傟偼 兟乣亅兾乛2 偲側傞丅
丂偙偺応崌丄嬌戝偼 冎亖冎0 偱偼側偔偰 冎0 傛傝傕彮偟彫偝偄 冎 偱婲偙傞偙偲偵拲堄偝傟偨偟丅乥俠乥偑嬌戝抣偲側傞 冎 偼丄乥俠乥傪 冎 偱旝暘偟偨幃偑僛儘偲側傞忦審傛傝媮傑傞 冎亖乮冎02亅2兿2乯0.5 偱偡丅偦偺偲偒偺嬌戝抣偼
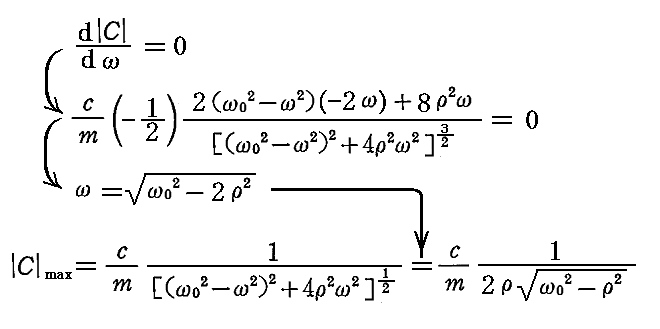
偲側傞丅
丂冎亖冎0 偼乥俠乥偑嬌戝抣傪庢傞強偱偼側偔偰懍搙怳暆乥俠乥冎偑嬌戝偵側傞 冎 抣偱偡丅懍搙怳暆偑嬌抣傪庢傞 冎 抣偼丄乥俠乥冎 傪 冎 偱旝暘偟偨幃偑僛儘偲側傞忦審偐傜媮傑傝丄妋偐偵
冎亖冎0 偲側傞偙偲偑夝傞丅偦偺偲偒偺怳暆偼
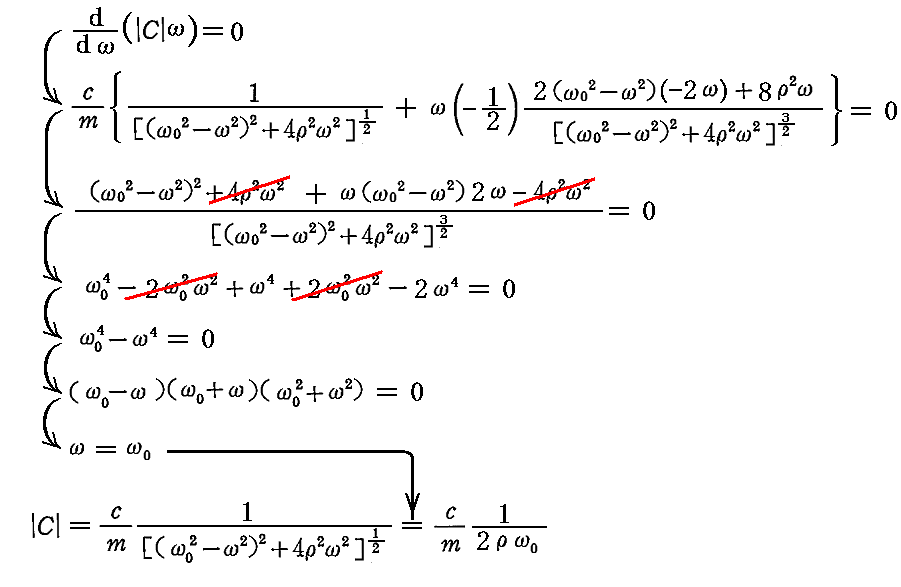
偲側傝傑偡丅
- 冎亜冎0 偺応崌
丂冎 偑屌桳妏怳摦悢 冎0 傪挻偊傞偲丄冎 偑戝偒偔側傞偺偵廬偭偰丄怳摦巕偺怳摦偺埵憡偺抶傟 偼兾乛2 傛傝抜乆戝偒偔側偭偰 冎仺亣 偺偲偒 兟仺亅兾 偵嬤偯偔丅傑偨怳暆偼抜乆彫偝偔側傝丄冎仺亣 偺偲偒僛儘偲側傞丅
丂
乮俁乯兿亙亙冎0偺応崌
丂懍搙偵娭學偡傞尭悐崁偺岠壥乮杸嶤乯偑彫偝偄応崌乮偮傑傝 兿亙亙冎0乯傪傕偆彮偟徻偟偔峫嶡偡傞丅
丂偙偺応崌 乮冎02亅2兿2乯0.5 偲 冎0 偲偺嵎偼擇師偺旝彮検偲側傝丄怳暆偺嵟戝抣偼傎傏 冎乣冎0 偱惗偠傞偲傒側偣傞丅偙偺偲偒 冎亖冎0亄兠 偲偍偔偲嫟柭偺嬤偔偺椞堟偱偼
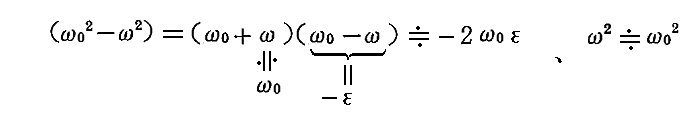
偲嬤帡偱偒傞偺偱
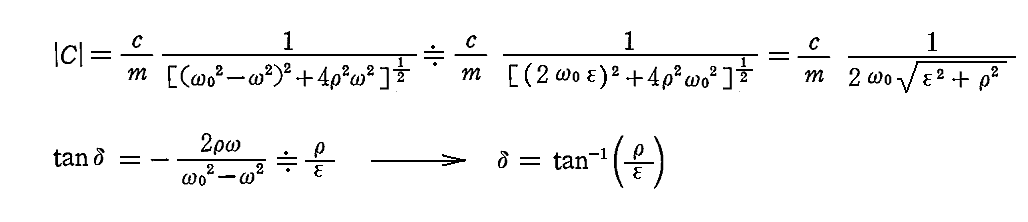
偲側傞丅
丂幃偐傜柧傜偐側傛偆偵嫟柭偼 兠亖0乮偡側傢偪冎亖冎0乯 偱婲偙傞丅偦偺偲偒偺怳暆偼嵟戝抣
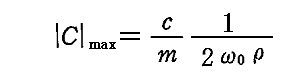
偲側傞丅偮傑傝怳暆偼尭悐學悢兿偵斀斾椺偟偰曄壔偡傞偙偲偑夝傞丅傑偨丄偙偺偲偒兠偑兿掱搙嫟柭怳摦悢 冎0 偐傜棧傟傞乮偮傑傝 冎亖冎0亇兿 乯偲怳暆偼 侾乛20.5乣0.7攞 偵彫偝偔側傞丅偙傟偼尭悐學悢兿偑彫偝偔側傞偲嫟柭嬋慄偼塻偔側傞偙偲傪堄枴偡傞丅偡側傢偪嫟柭嬋慄偼尭悐學悢兿偑彫偝偔側傞傎偳嫹偔偐偮崅偔側傞丅
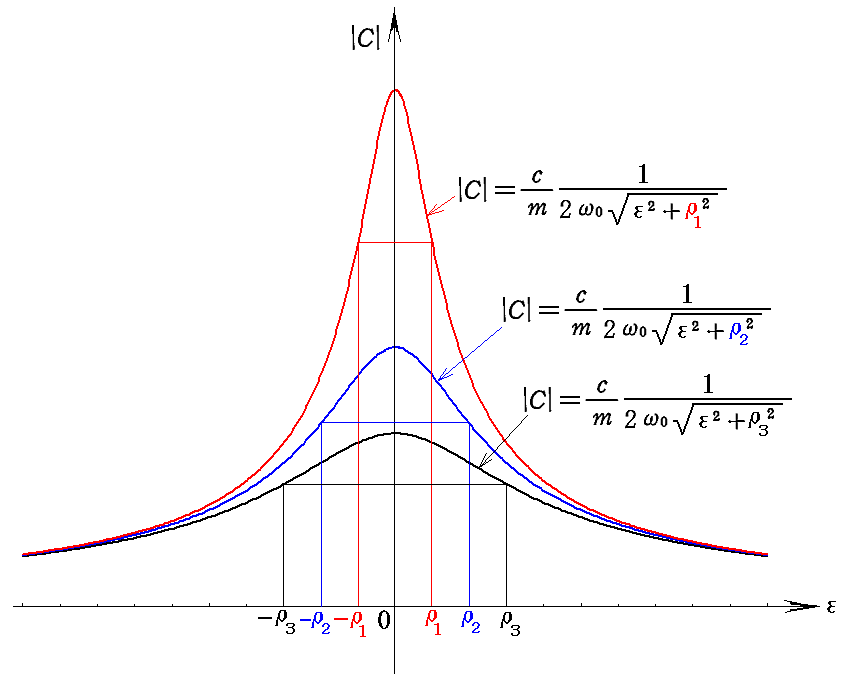
丂嫮惂椡偺怳摦悢偑曄壔偡傞偝偄丄怳摦偲嫮惂椡偲偺埵憡嵎 兟 偼忢偵晧偲側傞丅偡側傢偪怳摦偑奜椡偵懳偟偰抶傟傞丅嫟柭偐傜墦偞偐傞偲 冎亙冎0乮偮傑傝兠亙0乯 偺懁偱偼 兟 偼僛儘偵岦偐偄丄冎亜冎0 偺懁偱偼 亅兾 偵嬤偯偔丅冎亖冎0 偺偲偒偺埵憡嵎偼 亅兾乛2 傪捠夁偡傞丅兟 偺僛儘偐傜 兾 傑偱偺曄壔偼怳摦悢偱尵偊偽 冎0 傪拞怱偲偟偨2兿掱搙偺暆偱婲偙傞丅
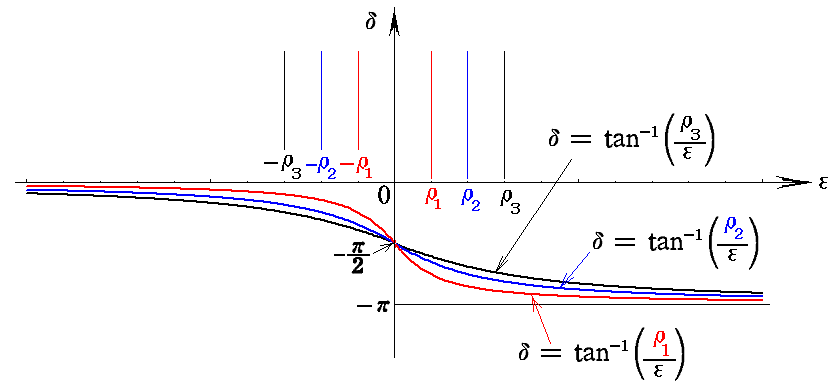
丂俁丏乮俀乯偱榑偠偨尭悐崁偺柍偄乮偮傑傝杸嶤偺柍偄乯嫮惂怳摦偺埵憡嵎 兟 偼 冎亖冎0 偱 兾 偩偗旘桇偟偨偑丄尭悐崁 兿 偑懚嵼偡傞偲偙偺旘桇偑 冎0 傪拞怱偲偟偨 2兿 掱搙偺暆偵側傜偝傟偰偟傑偆丅
丂
俇丏嶲峫暥專
丂偙偺峞偼堦斒揑側撪梕側偺偱偨偄偰偄偺嫵壢彂偵嵹偭偰偄傑偡偑丄偙偙偺愢柧偼庡偵
丂丂傾乕僲儖僪丒僝儞儅乕僼僃儖僩挊乽棟榑暔棟妛島嵗嘥丂椡妛乿島択幮(1969擭姧)仒3丄仒19傗
丂丂儔儞僟僂丄儕僼僔瘍c挊乽椡妛乿搶嫗恾彂(1971擭姧)丂戞5復仒26
摍傪嶲峫偵偟偰偄傑偡丅暿峞偺弨旛偺堊偵帺暘帺恎偺暅廗傪偐偹偰嶌傝傑偟偨丅