このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
高校物理のエネルギーの所に保存力というものが出でくるが高校生には非常にわかりにくい。しかしその定義は
2点間の移動に於いて力のする仕事が2点の位置で決まり物体を動かす道筋によらない場合、その力を保存力という。
というだけで、非常に簡単です。以下この定義が意味するところを説明する。
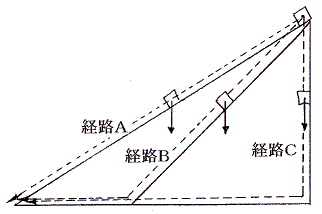
下図の経路A、B、Cで重力によりなされる仕事は全て同じになる。

経路A、B、Cの仕事が全て同じになることは下図の思考実験を考えれば明らか。
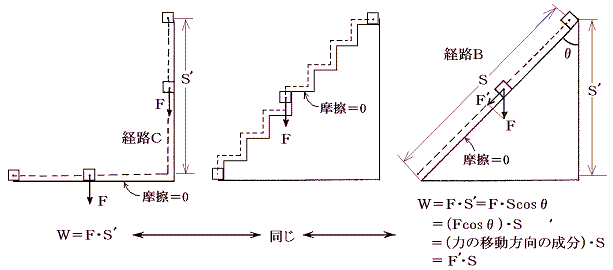
経路Bの動きを重力に垂直な方向と平行な方向の動きを組み合わせた階段上の経路で近似する。床面に摩擦が無いとすると、水平方向の仕事は零だから垂直方向の移動のみ仕事がなされ、階段状経路の仕事も経路Cと同じになる。階段の刻みの大きさを無限小にすれば斜面が実現されるので結局経路Bの仕事は経路Cの仕事と同じになる。
階段の刻みを無限に小さくすると物体が転がり落ちてしまうと心配する向きには下図のような状況の移動を考えればよい。
この思考実験から力の方向と移動方向が一致しない場合は
仕事:W=(力の移動方向の成分)×(移動距離)=F・Scosθ
であるという一般的な規則が導かれる。この公式を用いれば経路A、B、Cの仕事が全て同じになることは明らかである。
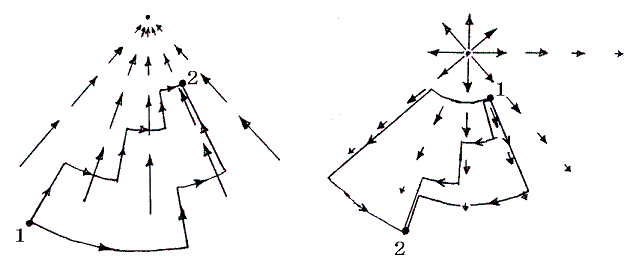
この場合も下図の様に点1から点2へ移動する様々な経路を、中心からの放射線の方向と円周方向の線分の組み合わせで近似する。そうすると円周方向の仕事は零になるから、点1から点2へ移動するときなされるき仕事量はその経路によらず全て同じになる。
もちろんW=(力の移動方向の成分)×(移動距離)=F・Scosθを用いて証明する事もできる。
これらの例は応用上重要である。下図のような単振動やクーロン力、万有引力の場合がそれに当たる。
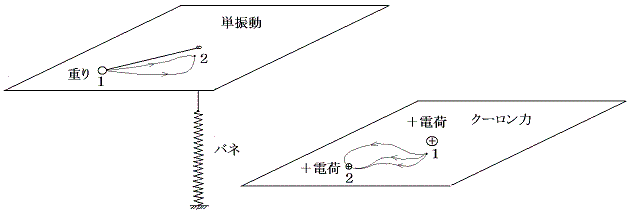
つまり[一様な力]や[中心を向くかその反対方向を向きその大きさが円周方向に等しい球対称な力]の場合は、上記のように力に垂直な方向の移動と、力に平行な方向の移動の組み合わせで経路を近似することができる。そのため、どの経路をたどろうとも、力によって2点間の移動に対してなされる仕事量は同じになる。つまり力は保存力になる。
もう少し注意しておくと、電荷が多数存在してもそれらの電荷が静止していれば、各々の電荷が生み出す電場を重ね合わせたものが生じるだけだから、電場の重ね合わせの原理と力の合成法則から、その重ね合わされた電場が電荷に及ぼす力は保存力になる。つまり静電場は必ず保存力になる。
上記以外に保存力はないのだろうか?もっと一般的な場合を考えてみる。保存力とはWi=Fi×SicosθiでSiを加え合わせて仕事を計算するとき、加え合わせた仕事W=ΣWiが、たどった道筋によらないFiのことである。
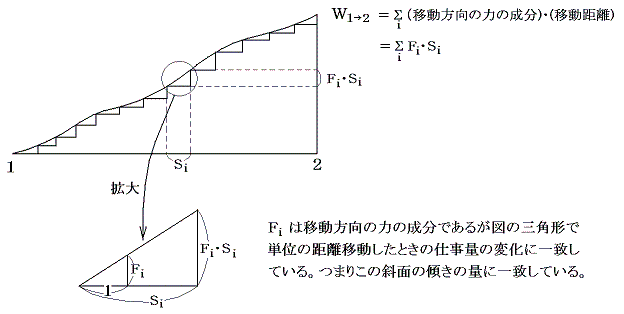
今簡単のために力は2次元平面上で働き、その力による物体の移動も2次元平面に限られるとする。そして平面上の物体の移動に伴ってなされる仕事量の積算値をその面に垂直な座標にプロットする。
位置の変化が二次元平面上に限られる場合、ある位置から別の位置へ物体を移動させて仕事を行うとき、その仕事量が移動させた道筋によらないということは、例えていえば下図の経路AとBで同じ高さの頂に到着するということで、下図に描いた様なことが起こらないということである。

上図の移動量(横軸)と仕事の積算量(縦軸)の三角図形の意味を考えてみると、物体に働く力の大きさは例えていえば斜面の勾配に物体を置いたとき、その斜面の勾配にそって転がり落ちようとする力の様なものであり、力の方向はなされた仕事が増大する方向である。実際に働く力は重力の斜面に沿った成分とは異なるのでこの例えは良くないが、斜面の傾きtnaθがsinθで近似できるようななだらかな斜面の場合この例えは便利である。
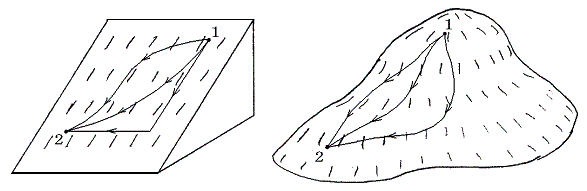
上記のことは言葉を変えれば、位置変化が二次元平面上に限られる場合、その平面上に斜面を形成する一つの連続的な曲面が存在して、二次元平面上の位置が決まるとその点の高さが一つに決まることを意味している。この連続的な曲面をポテンシャル関数と言い、そのような関数が存在することが保存力であることである。
普通は前記の曲面の値は正負を逆にして、なされた仕事量だけ曲面の高さが下がっていくように描く。そうすると斜面の真下の二次元平面上に存在する物体に働く力は斜面の下向きの傾きに関係すると考えることができて都合が良くなる。
ポテンシャル関数をV(x,y)であらわすと、物体が保存力の場から受ける力は
で表される。これはポテンシャル関数が表す斜面の勾配が力の大きさに比例することを意味している。
その様な曲面上を移動する運動の場合、力に依って物体になされた仕事(斜面高度の降下量)は、最初と最後の位置が同じならば物体が動いた道筋(斜面上の位置座標を平面上に射影した点の動く道筋)に依らずいつも等しくなる。このような力が保存力と言われるものである。
物体が2点間を移動するとき、2二次元平面の上に作られたポテンシャル関数の値は、保存力がした仕事の積算値だけ減少していく。つまりポテンシャル関数こそが位置エネルギーといわれるものである。そして保存力だけが仕事をするということは、物体がポテンシャル関数の上を移動してその高さを失うことである。つまり位置エネルギーが減少し、その減少分が運動エネルギーの増加分となり、位置エネルギーと運動エネルギーの和は常に一定となり、力学的エネルギーが保存する。
この当たりは別稿「エネルギー保存則の証明」4.を参照されたし。また、2.項でのべた中心力の場合の具体的な議論とポテンシャル曲面の形については、別稿「質点の二次元運動」を参照して下さい。
位置が三次元空間内で変化するとき、仕事の積算量(ポテンシャル関数)を一つの曲面で表現することはできない。しかし三次元空間の各点に付随する数値の集まりで表現することはできる。つまり出発点の値を基準とすると、そこから保存力によって仕事をされながら物体が動いていくとき、動いた最終点までになされた仕事の積算値だけ差し引いた値が最終点に付随するポテンシャル値(負の値)になる。その積算値が出発点と最終点の位置のみにより、出発点から最終点までの移動経路にはよらないことが、力が保存力であることの条件である。それは前記の三次元空間に付随する数値が三次元の位置座標の連続でなめらかな関数であること。
つまり連続的な三次元の関数が存在し、移動方向の力の成分は物体が単位の距離移動したときの関数値の変化量、力の働く方向はその数値が減少する方向となる場合、その力を保存力というのである。
例えば磁場や電場が時間的に変化する場合がそうで、電磁誘導現象に伴う力は保存力ではない。そのあたりは閉じたループに沿っての仕事の積算値(和)が零にならないことから解る。別稿「交流電気回路」1.交流電圧の発生 を参照されたし。
この場合、力の場を、ある関数値の変化量(勾配)で表すことはできない。そのような関数を定めることはできない。