流体要素の運動を決める力の一つは、水面の勾配と水に働く重力によって生じる“圧力差”です。座標(x.y)にある質量ρ(D+h)ΔxΔyの流体要素について成り立つ運動方程式のx成分(max=Fx)は
となる。同様に考えて、y成分(may=Fy)は
となる。
1879年にウィリアム・トムソン(ケルビン)はコリオリ力を考慮した長波の理論を発表した。今日これはケルビン波の理論と言われ、このことを報告した下記論文は有名です。
W. Thomson (Lord Kelvin), “On gravitational oscillations of rotating water”, Proc. Roy. Soc. Edinburgh, Vol.10, p92~101, March 17, 1879年
これは、Phil. Mag. Vol.10, p109~116, 1880年やトムソンの論文集第4巻に採録されおりネットからダウンロードできます。また、次のURLから直接ダウンロードできます。
http://www.aos.princeton.edu/WWWPUBLIC/gkv/history/Kelvin1879.pdf
原論文を参照されながらこの稿をお読み下さい。
必要な予備知識として、波については「波動方程式と一般解」、潮汐現象については「潮汐力」、共鳴・共振については「共振(共鳴)」、コリオリ力については「コリオリ力」や「慣性力」、流体の運動方程式については「二次元・非圧縮性・完全流体の力学」や「吹送流の西岸強化」をご覧下さい。
ニュートンは万有引力と力学法則に基づいて、地球表面に存在する海水に働く周期的な力を説明した。今日その力は“平衡潮汐理論(静力学的潮汐理論)”における“起潮力”(周期が約12時間程度)と呼ばれる。ところが、この理論では実際に生じる潮汐現象を旨く説明できなかった。
そこでケルビンは、潮汐とは上記の起潮力によって駆動された“長波”が、広さが数十~数百km程度、深さが数十m~数百m程度の様々な形をした内海、海峡、湾などに進入し、それが起潮力の周期と共鳴して大きな海面振動を引き起こす現象だと考えます。これは今日“動力学的潮汐理論”と呼ばれるもので長波の波動理論そのものです。
ケルビンの理論が画期的だったのは長波の理論に“コリオリ力”を導入したことです。そのことにより、現実に起こる潮汐現象を的確に説明できるようになった。
潮汐波は広くて浅い海を伝播する長波で、一般に[波長λ]≫[水深D]と仮定できる。これは重力波の中で特に波長が長大なものを意味します。[別稿「波動方程式と一般解」2.(4)を参照。]
長波の伝播に伴う流体粒子の移動はその水深方向についてほぼ均一であり、流体粒子の平面(二次元)的な運動のみを考慮した二次元流体の運動方程式で旨く説明できる。
考察の対象とする海域は、地球表面の曲率による変化が無視できる限られた緯度、限られた面積の領域とし、その領域内は平らで同一のコリオリ力パラメータが適応できるとする。またその海域の水深Dの最大値は、その海域の最小直径に比較して十分に浅いと仮定でき、また[波高h]≪[水深D]であるとする。
そして、さらなる簡単化のために、[水深D]=一定とし、側壁は垂直に切り立っていると仮定する。
下図の様な広くて浅い海の中に、柱状の流体要素を考える。
流体要素の運動を決める力の一つは、水面の勾配と水に働く重力によって生じる“圧力差”です。座標(x.y)にある質量ρ(D+h)ΔxΔyの流体要素について成り立つ運動方程式のx成分(max=Fx)は
となる。同様に考えて、y成分(may=Fy)は
となる。
ここで、圧力の場所的変化は波高の場所的な変化に置き換えることができる。このとき、“圧力差”は今考えている水柱の深さ方向に関しては一定になることに注意されたし。
この関係式を用いると前述の式は、以下の様に変形できる。
[補足説明]
これは座標空間に固定された座標値を変数とするオイラー形式の運動方程式です。そのため、左辺の時間微分∂v/∂tは本来ならばラグランジュ微分[Dv/Dt=∂v/∂t+(v・grad)v]にしなければならない。[別稿「二次元・非圧縮性・完全流体の力学」1.(2)2.を参照]
しかし、そのようにするとあまりにも複雑になるので、(v・grad)vの部分を省略して簡略化してある。そのような簡単化が許されると考えて議論していることに注意してください。一般的に、[波の振幅h]≪[波長λ]の場合には、この様な近似が許される。
地球規模の流体運動を論じるには自転する地球の表面に固定した座標系で論じるのが便利です。そのとき、回転系(地球表面)に固定した座標系での運動を論じるには、運動方程式の力の項に座標系が運動していることに伴う慣性力を付け加えておけばよい。[別稿「慣性力」5.まとめの最後を参照]
回転する座標系上の質量mの物体には、回転の角速度ω’と移動速度v’の積に関係する見かけの力である“コリオリ力”(慣性力の一種)が働きます。コリオリ力の大きさは
で表される。[別稿「コリオリ力」2.(1)参照]
また、それが働く方向は[北半球の地球表面に固定した座標系上では]流体の移動方向に対して右向きです。[別稿「コリオリ力」1.(1)参照]
今用いている座標系の回転角速度ω’は、座標系が存在する位置の緯度θと地球の自転角速度ωから以下の関係で導かれる。[別稿「大気大循環」2.参照]
例えば、日本付近(緯度θ=35°)の海における潮汐現象を論じる場合、座標系の回転角速度ω’は
程度となります。正確には1太陽日(24時間)ではなくて1恒星日(23.9344696時間)を用いて割り算すべきです。
いずれにしても、前述の角柱流体要素に働くコリオリ力が関係する運動方程式のx成分は、y方向の速度成分vを用いて
となる。ここで、uはx方向の速度成分です。右辺の正負の符号は北半球の海洋に付いてのものであることに注意されたし。北半球で、コリオリ力は進行方向に対して直角右向きに働きます。
一般に、回転する座標系では別種の慣性力である“遠心力”も現れます。しかし、別稿「コリオリ力」1.(3)で説明したように、地球は自転による回転運動により地球回転楕円体に変形しています。
そのため、その表面に張り付いた海水に対する遠心力の効果は[重力の大きさの変化]と[重力が働く方向の変化]ですでに調整されており、その中に取り込まれています。
そのため、“遠心力”を運動方程式の中に導入する必要は無くなります。この当たりは非常に解りにくいところですが、別稿「回転地球に固定された座標系におけるニール(Neil)の放物線とフーコー(Foucault)の振り子」1.(3)で説明しておりますのでご覧下さい。
前節の圧力傾度とコリオリ力を同時に考慮すると、座標(x.y)にある単位体積の流体要素に対して成り立つ“運動方程式”として
が得られる。
[補足説明1]
すでに注意したように、本当に正しい式はラグランジュ微分[Dv/Dt=∂v/∂t+(v・grad)v]を用いた
です。しかし、それは複雑なので、(v・grad)vの部分を省略して簡略化してある。
運動方程式(1a)と(1b)の両辺をtで偏微分すると
となる。
(1a’)式に(1b)を代入すると
となる。同じく(1b’)式に(1a)を代入すると
となる。これらは波高hと速度(u,v)の間の関係を定める方程式です。
(1a)式の両辺をyで偏微分、(1b)式の両辺をxで偏微分すると
となる。これの辺々を引き算すると
が得られる。
(3)式は現在の状況[つまり流体が回転系に乗っているため、流体を回転させる力(コリオリ力)が働く]において、各地点の“渦度”の変化を表す式、すなわち“渦度方程式”です。渦度の意味については別稿「カルマン渦列(動的安定性解析)」2.(2)を参照されたし。
[補足説明2]
(3)式の意味は
と書き直したとき、右辺の(∂u/∂x+∂v/∂y)が別稿「カルマン渦列(動的安定性解析)」2.(1)で説明したベクトルの“発散”を表すことを思い出せば理解できる。前に負符号がついているから、この項は次節 (3)連続の式 で説明する柱状領域に周囲から流体が流入する事を意味する。
柱状領域に流入するときコリオリ力を受けるので、渦を巻くように入っていき回転運動を生じる。つまり“渦度”のz成分が増大する。そのときω’がかかっているので座標系の回転速度が速いほどその効果は大きくなる事を言っている。
[別稿「二次元・非圧縮性・完全流体の力学」3.(3)2.の議論と比較して見られたし。]
非圧縮性流体の場合、海面高hの時間的変化は角柱(D+h)ΔxΔyの側面を通して出入りする流量の差に依存する。簡単化して水深Dが一定の場合を考察する。
x方向の流量差とy方向の流量差を加えたものが水面高hの時間的変化になる。入ってくる流量を正、出て行く流量を負とすると
となる。同様に
となるので
が得られる。これが“連続の式”と言われるものです。
“連続の式“(4)を“渦度方程式”(3)に代入して時間tで積分すると
が得られる。
この式は、波高が高いところの柱状領域の“渦度”が大きいことを意味する。なぜなら波高が高いのは過去に於いて、その柱状領域に周囲から流体が流入してきたことの結果なのですが、それは1.(2)[補足説明2]で説明したように“渦度”の増大を生じるからです。
これは運動方程式(1)や連続の式(4)以上のものを含んでいるわけではありませんが、便利で有益な式です。次章で繰り返し利用します。
前記の運動方程式と連続の式は未知関数が入り交じっているので、それらを整理して未知関数を一つだけ含む式にする。
運動方程式(1a)の両辺をxで偏微分すると
となる。同じく運動方程式(1b)の両辺をyで偏微分すると
となる。
ここで、“連続の式”(4)の両辺をtで偏微分したものに、“運動方程式”(1)の両辺をxやyで偏微分した(1a”’)と(1b”’)を代入し、さらに“渦運動を表す式”(5)を用いると
が得られる。
“渦運動を表す式”(5)の両辺をyで偏微分すると
となる。同じく(5)の両辺をxで偏微分すると
となる。
ここで、“連続の式”(4)の両辺をxで偏微分したものに、“運動方程式”(1a)の両辺をtで偏微分した(1a’)と“運動方程式”(1b)を代入し、さらに“渦運動を表す式”(5)をyで偏微分して得られた(5’)用いると
が得られる。
同様にして、“連続の方程式”(4)の両辺をyで偏微分したものに、“運動方程式”(1b)の両辺をtで偏微分した(1b’)と“運動方程式”(1a)を代入し、さらに“渦運動を表す式”(5)をxで偏微分して得られた(5”)用いると
が得られる。
結局、三つの量h、u、vは全て同じ形の“2階の同次波動方程式”(6)、(7)、(8)を満足する。これらはおなじみの波動方程式に、4ω’2の項が付け加わった形をしている。これがコリオリ力の影響で現れた項です。
本来ならば、この式中に周期的な起潮力を表す非同次項が導入されていてしかるべきです。しかし、それを考えると難しくなるので、とりあえずそれを省略した“自由振動”を表す波動方程式で議論しています。
論文の最初でケルビンも言及しているように、地球規模での潮汐現象を動力学的理論で最初に論じたのはラプラスです。彼はそのとき、ニュートンの発見した起潮力を潮力ポテンシャルとして導入していますが、それはとても複雑な方程式で簡単に解けるものではありません。
前章で求めた波動方程式の一般的解法は詳しく研究されていますが、ここでは簡単に説明する。
波高hに対する偏微分方程式
は線形・同次の微分方程式だからだから、解関数h(x,y,t)は変数分離できて三つの変数をそれぞれ単独に含む三つの関数の積で表すことができる。つまりh(x,y,t)=φ(x)χ(y)ψ(t)とおける。
これを(6)式に代入すると
となるが、左辺と右辺は互いに独立だからパラメータλ2を含む二組の方程式が得られる。二乗の形にしたのは、後の表現を簡単にするためで、それ以上の意味はありません。
ここで、最初の式はさらに
と変形でき、左辺と右辺は互いに独立だからパラメータα2を含む二組の方程式に分離できる。
結局、次の互いに独立な三つの連立方程式を解けばよい。
この連立偏微分方程式は直ちに解けて
が得られる。[別稿「調和振動子」2.(2)等を参照]
この式を元の波動方程式に代入すればα、β、γ間に成り立つ前述の関係が再び導ける。
このとき、振動する波に対しては
としなければならない。
節線を有するモザイク状の振動モードの解に対しては、
としなければならない。eix=cosx+isinxのオイラーの関係式により虚数成分を適当に組み合わせると、解として
が得られる。
このときm、n、σは以下の関係を満足する。
この様な波高hに対する解に対応するuとvの解を見つけるために、任意の形状の海洋に於いてモザイク状振動が生じる為には、どのような境界条件が許されるのかを見てみよう。
束縛ライン(境界線)上で、それに垂直な速度の水平成分がつねに零である様な境界ラインを引くことができない。そのため、単純な調和振動タイプの振動が生成され許される為には、水は境界の全ての周りで交互に押し込まれたり引き出されたりしするか、境界の全部とは言わないが、それに垂直な水平線分が零でない境界部分が存在しなけばなならないことになる。
それ故に、回転する方形の水槽における水の振動は単純な調和振動タイプとはならない。そういったタイプの解を求めようとする問題は解けない。
もちろん、もしω’=0ならば、回転しない水槽中の水にたいする解としてよく知られている単純な調和振動タイプの解となる。
[補足説明]
ここはケルビンの論文の該当部分の直訳ですが、説明が不十分で何のことか解りにくい。
要するに、ω’=0の場合の波動方程式の解として良く知られている単純な調和振動タイプの解[例えば矩形膜の振動として現れるモザイク状の定常波の様なもの。ただし、今考えているhは境界部分が腹になる。]は、ここでは解となり得ないと言っている。
それは、そのような解を仮定して1.(2)で求めた(2a)や(2b)に代入して、uやvを求めてみると、境界に於いてuやvが満足しなければならない“境界条件”[境界を横切る様な流れは存在できない]を満足できないことから解ると言っている。
最初に、もっとも簡単な境界条件を設定して、それを満足する解を考察する。
側壁がx軸に平行に存在し、y軸の正方向に無限に広がっている海域における解を考察する。
このような海域に対して、時間tおよび距離xに関して振動する解は、(9)式においてα=im、γ=iσとして
が得られる。iは虚数単位、l、m、σは実数を意味する。
解(10)式が波動方程式(6)式を満足することは代入してみれば直ちに了解できる。また、そのとき同時に、l、m、σは以下の関係式を満足しなければならないことが解る。。
次に、h(x,y,t)に対応するu(x,y,t)やv(x,y,t)の解をを求めよう。そのためには、(10)式を(2a)式や(2b)式に適用すればよい。そうすると
や
が得られる。
ここで
が成り立てば(2b’)式は
となり、y方向の速度成分v(x,y,t)が常に零となる解が存在する。このとき、上記の解(10)はx軸に平行な境界側壁において速度成分が満足しなければならない境界条件v(x,y=境界,t)=0を確かに満足することができる。
このときさらに、(11)式に(12)式を代入すると解るように
で無ければならない。
これらの関係式を(2a’)式に適用すると
となる。ここで正負の符号の内、物理的に可能で妥当なものを選択すると。
となる。これはx軸の正方向に伝播する波を表している。そのとき、指数項の前の符号として負が選択されている。なぜなら、そうしないとy→∞で解が発散してしまうからです。
同様に(10)式を書き換えると
が得られる。
(10’)や(14a)から解るように、波の振幅や流速uの大きさは、壁(岸)から距離y=(gD)0.5/2ω’だけ離れると、壁(岸)での値の1/e倍に減少します。この中にコリオリ力項2ω’が含まれていることから明らかなように、岸から沖へ向かう振幅や潮流速度の変化はコリオリ力が決めています。
この特徴的なスケール(gD)0.5/2ω’は、重力とコリオリ力の作用が同程度になる水平スケールと見なせますが、これを“ロスビーの変形半径”(radius of deformation)と言います。
y=0の位置にx軸に平行な側壁が存在する場合の波の様子をグラフで表してみる。解りやすくするために、この図は波高hが拡大され、波長λが縮小されている。
この図はx軸の正の方向へ伝播(赤→)する波を表している。水中に描かれている青→は流体の速度ベクトルを表している。x軸の正方向へ伝播する波の場合、速度ベクトルは波の峰でx軸の正方向を、谷で負方向を向いている。そのとき、速度の大きさは深さ方向では変化しない。そのとき、[波の伝播速度]≫[流体の移動速度]であることを忘れないでください。
yが大きくなるにつれて振幅が減少していることに注意。コリオリ力のために進行方向に対して右側(北半球)の振幅が大きくなる。今日、このような波を、その発見者にちなんで、“ケルビン波”と呼ぶ。
別稿「波動方程式と一般解」3.(3)で説明したように、(14a)、(14b)、(10’)式中のcos項を
の様に書くと、波の波長、周期、伝播速度、流体の移動速度は
で表されることが解る。
ここでの振動周期Tは当然のことながら“平衡潮汐理論(静力学的潮汐理論)”における“起潮力”の周期(T=12.42時間)を当てはめるべきです。つまりその周期に同期した潮汐波が顕著に存在できるとする。これらの式から直ちに以下のことが読み取れる。
1.波の伝播速度は別稿「波動方程式と一般解」2.(4)で説明した普通の長波の場合と同じ式で表される。
2.潮汐波の[波長λ]は、波の式μ=λ/Tに[周期T]、[伝播速度μ(水深Dに依存)]を代入した値となる。
3.[波高h]と[流体粒子の速度u]は、別稿「波動方程式と一般解」3.(5)で説明したのと同じ関係式を満たす。
地球自転に伴って水路が回転することによって現れるコリオリ力の効果は、ω’が現れている指数項
で表現されている。そのメカニズムは下記の様に説明できる。
波の峰にある水は、波の進方向と同じ方向に動いている。コリオリ力の効果によって、水は(北半球では)右横方向へ積み重なるために、波の峰は左側から右側に向かって少しずつ高くなるようになる。
波の谷がやってくると、流れの方向は逆転して、今度は水はもとにもどるように流れる。そのため、水面の横方向への傾斜の方向も、ちょうど逆になる。
つまり、波が進行するのに従って、水面は右側の壁の最も高くなった位置から左へ下がるように傾き、次には、左側の低い位置から、右側の壁に向かってさらに下がるのである。下記の[補足説明1]参照
北半球では進行方向に対して右側の側壁で最大の振幅となり、側壁から離れるにつれて振幅が次第に減少する潮汐波が生じる。。
[補足説明1]
x軸に沿って側壁があり、x方向のみに流体が運動する現在の状況における上記の解をもう一度1.(2)の運動方程式、や1.(3)の連続の式と照らし合わせてみる。
今v=0とおけるので(1a)(1b)(4)式は
と簡単化できる。
(A)式は、柱状領域に含まれる流体のx方向の加速度は波高のx方向の傾斜(これがx方向の圧力差を生じる)に依存する事を示している。これを簡略化された連続の式(C)式と一緒にすると、“波動方程式” ∂2u/∂t2=gD・∂2u/∂x2 または ∂2h/∂t2=gD・∂2h/∂x2 となり、x方向に非定常な波動運動を生じさせる。
また(B)式はy方向に関しては、y方向の波高の傾斜(これがy方向の圧力差を生じる)が柱状領域の流体に働くコリオリ力(y軸方向を向く)と釣り合っている事を示している。つまり瞬間的に考えれば速度のx成分であるuが正方向を向いたときであろうと、負方向を向いたときであろうと、その流れは“地衡流”となっていることを示している。
地衡流(風の場合は“地衡風”と言う)とは、別稿「台風のメカニズム」2.や「吹送流の西岸強化」で説明したように、圧力傾度とコリオリ力が釣り合った流れの事です。
[補足説明2]
1.(2)の[補足説明2]、あるいは1.(4)で、場所(x,y)の位置の微少柱状領域の流体の持つ渦度の変化を表す“渦度方程式”を説明した。この方程式の意味をここで求めた解と照らし合わせてみる。上記の解を図示した海域を真上からみて、各地点の波高と流速を記すと下図の様になる。
この図から明らかなように波高の高い部分はx軸の正方向を向く流速が大きな部分で、波高の低い部分はx軸の負方向を向く流速が大きな部分です。
そのとき別稿「カルマン渦列(動的安定性解析)」2.(2)2.で注意したように、渦度を持つと言うことは流体が回転するように流れているかどうかではなくて、流体が互いにずれあうように流れているかどうかが大切なのです。そこの例の様に回転するように流れていても渦度はゼロの場合があるし、下図の様に直線的に流れていても隣り合った流体部分との間に速度勾配があれば渦度が存在します。そのあたりはもう一度別稿「カルマン渦列(動的安定性解析)」2.(2)1.の渦度の定義を思い出してください。
まさに、ここで求めた解は、この図の例です。つまり波高の高い部分は渦度が正で増大しており、波高が低くなった部分は負で増大しています。
1.(4)で説明したように波高が高くなった部分の渦度が増大しているのはコリオリ力のためでした。ところで、上で求めた波動方程式の解で岸壁側の振幅が大きくなるのもコリオリ力のためでした。すべてつじつまが合っています。
日本近海(緯度θ=35度とする)の潮汐について数値的な検討をしてみよう。この場合、1.(1)2.で求めたようにω’=0.000417rad/s程度となる。大陸棚や内海を伝播する潮汐を考える場合、水深D=100m程度、重力加速度g=10m/s2として良いであろう。また潮汐周期T=12.42時間を用いる。
潮汐波の波高の最大振幅をH~0.5m程度と仮定すると
となる。潮流速度の最大値umax=16cm/sや波長λ=1400kmは、日本近海の潮汐波としては代表的な値です。
ちなみに瀬戸内海の平均水深Dは40m程度、対馬海峡は100m程度、東シナ海は大半を占める大陸棚部分で50~200m程度ですが、奥まった黄海では50m程度になる。
このとき、潮汐波のx方向の水面傾斜が最大の所の水面傾斜は
程度となる。この傾斜でΔx=100km離れた位置の波高の変化量はΔh=0.0000023×1000000m~0.23m程度です。
一方y方向の水面傾斜が最大の所の水面傾斜は
程度となる。この傾斜でΔy=100km離れた位置の波高の変化量はΔh=0.0000014×100000m~0.14m程度です。
つまり、両者は大きさの程度に於いてほぼ同じオーダーとなるので横方向(y方向)の振幅の変化を縦方向(x方向)の振動に対して無視することはできないことか解る。
ケルビンは論文中で、イギリス海峡を東西に伝播する潮汐波やアイリッシュ海を南北に伝播する潮汐波に於いて上記の傾向が実際に認められることを述べている。
イギリス海峡では南のフランス海岸に比較して北側のイギリス海岸側がほぼ節的(nodal chracter)だから、潮汐波は東から西に向かう弱い波と西から東へ向かうより強い波の伝播からなることを表している。つまり、イギリス海峡ではフランス側海岸に沿って西から東へ伝播する“ケルビン波”(M2-constituent)が見られる。
ちなみに、イギリス海峡の水深は80m(西側)~30m(東側)で、平均水深は約40m程度です。その水深での長波の波長はλ~900km程度ですが、実際の波長もその程度の“進行波”であることが読み取れます。
また、アイリッシュ海ではアイルランド側がほぼ節的なので、潮汐は北から南に向かう弱い波と南から北へ向かうより強い波の伝播からなることを表している。下図は文献2から引用した(M2-constituent)。
[補足説明3]
ついでに説明すると、図中の英国西岸のブリストル湾は世界で二番目に潮汐が大きな湾で、潮差は最大で13mに達する。ちなみにブリストル湾の平均水深は20m程度で、長波の伝播速度は14m/s程度、波長はλ=μT=14×12.42×60×60=632000m~630km程度になります。湾口から湾奥までの距離Lが160km~λ/4程度になり、潮汐周期に共鳴する“定常波”が生じて大きな潮差が生じる。
ケルビンは、前章の議論に引き続いて、無限に長い海峡に生じる“定常波解”を考察しています。今座標を下記のように取る。ただし、波長λ≫水深D≫波高hであることを忘れないこと。
線形の波動方程式だから任意の解を重ね合わせたものも解となる。そのため、定常波の解は、x軸の正方向に進む波と負方向に進む波を重ね合わせたものを考えればよい。すなわち
となる。
ここで第1項はx軸の正方向に伝播する波を、第2項は負方向に伝播する波を表している。第2項を負で重ね合わせたのは、後で説明する“無潮点”がちょうど原点になる様にするためです。正で重ね合わせてもかまわないが、そのときには無潮点の位置がずれる。
このとき第2項の指数部分の符号を逆にしているのは本質的です。そうしておかないx軸の負方向に進む波の解となり得ない。
またH’はy=0での最大振幅を表している。前節の様に側壁での最大振幅ではないので、Hではなく新たにH’と置き直している。
u(x,y,t)やv(x,y,t)の解を求めるには、(15)式のh(x,y,t)を1.(2)の(2a)、(2b)式に代入して得られる微分方程式を時間tに関して積分すればよい。
(2a)(2b)は線形の微分方程式だから、流体の移動速度も同様に重ね合わせたものとなる。
ここで、第2項につく符号が逆転していることに注意。第2項はx軸の負の方向へ進む波に伴う流体粒子の移動速度を表しているのだが、移動速度と波高の関係は正方向へ進む波とは逆の関係になるからです。すなわち波の峰では流体の速度ベクトルは波の伝播方向を向き、波の谷では流体の速度ベクトルは波の伝播方向と逆の方向を向かねばならないからです。
ここのところは解りにくいが、x=0、t=0の特別な場所と時間を考えてみれば了解できる。そのとき(15)式からx軸の正方向に進む波は峰が、x軸の負方向に進む波は谷がきている。一方(16a)から解るように、x軸の正方向に進む波に付随する速度ベクトルはx軸の正方向を向き、x軸の負方向に進む波に付随する速度ベクトルもx軸の正方向を向く。なぜならx軸の負方向に進む波に関しては丁度谷がきているからです。その瞬間の合成波の振幅は丁度ゼロになっているのですが、流速は正方向に最大になっているのです。
このあたりは、後の4.(3)でもう一度確認する。
式の意味を解釈しやすくするために、3.(3)3.で説明した
の関係式を用いて、式中の係数を波長λ、潮汐周期T、伝播速度μで書き直す。
これらの関係式を用いると、(15)(16a)(16b)は
の様に書き直せる。
以下でアニメーションを利用しますが、これらはIBMホームページビルダーに添付されているウェブアニメーター(animator.exe)で作りました。ウェブアニメーターあるいは類似のソフト(フリーソフトもあり)をお持ちなら、アニメーションファイルをダウンロードされて読み込ませて見てください。表示速度を変えたりコマ送りで見たりできますし、再編集も可能です。
最初に波高解h(x,y,t)の様子を調べる。一般的な議論では解りにくいので、適当な関数形を仮定して説明する。
すなわち H’=1、 2ω’/μ=0.1、 波長λ=40、 周期T=12、 水路幅W=20 とする。
側壁におけるyの値λ/4=±10を指数項に代入すると
となるが、日本付近の緯度では
であるから、実際の場合でも
となり、この数値例はコリオリ力の影響を考える上で適切であることが解る。
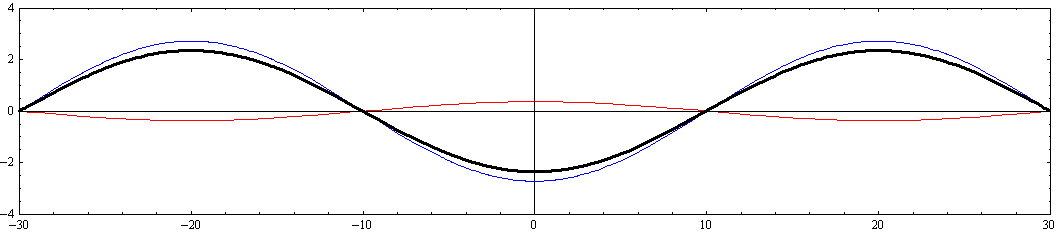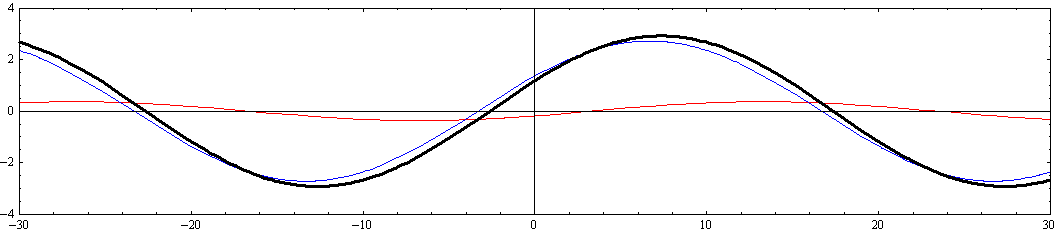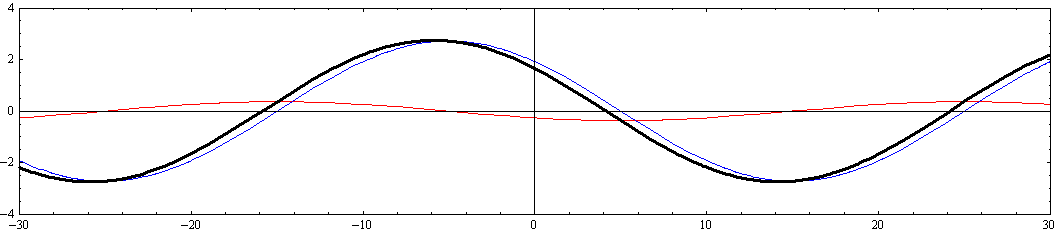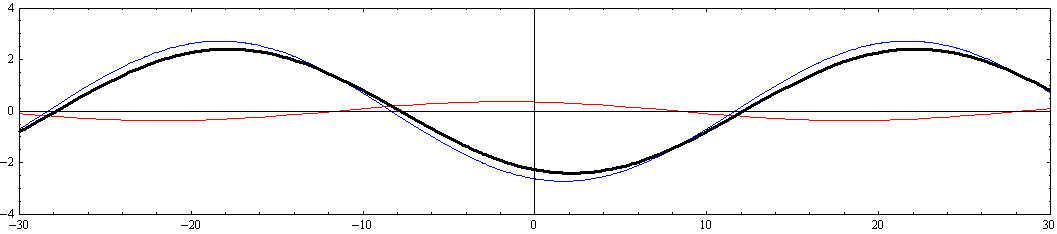
x軸の正方向に伝播する波の、y=0の水路中心部、y=-W/2の側壁部、y=W/2における最大振幅hmaxの様子をグラフにすると下記の様になる。波は手前に伝播してくる。
負方向に伝播する波の場合は下記の様になる。波は向こう側に伝播する。
グラフでは最大振幅hmaxと水深Dが誇張されているが、本当は水路幅W≫水深D≫波高hです。
最初に、特定のyの値で切った断面での解の様子を調べる。
[y=0(水路中心部)の断面]
y=0においては、x軸の正方向へ伝播する波と、負の方向へ伝播する波の最大振幅hmaxが同じになるので、前記の式はさらに簡単化できる。
このとき生じる合成波は、“互いに逆方向に進む[同じ最大振幅]、[同じ波長]、[同じ伝播速度]の二つの波を重ね合わせた場合に生じる定常波”となる。これは高校物理の「波」で習いますが、“全く振動しない部分(節)と激しく振動する部分(腹)が交互に並んで存在し、隣り合う節から節まであるいは腹から腹までの距離は進行波の波長の半分になる”。
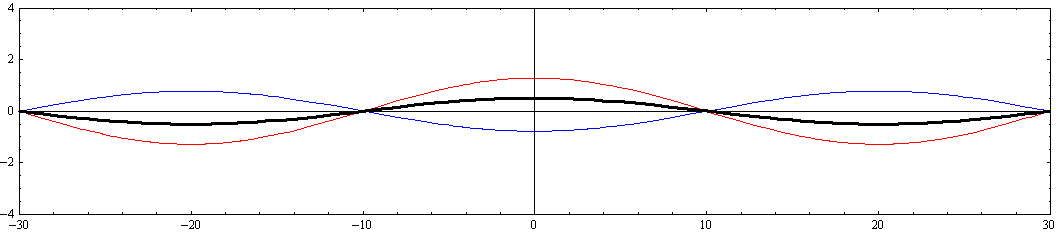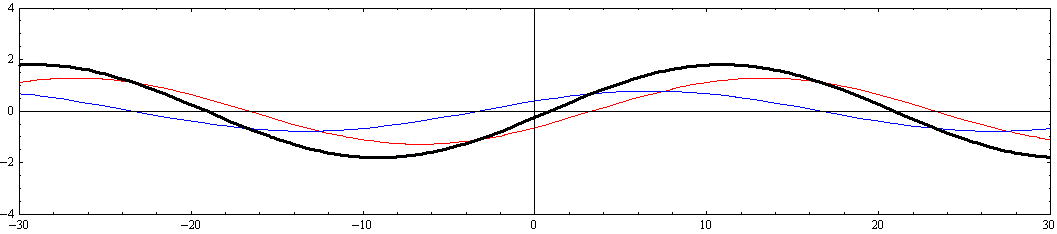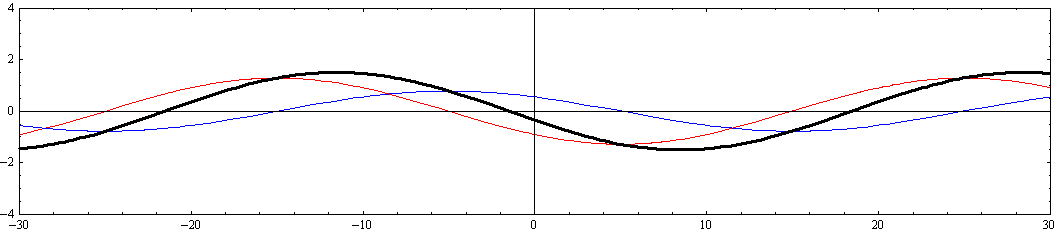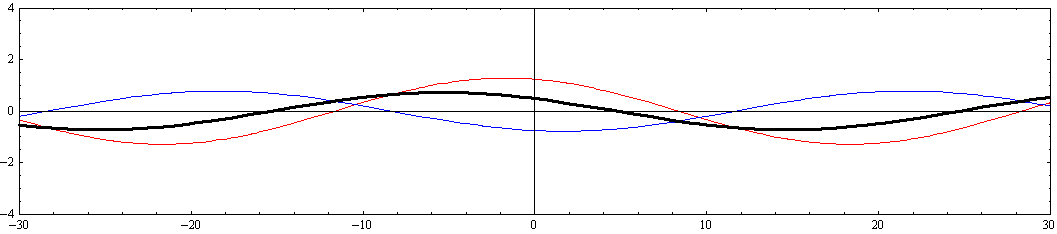
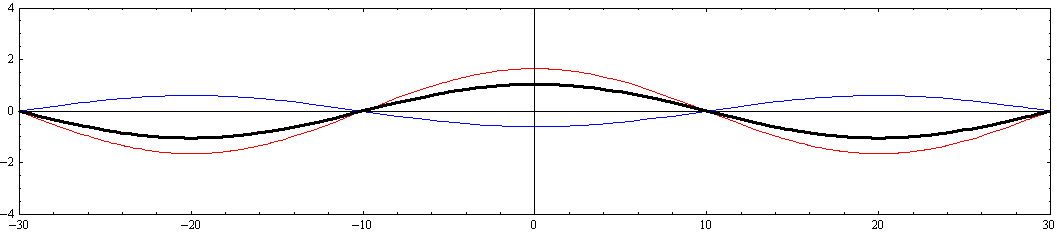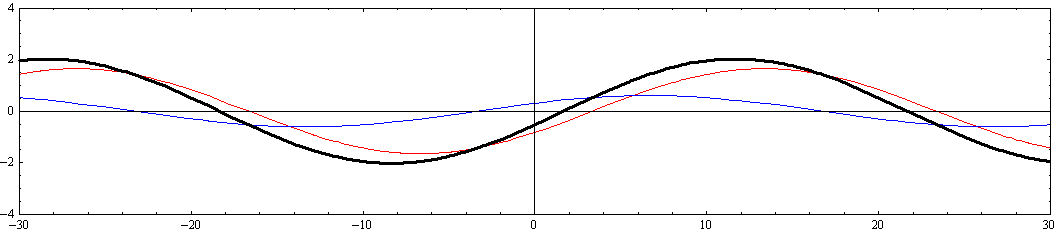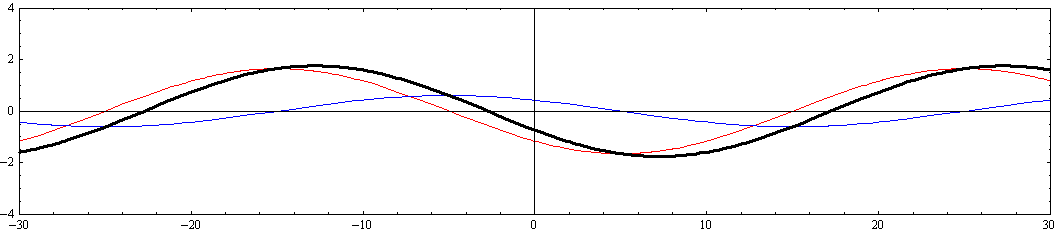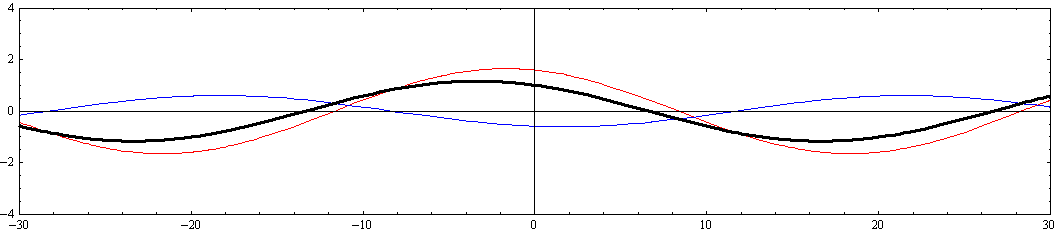
その時間的変化の様子を波高を強調したアニメーションで示す。
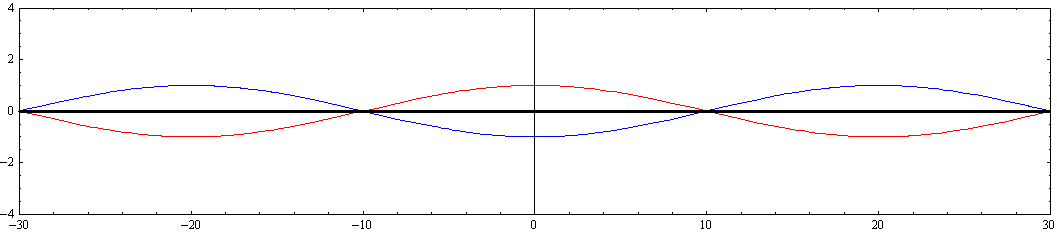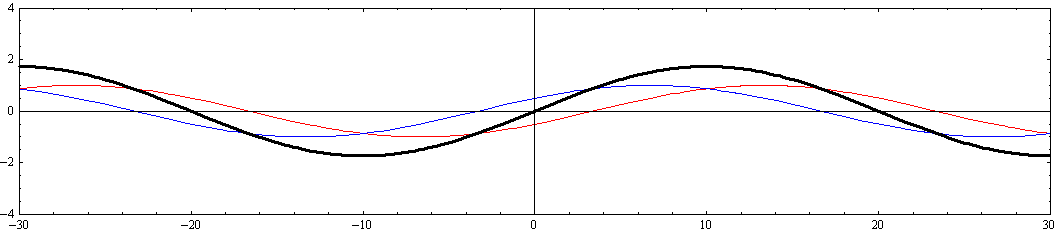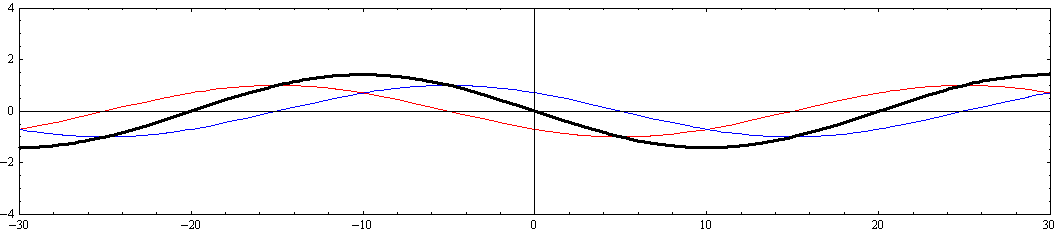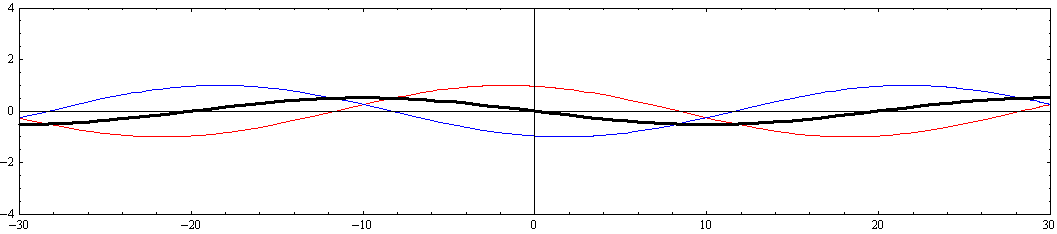
ここで赤色波はx軸の正方向に伝播する波を、青色波はx軸の負方向に伝播する波を表す。黒色太線が両者を合成した波を表す。
y=0(水路中心部)からyの負方向へ移動して、y=-W/8=-2.5、y=-W/4=-5、y=-W/2=-10(側壁部)の三つの位置におけるx軸に平行な断面での様子を調べる。
この場合、x軸の正負に伝播する波の最大振幅hmaxが異なるために三角関数の合成公式が使えないので簡単な式にならないが、アニメーションで示すと以下の様になる。
[y=-W/8=-2.5の断面]
[y=-W/4=-5の断面]
[y=-W/2=-10(側壁部)の断面]
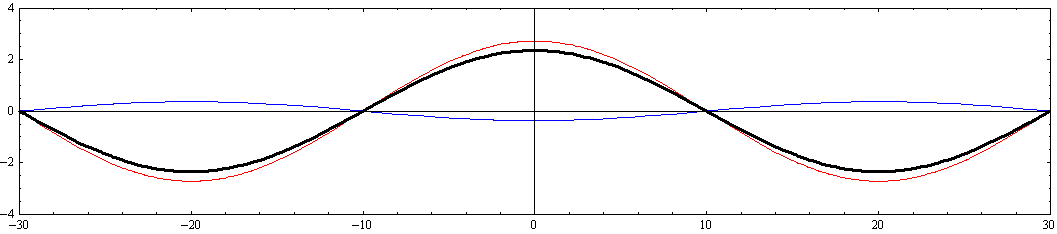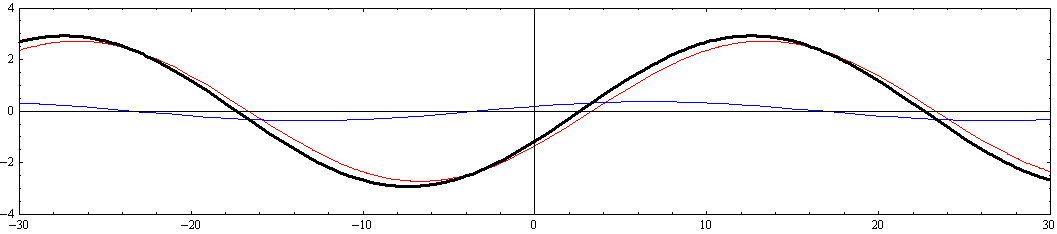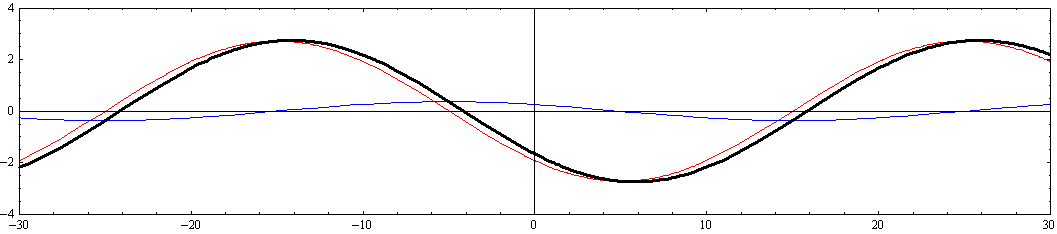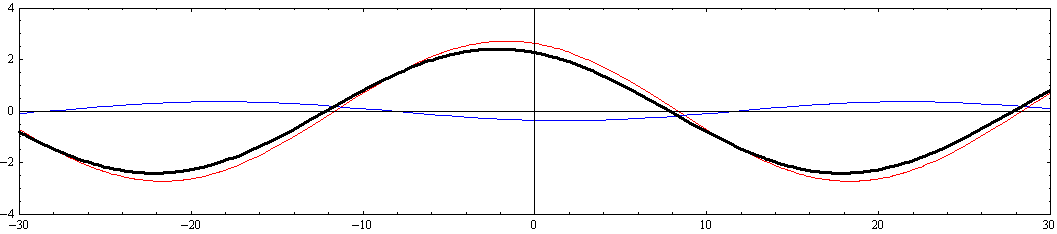
このとき、注意すべきは、“x軸の正と負に伝播する波の振幅の差が大きくなると、それらを合成しても静止した定常波とはならずに最大振幅の場所が移動していく進行波になる”ことです。
そうなることは、振幅の違いを拡大して一方をゼロにすれば、一方の方向に伝播する波のみが残ることからも明らかです。つまり振幅がより大きな波が伝播する方向に移動していく。
さらに注意すべきは、“x軸の正と負に伝播する波の最大振幅の差が変化しても、 x=-20、0、+20 の位置は常に振幅が最小になる位置(節)として固定されている。同様に、
x=-30、-10、+10、+30 の位置は、常に振幅が最大になる位置(腹)として固定されている。”ことです。
y=0(水路中心部)の断面の場合はもちろんですが、それ以外でもそうなることを、以下の二つの例で確認されたし。
[y=-W/8=-2.5の断面]
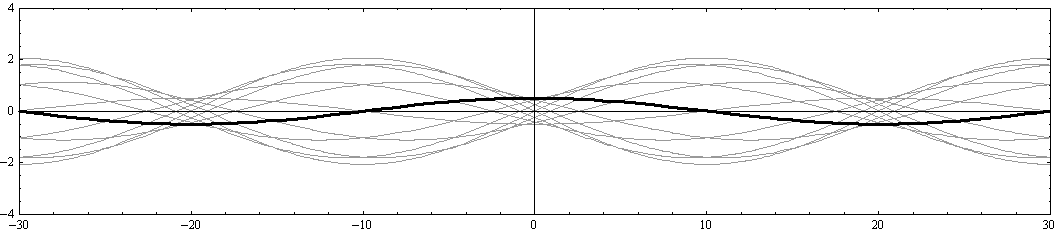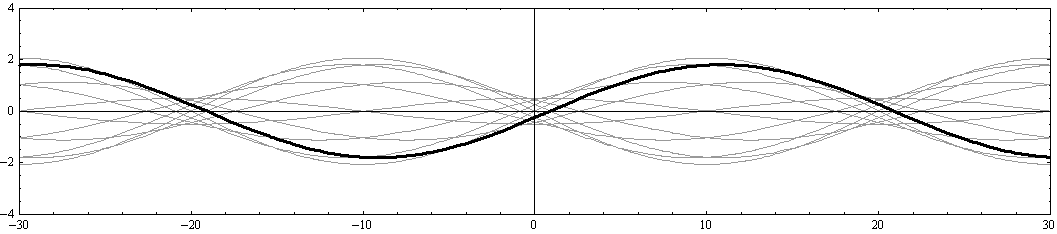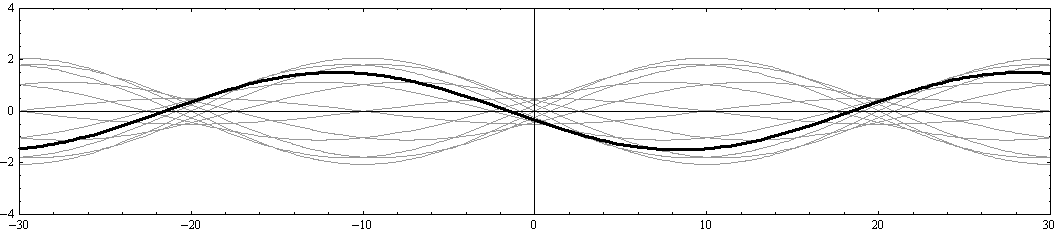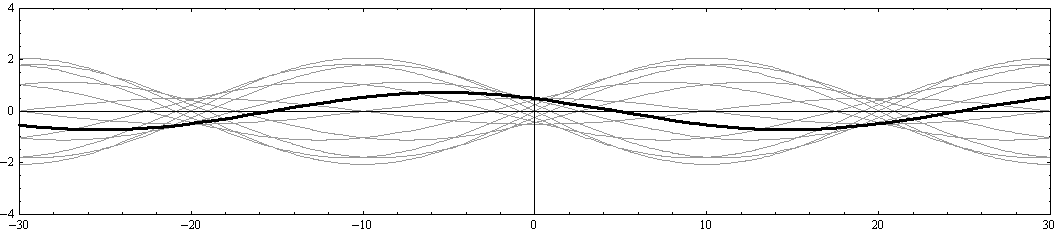
[y=-W/4=-5の断面]
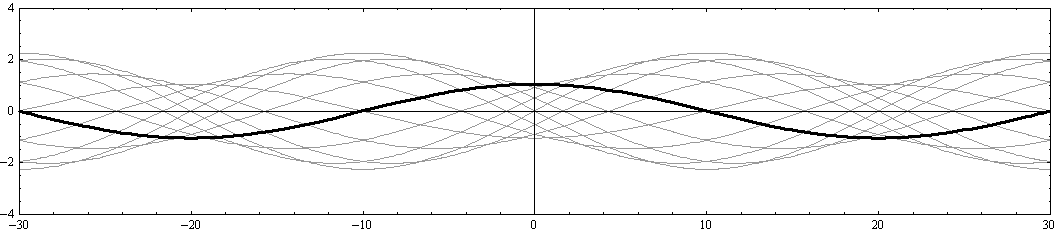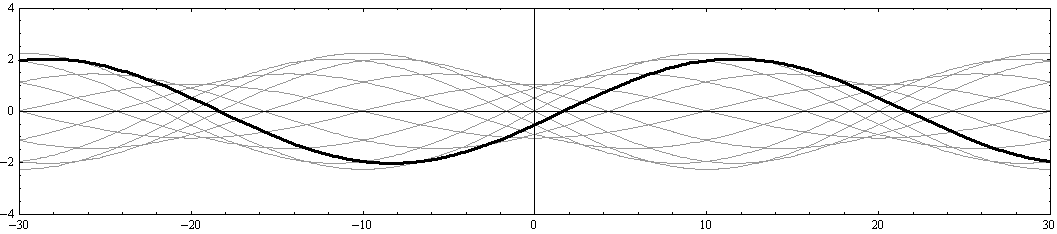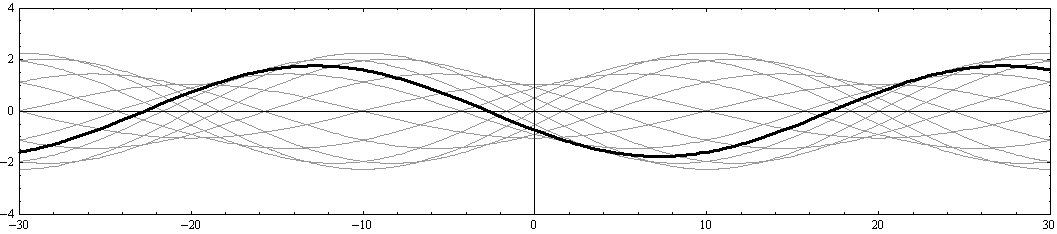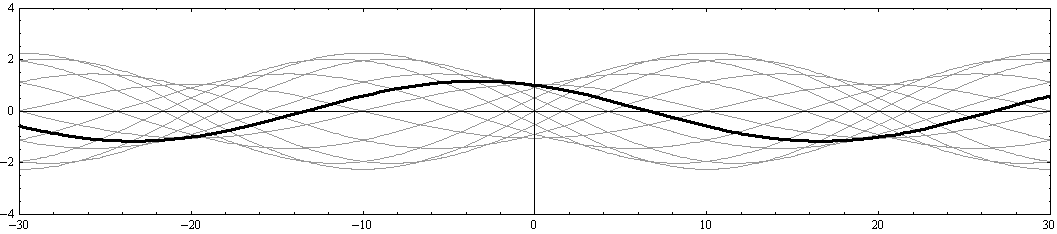
このあたりの事情は別稿「波の反射と屈折率」3.ですでに説明した。そこではcos関数ではなくてsin関数で表していますが、反射壁手前の合成波の様子をここのアニメーションと比較してみてください。x=+10あるいは+30の位置に反射壁があり、そこが腹になる場合と似ている。
yの正方向、すなわち、y=W/8=+2.5、y=W/4=+5、y=W/2=+10(側壁部)へ移動しても、伝播方向がx軸の負方向へ変わるだけで、全く同様な事情が成り立つ。例としてy=W/2=+10の側壁部の様子をアニメーションで示す。
[y=W/2=+10(側壁部)の断面]
最初に設定した関数形
を用いてアニメーション表示してみる。
ここでも H’=1、 2ω’/μ=0.1、 波長λ=40、 周期T=12、 水路幅W=20 と考えてください。図中の曲線は等高線です。また y=-5、0、+5 と x=-20、-10、0、+10、+20 の位置ラインも表示されている。
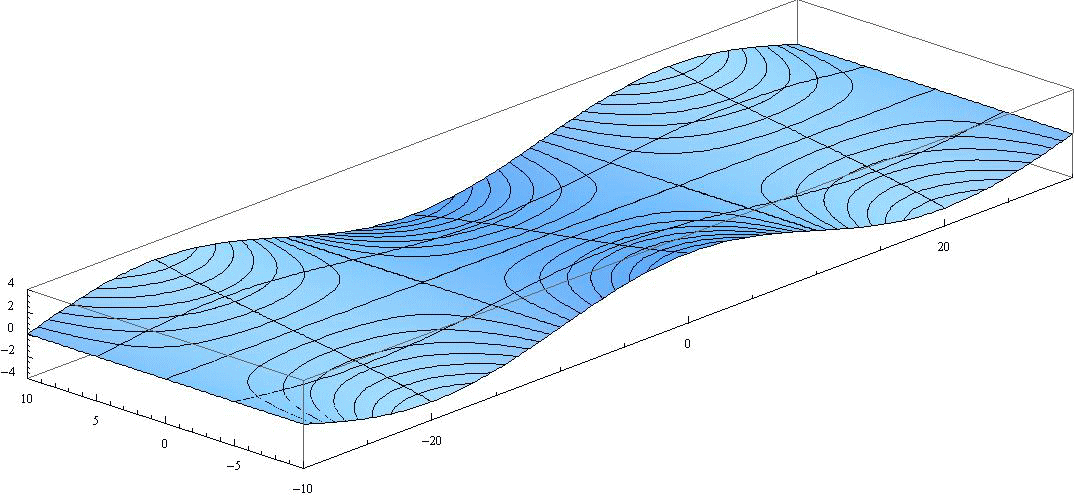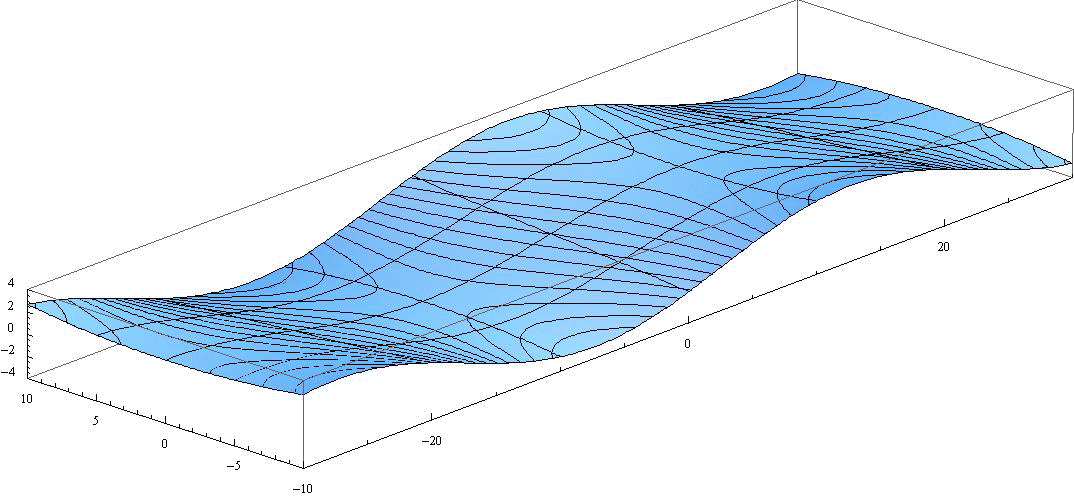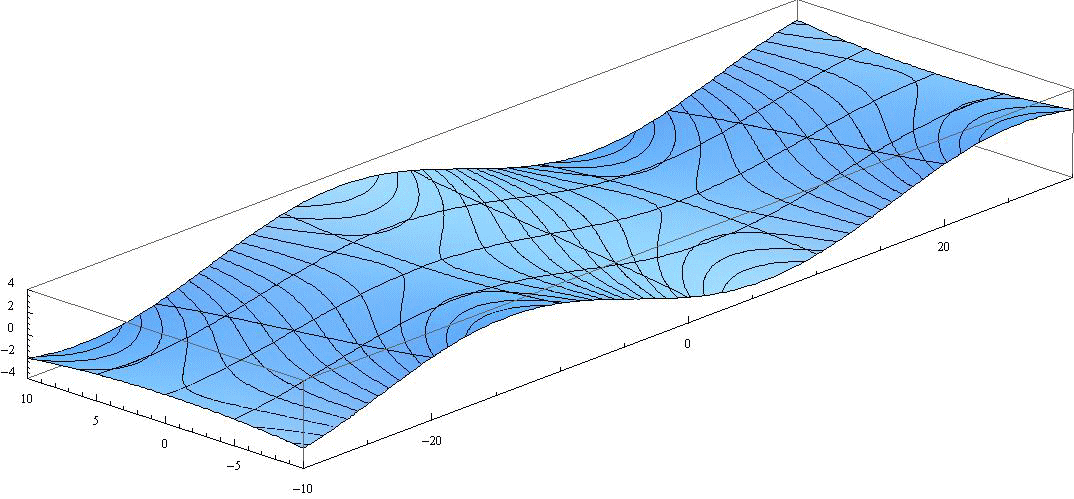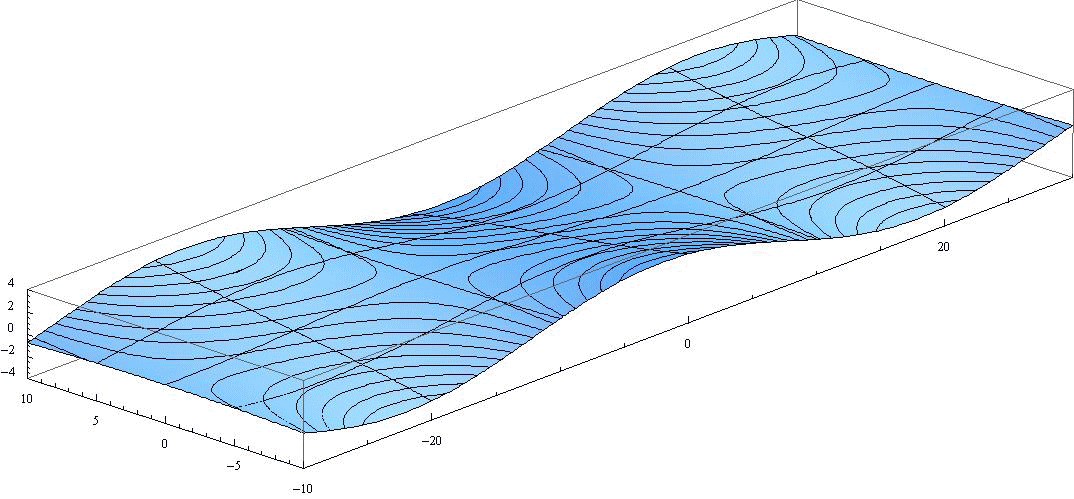
この図の y=0、y=-2.5、y=-5、y=-10 断面の変化が前項のぞれぞれのアニメーションに対応する。
図中の (x,y)=(-20,0)、(0,0)、(+20,0) に於いて、水面が全く振動していないことに注意。この様な位置を“無潮点(amphidromic point)”と言う。
さらに、x=-30、-10、+10、+30のライン上 に於いて、水面が最大振幅で振動することに注意。
潮汐波の伝播の様子を観察するには、等潮時線の概念が便利です。“等潮時線(co-tidal lines)”は“その瞬間の波高の時間的変化がゼロの位置を結んだライン”です。これは、各瞬間の波形の峰あるいは谷を結んだラインではありませんが、潮汐波が伝播していく様子を表す線だと考えることができます。
ある時刻の等潮時線は、(15’)式の時間微分がゼロとなる関数で表される。すなわち
を満足する点(x,y)の連なりが、時刻tにおける等潮時線です。
ここでも、前述の例についての“等潮時線”
をアニメーション表示すると以下のようになる。ここでは見やすくするために表示速度を、4.(2)2.や3.の半分にしています。
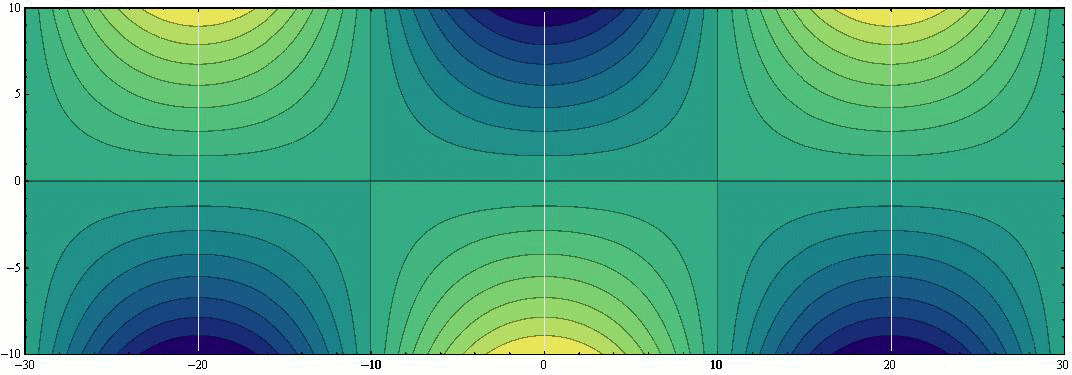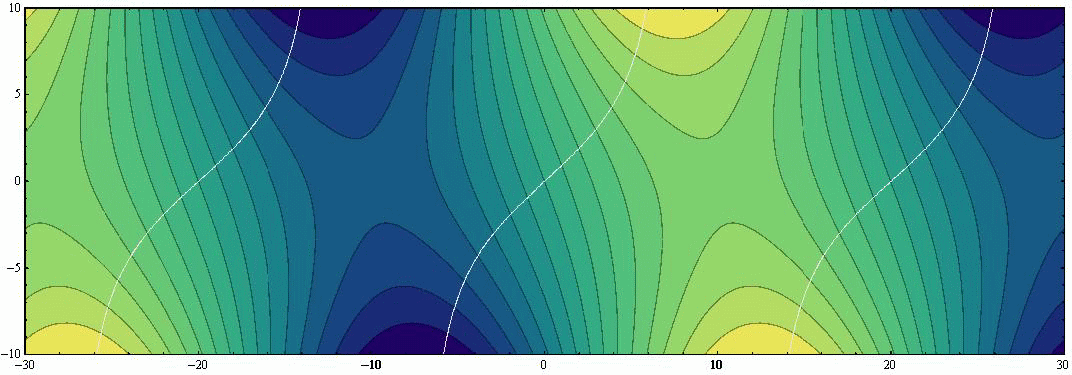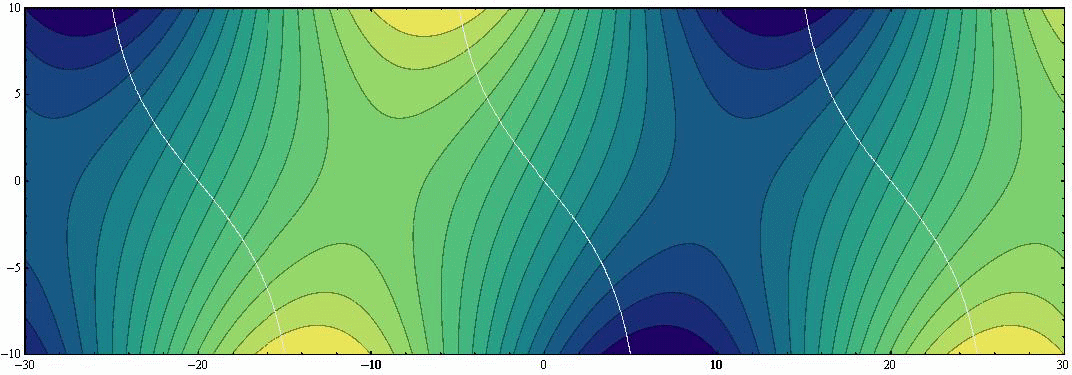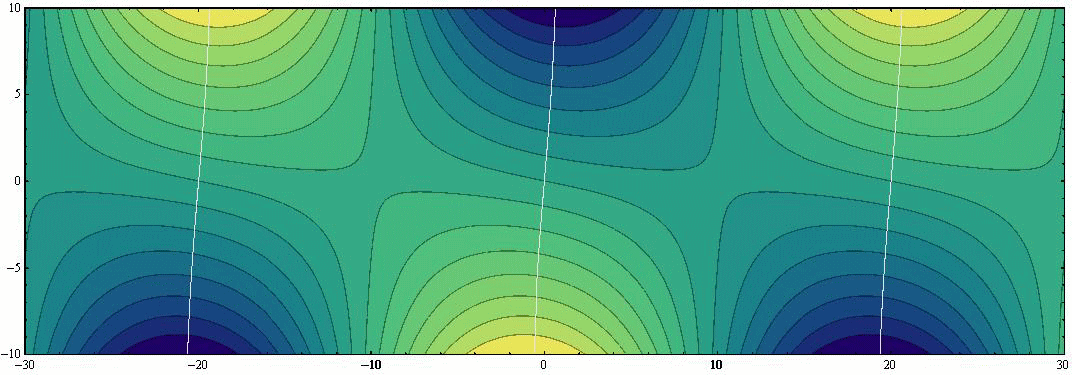
波高は黄色が濃いと高く、青色が濃いと低くなります。緑色部分が波高ゼロに対応します。図中の黒色曲線は等高線を、白色曲線は等潮時線を表しています。
様々な時刻の“等潮時線”を重ねた図を描いてみると下記のようになる。
図中の数字は“太陰時(lunar houres)”を表している。潮汐周期(12.42h)は12時間に近いので、図中のラインはほぼ1時間ごとの等潮時線の移動の様子を表していると言ってもよい。
グラフからも明らかなように“等潮時線(co-tidal lines)”は常に、x=±nλ/2、y=0に生じる“無潮点(amphidromic point)”と交わり、無潮点を中心として北半球では反時計回りに回転する。
このことは式の上からも確認できる。“無潮点”の近くで許される近似を用いると
で表される関数に従って、等潮時線のxy座標における傾きy/xが変化していく。
ところで
であるから、
となる。このグラフは
の様になるから、“無潮点”付近で“等潮時線”はほぼ等角速度ω~2π/Tで回転し、潮汐周期Tで(北半球では反時計回りに)1回転することになる。
ここで 水路幅W≪波長λ の場合を考察する。例えばW=λ/8 の場合は、水路幅Wの値以外はすべて同じだから、前出のアニメーションで-λ/8<y<+λ/8(すなわち-2.5<y<+2.5)以外の領域をマスクすればよい。つまり下記の様なアニメーションで示される。ここでも表示速度を、4.(2)2.や3.の半分にしています。
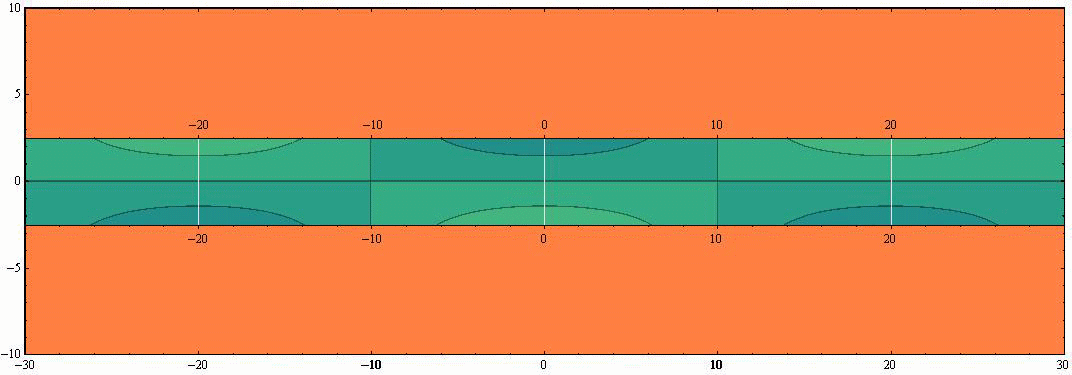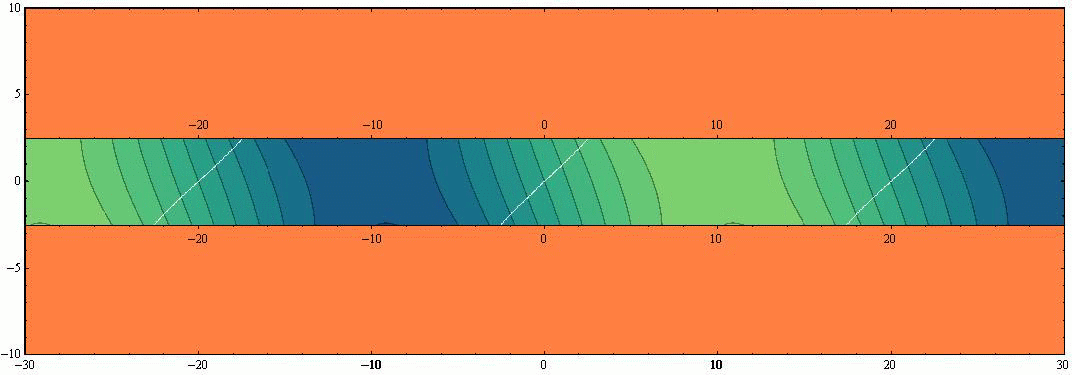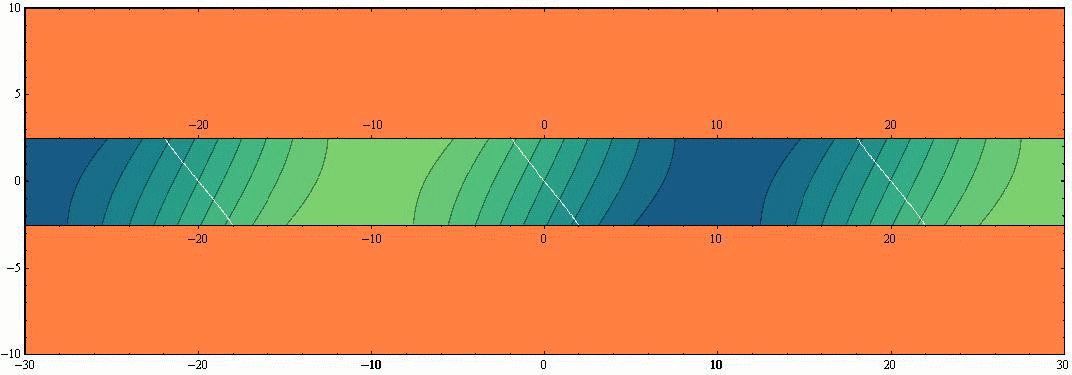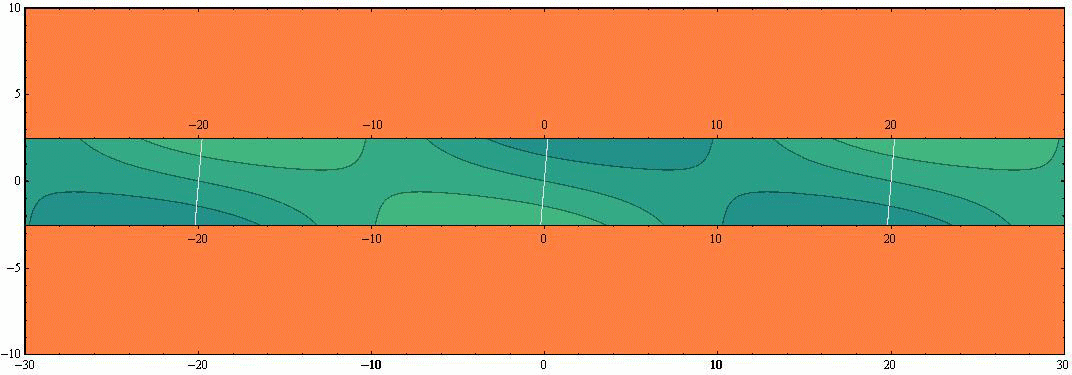
この例は教訓的です。つまり、水路幅W≪波長λ の水路や湾では、水路や湾を横断する方向に関して振幅の違いはほとんど目立たなくなり、水路や湾の縦方向での振幅の変化が主となる。
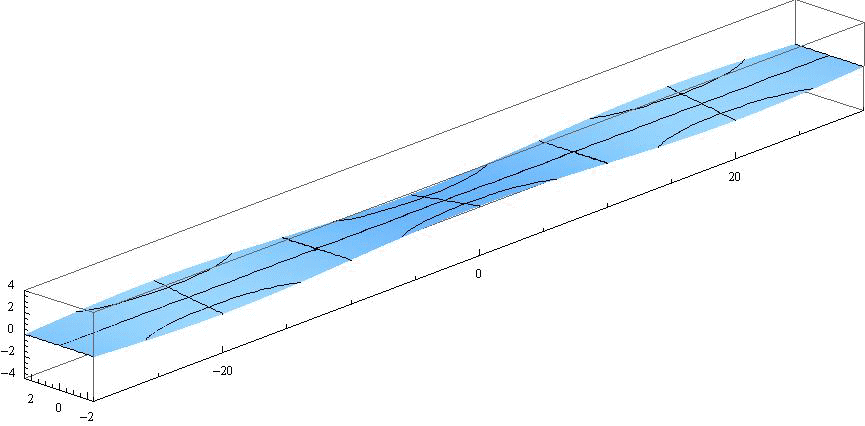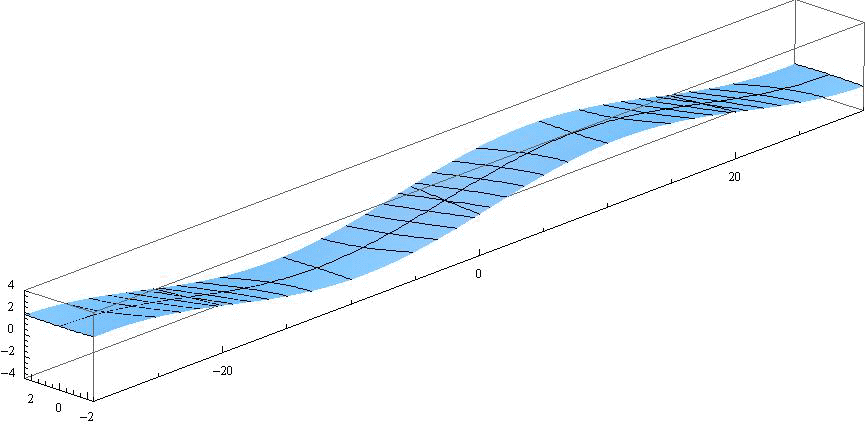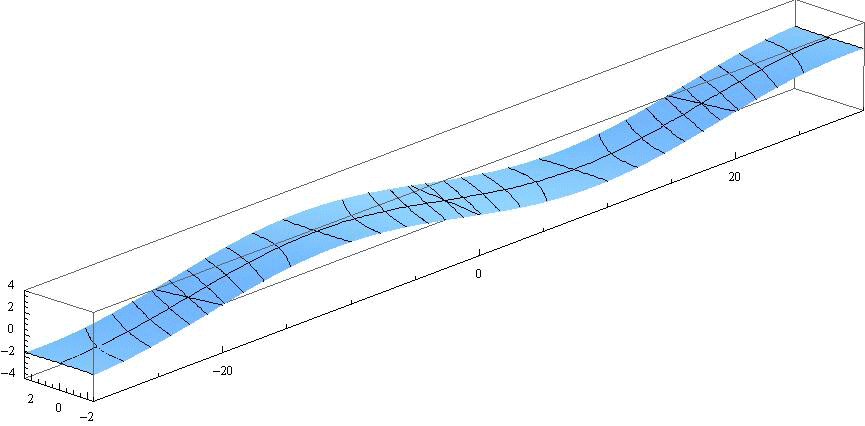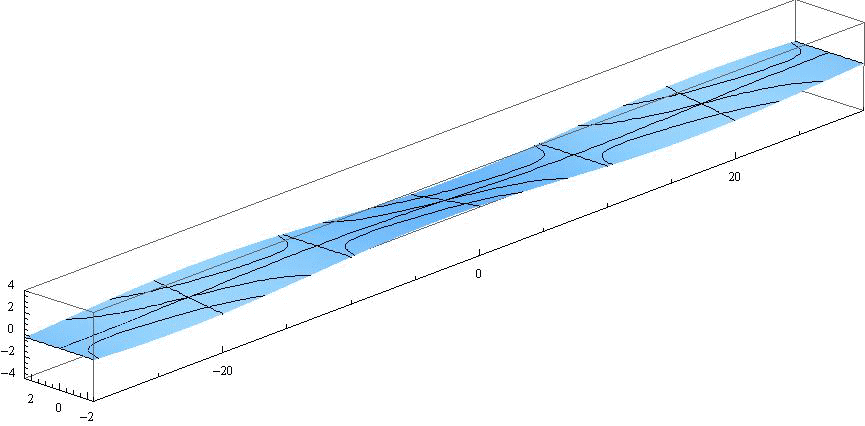
ここで注意すべきは、“最大振幅(腹)になる位置(x=-30、-10、+10、+30)でx方向の流速u(x,y,t)の値はほぼゼロになる”ことです[4.(3)1.参照]。つまりこの位置に壁があって水路が遮断されていても境界条件が常に満たされるのです。
そのため、このアニメーションは、湾奥の壁(上記の位置に設置された)で反射された反射潮汐波と入射潮汐波が合成されてできた定常波の解を表していると考えてもよいのです。
別項で説明したファンデー湾や前述のブリストル湾(3(3)5.[補足説明3])がまさにそのような例です。これらの湾の幅Wはλ/8以下でして、この様な縦長の湾での潮汐振動はコリオリ力効果を無視した議論でほぼ説明できます
さらに注意すべきは、“この様な縦長の湾でも“等潮時線”を定義できて、幅広の湾と同じ角速度で潮汐波の進行に伴って回転する”ことです。ここでのアニメーションがそのことを端的に示しています。
しかし、今の場合は水路を横断する方向での水面傾斜はほとんどありませんから等潮時線の回転する様を表示してもたいした意味はありません。
ここで、等潮時線の等波高点の軌跡である“等振幅線(co-range lines)”を求めてみる。話を簡単にするために無潮点の近くで考える。その場合には前記の近似が使えるのでh(x,y,t)は
となる。これを整理すると
が得られる。
ところで、“等潮時線”は4.(2)4.の(18)式を満足する(x,y)です。(18)式を整理すると
が得られる。
“等振幅線”は回転する等潮時線の同じ波高の点の軌跡だから、(19)式と(20)式の両方を同時に満足する(x,y)値で表される。つまり(19)式と(20)式から時間の依存性を消去すればよい。それは、(19)式と(20)式を未知数sin(2πt/T)とcos(2πt/T)の連立方程式と見なして解くことによって達成される。
この連立方程式は簡単に解けて
となる。これらを恒等式
に代入すると、“等振幅線”の軌跡を表す方程式として
が得られる。
この式は“無潮点”の近傍のみで成り立つ近似式ですが、同じ波高hの部分は“等潮時線”の回転に伴って楕円軌道を描くことが解る。等潮時線の波高hの点が描く楕円軌道の半軸長は下図の様になります。ω’、λ、μとの関係に注目。
4.(2)4.で示したアニメーションで、適当な高さの等高線(黒色曲線)と等潮時線(白色曲線)の交点が時間的に移動していく様子を観察してみてください。無潮点を中心とした楕円軌道を描いていることが見取れます。
y方向の成分v(x,y,t)は常にゼロだから、x方向の成分u(x,y,t)のみを考察する。
先に求めた(15’)式と(16a’)式
を比較すれば解るように、任意の場所と時間における流速の大きさu(x,y,t)は、波高h(x,y,t)の
倍となる。ここで、(g/D)0.5<1であり 波高h≪水深D だから、流速u~波高h×(g/D)0.5 ≪ D×(g/D)0.5~(gD)0.5~伝播速度μ となる。すなわち 流速u ≪ 伝播速度μ であることに注意されたし。具体的な値は3.(3)4.ですでに検討しているので参照されたし。
振幅の変化の様子も波高の変化と同期しています。そのため、正負のそれぞれの方向に伝播する波に伴う速度成分の合成は波高の場合と同様に合成すればよい。
ただし、(15’)式と(16a’)式では重ね合わせる符号が-から+に変わっていることに注意してください。そのようになったのは、流速の方向に関して、x軸の正方向へ伝播する波と負方向に伝播する波で逆転しているからです。すなわちx軸の正方向へ伝播する波では波高が正の位置で、流速はx軸の正方向を向き、負方向へ伝播する波では波高が正の位置で、流速はx軸の負方向を向きます。そこさえ注意すれば、正負のそれぞれの方向に伝播する波に伴う速度成分の合成は全く同様にすればよい。
速度の重ね合わせ符号が振幅のときと逆転しているので、“波高振幅が最小(節)になる位置(x=-20、0、+20)で流速振幅が最大(腹)になり、波高振幅が最大(腹)になる位置(x=-30、-10、+10、+30)で流速振幅が最小(節)になる”。
この事実は、水路幅が狭い場合には、無限長水路で考察した定常波解が、x=-30、-10、+10、+30の位置のいずれかに仕切り壁を設けて生じる反射波と入射波が合成されて生じる定常波の解となり得る事を示している。[4.(2)5.のアニメーションを参照]
もちろん、水路幅が広い場合には、このことは言えないのですが、近似的には言える。仕切り壁でのx方向の速度ベクトルuをy方向へ流体を移動させる速度ベクトルvと考えれば、奥の仕切り壁に沿って波が移動する解を近似的に表していると考えることができる。[4.(2)3.のアニメーションを参照、また5.(1)2.の考察を参照]
流速解u(x,y,t)の様子を表すグラフは、前節で求めた波高解h(x,y,t)に関するグラフをx軸方向にλ/4(すなわち10)だけスライドしたものになる。もちろん、垂直方向(正)の変位で水平方向(正)の速度ベクトルを表していると解釈しなければなりません。つまり縦波の横波表示をしている。
いずれにしても、グラフ(アニメーション)の位置を原点に対してλ/4だけスライドするだけですから改めて描きません。前節のグラフを参照されてください。
次図の様な矩形の湾を考える。
この様な場合、湾奥の壁に於いて、常にu(x,y,t)=0の境界条件が満たされねばならない。
細長い湾の場合、4.(2)5.で説明した水路の場合で波高が腹となる部分を壁で仕切ればよい。湾の奥行きLに比べて湾の幅Wが狭い(W≪L~λ/4)場合には、4.(3)1.で説明したように、湾奥の壁の位置で境界条件u(x,y,t)=0が常に満足されている。
この様な場合にはコリオリ力が無視できて、別稿のいくつかの例で説明したように、波高の振動について湾奥が腹、湾口が節、流速の振動に関しては湾奥が節、湾口が腹になる定常波となる。
湾の奥行きLが湾の水深D、潮汐周期Tにもっとマッチして顕著な潮汐現象が生じるのは、湾の奥行き長L=(1/4)×波長の場合です。
湾の幅が広くなるとコリオリ力の効果が出てきてケルビン波の取り扱いをしなければならない。湾の形がほぼ方形をしていて、湾の奥行きと幅が同じ程度の場合[例えば次節の黄海]には、前章で説明したように、波高hの振幅が最大(腹)になる位置(x=-30、-10、+10、+30)においても流速uの振幅が完全にゼロになることはない。
y=0の中心線上では確かに流速uは常にゼロになるが、水路中心線からyの正方向あるいは負方向に移動するにつれて、流速uの振幅はゼロでなくなり次第に大きくなる。そのため、前出の無限長水路に対する定常波解は、湾幅が狭い場合を除いて、仕切り壁で閉じられた湾において境界条件を満足する解とはなりません。
前章4.(2)4.のアニメーションのx=10の位置の波高変化の様子を詳しく見ると以下の事実が明らかになる。
いま仮にx=+10の位置に仕切り壁を入れて波が反射されたと考え、前節の解が成り立つとしてみる。アニメーションから明らかなように、y=-10側の側壁をx軸の正方向へ伝播し行く潮汐波の最大波高点がx=10の地点に達した瞬間に、同じx=10のy=+10の地点も最高点となっており、その最高点は次の瞬間からy=+10の側壁に沿ってx軸の負方向へ動いて行く。
つまり潮汐波の最高点が、方形の湾の周囲に沿って座標値(x,y)が(-10,-10)→(+10,-10)→(+10,+10)→(+10,-10)→(-10,-10)と伝播して行くと考えると、(+10,-10)→(+10,+10)と(+10,-10)→(-10,-10)の間の伝播に於いて湾幅Wの距離20を瞬時に移動していることになる。
現実には、すでに述べたように無限長水路における定常波解はx=10の湾奥が壁で仕切られていると考えた場合、そこでの速度成分uに関する境界条件を満たしていないのですから、上記の様な事が生じるのです。
境界条件を満たすためには、y=-10側の側壁をx軸の正方向へ伝播してx=10の地点に達した潮汐波は、そこで向きを変えて(+10,-10)→(+10,+10)の行程を時間を要しながら進んでいくと考えなければならない。(+10,-10)→(-10,-10)の間の行程についても同様です。
そのとき、 方形の湾でも、4.(3)1.の最後で注意したように、無限長水路に生じる定常波解は、x=-30、-10、+10、+30の位置のいずれかに仕切り壁を設けて生じる反射波と入射波が合成されて生じる定常波の解と近似的にはみなし得る。そのような近似が成り立つと考えて、4.(3)4.に表示したアニメーションのx<-10 と +10<x の領域を紙でマスクして、 -10<x<+10 の方形領域で波高の動きを眺めてみてください。方形の側壁に沿って波動が反時計回りに回転しているように見える。
それでは、湾奥の側壁においても境界条件を厳密に満たす解とはどのようなものであろうか?
ケルビンは文献1.で円形水槽を伝播する波について論じています。円柱座標で表した偏微分方程式を解く必要がありますが、その解はおよそ次のようなものです。
湾の中心部が振幅、流速について節(無潮点)となり、湾の外周に沿って“ケルビン波”がぐるぐる回る様な解となる。それは、ちょうど水路の両端を繋いで作った円形水槽の中をケルビン波がグルグルと回っているようなものです。
その場合は、ちょうどボーアの原子モデルにおける量子条件をド・ブロイ波の仮説によって説明したのと同じで、“湾の外周の長さが、波長の整数倍に一致する”ことが共鳴条件となる。実際には外周の少し内側に沿った一週長が波長の整数倍となるのだろう。
そのとき、[波長λ]は、波の公式v=λ/Tにより、[湾の水深D→波の伝播速度v]と[潮汐周期T]から決まりますが、方形の湾の場合は奥行きLと湾幅Wが λ/4~λ/2 であれば湾壁の少し内側の一周長が一波長程度になります。
ちなみに、前項で説明した細長い湾の様に湾奥で単純に反射して定常波ができる場合は無潮点(節)から湾奥(腹)の反射壁までの距離は波長の1/4程度でしたが、方形の湾の場合は湾の一辺がλ/4~λ/2程度[“無潮点”(等潮時線の回転中心)から岸までの距離がλ/8~λ/4程度]の間になることが境界条件を満たす上で妥当なところであろう。
このあたりは、次節で述べる具体例で確かめください。
例にあげた海域の水深分布はGoogleEarthの地図画面上でマウスポインターを動かせば読み取れます。是非確認して見てください。
イタリアとクロアチアに挟まれたアドリア海は全長780km程度の内海です。水深は北部で30~150m程度ですが、南部の中央部は1000m近い深度があります。下図の“等潮時線”が示されている領域の平均水深は、“無潮点”の北側で40m程度、“無潮点”の南側で100m程度です。GoogleEarthで水深の分布を確かめてみてください。
3.(3)4.の公式を利用して波長λを見積もると、水深40mの海域でλ~900km程度、水深100mの海域でλ~1400km程度となります。図を見る限り、アドリア海は前節で説明した1.と2.の効果が混じりあった潮汐振動になるようです。
[拡大版はこちら]
水深は、渤海で10~20m程度、黄海で30~80m程度、東シナ海の大陸棚部分で100m程度です。
実際の観測結果は下図に示されています。長波の波長λは水深40mの海域でλ~900km程度、水深100mの海域でλ~1400km程度でしたから、渤海や黄海に現れている潮汐波の“無潮点”(等潮時線の回転中心)から岸までの距離がλ/4程度になっていることが解る。
無潮点が海域の中心からずれているのは、例えば黄海では西側が浅く(30m程度)、東側が深い(80m程度)からです。GoogleEarthで水深の分布を確かめてみてください。そのとき、深いほど伝播速度は速く、波長は長くなり、逆に浅いと伝播速度は遅く、波長は短くなります。
[拡大版はこちら]
上図の説明はこちらを参照して下さい。
黄海の東側(朝鮮半島の西岸沖)は、潮汐差が大きく、“潮流速度“が速いことで知られています。
朝鮮半島の西岸に沿った海域の大潮時の干満差は (木浦付近で)3.6m ~ (仁川付近で)8m 程度だから、最大振幅hmaxに直すと (木浦付近で)1.8m ~ (仁川付近で)4m 程度となる。
木浦から仁川に向かって潮汐波が移動するにつれて波高が増大するのは、その方向に向かって水深がだんだん浅くなるからです。それはちょうど津波が海岸に近づくとき、水深が浅くなるにつれて伝播速度が遅くなり、後から来る波が積み重なって波高が高くなるのと同じです。そのあたりは“等潮時線”の間隔の変化から読み取れます。GoogleEarthで水深の変化を確かめてみてください。そのため仁川付近は黄海沿岸の中でも特に潮差が大きな海域となります。
水深D~40m程度として振幅の最大値hmaxから潮流の最大値umaxを計算してみる。別稿「波動方程式と一般解」3.(5)で説明した様に “潮流速度“=(g/D)0.5×h (hは波高振幅、すなわち干満差の1/2) です。
(g/D)0.5~1/2 である事を考慮すると、
umax=(g/D)0.5×hmax= (木浦付近で)0.9m/s ~ (仁川付近で)2m/s
となる。すなわち、これらの海域では、大潮の満潮・干潮時にかなりの潮流速度となることが解る。
このことに関しては別稿「共振(共鳴)」5.(4)も参照されたし。
イランとサウジアラビアに挟まれたベルシャ湾の全長は800km程度、水深は20m~60m程度です。
[拡大版はこちら]
潮汐を生じる“起潮力”には様々な周期のものがあります。主なものをあげると 主太陰半日周潮M2(28.098度/時)、主太陽半日周潮S2(30度/時)、日月合成日周潮K1(15.04度/時)、主太陰楕率潮N2(28.44度/時)、主太陰日周潮O1(13.94度/時)、主太陽日周潮P1(14.96度/時)、・・・・・・などです。括弧内の数字は角速度(度/時)を表しています。周期については次表を参照されてください。
“起潮力”周期の大多数は、ほぼ半日周期とほぼ一日周期の二つのグループに属します。そのとき、例えばM2とS2のように周期がほとんど同じでも、月齢が進めば周期のわずかな違いにより、それぞれの振動の位相はどんどんずれていきます[例えば別稿の広島湾での例参照]。そのため周期が似ていても、それぞれの起潮力による潮汐は、潮位の時間的な変化を解析すれば明瞭に区別できます。
実際に起こる潮汐はこれらがすべて混じり合った形で起こりますからとても複雑な動きになります。以下はペルシャ湾沿岸の様々な観測地点における実際の潮汐を調和解析(フーリエ級数の和で表したときの各固有振動の振幅)したものです。こういった調和解析を行うフリーソフトはネット上にたくさんあります。
[拡大版はこちら]
各潮汐振動成分ごとに解析しないと、振動分布図に明瞭な形は見えてきません。たいていは、圧倒的な主成分である M2(潮汐周期T=12.42時間)についてのものですが、図を見るときにはどの成分に関するものか気をつけてください。
以下に示す様な図を描くには、湾岸の多数の地点の潮位記録を調和成分に分けて、特定の潮汐要素を選ぶ。そして潮流の変化も参考にしながら、等潮時線の移動を予測する。そうして予想される無潮点が確かに存在するのかその地点の潮位記録と照らし合わせる。
下図はM2(潮汐周期T=12.42時間)に対応する潮汐振動の様子を表しています。ベルシャ湾の平均水深はD=40m程度ですから、長波の伝播速度はμ=(9.8×40)0.5=20m/s程度、波長はλ=μT=900km程度になります。その値から下図の様なケルビン波が生じるのも頷ける。まさに4.(2)4.で示したような状況が生じている。
[拡大版はこちら]
ちなみに、K1(潮汐周期T=23.93時間)成分については、下図のようになる。この場合潮汐周期TはM2のほぼ2倍ですから、波長λも2倍になり、無潮点も湾の中心部に一つだけ現れます。
[拡大版はこちら]
このとき、無潮点を中心として回転する等潮時線のy/xは無潮点付近で
に従った時間変化をします。すなわち等潮時線の回転角速度はM2の場合のほぼ半分になります。
下図は起潮力ポテンシャルを考慮して2度間隔メッシュで数値計算したM2潮汐波の伝播の様子を示しています。図中の連続線が“等潮時線(co-tidal lines)”を、破線が“等振幅線(co-range lines)”を表す。
等潮時線は、同じ位相を持つすべてのポイントを結びます。 数値は、月がグリニッジ子午線(0°)を通過した後の満潮の時間遅れ、またはグリニッジを基準とした潮の位相(たとえば、位相が
0° の場合、月がグリニッジ上空を通過すると同時に満潮になります) 、180°はこの時点で干潮です)
[拡大版][超拡大版] [図の説明]
大洋に生じるM2潮汐の振幅は最大で50cm程度であることに注意してください。また、いずれの等潮時線も“無潮点(amphidromic point)”を中心にして、潮汐周期(12.42時間)で一回転する。
大洋の水深はD=4000m程度ですから長波の伝播速度はμ=(9.8×4000)0.5=200m/s程度になります。実際に大洋表面上を“等潮時線”が進んでいく速度はその程度であることが図から読み取れます。
そのとき周期Tを潮汐周期12.42時間とすれば、進行波の波長はλ=μT=9000km程度になります。一週9000kmの円の直径は3000km程度になりますから、直径2000~4000km程度の回転運動をするケルビン波が大洋の中に配置され並ぶ事になる。それらが互いにうまく配置されるように“等潮時線”の回転方向が決まるようです。
ちなみに、地球半径は6370kmですから地球の赤道一周長は40000kmになることと、メルカトール図法のために高緯度が拡大されていることを考慮して図をご覧ください。
そのとき当然のことですが、等潮時線に沿っての海面の振幅の大小は、北半球では反時計回りの等潮時線で移動方向の右側が大きくなっています。しかし北半球で時計回りをする等潮時線に関してはそうはなっていないようです。
南半球では時計回りの等潮時線で移動方向の左側が大きくなっている。しかし南半球で反時計回りする等潮時線に関してはそうなっていない。
[補足説明0]
特に興味深いのは北大西洋に生じている無潮点と等潮時線の様子です。北大西洋は北の方が実質的に閉じていて巨大な湾の様な形をしている。
前図ではメルカトール図法のために北側の距離が拡大されているが、実際は東西、南北3000km程度の広さを持つ、水深3000~4000mの巨大な円形湾だと考えることができる。このことは地球儀の上で是非ご確認下さい。
また、月の公転と地球の自転との関係は別稿「潮汐周期」をご覧下さい。
さらに、下記の説明で最も解りにくいところは“ケルビン波”が絡んで来るところですが、そこの所はこちらのクランシーの説明を復習されて下さい。
[下図の拡大版]
上図説明文中の“静力学的平衡論”、“動力学的潮汐理論”、“定常波説”については別稿須田晥次著「海洋科學」のp592~p599をご覧下さい。
そこで、紹介されている (1)静力学的平衡論、(2)動力学的潮汐論、(3)定常波説 はそれぞれが単独で潮汐現象を説明できる様なもので無くて、これらを統合した形で説明されるべきものです。
すなわち、上図で説明した様に、“ケルビン波理論”を加味した“動力学的潮汐理論”に、“静力学的平衡論”と“定常波説”を援用して説明するのが、最も納得できるやり方だと思います。
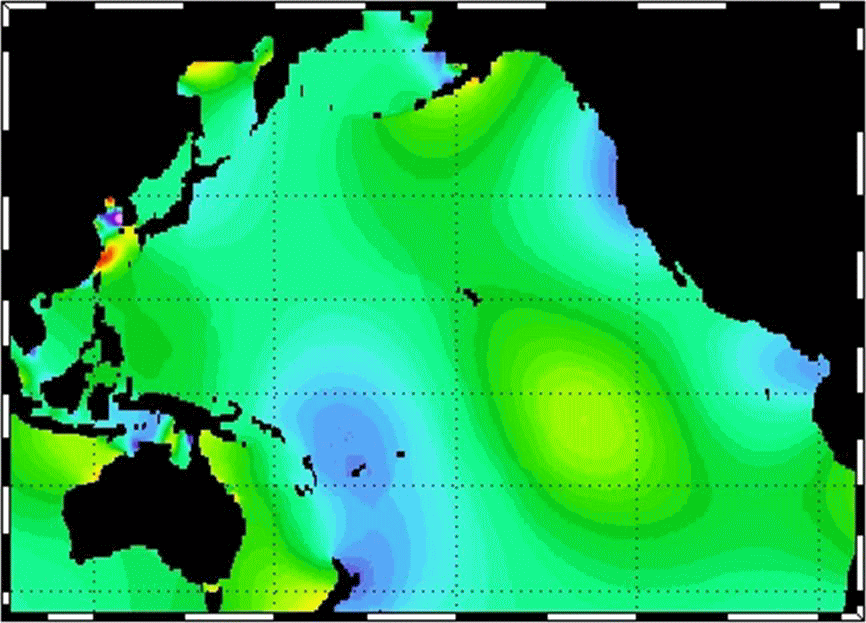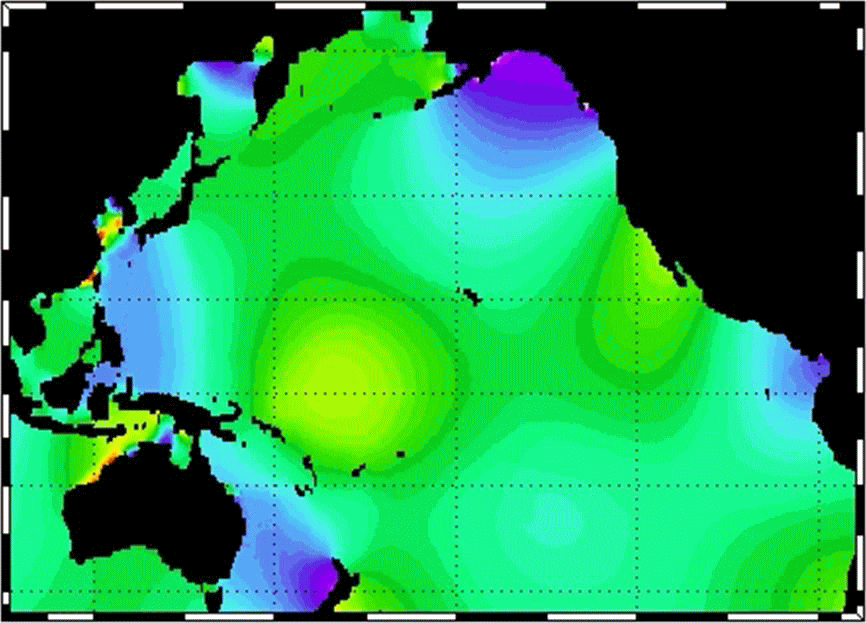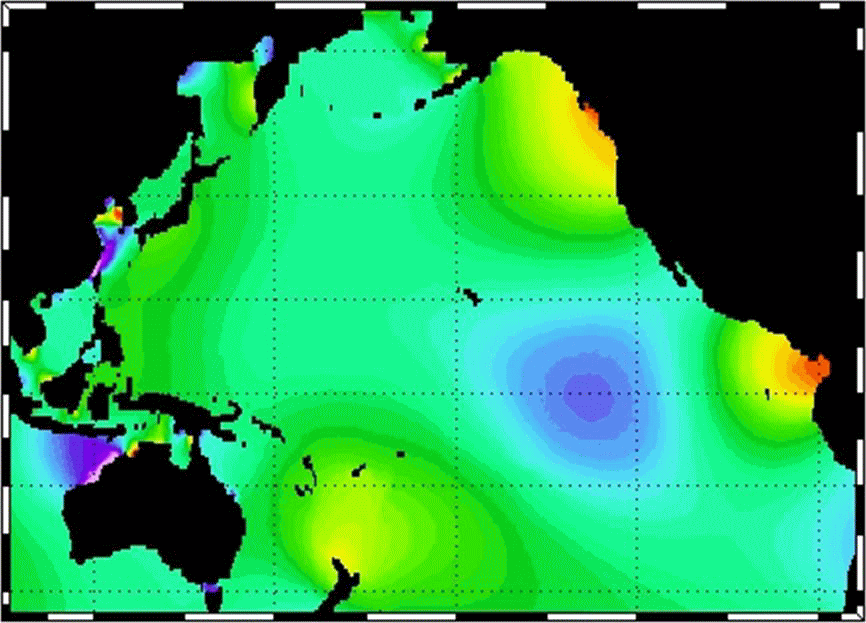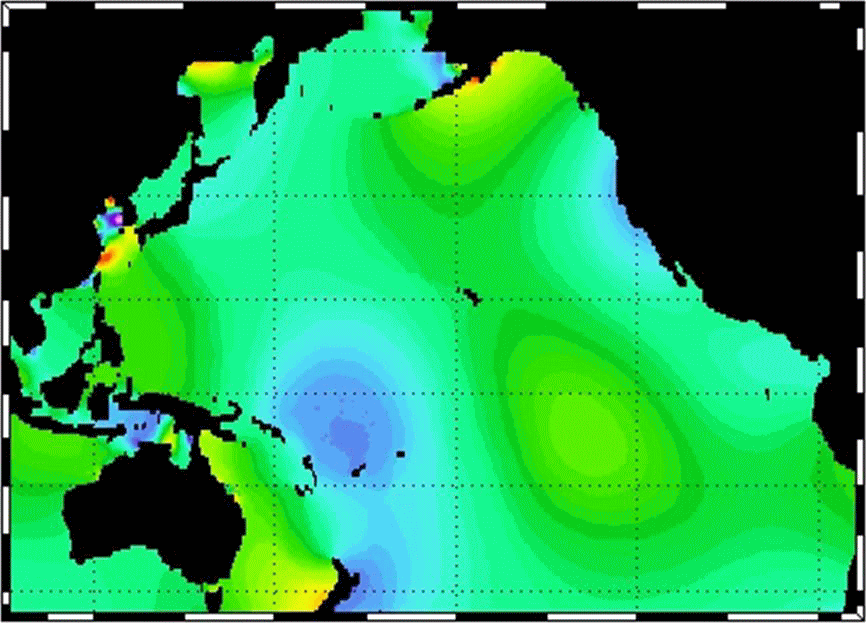
以下のアニメーションは、太平洋に於ける潮汐波の様子を示す。これは
http://www.o3d.org/eas-4300/lectures-2012.php 18-Tides.ppt
から引用した。少し改竄しています。太陰時で0.5h刻みの推移です。
[補足説明1]
ケルビン波の振幅や潮流速度uの大きさは、壁(岸)から距離y=(gD)0.5/2ω’だけ離れると、壁(岸)での値の1/e倍に減少します。この特徴的なスケール(gD)0.5/2ω’を“ロスビーの変形半径”(radius of deformation)と言います[3.(3)1.参照]。
ちなみに緯度45°に於いて2ω’=0.0001rad/s程度[1.(1)2.参照]ですから、緯度45°水深D=40mの内海の場合にはロスビーの変形半径は200km程度、D=4000mの大洋の場合には2000km程度になります。
上のアニメーションの黄海や北東太平洋の状況はまさにそのことを表しています。
[補足説明2]
上のアニメーションの赤道付近をよく観察すると、波長9000km程度の潮汐波が常に東に向かって伝播しているように見える。これは潮汐波が“赤道ケルビン波”となって西から東へ向かって伝播しているのかもしれない。もちろん様々な原因の潮汐波が重なっていますから、それらのノイズを取り除いたら、赤道ケルビン波が存在しているように見えると言うことです。
赤道ケルビン波はケルビン波と似ていますが、コリオリ力の緯度依存性(β効果)によるものです。赤道ケルビン波の特徴は、常に東へ伝播することです。高緯度へ移動したとき波高や潮流速度が赤道での値の1/eとなる特徴的スケールは、水深D=4000mの大洋の場合、4000km程度になります。アニメーションの様子はそのようになっていると見えないことはない。
赤道ケルビン波については、別稿「慣性重力波とロスビー波、そして赤道波」4.で説明しています。
[補足説明3]潮汐現象の教え方について(2017年7月追記)
読者の方から、「平衡潮汐理論では、実際の潮汐現象を旨く説明できません。実際の現象を解りやすく説明するにはどのようにしたら良いと考えられますか?」という趣旨の御質問を頂きました。以下は潮汐現象の教え方についての私見です。
潮汐現象は月及び太陽の引力による強制振動なのですが、具体的な海洋の形の中で潮汐力が誘起する強制振動がどのような共鳴現象を引き起こすのかを説明するのは難しい。ケルビン波として潮汐波が伝播すると教えるのが一番簡単そうです。
大洋の水深は4000m程度ですから、長波の伝播速度は200m/s(時速720km/h)程度です。月の潮汐力強制振動の周期はT=12.42時間です。別稿の説明を参照すると、進行波の波長はλ=v・T=9000km程度になります。
これは直径3000kmの円の周長となりますが、ちょうど北大西洋がこの程度の大きさの海です。それで北大西洋では丁度12時間程度で一週するケルビン波が月の起潮力によって共鳴して潮汐現象が生じるとして良いでしょう。実際の観測値はケルビン波の伝播で旨く説明できそうです。5.(2)4.[補足説明0]を参照。
ところが、北太平洋は、北大西洋の四倍程度以上の大きさがありますので、単純なケルビン波の周回共鳴にはなりません。幾つかの部分に分かれた周回共鳴が複雑に組み合わされた形になります。前出の北大平洋潮汐アニメーション参照。
5.(2)2.日本近海図の日本列島太平洋岸を東から西に伝播する潮汐波の伝播速度は、その等潮時線Ⅴ→Ⅵの間隔から計算して700km/h程度です。これはまさに水深4000m程度の大洋に於ける長波(ケルビン波)の伝播速度720km/h=200m/s にほぼ一致します。
また、等潮時線図に於いて、月の南中時間と日本列島太平洋岸の満潮時間が6時間程度ずれていますが、これは月が南中したときに日本の南方赤道付近の海水面が月の引力の為に最も高潮位になるためだと思われます。潮汐振動が月の起潮力に共鳴して共鳴振動しているならその様になるはずです。
それがケルビン波として周回伝播して、北にある日本の太平洋岸を通過する時刻が丁度半周期の6時間後ということです。その波がさらに6時間後に南方海域に達したとき、月は丁度日本から見て地球の裏側で南中していることになります。
実際の潮汐波の伝播の様子を知るには、海底地形・海岸地形の境界条件の下で各海水部分に働く強制起潮力を考慮した波動方程式を解かねばならないが、それは数値計算でしか実行できません。そのようにして解いた北太平洋解のアニメーションを先に引用しましたが、それをご覧いただくと実際の潮汐波をケルビン波の伝播でほぼ説明できることが了解できます。
アニメーション中の黄海・渤海部分のケルビン波伝播については、それらの内海の南側開口部“東シナ海”に働く起潮力強制振動に伴うケルビン波の周回伝播で旨く説明できます。もちろん海岸地形が入り組んでいますから、アドリア海やアラビア海のようには旨くはいかないようですが。
実際[黄海の水深から計算される長波の伝播速度]と[黄海の大きさ]と[月の起潮力周期]は共鳴条件を旨く満たしています。
日本海に潮汐がほとんど存在しないのは、[日本海の平均水深]と[日本海の周囲長を含めた大きさ]と[月の起潮力周期]が共鳴条件を満たさないからです。
以上のように、潮汐現象はケルビン波の周回伝播の共鳴条件で説明するのが一番簡単です。そのレベルを超えて説明するには、ラプラスの潮汐方程式を数値計算で解かねばならないでしょう。
このページはある読者の方からの質問が切っ掛けで作りました。作るに当たって若い頃読んだ文献2.を読み直してみたのですが、青焼きの縮小コピー版なので、老眼・乱視・緑内障の我が身には、目はウロウロ、頭はクラクラする作業でした。その内容をすっかり忘れていて、思い出すのにシクハックしたのですが、自分の青春時代が少しよみがえった気がします。