Louis de Broglie著「波動力学研究序説」(1930年刊)
ルイ・ド・ブロイが1930年に書いた波動力学の教科書です。渡邊慧翻訳で1934年に発刊(岩波書店)された訳本から引用しています。訳文はカタカナ表記の堅苦しい文章ですので、大幅に改変しています。原文はこちらでご確認下さい。
般的序論
1.古い質点力学
(1)Hamiltonの原理
(2)Lagrangeの方程式
(3)Lagrangeの関数、運動量とエネルギー
(4)Hamiltonの原理の他形式、Maupertuisの原理
(5)Hamiltonの正準方程式
(6)接触変換
2.Jacobiの定理
(1)Jacobiの方程式
(2)Hamiltonの積分およぴJacobiの関数
(3)短縮形のJacobiの関数
(4)Jacobiの方程式の種々の形
(5)一様な直線運動に対するJacobiの関数
(6)一様不変な場におけるJacobiの関数
3.波動力学の基礎的な考え
(1)出発点
(2)前述の結果を見出す他の方法
(3)屈折率、波Ψの群速度に関数基礎定理
(4)波動的な諸量と力学的な諸量との間の関係
(5)最小作用の原理とFermatの原理
4.波の伝播に関する一般的事項
(1)均質で時間的に不変な媒質内における波の伝播
(2)分散
(3)波連と波群
(4)不均質だが時間的に不変な媒質内における波の伝播
(5)波の包絡面の作用とFermatの原理
(6)不均質だが時間的に不変な媒質内における波群
(7)時間的に変化する媒質内における波の伝播
5.粒子の連合波の伝播方程式
(1)伝播方程式の選択に対する判別の基準
(2)場の無い場合の伝播方程式
(3)恒常の場における伝播方程式
(4)変わる場における伝播方程式
(5)方程式を自動的に見出す為に役立つ方法
6.古典力学と波動力学
(1)古典力学における振幅aの意味
(2)存在確率
(3)具体的な例
(4)第6章の摘要
7.干渉の原理およぴ結晶による電子の回折
(1)干渉の原理
(2)結晶による電子の回折
(3)G.P.Thomsonの実験に関する予備知識
(4)G.P.Thomsonの実験
(5)Ponte氏の実験(1929年)
8.干渉の原理および固定中心による荷電粒子の散乱
(1)古典力学による荷電粒子の散乱
(2)波動力学による計算
9.新力学における存在確率の運動
(1)確率の雲
(2)確率要素の運動方程式
(3)Ehernfestの定理
(4)関数φおよびaの計算
(5)嚮導波(キョウドウハ)の理論
10.光子の波動力学
(1)光子とその連合波
(2)光子に結び付けられる確率の雲
(3)干渉現象の解釈
(4)完全反射をする平面鏡の付近における光の干渉
(5)不完全反射をする鏡の付近における光の干渉
(6)二つの単色平面波の合成
11.Heisenberg およひ Bohr の理論
(1)分光的分解の原理
(2)Heisenberg およひ Bohr の理論. 不確定性関係式
(3)Heisenberg およひ Bohr の理論における波の意味
(4)古い力学との一致
(5)Einsteinの異議. 粒子は位置を指定し得ないのか又は位置を有しないのか?
(6)結語
12.測定の可能性とHeisenbergの関係式
(1)測定の操作とHeisenbergの関係式
(2)Heiserbergの顕微鏡
(3)Doppler効果を用いる電子の速度測定
(4)粒子の細孔通過
(5)速度の測定に関する注意
13.場が無い場合および場が一様な場合の波束Ψの伝播
(1)伝播方程式の場が無い場合における厳格な解
(2)特別の場合への計算の発展(Darwin)
(3)二回の相次ぐ観測による速度の測定
(4)一様にして変わらない場における波束Ψの伝播の厳格な解
(5)特別の場合への計算の発展
14.粒子系の波動力学
(1)系の古い力学の諸原理の摘要
(2)系の古い力学から系の新しい力学への移行
(3)数学的予備定理
(4)配置空間における伝播方程式
15.系の運動に結び付けられた波の解釈
(1)幾何光学の近似
(2)一般の場合. 確率の運動
(3)Ehrenfestの定理
(4)BohrとHeisenbergの解釈
(5)注意
16.古い量子論と周期運動の安定
(1)周期運動の量子化の第一例
(2)Wilson-Sommerfeldの条件
(3)Einsteinの言い表し
(4)Kepler運動の量子化
(5)變退(ヘンタイ)の問題
(6)古い量子論の不充分さ
17.量子化された運動の安定の波動的解釈
(1)波動力学における量子化の意義
(2)固有振動の簡単な例: 振動する弦および膜
(3)方程式(9)の一般的な場合の研究
(4)粒子系の量子化
18.量子化された系に対する波Ψの解釈
(1)一般的原理の量子化された系への適用
(2)量子化された系に及ぼす外よりの作用の影響
(3)確率の雲とHeisenbergの行列
一般的序論
ここは、本書の序文(前書き)です。しかし、カタカナ表記の読みにくい文章なので別ページで紹介します。原本をそのままをコピー引用していますのでリンク先を開いてご覧下さい。。
これは1930年に書かれた教科書の序文である事に留意してお読み下さい。
1.古い質点力学
二つの古い力学がある。一つは《Newtonの古典力学》で、もう一つは《Einsteinの相対論的力学》です。Newtonの力学は長い間科学の諸要求に対して満足なものであったが、Einsteinの深遠な考察はこの力学を修正して、考えている質点の速度が真空中の光速度cに比較して小さいときにはNewtonの力学と一致するが、速い速度に対してはそれから離れて仕舞うような力学を作らなければならないことを示した。
この二つの古い力学は、互いに区別する相違点があるにも拘わらず、重要な類似点も示している。というのは、二つの一般方程式は同一の形をもち、共に“最小作用の原理”から導かれる。この理由により、二つの古い力学の一般原理を同時的に述べることが容易になる。重要なことは、真空中の光速度cが無限に大きな値を持つと考えると、Einsteinの力学からNewtonの力学のすべての公式が導かれることです。つまり、β=v/cについて級数展開して高次の項を無視すれば《相対論的力学》の公式は《Newton力学》の公式に帰着する。
[補足説明]
上記の事柄に付いては別稿「相対論的力学」などを復習されると良いのですが、このことに付いては本著書において後ほど詳しく説明されます。
ここでは、まず質点の力学を扱う。すなわち力の場が与えられたと考えて、その中での一つの粒子の運動を研究する。今、この力の場を空間座標と時間の関数であるポテンシャル関数F(x,y,z,t)で定義する。
古い力学(《Newton力学》と《相対論的力学》)では、質点(粒子)は空間内でハッキリ定まった位置を有して、その位置は三つの座標で指定することができる。よって、質点(粒子)の“速度”を次の様に定義することができる。すなわち、道筋に沿って走った空間を、それを走るに要した時間で割った値で、しかも走る時間を零に近づけた極限の値とする。
粒子の位置が直角座標で指定される場合、粒子の速度は
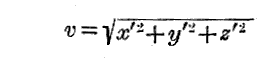
と表される。ただし、肩に付いている ’ は時間に関する導関数を示す。
一般の場合は、何らかの曲線座標q1,q2,q3を用い、速度はqi及びqi’のある関数として表される。
二つの力学の基礎原理は “Hamiltonの最小作用の原理” です。質点(粒子)が時間t0のときに空間点M0に、時間t1のときに空間点M1を占めるとすると、質点力学の問題とは時間t0と時間t1の間の時間に於ける質点(粒子)の運動を決定することです。
“Hamiltonの最小作用の原理” は、qi、qi’、t の関数 L(qi、qi’、t) に関して述べられる次の性質によってt0とt1との間における動点の運動が特徴づけられる様な関数 L が存在することです。
その性質とは、実際の運動に対する積分

の値が、この実際の運動より無限小だけ異なり、且つt0にM0に在る粒子をやはりt1にM1に持ってくるような他のいかなる運動に対するこの積分の値より小さいという事です。上記の積分を “Hamiltonの作用積分” と言い、関数 L(qi、qi’、t) は “Lagrange関数”(運動ポテンシャル) と称される。
それ故に、“Hamiltonの最小作用の原理”は次の公式で表される。
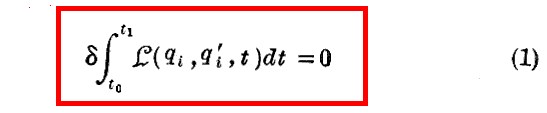
ここで、t0 と t1 は変えられないものであり、δなる記号は q の始め及び終わりの値を変えない様にして qi(t) 従って qi’(t) なる関数形について無限小の変化を行わせることを意味する。
(2)Lagrangeの方程式 目次へ
“変分法”の一般的方法に従って “Lagrangeの方程式” を導く。
時間tの各値に対する関数 qi(t) に qi(t)+δqi(t) なる値を与える様に修正すると、qi’(t) は qi’(t)+δqi’(t) となるので
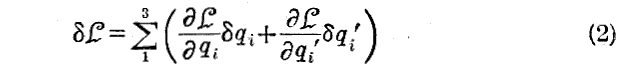
となる。
t0 と t1 は変えないので
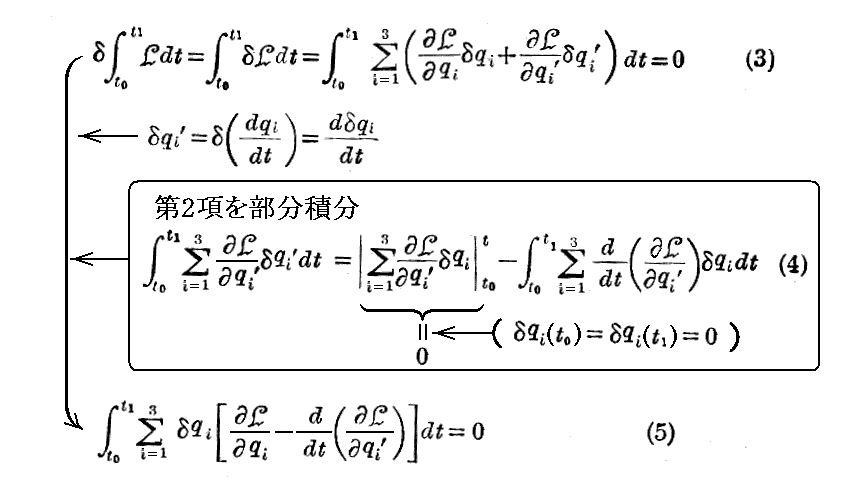
となる。ここで δqi は任意なので以上の結果は
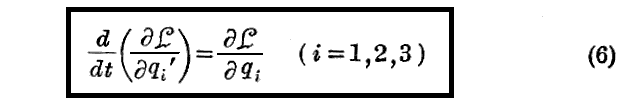
となることを意味する。
これが“Lagrangeの方程式”で、質点(粒子)の運動を“6個の任意定数”の関数として決定する。6個の任意定数は例えば、最初の位置の3座標と、初速度の3成分の様なものです。
この当たりについてはランダウ・リフシュツ著「力学}の第1章もご覧下さい。
(3)Lagrange関数、運動量とエネルギー 目次へ
1.Lagrange関数
以上の力学の理論に於いて、(NewtonとEinsteinの)二つの古い力学の区別が生じるのは“Lagrange関数”Lの選択の相違による。
《Newton力学》では
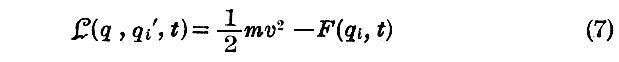
と置く。mは粒子を特徴づける定数で“質量”と呼ばれている。関数F(qi,t)は“ポテンシャル関数”であり、vは粒子の速度でqi’の関数として表されねばならない。
一方《Einsteinの相対論的力学》では
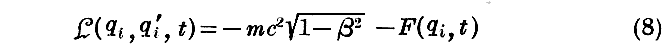
を選ぶ。ただしβ=v/cです。
ここで
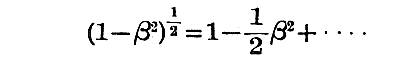
と冪級数に展開して、ここに書かない項を無視するならば“Lagrange関数”Lは
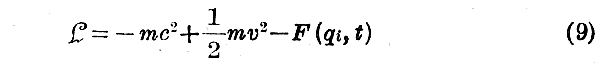
となる。だから相対論的な“Lagrange関数”は、この程度の近似では古典的な“Lagrange関数”と定数項−mc2だけ異なることが解る。
(1)式積分に於いてこの項は−mc2(t1−t0)なる項を生じるがこれは変分が行われず従って度外視できる。それ故に、前述の様に二つの古典力学はβの高次の巾を無視すると互いに融合してしまうことが解る。
[補足説明1]
Newton力学で“Lagrange関数”を(7)式の様に置いたのは、これを“Lagrangeの方程式”に代入するとNewtonの運動方程式が得られるからです。
また、(8)式がどこから導かれるのか不思議に思われるかも知れませんが、これも、“相対論的運動方程式”を“Lagrangeの運動方程式“と比較して求めたのです。それ以外の理由はありません。
ここは別稿「相対論的力学」2.[補足説明6]、あるい別稿「電磁場中の荷電粒子の運動」2.[補足説明1]、等々をご覧下さい。
次項で説明されている内容は、その手順を逆に展開しているだけです。
[補足説明2]
ド・ブロイが、最初から特殊相対性理論を含めた解析力学を展開しているのは、別稿「相対論的力学」3.(4)[補足説明4]で説明したようにド・ブロイの“物質波の仮説”は特殊相対性理論を基にして初めて導けるものだからです。
2.運動量
ここで、先ほどの“Lagrangeの方程式”に帰る。そこで、
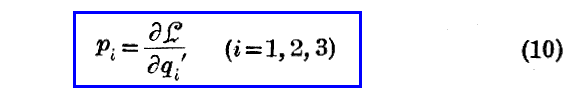
と定義して、このpiを変数qiの“共役運動量”と呼ぶことにする。つまりこれが“一般化運動量”の定義式を表している。
そうすると“Lagrangeの方程式”は

となる。これはLagrange方程式に(10)式を適用して得られる式だが、後で解るようにこれが“運動方程式”に相当する。そして、(11)式の右辺は“一般化力”を表していると見なせる。
しばらくの間座標qiが直角座標である特別な場合を取り上げる。そうすると
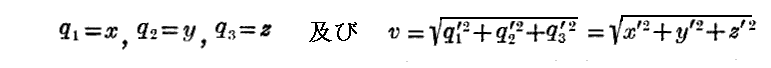
となる。
Lを《Newton力学的》に選ぶと
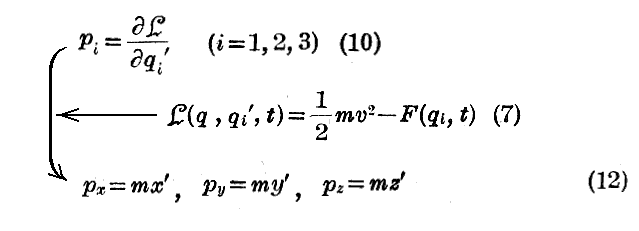
となるので、piはいわゆる運動量ベクトルmvの成分である事が解る。
もし《相対論的》な関数Lとして(8)式を取れば
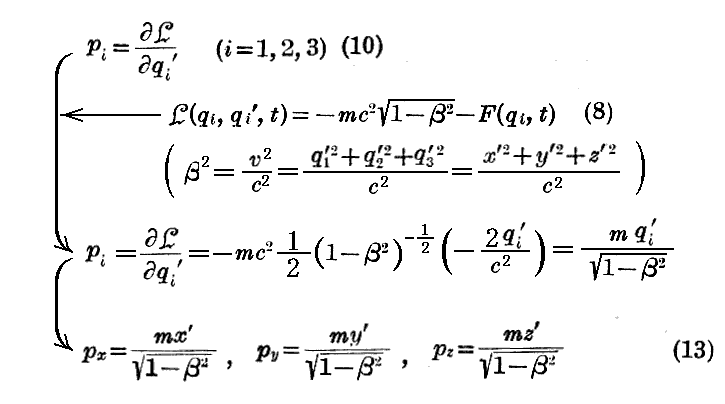
となる。もし相対論的力学における運動量ベクトルを
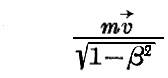
に等しいと定義すれば、piは再びこのものの成分となる。
さて、以上どちらの場合に於いても直角座標を選択すると、その結果としてLは関数F(qi,t)を通してのみqiの関数となる。従って

である。
ここで
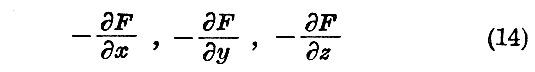
なる成分を持つベクトル−grad F を考え、且つこのベクトルを粒子に働く“力”と名付けるならば方程式(11)は【古典的運動方程式】
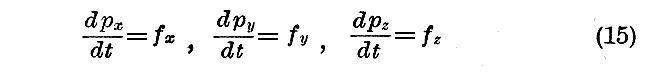
を与える。
この式は二つの古い力学すなわち《Newtonの古典力学》と《Einsteinの相対論的力学》のどちらにも適用できる。
3.エネルギー
次に、エネルギーの概念を導入しよう。その為には、“Lagrangeの方程式”の一般的な式から出発する。
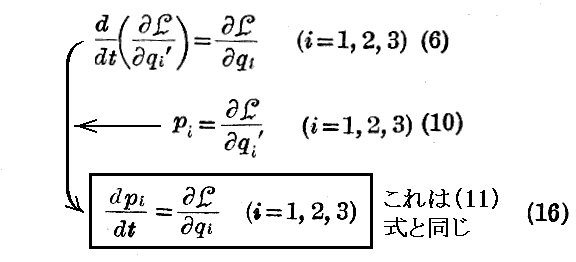
ここで、

なる量を考え、その時間に関する導関数を計算すると
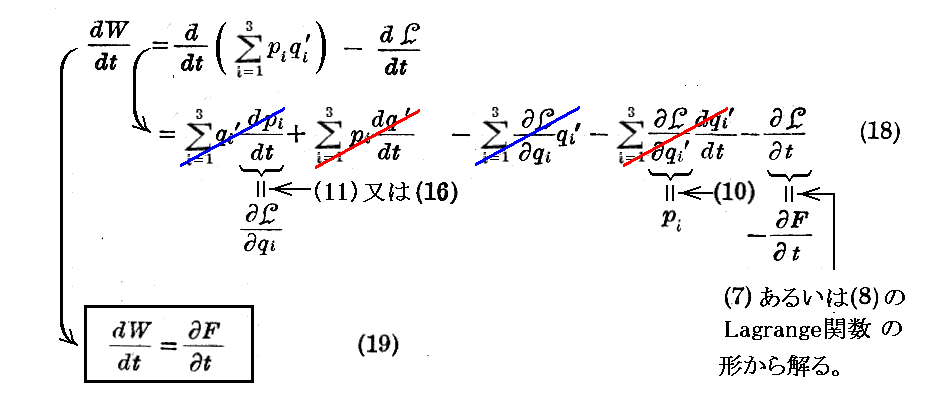
となる。これより次の定理が得られる。
“もし関数Fが時間を陽に含まないならば(17)式で定義されるWなる量は一定値を保つ。”このWを粒子の“エネルギー”と呼ぶことにすれば、これはいわゆる“エネルギー保存則”を意味する。
[補足説明1]
別稿「エネルギー保存則の証明」で述べた様に運動方程式を時間tについて積分すれば、“エネルギー保存則”が導ける。Planckがいみじくも指摘している様に、運動方程式の両辺を時間で積分したとき、その積分値がエネルギーの次元を持つ場合、それはエネルギー保存則を表していると見なせるのです。
ならば、運動方程式を一般化した、“Lagrangeの方程式”を時間tで積分すればエネルギー保存則を導く事ができるだろう。ド・ブロイは相対論的なLagrange関数も含めて説明しているので解り難いが、非相対論的力学に限ればその事を理解しやすい。
実際、Lagrangeの方程式の時間積分から直ちにエネルギー保存則が導かれる。(文献2.p129〜131より)
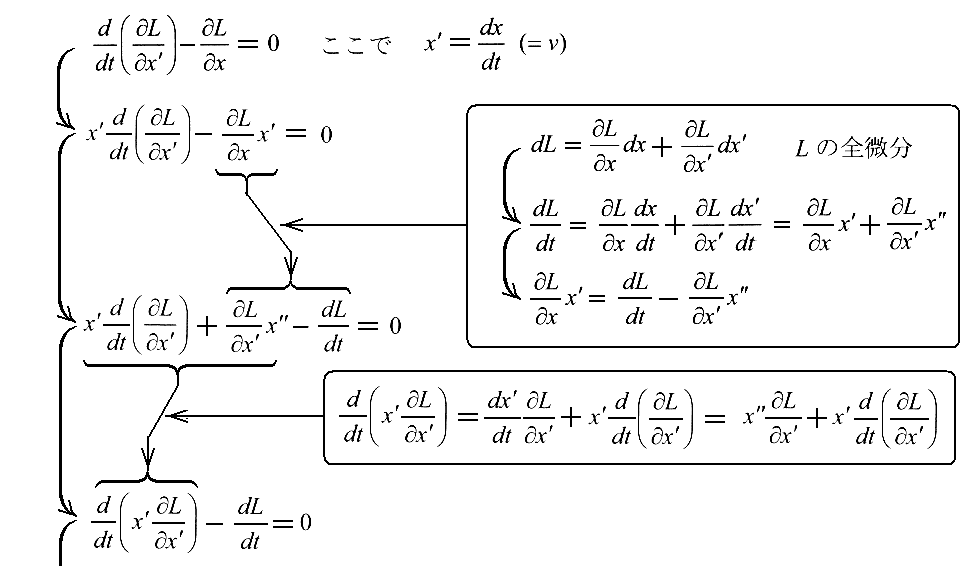
[補足説明2]
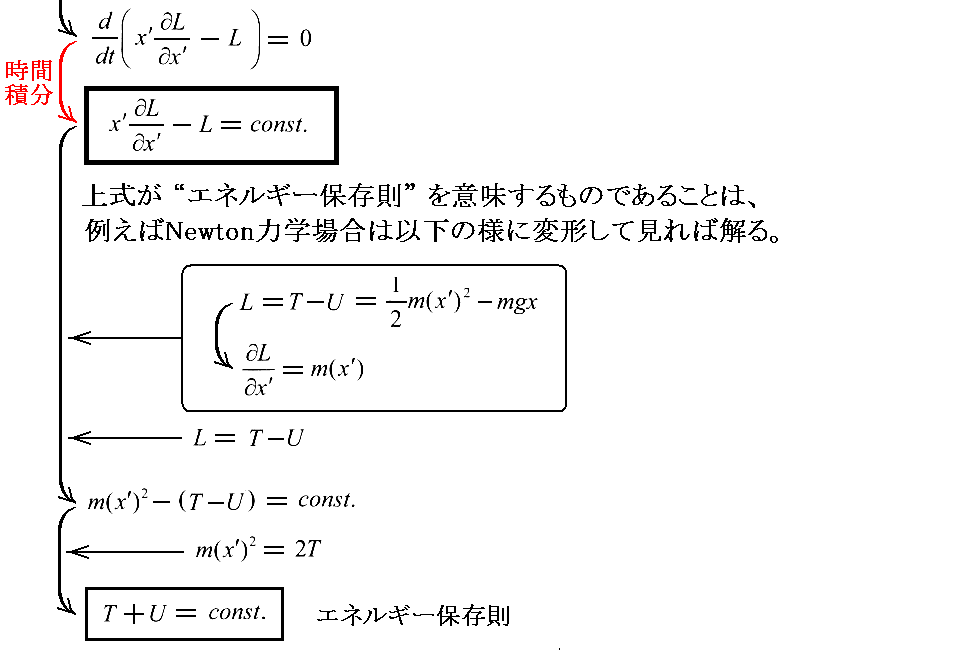
(17)式は“エネルギー関数”(Hamilton関数)の定義式ですが、非相対論的力学に限れば、以下の式変形でそのことは確認できる。
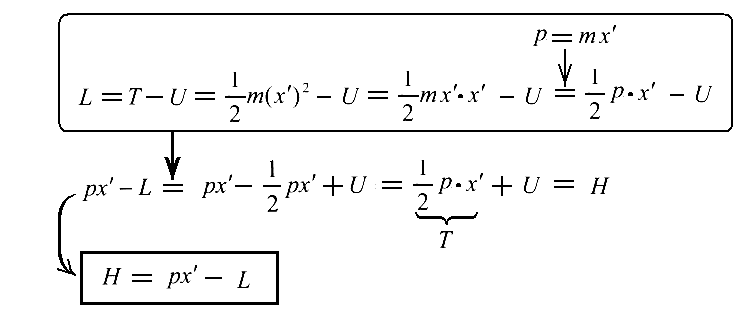
三次元でも同様です。
《Newtonの古典力学》に於いて、“エネルギー”がいかに表されるかを見てみる。
このときには
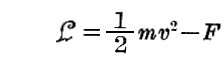
であり、座標の選択の如何に拘わらず(1/2)mv2の項はqi’の同次二次関数です。なぜならv2=x’2+y’2+z’2であり、x’、y’、z’なる項はそれぞれqi’の一次関数だからです。
それにゆえ
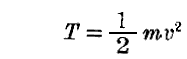
と置くことにすれば、同次二次関数に関する“Eulerの公式”によって

となる。上記式変形で“Lagrange関数”L は T の仲介に因ってのみ qi’ の関数となることに注意して下さい。
(17)式に(20)式を適用すると
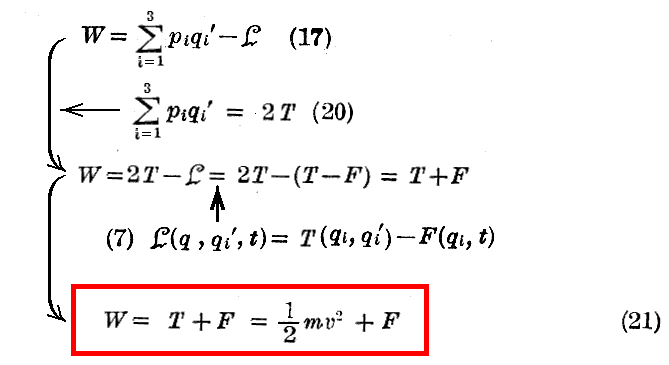
となる。つまり、粒子の“エネルギー”は、粒子の“運動エネルギー”と呼ぶべき T=1/2mv2 と“ポテンシャルエネルギー” F との和となる。
[補足説明3]
運動エネルギー T(qi’) は、直交座標の場合 qi には依存しないが、一般化された座標(例えば極座標の(r,θ)など)の場合には、rやsinθなどに依存する場合もあるので、T(qi,qi’)とした方が良いかも知れない。
ポテンシャルF(qi,t) が保存力を表す場合、ポテンシャルは qi’ に依存しないが、qi’ に依存する形にすると、ローレンツ力の様な保存力でない力も取り扱うことができるようになる。このことについては別稿「電磁場中の荷電粒子の運動」2.などをご覧下さい。
次に、《Einsteinの相対論的力学》に移る。
ここでは
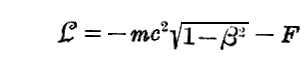
であるが、この第1項はもはや qi’ の同次二次関数では無いので、Newton力学と同じ様に展開できない。
しかし、

の関係があるので、
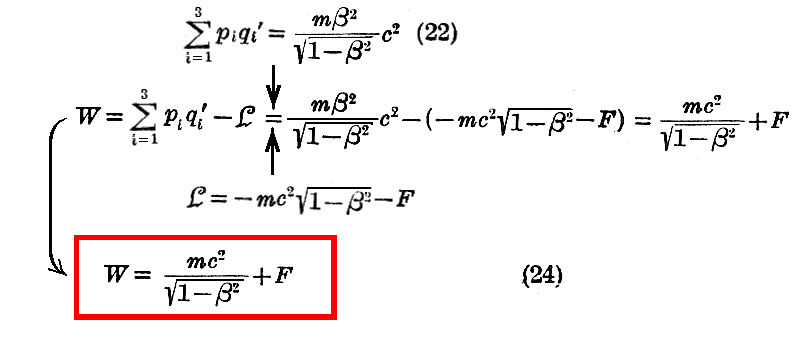
となる。右辺第1項は相対論的な力学に於いて運動状態にある粒子の“エネルギー”を代表する。
[補足説明4]
(21)式や(24)式は“Eulerの公式”を用いなくても地道に計算すれば導けます。例えば別稿「相対論的力学」2.[補足説明6]など参照。
さらに補足しますと、“Lagrange関数”を適切に設定すると、 “力学の運動方程式” のみならず、 “Maxwell方程式” や “一般相対性理論の重力場方程式” なども“最小作用の原理”によって定式化できます。
もし粒子が止まっているならばβ=0ですから、(24)式の第1項は mc2 となる。これは粒子の静止エネルギーです。これは“固有質量”mの存在に対応する内部エネルギーで、[固有質量m]×[光速度cの二乗]に等しい。
また、粒子が運動しているときには、第1項に於いてc2が掛かるべき
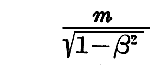
なる量は“運動状態にある粒子の質量”とみなすことができる。
粒子の“固有質量”mが零でないならば β→1 と共にこの量は無限大となるので、“可秤量物質粒子”の速度は決して光速度 c を超えることはできないことが解ります。
[補足説明5]
mの事を“静止質量”と呼んでいる文献が多いのですが、本書の様に“固有質量”と呼ぶ方が適切です。このことについては別稿「アインシュタインの公式E=mc2の証明」4.[補足説明3]をご覧下さい。
また上記“運動状態にある粒子の質量”については、別稿「相対論的力学」2.[補足説明4]をご覧下さい。
(24)式の右辺第1項をβ2の巾級数に展開して、高次の巾項を無視すると
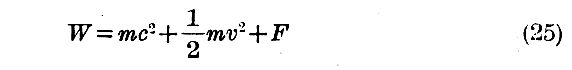
となるで、β2の高次の項が無視できる程度の近似では、相対論的粒子のエネルギーはNewtonの古典力学のエネルギー(21)式に mc2 の項を加えたものに等しい。逆に言えば、Newtonの古典力学に於けるエネルギーは内部エネルギーmc2 の項を最初から無視したものです。この事実は重要です。
このことは、《Newtonの古典力学》では粒子の質量が変化するなど思いもしなかったので、エネルギー保存則を考えるときに質量の変化をエネルギー保存則の中に取り込む必然性などなかったことに由来します。
つまり《Newtonの古典力学》では“質量保存則”は、“エネルギー保存則”が成り立つあるいは成り立たないの如何に関わらず常に成り立つ自明の真理だと考えられていたのです。
[補足説明6]
この当たりについてはランダウ・リフシュツ著「力学}の第2章もご覧下さい。相対論的な部分については別稿「相対論的力学」2.をご覧下さい。あるいはEinsteinの総説論文(1907年)の3.をご覧下さい。
[補足説明7]
【Lagrange方程式の共変性】
“Lagrange方程式”は座標変換に対して、その形を変えません。これは方程式を導く元になった“最小作用の原理”が座標の取り方によらない形式の原理だからです。なにはともあれ、Lagrange方程式の共変性は重要な性質なので以下で証明しておきます。
座標系 q1,q2,・・・qn から座標系 Q1,Q2,・・・Qn への変換が
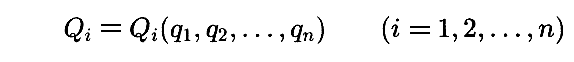
で与えられるとする。またその逆変換が
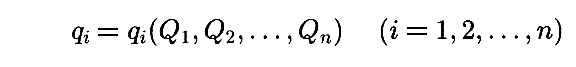
で与えられるとする。
ここで、Qjは q1,q2,・・・qn のみで決まり qj’ に依存しないので
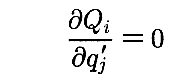
となる。また
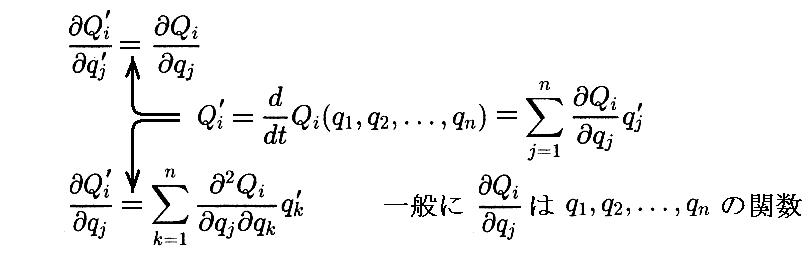
が成り立つ。
qiとQiは対称なので、同様な関係式
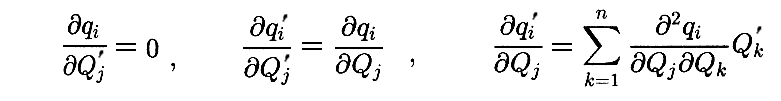
が成り立つ。
これらの関係式を用いて、L の Qi,Qi’ に対する偏微分を求めると
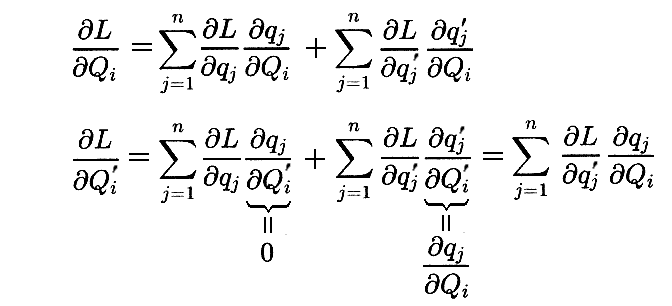
となる。
これらの式を用いると
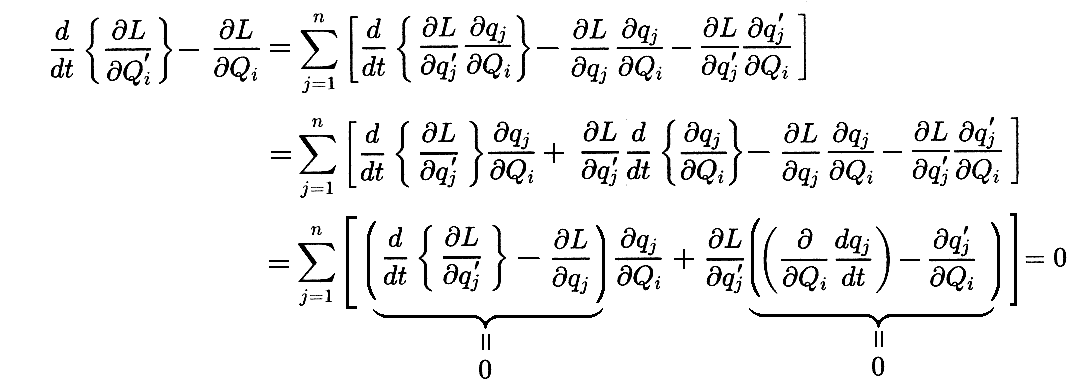
となり、Lagrange方程式の共変性 が証明される。
[補足説明7]
【Hamilton関数の共変性】
Hamilton関数の定義式に現れる Σpiqi’ も共変性が保たれる事が示される。
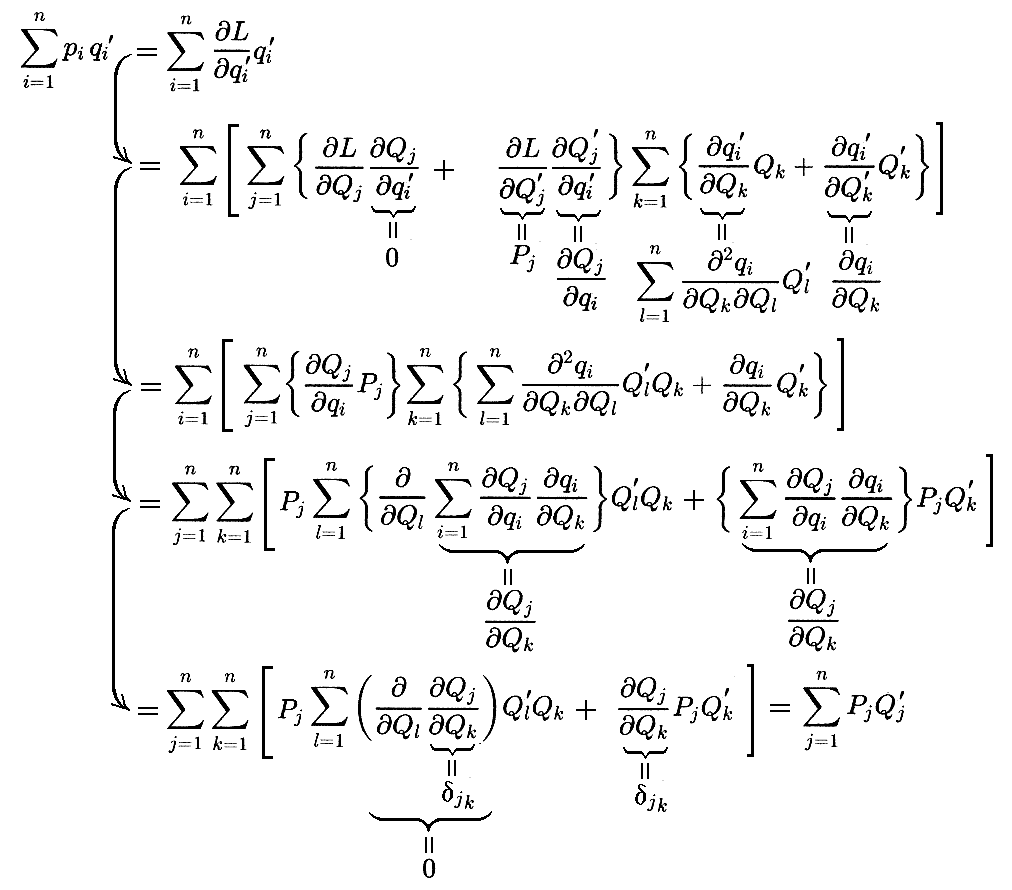
(4)“Hamiltonの原理”の他形である“Maupertuisの原理” 目次へ
これから、“Hamiltonの作用積分”に線積分の形を与えることができる事を示そう。
その為には、粒子の3座標qiと時間tとを一緒にしてできる4次元の抽象的な空間を考える。粒子の運動はqi=fi(t)なる3個の関係により表されるから、粒子の運動はこの4次元空間の或る一つの曲線によって表される。この曲線は相対性理論に於いて粒子運動の“世界線”と名付けられているものです。そのとき、この曲線に沿って各座標qiは時間tの関数となります。
エネルギーの表現式(17)を考慮すると、第1章§1.で導入した“Hamiltonの作用積分”は
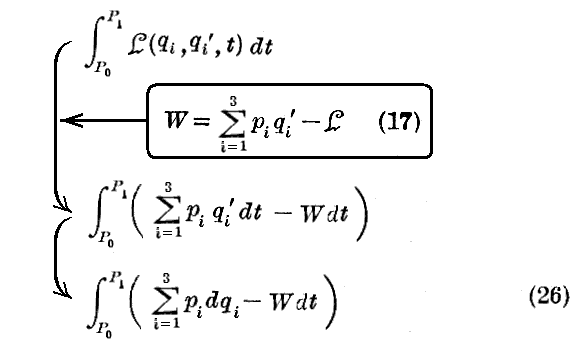
と書かれる。P0およびP1なる点は世界線上に於いて時間t0およびt1に相当する4次元空間内の点です。
それ故に、第1章§1.の(1)式で示される“Hamiltonの最小作用の原理”は
「曲線の両端P0およびP1を固定して、この線積分曲線を無限小変形した場合の線積分に対しても、その積分値が変化しないような曲線が粒子の満足する運動を表す」
ポテンシャルF が時間的に変化しない場合の、“Hamiltonの最小作用の原理”には特に興味がある。この場合には1.(3)3.で説明した(19)式により
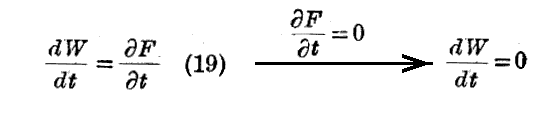
だから、エネルギーWは一定である。
この場合の最小作用の原理を“Maupertuisの最小作用の原理”と言う。
この場合、粒子の始点と終点に於ける時間および座標を固定して行う変分を考える代わりに、それらもδt0、δt1、(δq0)、(δq1)という微小量量だけ変化させることにする。、そうすると、“Hamiltonの作用積分”の変分は両端が変化されなかった場合の変分と両端に於ける変化による積分の変化との和となる。
始点の時間をδt0だけ、始点の座標を(δq0)だけ変えると、考える積分は
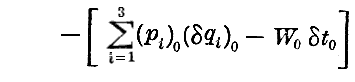
だけ変化し、積分の終点に於けるδt1と(δq1)の変化のために
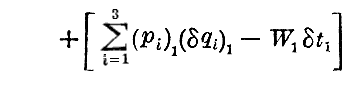
だけ変化するので、“Hamiltonの作用積分”の変分は以下の様に表される。
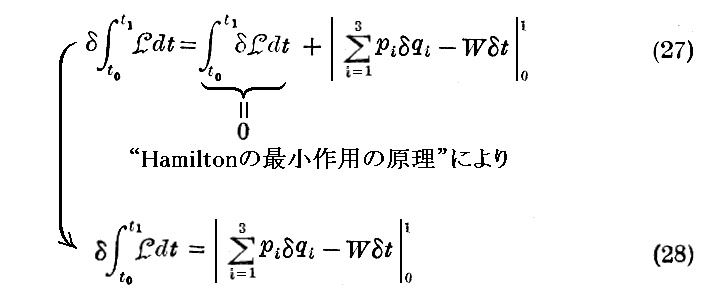
となる。これが作用積分の変分を表す式です。
Sによって“Hamiltonの作用積分”を表したが、S1によって次の線積分を表すことにする。

ただし、この積分は始点M0から終点M1までの道筋に沿って行うものとする。このときM0とM1は4次元の抽象的座標の中の空間点のみを取り出して、それら指定していることに注意して下さい。このとき(29)なる積分 S1 を“Maupertuisの作用積分”と言う。
ここで定常場に於いては(21)式または(24)式の“エネルギー公式”は、【速度したがってpi】を【座標qi】および一定値を有する【エネルギーW】の関数として表現できることを示しているから、“Maupertuisの作用積分”は時間に全く関係しない。
明らかに
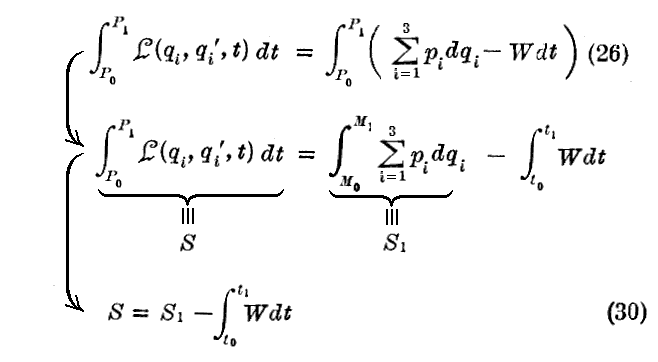
だから、一般に勝手な変分に対して
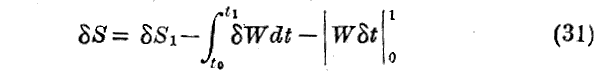
となる。これを(28)式と比較すると
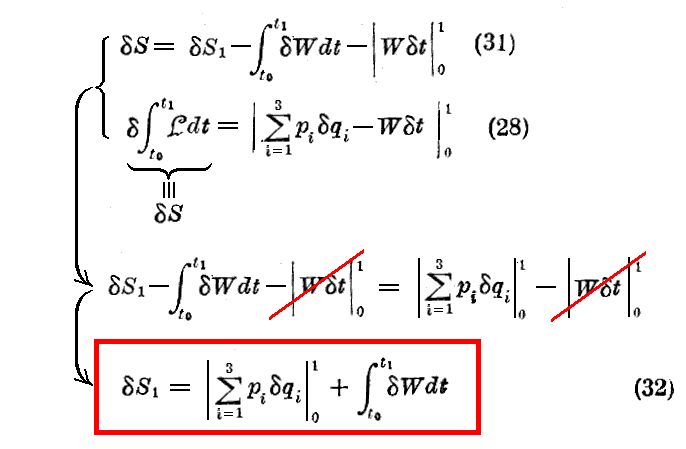
を得る。
だから、もし両端M0およびM1を固定し、且つエネルキー値を一定に保存して道筋を変えることとすれば“Maupertuisの作用積分”S1は一定となる。これは、“Maupertuisの原理”と言う。
今、qiに対して直角座標を採用すると
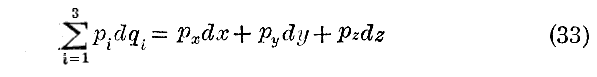
となるので、積分S1は運動量ベクトルの道筋に沿っての線積分の意味を持つことが解る。
(29)式“作用積分”中の(33)式に、1.(3)2.の(12)(13)式を適用するか、1.(3)3.で説明した“2次同次関数”に関する“オイラーの公式”を適用すると、S1は二つの古典力学それぞれに於いて
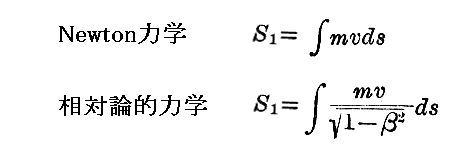
の意味を持つことになる。ここでdsは道筋曲線(世界線)の線素です。
(5)Hamiltonの正準方程式 目次へ
以下で、力学の方程式を“Hamiltonの正準方程式”といわれる形に変形する。
“Lagrange関数”はすでに見たように、qi、qi’、t の関数だから、(10)式のpiはこれらの変数の関数として表すことができる。従ってまた
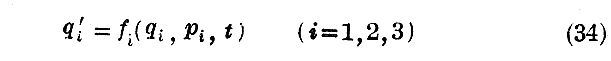
と表すことができる。
それ故にqi、qi’、t の代わりに、変数としてqi、pi、t を取ることができる。今後は qi、pi、t はそれぞれ“正準変数”と呼ぶことにする。
今、qi、pi、t を変数としてH(qi、pi、t )と表される“エネルギー関数”
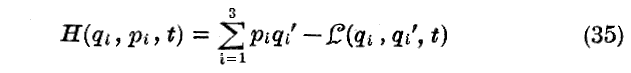
を考える。この右辺のすべてのqi’は(34)式を用いてqi、pi、t の関数として表されるものとする。つまり、H(qi、pi、t ) は(17)式のエネルギー関数Wの変数を(qi、qi'、t )から(qi、pi、t )に変更したものです。これを新たに“Hamilton関数”と称することにする。
次に、“Hamilton関数”の“正準変数”pj、qjの導関数を計算する。ここで j は1,2,3のいずれかの定まった値を取るとする。
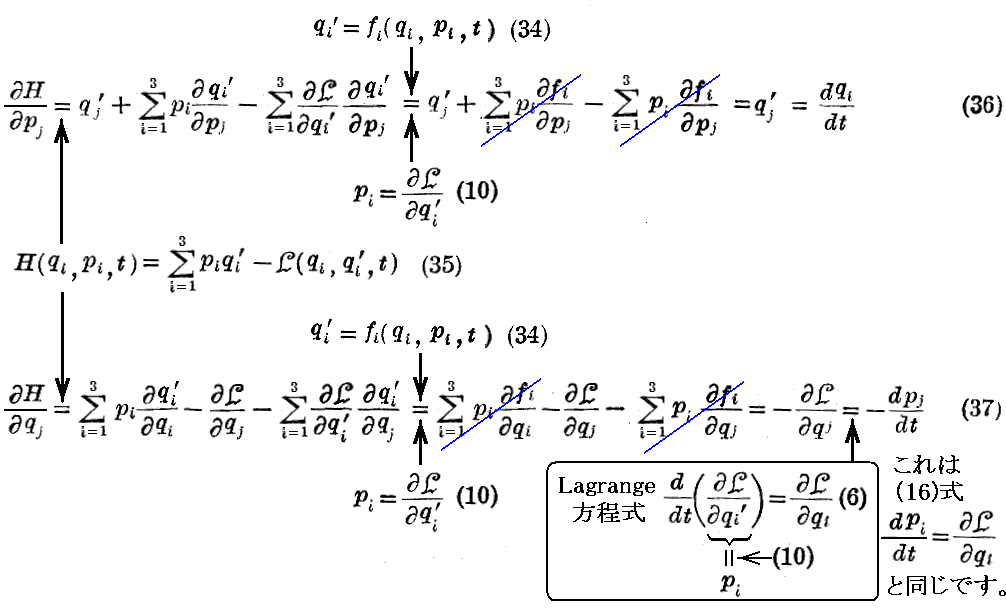
[補足説明1]
非相対論的な話に限ればもっと簡単に導ける。
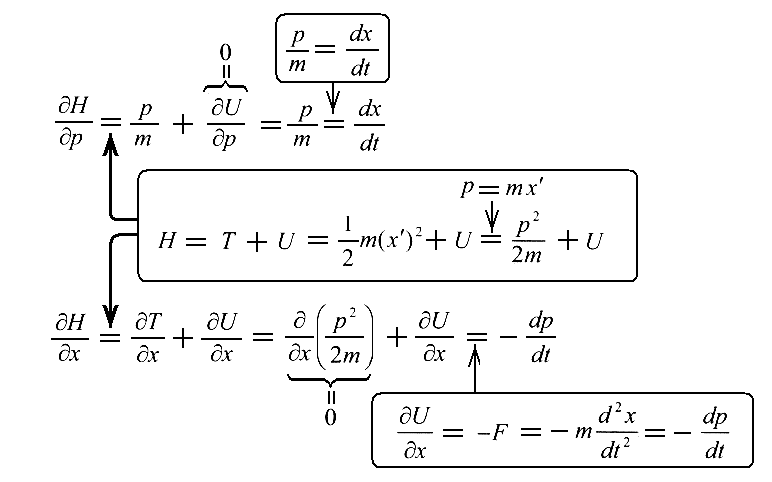
かくして、“Hamiltonの正準方程式”
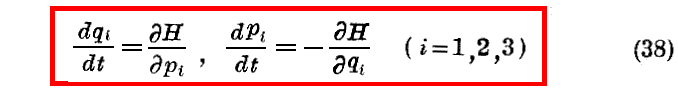
が得られる。
ここで、“Hamilton関数”の時間微分を計算してみると
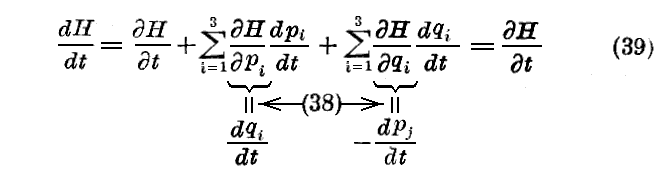
となるが、(35)式に於いて、“Lagrange関数”Lが、時間tを陽に含まなければ、(35)式から解るように“Hamilton関数”Hも時間を陽に含まないので(39)式の右辺は零となる。
(18)式で述べた様に“Lagrange関数”Lが、時間tを陽に含まなければ、エネルギーWの保存が成り立っていた事を考慮すると(39)式は“エネルギー保存則”が成り立つことを意味する。
次に、“Hamiltonの正準方程式”が古い二つの力学でどのように表されるか考察する。
最初に《Newtonの古典力学》について調べる。直角座標
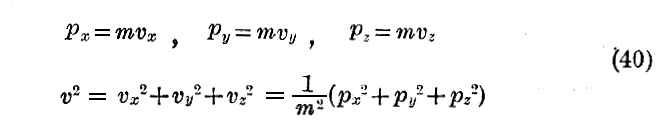
を用いると、1章§3.の(21)式を考慮すると
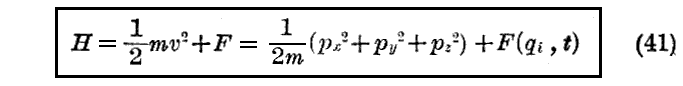
となる。それ故に
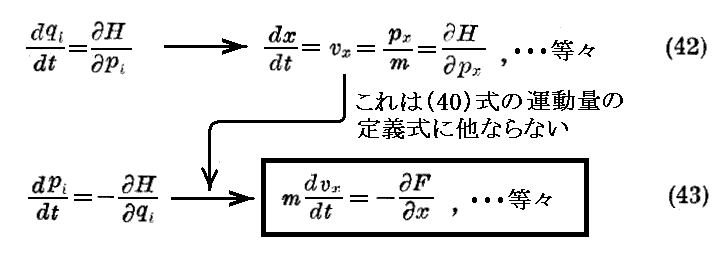
が得られる。これはNewtonの運動方程式に他ならない。
次に《Einsteinの相対論的力学》の場合を考察する。この場合も直角座標を用いることにすると、第1章§3.の(24)式を考慮すると
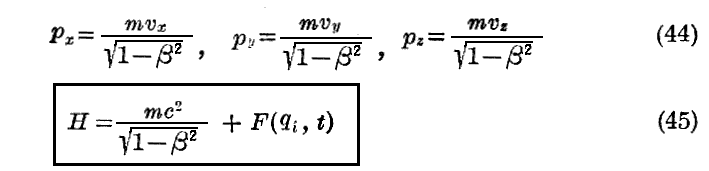
となる。
まず、H を qi、pi、t の関数で表そう。
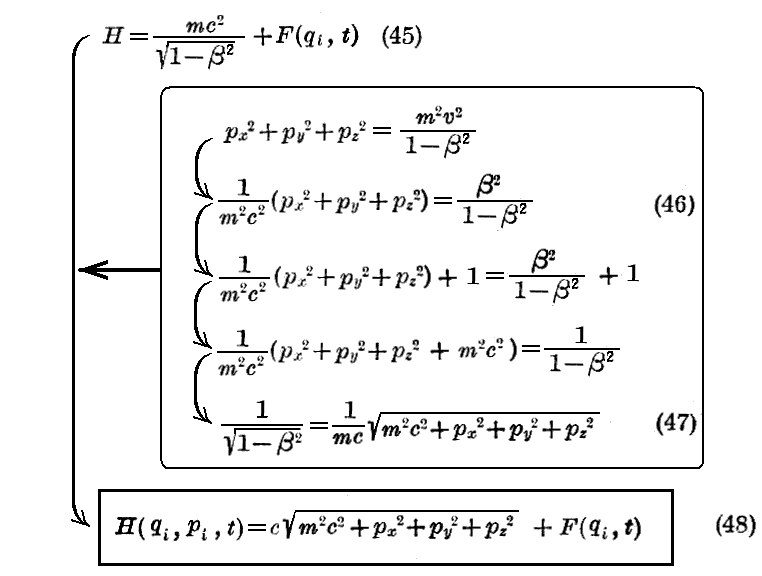
となる。従って
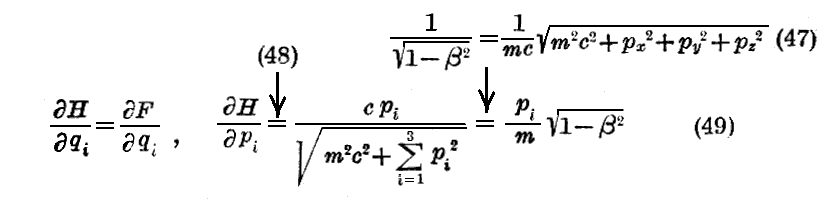
を得る。
この関係式を用いると“Hamiltonの正準方程式”は
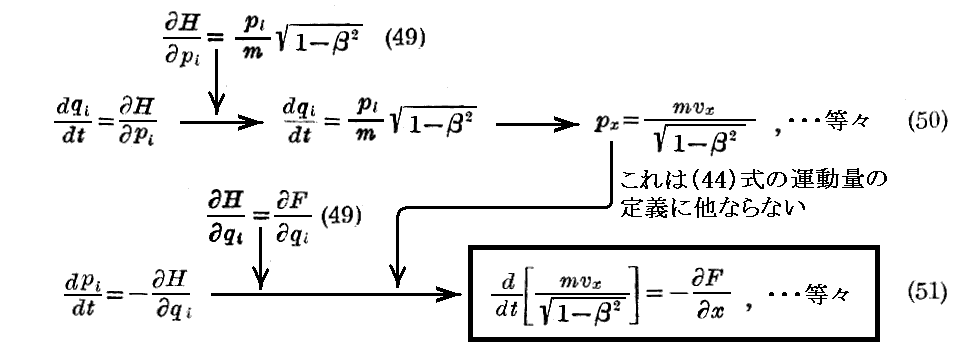
となり、相対論的な運動方程式が得られる。
[補足説明2]
相対論的エネルギー関数(“Hamilton関数”)Hの表現である(45)式や(48)式の導出については、別稿「相対論的力学」2.[補足説明6]なども復習されたし。
[補足説明3]
“Hamilton関数”H は、Lagrange関数L から
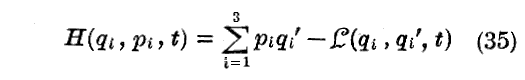
なるルジャンドル変換によって得られる。
この式を変形すると、“Lagrange関数”L は
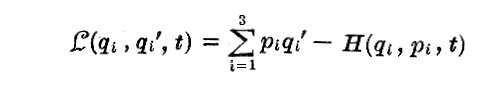
と与えられる。
この関係式を用いれば、“最小作用の原理”から“正準方程式”を直接導ける。以下 自由度1 の場合で説明する。
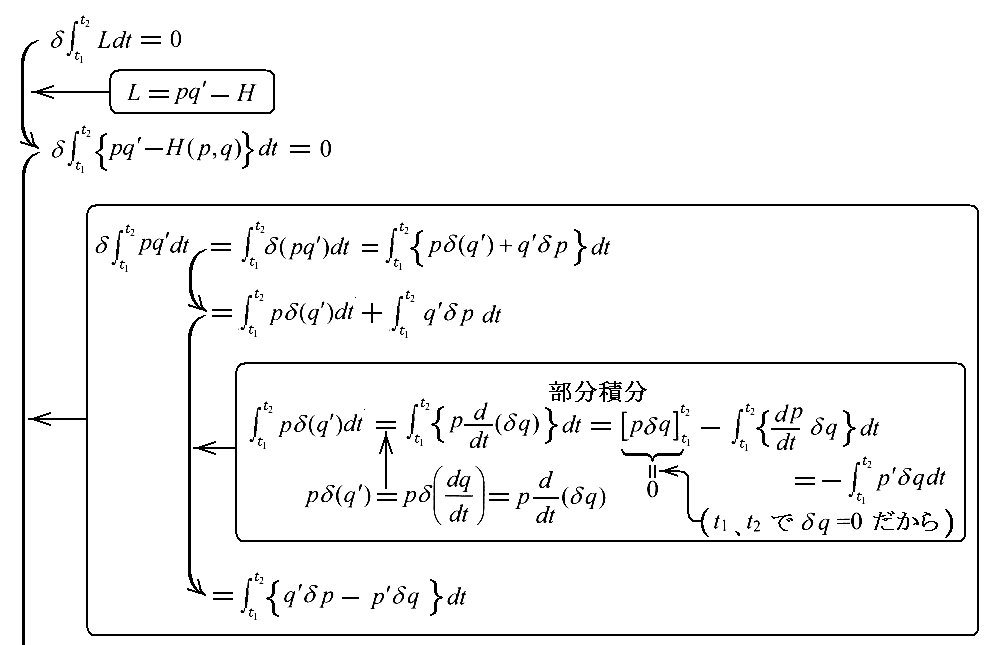
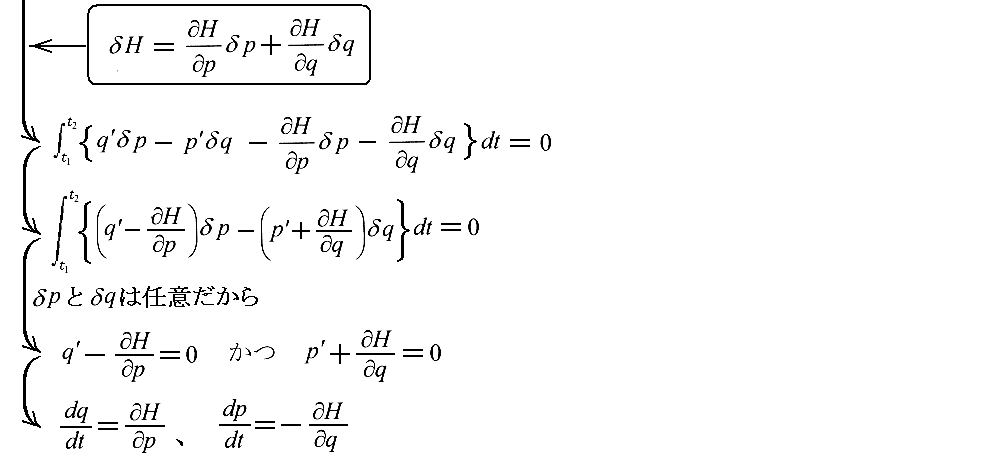
“Hamiltonの正準方程式”は時間t、三つの座標qi、三つの運動量pi (i=1,2,3)で与えられるのだが、今
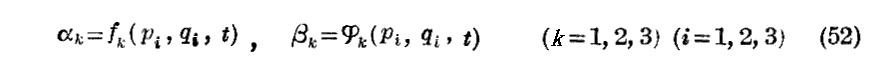
で定義される新しい変数に置き換えることを考える。
そのときこれらの式は
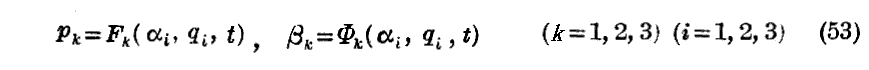
とも書ける。
このとき次の定理を得る。
[接触変換の定理]
もし
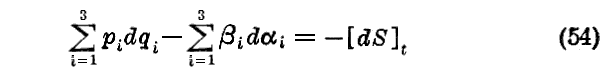
なる関数S(αi,qi,t)を見出すことが可能ならば、変数αi及びβiは
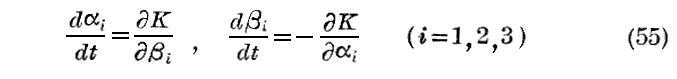
なる正準方程式を満足する。ただし
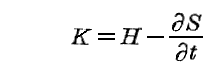
である。ここに[dS]tはtを変えないときのSの微分を意味する。
[証明]
まず、[dS]tはtを変えないときのSの微分である事を考慮すると(54)式から
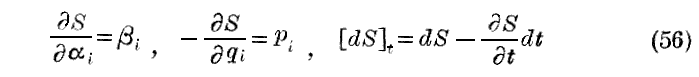
が成り立つ。次に(54)式より
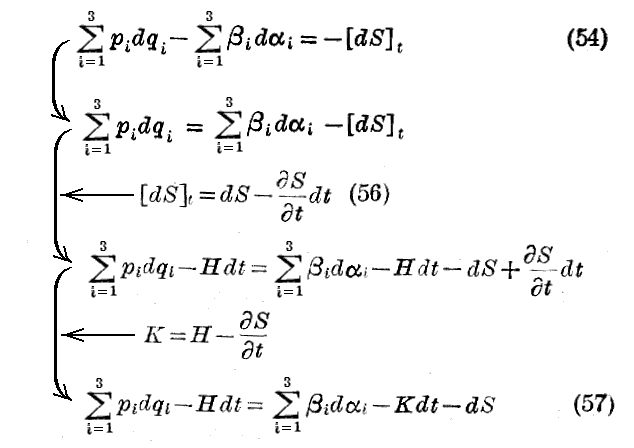
となる。
ここで始点M0((q1)0,(q2)0,(q3)0,t0)と終点M1((q1)1,(q2)1,(q3)1,t1)の4次元時空に於ける曲線Cに沿った次なる線積分
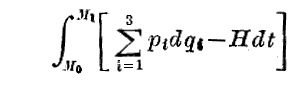
を考える。
曲線Cが粒子の運動を表すならば、(26)式の“Hamiltonの最小作用の原理”により、始点M0((q1)0,(q2)0,(q3)0,t0)と終点M1((q1)1,(q2)1,(q3)1,t1)を固定して、曲線Cを極めて僅か変形したときに一次の程度に於いては上記の線積分は値を変えない。すなわち
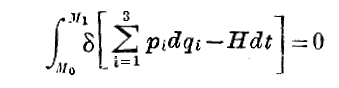
が成り立つ。
次に変数(α1,α2,α3,t)を用いる4次元時空を考える。曲線Cに対して、この空間に於ける曲線Γが対応する。それはCなる曲線上の各点に対して変数(q1,q2,q3,t)のみならず変数(p1,p2,p3)の確定した値が対応している。従って(52)式に依ってCの各点にそれぞれΓの一点が対応するからです。
((α1)0,(α2)0,(α3)0,t0)と終点((α1)1,(α2)1,(αq3)1,t1)がそれぞれ曲線Γの両端の座標であるとする。“Hamiltonの最小作用の原理”を適用する為に曲線Cを、その両端を固定して変化するらなぱ、それに依って曲線Γも変化させることになる。そのとき一般にはΓの両端が固定されたままに保たれる保証は無い。なぜならpiの始点と終点に於ける値はCの変化の影響を受けるため(αi)0及び(αi)1の変化を生じるからです。
そのため
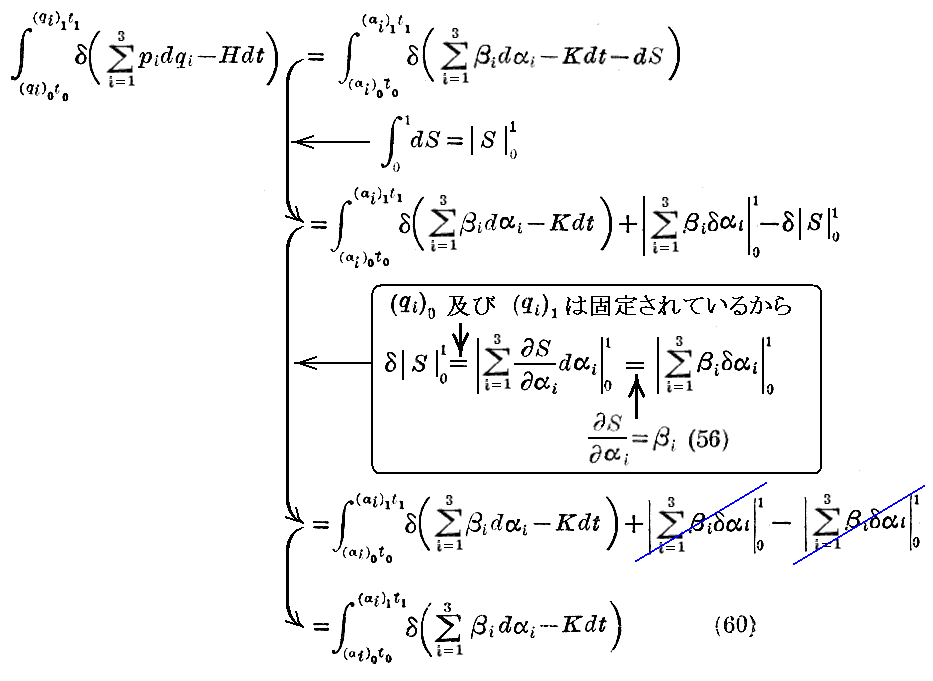
となる。ここで、右辺の変分はαi に対して始めと終わりは固定されて実行される。
(60)式の左辺は“Hamiltonの最小作用の原理”のために零だから、右辺も零となる。そのとき、右辺の積分における(β1,β2,β3)及び(α1,α2,α3)なる変数並びに K なる関数は、それぞれ左辺に於ける(p1,p2,p3)及び(q1,q2,q3)なる変数並びに H なる関数と同じ役割を演じているから、方程式(55)が証明されたことになる。
[証明終]
この定理は、(54)式を満足する変数の変換(“接触変換”と言う)をすれば、始めの 関数H を 関数K に置き換えることによって“Hamiltonの正準方程式”はそのまま満足されることを言っている。
2.Jacobiの定理
“接触変換の定理”から、“Jacobiの方程式の定理”が導ける。
K=0 となる様な“接触変換”が存在したとする。そうすると新しい基準変数αi、βiは次の“Hamiltonの正準方程式”を満足する。
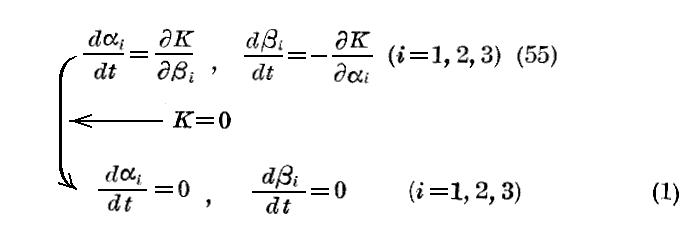
すなわち、αi、βiは定数となる。
ところで
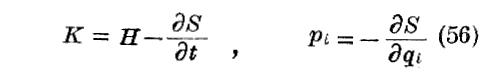
であるから、エネルギー関数Hを(qi,pi,t)の関数として表すと、K=0 なる条件は
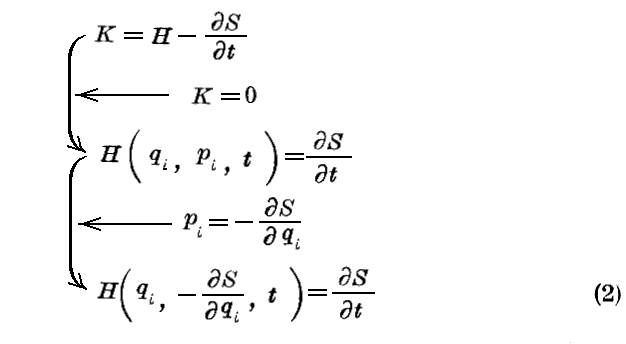
と等価です。S に付いての一次の編微分係数をもつこの方程式が、“Jacobiの方程式”です。
三個の任意定数αiを含むこの方程式の積分、すなわち方程式(2)の完全積分を一つ発見するならば、その関数S(qi,pi,t)なる変数と αi,βi=∂S/∂αi,t なる変数との間の変換を定義するものであり、その変換によれば K=0 であり、従って
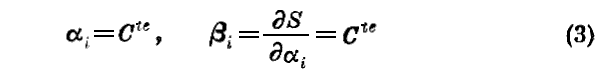
である。よって、つぎの“Jacobiの定理”を得る。
[Jacobiの定理]
一次編微分方程式(“Jacobiの方程式”)
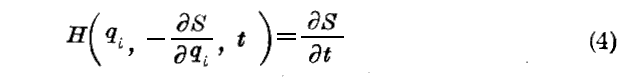
の完全積分S(qi,αi,t )を見出し得るならば、βi を三個の任意定数とするとき
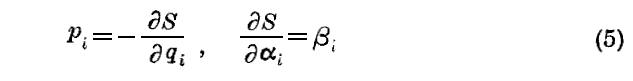
を得る。方程式(5)は変数(qi,pi,t)と定数(αi,βi)の関数として定義されるものであり、これによって粒子の運動が完全に定まる。
(2)Hamiltonの積分とJacobiの関数 目次へ
上述の接触変換に関する理論に於いて、変数αi、βiは6個の変数であるが、その力学的意義はまだ明確にしていない。従って例えばαiが座標であり、βiが運動量であると考える事もできる。関数S(qi,αi,t)においてはαiは常数であるから、その時はαiを粒子の座標の初期値と見なすことは自然の様に思われる。その事を明確にする為に、ただ一個の粒子を考える事を止め、共同の場に置かれ互いに相互作用する事の無い多くのまったく同一の粒子の雲を考察しよう。この雲の運動は与えられた場における同一粒子の可能なすべての運動を表すものです。時間t0より時間tまでの間の雲の運動の結果は、ひっきょう雲の粒子の時間t0における初めの座標(qi)をその粒子の時間tにおける終わりの座標(qi)に変換することになる。
今、Hamiltonの積分
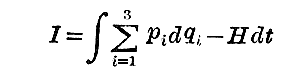
を、一つの粒子の道筋に沿って(qi)0よりqiまでとることにする。するとこの積分は(qi)0,qi,tの関数で
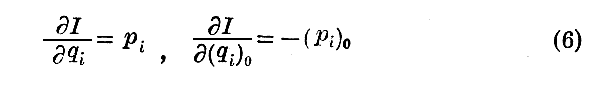
を満足する。ただし、(pi)0はpiの初めの値です。ゆえに、関数Iの符号をかえたものは変数qi,piと変数(qi)0,(pi)0との間の一つの接触変換を定義するです。さらに関数 S(qi,(qi)0,t)=−I は“Jacobiの方程式”を満足する。
それは
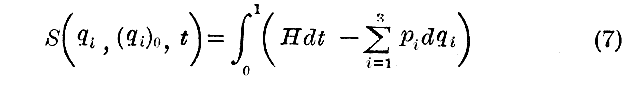
であるから、従って
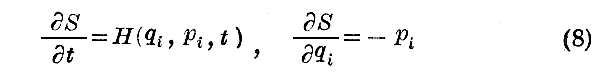
であり、故に
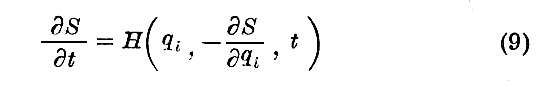
であるからです。
“Jacobiの定理”に従えば、(qi)0は運動中常数でなければならないが、このことは(qi)0が座標の初めての値であるという性質とは合致している。また(pi)0も常数でなければならないが、これは初めの運動量です。
(3)短縮したJacobiの関数 目次へ
αiは必ずしも初めの座標の値である必要はない。完全積分としては初めの運動量を含むものも見出されるし、あるいは又、他の常数を含むものも見出される。かかる積分が見出されるなら、いつでも
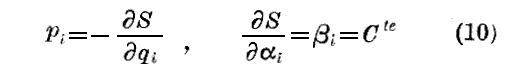
となり、これらの方程式が運動を決定する。
重要な特別の場合が恒常の場合です。この場合にはすでに見たように勢力(エネルギー)は常数となる。Wでこの常数を表すならば、Hamiltonの積分は
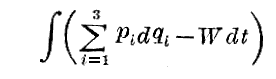
と書かれ、関数SとしてHamiltonの積分の符号を変えたものを採用すれば
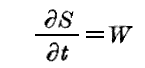
を得る。
一方
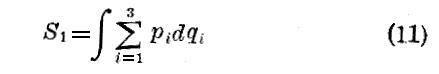
と置くと
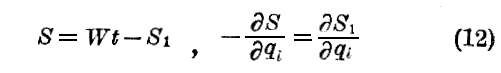
である。
最後にHは時間を陽に含まない。故にS1は
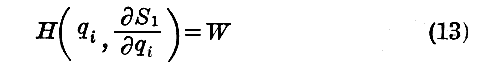
を満足する。S1は“短縮したJacobiの関数”と呼ばれる。もし(13)の完全積分であってWおよび二個の任意常数α1およびα2を含むものが見つかったら、関数S=Wt−S1(q1,α1,α2,W)はJacobiの完全な方程式の完全積分であって三個の任意常数α1,α2及びα3=Wを有している。しこうしてJacobiの定理によればこのときの運動は
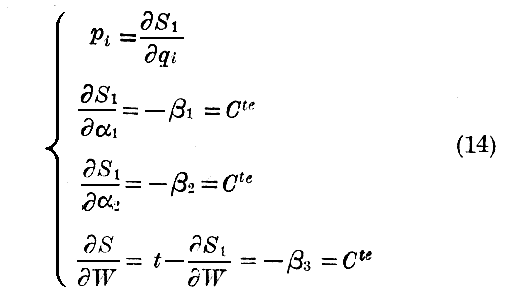
という関係により決定される。
−β3=t0と置いてみよう。そうすると一番終わりの方程式は

を与える。この方程式が時間を含む唯一の方程式であって運動の法則を与える。
一方
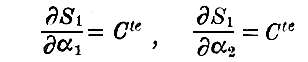
の二方程式はqiのみを含み道筋の形を決定する。
ここに再び運動の研究と道筋の研究の分離を見出したので、この分離が恒常な場の特性です。
(4)Jacobiの方程式の様々な形 目次へ
具体的な例を研究する前に、Jacobiの方程式が《Newton力学》および《Einsteinの力学》においていかなる形を取るかを明らかにしておこう。
まず《Newtonの古典力学》の場合を考察する。一般的にする為に、選ぶ座標qiは勝手なものとする。Newton力学においては運動エネルギーTは速度qi’の同次二次関数です。したがって
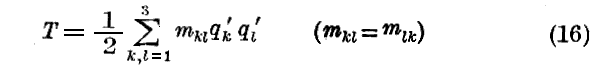
となる。ここにmkiは単にqのみの関数です。
(16)式より
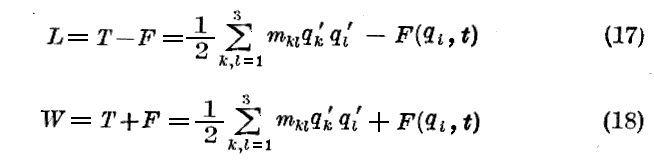
が導かれる。
piの定義に従って
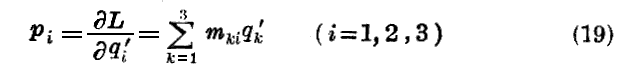
と書くことができる。もし(19)なる線形方程式をqiに関してとくと
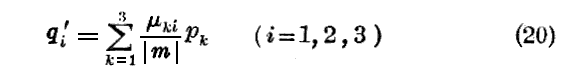
を得る。ただし|m|はmkiによって形作られた行列式であり、μkiはこの行列式において要素mkiに対する小行列式です。
[補足説明1]
連立1次方程式(19)式の解が(20)式となる事については、別稿「行列式と行列」1.(5)1.を参照されて下さい。
ここで、次の様に置くことにする。ここでmki=mikはmkiが対称行列であるこを示しているのでは無くて単に添字をその様に置くと言うだけで有ることに注意して下さい。
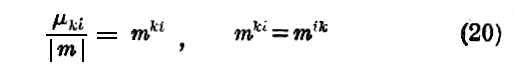
すると
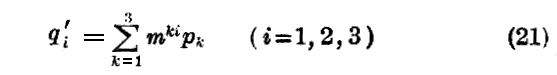
となる。
qi’を(21)の値で置き換えると、(16)式の代わりに
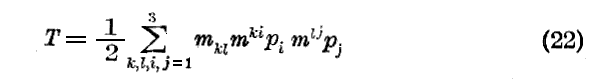
を得る。
しかるに行列式の性質によって
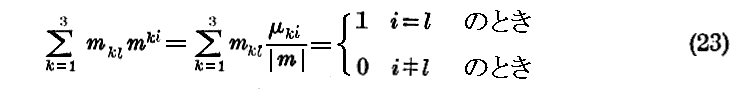
である。
[補足説明2]
(23)式の関係が成り立つ事は、別稿「行列式と行列」2.(3)を参照されて下さい。
そのため

となる。またその結果エネルギー関数Hをqi,pi,tの関数として表すと
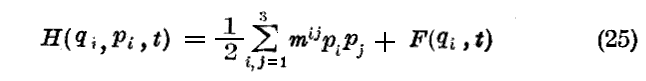
となる。
こうなると2.(1)で説明した“Jacobiの方程式”(2)式として
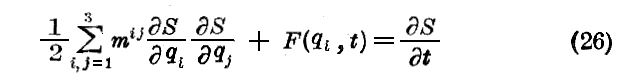
が得られる。
とくに直角座標を用いる場合には
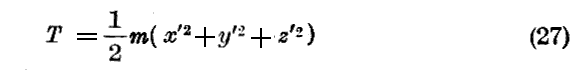
である。
故にmkk=mでありk≠lにたいしてmkl=0である。これより
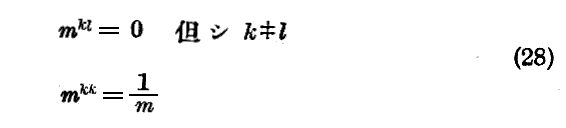
が導かれ、Jacobiの方程式は簡単な古典的形式
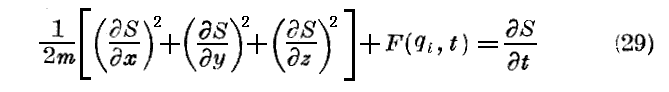
を取る。
次に《Einsteinの相対論的力学》に移ろう。本書において我々は相対論的力学をさほど多くは使わないから、直角座標の場合のみ扱う。すでに第1章§(5)の方程式(45)式として見出していたように、エネルギー関数Hは
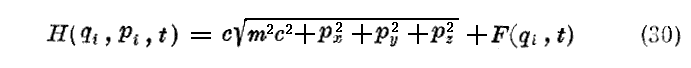
です。
このHの表現に依って、次の“相対論的Jacobiの方程式”
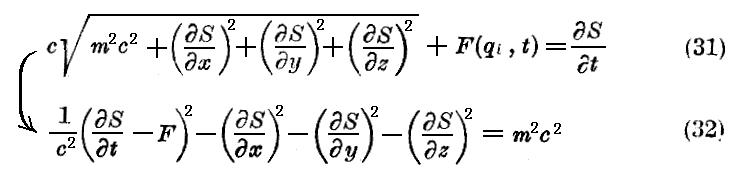
が導かれる。
(5)一様なる直線運動に対するJacobiの関数 目次へ
後で役立つ、二つの簡単だが重要な場合について、Jacobi関数の形を調べる。
《Newtonの古典力学》で満足する事にして、まずすべての場が無いときの粒子の一様な直線運動の場合から始める。その時は F=0 であるから方程式(29)式は
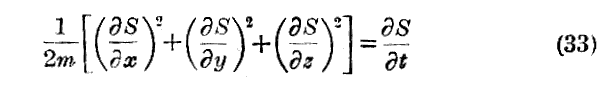
となる。
この一つの完全積分は
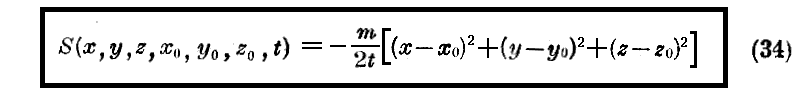
なる式で与えられることは容易に証明できる。
従って“Jacobiの定理”第2章§1.の(5)式に依れば
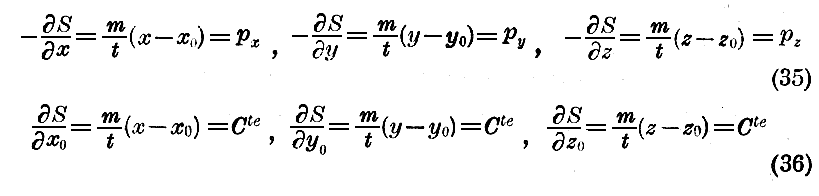
でなければならない。
従って(36)の右辺の常数はpx,pyおよびpzの一定値に等しく、運動の方程式は次の様にな良く知られた形をとる。
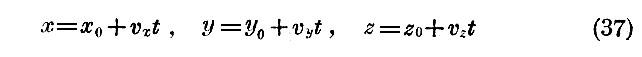
この完全積分の3個の常数x0,y0,z0は粒子のt=0における三座標であることが解る。
(34)なる積分はHamilton関数Hのtに関する積分の符号を変えたものに他ならない。実際、我々はHamiltonの積分を
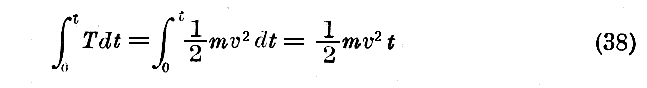
なる形に書くことができる。
しかるに、運動が一様であるから
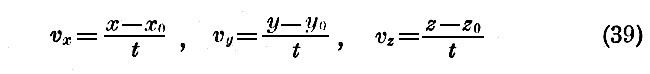
であり、また
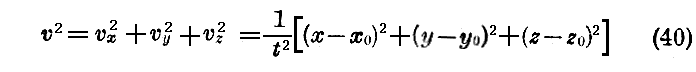
です。
ゆえに、Hamilton関数Hの積分の符号を変えたものは、確かに(34)式の右辺に等しい。
やはり同じく場のないときに、Jacobiの方程式の完全積分としてその任意常数が初めの三座標ではなくて三つの運動量(このものはこの場合常数)であるようなものを見出すことができる。
その完全積分は
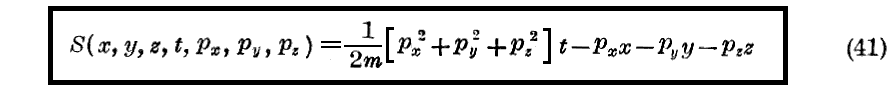
です。
このとき
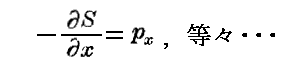
の方程式は恒等的に満たされている。またJacobiの他の3個の関係は
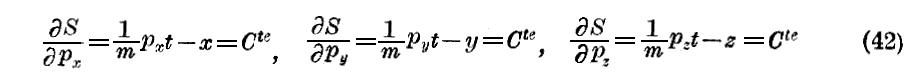
となる。この3個の常数を −x0,−y0,−z0 と呼ぶことにするならね我々は再び(37)式の運動方程式を得る。
(41)式の関数もまたHamiltonの積分から導かれる。それはHamiltonの積分は加性常数を無視すれば
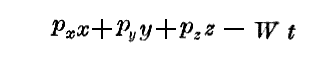
だからです。そのとき
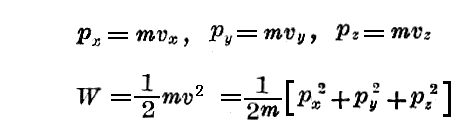
ですから、Hamiltonの積分の符号を変えたものは確かに(41)式を与える。
最後に恒常の場(常にゼロの場もこの中に含まれる)においてはJacobiの関数を Wt−S1(x,y,z,α1,α2,W) なる形に書けることをすでに知っている。ただしS1は方程式(13)式の積分である。Jacobiの関数をこの形に置く為に、運動量の一つ(例えばpz)を他の二つの運動量とWの関数として表すことのできる事に注意しておこう。それは
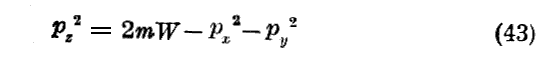
だからです。
(43)式によって与えられたpzの値を、符号を変えたHamiltonの積分の中へ入れると
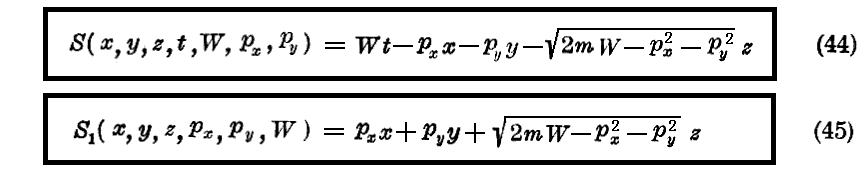
が得られる。
(14)および(15)の運動方程式は
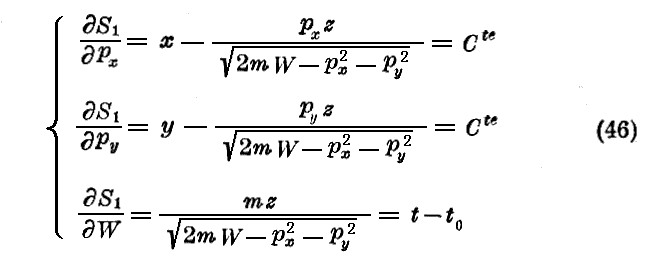
となる。この方程式中の最初の二つは
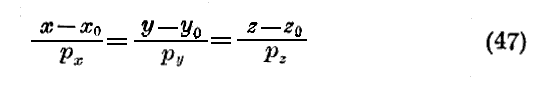
により定義された直線道筋を与える。
(46)の第三の方程式は道筋上の運動を決定する。それは
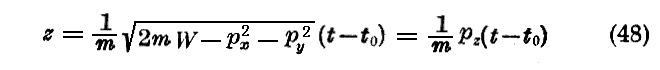
により座標zの時間の関数として与えられるからです。このとき t0 は z=0 の時を表す。
(6)一様で時間的に変化しない場に於けるJacobiの関数 目次へ
場が無い場合に次いで最も簡単な場合、すなわち一様にして変わらない場の場合を取り扱う。
至る処一定の力の成分をkx,ky,kzとしよう。すると
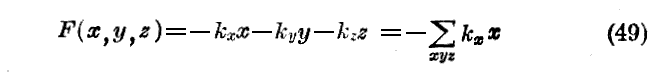
となります。それは
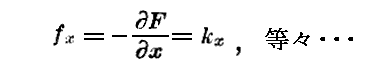
となるからです。
このとき“Jacobiの方程式”は
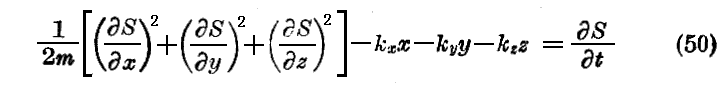
となる。
この方程式の一つの完全積分は次のものです。
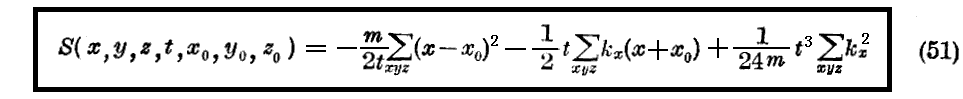
(51)が(50)を満足する事は代入して見れば容易に証明できます。
Jacobiの定理の方程式は第一に
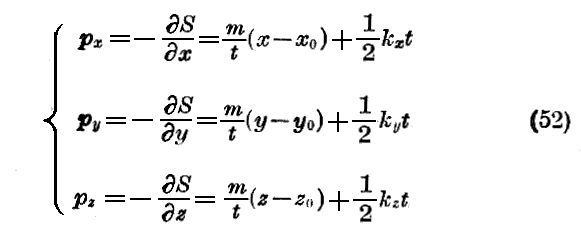
を与えます。
この関係は恒等的に証明されます。それは一様に加速される運動においては
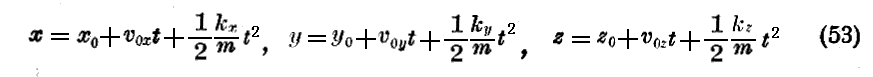
及び
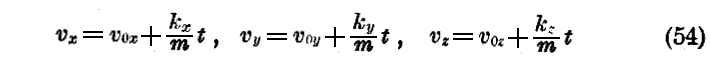
であり、これより
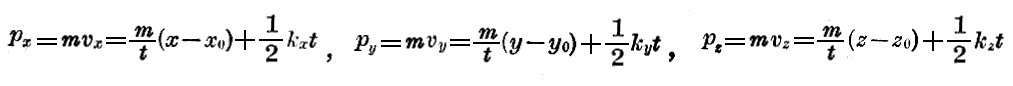
がえられ、これは(52)の関係に他ならないからです。
Jacobiの他の三個の関係、すなわち
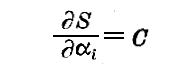
はこの場合
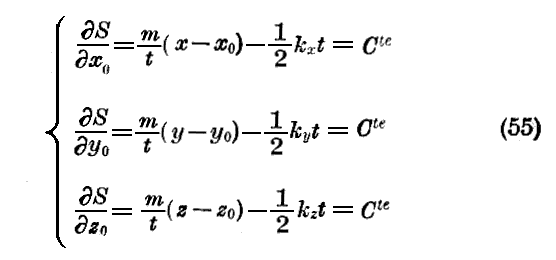
を与えます。
もしx0,y0,z0が初めの座標であるならば
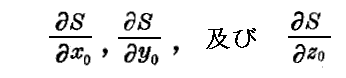
は初めの運動量mv0x,mv0y及びmv0zでなければならない。そして(55)は再び一様に加速される運殿方程式(53)となる。
(51)なる完全積分はHamiltonの積分から出発しても得られる事を示そう。Hamiltonの積分の符号を変えたものは実際
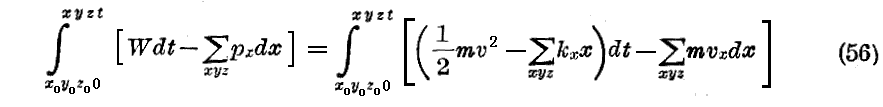
です。
しかるに、一様に加速された運動の公式(53)及び(54)は
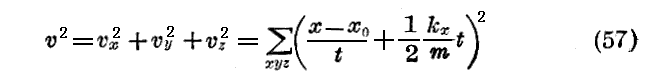
を与え、(57)を(56)に代入すると
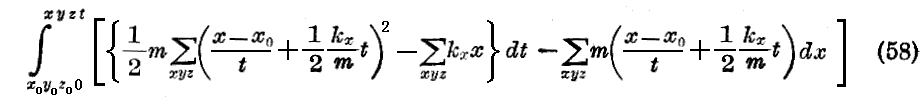
が得られる。
ここで∫なる記号内にある量は完全微分をなしている。それはdtの係数を任意の一個の空間変数で微分したものと、その空間変数の微分の係数を時間で微分したものと等しい事が容易に証明できるからです。
[補足説明]
上記のある関数が“完全微分”である必要充分条件に付いての説明は、例えば別稿「絶対温度とは何か(積分因子とは何か)」5.(2)などを復習して下さい。
そこで解析学の周知の方法によって(58)の積分を実行すると、(51)の値になる事を見る。したがって完全積分(51)式は、ここでもHamiltonの積分の符号を変えたものに等しい。
一様な運動の場合の様にJacobiの方程式の完全積分として三個の任意常数が初めの座標でなく初めの運動量である様なものも求められる。その初めの運動量は
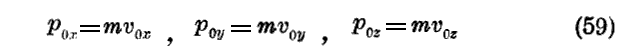
である。
もし(54)の公式を用いてHamiltonの積分の符号を変えたものを書くと
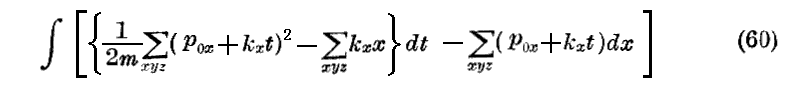
となる。
積分可能の条件は引き続き満足される。それは
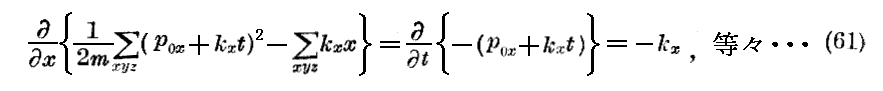
であるからです。そして(60)の積分に対して
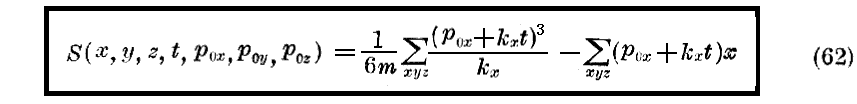
なる値を見出す。
(62)なる関数が(50)式の“Jacobiの方程式”を満足する事(それは改めて証明するまでもなく、この章の第2節によって初めから明らかではあるが)を実際に証明することは容易である。
方程式
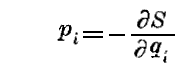
は(62)なる関数を得る為にとった方法それ自身によって恒等的に証明される。
また方程式
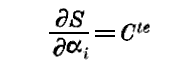
は
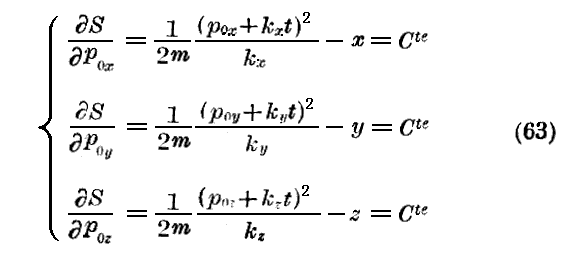
を与える。
所が
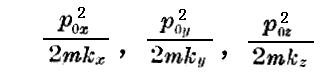
は常数であるから、次の様に書くこともできる。
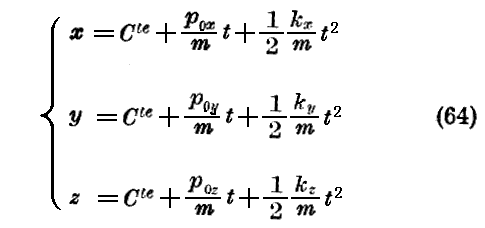
そしてこれらは再び古典的方程式(53)に他ならない。
最後に(50)の完全積分であって
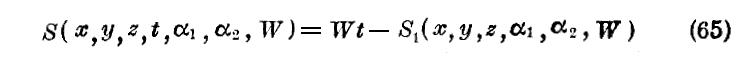
なる形を持つものを求めよう。
場が時間的に一定であるからこの事が可能なることが解る。この(65)なる関数もHamiltonの積分の符号を変えたものを計算することによって得ようと思うのであるが、計算を簡単にするためには、一様なる場の方向をx軸として取ろう。そうするとky=kz=0であり、運動量pyとpzは常数である。勢力(エネルギー)の表現
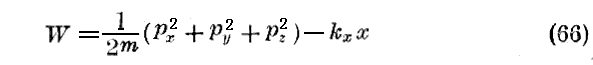
は次の関係を与える。
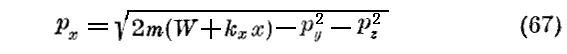
また、したがってHamiltonの積分の符号を変えたものは
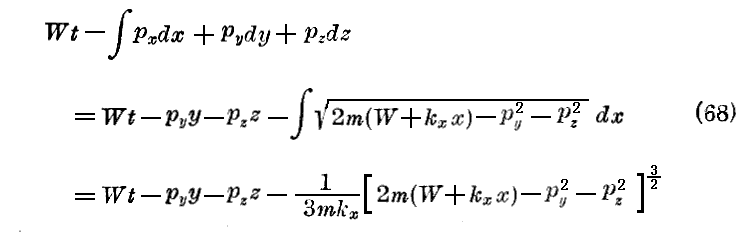
となる。
これを(65)に等しいとすれば
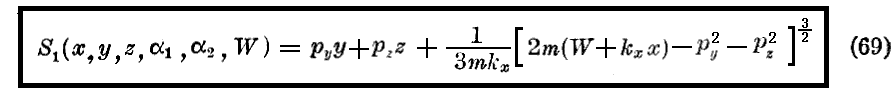
を見出す。
Jacobiの定理の方程式は次の通りである。
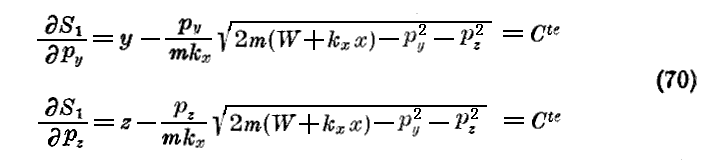
これらは放物線の道筋を定義するものであり、また
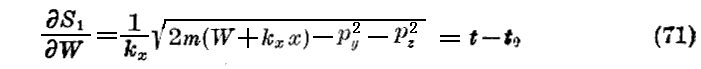
である。あるいは初めのpxの値をp0xと書くと
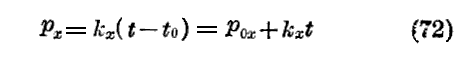
となるが、これは速度を時間の関数として表す周知の法則【方程式(54)式】です。
3.波動力学の基礎
波動力学の出発点は常に粒子の考えに周期性の考えを結び付け、そして粒子の運動と言う概念と波の伝播という概念を離さないように連合させる意図に在った。
まず最も簡単な場合すなわち場の外に在って自由に運動する粒子の場合を調べる。そのとき、波と粒子との間に設けられるべき結合はある意味において相対性理論の基礎原理によって要求せられるものであることが解るでしょう。
第一に、恒星全体に対して静止または一様直線運動をする直角座標軸系をガリレオの座標軸系と称することを思い出してください。そして力学の方程式が有効なのはその座標軸系に関してなのです。慣性の原理は仮定せる定義の一種なのですが、それの我々に教える所は、もし粒子が何らかの力を受けないのならば、その粒子は任意のガリレオ系に関して必ず静止又は一様直線運動をするという事です。
無限に多く在る“ガリレオ系”の中で特にその二個を考えよう。第一のものは、それに関して粒子が速度v=βcを持つもので、粒子の運動がoz軸に沿うように座標軸は配置されているものとします。これを
“xyz系” と呼ぶことにする。第二のものは粒子の“固有系”(あるいは“x0y0z0系”)と称せられるもので、第一の系に対して大きさ及び方向が速度vと同一なる運動をなすものとし、且つそのz軸は第一系のz軸上を滑るものとする。x0,y0,z0を以て“固有系”における点の座標を表し、x,y,zを以て第一系における点の座標を表すとしよう。つまり“固有系”においては、先ほどの粒子は静止しているように見える。
Einstein以前においては、人々は絶対時間の存在を承認してきた、従って “xyz系” に結び付けられた観測者は“固有系”に結び付けられた観測者と同じ時間の座標を用いるものと考えられた。それ故に、この二人の観測者の空間時間の変数は次の様な“ガリレオ群”の公式によって結構されていると考えられた。
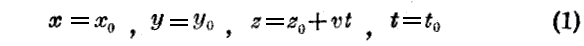
ところが、今日ではEinsteinの深遠なる探求の結果(1)式の関係を次の様な関係“ローレンツ群”で置き換えなければならないと考えられる様になった。
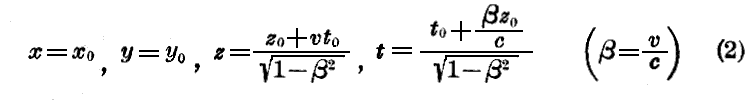
この逆変換は次の様になる。
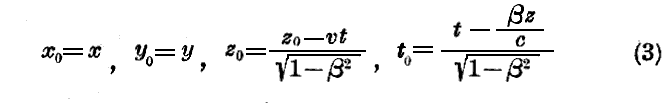
今は相対性理論の種々の考えの更に突っ込んだ議論には立ち入ることなく、(2)及び(3)なる公式を承認しよう。かかる議論は本書の範囲外に出るからです。
粒子に結び付けられた x0y0z0系 なる座標に於いて考えよう。元来我々の目的は波を粒子に結び付ける所にあるのだから、その波は固有系においては定常波の形を有する(つまり進行波では無い)と考えるのは自然です。換言すれば波の数学的表現が cos2πν0(t0−τ0) なる因子を通してのみ時間に関係すると言っている。更に時間の原点を適当に選ぶことにより τ0=0 と置くことが許される。すなわち

と表される。ここで、ν0 という常数を粒子の“固有振動数”という名で呼ぶことにします。
次に立場を変えて xyz系 に於いて考えよう。この系に関して粒子はv=βcの速度をoz方向に持つ。重要な問題は、粒子に結合している波の形が x0y0z0系 に於いていかなるものになるかを決定する事です。“固有系”に於いては位相の因子は cos2πν0t0 であったが、公式(3)の最後の式に従えば xyz系 に於ける位相の因子は
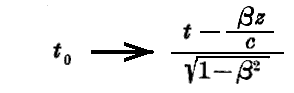
で置き換えることになるであろう。
ここで

と置くことにすると、位相の因子は
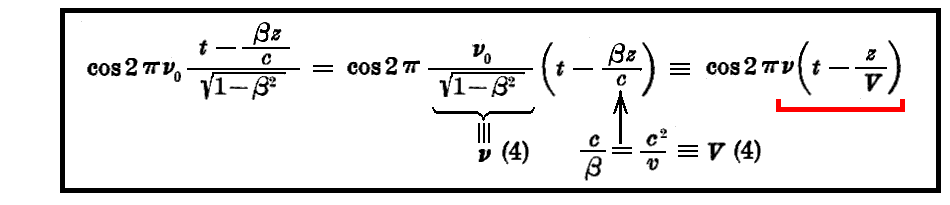
となる。従って xyz系 の観測者にとっては、この波は振動数νを持ちoz方向に“位相速度”Vで伝播する波の如く思われる。この事は一つの“ガリレオ系”より他の“ガリレオ系”に移る時に時間という変数の従う相対論的変換が生む所の直接の結果として表れる。
(4)の第2式から明らかな様に、【粒子に結合した波の位相速度】 V は【粒子自身の速度】 v に逆比例する。そのとき最大に重要なのですが、随伴波の位相速度Vと可秤量物質粒子の現実の移動速度vは、光速度cを仲介にして

の関係にある事です。従って “固有系” に関する粒子の速度はゼロであるから “位相速度” は無限大です。以前注意した様に相対論的力学に従えば【粒子自身の速度】 v は決して光の速度c以上の速度を以て行われることはできない。故に常に
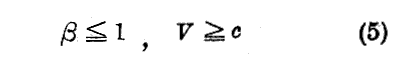
でなければならない。
(5)式の等号は粒子の質量(厳密に言えば“静止質量”あるいは“固有質量”)がゼロであるときにのみ実現される。それは光の粒子すなわち “光子” の場合です。この場合は後で再び立ち戻る。]
[補足説明1]
ここは何が言いたいのかとても解りにくいところですが、ド・ブロイの“物質波の仮説”でもっとも重要な所です。
ここの内容については、別稿「ド・ブロイの学位論文」1.(1)や、別稿「アインシュタインの特殊相対性理論(1905年)」3.(2)2.[補足説明7]あるいは、「相対論的力学」3.(4)[補足説明4]などをご覧下さい。
(2)前述の結果を見出す他の方法 目次へ
粒子に結合された波の位相に関する上記の結果は、より具体的な方法を用いても見出すことができます。この方法は種々の点においてより明確な理解を与えてくれます。
“固有系” に在っては、仮定から波はあらゆる点に於いて同一の振動数ν0 と同一の位相を持っている。故にこの系に於ける位相の分布を次の様にして表す事ができる。すなわち各点に小さな時計を想像し、これらの小さな時計はすべて同時的であり、その周期はT0=1/ν0であると考える事にする。
“xyz系” に於いては、これらの時計の各々は速度 v=βc を以て運動しているので、Einsteinの“遅れ”を受けるでしょう。この“遅れ”とは次の事を意味する。時計は “固有系” に於いてはz0という定まった座標を持っているが、xyz系 に於いてはその座標 z は時間 t の内に vt だけ増す。従って時計によって記される時間t0 の変化は Lorentz変換公式の4番目のものによって時間t の変化と結び付けられている。すなわち
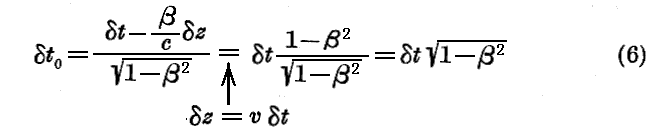
です。
時計が完全なる一振動を終わったとき、固有系 に於いては δt0=T0=1/ν0 だけ時間が経ったのであり、従って xyz系 に於いては
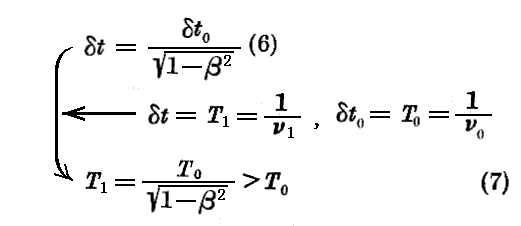
だけ時間が経った事になる。故に xyz系 の観測者は時計と共に運動する観測者よりも長い周期を時計に付与する。これがEinsteinの“時間の遅れ”です。
次に、周期から振動数に移ろう。xyz系 の観測者に対しては各々の小さな時計は
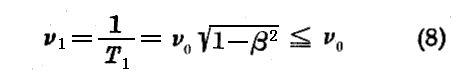
の振動数を持っている。ただし時計は速度 v の運動をしている。
そこでこの運動をしながらこの時計は常に
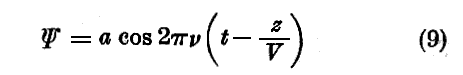
なる波と同一位相を保つことを示そう。ただし常数 ν および V は(4)式で定義される値を持つとする。
この事を証明するために、時間tのある時間t1に、時計が位置xyzの観測者に対して波Ψと位相が一致していると仮定しよう。そのときは
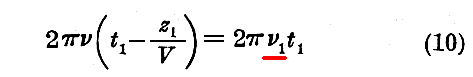
です。ここのz1は時間t1に於ける時計の位置の横座標です。
その後の時刻t2に於いて、時計は z2=z1+v(t2−t1) の位置を占める。その時計の占める位置における波Ψの位相は
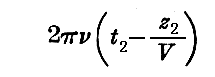
であり、時計の位相は2πν1t2です。
そのときになお二つの位相が一致するためには
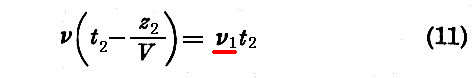
でなければならない。このことは(10)の為に次の様に書ける。
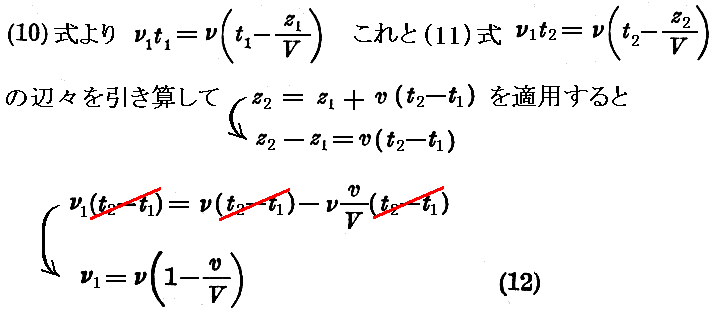
となり証明が完了する。
ところで、この関係式は
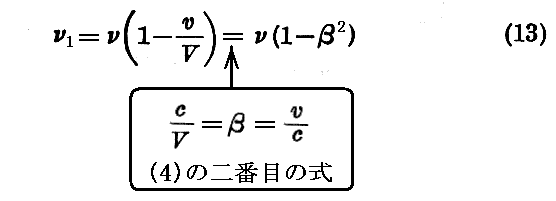
と書けるが、この関係(13)は、ν1の定義式(8)のν0に(4)の一番目の式【νの定義式】を適用すれぱ直ちに得られますから、その意味に於いても(12)式はすでに証明されています。
[補足説明1]
ここは何を言っているのか解りにくいと思います。別稿で引用している「ド・ブロイの学位論文」1.(1)[補足説明1]の後半の『位相一致の定理』の部分を参照して下さい。
(3)“屈折率”n、波Ψの“群速度”Uに関する基礎的定理 目次へ
位相速度V は xyz系 に於いて波Ψに対する屈折率を決定するのに役立つ。この“屈折率”n を

という普通の関係により定義しよう。この関係は(4)の二番目の式 V≡c/β 故に
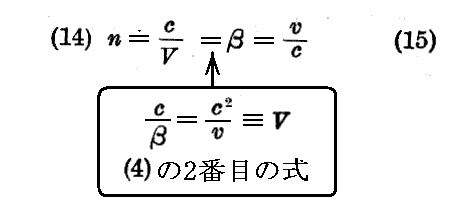
を与える。
(15)を(4)の一番目の式に代入すると
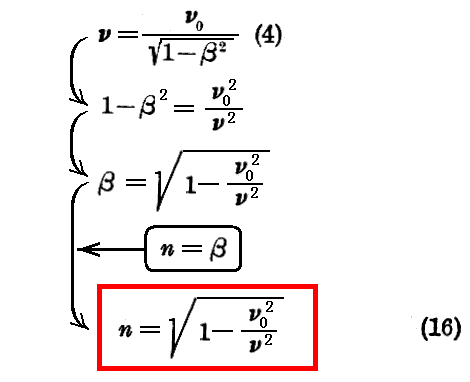
となる。
この公式は、ν0という常数により特徴づけられた粒子に結びつけられている波Ψに対する空間の分散を定義するものと考えられる。換言すれば、もしこの粒子が有すことができるすべての一様直線運動をxyz系に於いて考えれば、連合波の振動数と位相速度は常に(16)式の関係で結び付けられるのです。
(16)式は波の屈折率は伝播する波の振動数に依存して変化すると言うことを示している。つまり、波Ψが伝播するときの位相速度は振動数に依存して変化する事を示しています。
[補足説明1]
ド・ブロイが説明するところの可秤量物質粒子に付随する随伴波は仮想的なもので、当然真空中を伝わる波です。つまり、波が伝わる媒質は真空ですから、屈折率という説明は本来適切では有りません。
ただし、ド・ブロイは可秤量物質粒子に付随する随伴波は特定の波長や振動数を持っているとするのですが、そのとき波の振動数によって、その波の伝播速度(位相速度)は変化すると仮定します。そういった意味での屈折率であって、それを随伴波が伝わる仮想的媒質の屈折率としようと言うだけです。
その時、媒質の相対屈折率と媒質中の波の伝播速度との関係は別稿「光の屈折」1.(2)などを振り替えられて下さい。ただし、ここでは振動数の異なる随伴波ごとに違う屈折率の媒質を伝わると考えないといけませんから、そこまで屈折率という言葉にこだわると訳が解らなくなります。
我々が今得た分散の公式は、極めて重要な定理に導く。しかしこの定理を言い表す前に、“群速度”の概念を定義しなければ成らない。このものはかって Lord Rayleigh に依って分散物質中に於ける波の伝播の為に導入されたものです。振動数ν
の単色平面波で、ある一定方向(例えばox軸の方向)に伝播するものは、伝播位相速度V=c/nだから
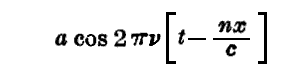
という関数で表される。ここに n は振動数ν にたいする媒質の屈折率です。
ただ一つの単色平面波を考えるかわりに、ox方向に伝播し振動数がν−δν,ν+δνという極めて小さな間隔の中に含まれる様な非常に多数の単色平面波を考えよう。これを“波群”と称そう。群に属する波の一つは
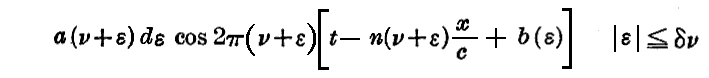
という関数で表される。ここでb(s)は位相の常数です。振幅aや屈折率nは振動数νの関数だからν+εの関数して表示されている。
今ある一瞬間にある一点においては合成された振幅は非常に大きいものとなるでしょう。分散性媒質に於いては種々の波の位相速度が多少異なるから、伝播につれて波は互いにずれて行くのである。しかるに位相の一致する点というものが常に存在してそれが位相速度とは一般に異なる一つの速度を以て移動して行くものであることを示そう。
実際、多数の波の重ね合わせを考えるのは難しいので、一つの群に属する二つの波の重ね合わせを考え、それらが振動数ν+ε1およびν+ε2という値に相当するものだとする(|ε1|≦δν,|ε2|≦δν)。我々の仮定に従って、ある一定のx及びtの値に対して、この二つの波は位相が一致している。そこでtをdtだけxをdxだけ変えてみよう。すると第一の波は
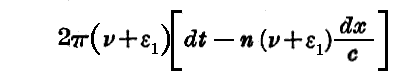
だけ位相が変わる。しかるにε1は極めて小さいから、n(ν)という関数を連続と考えて
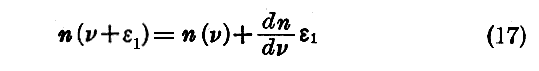
と置くことができる。従って二次の量を無視すれば、第一の波の位相の変化は
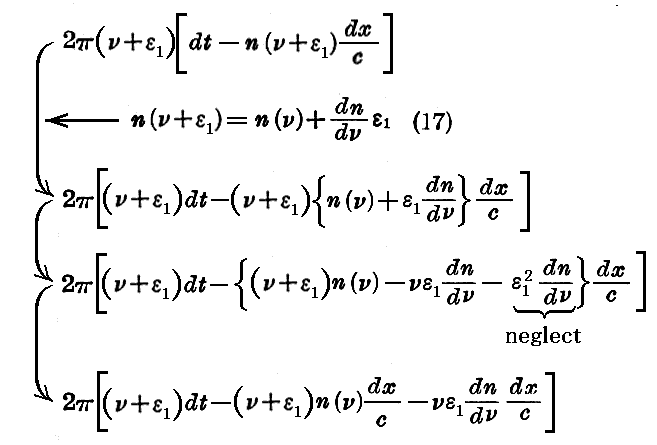
となる。
同様にして第二の波に対しては
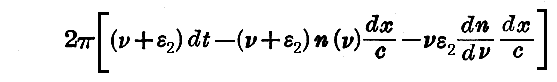
を得る。
上の二つの式の差を作ってみると、もし二つの波はなお位相が一致しているならば、 dx と dt とが次の関係で結び付けられていることになる。
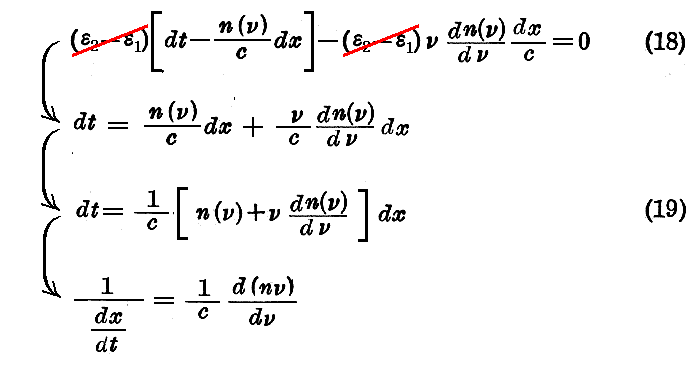
この関係は、次の式で表される一つの速度 U を定義する。
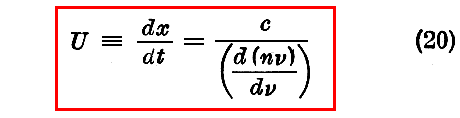
もし我々がx軸に沿って U なる速度で移動して行くと、二つの波ε1とε2は常に位相が一致している事を見る。所がε1とε2は任意なのであるから、我々の推論はその群に属するいわゆる一対の波に対して有効です。
すなわち、もし我々がx軸に沿って速度Uで移動して行けば、群に属するすべての波は常に位相が一致しているのを見る。言い換えれば位相の一致に依って起こされる極大はoxの向きに速度Uを以て移動する。“群速度”と称せられるものはこの速度です。
[補足説明2]
上記の説明は解りにくいのですが、ここで、いわゆる可秤量物質粒子に付随する随伴波の位相速度と、その振動数が少しづつ異なる随伴波を重ね合わせてできる波束の移動速度(“群速度”)との関係を説明しています。
その時注意して欲しい事は、重ね合わせる振動数が少し異なる随伴波の位相速度は、その振動数に依存して少し異なる事です。つまり随伴波の位相速度は随伴波の振動数に依存して変化するとしていることです。(16)式はその事を表しています。
ここは非常に解りにくい所ですので、別稿「慣性重力波とロスビー波、そして赤道波」5.(4)3.をまず復習されて下さい。そして別ページで引用するSommerfeld著「変形体の力学」をお読みになる事を勧めます。
上記の“群速度”の定義を踏まえて、我々は次の重要な定理を証明しよう。
[群速度の定理]
“随伴波(位相速度V)の連合波の群速度Uは可秤量物質粒子の移動速度vに等しい。”
[証 明]
(16)の分散の法則によれば
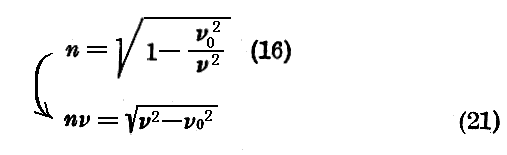
ですから
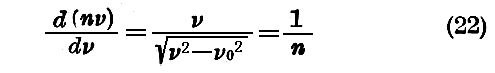
が成り立ちます。従って、この(22)式を(20)式に代入すれば、(15)式に依って 【随伴波を重ね合わせた波束の“群速度”】 U は 【可秤量物質粒子の“移動速度”】 v に等しくなります。
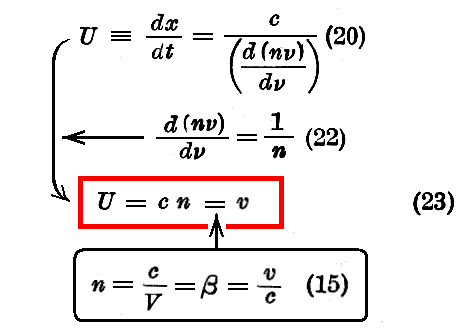
[証明終]
[補足説明1]
この節もわかりにくいところです。。別稿「ド・ブロイの学位論文」1.(2)を、特にそこの[補足説明1]や[補足説明2]などを参照して下さい。
(4)波動的な諸量と力学的な諸量との間の関係 目次へ
粒子を特性づける力学的諸量すなわち《質量》、《エネルギー》、《運動量》と連合波の波動的諸量すなわち《振動数》、《位相速度》、《屈折係数》との間に今まで何らの関係を導入しなかった。しかるに、もし連合波を用いて量子を理解しようとするならば、かかる関係がどうしても存在しなければ成らない。特に粒子のエネルギーWとその連合波の振動数νとは

という公式で結合されるとしなければ成らない。ここに h は“Planckの定数”です。(24)式は量子論が常にその出発点として取り上げる関係です。
相対性理論に従えば、粒子のエネルギーは xyz系 に於いて
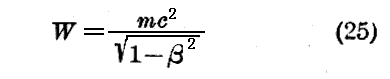
という値を持つ。固有系 に於けるその値は
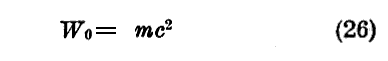
です。これより
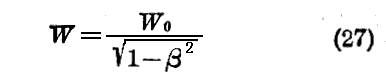
となる。
(27)なる公式はW0よりWへ移ることを許すものであって、ν0よりνに移る事を許す公式(4)の初めの式と同じ公式となっている。すなわち目標のガリレオ系を変える際に粒子のエネルギーは連合波の振動数と同じ様に変換されるのであるから粒子のエネルギーと連合波の振動数とを

という関係式で結び付けることが許されるのです。ここにhは一つの比例常数であって、我々はもちろん“Pranckの定数”に等しく取ろう。
次に運動量である。このものは道筋の向きに向いたベクトル量で、その値は相対論的力学では
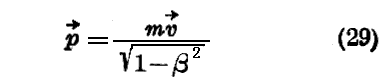
です。
(25)式と(29)式を比較することで、運動量ベクトルの大きさは

になる事が解る。
Wをhνで置き換え、c2/vを(随伴波の位相速度である)Vで置き換える。そうすると運動量は位相速度Vと同じ向きを向いたベクトルで、その大きさは
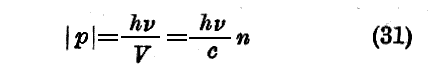
であるといえる。
この連合波の波長λを

という普通の関係で導入すると(31)式は

を与える。
(5)“最小作用の原理”と“Fermatの原理” 目次へ
要約すると、ある一方向に v=βc という速度で変位する質量 m なる粒子に対して、“振動数”
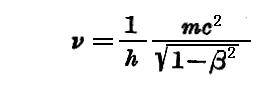
を持ち、“位相速度”
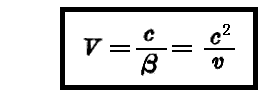
を持って同一方向に伝播する一つの波を随伴しなければ成らない。その波の“波長”は
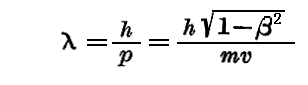
であり、その波束の“群速度”は v に等しい。
もしβ2が 1 に対して無視できるとき【つまりNewton力学の場合】は
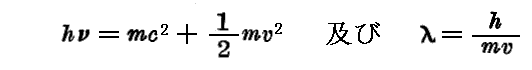
と置けば充分です。
終わりに一つの重要な注意をする。屈折率 n の媒質中において、幾何光学の意味に於ける光線は次の条件によって決定される。
“Fermatの原理”
二点AおよびBを通る光線は曲線積分
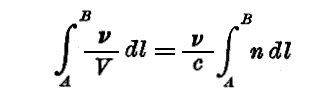
が最小となる様な形をとらなければ成らない。
ここに於いて、屈折率 n が全空間内に於いて一定である場合、Fermatの原理はAとBを結ぶ光線が最短の曲線すなわち直線となる。光線は直線であり、波は平面波となる。
ここで重要な点は、前節の結論から明らかな様に ν/V は p/h に等しいから、“Fermatの積分”は
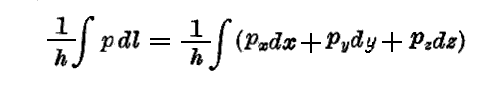
と書ける事です。この積分は常数1/hを除けば第1章§4.で述べた“Maupertuisの作用積分”とまったく同じものであることに気が付く。粒子に対する《Maupertuisの原理》と連合波に対する《Fermatの原理》との間に一つの類似が現れ始める。
この章に於いて、波と粒子との間に結合を設けたのは場の無い場合という極めて簡単な場合のみでした。この結合を一般化して場の内部において変位する粒子の場合に拡張する必要がある。
そのことを実現するには、ここで注意した“最小作用の原理”と“Fermatの原理”の類似に頼らなければならない。その為には光学に於いて屈折率が場所的・時間的に変化する媒質内の波の伝播の問題をあらかじめ詳しく研究しておく必要がある。
4.波の伝播に関する一般的事項
(1)均質で時間的に不変な媒質内における波の伝播 目次へ
我々はまず最も簡単な場合として、均質で時間的に変わらない性質を持つ空間内における波の伝播を取り扱う。例えば、均質な屈折率nを持つ媒質中に於ける光の伝播のような場合です。このとき光の波の伝播方程式は、媒質の屈折率をn、真空中での光の速度をc(c=3×1010 cm/s)とすれば、
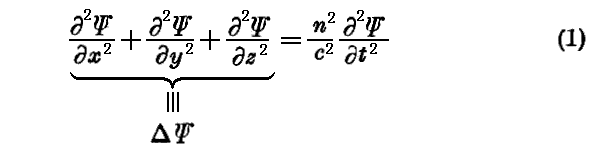
で表される。
この伝播方程式の解で、次の形をもつものを “簡単な正弦波” あるいは “単色平面波” と呼ぶことにする。
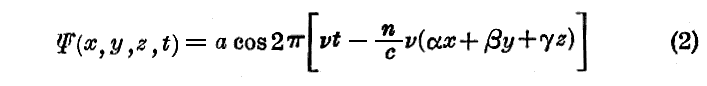
aは波の振幅、νは波の振動数であり、α,β,γは波の進行方向の方向余弦で α2+β2+γ2=1 を満足する。また、以下で表される部分
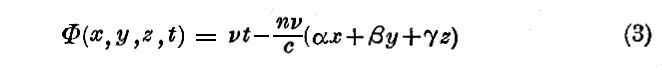
は平面単色波の “位相” と呼ばれる量である。
(2)式の“単色平面波”が方程式(1)の解である事は容易に確認できる。すなわち(2)式の形から
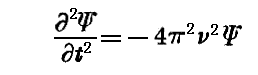
であるから(1)式は
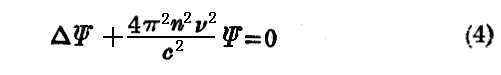
となる。ここで
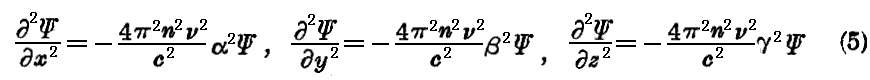
であるから、α2+β2+γ2=1 を考慮すれば、(2)式が(1)式を満足する事がいえ、(2)式が方程式(1)の解である事がいえる。ところで、今後
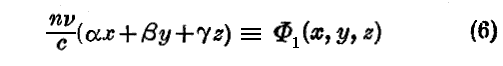
と置くことにする。
ある与えられた瞬間において(3)なる位相は平面 Φ=Cte 又は αx+βy+γz=Cte 上で一定です。この平面が位相の等しい平面(“等位相平面”)です。α,β,γは、この平面の法線の方向余弦です。時間が経つにつれて、位相Φの一定値は一つの“等位相平面”から他の“等位相平面”へと移りつつ空間内を進んでいく。つまり位相はα,β,γの方向へ移動するのですが、この方向が波の伝播する方向です。方向余弦α,β,γにより定義される互いに平行な直線が波の“射線”であり、位相速度を計算することができる。
位相速度とは、位相が一定の位置が射線に沿って移動していく速度のことです。いま dl を、射線に沿って測られた長さの要素とすれば
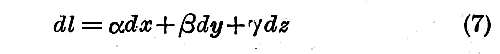
であり、与えられた dt および dl の値に対する位相の変化は
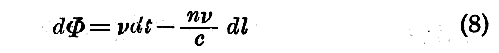
で表される。
もし我々が射線に沿って

の速度で移動していけば(8)式の辺かは零(位相の変化は無い)です。すなわちVが位相速度です。
波長λもまたこれに類似の方法で定義される。すなわち定まった時間において、斜線に沿って移動して位相Φが1だけ変わるために必要な長さが波長λです。位相Φが1だけ変わると言うことは、波Ψが初めの値と同じ値になることです。すなわち
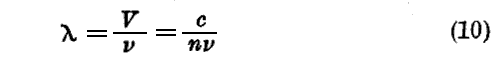
の関係式が成り立つ。
前節で我々はnを常数と仮定してきたが、(4)式の波動方程式に於いて屈折率nをνの関数としなければならない場合が生じる。つまり、波動方程式(4)のnは変数x,y,z,tには無関係であっても、その波動方程式の正弦解の振動数νと共に変わり得るとしなければならない事がしばしば生じると言うことです。
かかる場合を分散が起こるといい、nをνの関数として表す関係式を分散の法則と呼ぶ。このような場合が生じるのは、一般的な形で書かれた伝播方程式(1)の代わりに例えば
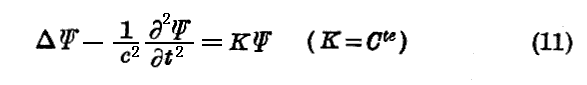
という形を取る場合です。なぜなら、(2)という解を(11)式に代入してみれば(11)式は
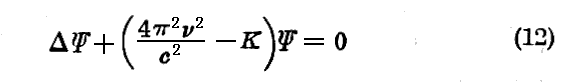
と書かれるのですが、これが再び(4)式の形の方程式であるためには
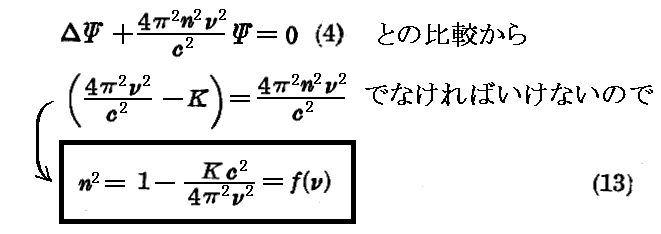
と置かなければならないからです。(13)式にあっては n は確かに ν と共に代わり得る。
“単色平面波”はある意味から言えば一つの抽象的存在と考えなければならない。なぜなら、このものは全空間にわたって過去未来永劫に存在すると言った代物だからです。
実際に於いては、波というものは、ある与えられた瞬間を考えれば、空間内の限られた領域を占め、またある与えられた一点を考えれば時間的な初めと終わりがあるのが常です。かくの如くの意味で限定された波の事を“波連”という。
一つの“波連”を表すために、我々は次の様な“単色平面波”の集まりを考える。
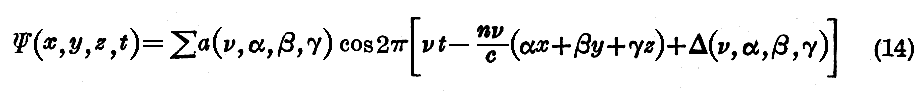
ここのΔ(ν,α,β,γ)という項は、それぞれ異なった単色波が一般に異なった位相を持っているという事を示す為に役立つ。もし α,β,γ が常に α2+β2+γ2=1 という関係で結び付けられているときは、前記の計算からして、ここの単色波が伝播方程式を満足する事がわかる。そして、この方程式が線型であるから、単色波の和も又一つの解となる。
有限個の項の和を考える代わりに
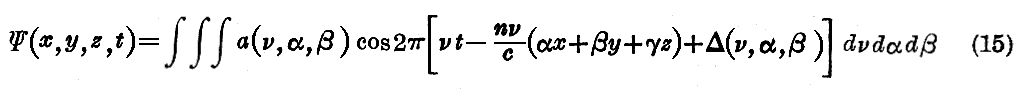
という積分を考える事もできる。ただし α2+β2+γ2=1 である。
もし n が ν の関数なら(14)及び(15)に於ける n は n(ν) の略記と見なすべきです。
一つの“波連”を如何にして“単色平面波”の和として表す事ができるかということを明確にする為に、次の様な場合を考える。今、z軸方向に伝播する一つの“波連”が
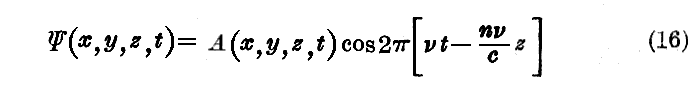
で表されるとする。時間の原点は適当に選ぶ。さらに我々は、この“波連”がz軸について対称であると仮定する。すなわちA(x,y,z,t)という関数がxおよびyという二つの変数に関して偶関数であるとする。
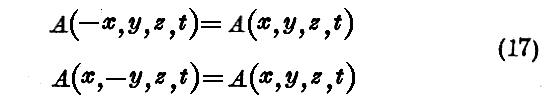
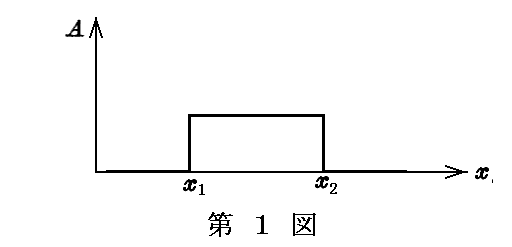
波連は定義により空間内に於いて限界がある故、関数A(x,y,z,t)は与えられた時間のある値に対して変数x,y,zがそれぞれx1とx2,y1とy2,z1とz2という限界内に含まれている所のみ零と異なるとする。この限界が波連の空間内の広がりの領域を決定するものである。
解析をもう少し簡単にする為に、与えられた瞬間に波連が占める領域内において関数Aが一定であるとみなしえるものと考えよう。ただし両端は例外でそこではAは急に零に帰るとする。換言すれば、今y,z及びtの与えられた値に対して関数Aはxのみの関数と考えられ、x<x1では零であるがx=x1の近傍において急に零から一定値に移り、続いてx=x2の近傍まで一定値を保ち、そのところで急激に零に帰るとす(第1図参照)。
yおよびzの関数としての変化も同一の形式であるとする。要するに“波連”のこの広がりの領域に於いて一つの“単色平面波”と一致するものであって、この領域の外においては当然この単色波とは異なる。
定義として、単色平面波にして振動数と伝播の方向が互いに極めて接近したものの集まりを “波群” と称することにする。
我々は、このように定義された “波群” によって波連の大きさが 波長c/nν に比較して大きく、波連の一定点における時間的継続が 周期1/ν に比較して大きい“波連”を表す事が可能である事を以下で示そう。
波連に付与されたz軸の周りの対称性故に、この波連を一つの 波群 により表すと
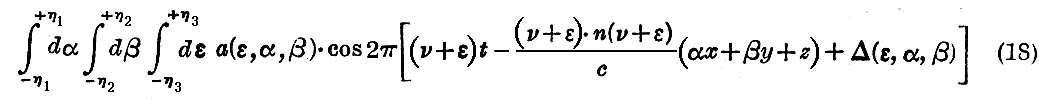
という形を持つであろう。
ここで γz と書かないで z と書いたのは、α及びβが極めて小さく(つまりz軸方向に沿った伝播をする)、
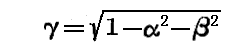
が1と異なる所はただ二次の量に依ってだけだからである。よって一次の量のみとることにするならば
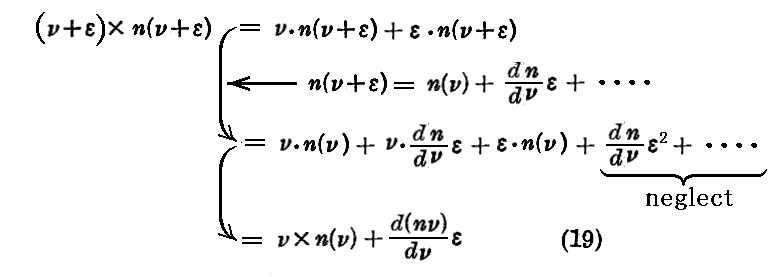
であり、(18)式中の余弦の引変数は
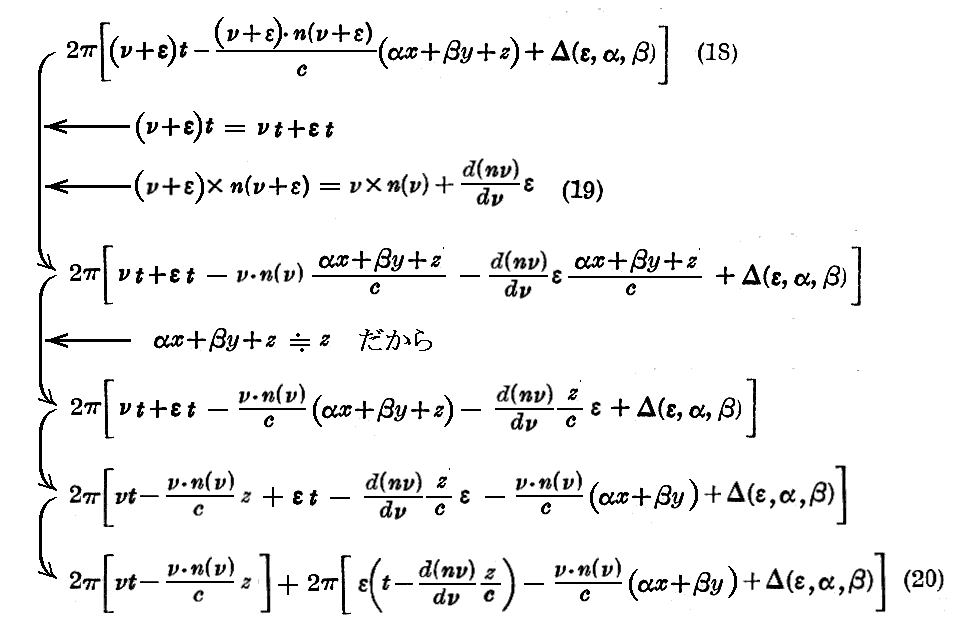
となる。
ここで、cos(a+b)=cosa・cosb−sina・sinb という公式を使うことによって(18)式は
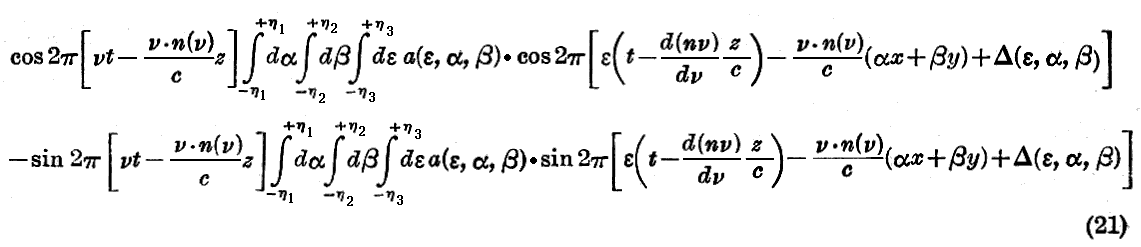
という形に書ける。
この(21)式の“波群”の表現を我々の“波連”の表現(16)式と同一のものとする為には、まず(21)式中の正弦の係数を零にしなければ成らない。その為に、関数Δが波群に属する単色平面波のすべてに対して同一の値を持つと考えよう。そうするとΔ=0と置くことが許される。
次にa(ε,α,β)に対して三つの引変数ε,α,βについて偶関数を採ろう。αおよびβに関して偶関数であるということは波群のoz軸の周りの対称性に相当し、εに関して偶関数であるということは中央の振動数νに関する群の分光的組成の対称性に相当する。(21)式を(16)式と同一のものにする為には
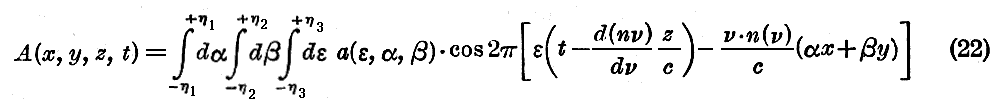
と置けば充分である。
(22)式が正確であるとき、つまり“波連”が一つの“波群”に依って表現される時は、(22)式に依って再び“Rayleighの群速度”を得ることができる。実際z方向に平行な直線を考えて、この直線上をdzだけ移動するのに
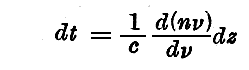
なる時間がかかることにして行くと、振幅Aの同一の値に随伴する事ができる。
従って我々が目下用いている近似の程度においては、“波連”の合成振幅は全体としてそのままz方向に
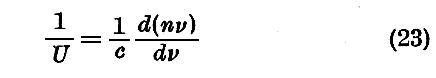
と言う式で定められる速度Uで移動して良くと考えられる。この速度は(第3章§3(20)式として)以前に導入した“群速度”に他ならない。もし n が ν に関係しないならば、U=c/nとなる。すなわち群速度が位相速度と一致する。
故に(22)式が有効なときは、A が z および t に関係するのは t−z/U という結合を通してだけである。従って z’=z−Ut という変数を導入するのは自然です。時間の与えられた値にたいしては、z’ は常数を除けば z という座標を計るものとなる。従って z1’ と z2’ が波連の前と後に相当する z の値ならば
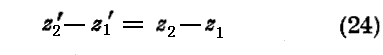
を得る。
波群(22)式は x および y について対称であると同じ様に z’ についても対称である事は容易に解る。(22)式のzにz=z’+Utを代入すると、(22)式は
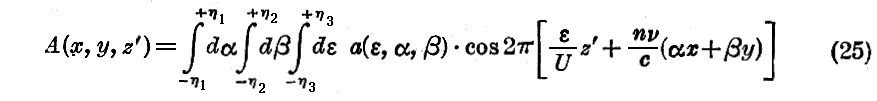
という形に書かれる。
もしここにおける余弦を三角関数の公式
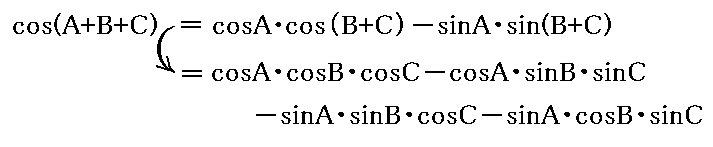
を用いて正弦や余弦の積に分解するならば、a(ε,α,β)が偶関数であるために三個の余弦の積の積分だけが零とならないで残る。すなわち
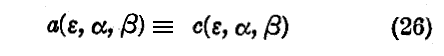
とおけば
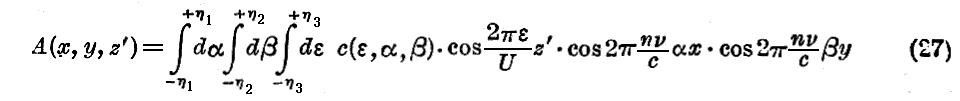
となる。
“波連”が一つの“波群”によって表現される様に A を書くことができるとすれば、それはこのようにして行われなければ成らない。ただし、いかなる時に A をこの様に書くことができるのか? ここに問題が起きる。
Fourierの積分の理論によれば、変数x,y,zに関して偶関数なる一つの関数 f(x,y,z) は極めて一般的な条件の許で
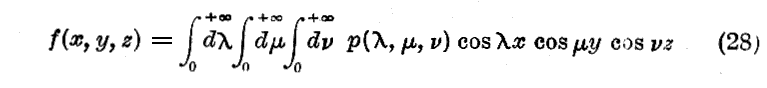
という形に書くことができる。ただし
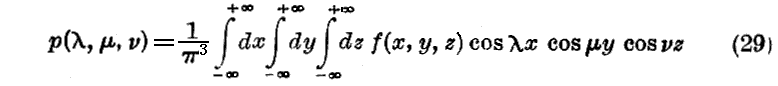
である。
故に変数x,y,z’について偶関数 A(x,y,z’) は
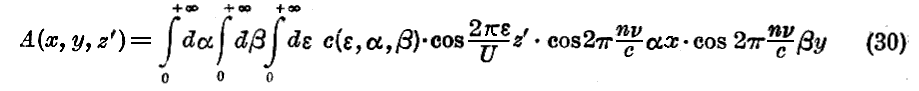
ただし
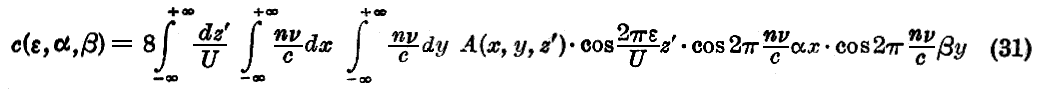
と書かれる。
しかし、我々の波連を一つの波群で表す事ができるためには、(27)と(30)とを一致させることができなくては成らない。すなわち(30)式に於いてα,β,εに関する積分範囲を 0〜η1,0〜η2,0〜η3, という極めて小さな範囲に縮めることができなくてはならない。その為には、(31)により決定される関数c(ε,α,β)がこの極めて小さな範囲の外においては零とならなくては成らない。しかるに、仮定により、A は x1<x<x2,y1<y<y2,z1<z<z2 に対して一定とみなされ、またこれらの範囲の外では零である。
もし公式(31)に於いてxに関する積分を考えれば

を持つ。ただしAは一定と見なされる。もし余弦が x1−x2 という範囲内で多数の周期を持つときは、c(ε,α,β)は零と考えられる。cが相当の値を持つためには
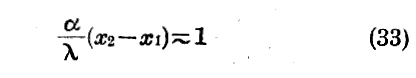
でなければならない。つまり、(33)の左辺は1と同程度の大きさをもためばならない。(33)式が、1より極めて小さいαに対しても成り立つためには

と言うことを必要とする。
“波連”のx方向の大きさは平均の波長λより極めて大でなければ成らない。y軸に平行な大きさに就いても同じ結果となる。
z方向に対しては
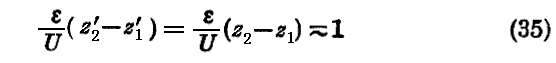
となる。ε が ν より極めて小さい為に
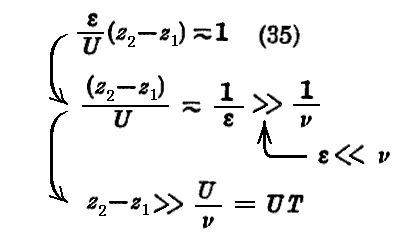
でなければならない。
UTなる積は一般に波長VTとは異なるが、多くの場合にこの二つの量は同程度の大きさです。そこで波連はその
すべての大きさが波長に比較して大成るときは、一つの波群で表現することが可能です。
波連全体が一定点をすっかり通過するのに要する時間は明らかに

です。
この時間は(36)式に従って周期T=1/νに比較して極めて長くなければならない。
(33)、(35)及びyに関するこれに相当する関係により
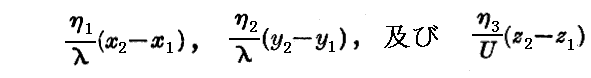
という量は少なくとも 1 と同程度の大きさでなければ成らない。伝播の方向を方向とし、単位長さ当たりの波数1/λに等しい長さを持つベクトルを考え、このものを“単色平面波”に対するベクトル“波数”と名付ける。そうするとその成分は
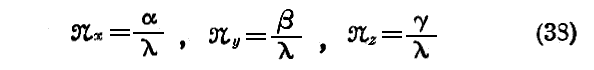
となる。
α、βおよびγに関する仮定ゆえに、“波連”のそれぞれの単色成分に相当する(33)式の変化の極大なるものは
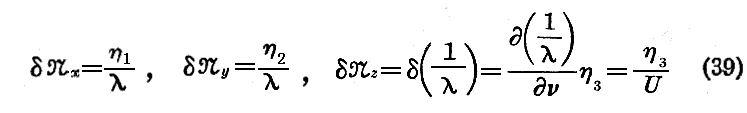
となる。
所で
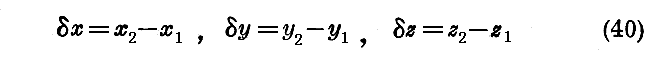
と置くことにする。これは“波連”の広がり内における座標の変化の極大です。これらの記号を定めると、量の大きさの程度について有効な不等式
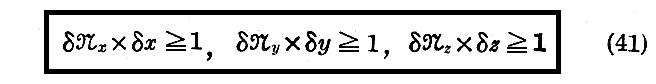
を書くことができる。
最後に

を以て一定点を波連が通過する時間を表し、δνで以て波群内に於ける振動数の変化の極大η3を表そう。そうすると(35)と(37)により

となる。
(41)式及び(43)式のBohr及びHeisenbergの理論に於ける重要性に就いては後に述べるでしょう。
(4)不均質だが時間的に不変な媒質内における波の伝播 目次へ
今まで我々は屈折率はx,y,zに関係しないと考えてきた。これからはnをx,y,zの関数とし時間的には一定と仮定しよう。これは光学に於いては均質で無い屈折媒質に対する場合として現れる。一般的には屈折率nは振動数νの関数であるから、均質ならざる屈折媒質も一般的には同時に分散性です。目下の場合に於ける簡単な正弦波の伝播方程式は
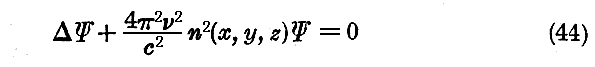
です。
正弦型の解
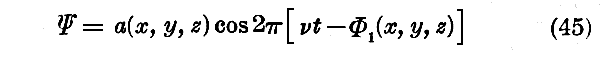
を取り上げよう。αは振幅であって今は場所に依って変化する。また
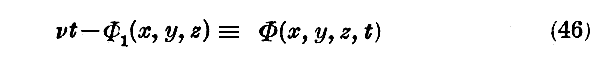
なる量は“位相”であって t に就いてはやはり一次であるが x,y,z に就いてはもはや一次ではない。
(45)を(44)に代入すると
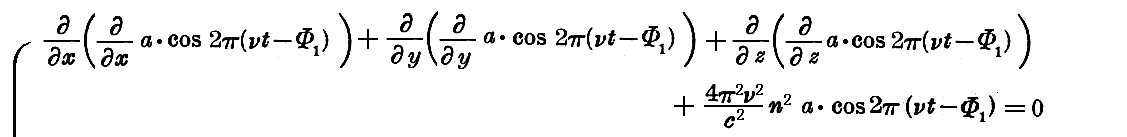
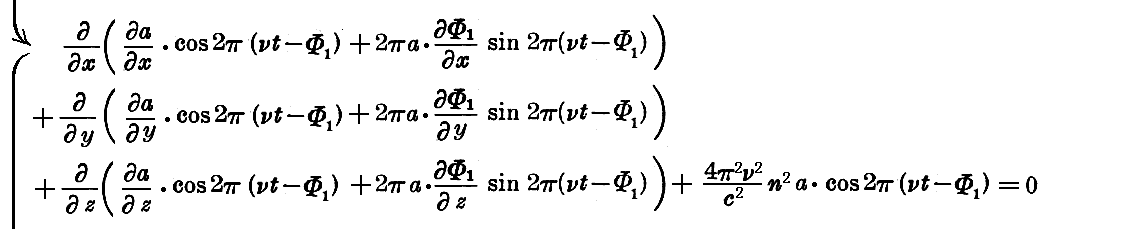
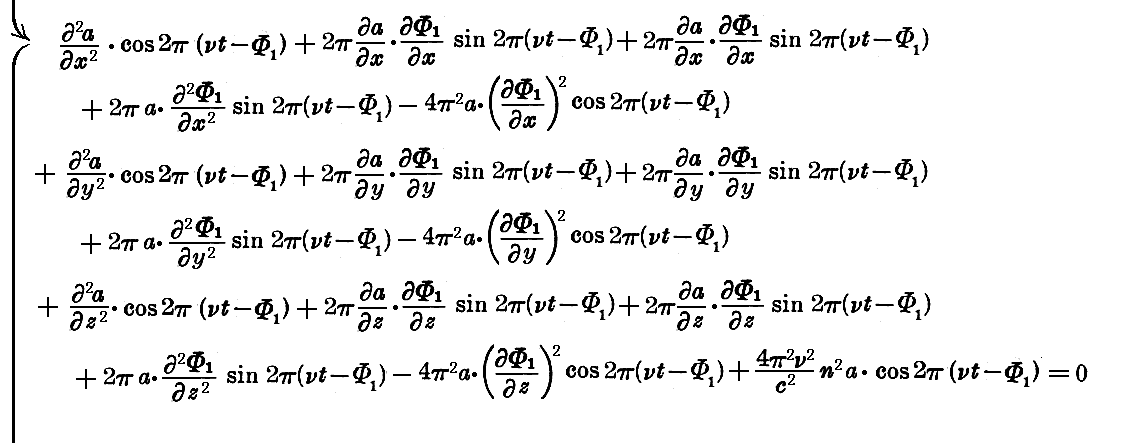
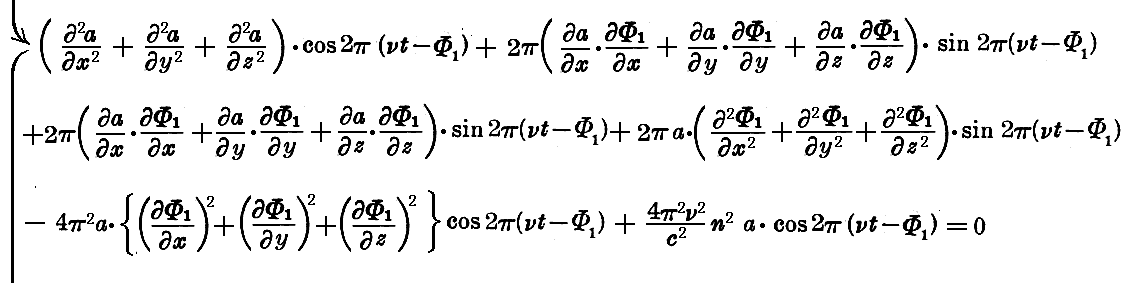
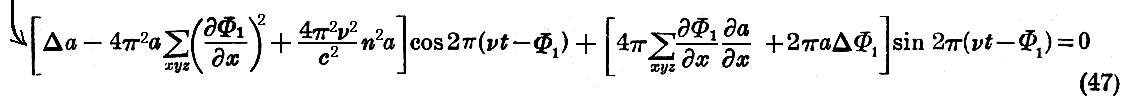
を得る。
この方程式は恒等的に成り立たねばならないので、 sin2π(νt−Φ1) 及び cos2π(νt−Φ1) の係数は別々に零とならなければならない。すなわち
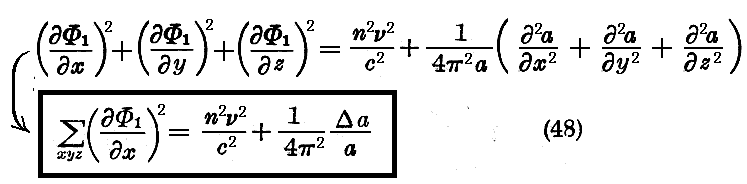
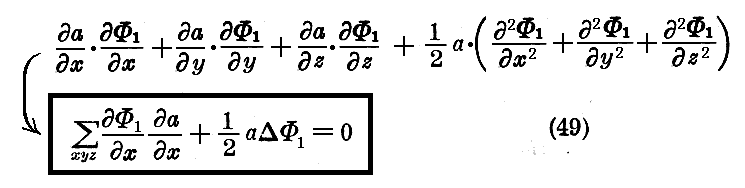
となる。
定義として、ある点に於ける波長とは
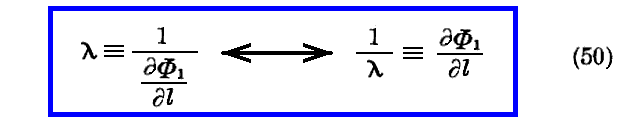
なる量の事であるとする。ここに dl は考える点に置いて Φ1=Cte という曲面の法線方向に取った長さの要素である。この長さλは今の場合、点に依って変わる。この定義は又nが一定の場合における普通の定義も含んでいる。というのは
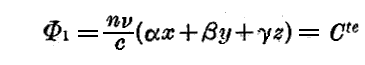
なる曲面は平面であり、その法線は方向余弦α,β,γを持ち、従って
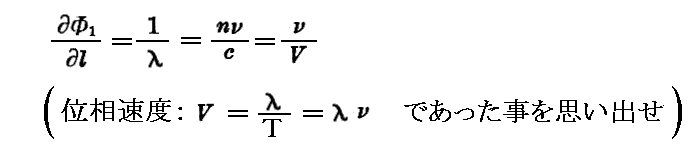
であるからです。
一様な媒質の場合の様に、Φ1=Cte という曲面を位相が等しい曲面(“等位相面”)と呼ぼう。このものはもはや一般に平面ではない。この曲面に直角なる曲線はやはり波の“射線”と呼ばれ、この射線の上をx,y,zより移動して位相の一定値に随伴する為に必要な速度を“位相速度”V(x,y,z)と名付けよう。Vの値は容易に計算される。すなわちもし斜線の要素dl を時間dt内に通過すると、位相Φの変化は
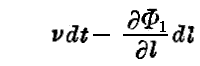
である。そしてこの変化が零なる為には
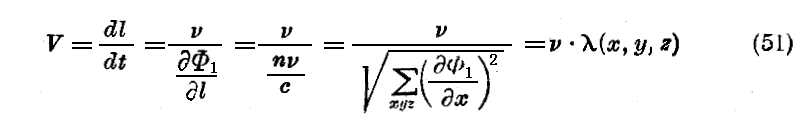
なる速度を以て移動する必要がある。
そこで関数(45)は
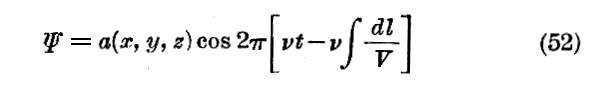
なる形に書かれる。積分は考える点 M(x,y,z) を通る射線に沿って、位相の原点として取った等位相面より M まで積分される。所が関数 V(x,y,z)
は一般に初めから解っているのではなく、その決定には連立偏微分方程式(48)及び(49)を用いて関数 a(x,y,z) 及び Φ1(x,y,z) を決定する事が必要です。
[補足説明]
ここは何を言っているのか解りにくいと思います。
ここの議論を理解するには、一次元の進行波の場合
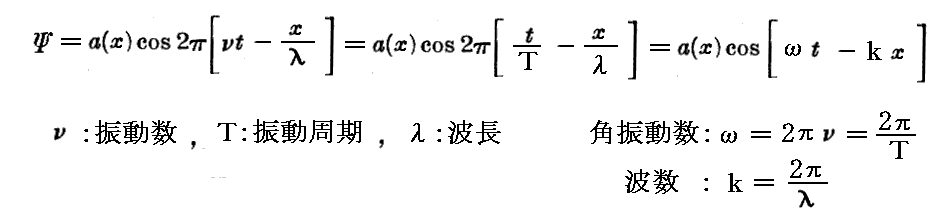
を思い出して下さい。
上記の表現における1/λの部分を
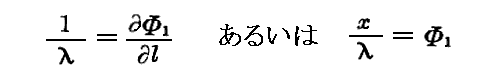
と置いて、三次元的な進行波の場合に、さらに場所的に屈折率が変わり波長が変化する場合に議論を拡張しているだけです。
そのとき、場所的に屈折率が変わル為に波動の解が変化するのですが、その様子を表すのが(45)式の形の解なのですが、逆に解がこの形で旨く表される為には許の波動方程式(44)が満たさなければならない条件方程式が得られます。
それが(48)、(49)式なのですが、これはポテンシャル関数Φ1が満たさなければならない方程式だと言うことです。
ただし、一つの面白い場合として、V と Φ1 の決定が a(x,y,z) を計算する必要なしに直ちに行われる場合がある。その場合と言うのは波長ていどの大きさの範囲では媒質が均質と見なされ屈折率が一定と考えられる場合です。その時は
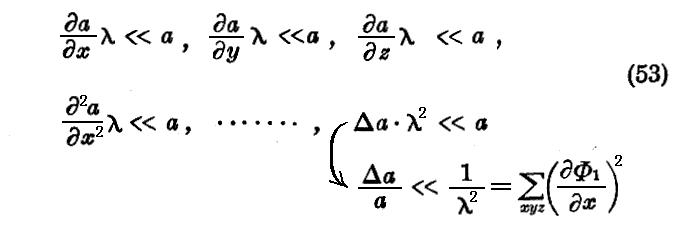
となる。
(53)の最後の不等式に(50)なるλの定義を結合すると方程式(48)に於いて

に対して無視し得ることが解る。
同様にして方程式(49)にλ2を乗じ且つ(50)を考慮に入れると
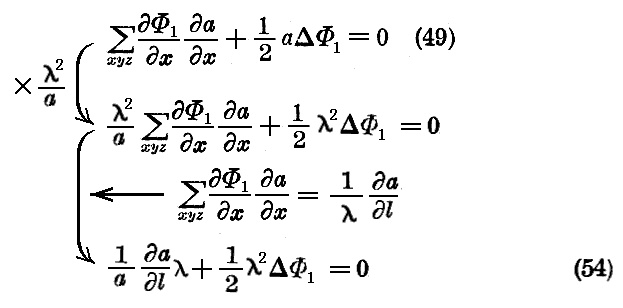
となり、この式の第一項は(53)式のおかげで無視できる。こうして 方程式(48)、(49)式 は
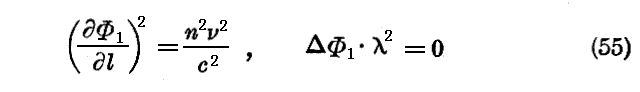
と書かれる。
故に(51)式に従って
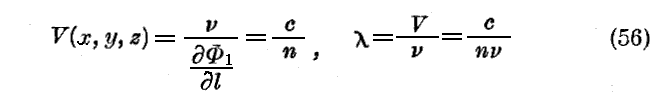
と置こう。
(55)の二番目の方程式はこのとき必然的に満足されている。なぜなら(56)に従えば Φ1 は波長程度の範囲では x,y,z に関して一次と見なされ、
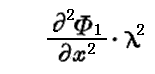
などの量は無視できるからです。
従って(52)は、この場合
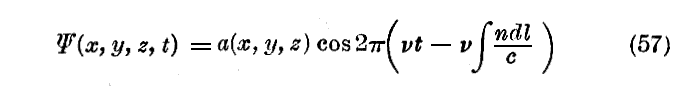
という近似解を与える。これは要するに Φ1 の決定が a(x,y,z) の計算等をする必要なしに初めからおこなわれるのである。 n(x,y,z) は与えられているのですから。
上記の近似で十分なときに、我々は“幾何光学”が有効であると言う。かかるときは、波長の程度の範囲では波は平面波であり単色であると言える。ただし波長を多数含む様な範囲に対しては伝播の条件の漸次的変化が起こり、この変化はこの大きな範囲に於ける振幅の変化及び位相の形の非線形性として現れる。
(5)“波の包絡面の作用”と“Fermatの原理” 目次へ
幾何光学の適用条件が満たされたと仮定して、その時に一つの波の伝播が如何様に研究することができるか見てみる。一つの等位相面を知っているとすると、その曲面上の各点Mの周りに
εV(M) という半径を持つ球を描くことに依って初めの曲面に無限に近い他の等位相面を作図する事ができる。。ただしεは無限に小さい定数であり、V(M)は点Mに於ける“位相速度”Vの値です。
この小球の包絡面二枚は共に等位相面です。なぜなら初めの曲面上で時間tに実現した位相の値を各々の曲面上に於いてそれぞれ t−ε および t+ε
という時間に於いて見出すからです。点Mと点Mを中心とする球がその包絡面に接する接点とを結ぶ二つの直線は“射線”の要素です。
このように漸次的に進めて行くと、すべての“等位相面”を作図する事ができ、同時に波の“射線”は少しずつ折れ曲がった直線の連なりとして決定される。
上記の方法は“波の包絡面の作図”という名称の許に知られているが、これに依れば幾何光学なるものはその根本仮定としてFermatの原理を容認するものであることが証明できる。Fermatの原理の言うところに従えば、空間内の二点AおよびBを通る射線は、AよりBまでその射線に沿って取った曲線積分
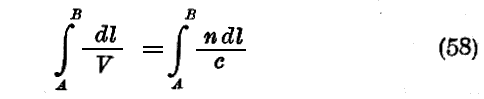
が定数であるようなものです。
A から B まである位相が移動するために要する時間が“射線”にそっては極小であることを意味する。このことを証明するために A を通る等位相面 Φ1(x,y,z)=c1 および B を通る等位相面 Φ1(x,y,z)=c2 を考え、次いでこの二つの中間に位置する総ての等位相面 Φ1(x,y,z)=c を想像する。ただし c の値は c1 と c2 の間にあって互いに無限に近い値を持っている。
A より B まで行く射線は互いに無限に近くにある Φ1=c なる曲面に垂直なる小さな直線分に依って形作られていると見なすことができる。射線に無限に近い少し変化した曲線はすべて二種の直線分により形成される。
その第一種の直線分は前記の如く決定された性質のものです。第二種の直線分はその両端を通る位相面に直角でない(垂直でない)様なものです。こうして第二種のものが少なくとも二個ふくまれている。この少し変化した曲線上の第一種一つの直線分に沿って取った
dl/V なる量は、射線上にて之に相当する直線分に沿って取った dl/V なる量に等しい。それは実際、いずれの dl も Φ1=c およひ Φ1=c+dc なる曲面を両端としかつこれに直角(垂直)であるから
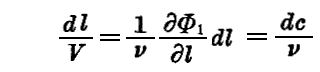
が両方の dl に対して成立するからです。
ところがもし少し変化した曲線の要素で互いに無限に接近した等位相面に直角(垂直)でないものを射線上でこれに相当するものと比較するならば、dl/V なる量は前者に対するものの方が後者に対するものより大きい。それは垂直線がいわゆる射線より短いからです。“Fermatの原理”はこのようにして証明される。ただし、波の理論に於いてはこのものはもはや根本仮定ではなく、幾何光学が適用され得るときのみ有効な一つの定理なのです。
(6)不均質だが時間的に不変な媒質内における“波群” 目次へ
波群の概念を不均質だが時間的に不変な媒質の場合に一般化しよう。
第4章§4の(55)式で示した様に、幾何光学が有効な場合は、関数Φ1は方程式
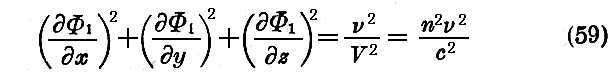
に従う。この方程式のことを“幾何光学の方程式”と呼ぼう。
波の包絡面の作図の出発点となる等位相面は
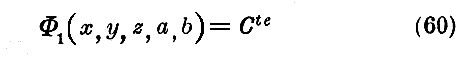
という方程式の完全積分の族に属する。そしてこの出発点の等位相面より作図法により導き出す他の等位相面も(60)の族に属する。右辺の常数のみが一つの曲面から他の曲面に移る時に変化する。それにえ定まった伝播に対して、等位相面は二つの媒介変数を持つ一つの族を形作る。一様な媒質の場合には、
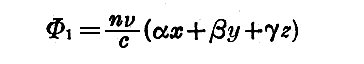
となり、二つの媒介変数 a 及び b は
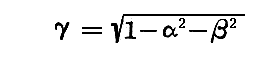
を取ればこの場合方向余弦 α 及び β となる。
次の様にして形作られた波群を取り扱う。その波群は極めて小さな範囲 ν−δν,ν+δν 内に含まれた振動数を有しその二個の媒介変数 a 及び
b は極めて小さな範囲 a−δa,a+δa 及び b−δb,b+δb 内に含まれる値を有する無限個の正弦波を含むものとする。時間t0,位置x0y0z0に於いてこれらの波の総ての位相が一致したとしよう。この位相の一致状態は如何に移動するのだろうか? 位相速度Vに関係する関数Φ1は一般には ν に関係し、群に属する波の総ての位相が、時間t0,位置x0y0z0に於いて一致するためには
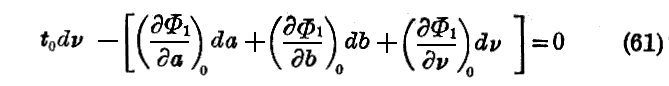
なる式を必要とする。ただし指数0は導関数が(x0,y0,z0)なる点の値を取ることを示し、da,db,dνはそれぞれの絶対値がδa,δb,δνより小さい値を取る。これより後の時間tに於いてこの位相一致の状態がx,y,zで実現される為には
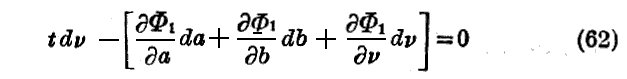
でなくてはならない。この場合はΦ1の導関数は点xyzに於ける値を取る。またda,db,dνは前の式と同一の値を持っている。(62)なる関係が(61)より当然導かれる為には
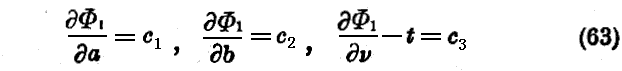
でなければ成らない。
最初の二つの関係は考える位相の一致点が空間に描く曲線を決定し、第三の関係はこの点がその道筋上を如何に運動するかを決定する。変化しない場に対する“Jacobiの定理”との類似が自ずと見え始める。
(63)の最初の二つの方程式に依り決定される道筋が等位相面に直角(垂直)なる事を示す事は容易です。実際、この二つの方程式を微分して
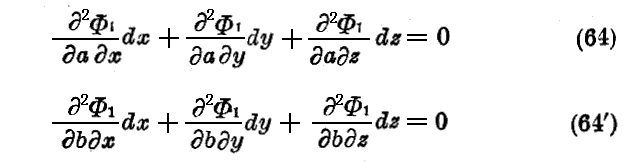
を得る。
しかるに、もし Φ1 により満足される方程式(59)を a 及び b に関して微分すると
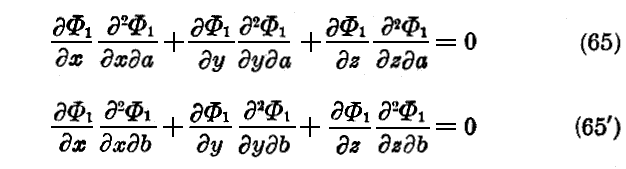
を見出す。
(65)−(65’)の一組を(64)−(64’)の一組と比較すると
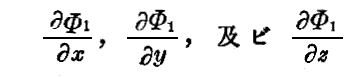
なる微分係数がそれぞれ道筋に沿って取った微分 dx,dy 及び dz に比例することが解る。すなわち道筋が確かに曲面Φ1=Cteに直角(垂直)なのである。
幾何光学が有効なときは、波長程度の大きさの範囲では伝播はあたかも屈折率一定であるかの如くおこなわれ、また波長のある個数を含む様な範囲に於いても(45)なる波はあたかも一定振幅を有する平面波と見なすことができる。さて、通常の場合に於いては波長なるものは我々が直接に計ることのできる程度の小さな大きさよりも更によほど小さいのである。従って波連にしてその大きさは人間的な大きさの範囲より見れば極めて小さいが波長のごとき長さは無数に包含するようなものを考える事が可能である。
(7)時間的に変化する媒質内における波の伝播 目次へ
我々がまだ語っていないのは、伝播の条件が場所に依って変化するのみならず、時間によっても変化する場合です。すなわち空間的に均質では無く、時間的にも一定ではない屈折媒質の場合です。
たとえば
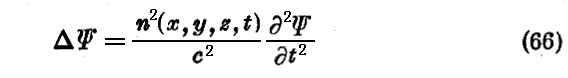
という伝播方程式を容認する事にしよう。
ここに於いては時間なるものはもはや何等特殊な役割を演じるものでは無くなる。従って位相が時間の一次関数である様な正弦型の解を取ることによって時間を取り除く事ができなく成る。それ故に正弦型の解の一般的な形として

の形を取ろう。
これを伝播方程式に代入して、正弦項と余弦項とを別々に零としよう。すると
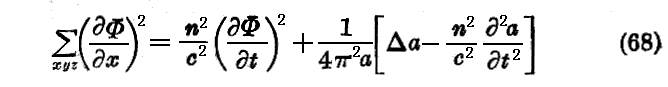
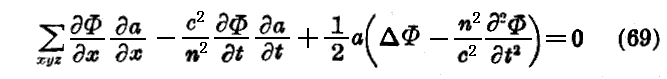
となる。
[補足説明]
(68)(69)式を導く手順は第4章§4で(47)式を求め、それから(48)(49)式を導いた手順と同じです。以下に、今回の場合の式変形の様子を追記しておきます。
定義として
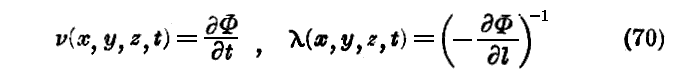
と置こう。dl は考える点、考える瞬間に於ける Φ=Cte 面の“法線要素”です。(70)によって定められた振動数及び波長は一般に両者とも変化するものである。 n が一定の場合は通常の意味の振動数及び波長と一致する。
λ の程度の空間的変位、及び周期 1/ν 程度の時間的経過に対して伝播の条件がほとんど変わらないときに“幾何光学の近似”が有効であると言う。しかる時は
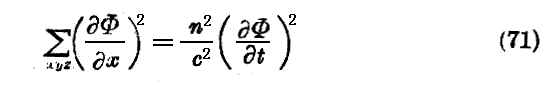
と書くことができる。また Φ の二次導関数を零と見なすことができる。方程式(71)は一般的な場合に適用した幾何光学の方程式の形です。波長程度の大きさの範囲、及び周期に比してあまり大でない時間の経過内に於いて、(67)なる波は平面波にして単色な波であると見なすことができる。このことから今の場合にも、波連にしてその空間的大きさ及び時間的経過が我々が計測し得ない程小さいけれどもなお波群として表す事ができる為に必要な条件を充足する様なものを想像することの可能性が出てくるのである。
(71)なる方程式の一つの完全積分を Φ(x,y,z,t,a,b,c) としよう。正弦波により形作られる波群があるとし、各正弦波に対して三つの常数 a,b,c が章範囲 a−δa,a+δa;b−δb,b+δb;c−δc,c+δc
に含まれるものとする。時間 t0 に於いてこれらの波が総て点 x0,y0,z0 に於いて位相が一致したと想像しよう。そうすると
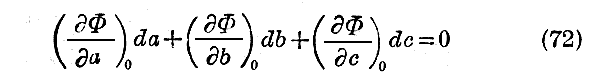
出なければ成らない。この式に於いて指数0は導関数が x0,y0,z0 に於いて時間 t0 の値を取ることを示し、又 da,db,dc はそれぞれその絶対値に於いて δa,δb,δc より小である。この位相一致の状態を更に点 x,y,z
時間 t において再び見出す為には
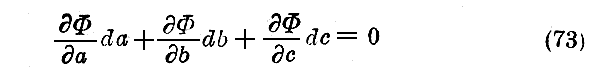
でなければならない。このときは導関数は x,y,z に於いて時間 t に於いて取られる。(73)が(72)の結果成立するためには
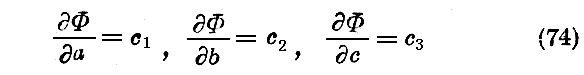
である事を要する。
この三つの方程式が位相一致点の運動を与える。“Jacobiの定理”との類似は今や明瞭である。
以上の波の伝播の研究に次いで、我々は波動力学に於いて粒子に連合せる波に対しいかなる“伝播方程式”を採用しなければならないのかを調べよう。
5.粒子の連合波の伝播方程式
(1)伝播方程式の選択に対する判別の基準 目次へ
すべての場の外に於ける粒子の運動という特別な場合に、我々はすでに波と粒子との間に一つの対応を設けることができた。この対応は次の様に行われる。
すなわち、勢力(エネルギー) W および 運動量 p を有す粒子に対して、運動の方向(ベクトル p の方向)に伝播し、振動数 ν=W/h および波長 λ=h/|p| を持つ波を結び付けなければならない。真空の空間がこの連合波に対してあたかも屈折率
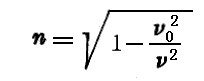
を持っているかのようにすべての事柄が行われる。ν0 は粒子の特性的常数であってその固有質量 m に対して ν0=mc2/h なる関係で結ばれている。粒子の速度はこの分散法則に相当する“群速度”に等しい。
一方に於いて、我々は第3章§5で “最小作用の原理” と “Fermatの原理” との間の関係が表れ始めるのを見た。こうして “古い力学” と “幾何光学” との間のこの類似は、波群の運動が幾何光学的近似に於いては “Jacobiの方程式” と極めて類似した方程式により行われるという事実を第4章に於いて確認したのである。
(2)場の無い場合の伝播方程式 目次へ
(3)恒常の場における伝播方程式 目次へ
(4)変化する場における伝播方程式 目次へ
(5)方程式を自動的に見出す為に役立つ方法 目次へ
6.古典力学と波動力学
(1)古典力学における振幅aの意味 目次へ
(2)存在確率 目次へ
(3)具体的な例 目次へ
(4)第6章の摘要 目次へ
7.干渉の原理およぴ結晶による電子の回折
(1)干渉の原理 目次へ
(2)結晶による電子の回折 目次へ
(3)G.P.Thomsonの実験に関する予備知識 目次へ
(4)G.P.Thomsonの実験 目次へ
(5)Ponte氏の実験(1929年) 目次へ
8.干渉の原理および固定中心による荷電粒子の散乱
(1)古典力学による荷電粒子の散乱 目次へ
(2)波動力学による計算 目次へ
9.新力学における存在確率の運動
(1)確率の雲 目次へ
(2)確率要素の運動方程式 目次へ
(3)Ehernfestの定理 目次へ
(4)関数φおよびaの計算 目次へ
(5)嚮導波(キョウドウハ)の理論 目次へ
10.光子の波動力学
(1)光子とその連合波 目次へ
(2)光子に結び付けられる確率の雲 目次へ
(3)干渉現象の解釈 目次へ
(4)完全反射をする平面鏡の付近における光の干渉 目次へ
(5)不完全反射をする鏡の付近における光の干渉 目次へ
(6)二つの単色平面波の合成 目次へ
11.Heisenberg およひ Bohr の理論
(1)分光的分解の原理 目次へ
(2)Heisenberg およひ Bohr の理論. 不確定性関係式 目次へ
(3)Heisenberg およひ Bohr の理論における波の意味 目次へ
(4)古い力学との一致 目次へ
(5)Einsteinの異議. 粒子は位置を指定し得ないのか又は位置を有しないのか? 目次へ
12.測定の可能性とHeisenbergの関係式
(1)測定の操作とHeisenbergの関係式 目次へ
(2)Heiserbergの顕微鏡 目次へ
(3)Doppler効果を用いる電子の速度測定 目次へ
(4)粒子の細孔通過 目次へ
(5)速度の測定に関する注意 目次へ
13.場が無い場合および場が一様な場合の波束Ψの伝播
(1)伝播方程式の場が無い場合における厳格な解 目次へ
(2)特別の場合への計算の発展(Darwin) 目次へ
(3)二回の相次ぐ観測による速度の測定 目次へ
(4)一様にして変わらない場における波束Ψの伝播の厳格な解 目次へ
(5)特別の場合への計算の発展 目次へ
14.粒子系の波動力学
(1)系の古い力学の諸原理の摘要 目次へ
(2)系の古い力学から系の新しい力学への移行 目次へ
(3)数学的予備定理 目次へ
(4) 配置空間における伝播方程式 目次へ
15.系の運動に結び付けられた波の解釈
(1)幾何光学の近似 目次へ
(2)一般の場合. 確率の運動 目次へ
(3)Ehrenfestの定理 目次へ
(4)BohrとHeisenbergの解釈 目次へ
16.古い量子論と周期運動の安定
(1)周期運動の量子化の第一例 目次へ
(2)Wilson-Sommerfeldの条件 目次へ
(3)Einsteinの言い表し 目次へ
(4)Kepler運動の量子化 目次へ
(5)變退(ヘンタイ)の問題 目次へ
(6)古い量子論の不充分さ 目次へ
17.量子化された運動の安定の波動的解釈
(1)波動力学における量子化の意義 目次へ
(2)固有振動の簡単な例: 振動する弦および膜 目次へ
(3)方程式(9)の一般的な場合の研究 目次へ
(4)粒子系の量子化 目次へ
18.量子化された系に対する波Ψの解釈
(1)一般的原理の量子化された系への適用 目次へ
(2)量子化された系に及ぼす外よりの作用の影響 目次へ
(3)確率の雲とHeisenbergの行列 目次へ
19.参考文献
この稿を作るに当たって、下記文献を参考にしました。感謝!
- Louis de Broglie著(渡邊慧訳)「波動力学研究序説」岩波書店(1934年刊 原本は1930年刊)
本稿はこの書籍を引用紹介するものです。
- 村上雅人著「なるほど解析力学」海鳴者(2016年刊
別稿でも紹介しましたが、とても解りやすく説明されています。購入されてご覧になることを勧めます。
- ルイ・ド・プロイ著(河野与一訳)「物質と光}岩波文庫(1972年
- ジョルジュ・ロシャク著(宇田川博訳)「ルイ・ド・ブロイ 二十世紀物理学の貴公子」国分社(1995年刊)
- Louis de Broglie, "Ondes et quanta", Comptes Rendus, Vol.177,
p507-510, 1923年
第一論文,“波と量子”、英訳版htmlはこちら
- Louis de Broglie, "Quanta de lumie`re, diffraction et interfe`rences",
Comptes Rendus, Vol.177, p548-550, 1923年
第二論文,“光量子”、回折と干渉”
- Louis de Broglie, "Les Quanta, la the`orie cine`tique des gaz et le
principe de Fermat", Comptes Rendus, Vol.177, p630-632, 1923年
第三論文,“量子、気体の運動論Fermatの原理”
上記三論文はページ数も少なく、断片的で論理的な飛躍があり解りにくい。そのため、次に紹介する学位論文の日本語抄訳をお読みになる事を勧めます。
- Louis de Broglie, "Recherches sur la the`orie des quanta", Ann.
de Phys., (10)3, p22-128, 1925年
これは1924年に受理されたド・ブロイの学位論文“量子論の研究”ですが、これはpdfファイルとして多くのURLからdownloadできます。
これは、前記三論文の内容をまとめて、更に肉付けしたものですが、100ページを越える大部なものです。ただし、その内容はとても難解です。
この学位論文の翻訳としては、1927年に岩波書店から出版された「物理学文献抄 第1輯」に芝亀吉氏による抄訳があります。この抄訳は42ページの大部なものです。
内容はかなり難解ですが、本稿をお読みになるとき平行して読まれると、理解の助けになるかもしれません。
- 小島智恵子著「日本における「物質波理論」の受容」(https://www.bus.nihon-u.ac.jp/wp-content/uploads/2021/09/KOJIMA_Chieko_2021-27-1.pdf)
このpdfファイルはこちらです。この中に上記ド・ブロイの三論文と学位論文の内容の簡単な紹介があります。
- 村上陽一著「ルイ・ド・ブロイ(1892〜1987)の功績」(http://www.wattandedison.com/deBroglie.pdf)
このpfファイルはこちらです。特にこの中の4.“ド・ブロイの理論”をご覧下さい。
-
-
-
-