レーマーが史上初めて光速度を測定した方法を説明します。その内容を要約した論文（日本語訳）を参考にしながらお読み下さい。
木星の衛星は木星のまわりを回っているのですが、地球から見て木星の裏側に隠れること［“食”と言う］が周期的に起こる。しかし、その食が起こる周期が時と共に少しずつ変動することが解ってきた。レーマーは長期間にわたって食が起こる時刻を観測して、その変動の原因をつきとめ、その変動量から光の速度を見積もった。
なぜレーマーはその様な単調な観測の仕事に関わり、また継続したのでしょうか。それには理由があります。当時拡大する新世界との貿易、航海の増大のために、ヨーロッパの国々は遠洋航海中の船の正確な位置を知ることや、新世界の正確な地図を必要としました。
そのときの問題点を、未開地の地図を作る場合で説明する。未開地の緯度はそこで観測される北極星の水平面からの高度角を測定すれば簡単に求まります。しかし、経度を知るのは簡単ではありません。それを知るには正確な時刻を知ることが必要だからです。未開地の観測点に於いて、正確なヨーロッパ時(例えばフランスのパリ時刻)が解れば、そのとき天頂を通過する星を観測することで、その地点とヨーロッパ(例えばフランスのパリ)との経度差を知ることができます。なぜならパリ時刻の同じ時間にパリの天頂を通過するのはどの星座のどの星かは正確にわかっているからです。
しかし、別稿で説明したように当時の時計［補足説明１］の精度は良くありませんでした。そのためヨーロッパを出発するときにいくら正確に時を合わせていても地図を作る目的の場所に移動するまでに時計が示す時刻は狂ってしまい正確なパリ時刻を知ることはできなかったのです。さらに、重力加速度の大きさは場所によって変化します。そのため当時使われていた振り子時計では、時刻そのものも狂って行きます［補足説明２］。
そのとき、毎日決まった時刻に起こる天体現象があれぱ、洋上の航海者や探検中の地理学者の時計をパリの時刻にあわせることができます。フランスの王立科学学士院は、その天体現象として、ガリレオが1610年に発見した木星の四つの衛星が周期的に木星の影に隠れる現象(食）が利用できると考え、実際に利用していました。地球の直径は木星と地球間の距離に比べてはるかに小さいので、木星の食現象は地球上の何処で観測しても同じ時刻に起こるからです。
［補足説明１］
マゼランの世界一周航海は1519年9月20日～1522年9月6日ですから、1600年代はまさに大航海時代でした。
ところで、振り子の等時性を利用して、実用に耐える振り子時計を作ったのはホイヘンスで1657年のことです。またひげゼンマイの等時性がフックにより発見（1654年）されて、これを用いた懐中時計をホイヘンスが作ったのは1675年頃のことです。
航海に於いて正確な計時を可能にしたハリソンの“クロノメーター”が発明・実用化されるのは、1735～1761年の頃です。ハリソンは合わせて５個のクロノメーターを制作したが、中でも1759年のH4型に至って懐中時計に似た形の実用性の高いものとなった。（当時の時計が狂う主な原因は、温度変化により、テンプゼンマイの長さが変わり、さらに弾性定数自体が変化することと、テンプの体積が膨張して慣性モーメントが変化することでした。ハリソンはバイメタルの温度による屈曲を用いてテンプゼンマイの実質的な長さを調整して、温度変化による影響を打ち消すことに成功したのです。山口隆二著「時計」岩波新書(1956年刊)参照）
ハリソンのクロノメーター H１～H5に付いてはこちらを参照。
ちなみに、キャプテンクックの第1回航海(金星の日面通過観測）が1768～1771年、第2回が1772～1775年、第三回が1776～1780年です。第１回航海に於いて、金星日面通過の観測地
(タヒチ島に設けた) の経度を知る方法として“木星衛星の食による方法”が用いられたようですが、クックは二度目の航海からラーカム・ケンドールが作ったH4型の複製クロノメータを携行し、後で述べる“月距法”と併用しながら正確な経度を測定することができた。ハリソンの“クロノメーター”については斉田博著「星を近づけた人々（上）」地人書院（1984年刊）§11の解説も興味深いのでご覧下さい。
［補足説明２］
別稿「古典天文学」３．（１）３．で説明したように、太陽系の大きさを知るには地球とどれか近くの惑星との距離を正確に知ることが必要です。そのためには地球上の離れた二点（例えばパリと南米のギアナ）から同時刻に近くの惑星（例えば火星）の方位を正確に観測して、三角測量の原理で地球-火星間の距離を求めます。もちろん火星の方位は、背景の遠くの星の位置との相対的な視差を測定することで求めます。
パリとギアナの時刻を合わせるのに木星衛星の“食”現象を利用します。これはパリから見てもギアナから見ても同時に起きるからです。そのようにして時刻を合わせた振り子時計で火星の天球図上の位置とその時間を継続して測定します。その様にしてパリとギアナの様々な時刻の火星の天球上での位置を観測します。遠征隊がフランスに帰国した後で、同時刻のパリとギアナでの火星の位置をつきあわせることで、火星までの距離を求めます。
1672年の火星はちょうど“衝”の位置にあり地球に最も接近することが解っていましたので、カッシーニは火星視差の観測のために南米ギアナのカイエーヌ島（赤道付近）に助手リシェーとマーリスを1671～1673年に派遣します。仏領ギアナが選ばれたのは1600年代の初めからフランス人が入植しており、定期船も就航していたからです。
ギアナでの時刻の較正には、もちろん木星衛星の“食”現象の運行表が使われたのですが、そのときリシェーは、持参した振り子時計 （パリで正確な時を刻むように振り子の長さが厳密に調整されていた） がギアナでは定常的に遅れる事に気付きます。1日当たり二分ずつ遅れたのです。時計が正しい時刻を示すようにするためには、3パリフィート8・3／5ラインだった振り子の長さを5／4ラインだけ短くしなければ成りませんでした。これらの結果は帰国後『カイエンヌにおける天文学、物理学の観測』として発表されます。［1パリフィート＝0.3248406m、1ライン＝2.255837mm］
これは直ちに、ホイヘンスやニュートンによって、遠心力の為に赤道地方の重力加速度がパリよりも小さくなるためであると説明されるのですが、実際に重力加速度の変化が観測された最初の例です。［振り子の振動周期から重力加速度を求める方法は高校物理で習う］
ちなみに、1673年にカッシーニは上記の2ヶ所で観測された火星視差を用いて計算することで、地球と太陽までの距離を1億3800万km（引用元の資料１と、資料２）と見積もっています［この値は２．(３)で用います］。（ここで注意して欲しいのですが、別稿「古典天文学」3．（1）3．で説明した様に、地球と火星の間の距離が測定できれば、他の惑星までの距離や、それらの惑星の公転半径は計算できます。）
また、ニュートンは1687年に出版される『プリンキピア』の第３篇、命題19，20で、この重力の変化について詳しく説明しています。
このようなことが解ったのはまさにこの時代であったことに注意して下さい。
木星衛星の“食”現象を前節で説明した事柄に利用できることに最初に気付き、木星の衛星の位置推算表を作ることを始めたのはガリレオです。彼はオランダ連邦の援助を得て実際に観測を始めたのですが、残念なことに彼の肉体的衰えと死（1642年）によって未完の仕事となってしまいました。（ダンネマン「大自然科学史」より）
このガリレオの仕事を完成させたのがボローニャ大学で天文学を教えていたカッシーニです。彼はボローニャで木星の運行表を作り上げて1668年に『メディチ家の星に関するボローニャの推算法』として発表します。これは上記の方法による正確な経度の計算法を可能にした画期的な運行表でした。カッシーニはこの業績が認められて1669年にパリ天文台（1667年設立）に招かれます。そして、1671年から彼が亡くなる1712年までの40年間パリ天文台長の地位にとどまり様々な大発見を行います。
天文台長となったカッシーニは、ボローニャで作った木星の衛星の運行表をさらに精密なものにするためにパリでも木星衛星の観測を継続していました。そして、この仕事に協力することになったのが、天文台に新しく雇われたデンマーク人の若い天文学者であったオーレ・レーマーです。フランスの天文学者ジャン・ピカールがデンマークを訪問した際にレーマーを紹介されて、彼にパリ天文台で働くことを勧めたのです。1672年からパリ天文台で働くことになったレーマーは、木星の衛星の運行表の精度を高めるための観測に従事して、地道な観測を数年間にわたって続けます。
［補足説明１］
“木星食”を利用する前に経度を決定する方法として用いられたのは、“月食”を利用する方法と“月距(月と他天体の間の測定角度)”を利用する方法 （つまり月の移動を巨大な天体時計として利用） です。そして18世紀後半になってからは“クロノメーター”を利用する方法となります。
上記の“月距法”の原理は古くから知られていたが、簡便で正確な角度測定器具である四分儀（1731年ジョン・ハドリー）や六分儀（1760年ジョン・キャンベル）が発明され、実用に耐える航海年鑑（太陽や星と月の角距離の様々な経度における数表）が整備されるのは18世紀になってからです。
この当たりの説明は
デーヴァ・ソベル著「経度への挑戦」藤井留美訳 翔泳社（1997年間）、角川文庫(2010年刊)
デレク・ハウス著「グリニッジ・タイム」東洋書林（2007年刊）の補講
石橋悠人著「経度の発見と大英帝国」三重大学出版会（2010年刊）第1章2節
が詳しい。これらはとても面白い本ですから読んでみられることを薦めます。
［補足説明２］
高橋憲一著「ガリレオの迷宮」共立出版（2006年刊）p266に “1629年11月には木星の衛星を利用した経度測定法についてスペイン政府と交渉を再開している” と書かれています。この根拠が何にもとづくものかは書かれていませんが、もしこれか本当だとすると、ガリレオはかなり早い段階で、木星衛星の運動を経度測定に利用しようとしていたことになる。
［補足説明１］
別稿で説明した当時の時計の精度から解るように、一回ごとの食が起こる周期を秒単位まで正確に測定することは困難でした。さらに当時の望遠鏡は、色消しレンズが発明（1733年）されるよりも以前のため、光の分散で滲んだ像しかえられないものであったことに注意して下さい。そのため当時の観測では、一回ごとの食周期の変動を計測するのは不可能だった［文献2．参照］。
しかし長期間観測を続ければ、地球の１年の間に衛星が何回食を起こすかは正確に数えられます。またその回数が数えられればその1年の期間をその回数で割ることで正確な食周期Ｔを求めることができます。その正確な食周期Ｔを用いれば、ある一つの食が起こった後にｎ回目の食が起こる時刻はｎＴ時間後であると正確に予測できます。
ただし、この正確な食周期を求める事に付いては２．(３)［補足説明２］で説明する事柄に注意して下さい。
ところが、その予想時刻が時と共に段々ずれてくることが解ったのです。何年にもわたる観測から解ったのは、太陽－地球－木星が一直線に並んだ“衝”の時Ｅ1を起点として食の起こる時間を予測すると、地球－太陽－木星が一直線に並ぶ“合”の頃Ｅ3の“食”開始時間が予測時間から最も大きくずれました。衛星イオの場合、予測よりも22分（1320秒）も遅れて実際の食が起こったのです。（ただし、この22分の意味については、2．（3）［補足説明２］をご覧ください。）
さらに奇妙なのは地球の位置が木星が衝となる位置Ｅ5に近付くにつれて、その遅れは少なくなり、再び“衝”の位置に戻ると、“食”の予測時間の遅れは無くなったのです。
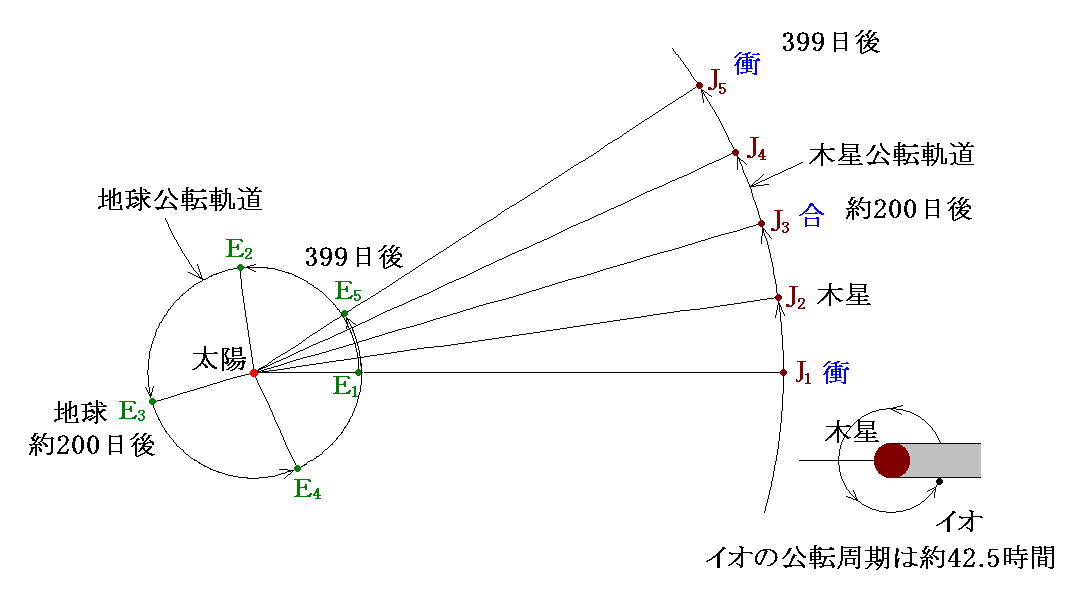
優れた観測者だったカッシーニもこの変動には当然気付いていました。当時、地球も木星も、またその衛星も楕円軌道を描き、その軌道上での速度はケプラーの第二法則（面積速度一定の法則）に従って変化することは解っていました。さらに互いの運動のために生じる互いの距離の変化に伴う引力の変化で生じる公転速度の変化も解っていました。そのため、このような変動が生じることは当然予想されることです。だからこそ運行表の精度を高めることが必要とされ、カッシーニは観測を続けていたのですから。
そういった状況の中で途中から、この観測に協力することになったのがレーマーです。彼は観測を継続しているときこの変動を説明する独創的な考えに思い至ります。
［補足説明２］
上記のケプラーの第一、第二法則の発見は1609年であり、第三法則の発見は1619年です。
また、上記の“距離の変化に伴う引力の変化で生じる公転速度の変化”についてですが、文献１．では“天体運動の原動力（premier
mobile）の回転にもむらがある”と記されています。これはニュートンによって惑星の軌道運動が万有引力によって説明される【『プリンキピア』の出版は1687年】よりも前であることを考えると、非常に興味深い記述です。
ただし、この記述がニュートンが発見した天体法則を意味しているのかどうかは解りません。実際、ケプラーはここに引用する様に考えていたようですから、当時の天文学者の間に行き渡っていたのは、おそらくこれに類する考えだったのでしょう。
レーマーは、木星の食が起こる周期が時と共に変動するのは光の速度が有限なためであると気づきました。楕円軌道上を速度を変えながら運行する天体間の関係ですから、食周期の変動には様々な原因が考えられます。様々考えられる中でレーマーの仮説は独創的なもので、この仮説に基づくと食が起こる予想時刻の変化が見事に説明できるのです。
木星の公転半径（7.78×108km）は地球の公転半径（1.50×108km）の約５倍です。またその公転周期は約12年（11.86155年）です。そのため木星との会合周期は約398.88日となります ［会合周期の意味と計算法は別稿「古典天文学」４．参照］。
そのため、地球と木星の関係は１．（３）の図の様になります。この図に於いて地球の位置がＥ1→Ｅ2→Ｅ3→Ｅ4→Ｅ5と変化するときの対応する木星の位置はＪ1→Ｊ2→Ｊ3→Ｊ4→Ｊ5と成ります。
ここで、簡単化のために木星の衛星の（地球から見た）公転周期が地球時間で20日だと仮定しましょう。また木星との会合周期も切りのいい400日とします。また地球軌道も木星軌道も完全な円軌道と仮定します。木星の回りを衛星が１回転する度に“食”が起こるのですが、その時の地球の位置は下図の様に移動していくことになります。木星の衝から衝までの会合周期400日の間に木星の食は20回起こることになります。
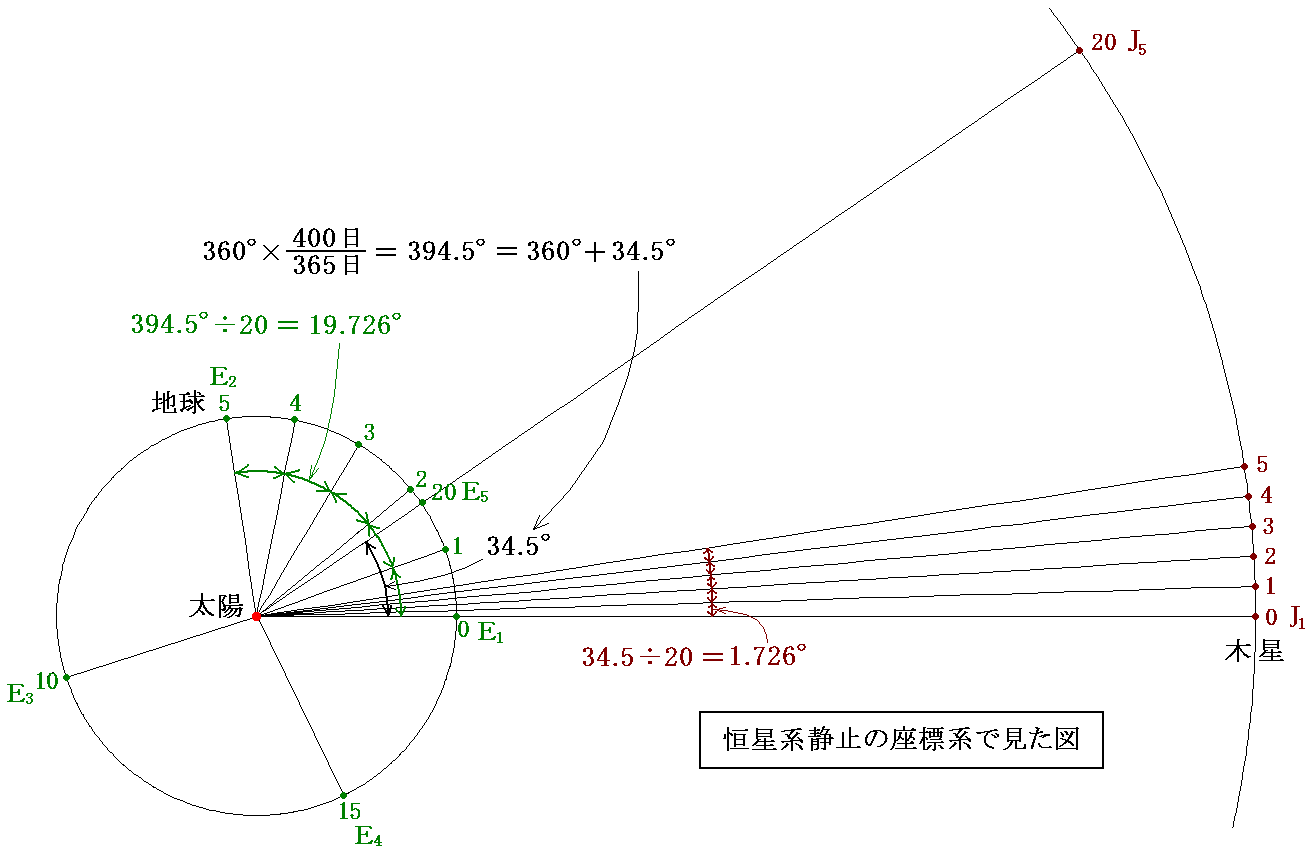
このとき、木星との会合周期400日の間に、地球は地球軌道上を360度×（400日／365日）＝394.5度回転することになります。つまり衛星の食周期20日の期間毎に、地球は地球軌道上を
394.5／20＝19.726°ずつ回転して行くことに成ります。
一方、木星は会合周期の400日の間に394.5－360＝34.5°回転しますので、食周期20日毎に34.5／20＝1.726°ずつ回転して行くことになります。
そのため木星が静止した座標系で考えると、衛星の食周期20日毎に地球は木星に対して相対的に
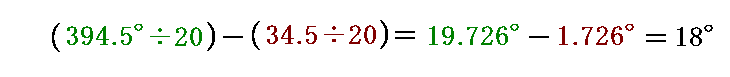
度ずつ進んだ位置に居ることになります。
そのため、木星静止の座標系で互いの位置関係を描くと下図の様になります。
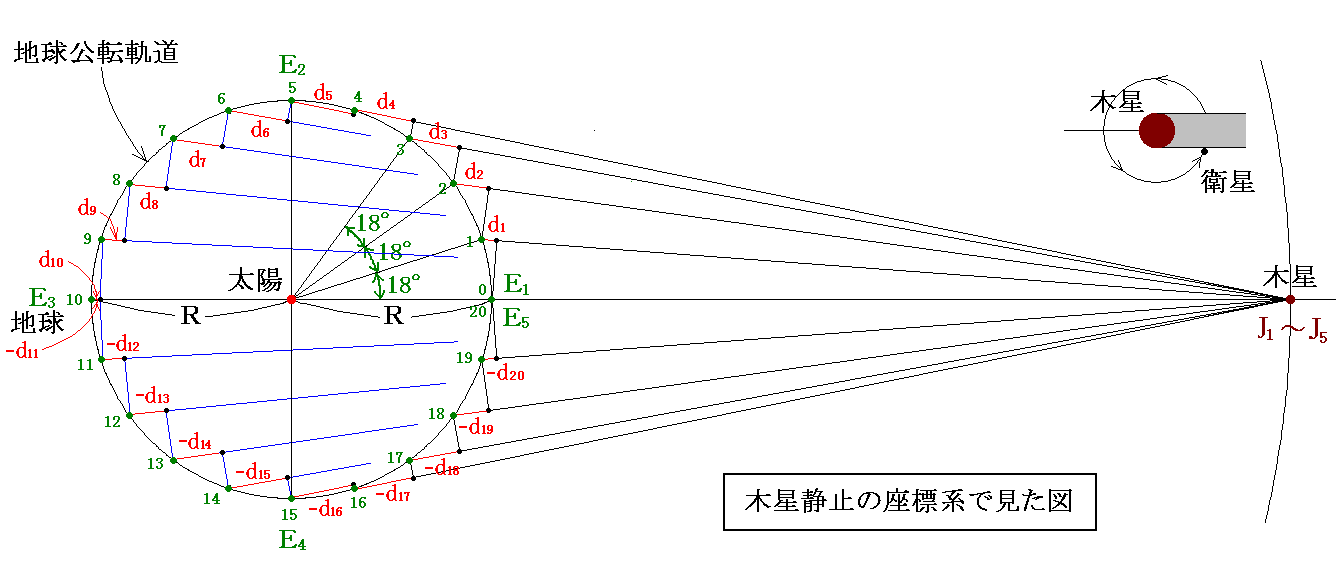
図中の0～20番の位置が、それぞれ衛星の食が生じた時の地球の木星に対する相対的な位置を示しています。そのとき、木星と地球の間を“食”が生じたという信号が光の速度で到達する時間は34分56秒（Ｅ1ｏｒＥ5の位置）から51分34秒（Ｅ3の位置）程度掛かりますが、その伝達時間は衛星の公転周期20日に比べると短いので、上記の0～20番の位置は、地球上の観測者が食が生じたという信号を受け取った時の位置と見なしても良いでしょう。
［補足説明１］
前節の図に於いて、例えばｉ番目の食が起こったことを観測する地球の位置は、ｉ－1番目の食を観測した地球の位置に比較して距離ｄｉ だけ木星より遠ざかっていることに注意して下さい。つまりｉ番目の衛星食が起こる時刻は、ｉ－1番目の木星食が起こった時間に衛星の公転周期Ｔを加えたものではなく、さらに距離ｄｉ だけ光が進むのに要する時間だけ経った時間となります。
以下同様に、地球がＥ1からＥ3に移動する間地球は木星から遠ざかり続けていますので、衛星の食が起こる時間は遅れ続けてゆきます。その遅れの合計値は結局光が距離 ｄ1＋ｄ2＋・・・＋ｄ10＝地球公転軌道の直径2Ｒ だけ進むのに要する時間となります。それはとりもなおさず、前述Ｅ3とＥ1に於ける到達時間の差である51分34秒－34分56秒＝16分38秒です。
地球がＥ3からＥ4に向かって移動するときには、地球は次第に木星に近付いて行きますから、上記の事情の逆のことが起こります。衛星食の起こる時間の遅れは次第に減少してゆきます。そうして地球がＥ5に到達したときに起こる食の時刻は、衛星の公転周期から予想計算される時刻に正確に一致します。
これが、レーマーの気付いたことです。
ここは解りにくいところですからグラフの上でもう一度説明しましょう。
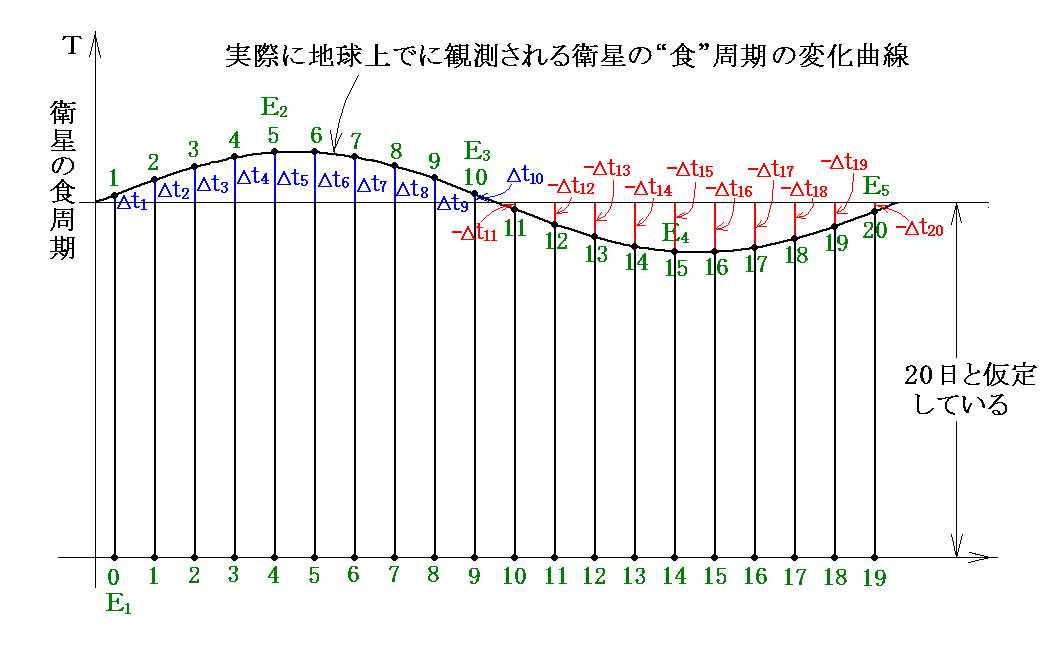
上図の中の青色部分の和は、光速度をｃ、地球の公転半径をＲとすると
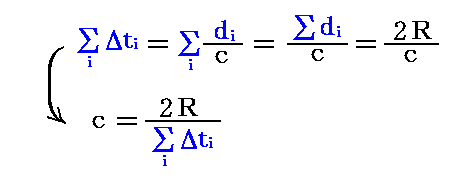
となる。
一方、赤色部部の和は遅れが減少してくる部分ですが、同様に
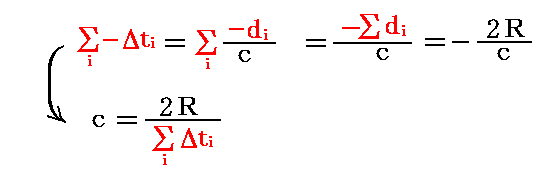
となる。
いずれにしても、地球の公転軌道の直径 2Ｒ を時間的遅れの最大値 ΣΔｔi で割れば光の速度が求まることになる。
実際にレーマーが光速度を求めた衛星イオの観測データについて説明します。イオはガリレオが発見した４つの衛星（イオ、ユーロパ、ガニメデ、カリスト）の中で最も木星に近い軌道を回るものです。これは離心率0.0041のほぼ真円の軌道を描くことが今日解っていますので、ここで議論している目的には特に適したものでした。その（地球から見た）平均公転周期は1.7698日＝42時間28.6分程度です。このことに付いては［補足説明１］を参照して下さい。いずれにしてもこれは１．（３）で注意したように、当時においても正確に求まったと思われます。
そのため地球がＥ1→Ｅ2→Ｅ3→Ｅ4→Ｅ5と移動する期間では399日÷1.7698日≒約225回の食が起こります。その半分のＥ1→Ｅ2→Ｅ3まで移動する期間では（399日／2）÷1.7698日＝112.7回≒約113回の食現象が起こることになります。そのため前節のグラフを衛星イオの場合について描いてみると
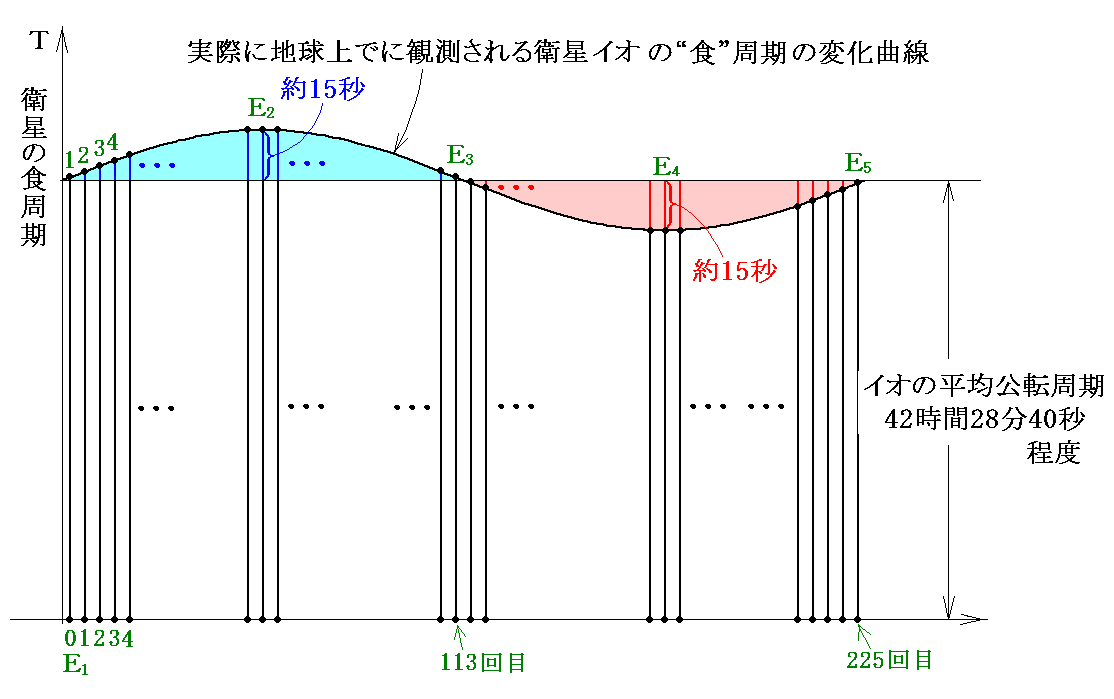
のようになります。
［補足説明１］
恒星空間に対するイオの公転周期は1.7691日＝42時間27.6分≒152856秒程度ということですから、地球から見た （正確には太陽から見た）
イオの公転周期はそれよりも約65秒程度長くなります。
それは、地球から見た （正確には太陽から見た） 木星はイオが225回公転する間に地球から見て （正確には太陽から見て） 約34.5度移動しますから、イオは一公転毎に34.5°÷225＝0.153°余分に回転しないと地球から見た
（正確には太陽から見た） 食は起こらないからです。もちろん地球も公転して位置を変えますのでその角度は季節により変動します （この変動幅は２．（３）［補足説明３］で説明する様に結構おおきなあたいです） が平均的にはその程度の増分があると見なしても良いでしょう。
そのため地球から見た （正確には太陽から見た） イオの平均公転周期は恒星空間に対する公転周期より約152856秒×（0.153／360）≒65秒程度長くなるはずです。
このとき、地球がＥ2の位置に居るときのイオの見かけの公転周期は平均公転周期に対して約15秒程度長くなります。なぜなら、地球の公転速度は29.8km／sですから、Ｅ2の位置に於ける地球は、イオの公転周期の42.5時間の間に、木星から約29.8×103m／s×42.5×3600s＝45.6×108m程度遠ざかります。そのため、その距離を光が伝播するのに約45.6×108m÷3.0×108m／s＝15sだけ余分に必要としますので、見かけの公転周期もそれだけ長くなるからです。また、地球がＥ4の位置に居るときには約15秒程度短くなります。
しかし、レーマーがこの変分を実際に観測できていたとは思われません。なぜなら、文献１．にはこのように記されており、文献の何処にもこの変分についての記述が無いからです。おそらく当時の時計の計時精度と当時の望遠鏡の観測精度では難しかったのでしょう。
１周期毎の時間の変化を観測することはできなかったが、２．（２）で述べたように、Ｅ1→Ｅ2→Ｅ3までに積算する遅れの総量 ΣΔｔi は観測できます。
もちろん、観測の途中には雨の日や曇りの日もあるだろうし、また木星が太陽の方向にあれば観測できません。しかし食の周期はほぼ一定間隔で起こりますから、途中観測できない日があっても、今観測している“食”が起点の日から数えて何回目の“食”であるのかは正確に解ります。だからその回数番目の食が起こる予測時刻は計算できます。だから予測時刻と実際に食が起こった時刻との差であるΣΔｔi は観測できたのです。
レーマーは文献１．の中で“衝”Ｅ1を起点として113回目Ｅ3に於けるトータルの時間的な遅れはΣΔｔi＝22分であると報告しています。実は、文献１．の中のこの部分の記述は曖昧で“22の割合で起こる”と記されているだけです。そのため、この22が時間の22分を意味するのかどうかはハッキリしません。
しかし、続きの文章中で、地球が木星に最接近（つまり“衝”の位置）した8月を起点として、イオの平均公転周期から三ヶ月後の11月9日の食の起こる時間を予想してみたところ、“イオはその予想時間よりも10分遅れて食を起こした”と記されています。この三ヶ月の積算の遅れから上記の113回目までの積算の遅れを計算すると約22分となります。そのため、文中の“22の割合で起こる”の22は22分のことであろうと科学史家は解釈しています。
［補足説明２］
更に補足しますと、この報告書には“22の割合で起こる”という表現で書かれているのは、木星が合の地点に達した時の225回目の食開始時間の実際の観測値から判明した22分の遅れでは無く、合の位置での遅れは22の割合になるだろうという計算予測値を示すものだからです。
実際のところ、地球から見て木星が太陽の方向にある“合”の位置で生じるイオの食現象など観測できないのですから。
レーマーが、この“22と言う割合になる”を、実際のところどうやって求めたのかを文献2．の説明で解説しますと
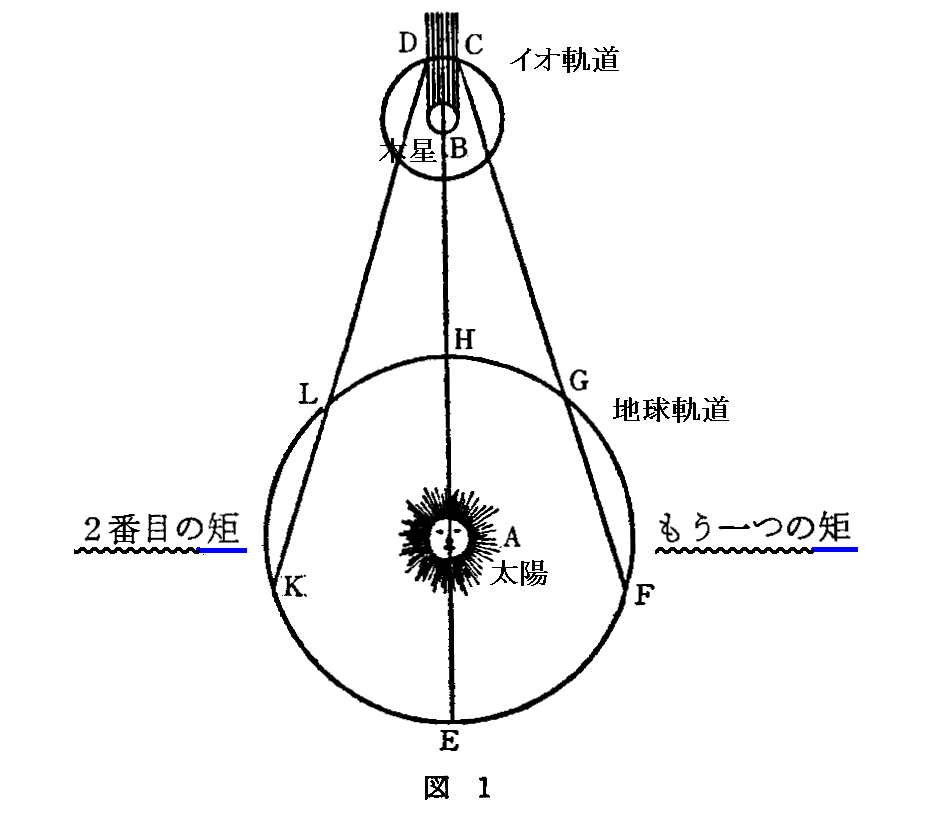
図1の2番目の矩の付近（先ほどの図のＥ２付付近）の40回の公転時間と、もう一つの矩の付近（先ほどの図のＥ4付付近）の40回の公転時間を観測で得て、その合計80回分の公転時間を80で割って、イオの食周期（公転周期）を求めたようです。これが【真の食周期（公転周期）】です。このことについては文献2．［補足説明３］を参照されたし。
そうすれば、2番目の矩（先ほどの図のＥ２付付近）における1公転周期の増大分は、【2番目の矩の部分の40回の公転時間÷40】－【真の食周期（公転周期）】により求める事ができます。おそらくそれは＋15秒より少し短めの＋14秒程度になったかも知れません。なぜなら40回の公転時間は先ほどの図のＥ２付付近の変動の平均値ですから。
もう一つの矩（先ほどの図のＥ4付付近）における1公転周期の減少分も同様に、【もう一つの矩の部分の40回の公転時間÷40】－【真の食周期（公転周期）】により求める事ができます。おそらくそれは－15秒より少し短めの－14秒程度になったかも知れません。なぜなら40回の公転時間は先ほどの図のＥ4付付近の変動の平均値ですから。
そして、その15秒（14秒程度かも知れない）が、矩の位置におけるイオの1公転周期時間にすすむ地球の移動距離を光が通過するのに要する時間となります（その事は文献2．のこちらに記されています）。
そのため、地球の公転軌道の直径（上図１のＨＥ間の距離）を光が通過する時間に換算すると、２２の割合になる。
ここで、レーマーの観測値 ΣΔｔi＝22分＝22×60＝1320秒 を利用し、地球－太陽間距離として1673年にカッシーニが求めていた値 1億3800万km＝1.38×1011ｍ を用いると、光速度ｃは
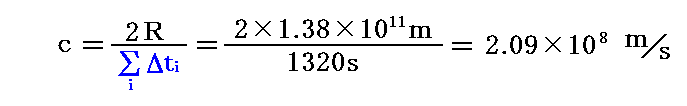
となります。
ちなみに、今日の正確な観測によると ΣΔｔi＝16分38秒＝16×60＋38＝998秒 であり、地球－太陽間距離は 1億5千万km＝1.50×1011ｍ ですから、光速度ｃは
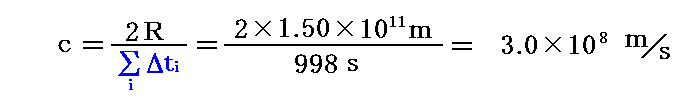
となります。
これと比較するとレーマーの得た値はかなり誤差があることになります。しかし、当時の観測技術を考慮するとまずまずの値ではないでしょうか。
［補足説明３］ （2023年4月14日追記）
イオの食周期（公転周期）の測定についてですが、食周期の変動偏差の現在の観測値を113回分集計した 16分38秒（＝998秒） とレーマーの予測計算値
22分（＝1320秒） との差 1320－998＝322秒 を 113回 で割った値は 322秒÷113回≒約3秒／回 程度になります。
つまり前記［補足説明２］で説明した、レーマーが得た【真の食周期（公転周期）】は、現在の観測値よりも約３秒程度短かったと言うことです。
食周期の実際の観測ですが、当時利用できた望遠鏡は色消しレンズが発明される以前の望遠鏡ですので、望遠鏡視野中の木星も、その衛星も滲んだぼんやりとした像でしか観測できなかったと思われます。木星衛星の食が生じる時刻を正確に測定するのはかなり難しく数十～数百秒程度の観測値のばらつきはあったでしょう。また、当時は振り子時計が発明されて時計が実用化されたばかりでして、時計精度誤差は1日当たり数秒程度はあった時代です。
しかし、先の2.（3）［補足説明２］で説明した様に、連続する40回の公転時間を観測して、それを40で割って平均化すれば、その測定精度の誤差は数秒程度以下にできたはずです。
そのとき、上記の3秒という差が、避けることができない測定精度誤差によるものなのか？、それとも、レーマーがまだ気付かない系統的な誤差を生じる原因があるのか？ということですが、以下その事に付いて考察してみます。
先の１．（３）［補足説明１］に於いて、衛星イオの正確な食周期（公転周期）を求めるには、地球の１年の間に衛星が起こした食回数で以て、その１年の期間を割れば良いと説明しました。
しかし、木星が太陽方向にあるとき、相当な長期間にわたって食現象を観測できませんので、絶対的に信頼できる正確な１年間の食回数（公転回数）を観測するのはある意味で難しいかも知れません。特に、１．（３）で述べた様に、カッシーニは当時イオの食周期（公転周期）が１年の間で変化しているらしいという事実をすでに観測でつかんでいたのですから。
そのとき、レーマーが自らの光速度測定理論を展開するために必要としたイオの【真の食周期（公転周期）】の測定に、木星がちょうど衝の位置付近にいるときの連続した何回かのイオ食周期（公転周期）を観測して平均値を求める方法をなぜ用いなかったのでしょうか？
木星が衝の位置にいるときには、１食周期の時間変化の間の地球と木星の間の距離変化はありませんので、測定した食周期（公転周期）には光の速度が有限である事の効果は介在せず正確な食周期が求められるように思えます。また、木星が衝の位置にあるときが、連続する食を観測する機会（つまり木星が夜間に天上にある割合）は最も多いのですから。
しかし、レーマーはそうしないで2．（3）［補足説明２］で説明する方法を採っています。
上記の疑問に少し関係するのですが、“食周期”と言った場合には下図のＡ地点到達までの１回転の時間です。“公転周期”と言った場合もＡの周期とＢの周期の内のＡの意味です。
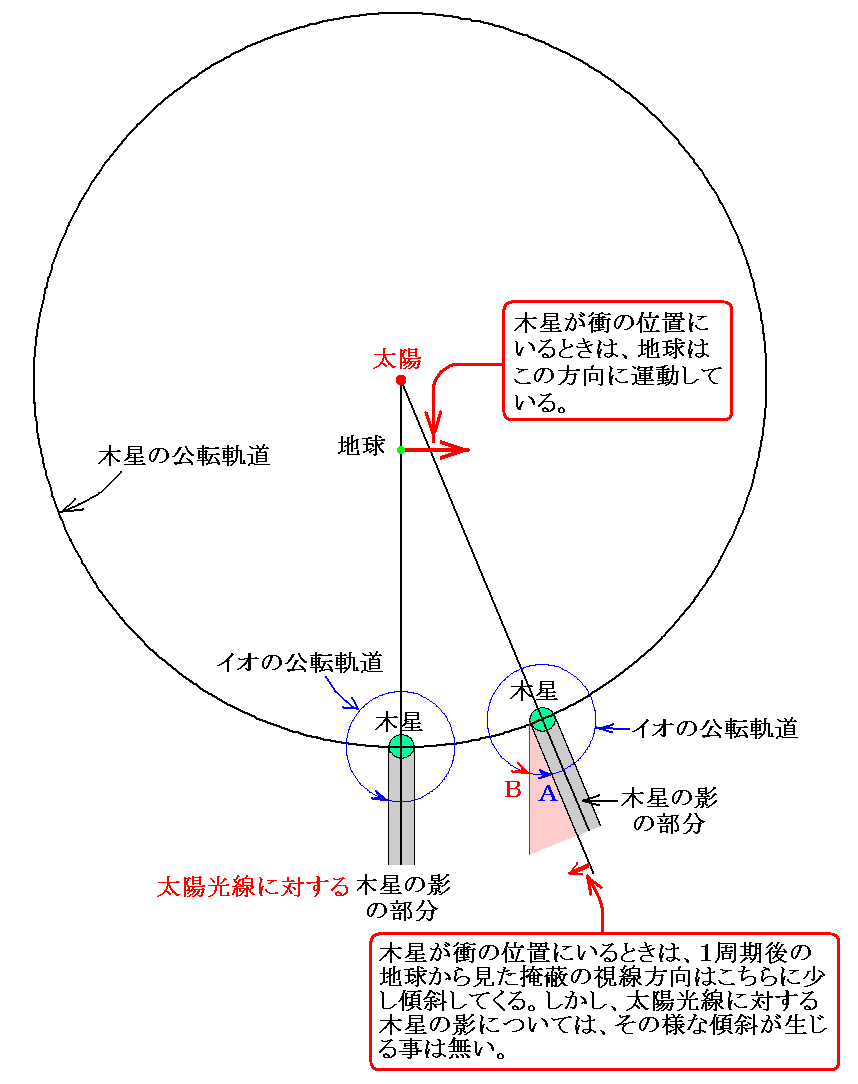
実際、レーマーはイオの食周期を 【イオが太陽光線に対する木星の影の中に入った時あるいは出た時を基準にして測定】 したのです。このことに付いては文献2．［補足説明２］を参照して下さい。
レーマーは文献2．の図１の説明文のなかで、２番目の矩の位置ではＤ点における出で食周期を測定し、もう一つの矩の位置ではＣ点における没で食周期を測定したと言っています。何ぜ２番目の矩の位置では出を用い、もう一つの矩の位置では没を用いたのかといいますと、２番目の矩の位置では没は観測できず、もう一つの矩の位置では出が観測できないからです。
ところで、 【木星本体によるイオの掩蔽（えんぺい）を利用する測定】でも、２番目の矩の位置で没が利用でき、もう一つの矩の位置では出が利用できます。そのとき掩蔽を利用する場合でも、２番目の矩の位置での出と、もう一つの矩の位置での没を観測するのはやはり難しくなります。それは太陽光線が作る木星の影の部分になるからです。
どちらを利用しても食周期は観測できそうなのに、何故レーマーは 【木星本体による掩蔽】 ではなく、 【太陽光線に対する木星の影への出入り】 で食周期を観測したのでしょうか？それは、 【木星による掩蔽を利用して食周期を測定】 すると、問題が生じるからです。
その理由を木星が衝の付近にいるときを例に取って説明します。木星が衝の位置にいるとき、地球は上図の赤矢印で記した方向に動いています。そのため木星の影の部分ではなく、地球から見た木星の掩蔽の視線方向を利用すると、１公転ごとに通常よりも図中に記した方向に移動します。そのことによって衝の付近で【掩蔽を利用して】観測した食周期は通常の食周期よりも短めになります。
実際、衝付近でのこの効果による短縮は177秒程度となり、かなり大きなものです。だから衝付近での【掩蔽を利用した】食周期の観測には、この効果を考慮した補正計算をしなければなりません。しかし、１．（１）［補足説明２］で説明しましたように、当時木星の公転半径もイオの公転半径も正確な値はまだ得られていなかったので、その補正計算にはかなりの誤差が介在するでしょう。
このとき、【太陽光線に対する木星の影への出入り】 で食周期を観測した場合には、地球の運動による観測誤差は発生しないことに注意して下さい。
また、衝付近での食周期の観察では 【木星本体による掩蔽】 と 【太陽光線に対する木星の影への出入り】 が、微妙な差で重なってきます。その重なりの中に存在する微妙な差は観測精度に悪さをするでしょう。その意味でも、衝付近での食周期の観則は適当ではありません。
そう考えると文献2．で紹介されている太陽光線に対する木星の影の出入りを利用し、しかも二つの矩における４０回転の公転時間を測定する方法 （2．（3）［補足説明２］で解説したもの） は地球の移動による誤差を生じない極めて優れた方法でした。レーマーはその事を十分把握していたのでしょう。
それで、最初の食周期測定値の3秒の違いの原因にもどるのですが、上矩（じょうく）における40回転分の公転時間と下矩（かく）の40回転分の公転時間を足して80で割って求めた【真の食周期（公転周期）】にも3秒程度の観測誤差はあったのだろうと言うことです。結局、当時の望遠鏡と時計の精度から避けられない観測誤差だったのでしょう。
以下で引用・紹介します 東北大・理 惑星プラズマ・大気研究センター (https://pparc.gp.tohoku.ac.jp/post_13/)のイオの食現象が示す様子の説明から解るように、食が生じる時刻を決定するのに、レーマー時代では数十秒～数百秒程度の誤差はさけられなかった。だから80回転分の公転時間を80で割っても一公転当たりに数秒の誤差は生じた。
木星には、ガリレオ衛星と呼ばれる4つの大きな衛星があり、木星の周りを2～17日の公転周期で回っています。この様子は5cm程度の小さな望遠鏡を使っても観察することができます。おそらくレーマーの観測条件もその程度だったでしょう。
これらの衛星は、木星の背後に近付き、太陽がつくる木星の影に入ってしまうと、地球から見える位置にあるにも関わらず、数10秒の内にふっと消えたように見えることがあります。これをガリレオ衛星の木星食と呼びます。
下の画像は、ハワイの60cm望遠鏡に同架した口径5cmの望遠鏡で、衛星イオ(Io)の木星食の様子を観察したものです。画像下の図は、同時刻の木星の影と衛星の位置を示しています。［拡大図］。
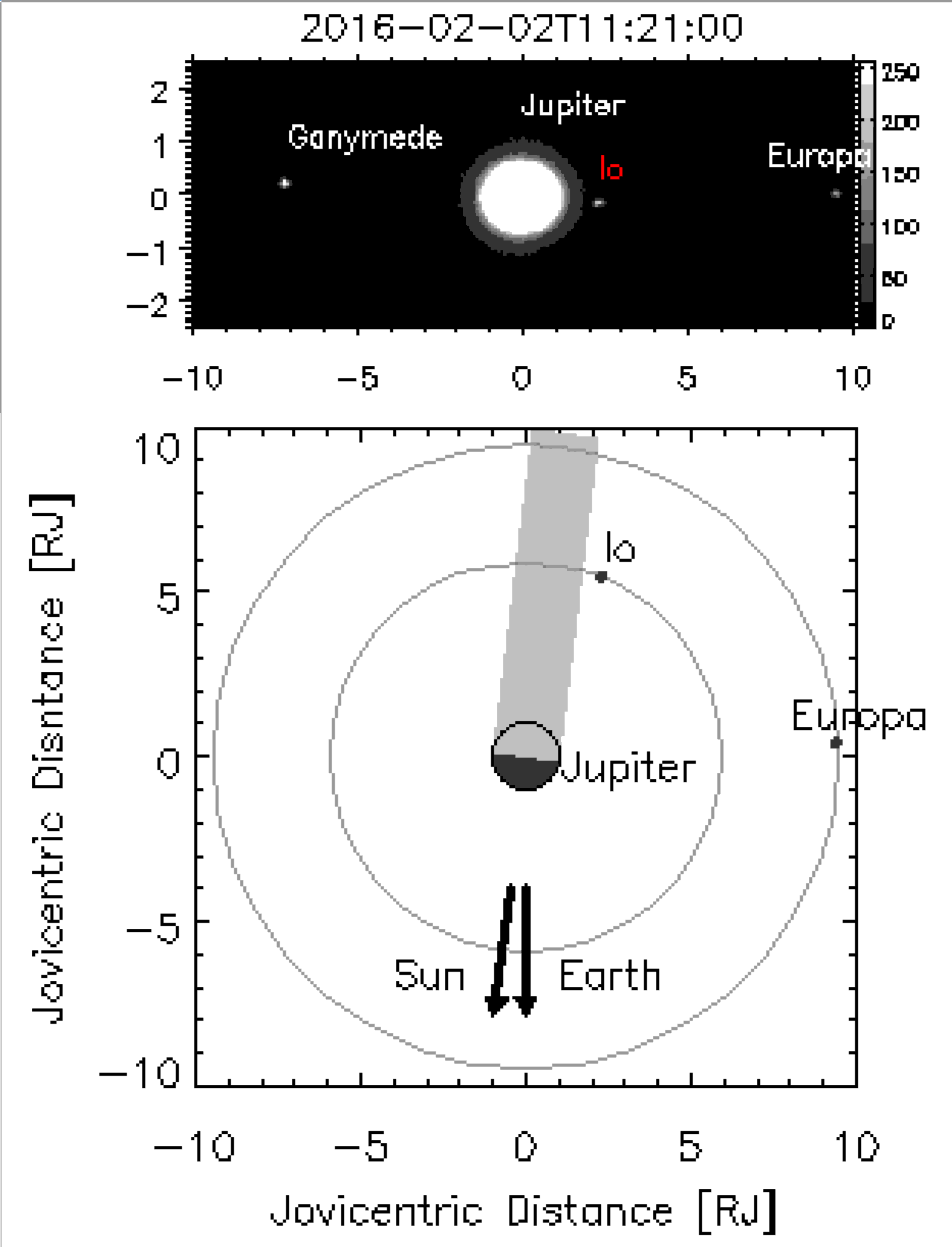
引用先のＵＲＬでは 12:15 UT あたりで、イオが突然見えなくなっている様子がアニメーション表示されていますので是非参照されて下さい。
以上の考察から解るように、レーマーはイオの食周期（公転周期）を誤差数秒程度で求めていたのですが、当時の天文学者の観測技術に驚嘆させられます。
こちらのページに、当時のカッシーニやレーマーの天文観測の様子の説明が有りますのでどうぞご覧下さい。図中に示されている観測時刻測定用の時計は、どうやら振り子時計の様ですね。
いずれにしても、この数秒の誤差が、レーマーの求めた光速度が現在の光速度から数十パーセントずれた原因です。その事に付いて興味深い解説を下記に引用・紹介しておきます［拡大版はこちら］。
いずれにしても、史上初めて光が有限な速度で伝わることを明らかにし、その具体的な値を得たことは画期的な業績です。
［2023年4月22日追記］
私は、長い間文献2．のこの部分に書かれている“22の割合で起こる”の根拠を、この部分に書かれている8月の衝から11月9日までのイオの食の出の遅れの10分を計算した“真の食周期”と同じものを用いて、113回目の食の遅れが22分になる事を計算したのだろうと思っていました。そのとき、レーマーがその“真の食周期”を求めた方法が文献2．の報告書の中には書かれていないので、過去8年間にわたる観測で得られた1年間の食周期の合算値を1年の食回数225回で割ることで、“真の食周期”を求めたものと思っていました。これは1．（3）［補足説明1］で説明したものです。
しかし、この部分の説明文の曖昧さと、“22の割合で起こる”を記した文との前後の位置関係から、この解釈については当初から疑問がありました。さらに、“22の割合で起こる”を説明した文の直前文の内容の意味不明さが、その疑問に拍車をかけていました。さらにもう一つ、文献2．の図1について疑問がありました。文献2．では図1のＬKとFGの距離について、イオの1食周期の間に地球が移動する距離として説明していますが、もしそうならばＬKとFGの長さがあまりにも不自然です。
ところが最近、ある読者の方から 『レーマーの言う22分と、今日の正確な値16分38秒との差が生じた原因について何か考えられることはありますか？』
という趣旨のご質問を頂いたのです。
そのご質問を受けて、レーマーの観測値の誤差の原因を色々考えて見ました。
そのとき、改めて文献2．を詳細に読み直してみたのですが、この部分に書かれている “何回かまとめて考えれば、非常に顕著になってくる” と “Ｆの側から観測された40回の公転時間は，･･･” と言う記述に啓発・覚醒されました。
そして、文中に記述されているすべての数値について検証してみたのですが、特にこの部分の数値が支離滅裂であることに気付きました。実際この説明文中の数値の不可解さについてはこちらで説明しています。
それらの気付から、最終的に 文献2．［補足説明3］ と、本稿の 2．（3）［補足説明２］ と 2．（3）［補足説明３］ に記した結論に到達しました。これらは、憶測を含んでいますが、おそらく真実ではないでしょうか？ 読者のご意見を伺いたいところです。
このページを作るに当たって参考にした文献を挙げておきます。
