�@���̃y�[�W�������������������̃o�[�W�����������p�������B�u���E�U�[�ł͌��ɂ����̂ł�������͑N���ł��B
�d����̉��́i�}�N�X�E�F���̉��́j
�@���Z�����u�d���C�v�̏��ŁA�d�C�͐��⎥�͐��́A���������S���łł����ǂ̗l�Ɏ��k�E�c�����鐫���������Ă���ƏK���i�܂�d����̒��ɉ��͂����݂���j�B���̐�����p����ƁA�d�ׂ�d���������������蔽�������肷�邱�Ƃ��d�����ʂ��ē������Ƃ��|�������ł���B������MKSA�L�����P�ʌn�ŋL�q�B�P�ʌn�ɕt���Ă��u�d���C�w�̒P�ʌn��������R�v���Q�ƁB
�P�D�t�@���f�[�̊ώ@
�@���Z�����̓d�C�̂Ƃ���ŁA�d�C�͐��⎥�͐���������������@������K���B�t�@���f�[�͂����Ɨގ��̕��@��p���āA���ɑ����̗�ɂ��āA��̂ȗ͐��̗l�q���ώ@�����B
�@�ނ́A�����̎��Ⴉ��A�͐��͏�ɐ��̕����ɏk�����Ƃ��͊ǂ͖c���ő����Ȃ낤�Ƃ��鐫���������ƂɋC�Â����i1837�N�j�B���̐����𗘗p����ƁA�Ⴆ�Q�̔��Γd�ׂ�тт����̊Ԃɓ������͂��|�������ł���B
�@�܂����̊Ԃ̋�Ԃɉ��͂����݂���ƍl����B���̉��͂͊e�_�ɂ�����d�C�͐������̈��́i�܂蒣�́j�ƁA�d�C�͐��̑��ݔ����́i�܂艡�����̈��́j�ŕ\�����Ƃ���B�����Ă��̋��x�͓d�C�͐��̖��x�ɊW����ƍl����B���̌��ʁA�͐�������̋��ŏI��鏊�̖ʂɂɂ͒��͂��������邱�ƂɂȂ�B
�@������̋��̋������傫���\������Ă���ꍇ�ɂ͋��̎���̗͐��́A���ˏ�ɐL�тċ��̒��S�ɑ��đΏ̓I�ɂȂ�B���̂��ߋ��ɓ����͕͂��ˏ�̑Ώ̓I�ɂȂ�A���ɓ������͂͗�ɂȂ�B
�@��̋����߂Â��ƁA���Z�����ŏK���悤�ɋ��̌����������������̗͐��̖��x����薧�W���A���Α��͂��܂�ɂȂ��Ă���B���̂��ߓ�̋��������������������̒��͂��A���̕����̒��͂�������A��̋��͈��������ƌ����̂ł���B
�@����͓d�ׂ̊Ԃɓ����͂��A�d�Ԃʼn��u��p�I�ɓ����̂łȂ��āA�d�ׂ����̎���̓d���ω������A���̕ω������d���ʂ��ċߐڍ�p�I�ɓ����Ƃ�������I�ȍl�����ł���B���̋ߐڍ�p�I�ȍl�����́A���̌�̓d���C�w�̔��W�������悤�ɁA�L���Ȗ���������炵���B
�@�d������ɑ��݂��鉞�͂̊��S�Ȍ`�́A��Ƀ}�N�X�E�F���ɂ��^����ꂽ�̂��}�N�X�E�F���̉����ƌĂ��B
�@
�Q�D�Ód����̉���
�@�d��̒��Ɉ��͂���ђ��͂����݂��邱�Ƃ͈ȉ��̂悤�ɍl����Η����ł���B�����ł͊ȒP�̂��߂��Ód���Ɍ����āA���͂Ɠd����W�Â���B
�i�P�j���̕\�ʂ̒P�ʖʐςɓ�����
�@���Z�����ŏK���悤�ɁA���̂ɏo���肷��d�C�͐��͓��̕\�ʂɐ����ł���A���܂��K�E�X�̒藝���P�ʖʐς�����̓d�C�͐��̖{���͕\�ʓd�ׂ̖ʖ��x�ɔ�Ⴗ��B�܂��\�ʂ̓d�ꋭ�x�͕\�ʓd�ׂ̖ʖ��x�ɔ�Ⴗ���B�i�ڂ����͕ʍe�u���̂̎���̓d�E�Ɠd���v�Q�Ɓj
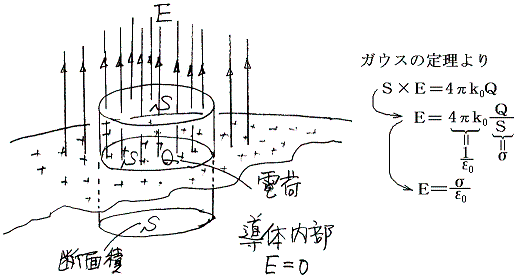
���̎��A���̕\�ʂɑ��݂���d�ׂɂ́A���̂̒P�ʖʐϓ�����
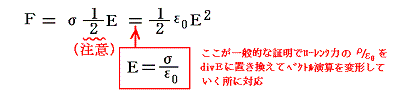
�̗͂������B�����ŁA�Ђ͂��̏ꏊ�̒P�ʖʐϓ�����̓d�ׂ̖ʖ��x�A�d�͗͂����߂��ʒu�ł̓��̕\�ʂ̓d��̋����ł���B���̂̓����͓��R�d��0�ł���B
�@���̂Ƃ����̂̕\�ʓd�ׂ���͂́A���̕\�ʂ̑��̕����ɕ��z����d�ׂ���̃N�[�����͂̍��͂ł���B���̂�����ŕ\�ʂɓd�ׂ���l�ɕ��z���Ă���ꍇ�́A�ʍe�u���w�����v��u���L���̖͂@���ւ̕⑫�v�ŏq�ׂ��悤�ɁA���k��ɕ��z���Ă���d�ׂ̊O���ɑ��݂���d�ׂɓ����͂͋��k��̑S�d�ׂ����S�ɑ��݂����ƍl�����Ƃ��Ɠ����͂������A�܂����k��d�ׂ̓����ɑ��݂���d�ׂɓ����͂͗�ɐ���B
�@���̏ꍇ�́A���̂ǂ���ɂȂ�̂ł��낤���H
�@�����͂��̕��ϒl�ł���B�܂��\�ʓd�ׂɓ����͂͋��k�̊O���̓d��Ɠ����̓d��i��0�j�̕��ρi�dout�{�din�j�^2�̓d��̒��ɑ��݂���ƍl�����ꍇ�Ɠ����ɂȂ��B����𗝉�������@�͕\�ʓd�ׂ�����0�̑w�ƍl����̂ł͂Ȃ��A����������������������w�̒��ɑ��݂��Ă���̐ϓd�ז��x�ς��l���鎖�ł���B���̌��ʂƂ��ĕ\�ʂ̒P�ʖʐϓ�����Ɋ܂܂��d�חʂ��Ђɐ����Ă���ƍl����B�܂胢�����ǂ̂悤�Ȓl���Ƃ��Ă��Ё��σ����ɐ���悤���������B
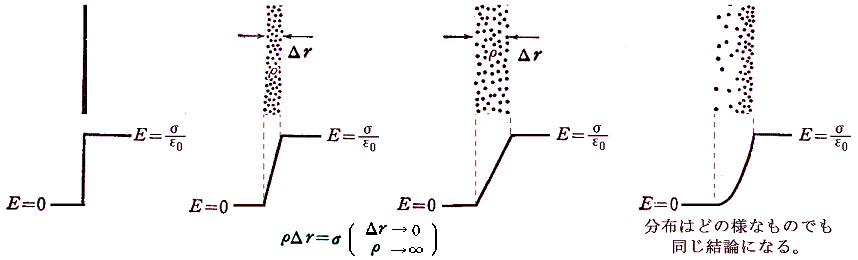
�@���̏ꍇ�ɂ͓d��͑w�̓������d��0�ŁA�w�̌��݂̕����ɒ����I�ɑ������ĊO�����d���Ё^��0�ƂȂ�B���̔�̑̐ϗv�f�Ɋ܂܂��d�ׂɓ����͂̕��ϒl�͖��炩�Ɂi�dout�{�din�j�^2�̓d��̒��œ����ƍl�����͂Ɉ�v����B���̂�����L�̎���1�^2�̌W�������ꂽ�̂ł���B
�@���̋����̓d�ׂ����̒��͂ɂ��d���ԓ��ɔ�яo�čs���Ȃ��̂́A�d�ׂ̋����ɂƂǂ߂悤�Ƃ���ʂ̋����͂������Ă��邩��ł���B
�@
�i�Q�j�d����̉���
�P�D�d�C�͐��ɐ����Ȗʂɓ�����
�@�d����ɉ��z�I�ɍl�����d�C�͐��ɐ����Ȗʂɓ����͂��Q�D�i�P�j�̓��̕\�ʂł̗͂�d��̒��ɍL���čl����悢�B�܂�d��d�̏ꏊ�œd��x�N�g���ɐ����ȒP�ʖʐςɓ����͖͂ʂɑ��钣�͂ƂȂ�A���̑傫����
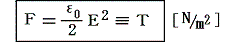
�ł���ƍl����B
�@
�Q�D�d�C�͐��ɕ��s�Ȗʂɓ�����
�@�d����̓d�C�͐��ɕ��s�Ȗʂɓ����͂́A�P�D�̌��_�Ɠd�ꂪ���݂����ԑ̐ϗv�f�����͂̒ލ���Ԃɂ���Ƃ����������猈�肷��悢�B���̂Ƃ���ʓI�ȋȗ��̓d�C�͐��̏�Ő�������̂́A���Z���x���ł͓���̂ŁA�ȒP�ȏ̏ꍇ�𗘗p���ē����B����͕\�ʂɈ�l�ȓd�ז��x�Ђőѓd�������̂̎���̓d��ł���B�ʍe�u�ѓd�������̋��̎���̓d��̎��G�l���M�[�v��u���̂̂܂��̓d�E�Ɠd���v�Ő��������悤�ɁA���̎���̓d��͋��̒��S������ˏ�ɊO�����ŁA���̒��S���狗�����̈ʒu��

�ƂȂ�B
�@���̎����S���甼�a���Ƃ��{�����̓�̓��d�ʖʂƓd�C�͊ǂŐ���ꂽ�����k����̑̐ϗv�f���l����B
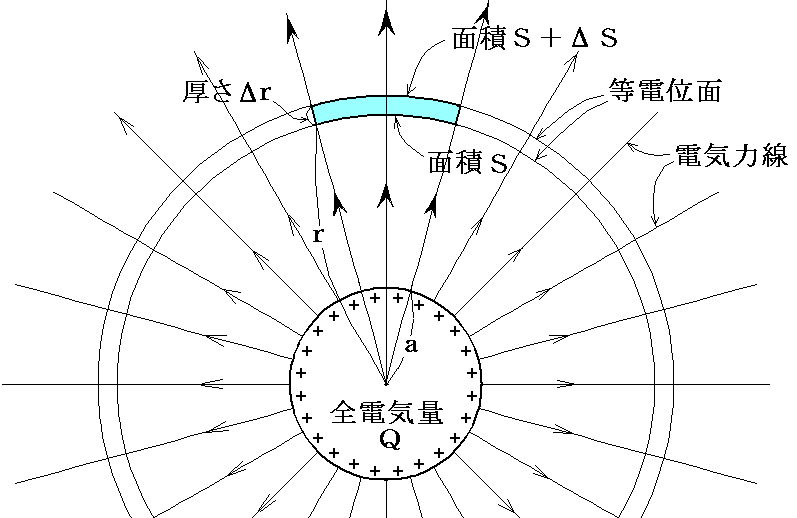
�@���̊k���̐ϗv�f�̏㉺�̖ʂɓ����͂ƁA�d�C�͊ǂŐ���ꂽ���ʂɓ����͂̒ލ����l����B����͂��傤�ǃV���{���ʂ̉t�̖��ɂ�����͂̒ލ����l����̂Ɠ����ł���B���̂Ƃ��A�A���̂̓����̖ʂɓ����͂́A�ǂ���̑̐ϗv�f�ɒ��ڂ��邩�ŕ������t�]���鎖�ɒ��ӁB
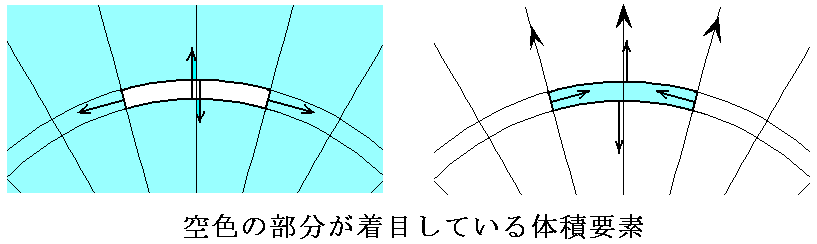
�@���}�̗͂ƉE�}�̗͖͂ʂ̔��Α��ɍ�p����͂ō�p����p�̖@�����疾�炩�Ȃ悤�ɑ傫���͓����������͋t�ł���B�����Œ��ڂ��Ă���̂͌��ł͂Ȃ��Ċk����̑̐ϗv�f�������E�}�̗͂̒ލ����l����悢�B
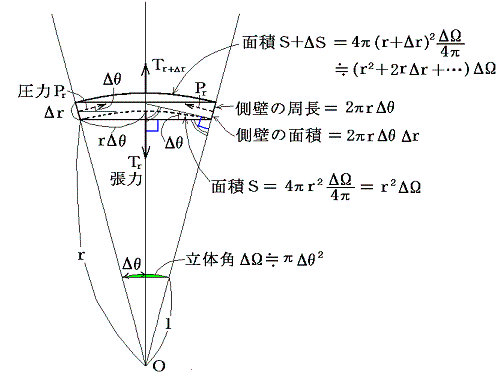
�@�܂��}�̊k���̏㉺�̖ʂɓ������͂̍����A���ǁi�d�C�͊ǖʁj�ɓ������͂̓��a���������̘a�ƒނ荇���Ă���ƍl����B�㉺�̊k���ʂɓ����P�ʖʐϓ�����̒��͂sr�ɂ����Q�D�i�Q�j�P�D�̌��_��p�����
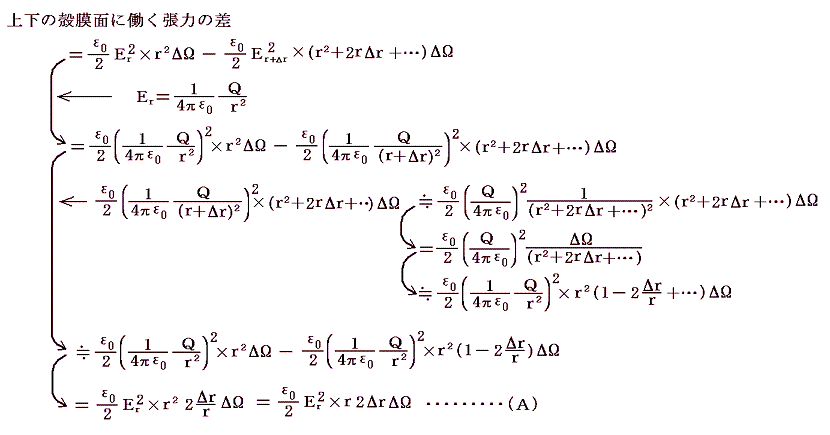
�ƂȂ�A���̕����͋��̒��S�n�̕����������Ă���B����P�ʖʐϓ�����̈��͂��o�Ƃ����
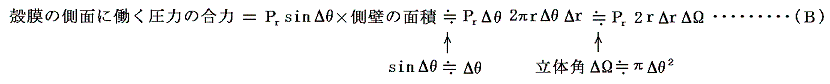
�ƂȂ�A���̕����͋��̒��S����O�����ł���B
�@�̐ϗv�f�ɑ��鉞�͂̂荇���̏�������(�`)��(�a)�łȂ���Ȃ�Ȃ��̂ŁA�d�C�͊ǂ̑��ʂɓ������͂or(�d�C�͐��ɐ����ȕ����j�͒P�ʖʐϓ�����
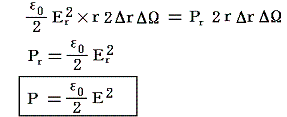
�łȂ���Ȃ�Ȃ��B����͓d�C�͐��ɐ����Ȗʂ̒P�ʖʐϓ�����ɓ������͂s�Ɠ����傫���ł���B
�@
�i�R�j�C�ӂ̕������������P�ʖʐ��ɓ������̓x�N�g��
�P�D���͂̕���
�@�d�ꒆ�ł��剞�����Q�D�i�Q�j�ŏq�ׂ��悤�ɒ�܂�ƁA�C�ӂ̕������������ʂɓ������̓x�N�g���e�����܂�B����́A���}�̗l�ɖʐϗv�f�r���d��ɕ��s�Ȏˉe�����rcos�����d��ɐ����Ȏˉe�����rsin���ɕ����āA���ꂼ��̖ʐϗv�f���Q�D�i�Q�j�̌��_��K�p����B���̗��҂��x�N�g���I�ɉ������킹�����̂����߂鉞�̓x�N�g���e�ł���B
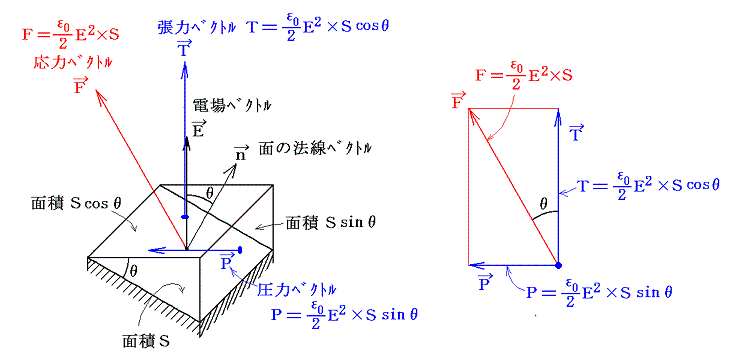
�����ŁA���̎����ɒ��ӂ��ׂ��ł���B
�@�P�ʖʐςɓ������͂̑傫���́m�d��̃G�l���M�[���x�n��(1/2)��0�d2�@�ɓ���������̕����͂d�ւ��Ă��Ɣ��Α��̑Ώ̓I�ȕ������Ƃ��B�C�ӂ̕������������ʂɂ́A��ʂɖʂɐ����Ȑ����Ɩʂɉ����������������B����́A���Z�����u���C�v�̂Ƃ���ŏK���u��ʂ̍R�̓x�N�g���͖ʂɑ��鐂���R�͂Ɩʂ̖��C�͂̍��͂ł���v�Ɠ����ł����B�܂�ʂ̗����̑̐ϗv�f�����̖ʂɉ����Ă��炷�l�ȗ͂������B(���}�Q��)
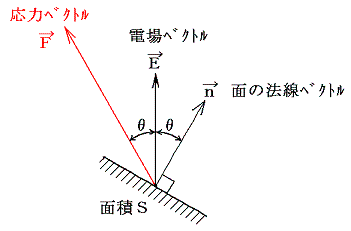
�@�ʐϗv�f�̖@���x�N�g�����Ɠd��x�N�g���d�̊Ԃ̊p�x��0����45����90����180����270���Ƒ�����ɂ��������ĉ��̓x�N�g���e�̕����͉��}�̗l�ɕω����Ă����B
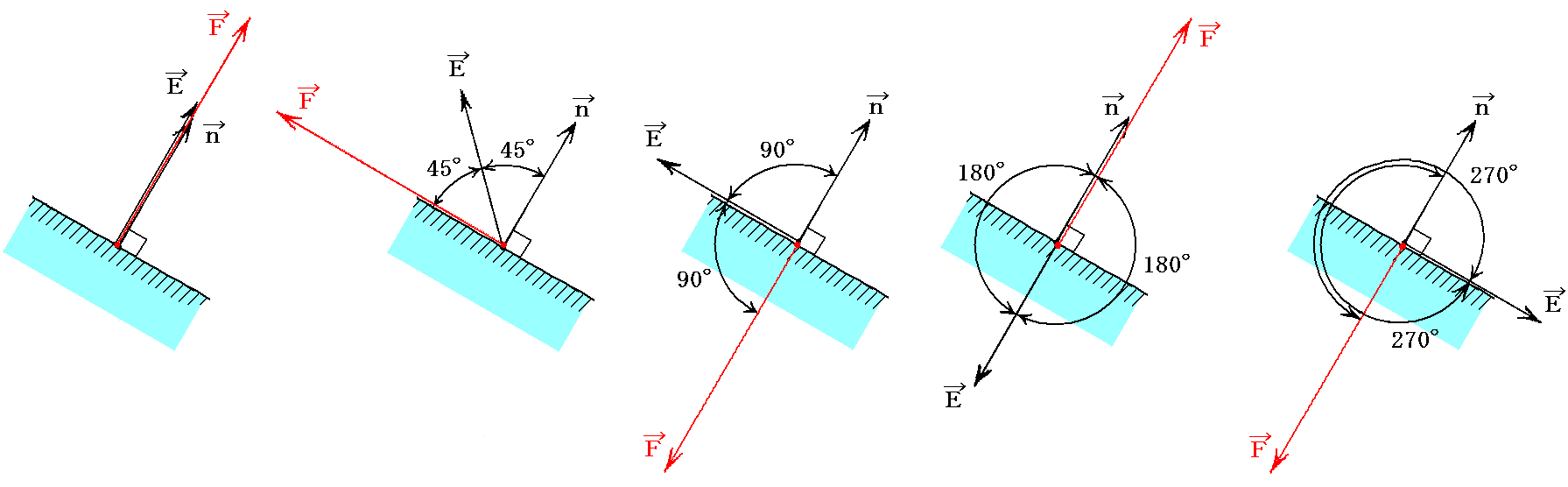
�@���̐}�Ŏ��̓_�ɒ��ڂ��ė~�����B�Ɓ�0����180���̂Ƃ��d��͖ʂɐ��������A�d��̕����͐^���ɂ��ւ�炸�ǂ���̉��͂��ʂ��`������̐ϗv�f�ɑ��Ē��͂ɂȂ��Ă���B�܂��A�Ɓ�90����270���̂Ƃ��d��͖ʂɕ��s�����A�d��̕����͐^���ł���ɂ��ւ�炸�ǂ���̉��͂��ʂ��`������̐ϗv�f�ɑ��Ĉ��͂ɂȂ��Ă���B
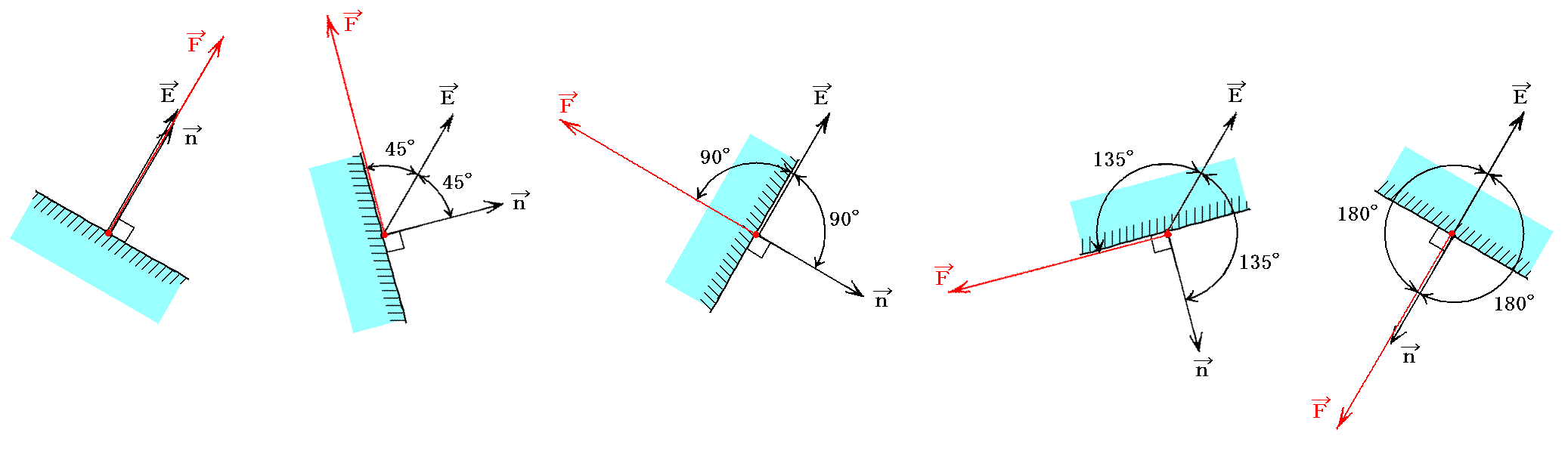
�@�������Ƃł����A�d��x�N�g���d���Œ肵�Ėʐϗv�f�̖@���x�N�g�������p�x0����45����90����135����180���Ɖ�]�����}�ɂ���ƁA�ʂɑ��ĉ��̓x�N�g�����ǂ̗l�ɕω����Ă��������ǂ�����B
�@
�Q�D��ʓI�ȃx�N�g���\��
�@���̓x�N�g���e�i�e���C�e���C�e���j�̓x�N�g���d�i�d���C�d���C�d���j�Ɩʂ̖@����\���P�ʃx�N�g�����i��x�C�����C�����j�m��������x2+����2+����2��12�n��p����Ǝ��̂悤�ȃx�N�g�����Z�ŕ\���ł���B
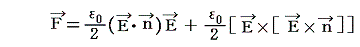
�@���̒����i�d�E���j�̓x�N�g���̓��ςŁA�����\���ŕ\�����i�d�E���j���d������+�d������+�d���������d�E1cos�ƂƂ����X�J���[�ʂƂȂ�B�������i�d�E���j�d�͑傫���d2cos�ƂŃx�N�g���d�̕����i�O�����s�̕����j�������x�N�g���ł���B
�@�܂��m�d�~���n�̓x�N�g���̊O�ςƌ�������̂ŁA���̉��Z���ʂ���̃x�N�g���ƂȂ�B���̃x�N�g���̕����̓x�N�g���d�ƃx�N�g��������镽�ʂɐ����ŁA�x�N�g���d����x�N�g�����̕����։E�l�W�����Ƃ��A�E�l�W�̐i�ޕ����������B���̑傫���̓x�N�g���d�ƃx�N�g�����̂Ȃ��p�����̏ꍇ�@�d�E1sin�Ɓ@�i�d�������ӂƂ��镽�s�l�ӌ`�̖ʐρj�ƂȂ�B���̃x�N�g���̂��A���A���������̐����́i�d�������|�d�������C�d�������|�d�������C�d�������|�d�������j�ƂȂ�B�m�d�~�m�d�~���n�n�͂d�Ƃ��̃x�N�g���̊O�ςł��邩��A����͑傫���d2sin�ƂőO���ł��Ƃ߂��o�̕����������x�N�g���ɂȂ�B
�@�㎮�̓x�N�g�������@�m�`�~�m�a�~�b�n�n���i�`�E�b�j�a�|�i�`�E�a�j�b�@��p����Ǝ��̂悤�ɕό`�ł���B�i���̃x�N�g�������͍��ӂƉE�ӂ����ꂼ�ꐬ���\���œW�J���ĕt�����킹�Ă݂���ؖ��ł����B�j
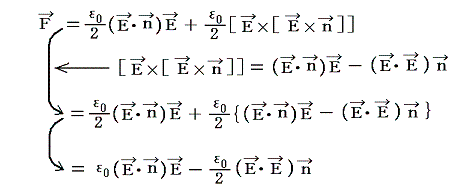
�����̃x�N�g���̊W��}�������
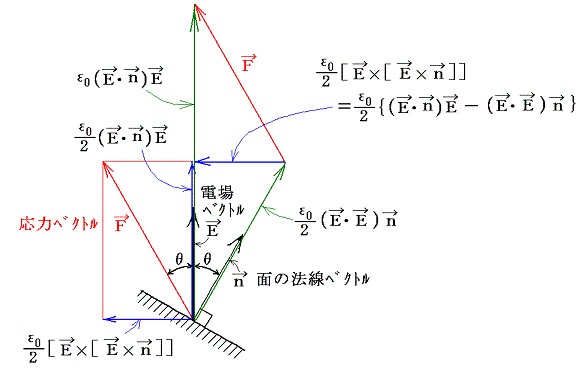
�ƂȂ�B���̐}������x�N�g�������@�m�`�~�m�a�~�b�n�n���i�`�E�b�j�a�|�i�`�E�a�j�b�@�����藧�͖̂��炩�ł���B
�@
�R�D���̓e���\��
�O�L�̃x�N�g���e�𐬕��\�������
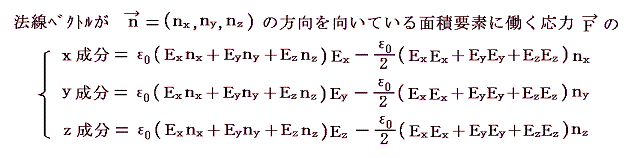
�ƂȂ�B
�@�ʐϗv�f�̖@���x�N�g�������i1�C0�C0�j�A�i0�C1�C0�j�A�i0�C0�C1�j�̓��ʂȏꍇ�ɂ��ċL���ƈȉ��̂悤�ɂȂ�B

�@�ʂ̕����x�N�g�������i1�C0�C0�j�ƌ������Ƃ�����A��L�̉��͖͂ʂ�肘���̕����̓d��̐ϗv�f�ɑ��ē����Ă���͂��Ӗ�����B�ʂ̐����̓d��̐ϐ����ɓ������͍͂�p����p�̌��������L�̕������t�ɂ������̂ł��B�܂��A�������͖ʂɐ����ɓ������͂ł���A�������Ƃ������͖ʂɉ����ē������f�͂ł��B
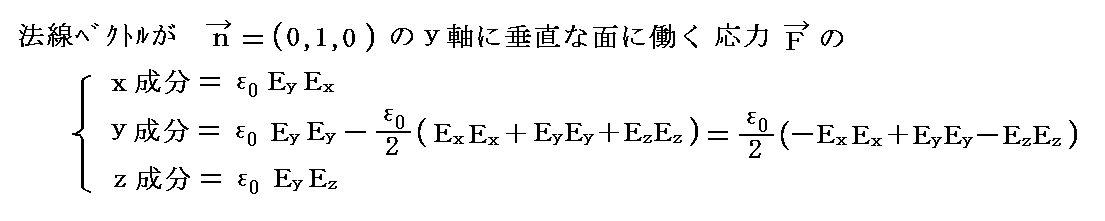
�@�ʂ̕����x�N�g�������i0�C�P�C0�j�ƌ������Ƃ�����A��L�̉��͖͂ʂ�肙���̕����̓d��̐ϗv�f�ɑ��ē����Ă���͂��Ӗ�����B�ʂ̐����̓d��̐ϐ����ɓ������͍͂�p����p�̌��������L�̕������t�ɂ������̂ł��B�܂��A�������͖ʂɐ����ɓ������͂ł���A�������Ƃ������͖ʂɉ����ē������f�͂ł��B

�@�ʂ̕����x�N�g�������i0�C0�C1�j�ƌ������Ƃ�����A��L�̉��͖͂ʂ�肚���̕����̓d��̐ϗv�f�ɑ��ē����Ă���͂��Ӗ�����B�ʂ̐����̓d��̐ϐ����ɓ������͍͂�p����p�̌��������L�̕������t�ɂ������̂ł��B�܂��A�������͖ʂɐ����ɓ������͂ł���A�������Ƃ������͖ʂɉ����ē������f�͂ł��B
�@������s��\������
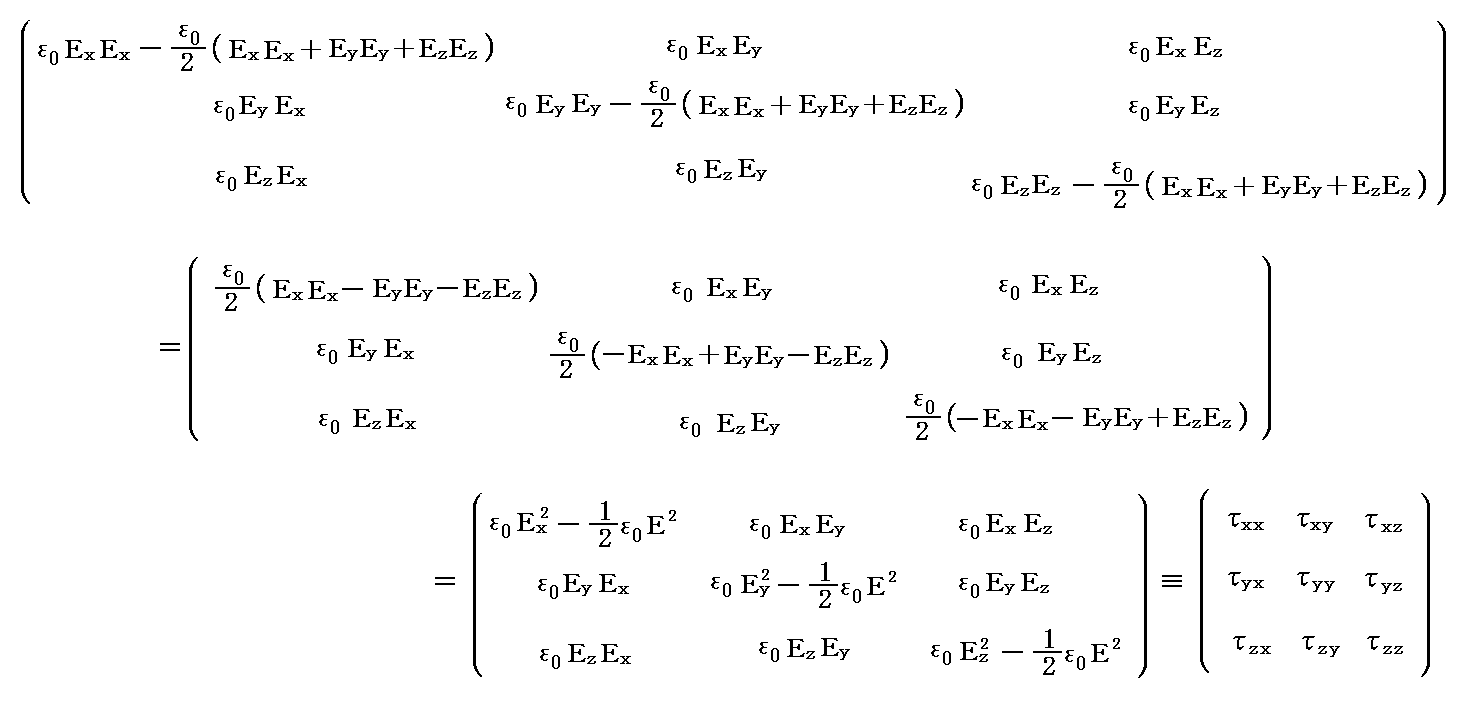
�͓d��ɂ��������}�N�X�E�F���̉��̓e���\���ƌ�����B
�@�����ʼn��͐������E���̂悤�Ȉ�ʓI�Ȍ`�ł���킷�ƁA ��ij �� �� ���ɐ����ȒP�ʖʐ��ɓ��� �� �������̗͂̐������Ӗ�����B�����̕\�����疾�炩�Ȃ悤�ɁA���̍s��͍s�Ɨ�����ւ����s��i�g�]�u�s��h�Ƃ����j�Ɠ����ɂȂ�B�܂� ��ij����ji �ƂȂ�B���̂悤�Ȑ��������s����g�Ώ̍s��h�i�Ώ̃e���\���j�ƌ����B
�@�e���\���ƂȂ�Ƌ}�ɓ�������邪�A��L�̈Ӗ��ȏ�̂��̂͂���܂���B�����𐳕��`�ɕ��ׂ������ł��ł����A���̂悤�ɕ��ׂĂ����Ǝ����Ő�������悤�ɕ֗��Ɏg����B
�@
�S�D�e���\���Ƃ͉����m�@���x�N�g�������i��x�C��y�C��z�j�̖ʂɓ������͂e���i�ex�C�ey�C�ez�j�Ƃ̊W�n
�@�@���x�N�g�������i��x�C��y�C��z�j���C�ӂ̕������������ʐϗv�f�ɓ������͂e���i�ex�C�ey�C�ez�j�����߂����B���������ɂ͉��L�̗l���l�ʑ̂`�a�b�n���l���āA�͂̒ނ荇�����l����悢�B
�@�}�����x�N�g�����r�A���rx�A���ry�A���rz�́A���ꂼ��̖ʗv�f��\���@���x�N�g���ɂ��ꂼ��̖ʐς��悶�����̂ł��B
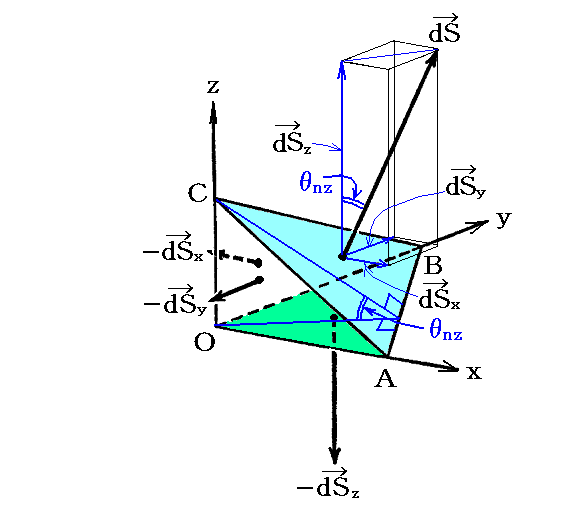
�@�O���ŋ��߂��l�ɁA�O�p�ʂa�b�n�A�O�p�ʖʂ`�b�n�A�O�p�ʖʂ`�a�n�ɓ������͐����͉����Ă���B�̂�����A�����𑫂����킹�邱�Ƃɂ��A�O�p�ʂ`�a�b�ɓ������͂e���i�ex�C�ey�C�ez�j�����߂�悢�B
�@�������A�O���̉��͂͂�������P�ʖʐϓ�����ŋL�q����Ă��܂����A��L�̒ނ荇�����l�����l�ʑ̂̊e�ʂ͒P�ʖʐςł͂���܂���B���̂��߁A�O�p�ʂ`�a�b�A�O�p�ʂa�b�n�A�O�p�ʂ`�b�n�A�O�p�ʂ`�a�n�݂̌��̖ʐϊW���l�������ނ荇�����l����K�v������B
�@�}���疾�炩�Ȃ悤�ɁA�ʐς��r�Ɩʐς��rz��
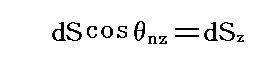
�̊W�ɂ���܂��B���̂Ƃ���nz�͖ʂ`�a�n���@���P�ʃx�N�g�����Ƃ����̂Ȃ��p�ł�����Acos��nz���x�N�g�����r�̂����ɑ�������]�����Ӗ����܂��B���̖ʂɊւ��Ă����l�� ���rcos��nx�����rx�A���rcos��ny�����ry �����܂��B���̂Ƃ�cos��nx���@���x�N�g�����̂����ɑ�������]�����Acos��ny���@���x�N�g�����̂����ɑ�������]�����Ӗ�����B�܂� �icos��nx�Ccos��ny�Ccos��nz�j���i��x�C��y�C��z�j �ł��B
�@���̂���
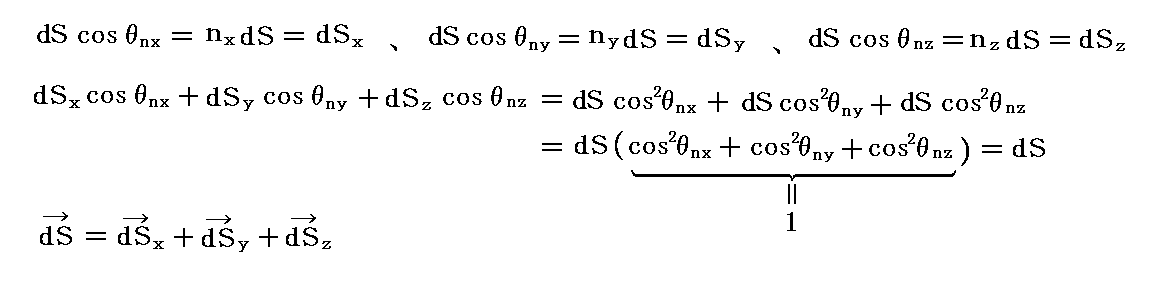
�����藧�B
�@���̂��Ƃ���A�@���x�N�g�������i��x�C��y�C��z�j�̕�����ۂ����܂܁A�n�_�Ɩʂ`�a�b�̋����߂��āA�ʂ`�a�b�̖ʐς�1�ɁA���Ȃ킿���r��1�Ɛ���悤�ɒ��߂����ƁA�O�p�a�b�n�̖ʐς��rx�A�O�p�b�`�n�̖ʐς��ry�A�O�p�`�a�n�̖ʐς��rz�͂��ꂼ�� cos��nx�Acos��ny�Acos��nz���邢�͂�x�A��y�A��z�ƂȂ�܂��B
�@���̂��߁A�O�p�ʂ`�a�b�i�ʐς�1�j�ɓ��� ���͂e���i�ex�C�ey�C�ez�j �̊e�����́A�O�p�a�b�n�̖ʁA�O�p�b�`�n�̖ʁA�O�p�`�a�n�̖ʂɓ������͐����ɁA���ꂼ��̖ʐς��悶�����̂��������킹��悢�B������̂Ƃ��l�ʑ̂̑̐ϐ����ɑ���ʂ̕����ƁA��p����p�̖@�����l�����āA���ׂẲ��͂��ނ荇���Ă���Ƃ��Ă̘b���ł��B
�@���Ȃ킿
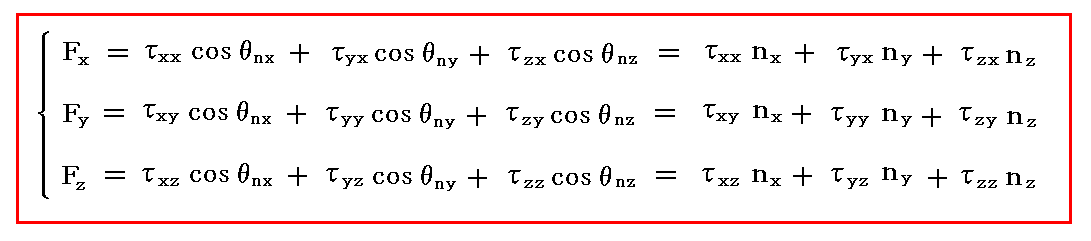
�ƂȂ�B����͂������Q�D�i�R�j�R�D�̍ŏ��Ɏ�������
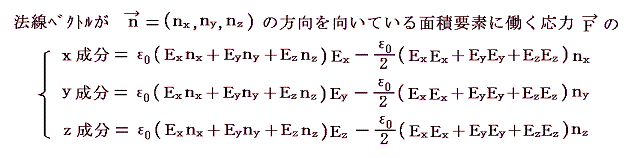
�Ɠ����ł��B
�@������ɂ��Ă��A�����̌��ʂ͉��͂̍s��\����p����
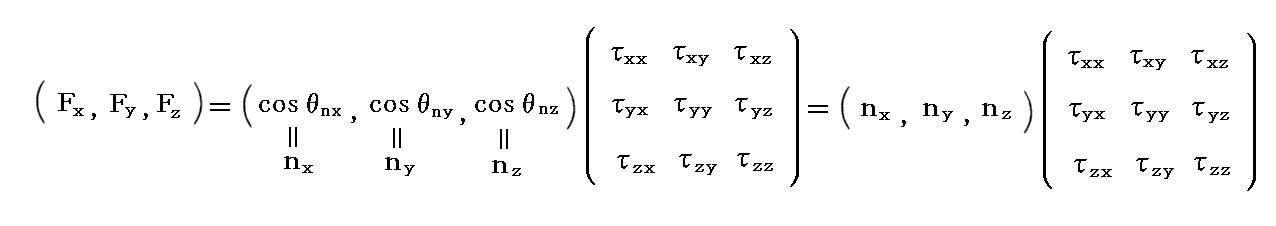
�Ƃ��āA�i1�s�C3��j�̕����]���x�N�g�����Ɂi3�s�C3��j�̉��͍s��̏�Z�����{���āi1�s�C3��j�̉��̓x�N�g���e�����߂�悢���Ƃ��Ӗ����Ă���B
�@���邢��
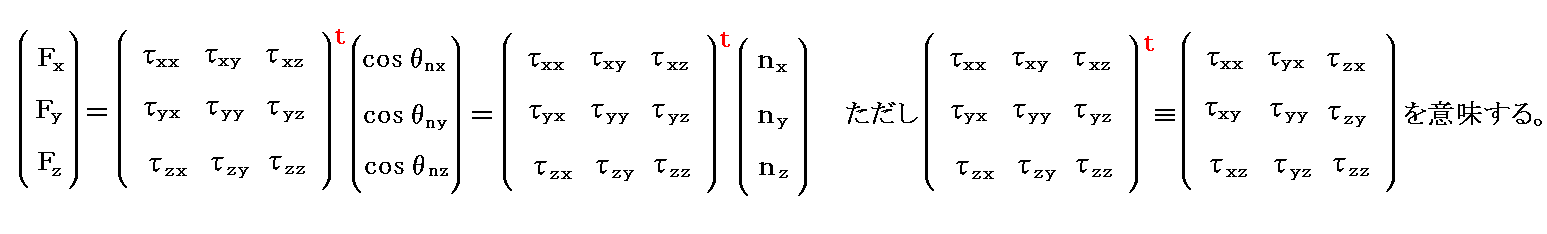
�Ƃ��āA�i3�s�C3��j�̉��͍s����g�]�u�s��h�Ɂi3�s�C1��j�̕����]���x�N�g�����̏�Z�����{���āi3�s�C1��j�̉��̓x�N�g���e�����߂�悢���Ƃ��Ӗ����Ă���B
�@�]�u�������̓e���\���̉E���ɕt���Ă��� �g���h ���]�u�s��itransposed matrix�j�̓������𗘗p���Ă���B
�m�⑫�����P�n
�@��L�̗l�ɁA�C�ӂ̕������������ʂɓ������́itension�j���o���s���̂��Ƃ��e���\���ƌ������̂ł��B�e���\���̖����Ƃ��Ă���ȏ�̂��̂͂���܂���B�܂�A�gtension�h���g�e���\���h�itensor�j�̌ꌹ�ł��B
�m�⑫�����Q�n
�@���̓e���\���̐����\���Ƃ�����ij �� �� ���ɐ����ȒP�ʖʐ��ɓ��� �� �������̗͂̐������Ӗ�����Ƃ������A��ij �� �� ���ɐ����ȒP�ʖʐ��ɓ��� �� �������̗͂̐������Ӗ�����ƒ�`���Ă��ǂ��B���̂悤�ɒ�`����Ƃ����ɐ����Ȗʂɓ������͐����͍s��̂P�s�ڂł͂Ȃ��āA�P��ڂɕ��Ԏ��ɂȂ�B�܂�s�Ɨ���ւ��B�����ɐ����ȉ��͐����Ƃ����ɐ����ȉ��͐����͂Q��ڂ�3��ڂɕ��ԁB
�@���̂悤�ɒ�`����Ə�L�̋L�q��
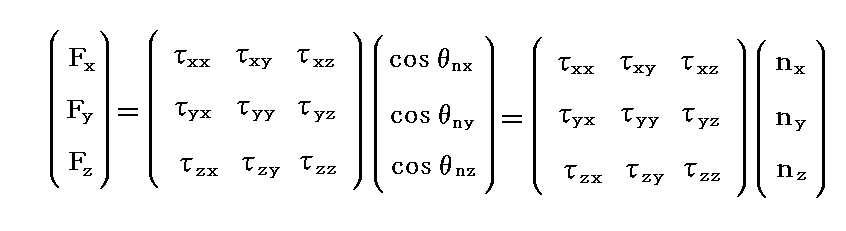
��
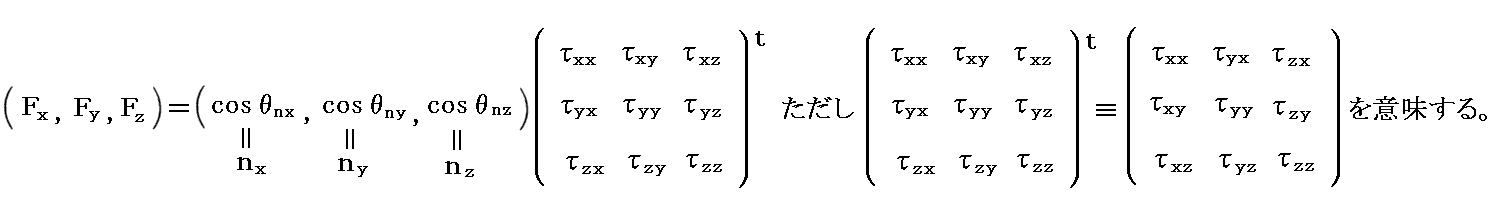
�ƂȂ�B�܂��]�u�s��̖���������ւ���B
�@���ȏ��ɋ����Ă͂�����̒�`��p���Ă���ꍇ������܂��̂Œ��ӂ��ĉ������B
�m�⑫�����R�n
�@�}�N�X�E�F�����̓e���\���͏����ij����ji �����g�Ώ̍s��h�i�Ώ̃e���\���j�ł����B���̐����͉��̓e���\���ł���ΕK�����藧���܂��B���̂��Ƃ͊ȒP�ɏؖ��ł��܂��B
�m�ؖ��n
�@��Ƃ�����xy����yx �Ɛ��邱�Ƃ��ؖ����܂��B���͐������l��������ȗ����̂�ݒ肷��B
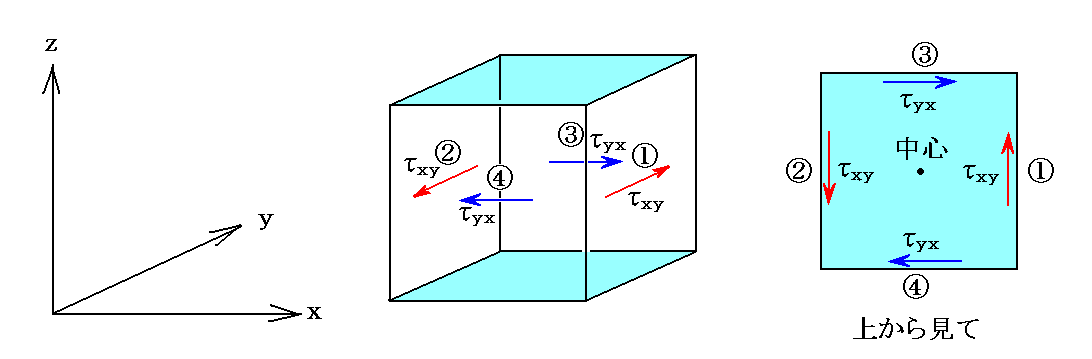
�@���̂Ƃ��A�ʇ@�ɓ���������xy �ƖʇA�ɓ���������xy �́A�傫�������������͋t�ɂȂ�܂��B�Ȃ��Ȃ�A�傫�����������Ƃ��ėǂ��͖̂ʇ@�ƖʇA�͂����߂��ɑ��݂��邩��ł��B�܂��A���͂̌������t�ɂȂ�̂́A���͂��l����̐ϗv�f�ɑ��Ėʂ̖@���x�N�g�����݂��ɔ��Ε����������Ă��܂��̂ō�p����p�̊W���炻���Ȃ�܂��B
�@���l�ɁA�ʇB�ɓ���������yx �ƖʇC�ɓ���������yx �Ɋւ��Ă��݂��ɑ傫���������A�������t�ɐ���܂��B
�@�����̐ϗv�f�͂��̒��S�_�ɑ��ĉ�]���Ă͂����܂���̂ŁA�����v���̃��[�����g���鉞����xy �Ǝ��v���̃��[�����g���鉞����yx �͓��R�������Ȃ���Ȃ�܂���B�܂���xy����yx �Ɛ���B
�m�ؖ��I���n
�@
�T�D�Ód����̈�ł̗͂̒ނ荇���i2018�N2���NjL�j
�@�Ód����̔C�ӂ̑̐ϗ̈�ɂ�����͂̒ނ荇�����l���܂��B
�Ód����̂���̐ϗ̈�u�̕\�ʂɓ���Maxwell�̉��͂̕\�ʐϕ����l���܂��B�܂�
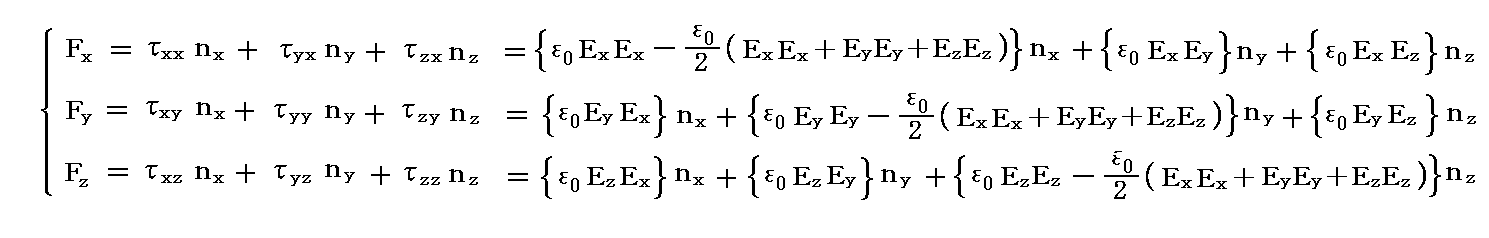
�̂��ꂼ��̃x�N�g�������̕\�ʐϕ����v�Z����B
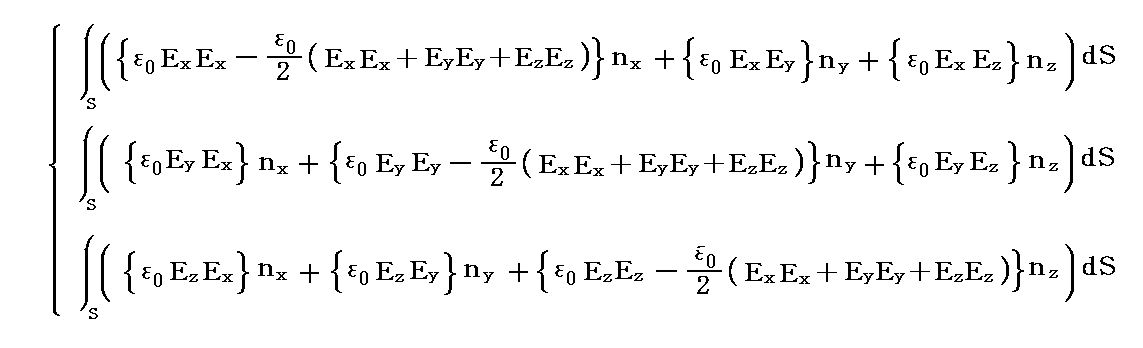
�@����́AMaxwell�̉��̓e���\�N�̊e�s�����ꂼ���̃x�N�g���ƌ��Ȃ����Ƃ��A���̃x�N�g���Ɨ̈�\�ʂ̖ʗv�f�����r�̓��ς�̈�\�ʑS�̂ɂ킽���ĕ\�ʐϕ��������̂�����A�K�E�X�̒藝�ɂ�艺�L�̑̐ϐϕ��ɒ������Ƃ��ł��܂��B���Ȃ킿
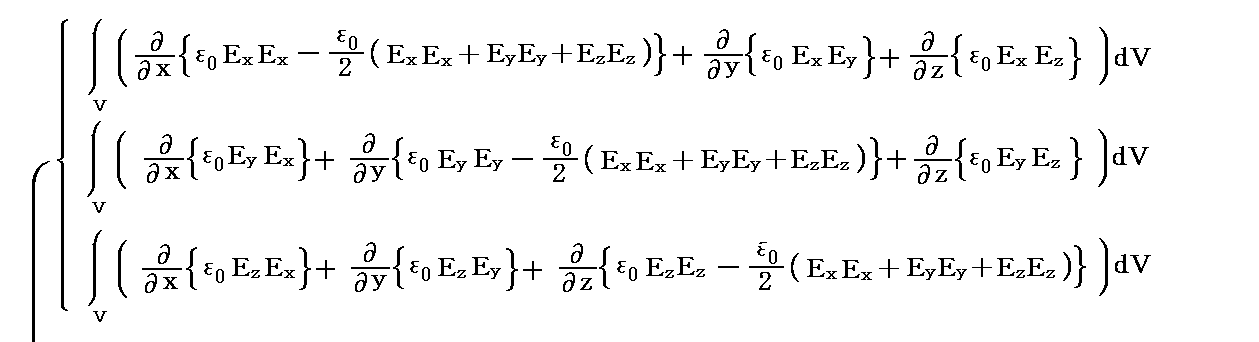
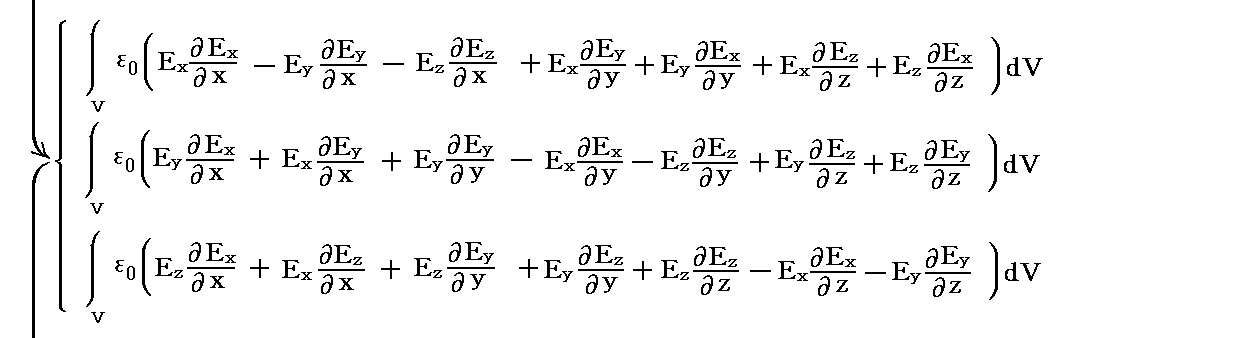

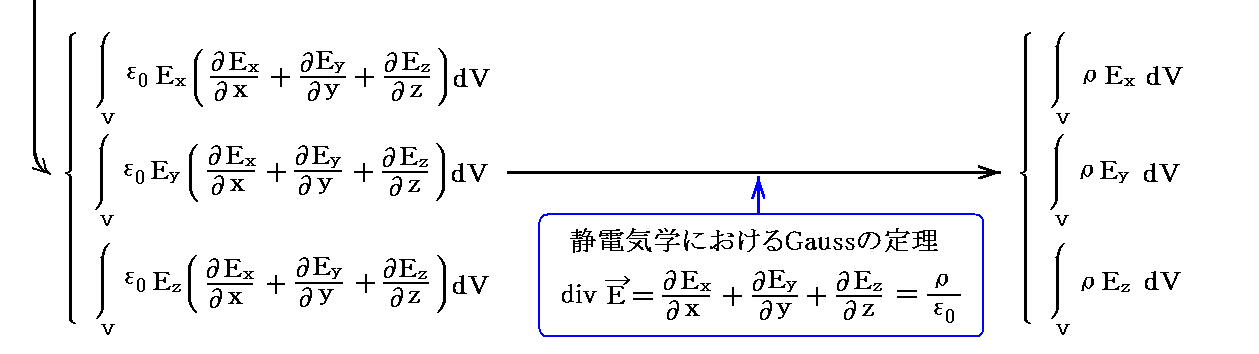
�ƂȂ�܂��B
�@���ʂ̋��ȏ��ł͏�L�̃x�N�g�����������e���\���\����p����
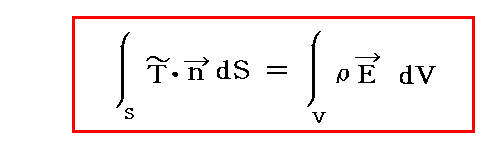
�Ə����Ă��܂����A��������\���Ă��܂��B
�@�e���\���\�L�ɂ���Ɠ�������܂����A�x�N�g���������̐����\�����܂Ƃ߂ď�����@�ɉ߂��܂����B�s��Maxwell�̉��̓e���\�N�ł��B�L�����g�`�h���s���e���\���ł��邱�Ƃ�\���ׂɂ��܂����B���傤���g���h��t���������d���x�N�g���ł��邱�Ƃ�\�����悤�ɁB�܂��A�e���\���ƃx�N�g���̓��� �s�E�����r �ɂ��Q�D�i�R�j�S�D�ŏq�ׂ��ȏ�̈Ӗ��͂���܂���B
�@�厖�Ȃ��Ƃ́A���̎��������Ӗ����邩�ł��B
�@�㎮���ȉ��̗l�ɏ��������Ă݂�Ή���₷���B
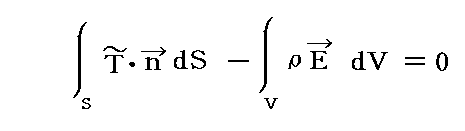
�@���ӂ̑�2���͓d����̈���ɑ��݂��镨���i�d�ׁj�ɓ����͂̔���p�́i����͓d����̒P�ʑ̐ςɓ����̐ϗ͂ƌ����ׂ����́j�������ڂ��Ă���̐ϗ̈�S�̂ɂ킽���đ̐ϐϕ��������̂ł��B���̗͂̍��v�͍��ӑ�1���̑̐ϗ̈�̕\�ʂɌ����d����̕\�ʉ��͂�\�ʑS�̂ɂ킽���ĉ������킹�����̂ƒނ荇���Ă��鎖�������Ă���B
�@����́A�̈���ɑ��݂��镨���i�d�ׁj���d���ꒆ�Ɍ���鉞�͂̌����Ȃ̂ł�����A��p����p�̌�������s���Ɠ�����O�ƌ���������܂��ł��B
�@��̗͂��ނ荇���Ă���̂́A���͕����i�d�ז��x�̕��z�j���������A�d������ÓI�Ƃ��Ă��邩��ł��B������d���ꂪ���ԓI�ɕω�����Ƃ��ɂ́A���̓�̗͂͒ނ荇���Ă��܂���B���̏ꍇ�ɂ��Ă��R�D�i�R�j�T�D���Q�Ƃ��ĉ������B
�@
�i�S�j����������
�P�D��ٕ̈����_��d�Ԃ̈���
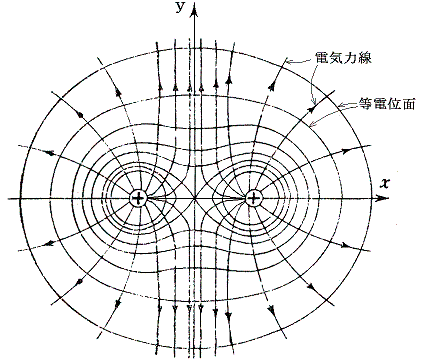
�@+����-���̓d�ׂ�2����������Č݂��Ɉ��������Ă���ꍇ���l����B���d�ׂ̐^�ɗ��d�ׂ����ԕ����ɐ����Ȗʂ��Ƃ�ƁA���̖ʏ�ł̓d��͍��Z�����ŏK���悤�ɉ��}�̗l�ɂȂ�B���̂Ƃ��A���̖ʏ�Ɍ���鉞�͂͂������݂̂ɂȂ�B
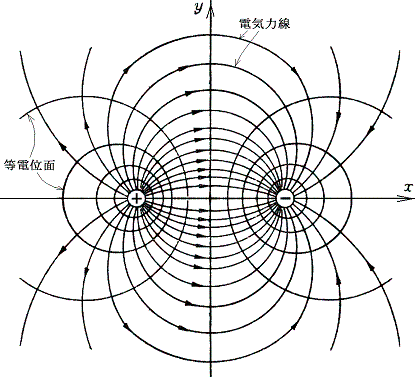
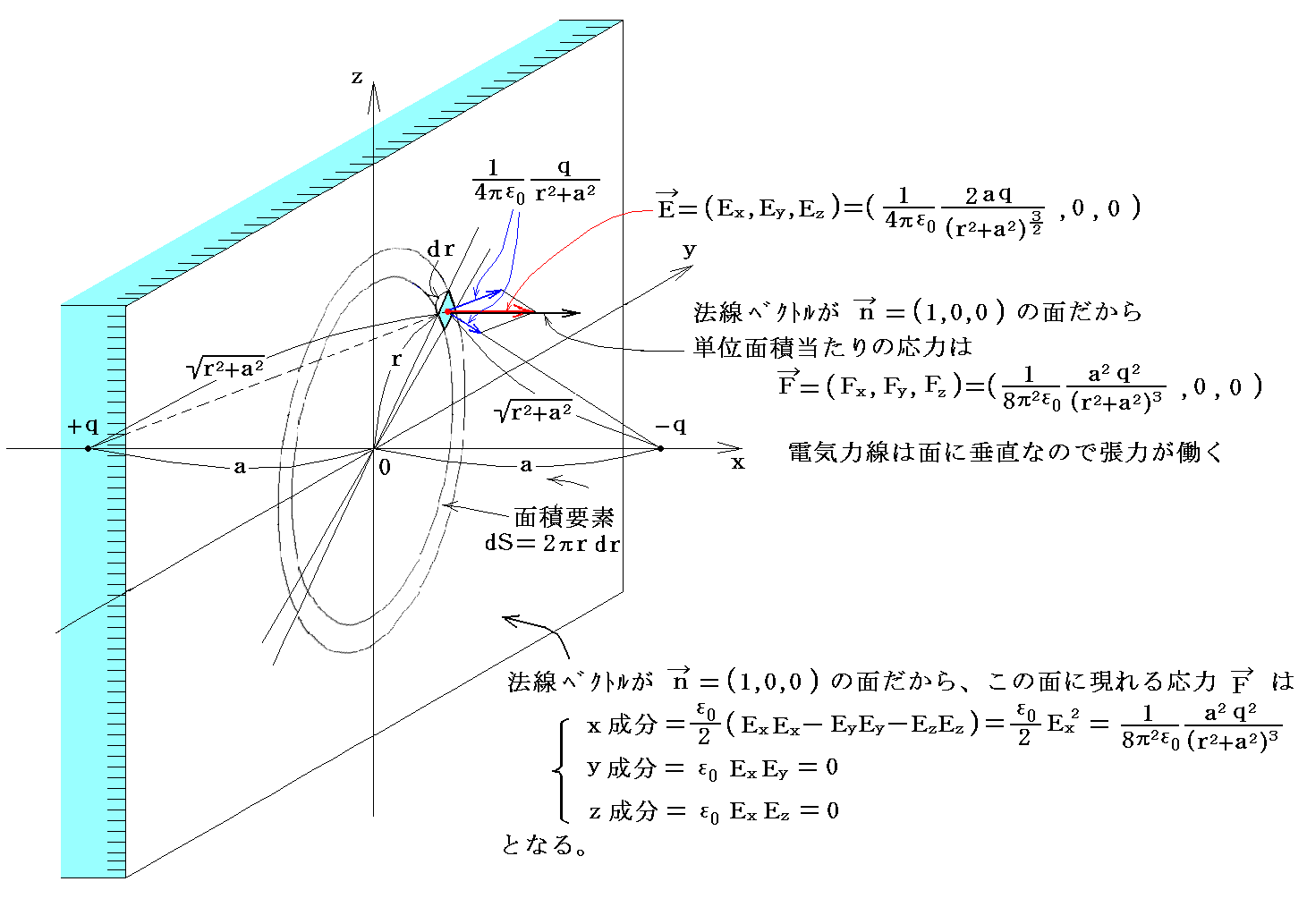
���̉��͂��������ʑS�̂ɂ킽���ĉ������킹�����̂��i���C0�C0�j�̈ʒu��-�����i-���C0�C0�j�̈ʒu��+���������͂ł���B����͈ȉ��̐ϕ������{����悢�B
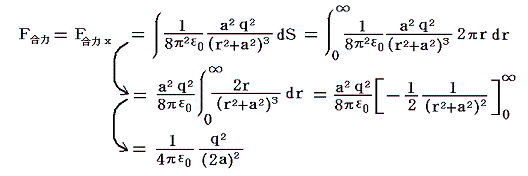
����́A�܂��������u��p�ɂ��ƂÂ��N�[�����̖@���̌��ʂƈ�v����B
�@������Q�D�i�Q�j�d����̉��͂̒�`����l���č݂�Ӗ����R�ƌ����Γ��R�ł���B�d�ׂ̈ʒu�ł̉��͂�d�C�͐��ɉ����Ċe�̐ϗv�f�Ɋւ��Ēލ��̏�����ۂ��Ȃ��玟�X�Ɖ��͂��e��ԂɊ��蓖�Ăčs���̂ł��邩��B
�@
�Q�D��̓������_��d�Ԃ̐˗�
�@+����+���̓d�ׂ�2����������Č݂��ɔ������Ă���ꍇ���l����B���d�ׂ̐^�ɗ��d�ׂ����ԕ����ɐ����Ȗʂ��Ƃ�ƁA���̖ʏ�ł̓d��͍��Z�����ŏK���悤�ɉ��}�̗l�ɂȂ�B���̂Ƃ��A���̖ʏ�Ɍ���鉞�͂͂��A�������݂̂ɂȂ�B
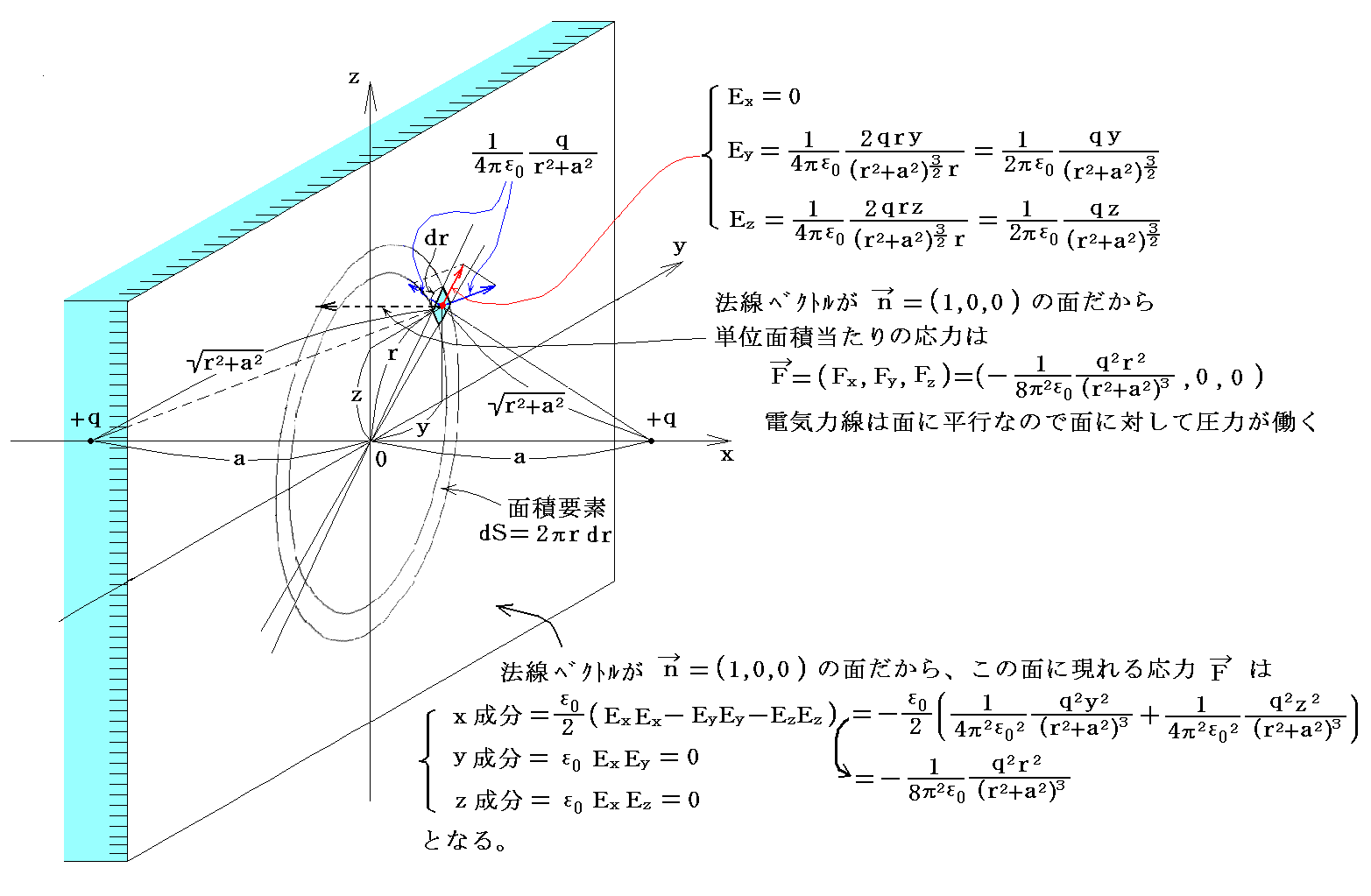
���̉��͂��������ʑS�̂ɂ킽���ĉ������킹�����̂��i���C0�C0�j�̈ʒu��+�����i-���C0�C0�j�̈ʒu��+��������͂ł���B����͈ȉ��̐ϕ������{����悢�B
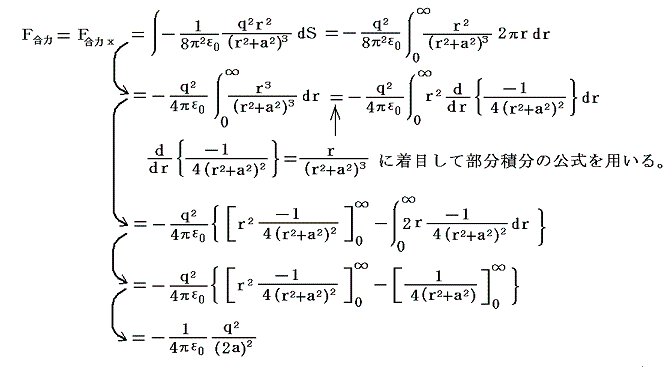
����́A�܂��������u��p�ɂ��ƂÂ��N�[�����̖@���̌��ʂƈ�v����B
�@
�R�D��l�ɑѓd�������k�̔��a���k�߂邽�߂̎d���Ɠd��̃G�l���M�[
�@��l�Ȗʖ��x�Ђőѓd�������a���̋��k�ɂ��A�Q�D�i�P�j�ŏq�ׂ��悤�ɒP�ʖʐϓ�����

�̗͂����k��c������������ɓ����Ă���B���̂��ߋ��k�̑S�d�ׂ����ɕۂ����܂܂Ŕ��a��(���|����)�ɏk�߂悤�Ƃ����

�̐��̎d���������Ȃ���Ȃ�Ȃ��B
�@���̂Ƃ��A���k���k�����ɐV���ɓd�ꂪ�������B�����ĈȑO����d�ꂪ���݂��Ă��������̓d��̑傫���́A�S�d�ׂ����ɕۂ����܂܂̎��k������A�����ł���B���̐V���Ɍ����d��̃G�l���M�[���������V���ɑ��������ƂɂȂ�B�Ƃ���œd��̎��G�l���M�[�͒P�ʑ̐ϓ�����@�i1/2�j��0�d2�@�ł��邱�Ƃ͕ʍe�u�d���ƃG�l���M�[�v�Q�D(�S)�i�T�j�Ő��������B���̌��_��p����Ƒ������d��̃G�l���M�[��
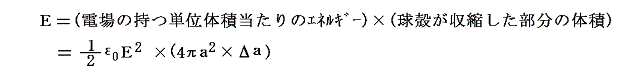
�ƂȂ�B
�@���҂͂܂�������v����B�܂�������d���̕������d��̃G�l���M�[�����������ƂɂȂ�B
�m�⑫�����P�n
�@����Ƃ͋t�ɁA�ѓd���k�\�ʂɓ����c���͂ɂ�苅�k��c�������ĉ��炩�̗͊w�I�d�������o���ƁA���k�̂܂��̓d��̃G�l���M�[���������Ă��̃G�l���M�[���܂��Ȃ��B����͌��Nj��k��ɕ��z��������d�Ԃ̔����͊Ԃ𗘗p���Ďd�������o���̂ł����A�d�ו��z�̕ω��ɂ��d���I�G�l���M�[�̕ω����d���ꕪ�z�̕ω��Ɏ|���Ή����Ă��邱�Ƃ������Ă���B
�@����͕ʍe�u�d���ƃG�l���M�[�v�Q�D(�S)(�T)�ŏq�ׂ����s�ŃR���f���T�[�̊Ԋu�����߂Ďd�������o���̂Ɠ�������ł��B���̏ꍇ�͗��ɔɕ��z���Ă���َ�d�Ԃ̈��͂𗘗p���Ďd�����Ƃ肾���̂ł����A���̂Ƃ����d�ו��z�̕ω��ɂ��d���I�G�l���M�[�̕ω����d���ꕪ�z�̕ω��Ɏ|���Ή����Ă��܂����B�B
�@
�R�D���d��������̉���
�ȒP�̂��߂ɒ��I�ȓd�������鎥��Ɖ��͂̊W���B
�i�P�j�~����d���ɓ�����
�P�D�r�I���T�o�[���̖@���ƃA���y�[���̖@��
�����̖@���͍��Z�����̎��ƂłȂ炤�̂ŁA�ȒP�ɕ��K����B
�@1820�N�ɃW�������o�e�B�X�g�E�r�I�ƃt�F���b�N�X�E�T�o�[���͒��d���̂܂��̎���ɂ��Ď��̖@���������B�d���h������Ă��铱���̃��r�̒��������́A���ꂩ�狗�������ꂽ�ꏊ�Ɉȉ��̒l�Ŏ�����鎥��g������B�i�r�I=�T�o�[���̖@���j
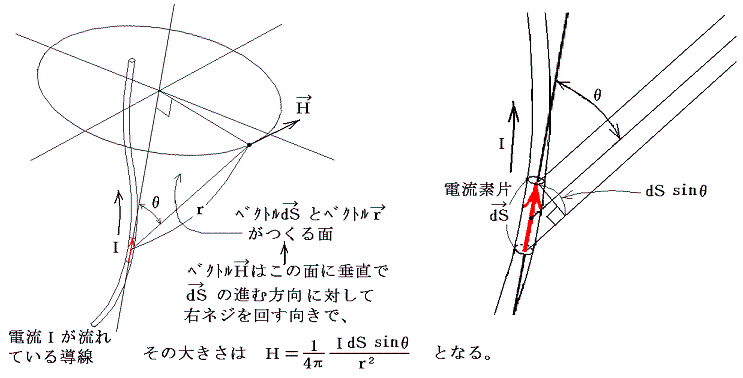
���̖@�����������菇�͕ʍe�u�r�I�E�T�o�[���̖@���i1820�N�j�����������@�v���Q�ƁB
�@������1820�N�ɃA���h�����}���E�A���y�[���͕����o�H�ɂ����Ď���̑傫���𑫂����킹��ƁA���̘a�͕����o�H���т��d���̘a�ɔ�Ⴗ�邱�Ƃ��������i�A���y�[���̖@���j
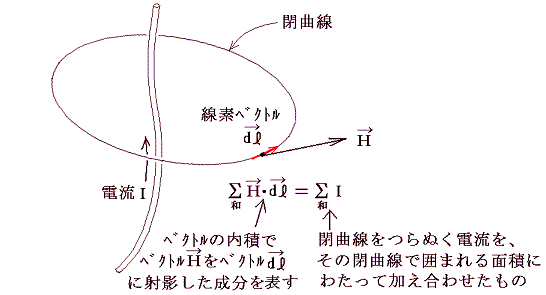
�@������̖@���͂���������d���̏ꍇ�̂ݐ������A�d�������ԓI�ɕϓ�����ꍇ�͐������Ȃ��B�B�Ȃ��Ȃ�A���I�łȂ��ꍇ�ɂ͓d��⎥�ꂪ�ϓ����A�l���Ă���_�ɂ��̓d����̕ω������B����̂Ɏ��Ԃ�������B�������A�����̖@���͂��̎��ԓI�x��̌��ʂ��l�������`�ɂȂ��Ă��Ȃ�����ł��B�����ɘ_����ɂ͂��̌��ʂ��l�������}�N�X�E�F���̕�������p���Ȃ���Ȃ�Ȃ��B�����������̋c�_�̖{���𗝉�����ɂ́A���I�ȏꍇ�ŏ\��������A�����̖@����p���ĊȒP�ɘ_����B
�@�܂��A������̖@���݂͌��ɓ����ł���A������瑼�������Ƃ��ł���i�ؖ��͏ȗ��j�
�@
�Q�D���������d�������鎥��
�@���Z�����ł́A�A���y�[���̖@����p���ē������A�����ł��r�I=�T�o�[���̖@����p���ċ��߂Ă݂�B���}�̗l�Ȗ����ɒ������������Ɉ��̓d���h������Ă���Ƃ���B�������狗�����������ꂽ�ʒu�̎���́A�r�I=�T�o�[���̖@�����d���ɑ��ĉE�l�W�̕����ɓ�������芪���悤�ɂł���B�����d�����狗�����̓_�̎���́A�ȉ��̎��ɉ����Ă��Ɋւ���-������+���܂ł̐ϕ������s����悢�B���ʂ͐ϕ��ϐ����Ƃɕϊ����Ď��s���邪�A���̂܂܂ł��ϕ��ł���B
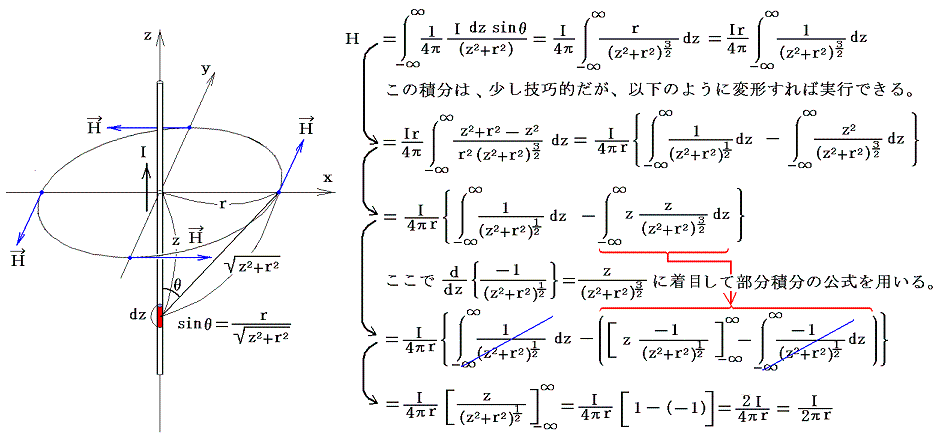
���̌��_�́A�w�I�Ώ̐����l�������A���y�[���̖@����p��������

�ƈ�v����B
�@
�R�D�~����d���̂��鎥��
�@���x�͉��}�̗l�ɂ��������ɖ����̒����������a���̉~���\�ʂ������̐������ɗ���Ă���d�����l����B����͑O���Q�D�̒����d�����~����ɂ�������z�u����Ă���ƍl����悢�B�e�X�̒����d�������鎥����d�ˍ��킹�����̂����߂鎥��ł���B
�@���̂Ƃ��A���y�[���̖@����p����A�~���̓����ł͗��ɁA�O���ł͉~��������i���̕����́A�d���̕������E�l�W�̐i�ޕ����Ƃ��āA�E�l�W�������j����ɂȂ�A���̑傫���͉~���̒��S���狗�����̓_�łg���h�^2���i�h�͉~���𗬂��S�d���j�ƂȂ����Ƃ��e�Ղɓ�����B
�@�����œ������Ƃ��r�I=�T�o�[���̖@����p���ċ��߂Ă݂�B����͕ʍe�u���L���̖͂@���ւ̕⑫�v�ŋ��k�ɑ��ėp�������@���~���ɑ��ēK������悢�B
�@�~���������P�ʕ�������ɗ����d�������Ƃ����
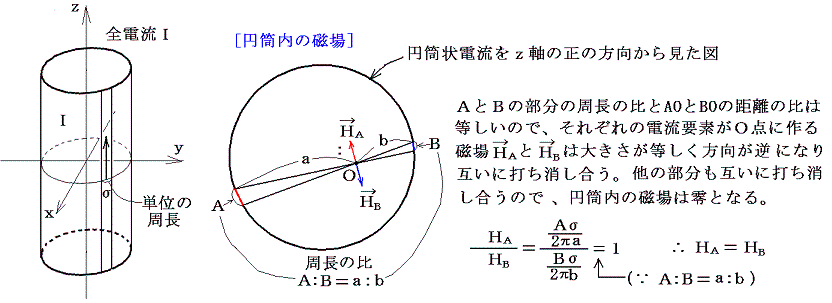
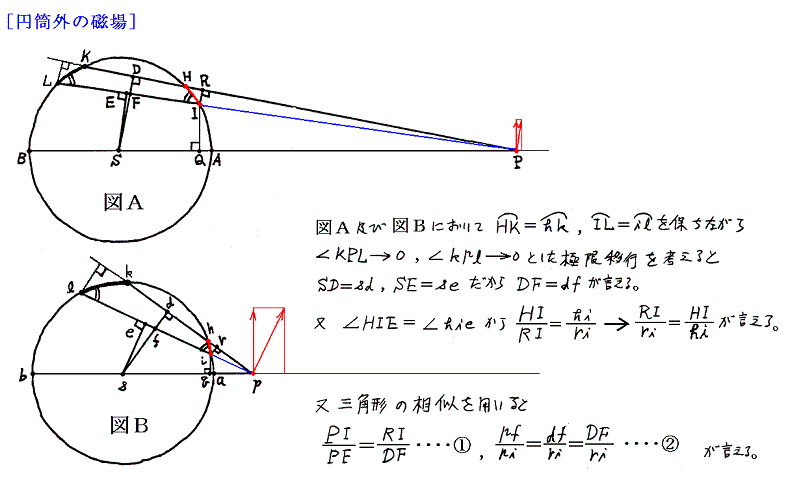
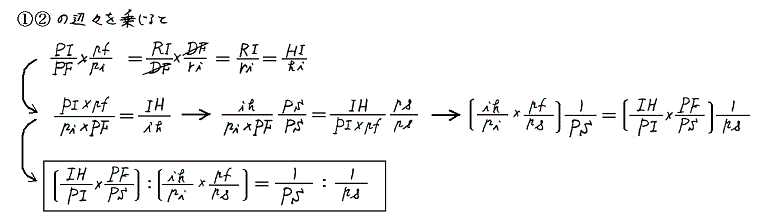
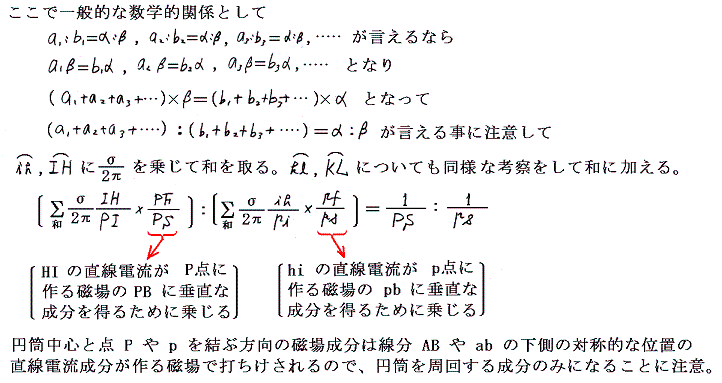
�ȏ�ʼn~���d���̊O���̓_�ɉ~���d������鎥��͉~���̒��S���ƒ��ړ_�Ƃ̋����̋t���ɔ�Ⴗ�邱�Ƃ��������B���ɉ~���̔��a�������������Ɍ��ڍs���l����Ɣ��萔�͓����Ȃ̂ŁA�����~���d�����_�o�ɍ�鎥��͑S�d�����~���̒��S���𗬂�Ă���ꍇ�Ɠ����ɂȂ�B���ǃA���y�[���̖@���œ���ꂽ�̂Ɠ��l�Ȍ��_��������B
�@
�S�D�~����d���̒P�ʖʐςɓ�����
����g�̒��x���ʼn^�����鐳�d��+���́A�ȉ��̎��ŕ\����郍�[�����c�͂���B
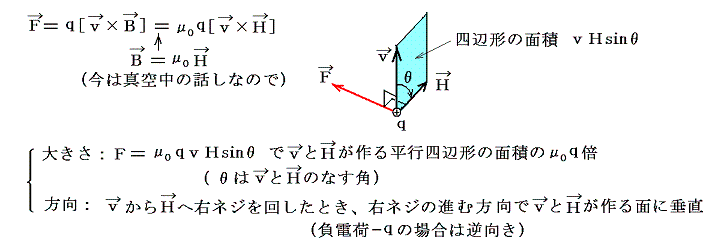
�����p����ƁA����ɑ��Đ�����������d���̒����k�̐����v�f����͂�
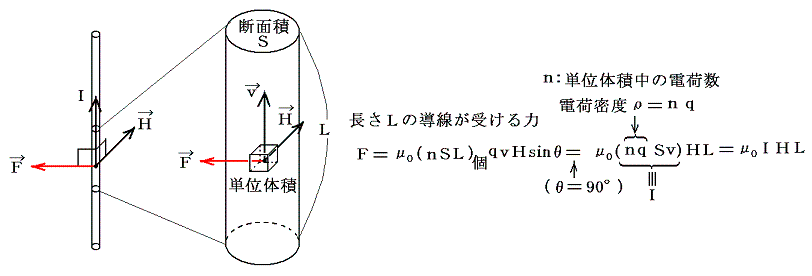
�ƕ\�����B���̌��_�͍��Z�����ŏK���B
�@�����p�����~����d���̒����k�A�����̖ʐϗv�f����͂ewL�����߂�B
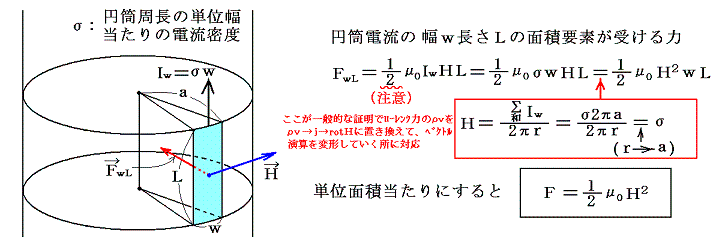
�@���̏ꍇ���Q�D�i�P�j�Ɠ����悤�ȍl������K�����Ȃ����Ȃ��B�~���d���ɓ����͉͂~���̊O���̎���Ɠ����̎���i��0�j�̕��ρi�gout�{�gin�j�^2�̎���̒��ɑ��݂���ƍl�����ꍇ�Ɠ����ɂȂ��B����𗝉�������@�͉~����d��������0�̑w�ƍl����̂ł͂Ȃ��A����������������������w�̒��ɑ��݂��Ă���ʓd�����x�� ���l���鎖�ł���B���̌��ʂƂ��ĕ\�ʂ̒P�ʎ���������ɗ���Ă���d�����Ђɐ���ƍl����B�܂胢�����ǂ̂悤�Ȓl���Ƃ��Ă��Х���������������i���͉~���̎��͂̂��镝���Ӗ�����j�ɐ���悤���� �����B
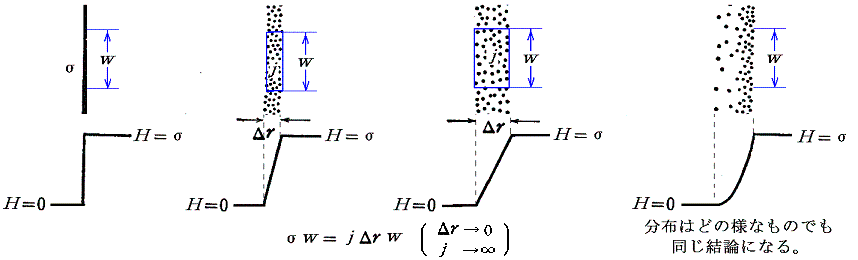
�@���̏ꍇ�ɂ͎���͑w�̓������g��0�ŁA�w�̌��݂̕����ɒ����I�ɑ������ĊO�����g���Х2���^�i2���j�����i�������������ɋ߂Â���j�ƂȂ�B���̔�̑̐ϗv�f�𗬂��d�ׂɓ����͂̕��ϒl�́A���炩�ɓd�ׂ��i�gout�{�gin�j�^2�̎���̒��œ����Ă���ƍl�����͂Ɉ�v����B���̂�����L�悤�Ɏ�����1�^2�̌W����������B
�@�~���̖ʓ��̓d�ׂ����̈��͂ɂ��~�������̋�Ԃɔ�яo�čs���Ȃ��̂́A�d�ׂ̖ʂɂƂǂ߂悤�Ƃ���ʂ̋����͂������Ă��邩��ł���B���ۓ��̒��̎��R�d�q�͎��R�d�q���O�ꂽ���̃C�I�����q�ɋ�����������Ȃ��痬��Ă���B���̂Ƃ����R�d�q�͕��̃C�I�����q�ɂ܂Ƃ����Ȃ��痬��Ă���̂ŁA�S�̂Ƃ��Đ����̓d�ׂ͑��݂��Ȃ��B���̂��ߓd��͑��݂��Ȃ��̂ŁA����Ɠd���̑��ݍ�p�̂ݍl����悢�B
�@
�i�Q�j������̉���
�P�D���͐��ɕ��s�Ȗʂɓ�����
�@������ɉ��z�I�ɍl�������͐��ɕ��s�Ȗʂɓ����͂��R�D�i�P�j�S�D�̓��̕\�ʂł̗͂�����̒��ɍL���čl����悢�B�܂莥��g�̏ꏊ�Ŏ���x�N�g���ɕ��s�ȒP�ʖʐςɓ����͈͂��͂ƂȂ�A���̑傫����

�ł���ƍl����B
�@
�Q�D���͐��ɐ����Ȗʂɓ�����
�@���͐��ɐ����Ȗʂɓ����͂́A�O�L�R�D�i�Q�j�P�D�̌��_�Ǝ��ꂪ���݂����ԑ̐ϗv�f�����͂̒ލ���Ԃɂ���Ƃ����������猈�肷��悢�B���̂Ƃ���ʓI�ȋȗ��̎��͐��̏�Ő�������̂́A���Z���x���ł͓���̂ŁA�ȒP�ȏ𗘗p���ē����B
�@����͕\�ʂɈ�l�ȓd�����x�Ђł����̐������֓d��������Ă���~���̂̎���̎���ł���B�R�D�i�P�j�R�D�Ő��������悤�ɁA���̎���̎���͉~���̒��S���ɑ��ē��S�~��ł��̕����͓d���ɑ��ĉE�l�W�̕����ł���B�����Ă��������ɑ��Ă͈�l�ł���B���̂Ƃ��m���S���甼�a���Ƃ��{�����̓�̎��͐��Ȗʁn�Ɓm���͐��ɐ����ȓ�̖ʁn�Ɓm���ɐ����ȕ��ʂł��Ƃ��{1�ɂ������̕��ʁn�Ő���ꂽ�����]�Ȃ�����̑̐ϗv�f�i���������ɂ͒P�ʂ̒����Ƃ���j���l����B
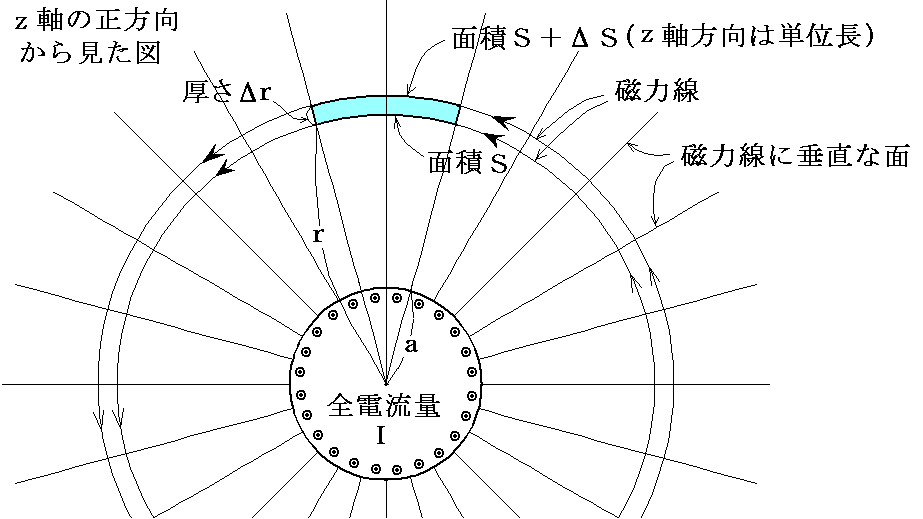
�@���̜]�Ȃ�����̐ϗv�f�̔��a�����ɐ����ȓ�ʂɓ����͂ƁA���ʂɓ����͂̒ލ����l����i�����ɐ����ȕ����̖ʂɊւ��Ă͏�ɂ荇�����������Ă���j�B���̂Ƃ��A�A���̓����̖ʂɓ����͂́A�ǂ���̑̐ϗv�f�ɒ��ڂ��邩�ŕ������t�]���鎖�ɒ��ӁB���}�̋�F���������ڂ���̐ϗv�f�ŁA����̑̐ϗv�f�ɓ����͂ł���B
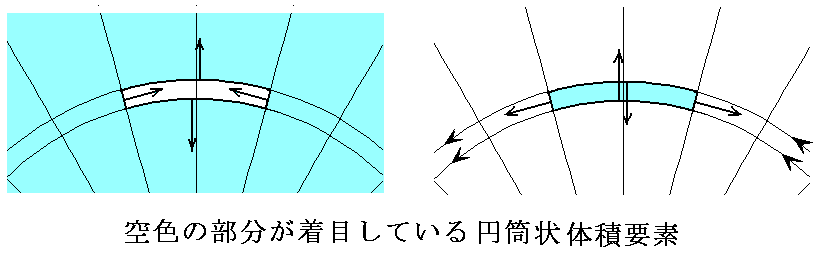
�@���}�̗͂ƉE�}�̗͖͂ʂ̔��Α��ɍ�p����͂ō�p����p�̖@�����疾�炩�Ȃ悤�ɑ傫���͓����������͋t�ł���B�����Œ��ڂ��Ă���̂͌��ł͂Ȃ��Ĕ�̑̐ϗv�f�������E�}�̗͂̒ލ����l����悢�B
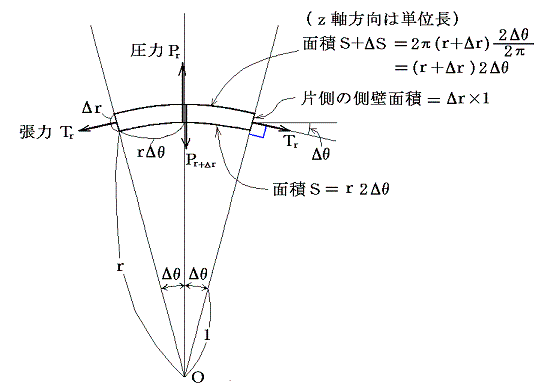
�@�܂��}�̜]�Ȃ����̏㉺�̖ʂɓ������a�����̈��͂̍����A���ǂɓ������͂̔��a���������̘a�ƒނ荇���Ă���ƍl����B���͐��ɕ��s�Ȗʂɓ����P�ʖʐϓ�����̈��͂or�ɂ����Q�D�i�Q�j�P�D�̌��_��p����Ɓi���������ɂ͒P�ʂ̒����Ƃ���j
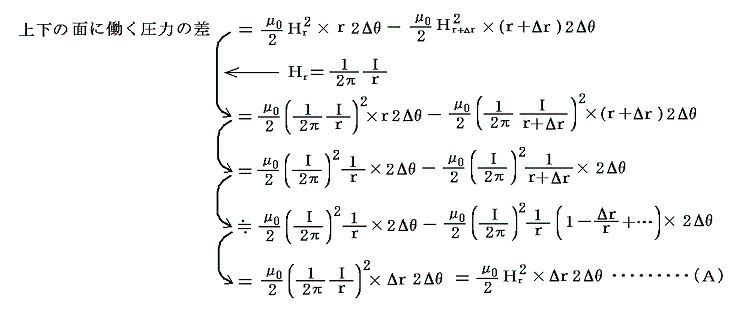
�ƂȂ�A���̕����͉~���̒��S������O�����ł���B
�@������ǂ̒P�ʖʐϓ�����̒��͂��sr�Ƃ����
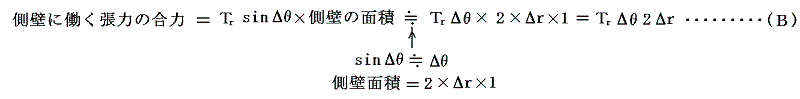
�ƂȂ�A���̕����͉~���̒��S���̕����������Ă���B
�@�̐ϗv�f�ɑ��鉞�͂̂荇���̏�������(�`)��(�a)�łȂ���Ȃ�Ȃ��̂ŁA���͐��ɐ����Ȗʂɓ������͂sr�͒P�ʖʐϓ�����
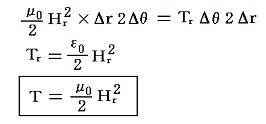
�łȂ���Ȃ�Ȃ��B����͎��͐��ɕ��s�ȒP�ʖʐϓ�����ɓ������͂o�Ɠ����傫���ł���B
�@
�i�R�j�C�ӂ̕������������P�ʖʐςɓ������̓x�N�g��
�P�D���̓x�N�g��
�@���ꒆ���剞�����R�D�i�Q�j�̗l�ɋ��܂�ƁA�C�ӕ������������ʂɓ������̓x�N�g���e�����܂�B���̋��ߕ����Q�D�i�R�j�P�D�ŏq�ׂ��d��̉��̓x�N�g���Ɠ����ł���B���̏ꍇ���d�C�͐��Ɠ����悤�ɁA���͐��ɐ����Ȗʂ������A���s�Ȗʂ������ƂȂ��B���̂��Ƃ���e�͈ȉ��̂悤�ɕ\�����B
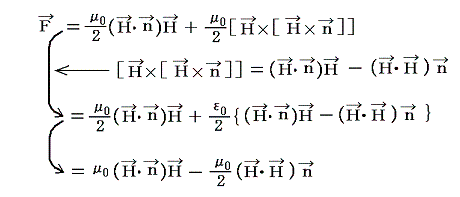
�x�N�g���̊W��}�������
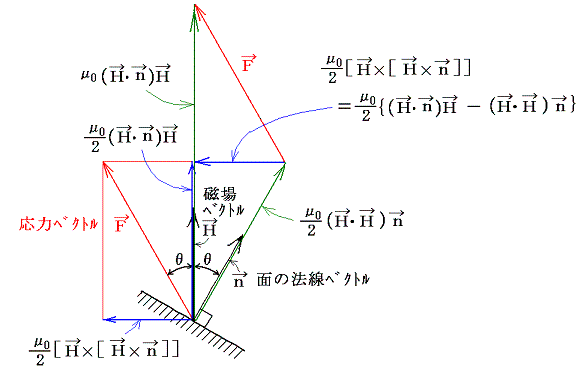
�ƂȂ�A�d��̏ꍇ�ƑS�������ɂȂ�B
�@
�Q�D���̓e���\��
�O�L�̃x�N�g���e�𐬕��\�������
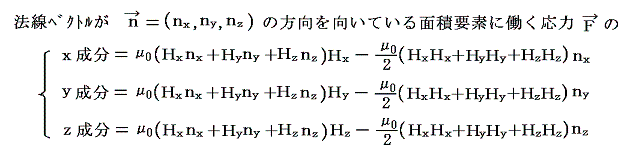
�ƂȂ�B
�@�ʐϗv�f�̖@���x�N�g�������i1�C0�C0�j�A�i0�C1�C0�j�A�i0�C0�C1�j�̓��ʂȏꍇ�ɂ��ċL����

�ƂȂ�B
�@������s��\������
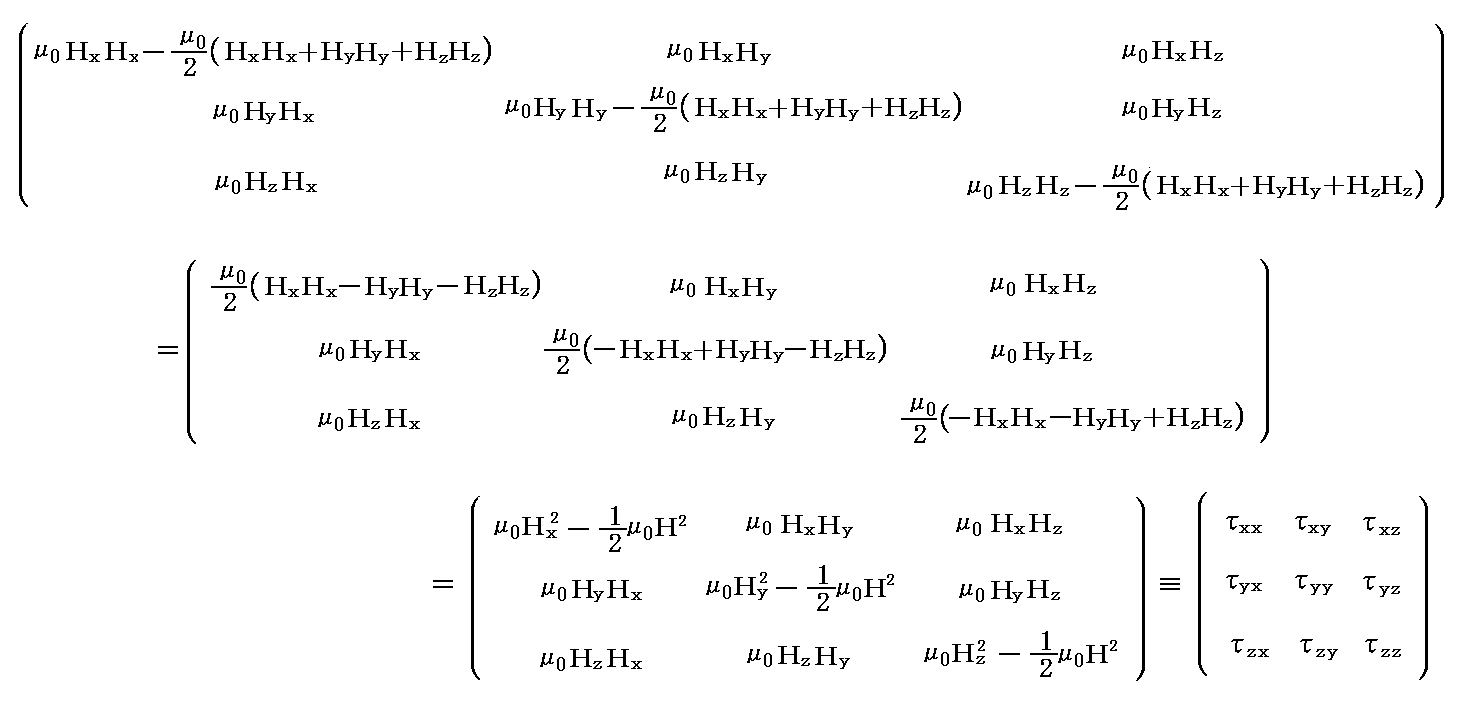
�͎���ɑ����}�N�X�E�F���̉��̓e���\���ł���B
�@���̃e���\���Ɋւ��Ă��Q�D�i�R�j�S�D�Ő����������������ׂĐ��藧���Ƃ͌����܂ł�����܂���B
�@
�R�D�Î�����̈�ł̗͂̒ނ荇���i2018�N2���NjL�j
�@�Î�����̔C�ӂ̑̐ϗ̈�ɂ�����͂̒ނ荇�����l���܂��B�Q�D�i�R�j�T�D�̐Ód��̏ꍇ�Ɠ��l�ɍl����悢�B
�Î�����̂���̐ϗ̈�u�̕\�ʂɓ���Maxwell�̉��͂̕\�ʐϕ����l���܂��B�܂�
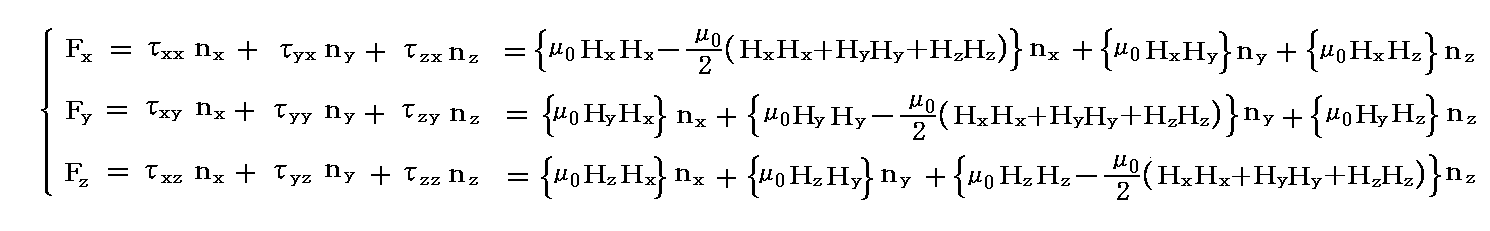
�̂��ꂼ��̃x�N�g�������̕\�ʐϕ����v�Z����B
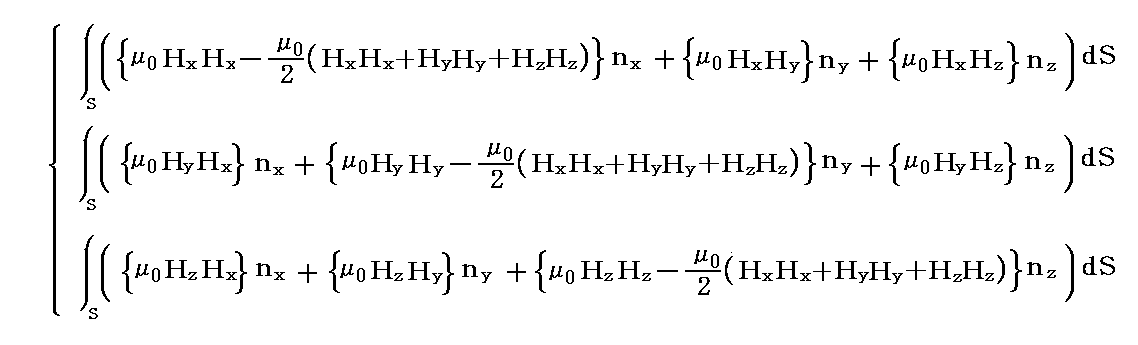
�@����́AMaxwell�̉��̓e���\�N�̊e�s�����ꂼ���̃x�N�g���ƌ��Ȃ����Ƃ��A���̃x�N�g���Ɨ̈�\�ʂ̖ʗv�f�����r�̓��ς�̈�\�ʑS�̂ɂ킽���ĕ\�ʐϕ��������̂�����A�K�E�X�̒藝�ɂ�艺�L�̑̐ϐϕ��ɒ������Ƃ��ł��܂��B���Ȃ킿
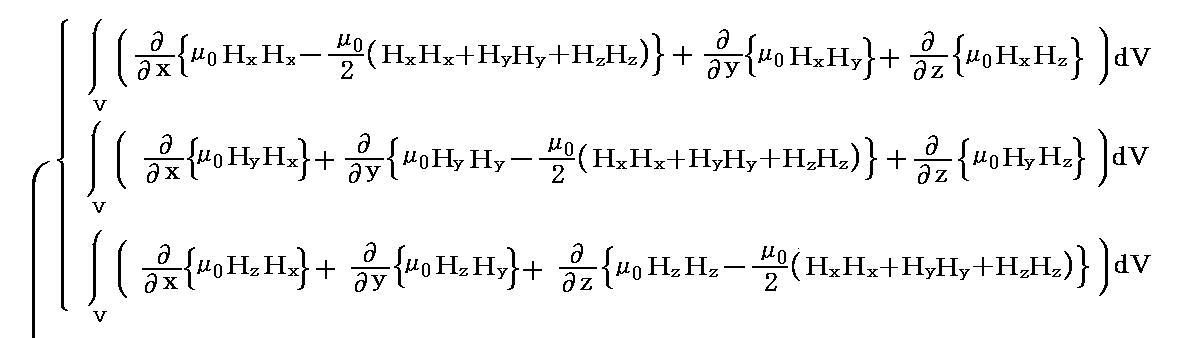
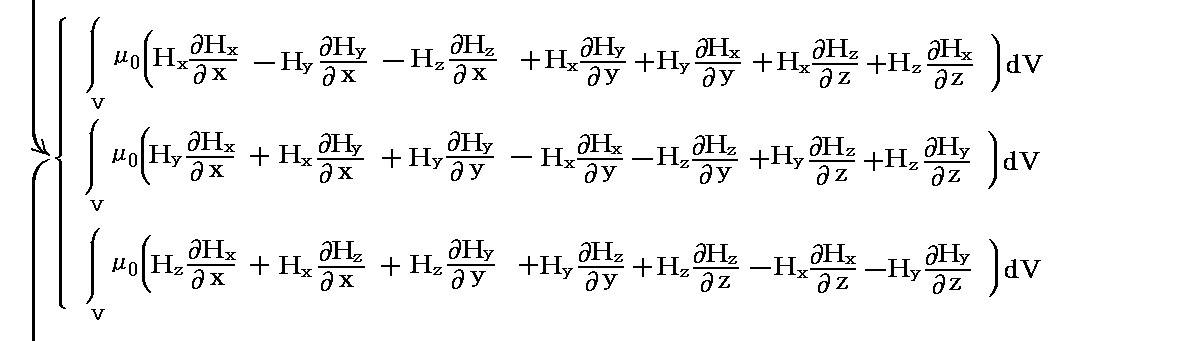
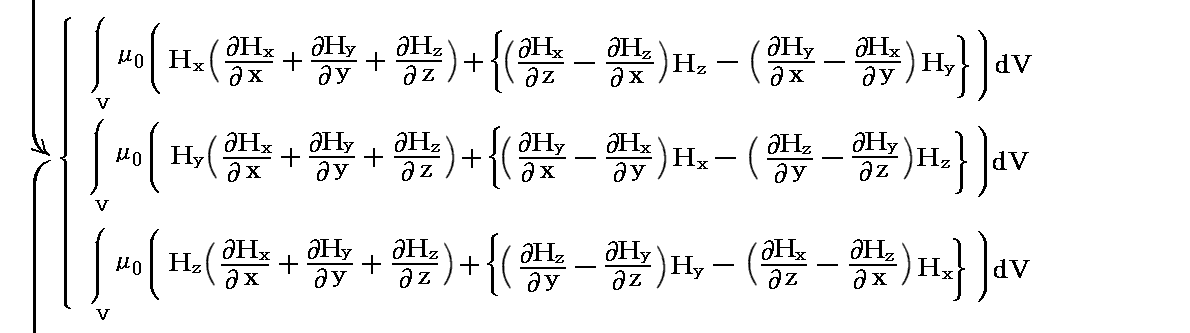

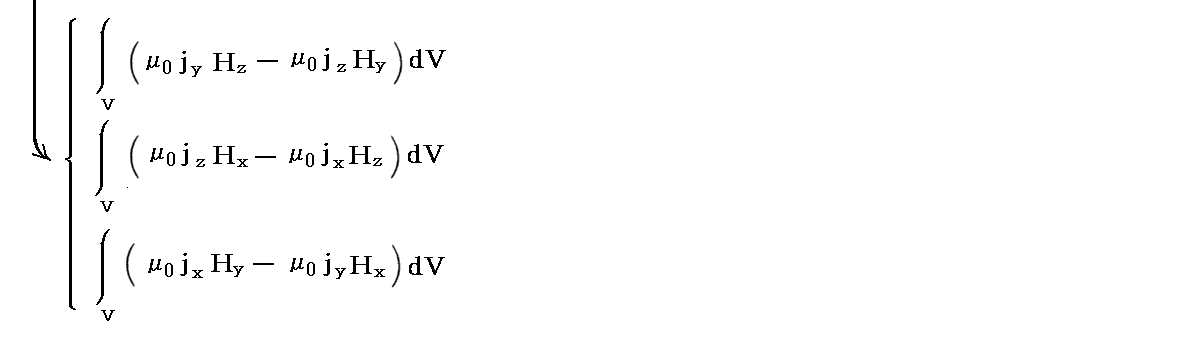
�ƂȂ�܂��B
�@���ʂ̋��ȏ��ł͏�L�̃x�N�g�����������e���\���\����p����
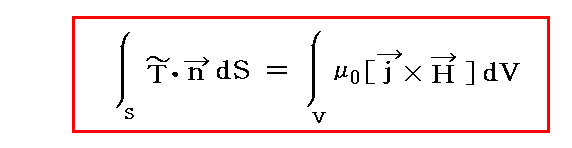
�Ə����Ă��܂����A��������\���Ă��܂��B
�@�e���\���\�L�ɂ���Ɠ�������܂����A�x�N�g���������̐����\�����܂Ƃ߂ď�����@�ɉ߂��܂����B�s��Maxwell�̉��̓e���\�N�ł��B�L�����g�`�h���s���e���\���ł��邱�Ƃ�\���ׂɂ��܂����B���傤���g���h��t���������g���x�N�g���ł��邱�Ƃ�\�����悤�ɁB�܂��A�e���\���ƃx�N�g���̓��� �s�E�����r �ɂ��Q�D�i�R�j�S�D�ŏq�ׂ��ȏ�̈Ӗ��͂���܂���B
�@�厖�Ȃ��Ƃ́A���̎��������Ӗ����邩�ł��B
�@�㎮���ȉ��̗l�ɏ��������Ă݂�Ή���₷���B
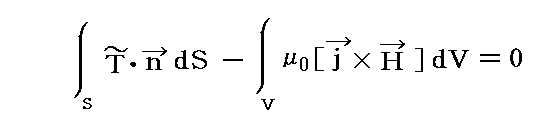
�@���ӂ̑�2���͓d����̈���ɑ��݂��镨���i�d���j�ɓ����͂̔���p�́i����͓d����̒P�ʑ̐ςɓ����̐ϗ͂ƌ����ׂ����́j�������ڂ��Ă���̐ϗ̈�S�̂ɂ킽���đ̐ϐϕ��������̂ł��B���̗͂̍��v�͍��ӑ�1���̑̐ϗ̈�̕\�ʂɌ����d����̕\�ʉ��͂�\�ʑS�̂ɂ킽���ĉ������킹�����̂ƒނ荇���Ă��鎖�������Ă���B
�@����́A�̈���ɑ��݂��镨���i�d���j���d���ꒆ�Ɍ���鉞�͂̌����Ȃ̂ł�����A��p����p�̌�������s���Ɠ�����O�ƌ���������܂��ł��B
�@��̗͂��ނ荇���Ă���̂́A���͕����i�d�����x�̑傫���ƕ��z�����A�܂���d���̂ݑ��݁j���ω������A�d������ÓI�Ƃ��Ă��邩��ł��B�����i�d���j��d���ꂪ���ԓI�ɕω�����Ƃ��ɂ́A���̓�̗͂͒ނ荇���Ă��܂���B���̏ꍇ�ɂ��Ă��R�D�i�R�j�T�D���Q�Ƃ��ĉ������B
�@
�S�D�d��Ǝ��ꂪ�����ɑ��݂���ꍇ
�@�d��Ǝ��ꂪ�����ɑ��݂���ꍇ�ɂ́A�e��ԕ����ɂ����鉞�̓e���\�����Q�D�i�R�j�R�D�̓d��ɂ�鐬���ƑO���R�D�i�R�j�Q�D�̎���ɂ�鐬���𑫂����킹�����̂ɂȂ�B�܂�
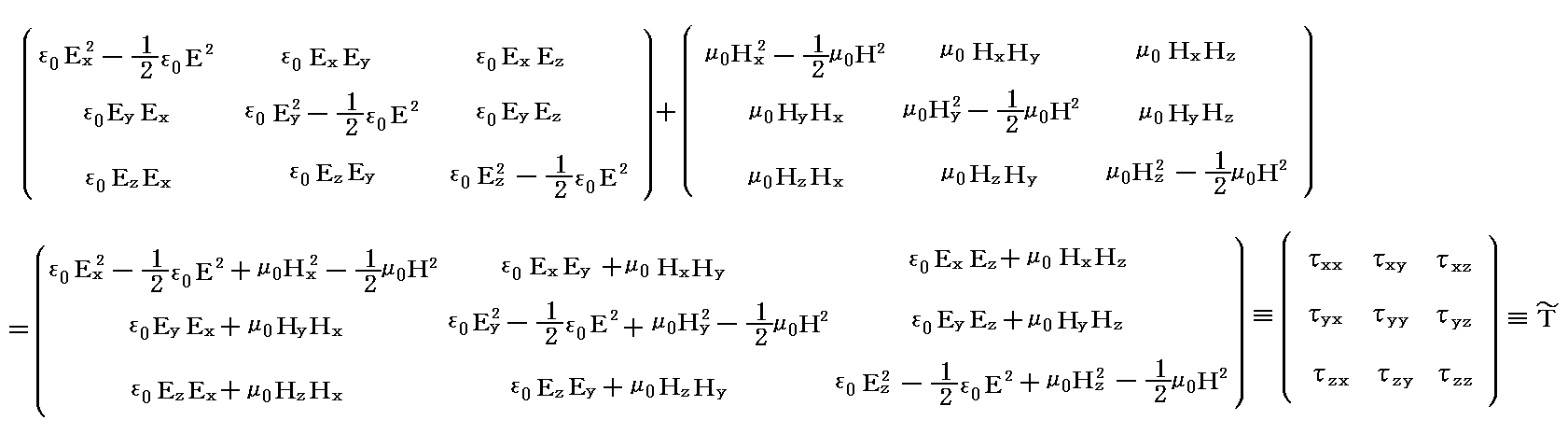
�ƂȂ�B�Ō�̋L�����g�`�h���s���e���\���ł��邱�Ƃ�\���ׂɂ����B���傤���g���h��t�����x�N�g���ł��邱�Ƃ�\�����悤�ɁB
�@����͎��ԓI�ɕω�����ꍇ���܂߂��C�ӂ̓d������̔C�ӂ̓_�ɂ�����Maxwell�̉��͂̃e���\���\���ł��B
�@�e���\���̈Ӗ��ɂ��Ă��Q�D�i�R�j�S�D���Q�Ƃ��ꂽ���B�����ł��q�ׂ��l�ɉ��̓e���\���͏�� ��ij����ji �������Ώ̃e���\���ł��B�܂��Ίp�v�f�̘a�� ��xx�{��yy�{��zz���|{(1�^2)��0�d2�{(1�^2)��0�g2} �ƂȂ�B�@
�@
�T�D���ԓI�ɕω�����d������ɂ�����͂̒ނ荇���i2018�N2���NjL�j
�@�Q�D�i�R�j�T�D�ł͐Ód����ł́A�R�D�i�R�j�R�D�ł͐Î�����ł̗͂̒ނ荇�����l�@���܂������A�����ł��d���ꂪ���ԓI�ɕω�����ꍇ���܂߂��C�ӂ̓d������ɂ�����̐ϗ̈�ɂ��Đ��藧���s�͂̒ނ荇���̖@���t�������܂��B
�@�������A�����i�d�ז��x���z��d�����x���z�j�����ԓI�ɕω����A����ɔ����d���ꂪ���ԓI�ɕω�����ꍇ�ɂ́A�Q�D�i�R�j�T�D�i�Ód��j��A�R�D�i�R�j�R�D�i�Î���j�̏ꍇ�̂悤�ɓd����̈���̑̐ϗ͐ϕ��Ɠd����̈�\�ʂ̕\�ʗ͐ϕ����݂��ɒނ荇���킯�ł͂���܂���B�̐ϗ̈���̓d����̉^���ʂ̎��ԓI�ω���\�������V���ɏo�Ă��܂��B
�@���̂��߁A�s�͂̒ނ荇���̖@���t�ł͂Ȃ����s�d����̉^���������t��\�����ƂȂ�܂��B
�@��L�̕��j�ɏ]���āA�@�Q�D�i�R�j�T�D�i�Ód��j��A�R�D�i�R�j�R�D�i�Î���j�̏ꍇ�Ɠ��l�ɂ��Ηǂ��̂ł����A����́A�Q�D�i�R�j�T�D�i�Ód��j�ŗp����

�͎g���܂���B
�@��

��p���Ȃ���Ȃ�܂���B
�@�܂��A�R�D�i�R�j�R�D�i�Î���j�ŗp����

�̌㔼�͎g���܂���B
�@�㔼�͓d��̎��ԓI�ϓ������܂߂�

��p���Ȃ���Ȃ�܂���B
�@�ȏ�̂Q�_���ς�邾���Ō�̓W�J�͓����ł��B
���ԓI�ȕω�������d������̔C�ӂ̑̐ϗ̈�u�̕\�ʂɓ���Maxwell�̉��͂̕\�ʐϕ����l���܂��B�܂�
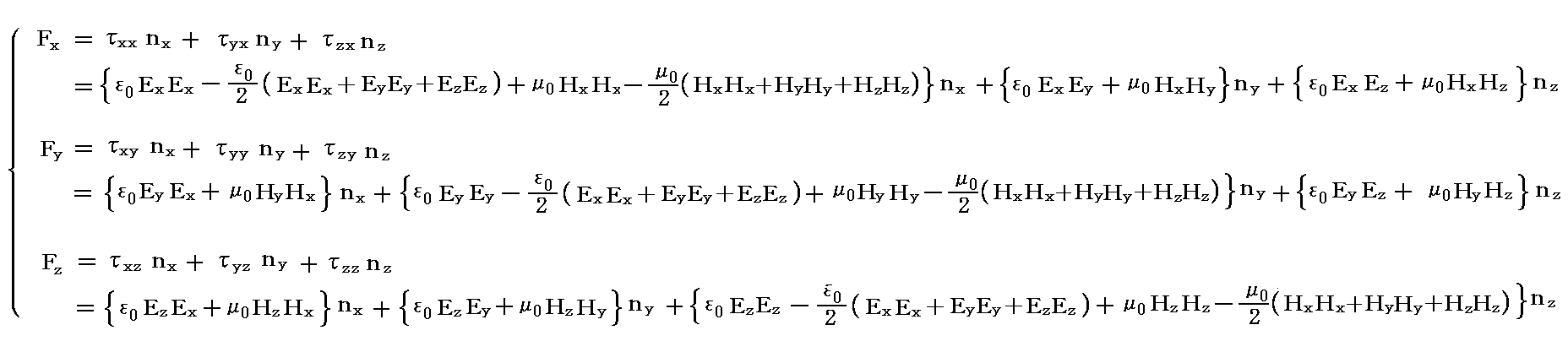
�̂��ꂼ��̃x�N�g�������̕\�ʗ̘͂a���v�Z����B
�@Maxwell�̉��̓e���\�N�̊e�s�����ꂼ���̃x�N�g���ƌ��Ȃ����Ƃ��A���̃x�N�g���Ɨ̈�\�ʂ̖ʗv�f�����r�̓��ς�̈�\�ʑS�̂ɂ킽���ĕ\�ʐϕ����܂��B���̂Ƃ��x�N�g����͂ɂ������K�E�X�̒藝�ɂ��̐ϐϕ��ɒ�����B
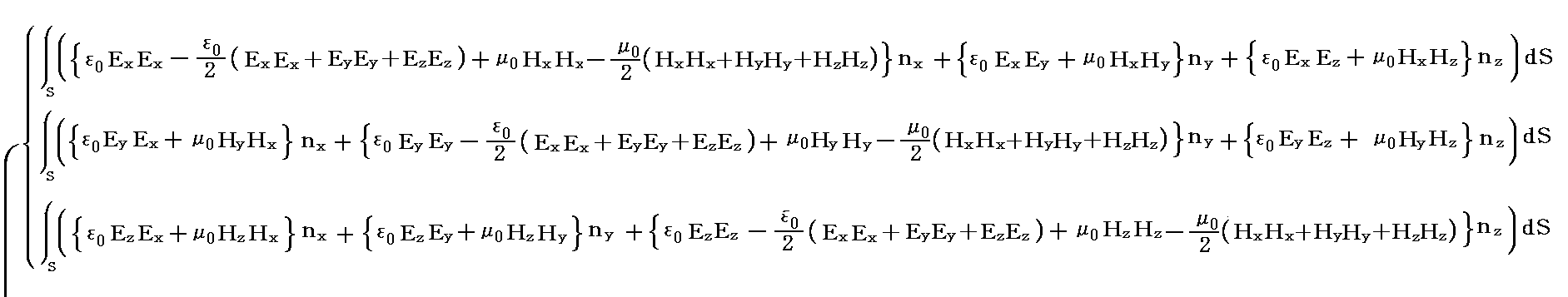
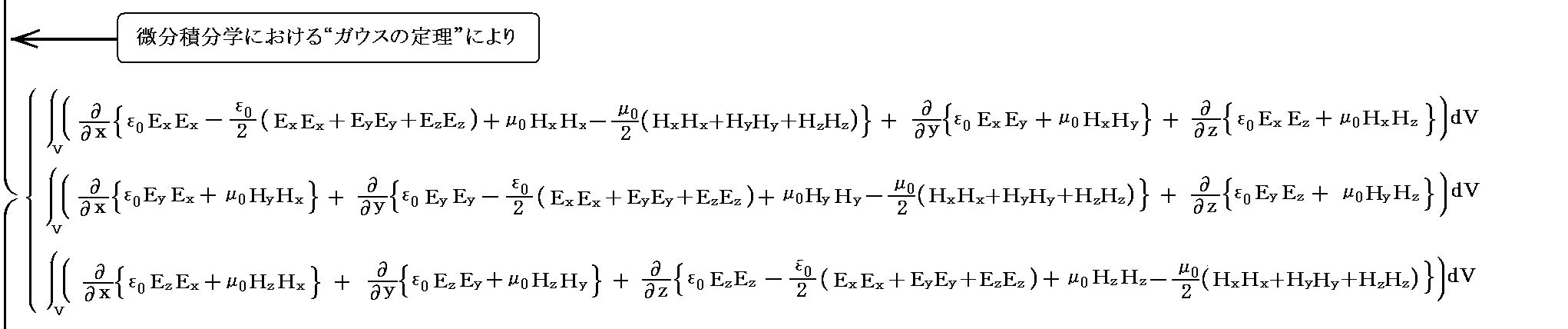
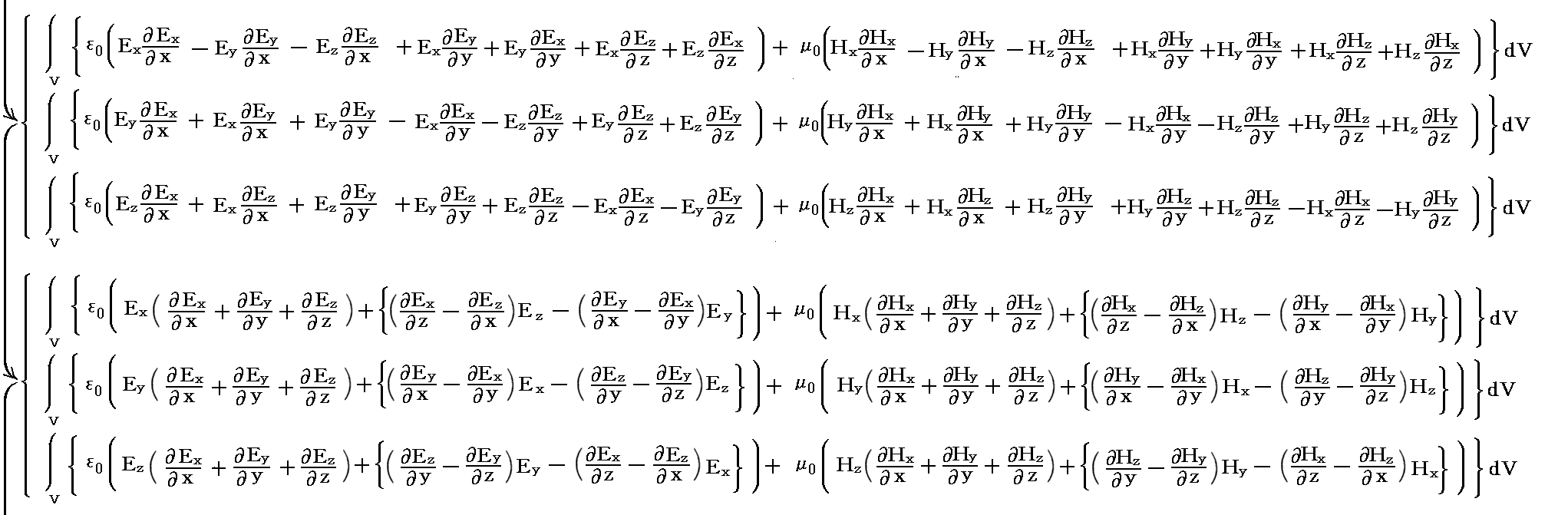

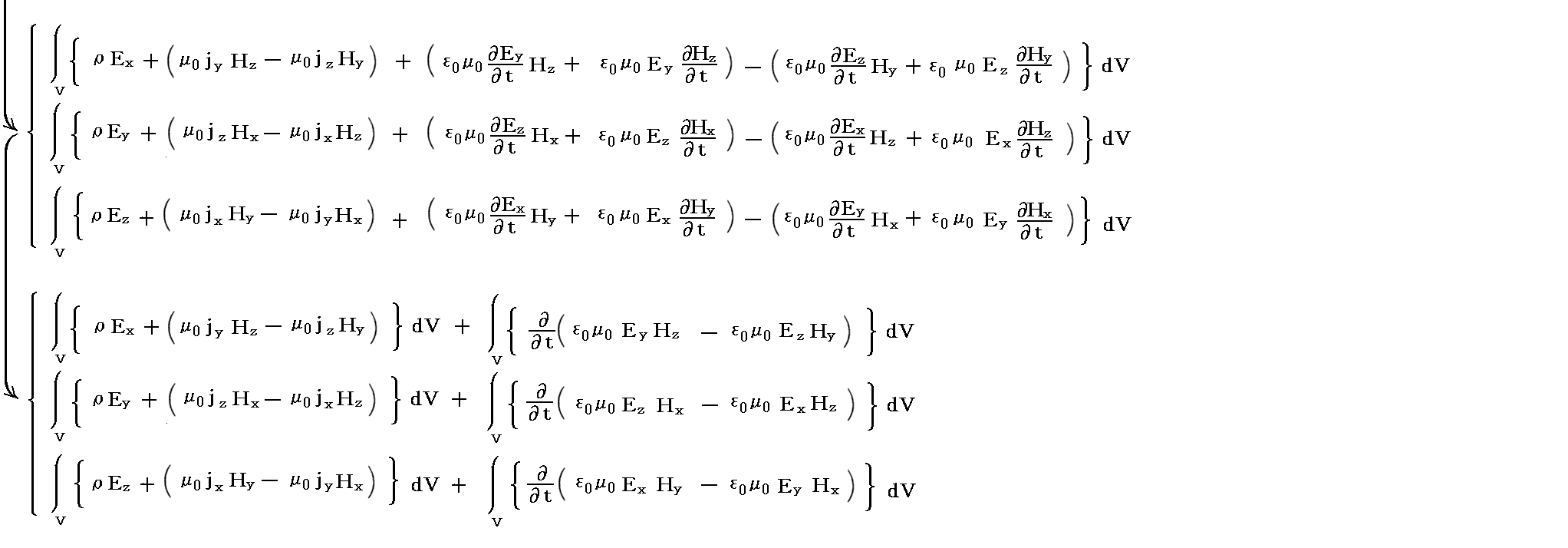
�ƂȂ�B
�@����͈ȉ����x�N�g����������\���Ă���B
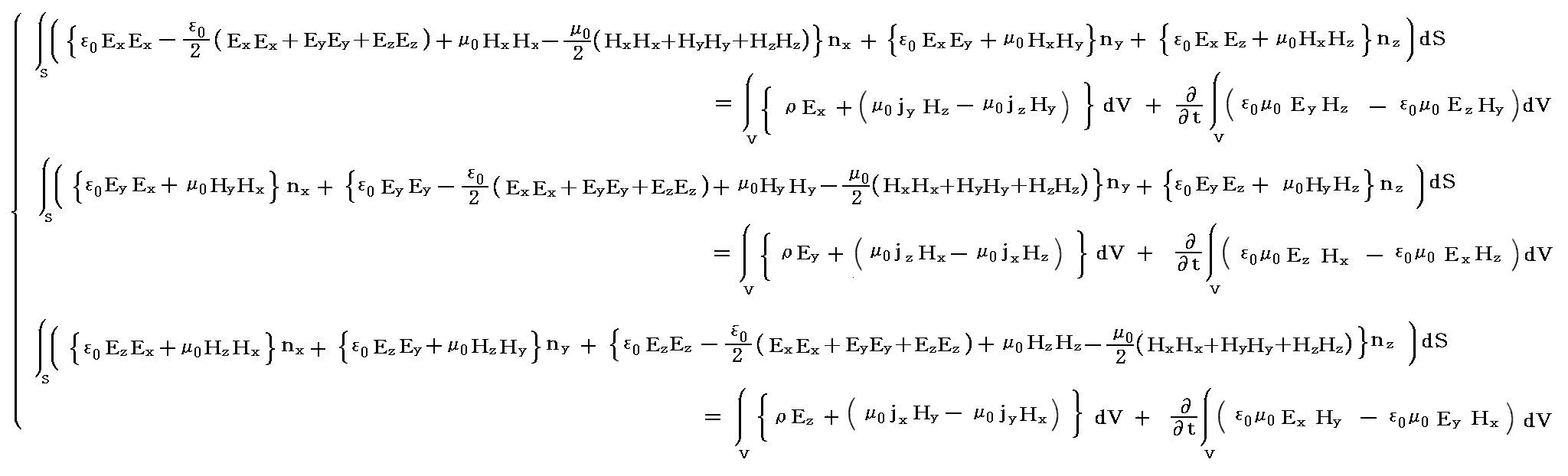
�@���̂܂܂ł͉���ɂ����̂ŁAMaxwell�̉������e���\���s�ŕ\����
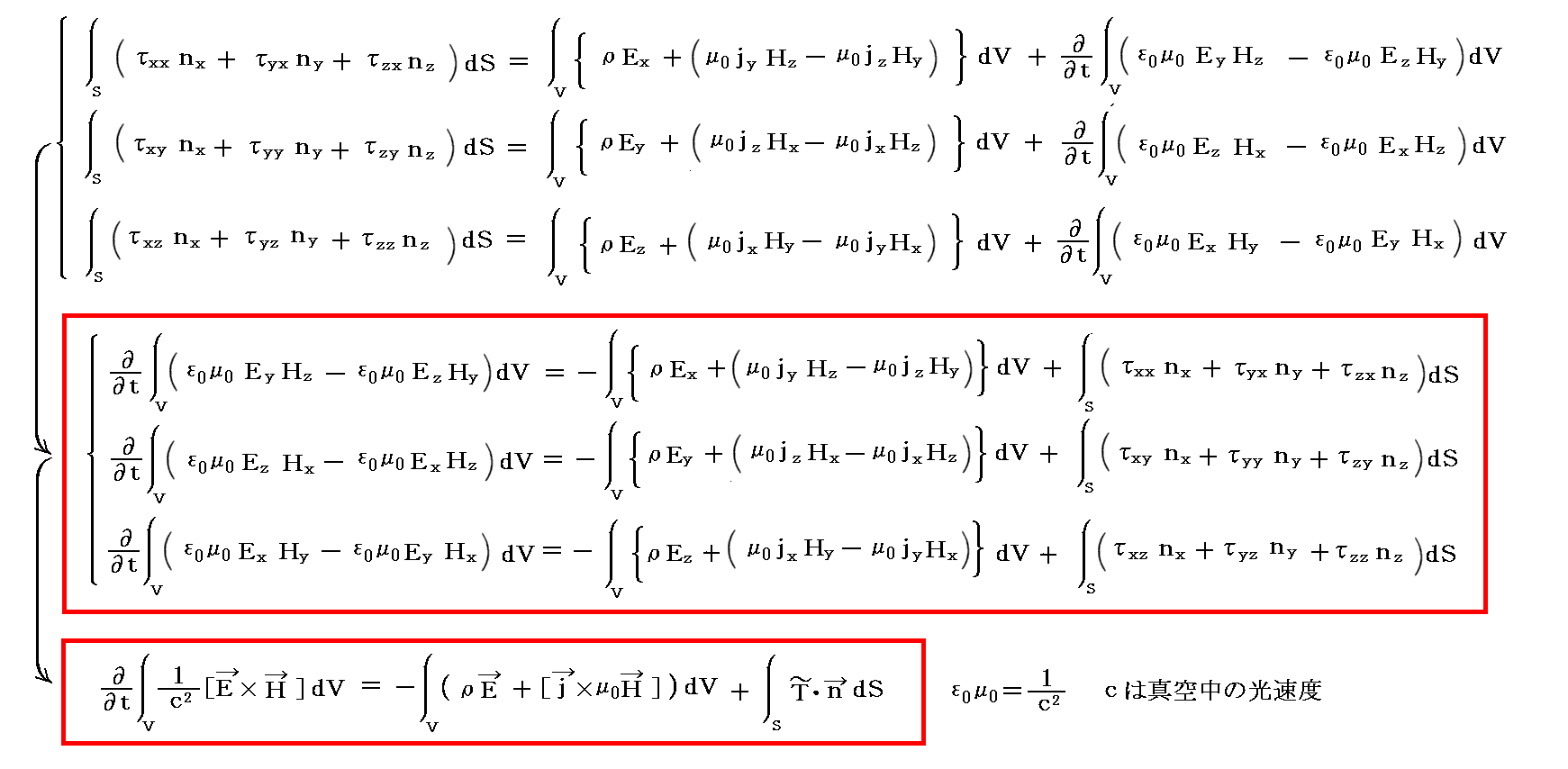
�ƂȂ�B
�m�⑫�����P�n
�@�厖�Ȃ̂́A���̎��������Ӗ����邩�ł��B
�s���Ӂt
�@�m�d����̉^���ʖ��x�̎��ԓI�ω��̑̐ϗ̈�S�̂ɂ킽��ϕ��l�i�������x�N�g���l�j�n��\���B�m�d�~�g�n�̓|�C���e�B���O�x�N�g���ł���A��0��0��1�^��2�ł�������A�G�l���M�[�����x�i���^���ʖ��x�j�̑̐ϗ̈�S�̂ɂ킽��ϕ��l�̎��ԓI�ω��̊�����\���Ă���B
�s�E�ӑ�1���t
�@�m�̐ϗ̈�ɑ��݂��镨�́i�d�ׂ�d�����\��������́j�ɓ������[�����c�͂̔���p�́i���ꂪ�d����ɓ����̐ϗ́j�n��\���B�|�����͔���p�͂ł��邱�Ƃ�\���Ă���B����͑̐ϗ̈�u�S�ʂɂ킽��̐ϐϕ��ł��邱�Ƃɒ��ӁB
�s�E�ӑ�2���t
�@�m�̐ϗ̈�̕\�ʂɉ����ēd����ɓ����\�ʗ͂̐ϕ��l�i�������x�N�g���l�j�n��\���Ă���B
�@
�@�܂肱�̎��́A�g�m�d����̉^���ʂ̎��ԓI�ω��n�͂����m�d����ɓ����̐ϗ́n���m�\�ʗ́n�̘a�ɓ������h�Ƃ����s�d����̉^���������t��\���ϕ��^���g�x�N�g���������h�ł��B
�@
�@�x�N�g�������������s���gMaxwell�̉��̓e���\���h�ł����A�g�e���\���h�Ƃ̓x�N�g���Ƃ̐ρi���ςɑ�������j����邱�Ƃɂ���Ĉ�̃x�N�g����\�����邽�߂̐��w�I�ȍH�v�ł��B�L�����g�`�h���s���e���\���ł��邱�Ƃ�\���ׂɂ��܂����B�E�ӑ�2���́A�̐ϗ̈�̕\�ʂɌ���鉞�͂̑̐ϕ\�ʑS�̂ɂ킽��ϕ���\���Ă��܂��B���C���C���������ꂼ��̐ϕ��l�i3�����j����̎��ŕ\���Ă��܂��B
�@���̂�������Q�D�i�R�j�S�D�K���ĉ������B
�@
�@�������|�C���e�B���O�x�N�g�����o�Ă��܂����A�����ł͕\�ʐϕ��ł͂Ȃ��āA�̐ϐϕ��ŊW���܂��B�������|�C���e�B���O�x�N�g�����̂��̂ł͂Ȃ��āA����������x�̓��Ŋ������x�N�g���ʂ̐ϕ��ł��邱�Ƃɒ��ӂ��ĉ������B
�@�����Ƃ悭�����W���Ƃ��āA�̐ϗ̈�u�ɂ������s�d����̃G�l���M�[���x�t��\���ϕ��^���g�X�J���[�������h������܂��B���̂Ƃ��̃|�C���e�B���O�x�N�g���͑̐ϗ̈�̕\�ʐϕ��l�Ƃ��ĊW���Ă��܂��B����Ƃ̈Ⴂ�ɒ��ӂ��ĉ������B
�@���̂��Ƃɂ��Ă͕ʍe�u�d����̃G�l���M�[���x�ƃ|�C���e�B���O�x�N�g���v�Q�D�i�R�j�m�⑫�����R�n�Ő������Ă��܂��̂ł����������B
�@
�@
�@����ɕt�������܂��ƁA�{�e���x�N�g���������Ə�L�ʍe���X�J���[�������́A�~���R�t�X�L�[����œ�������Ĉ���e���\�����������\�����܂��B�����āA��������[�����c�ϊ��ɑ��ĕs�ςȕ������ƂȂ�܂��B���̂��Ƃɕt���Ă͕ʍe�uMaxwell�������n�̐挩���Ɠd���|�e���V�����iLorenz gauge�j�v�U�D�������������B
�@�d���ꂪ���ԓI�ɕω�����͓̂d�����ԓ��ɑ��݂����g�����i�d�ׂ�d���j�h���g�d����h�����ݍ�p���邩��ł��B�܂�d�ׂ̑��݈ʒu�����ԓI�ɕς��A�d���̑傫����ʒu�����ԂƋ��ɕς�鎖�ɂ���ēd���ꂪ���ԓI�ɕω�����̂ł��B���Ƃ��g�t�@���f�[�̓d���U���̖@���h�́g���[�����c�̗̖͂@���h���ʕ\���ł��B
�@�����玞�ԓI�ɕω�����d����̗l�q��\���s�d����̉^���������t�����߂�ɂ́A�g���[�����c�̗̖͂@���h����o������Ηǂ����Ƃ�����B����͎��ԓI�ɕω������ɂ����Ă���������������ł��B
�@�܂�A���[�����c�̗̖͂@���̑̐ϐϕ���Maxwell�̓d�����������p���ĕό`���čs���A�̐ϗ̈�\�ʂ�Maxwll�̉��͂̕\�ʐϕ��ƊW�Â��邱�Ƃ��ł���ł��傤�B������x�͑̐ϗ̈���̓d����̎��ԓI�ω��ɔ������������͂��ł��B�������s�͂̒ނ荇���̖@���t���s�d����̉^���������t�ɂȂ�킯�ł��B
�m�⑫�����Q�n
�@���ʂ̋��ȏ��ł́A�g���[�����c�̗̖͂@���h����d����̉^�����������܂��B����͕ʍe�u�A�C���V���^�C���̌����d������2�̏ؖ��v�R�D�m�⑫�����P�n�̉E�����Ԏ����͂ݘg���Ő������������ł��B
�@���傤�Ǘǂ��@��Ȃ̂ŁA�����ł܂Ƃ߂Ă����܂��B�O�q�̋c�_���t�ɂ��ǂ邾���ł��B




�@
�i�S�j����������
�P�D���������ɗ���镽�s�d���Ԃ̈���
�@�^�ɏ\�������Q�{�̒�����̓���������2��[m]�����ĕ��s�ɒ���A���������ɂ��ꂼ��h�mA�n�̓d���𗬂��B���̂Ƃ��������݂͌��Ɉ��������B�����̒����k������̈��͂��A�Q�{�̓����̐^�̖ʏ�Ɍ����}�N�X�E�F���̉��͂��������킹�邱�Ƃɂ�苁�߂Ă݂�B
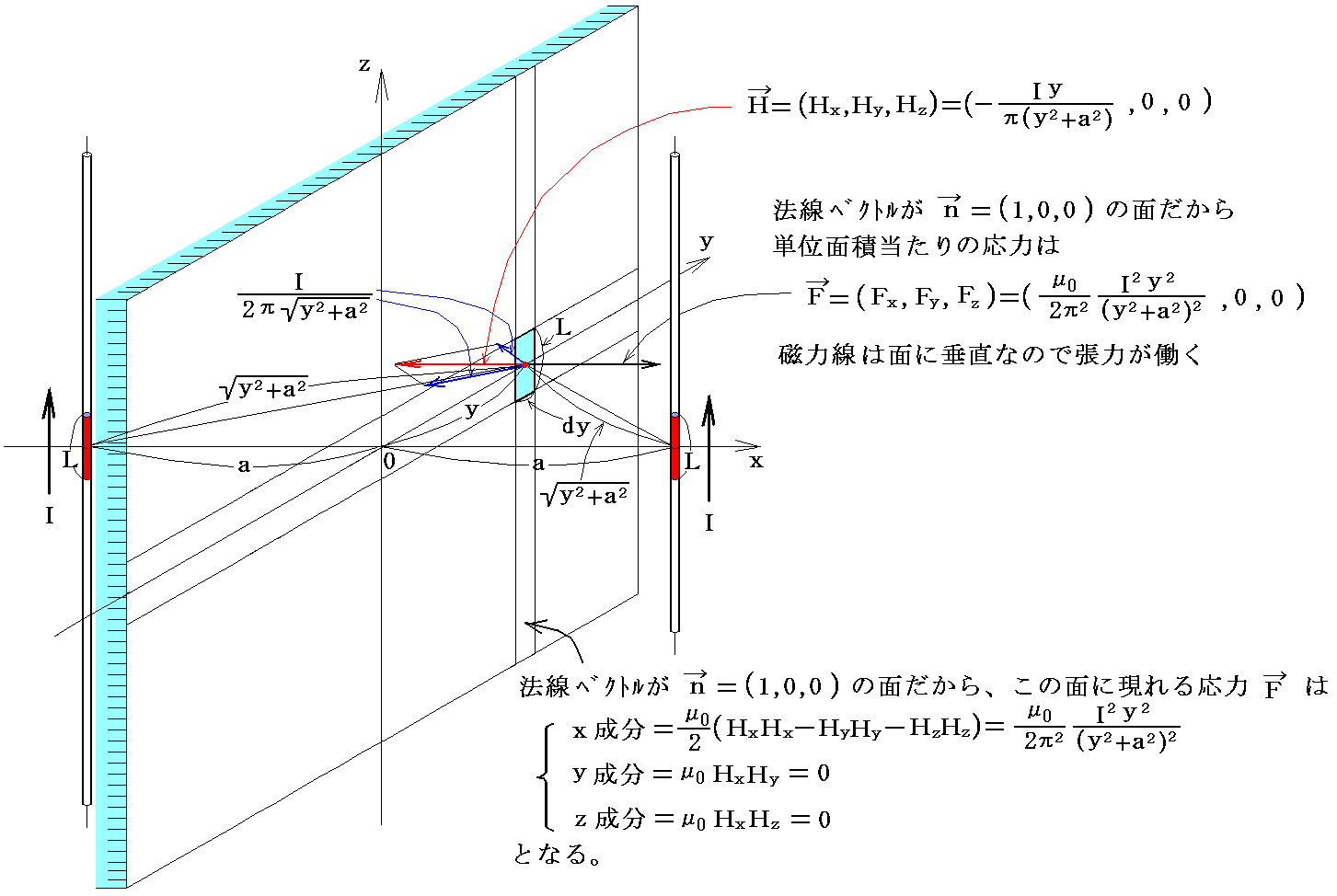
�@��L�̉��͂��k�̕��������|���`+���ɂ킽���ĉ������킹�����̂��i���C���j���i���C0�j�̈ʒu�̓d��+�h���i���C���j���i-���C0�j�̈ʒu�̓d��+�h�������k�̕����ɋy�ڂ����͂ł���B
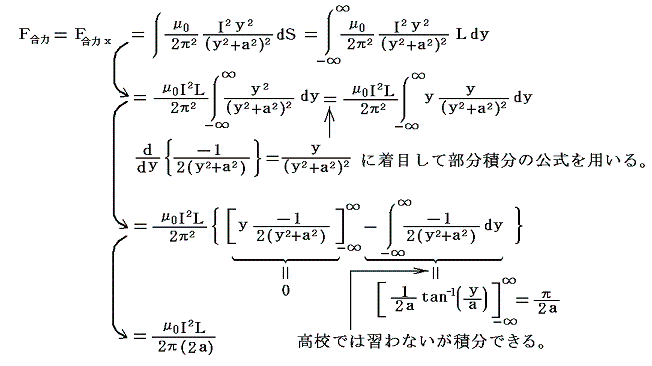
�@����́A�܂��������Z�����̎��ƂŏK�����u��p�ɂ��ƂÂ����ʁi���}�Q�Ɓj�ƈ�v����B
�@������R�D�i�Q�j������̉��͂̒�`����l���č݂�Ӗ����R�ƌ����Γ��R�ł���B�d���̈ʒu�ł̉��͂����͐��ɐ����ȕ����Ɋe�̐ϗv�f�Ɋւ��Ēލ��̏�����ۂ��Ȃ��玟�X�Ɖ��͂��e��ԂɊ��蓖�Ăčs���̂ł��邩��B
�@
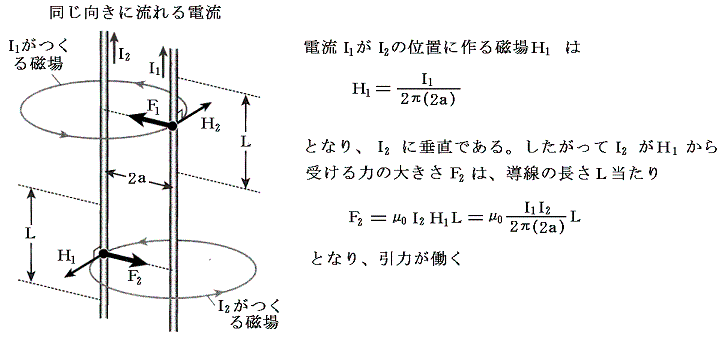
�Q�D�t�����ɗ���镽�s�d���Ԃ̐˗�
�@�^�ɏ\�������Q�{�̒�����̓���������2��[m]�����ĕ��s�ɒ���A�t�����ɂ��ꂼ��h�mA�n�̓d���𗬂��B���̂Ƃ��������݂͌��ɔ�������B�����̒����k������̔����͂��A�Q�{�̓����̐^�̖ʏ�Ɍ����}�N�X�E�F���̉��͂��������킹�邱�Ƃɂ�苁�߂Ă݂�B
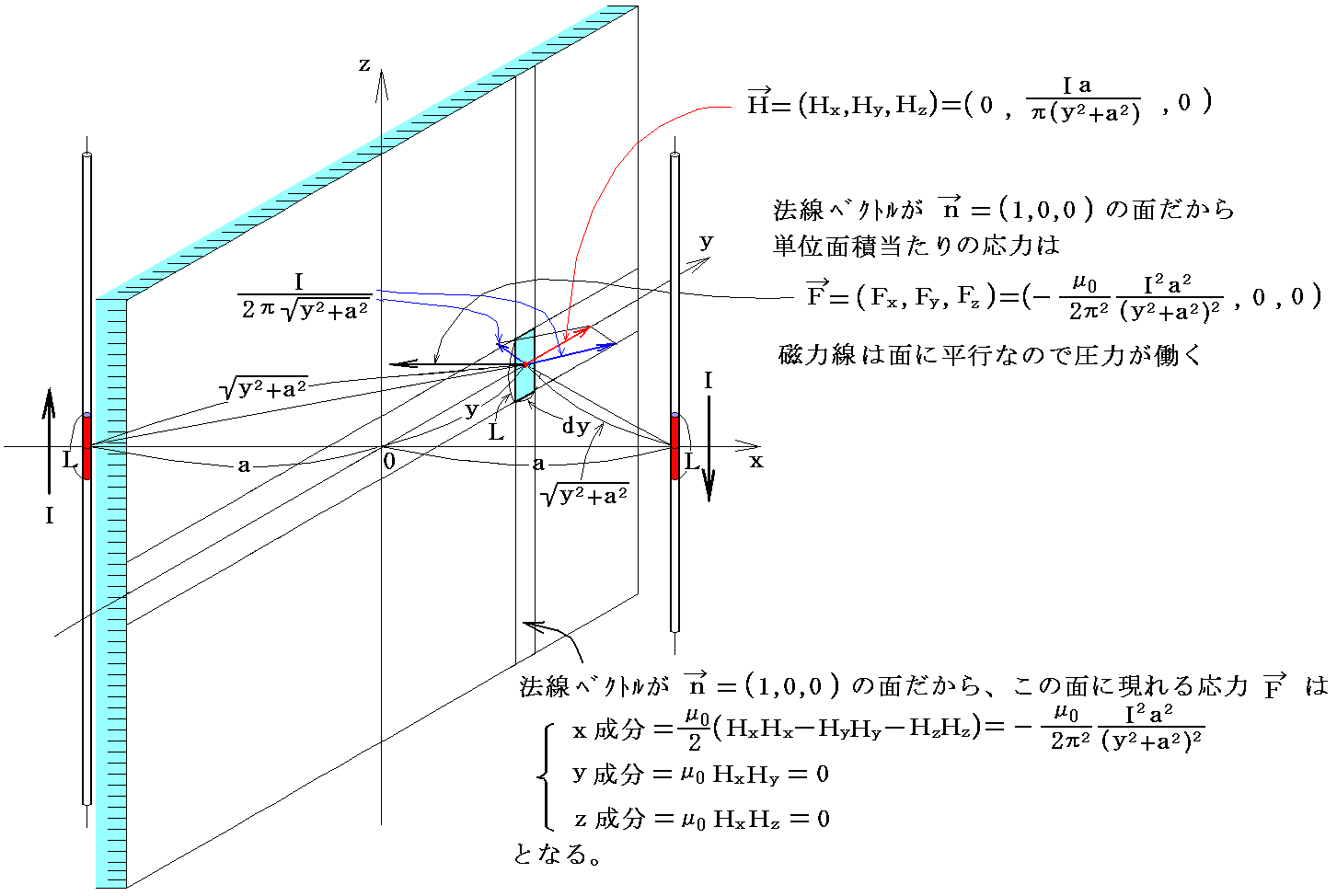
�@��L�̉��͂��k�̕��ł����|���`+���ɂ킽���ĉ������킹�����̂��i���C���j���i���C0�j�̈ʒu�̓d��-�h���i���C���j���i-���C0�j�̈ʒu�̓d��+�h�������k�̕����ɋy�ڂ������͂ł���B
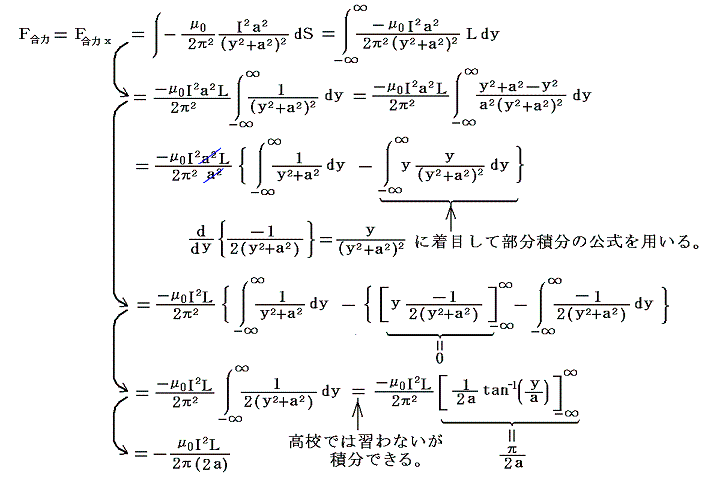
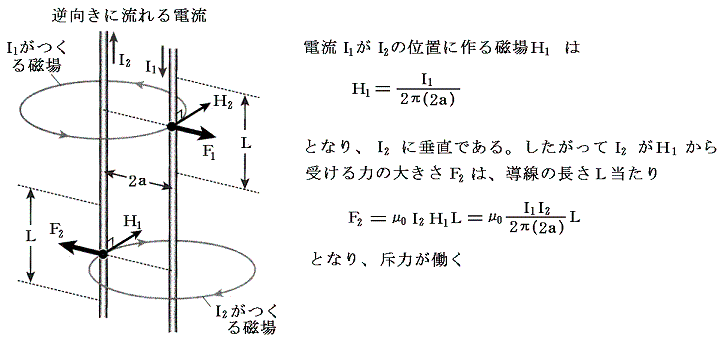
����́A�܂��������Z�����̎��ƂŏK�����u��p�ɂ��ƂÂ����ʁi���}�Q�Ɓj�ƈ�v����B
�@
�R�D�~����d���̔��a�����k������d���Ǝ���̃G�l���M�[
�@�~����d���̉~���̔��a��������i���|�����j�Ɏ��k������̂ɕK�v�Ȏd���ʁi�~���̒����k������j���A�~�������k�����̈�ɐV���Ɍ���鎥��̃G�l���M�[�i1/2�j��0�g2�~�i2���~�����~�k�j�ɓ��������Ƃ��Ă݂悤�B�����Łi2���~�����~�k�j�͐V���Ɏ��ꂪ�����̈�̑̐ςł���B�P�ʑ̐ϓ�����̎���̃G�l���M�[���i1/2�j��0�g2�ł��邱�Ƃ͕ʍe�u�d���ƃG�l���M�[�v�Q�D�i�T�j�i�Q�j�Ő��������B
�@�d��̏ꍇ�A���͂𗘗p���ċ��k�����k������d�����v�Z����ƁA���k�����k�������Ƃɂ���Đ�������Ԃɓd�ꂪ�V���Ɍ���āA���傷��d��̃G�l���M�[�Ƃ��܂��Ή����邱�Ƃ��m���߂�̂͊ȒP�������B�������A����̏ꍇ�A�~����d���̔��a�����k����Ƃ��ɗv����d���ʂƎ��k������ԂɌ���鎥��̃G�l���M�[�̑Ή��W���m���߂�̂͏����ʓ|�ł���B
�@�~����d���̉~���̔��a���A�d���l�����ɂ��������܂܁A�����炁�|�����Ɏ��k������Ƃ��̎d���́A�~���\�ʂɓ����Ă���͂��R�D�i�P�j�S�D�ŏq�ׂ��悤�Ɉ��͂ł��邩��A���ɂȂ��B���̂Ƃ��A����̒��œ��������Ɠ����ɂ͓d���̗����W����t�N�d�͂������邱�Ƃ��v���o���K�v������B���̓d���l��ۂ��߂ɂ͓d���ɑ��Đ��̎d�������������Ȃ���ΐ���Ȃ��B���̎d������������������������ʂ͐��̎d����������悤�Ɏv����B���������̋t�N�d�͂����߂�v�Z�ɂ�1�^2�̊|�������g��p����K�v�������̂ŁA���҂𑫂����킹�Ă���̎d�������o�Ă��Ȃ��B
�@���̎d���ɂ���ɂ͂���ɉ������K�v���B���ꂪ���Ԃ̌o�߂Ƌ��ɐV���Ɍ����̂�����d���U���ɔ����Đ�����d��̌��ʂ��l�����Ȃ���Ȃ�Ȃ��B�ȉ����Ԃɐ�������B
�@�܂��A�R�D�i�Q�j�P�D�Ő��������悤�ɉ~���ʂɂ͒P�ʖʐϓ�����i1/2�j��0�g2�̃}�N�X�E�F���̉��́i���́j�����݂���B���̂��߉~�����k�߂邽�߂̎d���͍����̔����ʂ�����ƁA�~���̒����k�E����������

�ƂȂ�B���Ƃ̂��A�O�͂Ƃ��Ă͂ewL�Ƃ͋t�����̗͂������Ȃ��炷��d���ɂȂ�̂ŁA���R�̎��Ȃ������̎d���ɂȂ�B
�@���̂Ƃ��A�~���d���͎���ɐ����ɓ������̂�����A���̒��̓d�ׂɂ����[�����c�͂������B����͓d���̗���Ă�������Ƃ͋t�����ƂȂ�t�N�d�͂���B���̗͂ɋt����čŏ��̓d���l���ێ����Ȃ���Ȃ�Ȃ��B����͓d���ɑ������̎d�������Ȃ���Ȃ�Ȃ����Ƃ��Ӗ�����B���L�̗l�ɋL�����߂āA���̒l���v�Z���Ă݂�B
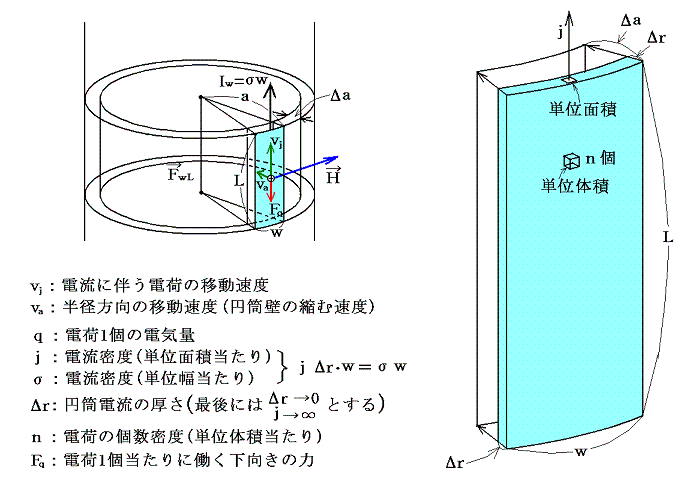
�@�d�ׂP������ɓ����t�N�d�͂ɔ����͈͂ȉ��̂悤�ɂȂ�B���̂Ƃ����A����g�͓d�ׂ̑��݂��郢���Ɋւ��Č���������0����g�܂ŕω�����̂��g�Ɋւ���(1/2)�̊|���������ϒl��p���Ȃ���Ȃ�Ȃ��B
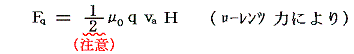
�@�d���d�ׂ͒P�ʎ��Ԃɂ�j���������̐������Ɉړ����Ă���B���̂Ƃ��ŏ��̓d���l���ێ�����ɂ́A�t�N�d�͂Ő�����͂ɑ�������͂�������ɉ����Ȃ���ړ������˂Ȃ�Ȃ��B���̎d�������k�~���~�����̑̐ϗv�f���̑S�d�ׂɑ��ĉ������킹��悢�B�܂肱�̑̐ϗv�f���̑S�d�ׂɑ���d�����o��
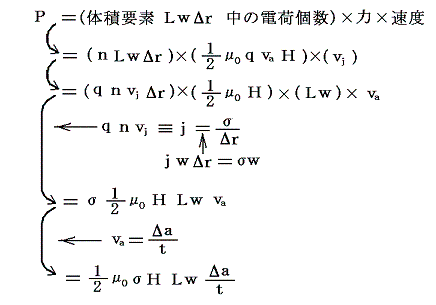
�ƂȂ�B�����ʼn~�����a�����������k�߂�̂ɗv���鎞�Ԃ��� t�������^��a ��p���Ă��邪�A���̎��Ԃ�������x���������̂��A�d���ɉ����Ȃ���Ȃ�Ȃ��d���v2�ł���B
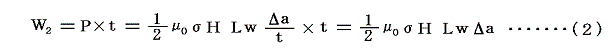
�������͏����Ă��܂��̂ŁA�ǂ�Ȃɂ������k�߂Ă�(�܂肖a��0�ɂ��Ă�)���ʂ͓����ł���B
�@�����ł���ɁA����������̎d���������Ȃ���Ȃ�Ȃ��B����͉~���̎��͂ɐV���ɐ����Ă��鎥�ꂪ�����N�����d���U���d��ɂ��t�N�d�͂ɍR���邽�߂̎d���ł���B�U���d��Ɋւ��Ă͕ʍe�u�d���g�v�P�D�i�P�j�Ő��������悤�ɁA�������x�a�����ԓI�ɕω����Ă���Ƃ��A���̏ꏊ�t�߂ɂ́k�������x���������Ă�������l�ɑ��āA�k���l�W�̕����l�ɓd��͑��݂���(�t�@���f�[�̓d���U���̖@��)�B
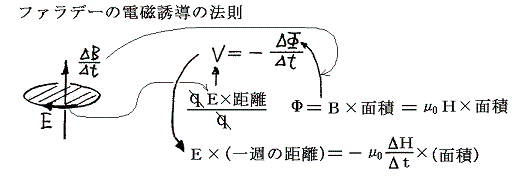
�ƋL�q�ł���B
�@���̂Ƃ��A�V���ɂł��鎥��͉~��������悤�Ɍ����̂ŁA���Z�����̎��Ƃœ����������t�����\���m�C�h���̎�����A���y�[���̖@���ŋ��߂��̂Ɠ����l�ȍl�������A�������x�̎��ԓI�ȕω����Ɣ�������U���d��ɑΉ������čl����悢�B�������ԂɃ����������a�����ɏk�ނƂ���ƁA�����k�~�������̖ʗ̈�ɐV���Ȏ������x�������Ă���B
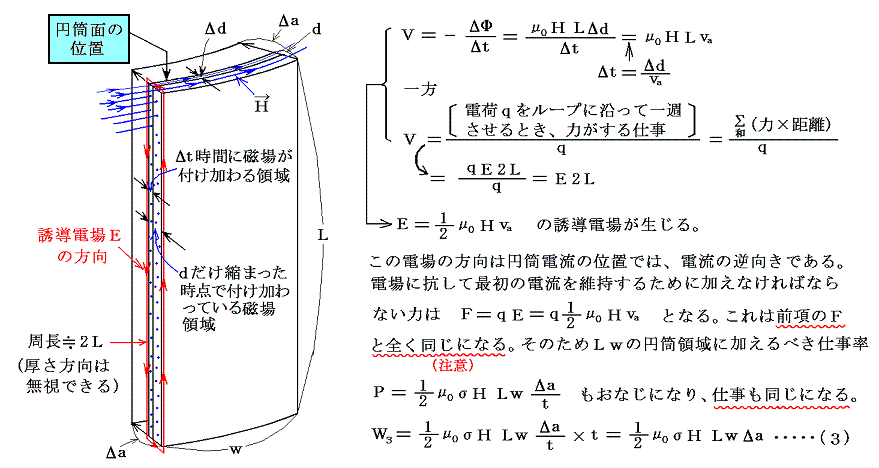
�@���̗U���d��ɊW����͂����߂�Ƃ��ɂ́A�d�Ɋւ����i1/2�j���悶��K�v���Ȃ����Ƃɒ��ӁB�܂����̏ꍇ�����͏����Ă��܂��̂łǂ�Ȃɂ������k�߂Ă����ʂ͓����ł���B�܂����̂Ƃ������U���d��́A�~���̎��k���I���Ə����Ă��܂��̂ŁA�d��̃G�l���M�[�̑������l����K�v�͂Ȃ��B
�@�i�P�j�`�i�R�j���̂v1�`�v3�����ׂĉ������킹�����̂��A�d���l�����ɕۂ����~����d���̔��a��������i���|�����j�Ɏ��k������Ƃ��ɕK�v�Ȏd���ʁi�����k�~�����̕����ɂ��āj�ł���B����͉~�������k�����̈�ɐV���Ɍ��������̃G�l���M�[�i1/2�j��0�g2�~�i�k�~���~�����j�Ɉ�v���Ă���B
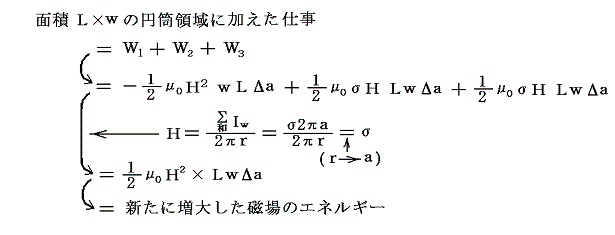
�m�⑫�����P�n
�@���̂Ƃ��d���Ɏd���������鎖�Ȃ��A�~����d���ɓ������k�͂ɂ��~�������k����̂ɔC���ĉ��炩�̗͊w�I�Ȏd�������o���ƁA�~���𗬂��d���ʂ��������āA���̂܂��̎���̃G�l���M�[�����������A���̃G�l���M�[���܂��Ȃ����ƂɂȂ�B
�@�t�ɁA�~���̎��k�͂ɋt����ĉ~����c�������悤�Ƃ���ƁA�d���ʂ̑���������A���̂܂��̎��ꂪ�傫���Ȃ�A����G�l���M�[�̑������B����͕ʍe�u�d���ƃG�l���M�[�v�Q�D(�T)(�Q)�ŏq�ׂ��\���m�C�h�R�C���̏ꍇ�Ɠ�������ł���A����Ɂu���d�@�ƃ��[�^�[�̗��_�v�ŏq�ׂ����d�@�̃��J�j�Y���ł��B
�@�܂��A����́A����v���Y�}�i�d�������C�̂œd�C��ʂ��j�̎������ɑ�d���𗬂��ƁA���o���ꂽ����Ɠd�����g�̑��ݍ�p�ɂ��A�v���Y�}�������ߕt�����Ē��S���ɍׂ��R��ɂȂ��ďW�����錻�ہi�s���`���ʁj�̃��J�j�Y���ł�����B���ہA10���A���y�A���x�̓d���𗬂��ƁA���k���ꂽ�v���Y�}���̓������͂�1000�C�����炢�ɒB����B�@
�@�����̋c�_�́A�������g����鎥��Ƃ̑��ݍ�p���W��������ǂ��̈�̘b���Ȃ̂Ŗ{���ɂ���ł悢�̂������^�₪�c�邪�A�����炭�������Ǝv���B
�@
�S�D�Ód�C�w�Ɠ��d�C�w�̊W
�@�������̓d�ׂ���l�ɑѓd�������s�Ԃɂ͐˗͂������ƍ��Z�����ŏK���i�ʍe�u��Γd�ʌv�Əی��d�ʌv�̑��茴���v�P�D�i�Q�j�Q�Ɓj�B���̂Ƃ��ѓd���s�����s��ۂ����܂ܔ̖ʂɉ����������ɓ����Ƃǂ��Ȃ�̂��낤���H
�@����̓}�N�X�E�F���̉��͂ɒ��ڊW�������A���̃y�[�W�ŗp�������������p�ł���̂ŁA�����Ő�������B
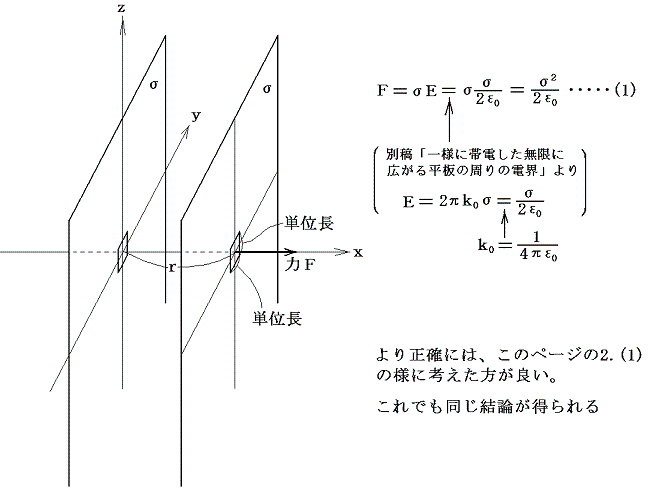
<���s���Î~���Ă���ꍇ>
�@�������̓d�ׂ��ʖ��x�Ђň�l�ɑѓd���������ɍL���̕����A���}�̗l�ɔz�u����Ă���Ƃ���B���̂Ƃ����s�Ԃɂ͐˗͂������A���̑傫���͒P�ʖʓ����艺�L�̂悤�ɂȂ�B�ʍe�u��l�ɑѓd���������ɍL���镽�̎���̓d�E�v���A���͂��̃y�[�W���Q�D�i�P�j�ɂ��
<���s�����x���œ����Ă���ꍇ>
�@�ѓd���s�����}�̗l�ɑ��x���œ����Ă���ꍇ�A����͓d�����x �����Ђ� �ł����̐������ɗ����ʏ�d���ƌ��Ȃ���B���̂Ƃ��R�D(�P)�Q�D�̌��_�����̂܂ܗ��p�ł���B
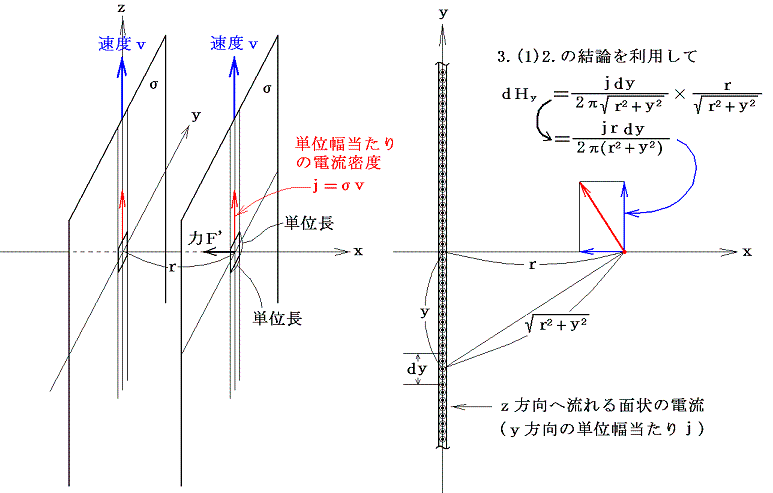
����0�̈ʒu�̖ʏ�d�����������̈ʒu�ɍ�鎥��́A���d�� ������ ����鎥�ꂄ�gy���������ɐϕ����ċ��߂�悢�B�������̎��ꐬ���͐ϕ��̌��ʑł����������̂ŁA�����̐���������������l�Ȏ���ƂȂ�B
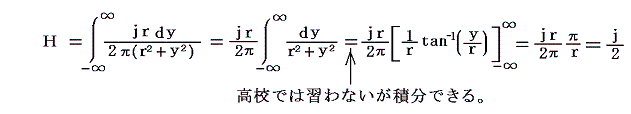
���̎���g�̏��𗬂��d�����x �����Ђ� �̖ʓd���̒P�ʕ��A�P�ʒ�������ɓ����͂̓��[�����c�̖@�����l������ƈ��͂ƂȂ�A
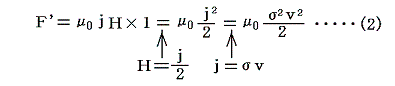
�Ƃ����l�ɂȂ�B
<�e�Ƃe�f�̊W>
�i�P�j���̐˗͂e�ƁA�i�Q�j���̈��͂e�f�̔��
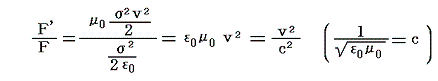
�ƂȂ�B�ɔ̓������������傫���Ȃ��ĂP�^(��0��0)1/2�ƂȂ�Ɨ��҂��������Ȃ�A��������͂������Ȃ��Ȃ�B���̒l�����������ł���A������d���C�w�̍����Ɋւ�鎖���ŁA�}�N�X�E�F���͔ނ̒����hTreatise�h��Art769�ŁA���̂��Ƃɒ��ӂ𑣂��Ă���B
�@
�S�D�⑫
�@Edmund T. Whittaker ���u�G�[�e���Ɠd�C�̗��j�i���j�v�u�k�Ёi1976�N���jP308�`309�@�ɓd����̉��͂̊ȒP�ȓ����@����������Ă���B���̃y�[�W�͂����̋L�q���Q�l�ɂ��܂����B������̉��͂������悤�ɍl�����̂ł����A�{���ɂ���ŗǂ��̂��C�ɂȂ�Ƃ���ł��B
�@�{���̗l�ɓd������ɉ��͂��`���Ă������A�^��̉��͂ʂ̈Ӗ��Œ��ڑ��肷�鎖�͂ł��Ȃ��B���炩�̕��̂�}�����ď��߂đ���ł���̂����A���̂�}������Ɠ��R���̓����̓d�ׂ��ړ����d��������d����̗l�q���ω�����B���̕ω������d����̏ŁA���̕��̕\�ʂɏ�L�̉��͂�������ł���B
�@��w���x���̓d���C�w�̓x�N�g����͂̌�����p���ĉؗ�ɓW�J�����B�`���͐����Y��ɐ�������邪�A�b�����ۓI�ɂȂ藝��������Ȃ�B�����ȂƂ��됔���̕ό`��������O�O�ɒǂ��Ă݂Ă��������C�����Ȃ��B���̂Ƃ������ɘf�킳���̂ł͂Ȃ��A�D�L����̓I�ȗ�ōl���邱�Ƃ�����Ǝv���B
�@�d���C�w�ł͋ߐڍ�p�̊�ɂȂ��̍l�������d�v�ɂȂ�B���̂Ƃ������̏�Ƃ��̌��̓d�ׁE�d���Ƃ̊W���A���ʂȏꍇ�ŏ\���ɋᖡ���Ă����Ɨǂ��B���̓��ʂȏꍇ�Ƃ��m�_�d�ׁn�E�m��������d�ו��z�n�E�m��������d�ו��z�n�E�m���k��d�ו��z�n�̎�����d���ƁA�m������d���n�E�m����d���n�E�m�~����d���n�E�m�T�[�L�b�g��~�d���n�E�m�\���m�C�h�d���n�̎���������ł���B
�@�H�w�I�ɏd�v�ȑ����̗�͂����̂ǂꂩ�ŋߎ��ł���̂ŁA�����̐������m�F�E�������Ă����ƈ�ʓI�ȓd����̐����̗����ɖ𗧂B