このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
運動の第2法則を言いかえたものが「エネルギーの変化は仕事に等しい」であり、運動の第3法則を(第2法則を用いて)言いかえたものが「エネルギー保存の法則」です。
物理学における仕事は力×距離(=F・S)で定義される。このように定義する理由は、実生活における仕事の量は[物体に加えた力]と[物体の移動距離]に関係するからである。その関係は例えば以下の経験事実から了解できる。荷物を高いところに運び上げるときの仕事のしんどさは荷物の重さ(力)が大きいほど、また持ち上げる高さ(距離)が高いほどしんどい。まさにそのしんどさの積が仕事の量に関係する。
力と移動方向が違う場合は以下の思考実験をしてみればよい。面に摩擦が無い場合下左図のAからBへ物体を持ち上げる仕事は下中図の様に持ち上げるときの仕事と同じである。階段の刻みを無限に小さくすると下右図の斜面を滑らせて持ち上げる仕事と同じになる。すると下右図下に記入した式の変形をたどれば解るように W=FScosθ とすればよいことが解る。
例えば摩擦のある床の上にある物体をズルズルと押していく場合を考える。このとき別稿「ニュートンの運動法則」2.作用反作用の法則 で述べたように力はいつも対(ペア)になって存在する。そのとき仕事の計算にはどちらの力を用いたらよいのだろうか?そのとき物理では次の様に考える。
物体になされた仕事は、[その物体に働いている力]と[その物体の移動距離]の積である。そのとき前項(2)の結論を用いると力の方向と移動方向が反対を向いている場合、cosθ=cos180°=-1 だから、仕事は負になる。そのとき作用反作用の法則から反対向きの力が必ず対(ペア)で存在するから正の仕事をなされたものがあれば、必ず負の仕事をなされたものがあることになる。そのとき負の仕事をされるもの(上図では人)が他に対して正の仕事をするものになる。
上図の物体に働く摩擦力はやはり物体に負の仕事をする。そのため、この力の反作用が他の物体(床)に正の仕事をする。今の場合床に対して正の仕事をする。ただし摩擦力の場合熱の形に変化してしまうので床の中の力は見えないし床は動かないが床に生ずる力と対(ペア)になることは間違いない。そして、この場合物体は人からもらった仕事分をすべて床に与えてしまうので、正味の仕事が物体の中に貯まることはない。
エネルギーとは仕事をする能力のことである。仕事をする能力は物体や空間(場と言われる)が持つ。物体や空間(場)はその状態を変えることにより仕事をする能力(エネルギー)を蓄える。
着目する状態の物体あるいは空間(場)のエネルギー(仕事をする能力)は、基準の状態(エネルギー=0とする)から、その着目する状態にするために、その物体あるいは空間(場)に加えた仕事の量で表される。または、ある着目する状態から基準の状態に戻るまでに、外に取り出すことのできる仕事の量で表される。
それゆえに、一般的に、エネルギー(仕事をする能力)は物体系または空間(場)の状態を記述する物理量で表される。その時、運動エネルキーと位置エネルギーという概念が出現するが、これらのエネルギーの意味に付いては別稿「調和振動子」1.[補足説明]をご覧下さい。そこでは、“エネルギー保存則”が成り立つための条件も明らかにされます。
以下で典型的なエネルギーを説明する。
質量を持つ物体は運動することによりエネルギーを蓄える。止まっている物体より、動いている物体の方がエネルギー(仕事をする能力)を持っている。止まっている物体は何もできないが、動いている物体は他のものをはじき飛ばしたり、ペチャンコに潰したりできる。自動車による交通事故はその不幸な例である。物体が動くことによって持つエネルギーのことを運動エネルギーといいKやEKの記号で表す。Kを用いるのは運動(kinetic)のエネルギーだからである。
その量はいくらか計算してみる。摩擦のない水平面上にある物体に力Fを加えて距離S押してW=F・Sの仕事を加える。このとき加えられた仕事を、別稿「ニュートンの運動法則」3.(2)F=一定 の場合に成り立つ公式③④または⑤を用いて変形すると1/2mv2 となる。
このとき大事なことはエネルギーの表現が質量と速度の関数で表されていることである。大事なのは質量と速度であって、どのような過程を経てその状態になったかは関係ない。だからエネルギーをF・Sで表しても意味がない。物体の状態を特徴づける速度vと質量mの関数(1/2)mv2の形で表されてこそ、物体が持つ運動エネルギーの値をすぐに知ることができる。運動エネルギーは止まっている状態を基準(=0)として測定する。
働く力が一定でない場合は、移動距離を細かく分割して各部分の仕事の和をとればよい。この場合も同じ結論が得られ、加速のされ方にはよらないことが解る。(下図参照)
このように仕事の積算値のみがエネルギーの変化に関係し途中の経過には依存しないのは、運動量の変化が力積の積算値のみに関係したことと同じである。運動量もエネルギーも最初と最後の状況の変化で議論でき途中の経過に依存しないことが役に立つ理由である。
摩擦が働き、動摩擦力以下の力で押す場合は以下のようになる。このときは、摩擦力は押される力と釣り合い、物体はズルズルと動くだけで運動エネルギーを蓄えることはできない。
動摩擦力よりも大きな力で物体を押していく場合は一部が運動エネルギーとして物体に蓄えられ、一部が熱エネルギーとなって失われる。
バネは自然の状態より、伸びたり押し縮められた状態の方がエネルギーを蓄えている。そのとき蓄えられているエネルギーのことを弾性力に伴う位置エネルギーと言いUバネやPバネで表す。U(ubiety位置)やP(potential潜在能力)の頭文字である。
その際より沢山伸ばされたり、縮められている方がより多くのエネルギーを蓄えている。また、バネの堅さをあらわす量をバネ定数kというが、蓄えられたエネルギーはバネ定数kにも関係する。
バネに蓄えられるエネルギーは伸び(縮み)xやバネ定数kとどのように関係するだろうか。バネをxだけ伸ばすのに必要な仕事はフックの法則を表すグラフとx軸で囲まれた部分の面積で表されるのは高校物理の授業で習うところである。バネの変形の中に蓄えられるこのエネルギーは一番解りやすい。
ここで注意すべきはバネを縮める場合も同様な形になり、正のエネルギーが蓄えられることである。xが負の値でもx2は正だからである。
ここで大切なことはエネルギーの表現がバネ定数kとバネの伸び(縮み)xの関数で表されていることです。バネの状態を表す量に関係付けられてこそ役に立つ。バネのエネルギーはバネの変形の中に蓄えられている。バネの状態を特徴づける伸び(縮み)xとバネ定数kの関数(1/2)kx2の形で表現してあれば、バネの状態からそれが持つ位置エネルギーをすぐに知ることができる。
バネの位置エネルギーは自然の状態のバネ(x=0)を基準(=0とする)として測定する。
質量がその存在する場所を変えることにより生じるエネルギーですが、それは質量の中にあるのではなく、質量とその質量に働く重力を生じる物体(地球)を取り巻く空間の中に蓄えられる。しかしこの説明は高校生にとって非常にわかりにくい。次に、そのあたりを説明する。
地球表面上の質量mの物体が持つ位置エネルギーは、仕事(W=F・S)とエネルギー(ある状態のエネルギーとは、基準の状態からその状態にするのに要した仕事の量で表わされる。)の定義からU=mghとなる。ここでのmgはもちろん人が物体に加えた力で、地球が物体を地球中心に向かって引っ張るmgと大きさが同じであるが、その方向は地球中心とは反対側の空の方向を向いている力である。(図1参照)
ところで物体が上空に向かって移動しているときに、同時に物体に働いている地球が下向きに引っ張る力のする仕事はどうなるのだろうか?もちろんこの力の方向は移動方向と反対向きだからこの物体にされる仕事は負で-mghであり、いま考えている物体に同時に働いているのだからこの仕事もエネルギー変化を考える時には考慮しなければならない。それなのに、なぜこの力がする仕事を無視して良いのだろうか?
普通物体の位置エネルギーは物体と地球を合わせた物を一つの系として考えるから、物体が地球に引かれる力は地球が物体に引かれる力と作用反作用の関係にあり、これらの力は内力として互いに打ち消し合うから無視できると考えるのだろうか?
以上の様な考え方から無視して良いのだとすると次の様な疑問がでてくる。高さhに在った物体を自由落下させると運動エネルギー(1/2)mv2 をえるが、このときには地球が物体を引っ張る力(それは当然下向き)に落下距離をかけてもとめる。(図2参照)
このときには地球が物体を引っ張る力は外力と考えて物体は外から仕事をされてエネルギーを得るとしている。これは奇妙だ?
更に、このとき物体が持っていた位置エネルギーは少しも失われていない。なぜならこの物体と地球の系はそれが持つエネルギーを失う様な外界への仕事は何もしていないのだから。もしそのような仕事を外界に対してすれば必ず外界に及ぼした力の反作用がその系の中の物体中に現われて、その力と物体の移動方向は逆向きになり、物体が負の仕事をなされたようになる。例えばなんらかのメカニズムが在って物体を支えながらゆっくりと降下させれば位置エネルギーから仕事を取り出すことができる。(図3参照)
しかし今はそのようなことは何も無い。だから物体の持つ位置エネルギーは失われていないはずだ。
以上の様な疑問の原因はすべて、本来重力は近接作用力であるのに、高校物理では瞬時に空間を越えて離れた所へ作用できる遠隔作用力であるかのように説明しょうとする所にある。世に出ている教科書の多くが近接力的な説明をすることを目論見て場を介在させる説明をしているが、運動エネルギーや位置エネルギーを担う実体が何であるかを明確に説明していないのでますます生徒を混乱させる。以下で、バネと重りの系と重力場と重りの系を対比させながら、この疑問に答える。
まずバネの先に重りを結びつけたバネと重りの系を考える。(図4参照)
この系では運動エネルギーを担うものは重りであってバネは運動エネルギーに関してはまったく関係無い。また位置エネルギーを担う実体はバネであってそのときには重りはまったく関係ない。
重りに力Fを加えて引っ張ったときに、おもりはバネにより後向きに引っ張る力も働き、重りは外力によりW=F・Sの仕事をなされるが同時にバネによりそれと同じだけの負の仕事もなされる。だから重りに加えた仕事はおもりを素通りして、バネの中に位置エネルギーとして蓄えられる。重りの中にはエネルギーは貯っていない。
次に引っ張った手を放すとバネは縮んで重りは運動を始める。そのとき重りはバネから引っ張られて運動エネルギーを得るがそれはバネが重りにした仕事による。バネは重りに仕事をするため、そのぶん位置エネルギーを失う。それらの仕事のやり取りはバネと重りの間に働く系内の内力を考えれば理解できる。そのときには重りとバネをあたかも別々の系のように考えて重りとバネの間に働く力を外力のように考えて各部分のエネルギーを計算する。そのときの力はもともと作用反作用の関係にある力だから大きさは等しく向きは逆で、バネと重りを合わせた系としてのエネルギーは保存される。
重力場と重りの系も、バネと重りの系の様なものだと考えれば良い。(図5参照)
ところがバネからの単純な類推ではいかないところが一つある。それは重りが場に及ぼす力である。つまり場が重りに及ぼす重力mgの反作用である。バネの場合は単純な反作用の力-Fであったが、この場合はそんな単純な力にはならない。場にエネルギーを蓄えるときの式が単純なW=F・Sでは無いのだから当然である。こういった困難は電磁場のエネルギーを考慮するときや、摩擦力の反作用がする仕事(結局それは熱になるのだが)の場合にもでてくる。それらの場合はW=F・S以外の形でエネルギーがやり取りされるからだ。重力場の場合の理解が難しくなるゆえんである。
だからやむをえず重力場の持つエネルギーを(図6)の様に地球と物体との間の距離(即ち高さ)hでもって表わす。(もちろんそのとき重りが持つ運動エネルギーの方はバネと重りの系と同じ様に重りの運動状態で表わせる。)
(図6)の様に重りと地球の間の距離で重力場が持つエネルギーを表わすのは、ちょうどバネと重りの系に於てバネに蓄えられたエネルギーをバネを持ち出さないで(図7)の様に壁と重りの間の距離によって表わそうとする様なものである。
もちろんバネと重りは分けて取り出すことができるから普通はバネの持つ位置エネルギーをバネの変形として表わし、重りの持つ運動エネルギーは重りの運動状態を記述することにより表現する。しかし、仮にバネと重りを分けて取り出すことができなかったり、バネが透明なものでできていて重力場の様に目に見えなかったり、質量がバネに及ぼす作用が単純な力にならず(質量が場にする仕事の様に)F・Sで表わせ無いようなものであったらきっと(図7)の様な表現をするであろう。
そしてバネと外界とのエネルギーのやり取りは重りにkxの力を加えて重りを移動することにより実現するだろう。そのとき重りにはバネから引っ張る力が働いているから、重りがバネにおよぼす力の形が仮に解らなくてもその反作用のバネが重りに及ぼす力-kx(重力場のmgに相当する)は解っているので、重りがその力によってなされる負の仕事は計算できる。(負の仕事をされたと言うのは言葉を変えれば、他に対して仕事をしたこと)それを利用してバネに蓄えられるエネルギーを計算できる。(図8参照)
そのとき明かなように重りを引っ張ることにより重りに加えられた仕事は重りを素通りしてバネに流れ込む。もともとバネと重りは不可分でいつも一つの系を形成しているとしているのだから、バネにエネルギーを蓄えることがいつも重りを経由してしかできなくてもいっこうにかまわない。
重力場と重りの系の場合にも同様に考えている。重力場は目に見えないから、目に見える質量の移動量で重力場の変形を表現している。質量の存在する場所を記述することで場の変化を代弁しているだけで、位置エネルギーを担うものは目に見えない場である。だから重りに加えた仕事は、地球が重りを引く力mgにより、重りを素通りしたのだ。
この様に考えると重力の位置エネルギーの難しさは結局
(1)重力場と質量を、バネと重りのように分けて別々に取り出せない。
(2)重力場はバネと違って目に見えない。
(3)質量から場に作用する力が、重りがバネに作用する力のように単純な形で表わせない。
の三点にあることが解る。だから場へなされる仕事を、バネになされる仕事のようにW=(バネに働く力)×(バネの伸び=力の作用点の移動距離)と表わせず、場への仕事(エネルギーの流れ)を質量になされた負の仕事-mgh(場から質量への力はmgで与えられる)を通じてしか表現できない。(図9参照)
こういった考え方は電場2.(4)(5)や磁場2.(5)(2)にも当てはまる。
万有引力は距離とともにk1/r2で変化する(k=GmM)。地球との距離が大きくなった場合の万有引力に伴う位置エネルギーを求める。バネの場合と同様に、移動距離を細かく分割して各部分の仕事の和をとればよい。
出発点の距離rのときの値を位置エネルギーの基準値(Ur=0)として、バネのエネルギーを求めたときと類似のやり方で、地球と重りの距離が無限大になったときの位置エネルギーを計算すると
となる。しかし、この形は非常に使いにくい。実際に求めたいのは無限に離れた点での値ではなくて、距離r離れたときの位置エネルギーの表現形式である。そこで無限遠はなれたときを位置エネルギーの基準値(U∞=0)とする。
このようにすれば距離rはなれたとき場に蓄えられる位置エネルギーの値を距離rの関数で表すことができる。そのために無限遠はなれた場合を位置エネルギーの基準値(U∞=0)にした。こうすると位置エネルギーの値が負(-GmM/r) になってしまうが、重要なのはrが変化したときのエネルギーの変化量だからこれで良い。離れている状態を表す距離rと、重力の大きさの目安である重力加速度g=GM/r2、質量mの関数で表されることが重要なのだ。
距離の変化量Δr=hが地球半径Rに比べて小さい場合には
となり、おなじみの表現形式になる。
コンデンサーに蓄えられるエネルギーの議論を利用して電場の持つエネルギーを求めよう。高校物理で、容量Cのコンデンサーに電荷Qが貯まってコンデンサーの極板間電圧がVになったとき、コンデンサーには
で表されるエネルギーが蓄えられていると習う。このことの意味を詳しく調べてみよう。
導体球が電気量Q(面密度σ)の電荷で帯電しているとき、ガウスの定理を用いて
故に点状電荷の場合の半径aにおける電位と同じになる。
電荷qを無限遠のかなたから点状電荷Qから距離rだけ離れた点まで近づけるのに要する仕事は2.(3)(4)万有引力による位置エネルギーと全く同様な議論で導くことができる。ただし力の方向が逆だから今回は正の値になり W=k0qQ/r となる。だから点状電荷Qから距離r離れた場所の電位V(r)は、その定義 V=W/q から V=k0Q/r(ただしr→∞でV=0) となる。
この結論を利用すると、導体球表面の電位は V(a)=k0Q/a となる。これは導体球の電位はその導体に貯まった電気量に比例することを意味する。
つまり、球形導体の場合電気容量はC=a/k0=4πε0aとなる。
導体球に電荷を蓄えるために必要な静電エネルギーを計算してみよう。ここでの考え方は、加えるべき力の方向が逆であることを除いて 2.(3)(4)万有引力による位置エネルギー の場合と同じである。電荷を少しずつ持ってくるときの仕事を考える。
導体球に蓄えられるエネルギーは、電荷を少しづつ付け加えるとき必要な仕事をすべて加えあわせればよい。Qまで帯電するために必要な仕事量は、導体球の電位が帯電している電気量に比例することを考慮して
となり、お馴染みの結論が得られる。ここで大切なことは、加えられた仕事は電荷の中に蓄えられているのではないことです。重力に伴う位置エネルギーのところで述べたのと同様に、外界が及ぼす力(上図の赤の矢印)が電荷に与える仕事は、電界が電荷に及ぼす負の力(上図の青矢印)により電荷を素通りしてしまう。(1.(3)仕事の正負 を参照)それでは外界が加えた仕事(エネルギー)はどこへ行ってしまったのかというと、重力の場合と同様に電場の中に蓄えられたと考えなければならない。実際、電場は電荷が導体に蓄えられるにつれて大きく変化している。その変化でもって蓄えられたエネルギーは測定されるべきである。エネルギーが電場とどのように結びつけられるかは2.(4)(5)で説明する。
ここでは重力と同じように一種の便法として、電場の量ではなくて電荷の集まりぐわいで蓄えられたエネルギーを表している。U=(1/2)QV=(1/2)CV2=(1/2)(Q2/C) これは重力場のエネルギーを質量の位置の変化で表したのと同じである。半径aの球形導体の場合電気容量はC=a/k0=4πε0aとなる。
エネルギーと電場を結びつける式を導くために平行版コンデンサーを利用する。そのためまず平行板コンデンサーの電気容量Cを計算する。
いま平行板にそれぞれ+Q(面密度σ)と-Q(面密度-σ)の電荷が貯まっているとき両極板の電位差Vを計算する。
無限に広い導体板が面密度σで一様に帯電しているとき、その周りの電界は導体板に垂直外向きで平板からの距離によらず一定値E=2πk0σ となる。電荷密度が負の-σの場合は導体板の方向を向きその大きさは同じである。この式を、高校ではガウスの法則を用いて導くが、クーロンの法則を利用して積分法で導くこともできる。
平行板の内側の電界は+σに帯電した導体板が作る電界と、-σに帯電した導体板が作る電界(前者と同じ方向を向く)を重ね合わせればよいのでE=4πk0σ となる。また、平行板の外では両極板がつくる電界は反対向きなので、重ね合わせると互いに打ち消しあってE=0 となる。このあたりは高校物理の授業で習う。(下図参照)
ここで電荷qを負極板から正極板に運ぶ仕事を考える。電位差の定義は、ある点から別の点まで電荷qを動かすのに必要な仕事がWのとき、その2点間の電位差をV=W/q で表すものだった。それを用いると極板間の電位差Vは両極に存在する電荷Qに比例する。
電気容量Cは電気量Qと電位Vの関係式の比例定数だったから、平行板コンデンサーの電気容量はC=(1/4πk0)(S/d)=ε0S/d となる。これは高校物理でお馴染みのものであるが、球形導体の場合のC=a/k0=4πε0a に相当する。
図1の様に帯電したコンデンサーにはエネルギーが蓄えられている。一見すると+Qと-Qは引力で引き合うので無限遠の彼方に離れて存在するときより安定化して、負のエネルギーを持つように思うが、そうではない。
正しくは以下の様に考える。+Qと-Qの電荷をそれぞれの極板に与えると言っても、それらの電荷は最初から塊で存在するのではない。何も無い所に、まず微少な電荷+qと-qを無限遠の彼方から持ってくる。そして、次に微少な電荷+qと-qを持ってくるときには、すでに存在する電荷の反発力に逆らって持ってこなければならない。以下同様で電荷が貯まるにつれて、それらからの反発力は強くなり(極板の電位は高くなる)外から正の仕事を加えなければ電荷は貯まらない。コンデンサーの持つエネルギーとは電荷を塊にするのに必要なエネルギーの事である。(図2参照)
そのとき正負の電荷を少し離れたところに同時に集めることの意味は何か。それは図3の様に正電荷を左から正極に持ってくる場合、正極にすでに貯まっている正電荷の斥力もあるが、負極に貯まっている負電荷の引力も働く。そのときr+<r-だからf斥力>f引力となり、正の仕事が必要になる。仕事は必要だが正電荷を単独で集めるより少ない仕事ですむ。
右方向から正電荷を正極に運ぶ場合、最初は負極の引力で引き寄せてもらえても、負極を越えて正極へ移動する区間では正極の斥力に打ち勝ち負極の引力を振り切らなければならず、合計するとやはり正の仕事となる。(図3参照)
たしかに正の仕事が必要だか、正負の電荷を離れた状態で集めるよりも、すぐ近くに隣り合って集める方が他の極板からの引力が利用できる分少ない仕事で集めることができる。この状況は色々な距離にある正極、負極が作る電位の重ね合わせを比較してみればよく解る。(図4参照)
正負の極板が同時に存在して、その間の距離が近いほど電位の山の高さは低くなり、谷の深さは浅くなる。電荷を一定にして極板間隔を狭めれば山と谷の高度差は少なくなる。これはV=Q/C=Q/(εS/d)=(Qd)/(εS) で表される変化に対応している。つまりコンデンサーとはより少ない仕事でより多くの電荷を貯めておく装置の事である。
以上の話では、正電荷、負電荷をそれぞれ無限遠の彼方から集めてきたが、正電荷を負極板から運んでも良い。そのとき負極板には負電荷が残り、ちょうど掘り出した土をすぐそばに積み上げて山と谷をつくるのに似ている。この場合に必要な仕事は前項と同じである。それは+Qと-Qが貯まった段階で、さらに+ΔQ、-ΔQを貯めるのに必要な仕事を比較してみれば解る。(図5参照)
コンデンサーの静電エネルギーは上記仕事ΔWの和である。故に図6の様な状況でコンデンサーに蓄えられたエネルギーは E=(1/2)QV となる。つまり-Qの事を考える必要はない。
コンデンサーに蓄えられたエネルギーとは結局、+-の電荷が同じ所に存在して互いの電場を打ち消している状況から、両者の引力に逆らって二つに引き離すのに要する仕事の量と同じである。正負の極板に分かれた正負の電荷は互いに引き合い再び結合しようとする。極板が近づいて接合するまでの過程で、蓄えられたエネルギーを使って他に対して仕事ができる。
最初帯電していない状態の平行板コンデンサーに負極板から正極板へ電荷を移動させて帯電させる場合を考える。正負の極板に電荷+Qと-Qが貯まったとき、コンデンサーに蓄えられているエネルギーを計算する。いま両極に+q、-qだけ貯まった状態のときΔqの電荷を負極板から正極板に移動させるのに要する仕事ΔWを求める。
この仕事ΔWの合計和がコンデンサーに蓄えられたエネルギーだから
2.(4)(2)で注意したようにここでも、電荷Δqに加えられた仕事は電場から受ける力-qEにより電荷を素通りする。つまりエネルギーは電荷の中に蓄えられるのではない。それでは何が蓄えるのかというと、電荷に仕事を加えたことにより変化した物理量である電場Eの中に蓄えられると考えねばならない。平行板コンデンサーの場合、電荷が移動したことにより、平板内部のみが一様な電場で満たされるので、エネルギーと電場を関係づける式を簡単に導くことができる。得られたエネルギーの式を変形してみる。
結局エネルギーは単位体積あたり(1/2)ε0E2の密度でコンデンサー内の電場に蓄えられると考えればよいことが解る。
つまり正負に帯電した平行板を、密着した状態から距離dだけ引き離された状態にするには、正負の極板間の引力に逆らって引き離すための仕事を加えなければならない。仕事を加えて引き離された結果何が生じるかというと、引き離された極板の間に一様な電場Eが現れる。これこそが仕事の結果生じた変化である。だからコンデンサーに蓄えられたエネルギーは電場の変化で表される。
外界である私が力を入れて[正負の極板を引き離す場合]には極板の間に電場が現れる。私が極板に加えた仕事(=力×距離)は極板が電界から受ける力により、極板を素通りして電場の中に蓄えられる。これはバネの両端を引き延ばして、バネの中にエネルギーを蓄えたのと同じである。
以上は話を簡単にするために平行板コンデンサーを用いたが、[正負の点電荷を引き離す場合]や、例(2)の様に[一カ所に電荷を集める場合]も電場の中にエネルギーが蓄えられる事情は同じである。
正負の点電荷を引き離す場合の計算は面倒だが、前記(2)の導体球に電荷を蓄える場合はそんなに難しくないのでこちらを参照。
加えた仕事が、実際にどのようにして空間に広がって行き、電磁場のエネルギーとして蓄えられるのかは別稿「電磁場のエネルギー密度とポインティングベクトル(1884年)」2.(5)2.[補足説明2]を参照されたし。
ここでは電荷に働く力について、コンデンサーの場合の静電場による力以外にファラデーの電磁誘導の法則が関係する力が重要になる。このとき高校生にとってわかりにくいのが起電力と言う物理量である。これは誘導電場E’に関係する量で、静電場とともに現れる電位(電位差)に似ているが、それとは異なる。
磁場が時間的に変化するとそのまわりに渦状の誘導電場E’ができる。そこにおかれた回路に沿って電荷が動くと誘導電場E’がローレンツ力の電場成分F=qE’に従って電荷に力を及ぼして仕事をする。単位電荷に誘導電場がする仕事が誘導起電力である。起電力という名称が与えられているが力ではない。それは電荷に加えられた仕事(エネルギー)を、その動かした電荷の電気量で割ったものである。これは静電場における電位と同じ次元(単位)となるので面食らうが、いわゆる静電場における電位とは異なる。このあたりをいくつかの例を用いて説明する。
以上述べたいずれの例の場合も、電荷にはローレンツ力
が働くと考えればよい。このときローレンツ力には例1~3のように誘導電場E’による力もあれば、例2のように静電場Eによる力の場合もある。また例4の用にv×Bによる力の場合もある。いずれも電荷eに力を及ぼす。これらの電荷に働く力が電荷に対して仕事をする。
v×Bはベクトルの外積といわれるベクトル演算で、その演算結果のベクトルはベクトルvとベクトルBが作る平面に垂直で、ベクトルvからベクトルBの方向へ右ネジを回したとき、右ネジの進む方向を向き、その大きさはベクトルvとベクトルBのなす角がθの場合 vBsinθ となる。
ここで注意してほしい事は、電荷eに働く力で直接dB/dtに関係するものは無いことです。dB/dtは誘導電場E’を生みだし、その誘導電場を通してeE’の力が働くと考えねばならない。もちろんdE/dtに直接関係する力も無い。eEの形で働くか、dE/dtが生み出すB(ビオ・サバールの公式を拡張したもの)に関してev×Bの形を通して力が働くだけである。
これはもともと電磁場の定義で、静止しているeに直接働いて力を生み出す成分をE、動いているeに働いて力を生み出す成分をBと置いた事による。
準備が整ったので磁場に蓄えられるエネルギーを論じよう。まず下図の様な電気抵抗のないリング状の導線に定常的な電流Iが流れている場合を考える。この場合リングを流れる電流は導線中を移動する電子によって担われている。そのとき電子は、電子がはずれたプラスイオン原子に寄り添うように流れているから、正味の電荷は存在しない。そのため電場Eは存在しない。定常的な電流 I が存在するだけである。時間的に変化しない電流は時間的に変化しない磁場Hを生じるだけである。このとき導線の抵抗はゼロ(いわゆる超伝導状態)と考えているので電流は永遠に流れ続け、磁場中のエネルギーは永遠に保持される。そのとき電子に働く力(電流方向の成分)はゼロである。
このときエネルギーは電流によって生じる磁場 H の中に蓄えられていると考えればよい。電流を担う電子も動いているので運動エネルギーを持っているが、その値は磁場の中に蓄えられているエネルギーに比較したら無視して良いくらいにごく微量である。(そのあたりの見積もりはこちらを参照)
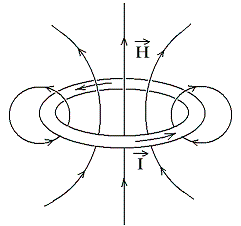
問題は以上のような状況から電流を増やしていく場合である。電流を増やそうとすると磁場の値が増える。そして時間的に変動する磁場は誘導電場E’を発生して加速されようとする電子の動きを妨げる。いわゆる電磁誘導(自己誘導)現象の発生である。つまり電流を増大させるためには、その妨げる力に抗して仕事をしなければならない。そのとき加えなければならない力は外部回路からの、たとえば電池による静電圧(静電場)による力の場合もあるであろう、また発電機の回転子の様に回路を磁場中で動かすことによって生じる力の場合もあるであろう。何らかのメカニズムにより、導線中の電子に力を与えて仕事を加えなければその電流を保持できない。しかしその加えた仕事は(電子の運動エネルギー増加分として電子中に蓄えられるごくわずかの部分を除けば)そのまま電子を素通りして磁場の中に蓄えられる。
その計算の仕方は高校物理の自己誘導のところで習う通りであるが、ソレノイドコイルの場合を例にしてもう少し詳しく見てみよう。いま下図の様なソレノイドを考える。コイル中は何もない真空とする。コイルに電流が流れていない状態から電流が I0 流れている状態にするときに加えるべき仕事の量を見積もる。
断面積がSの十分に長いソレノイド(単位長さあたりの巻き数=n)の導線に一様な電流 I が流れているとき、ソレノイド内部の磁界はソレノイド内の場所によらず一定値H=nI となる。この式を、高校物理ではアンペールの法則を用いて導く。ビオ・サバールの法則を利用して積分法で導くこともできるがその計算は面倒である。
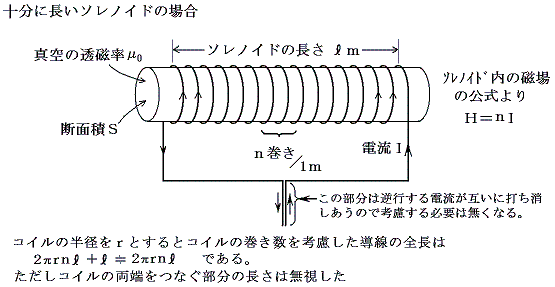
今ソレノイドに電流 I が流れており、その電流を I+ΔI に増やすために必要な仕事量を考える。電磁誘導の公式の磁束密度の時間的変化を電流の変化に関係づけた自己誘導の公式を用いると
の逆起電力が生じる。
電流を増やそうとしたとき生じる誘導起電力に逆らって電流値を I から I+ΔI まで増やすときに必要な仕事を計算してみる。このとき注意すべきは電流が増えるので電子の速さはvからv+Δvに増えるのだが、そのときの加えるべき仕事は誘導起電力により電子が押し戻されようとする力に逆らって、電子の移動速度を保持するために必要な仕事である。そのときΔvの変化分は無視できる。つまり今まで力が働かない状況で流れ続けていた電流を、新たに生じてきた押し戻そうとする力に抗して同じ電流を流し続けるために必要な仕事だと考えればよいのである。ところで、そのとき生じる誘導起電力Vとは前項2.(5)(1)例1 で説明したように
となる。つまりV=[F×(コイルを形成する導線の全長)]/e となる。
ここでコイルを作る導線の断面積をS[m2]、導線の単位体積中に含まれる自由電子の個数をne[個/m3]、電流 I のときの電子の移動速度をv[m/s]、電子1個の持つ電気量をe[C]とすると電流は I=eneSv[A]と表される。このあたりは別稿「オームの法則」を参照。
電流が増大しているΔt秒の間に電子に加えるべき仕事ΔWは、電流が増大している間磁場が増大し、その磁場の時間的変化により生じる電子を押し戻そうとする誘導電場による力に抗して、そのΔt秒の間電子を動かし続けるための仕事である。
導線中に存在する自由電子の全個数は N=neS×(コイルを形成する導線の全長)[個] であるから、
このときvはv+Δvまで変化するのだが、第1近似としてΔvの変化は無視できることに注意せよ。
次に、このΔWを I=0 の状態から I=I0 の状態になるまで加えあわせていけばよい。それは以下の図の三角形の面積を求める問題と同じで、お馴染みのものである。
一般に電流 I が流れているとき、自己誘導係数Lのコイルに蓄えられるエネルギーは W=(1/2)LI2 となる。
ここでは重力と同じように一種の便法として、磁場の量ではなくて電流の流れぐわいで蓄えられたエネルギーを表している。つまりU=(1/2)LI2 である。しかし、実際にはエネルギーは電流に蓄えられているのではなくて磁場に蓄えられている。
この当たりの事情は重力場のエネルギーを質量の位置の変化で表したり、電場のエネルギーを電荷の配置の変化で表したのと同じである。断面積S、長さ l 、単位長さあたりの巻き数nのソレノイドの場合自己誘導係数は L=μ0n2lS となる。
自己誘導係数 L=μ0n2lS を用いてエネルギーの表現形式を変形すると
となる。
つまりエネルギーは単位体積あたり(1/2)μ0H2の密度でソレノイドコイル内の磁場に蓄えられると考えればよい。
電子が止まっている状態からコイル内に電流 I が流れている状態にするには、自己誘導の逆起電力に逆らって電子を加速しなければならない。電子を速度vまで加速した結果何が起こったかというと、ソレノイドコイル内に一様な磁場Hが現れる。これこそが電子に加えた仕事の結果生じた変化である。だからコイルに蓄えられたエネルギーは磁場の変化量で表される。
もちろん電子は運動エネルギーを持つが磁場の中に蓄えられるエネルギーに比較すると無視して良いくらい少量で、エネルギーの大半は磁場の中に移動している。ここで、電流は磁場のエネルギーを代弁をする符帳にすぎない。符帳にすぎないのだが、電流は磁場の存在と表裏一体だから電流がエネルギーを担うといっても良かったのである。
以上の議論からあきらかなように、「質量と重力場」、「電荷と電場」、「電流と磁場」は表裏一体。
それに故に質量や電荷や電流に仕事を加えて、それらの在り様を変化させて重力場、電場、磁場にエネルギーを蓄える。
それらの場に蓄えられたエネルギーを外に取り出すときも、それらの場と表裏一体の相互作用をする質量・電荷・電流を通してしか取り出すことはできない。これはバネの中に蓄えられているエネルギーを、バネの両端の動きを通して取り出すのと同じである。
力学的エネルギー保存則を考えるとき重要なのは系と外界いう概念である。系とは色々なエネルギーを担う物体や場の集合体の事である。系に含まれないそれ以外の物体、あるいは場を外界という。そのとき系内の物体間で及ぼしあう力を内力、外界が系内の物体に及ぼす力を外力と言う。
たとえばバネとおもりをあわせた物を系と考え、それを引っ張っぱって伸ばす人を外界とすると、バネと重りの間に働く力が内力で人が物体を引く力が外力である。(下図参照)
物体と地球とその間に介在する重力場を一つの系と考えれば、場が質量に及ぼす万有引力は内力で、物体と地球の間に入ってそれを引き離そうとする人が物体や地球に加える力が外力である。(下図参照)
今考えている系が、外界と力のやりとりをせず、系内の物体の間での力のやりとり(内力)のみが働く場合、その系の持つエネルギーの総和は不変である。なぜなら系内の物質どうしが力を及ぼしあって互いに仕事をやり取りしても、その両者に働く力がいずれも系内に働く内力であるかぎり、作用と反作用が系内の物質に働くだけであるから。ニュートンの第三法則から明かなように作用と反作用は大きさが等しく向きが逆である。作用が系内の一方の物体に正の仕事をすれば、反作用が系内の他方の物体に必ず負の仕事をする。そのため系が持つエネルギーの増減を互いに正確に打ち消す。(下図参照)
だから系内の仕事のやり取りがすべてW=F・Sであらわされる内力で行われるかぎり力学的エネルギー保存則は成り立つ。
エネルギー保存則を利用するとき必要なのは、系を構成する部品が持つエネルギーの表現形式を覚えておくことである。高校物理では以下の3つを暗記すればよい。それらは、それぞれの部品の状況を表す量で記述されているので、部品の状況を見ただけでそれぞれの持つエネルギーを知ることができる。
以下、エネルギー保存則の利用例を幾つか説明する。
前項(2)の公式を用いて各状態におけるエネルギー値の和を書き表すと以下の様になる。
上記の図で状態0から状態1へ移行するときのみ外界は系に対して仕事をする。そのため系が持つエネルギーは状態0から状態1へ移行するときの仕事量だけ増える。
それ以後の変化に関しては外界は系に対して仕事をしないので、各部分の持つエネルギーは内力による相互作用で変化するかもしれないが、運動の第三法則(作用反作用の法則)のために総和のエネルギーは保存される。だから各状態での各部分の持つエネルギーを書き出して加えあわせたものはいつも等しいことが保証される。
高校物理の練習問題で計算するように E1=E2=E3 となることは、運動の第2法則を用いて証明できる。これがエネルギー保存則はニュートンの運動法則を言い換えたものにすぎないということの意味である。しかし3.(1)項で述べたように、それは証明するまでもなく成り立つことである。
前項(2)の公式を用いて各状態におけるエネルギー値の和を書き表すと以下の様になる。
状態0から状態1へ振り子を引っ張り挙げるときのみ、外界は仕事をして系のエネルギーは変化するが、それ以後は誰もバネとおもりの系にちょっかいを出していないので系のエネルギー総和は保存される。
この場合も E1=E2=E3 となることは、運動の第2法則を用いて証明できる。この証明は高校生にとって面倒だが可能である。別稿で説明した単振動の結論を旨く利用すればよい。しかし3.(1)項で述べたように、それは証明するまでもなく保証されることである。
前項(2)の公式を用いて各状態におけるエネルギー値の和を書き表すと以下の様になる。
状態0から状態1へ振り子を引っ張り挙げるときのみ、外界は仕事をして系のエネルギーは変化するが、それ以後はエネルギー保存則が成り立つ。
この場合も E1=E2=E3 となることは、運動の第2法則を用いて証明できる。しかしそれは高校生にとって簡単ではない。だからこそエネルギー保存則が成り立つという保証が有益なのである。
高校物理で習う難しい所である。しかし各状態でのエネルギーをそれぞれの状態で各部分が持つエネルギーを足しあわておき、どの状態からどの状態に変化するとき外界と仕事のやりとりがあるかに注意すればそんなに難しくない。
状態0から状態1へは外界である人がバネを引き延ばし、おもりを持ち上げて、系に対して仕事をする。その分だけエネルギーは増大する。状態1から2への変化も同様である。それ以後はバネと重りと地球の系が勝手に振動するのであって、系にたいして外界は仕事を加えていない。だからエネルギーは保存される。
状態1から2への変化で外界が加える仕事(エネルギー)は (1/2)k(l+a)2-(1/2)kl2 ではなくて (1/2)ka2 となるのは、重りが自らの位置エネルギーを失ってバネを伸ばす仕事を助けるからである。
だからバネについた重りを鉛直に振動させる場合、状態2における位置を中心としたバネの伸びでエネルギー値を計算すればよい。見かけ上、重力場の影響を考慮しなくて良くなる。
系内に摩擦力の様なものがはいってくると力学的エネルギーは保存しない。(下図参照)
物体に働く摩擦力に関してはW=F・Sがつかえる。しかし床に働く摩擦力の反作用-Fに関してはW=(-F)×Sがつかえない。床は動いたりしないのだから移動距離Sなど考えようが無い。そのときエネルギーの流れを表わすものはなんになるのか?
そのような場合もエネルギー保存則に含ませるには、仕事(つまりエネルギーのやりとり)がW=F・S以外の形で行われる場合も含むように拡張しておかねばならない。
そのようなもので最も身近な例は熱のやり取りである。その場合、仕事(つまりエネルギー)のやり取りの公式は熱のところで出てくる公式
Q=mct
となる。床(床の上の物体も含む)の温度上昇量tを知ることにより熱の形のエネルギーへのエネルギー入流量を知ることができる。だから系内に摩擦力を生じるような部分が含まれる場合、エネルギー保存則の形を、Q=mctの形のエネルギーも含むように拡張しておかねばならない。
熱以外では電磁場や重力場を含む場合も同様である。電磁場や重力場を含むように拡張されたエネルギー保存則を構築しなければならない。そのとき熱と電磁場、重力場とは決定的な違いがある。電磁場や重力場はエネルギーを可逆的にやり取りできるのに対して、熱はW=F・Sから熱への変換はいつでも可能だが、熱からW=F・Sへの変換は熱力学第二法則の制約がある。ただし、ここではこれ以上の議論はしない。エネルギー変換の様子を説明する模式図を掲げるにとどめる。