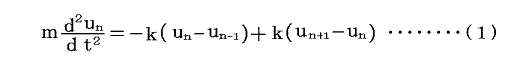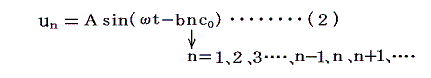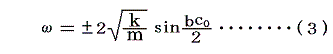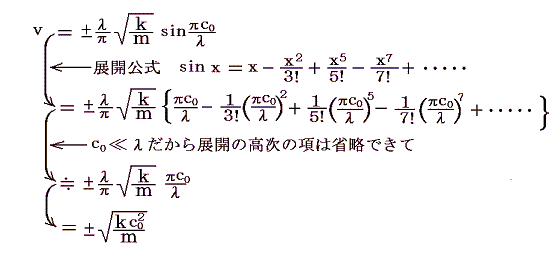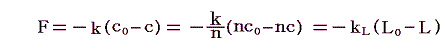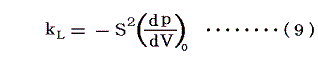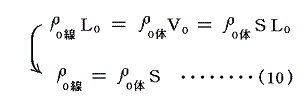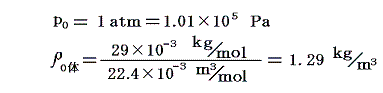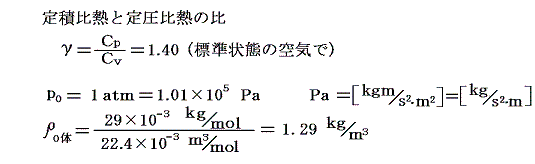このページを印刷される方はこちらのバージョンをご利用下さい。ブラウザーでは見にくいのですが印刷は鮮明です。
音速の理論
人は古代より、経験事実から音の伝播速度は光に比べてはるかに遅いことを気づいていた。そのため17世紀中頃より多くの人が測定を試み、また速度の理論式の導出に挑戦してきた。ここでは音速のできるだけ簡単な導き方を説明する。
1.バネと重りの縦波振動体モデル
波の伝播速度は、通常連続体についての波動方程式を立ててそれを解く方法で説明します。それ以外の方法で伝播速度を簡単に説明するのは難しい。だから波動方程式の解をいかにわかりやすく説明するかというところを工夫するしかない。そのとき最もわかりやすいのはバネ(自然長c)につながれた重りが一次元直線状に並んだモデルです。いま下図のように質量mの重りが多くのバネにより一直線につながれているとする。平衡状態での重りの間隔はc0とする。質点の大きさは無視できるとするのでc0は個々のバネの平衡状態における長さになる。
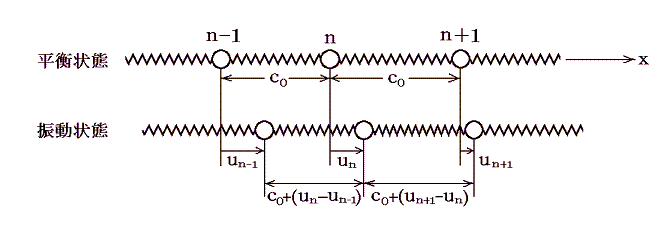
上図は重りが静止している平衡状態と波が生じている振動状態のある瞬間の状況を表している。このときn番目の質量に対する運動方程式(ニュートンの運動の第2法則)はバネについて成り立つフックの法則を利用して以下の様になる。ただしkは質量を結んでいるそれぞれのバネ1個についてのバネ定数です。
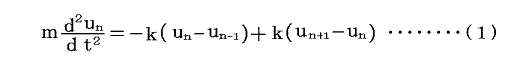
ここで注意すべき点は、平衡状態におけるバネの長さc0が、元々の長さがcであるバネがすでに圧縮あるいは伸長されている場合である。このとき例えば、n番目の質点の左側にあるバネがn番目の質点に及ぼす力Fは、右向きを正としバネの長さがc0のときにすでに存在する力をF0(圧縮あるいは伸長されているとしているのだからこの力が存在する)として以下のようになる。
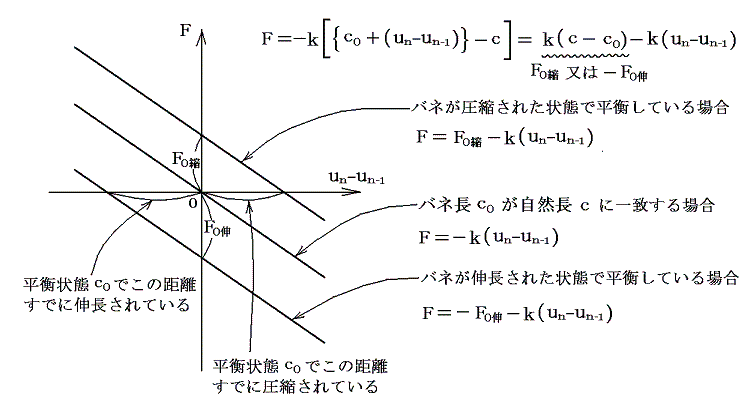
質点の右側のバネが質点nに及ぼす力についても同様な結論(ただし傾きと、F0縮またはF0伸の符号が逆になる)が成り立つ。両サイドのバネの効果を足し合わせるとF0の部分は符号が逆だから(1)式の中で互いにキャンセルして、見かけ上平衡状態でバネがすでに圧縮あるいは伸長されている効果は出てこない。
(1)式は、バネの先端に付いている重りに対する運動方程式 ma=-kx に似ている。この場合、重りの運動は単振動になることを高校物理Ⅱで習う。(1)式の様に右辺が重り(質点)に付いてるバネの単なる伸びではなくて、伸びの場所的な変化量の場合どの様な運動になるであろうか。その答を高校レベルで説明するのは難しい。
難しいが、質点運動の加速度が、その加速度運動を生じるバネの張力の場所的な変化量に依存することから、高校物理「波」で学習する進行するサインウェーブになることが予測される。実際、進行するサインウェーブが作り出す質点の動きが(1)式を満足することを示すのは簡単です。
ただしそういった解が(1)式を満足するには、その中に現れてくるバラメーターがある特定条件を満足しなければならない。その条件こそが波動の伝播速度に関する制約です。以下でそこを説明する。
今(1)式の解として
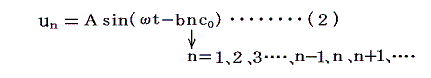
が成り立つと仮定すると

が成立しなければならない。
逆に
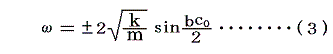
が言えれば、un=Asin(ωt-bnc0) は(1)の解となる。
ここで質点粒子が充分密に存在する場合は nc0=x とおけて
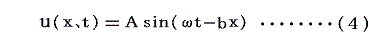
となる。この式は以下の意味を持つ。
- x=一定 の点の変異の時間的変化に着目すれば
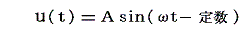
となるので、xの位置の媒質は周期T
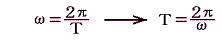
の正弦振動(単振動)をする。
- t=一定 のときの変異の空間分布に着目すれば
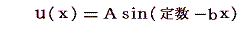
となるので、波形は波長λ
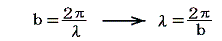
の正弦波(サインウェーブ)となる。
- 位相 ωt-bx=一定 の点は
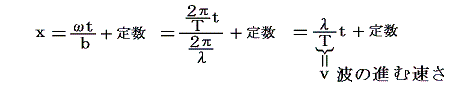
の式で表される点xとして、速度v
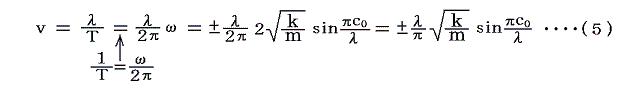
で移動していく。
(3)式や(5)式は波の角振動数ωや速度vが波長λにより変化することを示している。こういった現象を分散という。このようになったのは質点がとびとびに分布しそれらがバネでつながれている不連続な媒質を考えたからです。実際は、次に述べるように c0<<λ が成り立つ。上記モデルがあたかも連続体媒質のように取り扱える場合は、波長に関係しない一定値となる。
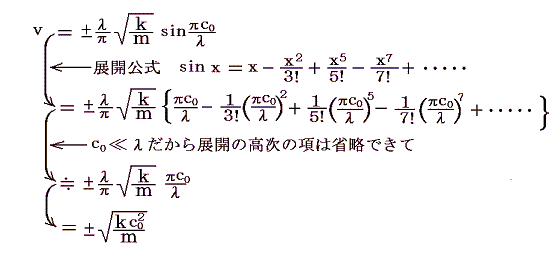
つまり波の伝播速度は媒質の振動数(周期)、波の振幅、波の波長に依存しない一定値となる。そして上式の伝播速度を満足する u(x、t)=Asin(ωt-bx) が(1)の解となる。 ここで、ωとbはv=(一定値)=ω/bを満足しさいすれば、任意の値でよいので(1)の解は無限に存在することになる。そして、それらの和も(1)式を満足することは実際に代入してみればすぐに確認できる。それらの個々の解の振幅Aは任意の値でよいので、そういった解の和を用いれば任意の波形の波も解となりうる。方程式(1)式の一般的な解の導出については別稿「波動方程式と一般解」参照。
上記式中のk、c0、mは全て微視的な原子レベルの量で簡単には知ることができません。そこで、それらを測定可能な巨視的な量に結びつける必要があります。その辺りを次に述べます。
2.音速
前節の結論を巨視的な量に結びつけるために式をもう少し変形する。
質量のないバネと質点が交互にならんだまま、個々の質点の質量を小さくしながら数を増やし、質点間の間隔c0を0に近づける。そうすると、質量を一様にバネに沿って分布させたスリンキーのようなモデルにすることができる。そのときには集中した質量や質量のないバネは存在しない。そのかわりに、それに沿って質量が分布した一つの長いバネがある。そのとき長いバネのバネ定数kLは個々のバネのバネ定数kをバネの数nで割ったものになる。その理由は別稿「直列と並列2.バネ定数」を参照。

上記のモデルを用いて音速を求める。いま、両端をピストンで区切られた円筒のなかに空気を詰め、一方のピストンを振動させて音を送り出し他端のピストンを揺らすとする。密閉容器に閉じこめられた空気は、容器の壁に外側に向かう圧力を及ぼす。このとき空気は圧縮されたn個のバネと(n-1)個の重りの系のモデルで近似できる。
まず最初に下図のモデルの長さL0をゆっくり圧縮して縮めたときの変化dLと加えた力dFの関係を求める。
圧縮されたn個のバネと(n-1)個の重りの系で、平衡状態における個々のバネの長さc0は自然長cより圧縮された状態であると考える。

個々のバネをn個つなげたバネ全体の長さをL0とする。このL0は空気を詰めた円筒の長さでもある。平衡状態における長さ L0=nc0 の自然長における値を L=nc とする。そのときバネがピストンを押す力Fは
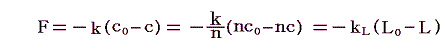
で与えられる。バネの長さLが変化したときのFの変化は上式を微分してえられる
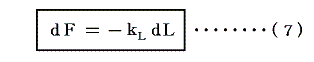
となる。
これをバネの変わりに空気が詰まっている場合と比較する。
円筒に詰められた空気の場合空気がピストンに及ぼす力Fは、圧力をp、円筒の断面積をSとして
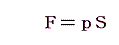
である。もしピストンが平衡点からほんの少しずれて長さL0からdLだけ変化したとすると、体積の変化は dV=SdLとなる。従ってFの変化は
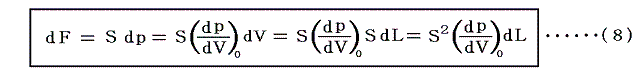
となる。(dp/dV)の添字の0は、dp/dVの平衡点での値である事を示す。
(7)式と(8)式を比較すると、バネと重りのモデルのバネ定数 kL は実際の空気についての量p、V、Sと以下のように関係づけられる。
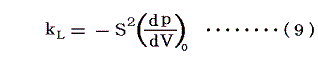
また、平衡状態の体積は SL0=V0 であるから、モデルのバネの線密度 ρ0線 は、実際の空気の体積密度 ρ0体 と以下の関係になる。
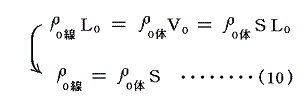
(9)、(10)式を(6)式に適用すると音速を測定可能な巨視的な量で表現できる。

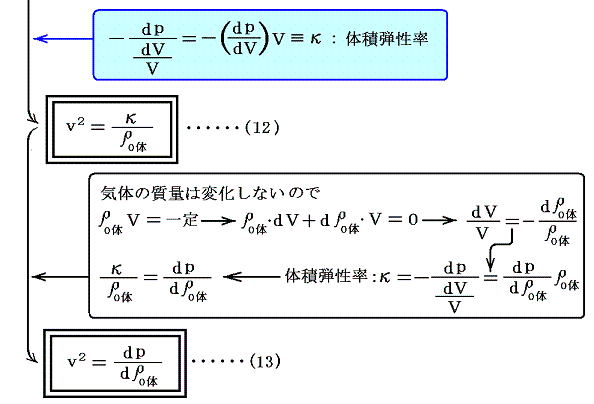
上記の“体積弾性率”κとは、圧力の無限小増加と、それによって単位体積に生じる体積減少量との比の事です。別稿「絶対温度とは何か(積分因子とは何か)」3.(2)4.などを復習して下さい。
また、添字の0はまだ音波が発生していない平衡状態での値を意味します。
(11)(12)(13)式はいずれも正しい結論で、ニュートンが求めています。(「プリンキピア」第8章命題48、定理38)
次なる問題は圧力が体積や密度の変化に、どのように関係するかです。これは、結局体積弾性率κを求めることと同じですが、このあたりを次で論じる。
3.圧力変化と体積変化(密度変化)の関係
(1)ニュートンの説明(1687年)
ニュートンは体積に対する圧力変化の割合を求めるとき、一定温度のもとでは圧力と体積の積は一定であるというボイルの法則を用いた。つまり彼は音が伝わるときの空気の局所的な圧縮・膨張の過程を等温変化とした。この場合
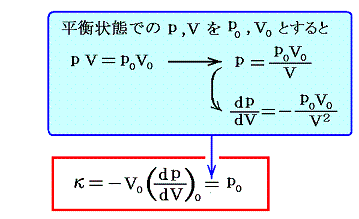
これを(11)式、あるいは(12)式に代入すると
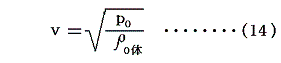
となる。
この式に空気が標準状態(0℃、1気圧)のときの値を代入してみる。
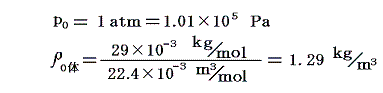
であるから、(14)式は以下の様になる。
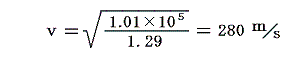
これは標準状態の空気中での音速の実測値332m/sに比べると15%も小さい。この誤差の原因は、一定温度という条件下でのみ成り立つボイルの法則を用いたところにある。
(2)ラプラスの説明(1816年)
音波の中では、温度は一定に保たれない。ある瞬間、圧縮領域にある空気は外から仕事をされたために、平衡温度より僅か高くなる。そこから1/2波長離れた膨張領域では、外に対して仕事をしたため温度が僅か低くなっている。つまり圧縮領域が得たエネルギーは膨張領域が失ったエネルギーに等しい。圧縮領域は温度上昇のために、その圧力はボイルの法則から導かれる値より大きくなり、膨張領域は逆に小さくなる。この効果は(13)式の値をより大きくする方向に働く。
上記の様なことが起こるのは気体の各部分が断熱的に変化するからである。気体の熱の伝導は、高温の部分の気体(より高速で飛び回っている)が低温の部分の気体に衝突して、低温部の気体の速度を上げる(温度が上がる)ことによって達成される。だから必然的に熱の伝導速度は気体分子の運動速度より速く伝わることはない。
ところで音波は気体密度の疎密の伝播である。圧縮されたとか膨張したという現象の伝播も、気体を構成する分子が熱運動にともなう運動速度でもって隣の部分の気体分子に衝突を繰り返すことにより伝わっていく。故に音の伝播速度も、気体の分子運動の速度よりは速くなることはない。ただし、その速度に近い速さで伝播していくだろう。
このとき、気体分子は長い距離を直進することはない。標準状態では10-7m程度進む間に衝突を繰り返しジグザグ運動をする。(このあたりは別稿「アボガドロ定数の測定法」 4.ロシュミットの測定法 を参照)そのため熱の移動が疎密の伝播速度を超えることはない。故に空気の各部分に起こる疎密の変化は断熱的に起こると考えて良い。
1816年、ラプラスは、圧力の密度(圧力)依存性に断熱変化の公式を用いて正しい音速の式を導いた。別稿「気体の断熱変化」で求めた公式を用いる。ここでγは“気体の定圧比熱と定積比熱の比”である。
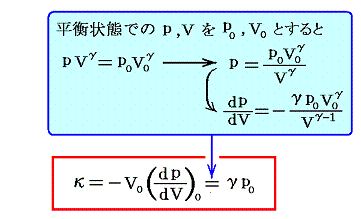
これを(11)式、あるいは(12)式に代入すると
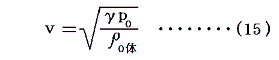
となる。
空気が標準状態のとき
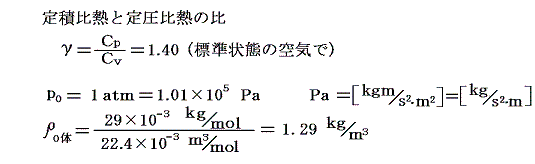
であるから、(15)式は以下の様になる。
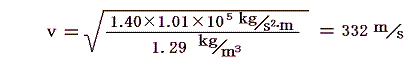
これこそ実測値に合う正しい結論である。
詳細は、ピエール=シモン・ラプラス著(竹下貞雄訳)「ラブラスの天体力学論 第5巻」(原本は1823年刊)の第12編、第3章 を参照されたし。
音速理論の歴史的な展開については、別稿山本義隆「熱学思想の史的展開」第15章Ⅰ~Ⅱを参照されたし。
(3)音速は圧力(気体密度)に関係するか[2018年2月追記]
ある読者の方から「音速は本当に圧力(気体密度)に関係しないのでしょうか?」という質問を受けました。確かに重要な疑問で、その当たりの説明が不足していましたので補足します。
結論から言いますと、気体が“理想気体”と見なせる場合は気体の圧力(密度)が変化しても音速は変化しません。温度の変化に依存するだけです。
それは音速が決まる物理的なメカニズムを考えれば解ります。音は気体が隣の分子に衝突して気体の疎密の状況を次々と伝えていく現象ですから、気体分子の運動速度に関係します。だから音速は気体の運動速度のみに依存します。もちろん、気体は一方方向のみに運動しているわけではありませんし、速度の大きさもMaxwellの速度分布則に従って変化しています。そのため音速は気体の平均的な運動速度にある定数をかけた値になります。
そのとき「気体中を伝わる音速は気体の圧力に関係するか?」という疑問の解答は、温度は同じだが気体の圧力が変わるというのがどういった事かを考えれば解ります。
同じ温度だが圧力が高い気体とは、気体の分子の飛び交う速度分布の様子は同じだが、分子密度が高いということです。分子密度が高いと、気体が次に衝突するまでに飛行する平均自由行程は短くなりますが、気体分子の速度分布が変わらなければ音速は同じです。
だから、温度が同じ(つまり速度分布が同じ)なら圧力を変えても(つまり気体の密度を変えても)音速は変化しません。
実際、音速を表す式
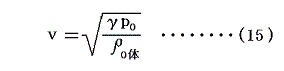
に於いて“理想気体”の圧力は気体の密度に厳密に比例しますから分母分子で打ち消し合ってp0/ρ0体は一定で、温度が同じ場合には、圧力(密度)を変えても音速は変化しません。
ただし、以上の話は理想気体の場合であって、気体分子に大きさがあり、分子間にファン・デル・ワースル力が働く“実在気体”の場合には、圧力(密度)変化の影響が極わずかですが有ります。理想気体と違って、実在気体の圧力は気体密度に厳密には比例しないからです。
音速の圧力(密度)依存性を知るには、ファン・デル・ワールス気体(実在気体)の音速公式を用いなけばなりません。それは別稿「熱力学関数(状態方程式曲面)の性質」1.(2)4.で説明するように
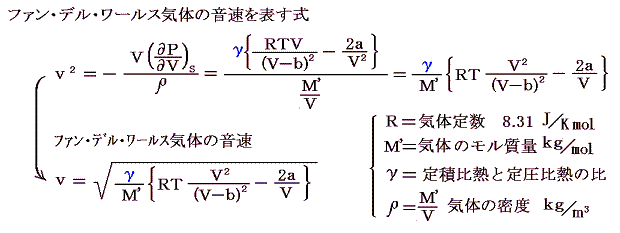
となります。
この公式は圧力ではなくて、体積Vの関数になっていますが、ファン・デル・ワールスの状態方程式を使って圧力の関数に直せば音速を圧力と絶対温度の関数として表せます。もちろんファン・デル・ワールス気体でも体積はほぼ圧力に反比例しますので、簡単に論じるには、上式中のVを理想気体の状態方程式V=(比例定数)/Pに従って置き換えればおよその圧力依存性は計算できます。ファン・デル・ワールス定数aとbの値は別稿「ファン・デル・ワールスの状態方程式」1.(1)などの数表から引用してください。
このとき、aやbは非常に小さな値ですから式の形から解るように圧力(密度)への依存性は極わずかです。よほど高圧(高密度)に圧縮した場合で無ければ音速の圧力依存性は無視しても良いでしょう。
4.音速の実測値
高等学校でならう理想気体の状態方程式を用いて(15)式をさらに変形する。
別稿「気体の断熱変化」 2.等温・定積・定圧・断熱変化の関係 の図を見れば解るように、気体の状態方程式は図中の曲面を意味するので、その中には等温・定積・定圧・断熱変化・等々・・・すべての変化が含まれている。
ここでM’は空気の平均分子量から求まる空気のモル質量(空気1molの質量)である。空気の平均分子量については別稿「ドルトンの分圧の法則と混合気体の状態方程式」を参照。
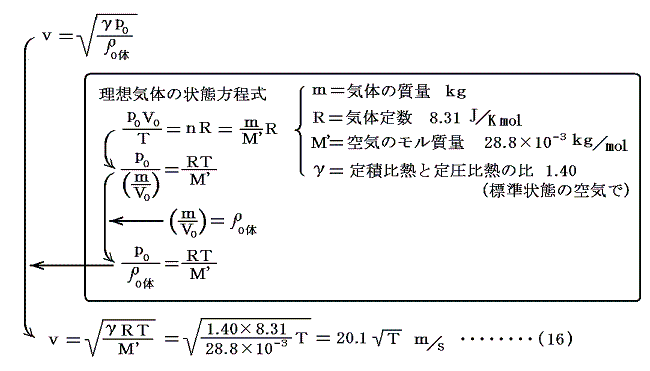
(16)式は下図の様なグラフになるが、0℃=273.15Kでの音速は v=332m/s となり実測値331.5m/sにほぼ一致する。、その付近のグラフの傾きは 0.6m/s・K であるから、お馴染みの常温付近での音速の表現式
v=331.5+0.6 t (tは空気の摂氏温度)
が得られる。
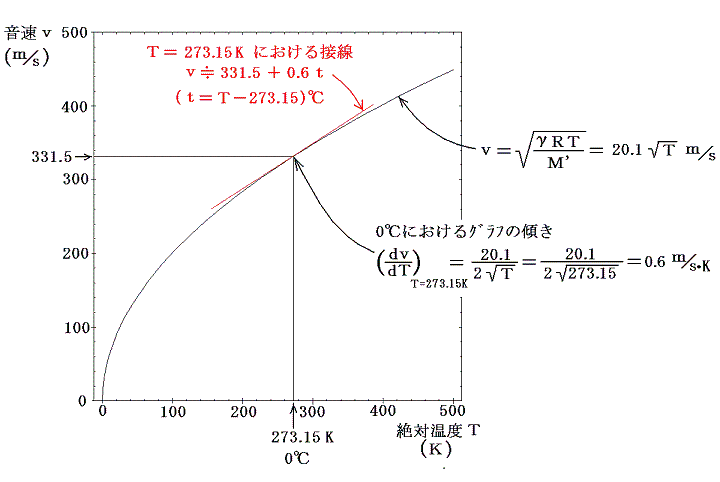
音速は絶対温度の平方根に比例して速くなる。これは、音を伝える媒質を構成する分子の運動速度が絶対温度の平方根に比例して大きくなるからです。
さらに、音速は気体の分子量Mの平方根に逆比例する。つまり軽い気体中ほど音速は速くなる。水素やヘリウムなどの軽い原子・分子で構成される気体中を伝わる音の速度が速くなる理由です。種々の気体の音速実測値は別稿「音速の理論2(分子速度と比熱比)」2.(2)をご覧ください。
[補足説明1]
上記グラフに付いて補足します。上記のグラフは、空気が理想気体の状態方程式を満たすものとして導かれた結論をグラフ表示したものです。
しかし、実際には空気は理想気体ではありません。特に温度が下がり空気密度が増大すると理想気体からのズレが大きくなります。そして1気圧下では摂氏-190℃以下まで冷やすと液化してしまいます。この当たりは別稿「冷凍・低温技術の歴史」1.(3)なと参照。
だから上記グラフの100K以下の部分はまったく正しくありませんし、空気中音速の議論には適用できません。
[補足説明2]
音速とは気体の疎・密の状況が次々と伝えられていくことですが、それは気体分子が隣り合った気体に衝突することで次々と伝えられていく。そのため音速は気体分子の速度vに関係するはずです。
簡単な分子運動論的な考察から、音速は[気体分子の運動速度の二乗平均値〈v2〉の平方根]に比例することが解ります。このことについては別項「音速の理論2(分子速度と比熱比)」2.をご覧ください。
[補足説明3]
水中も音は良く伝わる。そのメカニズムは空気の場合と同じで(11)(12)(13)式が適用できます。そのとき水は空気よりもはるかに圧縮されにくい。その体積弾性率κ(もちろん断熱変化)は標準状態の空気の14000倍程度である。また水の密度ρ0体は標準状態の空気の775倍である。故に水中の音速は(12)式より空気中の音速の(14000/775)0.5=4.24倍、つまり約1400m/s(0℃で)程度になる。
岩石についても同様に(11)(12)(13)式が適用できます。岩石中の音速こそ、地震のとき最初に到着する縦波P波(primary wave)の速度です。これは6×103~7×103m/s程度です。
5.参考文献
- 西條敏美著「物理学史断章」恒星社厚生閣 第6章 音速の理論式の成立をめぐって
音速理論成立の歴史が詳しく説明されている。
- F.S.Crawford著「バークレー物理学コース3 波動(上)」丸善株式会社
このページの記述はこの本に多くを依存している。波の本質を解りやすく教えてくれる優れた教科書。
- ニュートン著「自然哲学の数学的原理(プリンキピア)」中央公論社 世界の名著第26巻
第8章命題48、定理38 本文(11)式の導き方が書かれている。有名な本ですが、読みこなすには厖大な努力が必要です。
- ピエール=シモン・ラプラス著(竹下貞雄訳)「ラブラスの天体力学論 第5巻」大学教育出版 (2013年刊)
原本は1823年刊の古い本です。この中の 第12編、第3章 に音速の理論が記されています。