このページを印刷される方はこちらのバージョンをご利用下さい。図がより精細・鮮明に印刷できます。
ファン・デル・ワールスの状態方程式
(クラウジウス=クラペイロンの式、ジュール=トムソン効果)
ファン・デル・ワールスの状態方程式は原子・分子間力、実在気体の熱的性質、クラウジウス=クラペイロンの式、ジュール=トムソン効果、気体の液化技術に絡む極低温物理学への貢献・・・等々に深く係わった、きわめて霊妙な式です。その当たりを解りやすく説明します。
以下の議論は全て1モルの気体についての数式表現です。そのことを明示するために絶対温度T以外の量を全て小文字で表す。絶対温度・エントロピーについて馴染みの無い方は、先に別稿「絶対温度とは何か(積分因子とは何か)」をお読み下さい。
1.ファン・デル・ワールスの状態方程式
(1)状態方程式
オランダの物理学者ヨハネス・ディーデリク・ファン・デル・ワールス(Johannes Diderik van der Waals 1837~ 1923年)は博士論文「気体および液体の連続性」(1873年)で、気体の液化を表し、且つまた定量的に実在気体の状態変化を表す数学的方程式を提案した。
その方程式は1モルの気体に対して
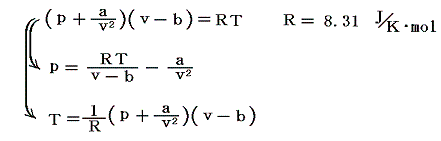
と表される。ここでpは気体の圧力、vは1モルの気体が占める体積、Tは絶対温度、Rは気体定数である。aとbは気体の種類に関係する定数です。その物理的な意味については次節で説明する。
これは非常に簡単な式だが、aとbの値を調整すれば、多くの実在気体の状態変化を近似的にうまく表した。実在気体の状態変化にもっともよく合致するように定めたa、b値の例を以下に示す。
ただし係数aとbは、実在気体の振る舞いのどの領域を重視して、その性質にあうように調整するかによってかなりの任意性がある。そのため文献によりその値はかなりバラツキがある。その当たりは3.(3)で説明する。
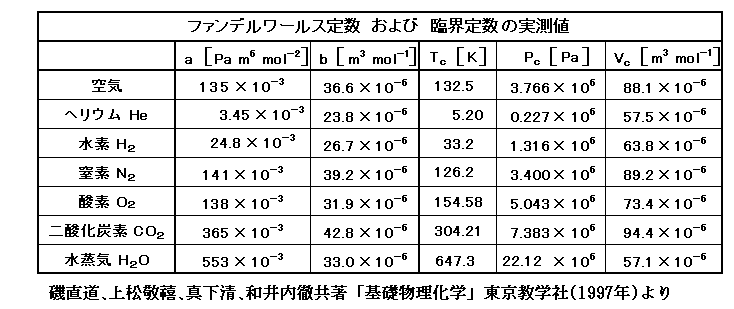
この中の二酸化炭素の三態の状態図は
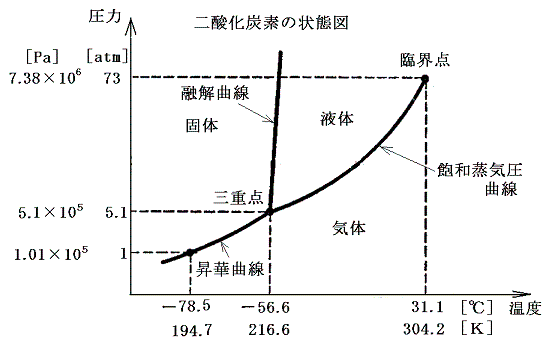
となる。
また、ファン・デル・ワールス式で近似した二酸化炭素の等温変化を表すp-v状態図は
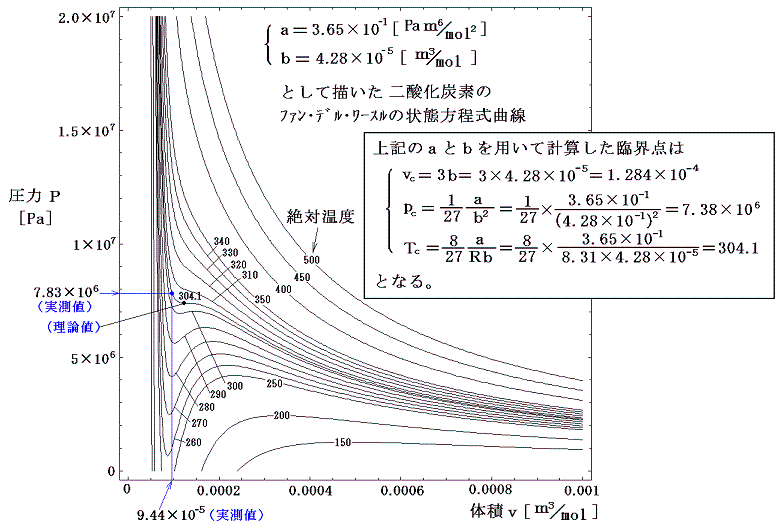
となる。ここで、Tが小さい領域における等温線はv=bとp=0を漸近線とする曲線となることに注意。これは式の意味を考えれば明らかです。
ここでa、bは広範囲にわたって実際のカーブに合う様に決められている。そのため実際の臨界点の位置は、この方程式から得られる値と必ずしも一致しない。逆に、実際の臨界点と一致するように定数a、bを決めると臨界点以外の領域でかなりの差が出てくる。
また、ファン・デル・ワールスの状態方程式には、現実には存在できない(∂p/∂v)T>0の領域を含んでいる。その領域の取り扱いについては3.(1)で議論する。
p-v状態図を三次元的に表すと次のようになる。ただし絶対温度200K以下は省略されている。
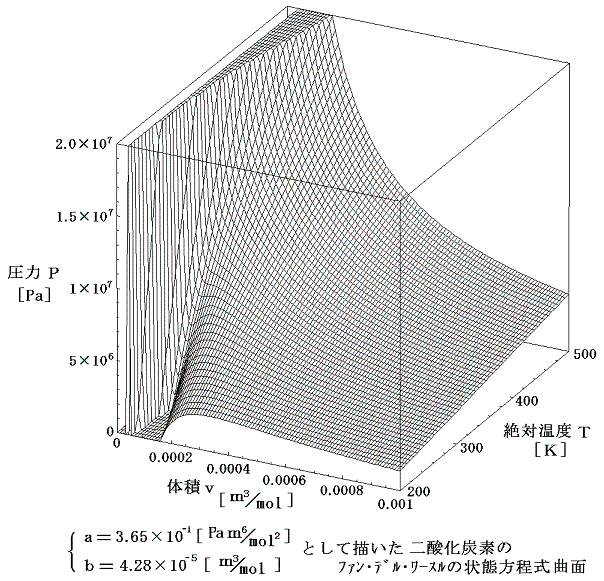
(2)係数aとbの意味
ファン・デル・ワールスは、彼の学位論文(1873年)の中でaとbの統計力学的な起源について詳しい基礎づけをおこなったのですが、それはかなり複雑で難しい議論です。その簡単な解説が参考文献1.§26や参考文献4.付録14にあるが、これも難しい。ここでは普通の説明に利用されるごく簡単な考え方のみを示す。
1.排除体積項 b
まず、分子が動き回れる領域の体積はvではなく、それから分子群自体が占める体積を引いたものになる。それは体積v中の分子数をN(以後1モルの場合を考える)とするとNに比例するはずです。比例定数をb’とすると、完全気体の状態方程式pv=RTのvが補正項Nb’だけ異なるはずです。このNb’が係数bです。
問題は、この補正項をどのように理想気体の状態方程式に導入するかです。圧力pにおける理想気体(ideal
gas)1モルの体積をvI’、実在気体(real gas)1モルの体積をvRとすると、同じ圧力pIに対して下左図の様にvRの方がvIよりも補正項分だけ大きくなるはずです。
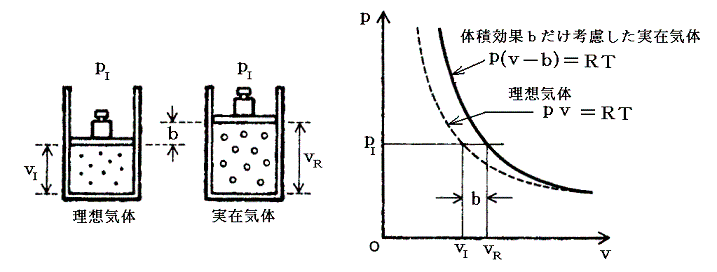
そのため実在気体の状態方程式は理想気体の状態方程式pv=RTのvを(v-b)に置き換えればよい。つまり
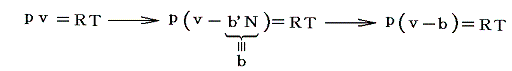
となる。ここでvR-vI=bは粒子が運動の場として使えなくなった無効な空間(排除体積)と考えられる。
2.引力項 a/v2
次に、圧力に関してですが、気体の容器の壁が気体に及ぼす圧力のほかに、分子間に存在する引力が影響するであろう。そのとき気体を詰めた容器壁の近傍では、気体が存在する内側からのみ器壁表面層の分子は引力を受ける。このことはすぐに説明する。そのため気体が器壁に衝突するときの衝撃力(圧力)は減少することになる。その減少の割合は、表面層に存在する分子の数密度(N/vに比例)と同時に、これに引力を及ぼす分子の数密度(やはりN/vに比例)に関係すると考えられる。そのため両者の積N2/v2に比例するであろう。比例定数をa’とするとa’N2/v2となるが、a’は分子間引力のポテンシャルカーブに依存する関数である。普通はa’N2を改めてaと置き補正項をa/v2と表す。
このとき、壁と気体の間に働く引力は測定される圧力に何の影響も及ぼさないことに注意すべきである。それは壁に衝突する気体分子は壁に近づくときに壁からの引力により加速されるが、壁から遠ざかるときには壁に引き戻され減速される。そのため別稿「惑星探査機のスイングバイ航法」2.で述べたことと同様に、衝突分子の運動量変化には何ら影響しないのである。壁との衝突では、そのような引力が存在しない完全弾性衝突と考えることができる。
このときの補正圧力は理想気体の状態方程式中にどのように組み込まれるであろうか。いま考察しやすくするために理想気体の体積vIには実在気体と同じ大きさ(ただし分子間力は無い)の粒子が同数個含まれるとしてこれをvI’とおき、そのvI’と実在気体のvRを比較してみる。気体の圧力は粒子が器壁に及ぼす衝撃力によるから、上記の補正項は実在気体に於いて衝撃力が弱まったことを意味している。つまり圧力が下がるのである。そのため同じ粒子数・温度・圧力で比較したときには、理想気体よりも実在気体の方が体積が小さくなる。
そのとき理想気体を実在気体と同じ体積にするには、理想気体により大きな圧力をかけなければならない。つまり、同じモル数の理想気体の体積を実在気体と同じに保つために加えるべき圧力が補正項a/v2である。これが理想気体に適応すべき補正項であって、その関係は下図から読み取れる。
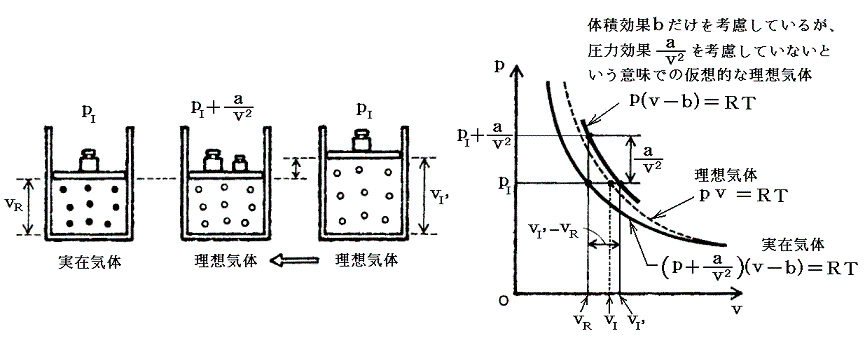
そのため実在気体の状態方程式は、上に述べた仮相的な理想気体の状態方程式p(v-b)=RTのpを(p+a/v2)で置き換えればよい。つまり
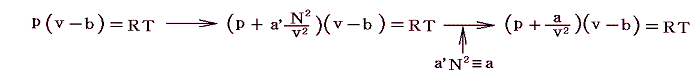
となる。これがファン・デル・ワールスの状態方程式です。
3.定数 a と b に付いての別説明(テル・ハール著「熱統計学」より引用)
気体の粒子が互いに力を及ぼす様子は、次図の様なポテンシャルエネルギー曲線から導かれるであろう。
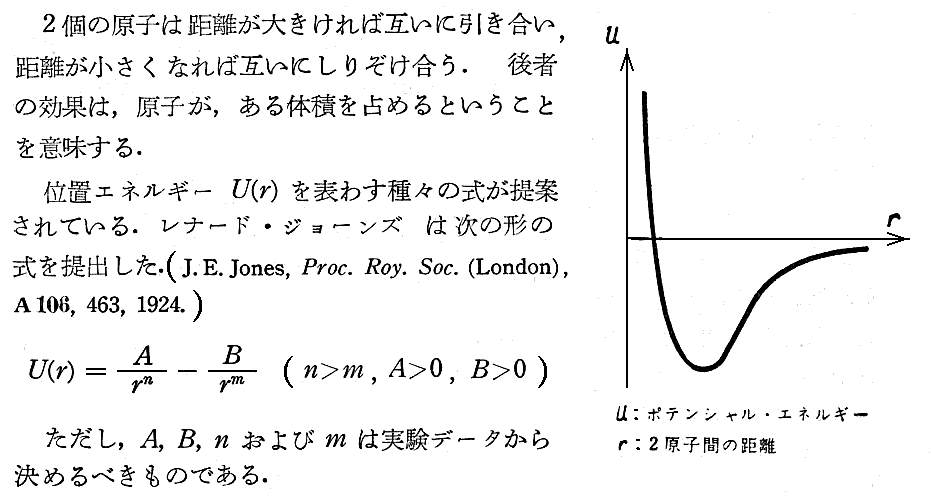
このとき、原子間のしりぞけ合う力(斥力)は、気体の動き回れる体積を小さくする効果を生む。そのため、理想気体の状態方程式 pv=RT における v を、これよりも僅かに小さいもの,例えば (v-b) で置き換えなければならないだろう。
斥力が、 v を因子 b だけ減少させるのであれば、ポテンシャル曲線の引力部分は、体積 v を増大する効果を生むと考える事ができる。その効果の補正を入れると v は、(v-b+a)で置き換えれば良いであろう。
すなわち、圧力と体積の関係式は
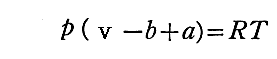
となる。
気体の圧力(あるいは密度)があまり大きくない限り、b と a は v に比べて非常に小さな補正にすぎないから、上式を
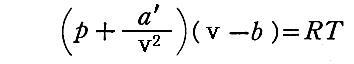
の様に書きなおすことが可能です。実際この式を展開して
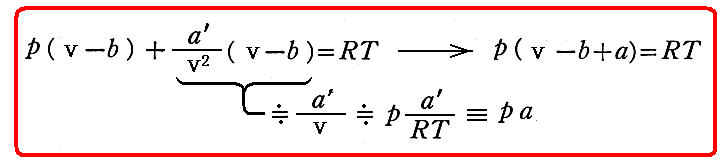
の様に変形して見れば明らかな様に
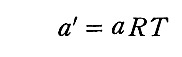
と置けば良いのです。
この a’ で表した形の式が、ファン・デル・ワールスの方程式と呼ばれるものです。
(3)式の検討
ファン・デル・ワールス状態方程式の圧力の表式を二つの部分に分けてみる。
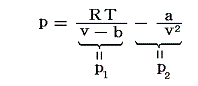
この中でp1の部分は理想気体のp-v線図をちょうど係数b(排除体積)だけv軸の正方向へスライドした形をしている。1.(1)の表を見ると係数bの値は気体の種類によらずほぼ一定な値で、20~40×10-6[m3/mol]=20~40[cm3/mol]の間に収まっている。ところで液体の水1molの体積は18cm3であるから、気体の排除体積がこの程度の値に収まるのはうなずける。そのため、p1のbはほとんど一定値としてよく、主に絶対温度による違いが重要になる。
一方係数aが関係するp2の部分ですが、係数aの値は、気体の種類に依存してかなり変化する。凝縮温度(沸点)が低い気体ほどaの値は小さくなり分子間力が小さくなることに対応している。
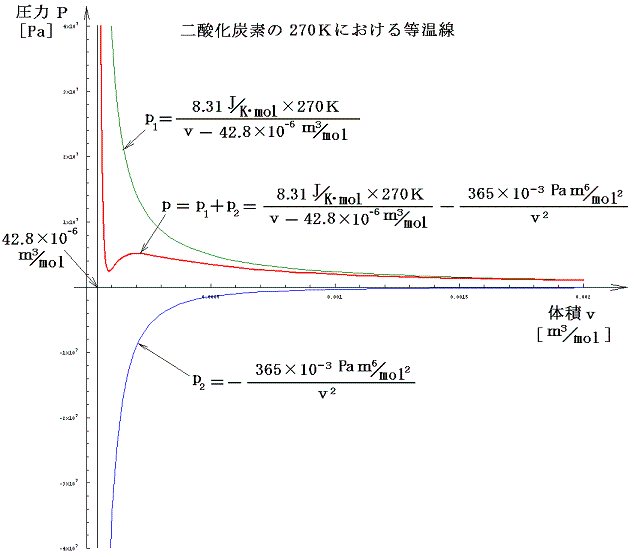
グラフを描いてみるとこれらの関係はより一層明瞭になる。下図の緑色線グラフはb=30×10-6[m3/mol]を固定して、絶対温度を変えて描いたp1のグラフです。青色線グラフは各物質のaの実測値を用いて描いたp2のグラフです。
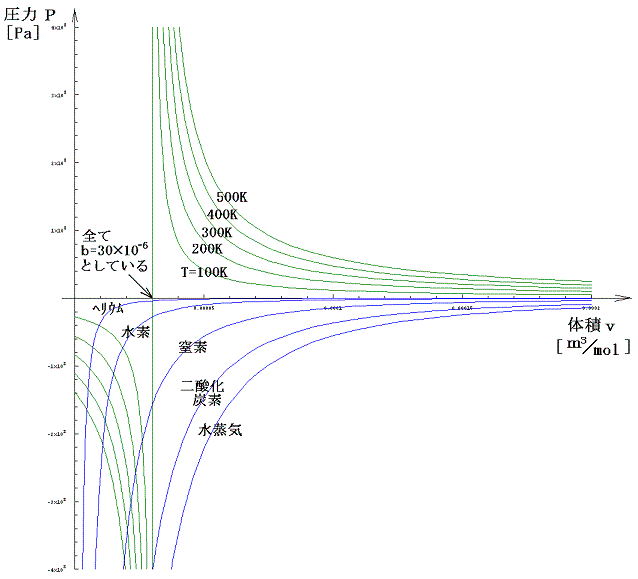
式の形から明らかなようにp1は1/vに比例してv→bとともに無限大に近づき、p2の絶対値は1/v2に比例してv→0とともに無限大に近づく。当然vの2乗に逆比例するp2の方が、その増大の割合は大きいのですが、無限大となる漸近線の位置がずれているために、p=p1+p2は下図の様になる。
次図は1.(1)表のaとbの値を用いて描いたT=270Kにおける二酸化炭素のp-v線図です。
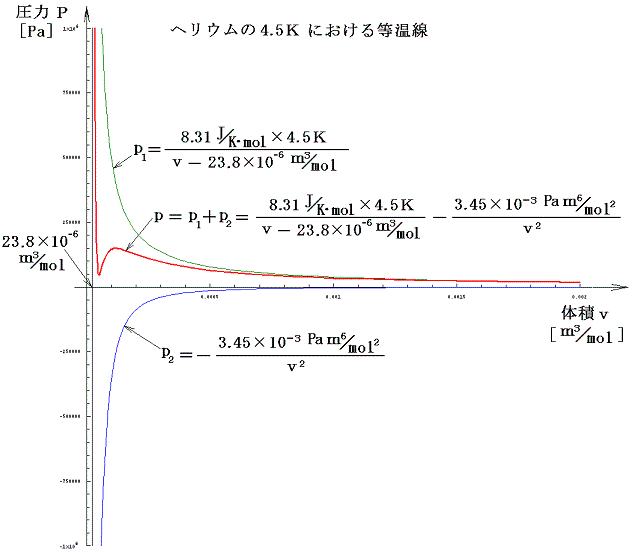
次図は1.(1)表のaとbの値を用いて描いたT=4.5Kにおけるヘリウムのp-v線図です。
すでに強調したが、ファン・デル・ワールス状態方程式はあくまで近似的な式です。しかし、近似的ではあるがとにかく実在気体の性質を普遍的にうまく説明した初めての数式表現(状態方程式)であることが重要です。数式で表すことができて初めて、以下に見るように、それに対して熱力学の基本原理を適応することにより様々な重要な結論を導き出すことができた。そして実在気体の振る舞いを通じて、原子・分子の本質を浮かび上がらせてくれた。その意味に於いてこの方程式が果たした役割は偉大です。
後に、実在気体の振る舞いにもっと良く一致する改良型の方程式が色々提案されたが、理想気体の方程式との関連性と、補正の物理的意味の明解さ、および、それから得られた成果の実り多さに関してこの方程式を超えるものはない。
2.ファン・デル・ワールス気体の性質
以下で、ファン・デル・ワールスの状態方程式で表される気体が満たすべき性質を調べる。
(1)膨張係数
別稿で理想気体の場合を説明したが、一般に状態方程式が定まれば、その方程式から定圧膨張係数(体積膨張率)αを数学的に定めることができる。

となる。a=b=0の理想気体の場合にはα=1/Tであったことを思い出されたし。ファン・デル・ワールス気体の膨張係数は絶対温度のみならず体積(圧力)にも依存する。
ファン・デル・ワールス気体と理想気体の膨張係数の差は
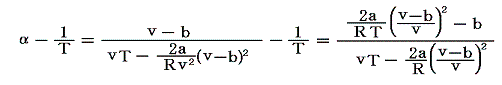
となる。大部分の気体(O2やN2)では、常温で右辺は正となり、熱膨張係数は理想気体よりも大きい。しかし水素H2と希ガスに関しては常温で右辺は負になる。そうなるのは、これらの気体では凝集力の大きさを決める状態方程式の(分子間引力に関係する)係数 a がきわめて小さい[1.(1)の表を参照]からです。
(2)内部エネルギーの変化
別稿「絶対温度とは何か」4.(1)1.で説明した様に、理想気体の内部エネルギーは温度のみの関数で体積や圧力に関係しなかった。ファン・デル・ワールス気体についてはどうなるのか調べてみる。
まず、熱力学第一法則に熱力学第二法則(エントロピー原理)を適用した式
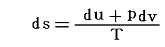
から出発する。この式についてなじみのない方は、先に「別稿5.(6)と6.(4)」をお読みください。
以下の議論は「別稿7.(1)1.と7.(2)1.」と比較しながら読まれると解りやすいと思います。ただし、ここでの議論は全て「別稿7.(4)まとめ」で説明したやり方に従うものです。

となる。ここで、sは状態量ですから、dsが完全微分であることの条件式から
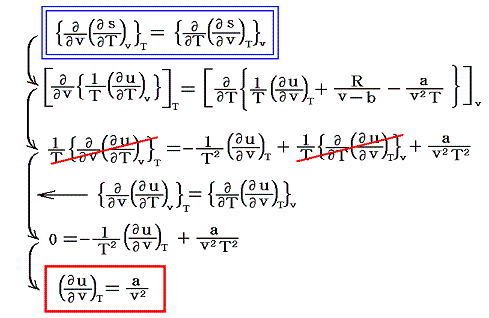
が得られる。
ここで、内部エネルギーの変動に b は関係しない事に注意して下さい。実在気体の性質に関係する b は内部エネルギーの体積依存性には関係しないのです。これはある意味当然予想されることです。
実在気体の内部エネルギーの体積依存性に関しては分子間力に関係する a に依存するのですが、“理想気体”の場合は a=0 ですから当然 (∂u/∂v)T=0 となります。理想気体の内部エネルギーは温度が変わらなければ、その体積や圧力の違いに寄らず一定であった事を思い出して下さい。
蛇足の説明ですが、“カルノーサイクル”の作業物質が“理想気体”であり、カルノー機関の内部エネルギーがその温度のみに依存して、体積や圧力に依存しない場合には別稿でポール・センが説明しているカルノーサイクルのメカニズムで(A)や(B)の部分が追加で言えます。
しかし、カルノーサイクルの作業物質が“実在気体”であっても“カルノーの原理”は成り立ちます。そのため、実在気体を用いたカルノーサイクルでも熱力学原理の議論が成り立つのですから、普通(A)や(B)の部分が成り立つ必要はありません。
理想気体の内部エネルギーは温度だけの関数で体積には関係しなかったが、ファン・デル・ワールス気体の内部エネルギーは同じ温度でも体積が変われば変化することを意味している。
これは、ファン・デル・ワールス気体の内部エネルギーは、理想気体のように分子の運動エネルギーのみによるのではなく、定数aで関係づけられる分子の凝集力のポテンシャルエネルギーにも依存することを意味する。
このポテンシャルエネルギーは、互いに万有引力で力を及ぼしあっている質点系の場合と同様に負のエネルギーを持ち、膨張するにつれて0に近づく。したがって、気体中に蓄えられている内部エネルギーuは、同じ温度であるという条件の基ではvが増すにつれて増大し、その増大の割合が上記の関係式
(∂u/∂v)T=a/v2 で与えられるということです。
それでは温度とは何かということになるのだが、熱力学では別稿「絶対温度とは何か(積分因子とは何か)」6.(3)で説明した以上の説明することはできない。しかし、とにかく上記の様な関係を導くときに一定値となる示強性の状態量です。
[補足説明1]
普通の教科書では上式は、最初の式の両辺をvで偏微分したものをMaxwellの関係式(∂p/∂T)v=(∂s/∂v)Tを用いて変形した後に、ファン・デル・ワールスの状態方程式を代入して導いている。Maxwellの関係式を用いると機械的かつエレガントに変形できるが、そのようにするとエントロピー導入の意義がわかりにくくなるので、あえて泥臭く変形した。
Maxwellの関係式は、もともとds[あるいはそれから導かれた様々な自由エネルギーの変分]の完全微分条件から求められたものだから同じ結論が得られるのは当然です。ちなみに(∂p/∂T)v=(∂s/∂v)Tはヘルムホルツの自由エネルギー f=u-Ts の変分 df=-sdT-pdv
が完全微分であるという条件から求める。
(3)比熱
定積比熱の定義より

がいえる。ファン・デル・ワールス気体の定積比熱は、温度が一定なら体積(圧力)によって変化しない。つまり理想気体と同じように定積比熱は温度だけの関数である。
ここで是非注意してほしいのですが、比熱の温度依存性はたとえ状態方程式が与えられていても、熱力学からは導くことはできません。熱力学の守備範囲外の事です。ただし、cvやcpなどの何らかの状態変化経路に沿った一種類の比熱の温度依存性が実測値等により求まれば、例えば次に説明するように、状態方程式から他の形式の比熱の温度依存性は求めることができます。
次にモル比熱の差cp-cvを求めよう。別稿「絶対温度とは何か」4.(2)2.で説明した様に理想気体の場合はcp-cv=Rであったが、ファン・デル・ワールス気体の場合は。
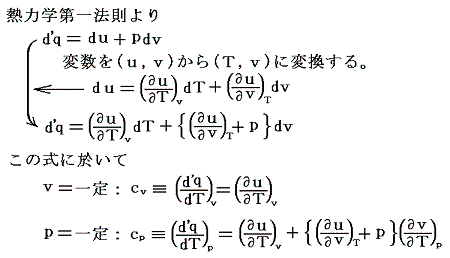
となる。この両式の差をとると

となり、体積(圧力)や温度に依存する。
ここでbは小さな量だから、近似的に
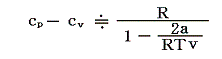
が成り立つ。
さらに補足すると、a→0 の場合はもちろん理想気体の公式
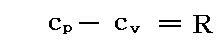
に一致する。本稿では物質量n=1の場合を議論していることを忘れないで下さい。
(4)エントロピー変化
最後にファン・デル・ワールス気体のエントロピーを計算しておく。理想気体の場合は「別稿6.(4)3.」ですでに求めたので、そこと比較しながらお読みください。

前項で定積モル比熱が温度だけの関数であることを示したが、ここでさらに気体領域におけるcvが理想気体の場合と同様にほとんど温度によらないと仮定できるとして積分を行い、ファン・デル・ワールス気体の(T,v)におけるエントロピー値を求める。
両辺を(s0,T0,v0)から(s,T,v)まで、可逆過程に沿って線積分を実施すればよい。sは状態量である故にdsの線積分値は積分路に依存しない。そのため、右辺第一項でv=一定の下に(T0,v0)から(T,v0)まで積分したものに、第二項のT=一定の下に(T,v0)から(T,v)まで積分したものを加えておけばよいので
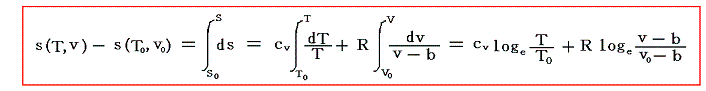
が得られる。
もちろん、このとき別項で説明した理想気体の場合と同様にファン・デル・ワールスの状態方程式を用いて変数を(T,p)や(p,v)に変換したs(T,p)やs(p,v)の関数形を求めることもできる。ただし、式の形は少し複雑になる。
さらに、密度が高い液体の領域に近づくと比熱はかなり変化するので、上記の様な簡単な式では表せない。そのときには比熱の実測値を用いて計算しなければならない。
3.ファン・デル・ワールス気体の液体・気体共存領域
(1)(∂p/∂v)T>0領域とMaxwellの規則
熱力学で相という言葉は、単一の物質の場合、その異なる凝集状態を指す(固体状態では結晶構造の違うものを指す場合もある)。ファン・デル・ワールスの理論では気体の相と液体の相との平衡状態も扱う。
まず言えることは、下図のAA’とBB’の領域についてである。
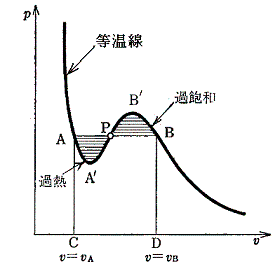
AA’の領域は過熱状態といわれ不安定な領域である。不安定ではあるが、振動が全くない容器の中で静かに過熱すると、液体端Aの圧力よりも少し低い状態で液体状態が保たれる。またBB’は過飽和状態といわれ、全く塵(ゴミ)を含まないない蒸気は、同じ温度で蒸気端の点Bよりも高い圧力を持つ。
これらはきわめて不安定な状態で、ごく僅かな刺激で液体・気体の共存した状況に推移する。そのため、これらの不安定な状態はAやBを行き過ぎた僅かな範囲でしか起こらないが、ファン・デル・ワールスの理論がAA’、BB’という分岐に沿った不安定状態があることを定性的にしろ説明できるのは注目に値する。
次に、上図のA’-P-B’の領域であるが、ここは(∂p/∂v)T>0となる領域で体積が増えれば圧力が増えることを意味している。しかし、現実にはそのようなことは起こりえない。この領域で実際に起こる現象は次のようなものです。圧力を一定に保って、系に熱を加えていくと、系は一定温度を保ったままで液体が水蒸気に蒸発していき体積が増大していく。同一圧力を保つように液体と気体の間で相変化が起こり、二相平衡を実現しながら体積が変化していくのです。[下図のA-P-B、A’-P’-B’、A”-P”-B”、・・・等々の変化]
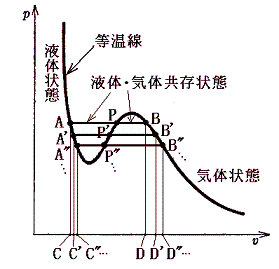
そのとき問題になるのは、上図のA-P-B、A’-P’-B’、A”-P”-B”、・・・等々の変化の内どれが実際に起こる経路かということです。この状況に対して熱力学はどのような事柄を教えてくれるか考察する。
[補足説明0]
《相転移に於いて、相転移前と相転移後のギブズの自由エネルギーは互いに等しい》
これは一定圧力pに調整され自由に動くピストンで蓋をした円筒状容器に封入された物質の二相平衡系に生じる変化です。系に熱を加えると一定圧力・一定温度の下で相A(液体)が蒸発して相B(飽和蒸気)に変化して体積が変化する現象です。
液相(相A)にあるときの物質1モルが持つ内部エネルギーをuA、気相(相B)にある物質1モルが持つ内部エネルギーをuBとすると、この相変化は一定圧力、一定温度の下での準静的可逆過程だから、転移温度をTとすると

となります。
これは
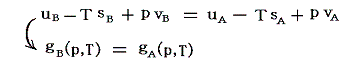
と変形してみれば明らかなように、相転移前と相転移後の1モルの物質のギブスの自由エネルギーg(状態量の一種)が等くなるように生じる変化です。これはエントロピーの性質から導かれる熱力学的結論です。
ギブスの自由エネルギーgは、状態量である内部エネルギーuに、同じく状態量であるpvとTsを加えたり引いたりしたもので、物質の状態を規定する状態量の一種です。
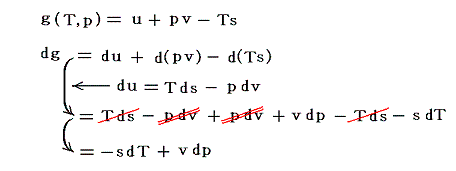
その独立変数はTとpになりますので、上のp-v図の各点に物質の状態量gが付随するということです。つまりpv座標平面に垂直に座標軸gを取ればpv平面上にg(T,p)曲面が決定できると言うことです。
その曲面の形は2.(4)でエントロピー関数s(T,v)の曲面を導出をしたのと同じような手順で求めることができる。上図のA点のギブスの自由エネルギーgAを基準にしてB点のそれgBを求めてみる。そのとき等圧、等温変化で結ばれる2点A-B、A’-B’、A”-B”、・・・等々のgAとgB、gA'とgB'、gA"とgB"、・・・の関係で両者が等しくなる場合が、実際に起こる変化のはずです。
以下の説明は、gB=gAすなわちgB-gA=0となる等圧線A-P-Bを探す操作です。
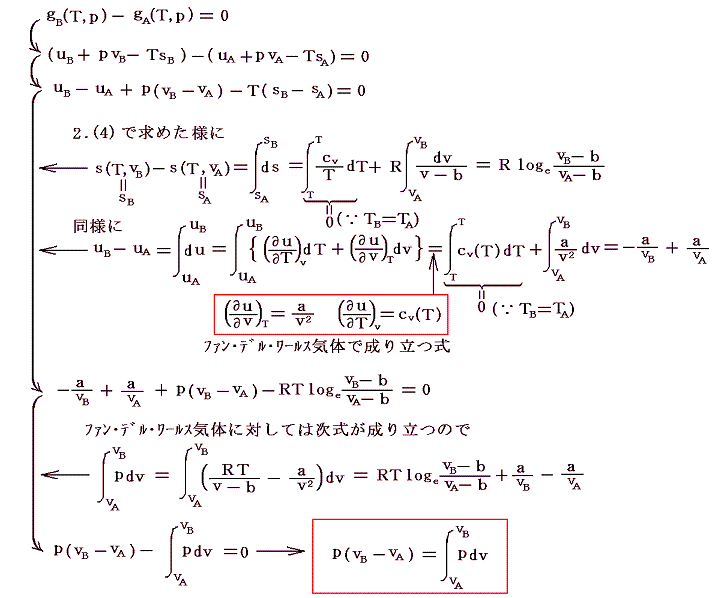
上式の左辺は下左図着色部の面積を、右辺は下右図着色部の面積を表している。
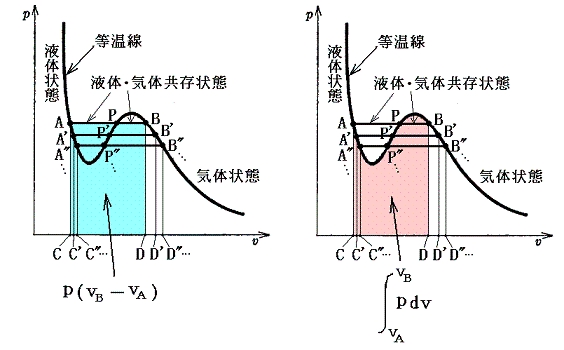
つまり、この両者の面積が等しくなる等圧線が求める状態変化曲線です。これは下図の面積Aと面積Bが等しくなるような等圧線に沿って実際の変化が起こる事を意味する。
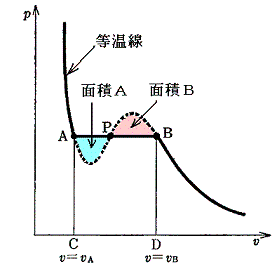
このことを最初に指摘したのはJ.C.Maxwell(Nature 1875年)なのでこの関係をMaxwellの規則という。
[補足説明1]
Maxwellはこの規則を見つけるとき、水平な線とファン・デル・ワールス等温線で作られるサイクルを考えた。このサイクルをたどると二つのループを一回りすることになるが、一つのループは左回りに、もう一つは右回りに回る。従って二つのループは符号が逆になる。このサイクルは等温過程だけから成るサイクルであるから効率はゼロであり仕事は取り出せない。ところで仕事はサイクルの面積で与えられるので、その面積はゼロでなければならない。つまり互いに逆回転する二つのループが囲む面積は等しくなければならないのである。
(2)液体とは何か
1.気体と液体の連続性
Maxwellの規則を、臨界点より下の全ての等温線について適用して作図を行うと、下図のようにな気相と液相が平衡を保って共存する領域(着色部)の境界線が得られる。この右側は気体のみが左側は液体のみが存在できる。この領域の最高点が臨界点(pc,vc,Tc)である。
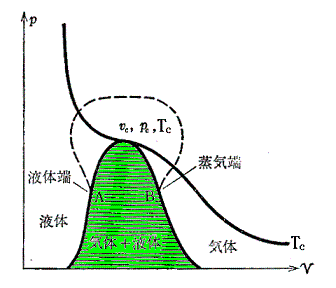
上図で明らかなように、二相共存領域(着色領域)を通ること無しに、安定状態のみを連続的にたどる(上図点線経路)ことにより気体と液体との間を自由に行き来することができる。これがファン・デル・ワールスが論文の表題を「気体状態と液体状態の連続性」とした理由です。
Maxwellの規則を求めるときに実行した線積分も、s、uがいずれも状態量であるために、その積分値は積分経路に依存せず同一の値を与える。そのためファン・デル・ワールス式の不安定領域(上図着色領域)を通ることなく、上記の点線経路のような熱力学的に安定に存在する領域を経過して線積分を実施したと考えればよい。ただし、pのdvに関する積分だけは、ファン・デル・ワールスの式が全ての領域に於いて成り立つと仮定して、等温線に関して積分している。
超臨界状態物質の興味深い利用法。

2.自由表面
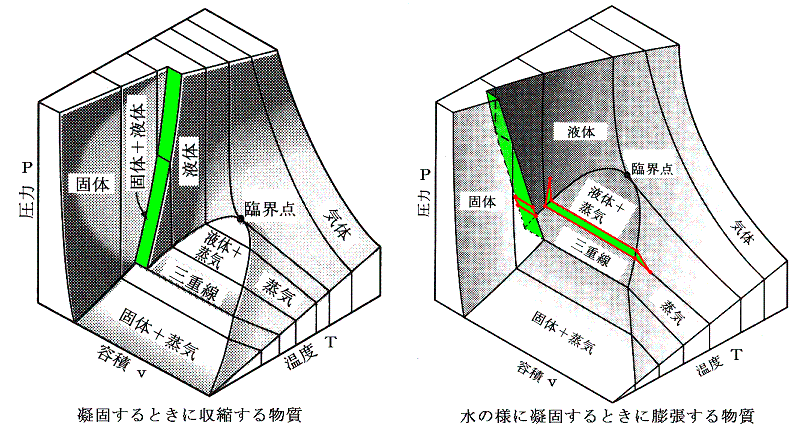
臨界点とはどのような状態なのか水を例にして説明する。氷1mol(18g)を内容積57.1cm3の頑丈な真空容器に入れ全体を熱浴の中につけて温度を変えられるようにする。そして体積を一定を保って温度を下図のようにA→B→Cと臨界温度647.3K(374.2℃)まで暖める。
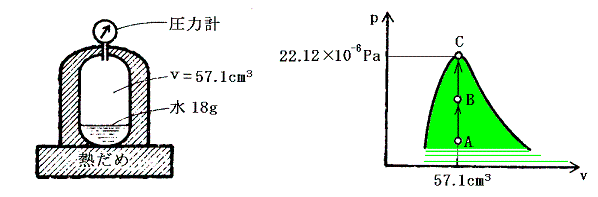
Aでは気体と液体の間に境界があるため、両者の区別ができる。過熱により気体は蒸発して気体の密度は温度とともに増大する。逆に液体はその質量が減少するのはもちろんであるが密度も減少してゆく。Bの状態がそれである。さらに温度を上げると気体と液体の境界がぼやけてやがて消滅する。それが臨界点Cでの状態である。そこでは境界面が消滅するので気体と液体の違いは意味を持たない。
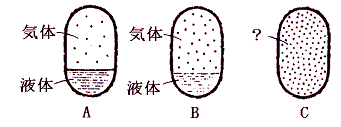
我々が「液体」なるものを認識できるのは、気体との境界に自由表面が存在するときのみであって、その他の状態では液体と気体の区別は意味をなさない。つまり、液体が定義できるのは上図の緑色着色領域だけである。だからこそ、臨界温度以下に冷却しないと、気体を液化することはできなかったのである。
3.二相共存領域
二相共存領域における等圧・等温線上の点Pが物理的にどのような意味を持つか考えよう。
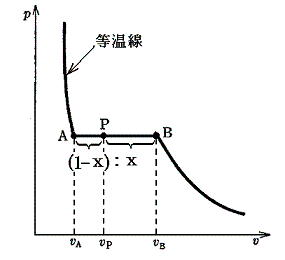
直線AB上の点Pの圧力、温度はA、B点と同じである。体積が異なるのは液相と気相にある質量比が異なるからである。A点ではモル体積vAの液体だけが、B点ではモル体積vBの気体だけが存在する。P点での液体の質量の割合をx、気体のそれを(1-x)とすると、線分AB上の任意の点Pの体積vPは
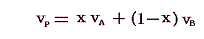
となる。当然のことであるがx=1の時にはvP=vA、x=0の時にはvP=vBとなる。したがって
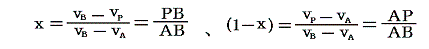
の関係が成り立つことが容易に解る。
(3)臨界点
前項の議論から明らかなように、ファン・デル・ワールスの状態方程式において(∂p/∂v)T>0の領域が消滅する温度Tが臨界温度Tcである。そのため、ファン・デル・ワールスの状態方程式が定まれば、臨界点の(pc,vc,Tc)はその状態方程式から数学的に求まる。臨界点は等温曲線の傾きがゼロでしかも変曲点となる点だから、そのこと示す関係式を利用すればよい。
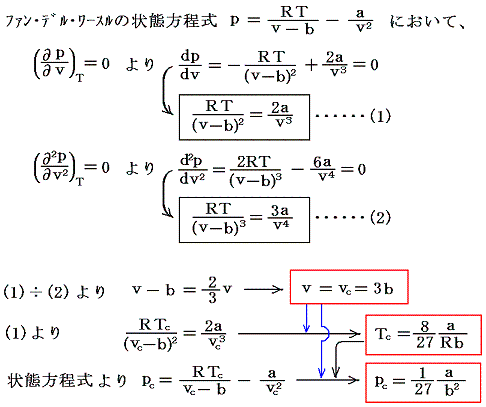
となる。
さらに、ファン・デル・ワールス理論では
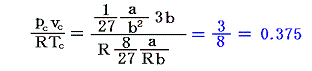
が常に成り立つことがいえる。
ファン・デル・ワールス状態方程式を臨界点での値(pc,vc,Tc)を単位とた変数(p†,v†,T†)で表すと
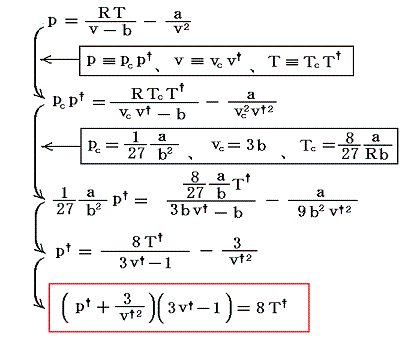
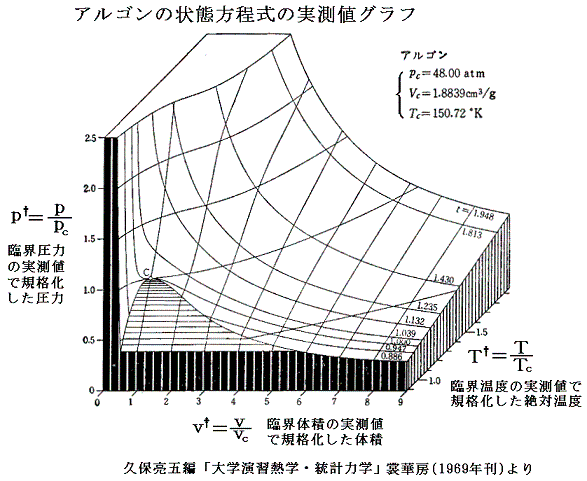
となる。これは気体の種類によらない(つまりa,bの違いに依らない)普遍的な式となる。参考に、二相共存領域を3.(1)項で説明したMaxwellの規則により定まる等圧線で置き換えたレリーフを示す。[拡大版]
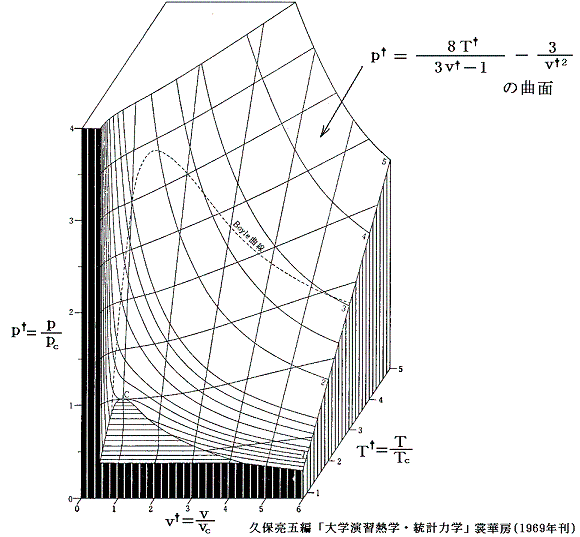
図中の“Boyle曲線”とは
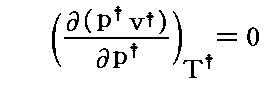
となる点を繋いだものです。その具体的な関数形と、この曲線の意味については別ページで説明していますのでご覧下さい。また、その意味を実際に示しているレリーフ図の例は4.(2)のこの図で引用していますので御覧下さい。
すでに注意したようにファン・デル・ワールスの状態方程式は、実在気体の本質をよく表しているが、あくまで近似的な式です。
そのため、現実の気体の振る舞いにできるだけ広い範囲で合致するように定数a、bを定めると、それから上式により計算される臨界定数は実際の測定値と必ずしも一致しない。
また実測された臨界定数の値から、上式を使ってaとbを求めてファン・デル・ワールスの状態方程式を構成すると、それは臨界点こそ一致するが、それから離れるにつれて実際の気体の振る舞いからずれてくる。[下図参照]
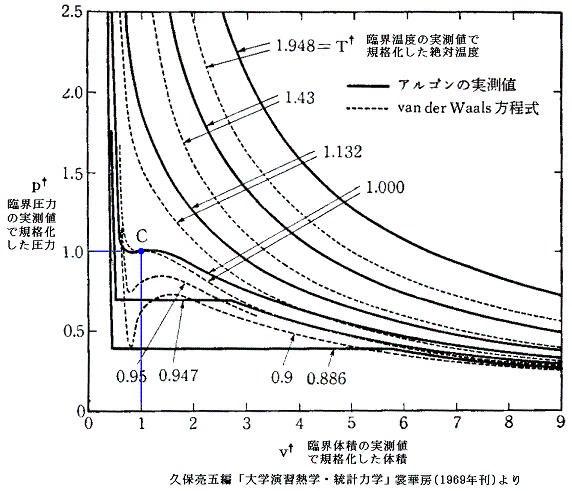
さらに、実在気体のpcvc/(RTc)は、上で求めた0.375にはならないで0.27~0.33の間にばらける。[下表参照]

だから上記の計算式は、あくまで近似的な関係式であると考えるべきです。しかし、臨界点のおよその値はa、b値から見積もることができるので、実在気体の液化装置の設計に於いて、きわめて重要な情報を提供する。
事実、オネスは100℃~-216℃の範囲でヘリウムの体積と圧力を精密に測定してファン・デル・ワールスの状態方程式の定数aとbを見積もり、上記の式を用いてヘリウムの臨界温度を6Kあたりであると推定したのである。[別稿「冷凍・低温技術の歴史」1908年参照]
4.クラウジウス=クラペイロンの式
クラウジウス=クラペイロンの式は相変化にともなう体積変化と潜熱を、二相平衡系の圧力の温度依存性に関係づける式です。相変化についてきわめて重要な情報を教えてくれる式ですが、その証明を理解するのは結構難しい。それは相転移を伴った特異点における議論のため、式を導くときに利用される変分の意味が非常にわかりにくいためです。ここでは、その当たりを重点的に解りやすく説明します。
(1)飽和蒸気圧曲線
実在気体の例として水蒸気を取る。円筒形の容器に水を入れて、その水の上に蓋をする形で可動ピストンを気密に取り付ける。ピストンに加えた圧力と系の温度を一定に保ちながらゆっくり加熱していくと、水の一部は蒸発して水面とピストンの間にできる空間を満たす。そして圧力を一定に保ちながら全体の体積は増大していく。ピストンと水面の間の空間は飽和蒸気で満たされており、その圧力を飽和蒸気圧という。熱を取り除くと蒸気は凝縮して水に戻り体積は減少する。したがって与えられた温度Tと系の圧力pの間には体積によらない方程式
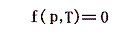
が存在する。これをp-T座標面にプロットすると水の場合下図の様になる。これは飽和蒸気圧曲線と言われるもので、1.(1)で示した二酸化炭素の場合の-56.6~31.1℃の間の曲線に相当するものです。
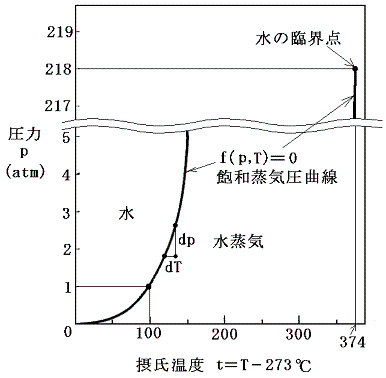
これは言うまでもなく、状態方程式曲面の液体・気体共存領域をp-T座標面に射影したものです。[拡大図]
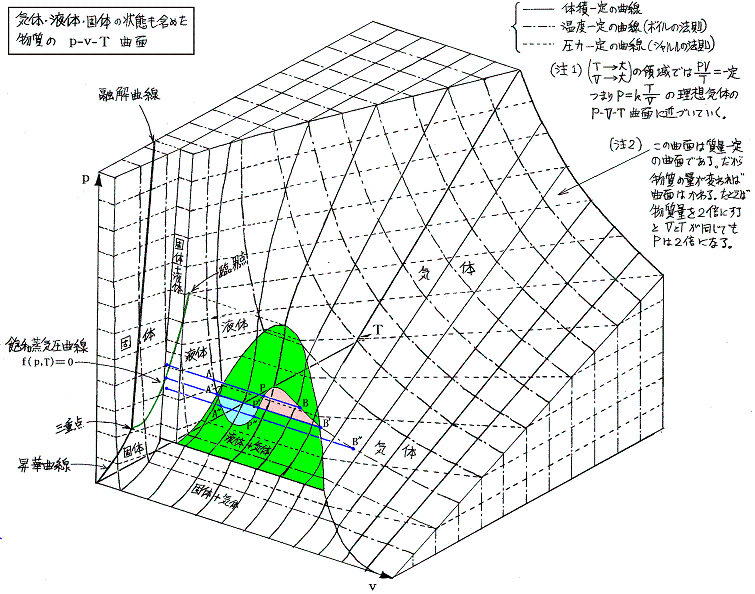
上図の A-P-B、A’-P’-B’、A”-P”-B” は、3.(1)で述べた等温・等圧線に相当する。その直線をp-T座標面に射影した点が4.(3)の図の何処に対応するかに注意されたし。
(2)p-T座標面上の様々な状態量の関数曲面
p-T平面に垂直方向の量として、前節に述べたvの代わりに、内部エネルギーu、エントロピーs、エンタルピーh、ギブスの自由エネルギーg、あるいは定積比熱cv、定圧比熱cpや、pv、Ts などを取ることもできます。これらの量はいずれも系の状態量ですから点(p,T)が決まればそれに垂直な方向の座標に対して連続的な関数曲面を形成します。
ところが上に述べた飽和蒸気圧曲線の真上の近傍では、それらの曲面は互いに食い違っています。その当たりが非常にわかりにくいので、参考文献3.久保亮五編「大学演習 熱学・統計力学」に載っている図を拾ってきて示します。これらの図は物質の種類やp-T座標の方向もバラバラですが、その当たりの様子はご理解いただけると思います。いずれの図も飽和蒸気圧曲線の真上で曲面が食い違っています。その部分が上図緑色の気体・液体共存領域に対応します。また、点Cが臨界点です。[拡大版]
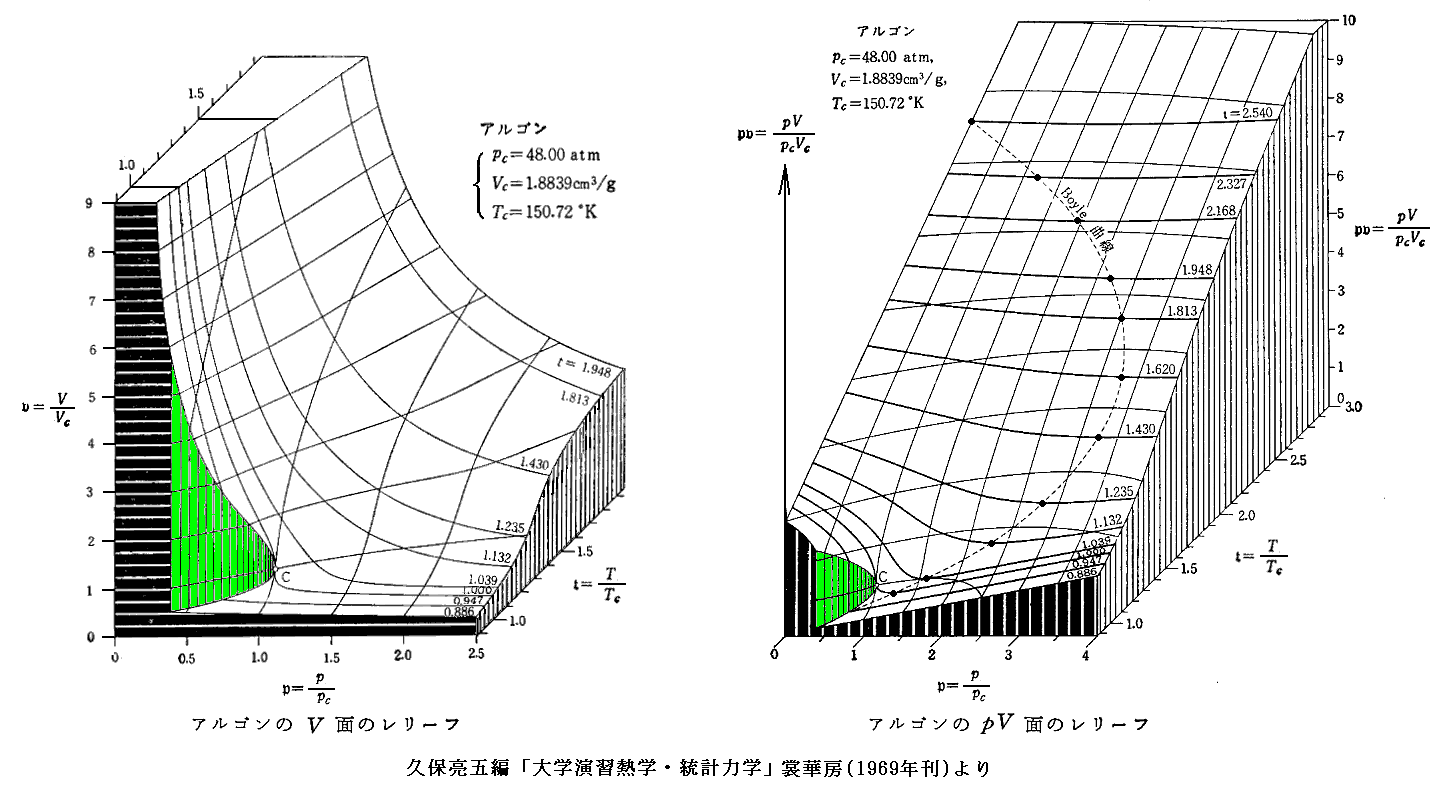
上左図の(p,T)の各点に於いて、そこのv値をp倍してプロットすれば上右のpv曲面図になります。
右図中の“Boyle曲線”[3.(3)で説明]の位置で T†=一定 の p†v†-p†曲線 の傾きが p† の増大に伴って負から正に変化することに注意して下さい。それが別ページで説明した
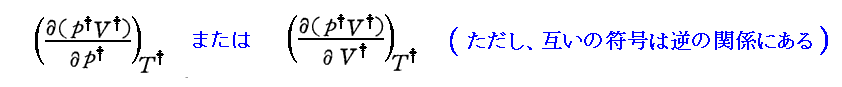
の正負の変曲点曲線である“Boyle曲線”の意味を表しています。
定積モル比熱Cv(T,v)の体積vに対する依存性や、定圧モル比熱Cp(T,p)の圧力pに対する依存性は状態方程式p=f(T,v) or v=f’(T,p)などが定まれば決定できます。(計算法は参考文献3.第3章例題[3]など参照)
ただし2.(3)で注意したように、比熱の温度依存性は状態方程式や熱力学からは求まりません。以下のレリーフの温度依存性はあくまで空気の実測値より求めてレリーフにしたものです。そのようにして求めた空気のモル比熱のp-v座標面上のレリーフですが、圧力が低い場合は理想気体と同様に温度の依存性はなくほぼ一定と見なせます。[拡大版]
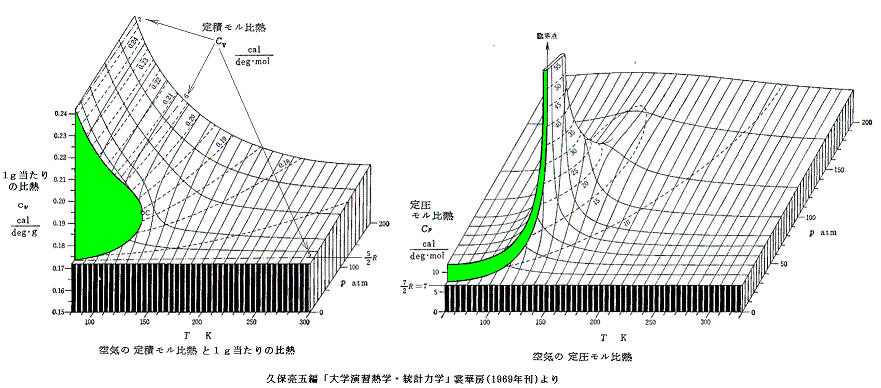
各(p,T)点における比熱が解ればp-v座標面上の内部エネルギーuの関数曲面が求まる。それは(p1,T1)から(p2,T2)へ変化したときの内部エネルギーの変化量は、その状態変化に伴って、その系に出入りする仕事量と熱量から計算できるからです。3.(1)でもそのような計算をした。
そのようにして求めた空気の内部エネルギーuのレリーフが下右図です。別稿「絶対温度とは何か」4.(1)1.で説明した様に、理想気体の内部エネルギーは温度のみの関数で体積や圧力に関係しなかったが、ファン・デル・ワールス気体ではそうはなりません。
統計力学に依ると“理想気体”の内部エネルギーは絶対温度Tに比例することが言えます。しかし、熱力学の範囲ではそこまでは言えません。現実には存在しない“理想気体”の比熱のデータが測定できれば、その事が言えるはずですが。
[拡大版]
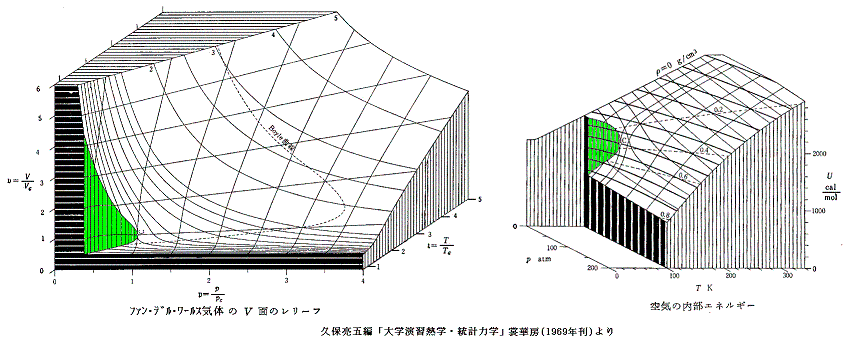
エントロピーsもuと同様にして求まる[下左図]。
このようにuやsのレリーフが求まれば、他のエネルギー形式は
エンタルピー: h=u+pv[下右図]
ヘルムホルツの自由エネルギー: f=u-Ts
ギブスの自由エネルギー: g=h-Ts=u+pv-Ts
の定義式にしたがって内部エネルギーuにpvやTsを加えれたり引いたりすれば直ちに求まる。
特に興味深いのは上右図のu図に最初に示したpv図を縦軸に於いて足し合わせてできるエンタルビーhを縦軸にした h-p-T のレリーフ図(下右図)です。ここでは気体の種類が違っていますが、もちろん同じ気体に付いての図で足し合わせます。
この図中の エンタルピーh=一定 の曲線で (∂T/∂p)h=0 となる点(赤点)を繋いだ線が“ジュール=トムソン係数”の“逆転温度曲線”[(∂T/∂p)h=0の曲線]です。この図の詳しい説明は5.(4)を御覧下さい。[拡大版]

これらのp-v座標面上の様々な状態量のレリーフの中でも下右図のギブスの自由エネルギーgの状態図は特に興味深い。これは参考文献3.の4章問[B][31]で説明されているものです。[拡大版]
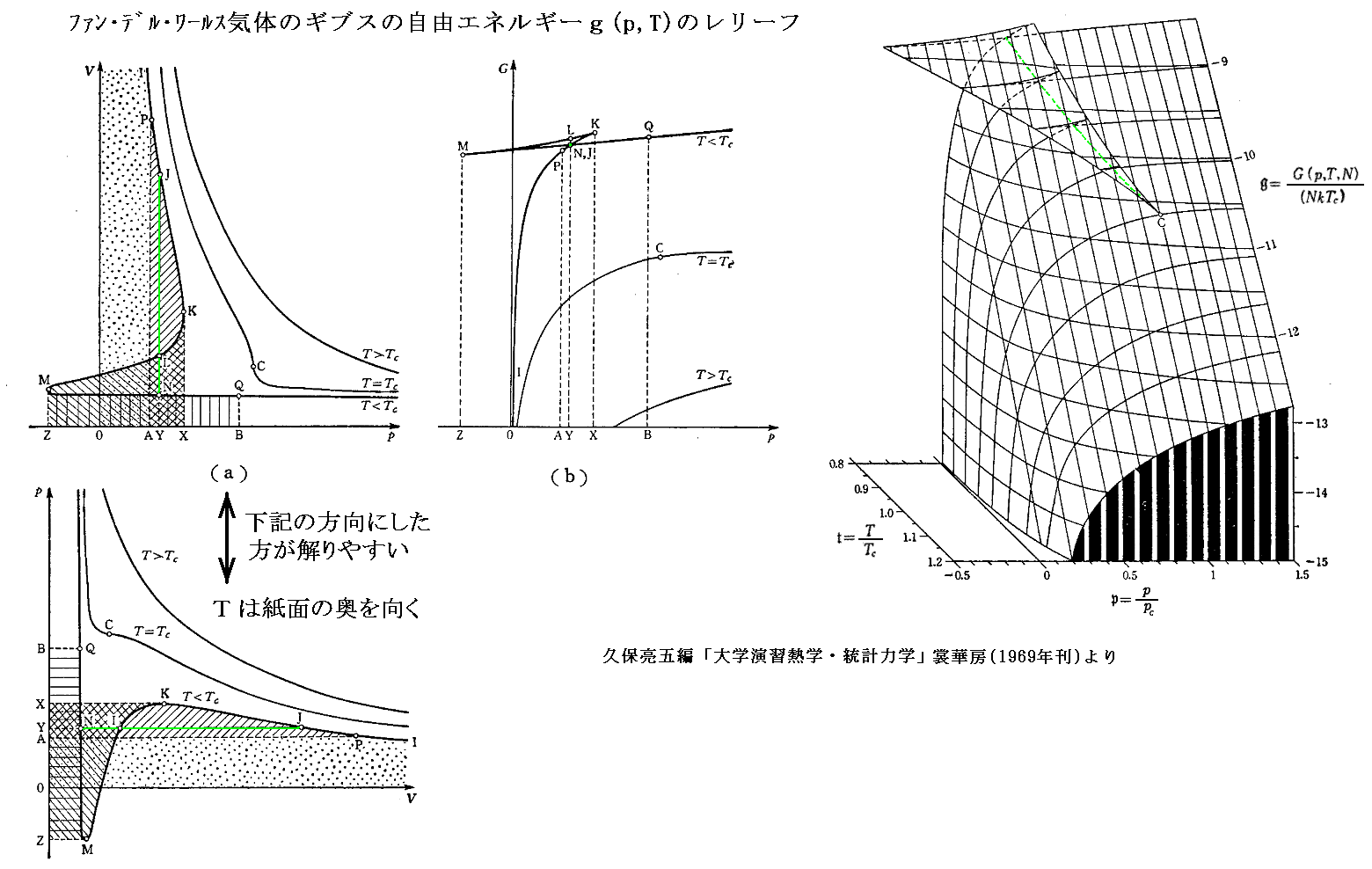
上右図のg(p,T)のレリーフ中の緑色の点線のp-T平面上への射影が、最初に述べた“飽和蒸気圧曲線”です。3.(1)[補足説明0]で説明したように、この曲線(つまり液体・気体共存領域)ではギブスの自由エネルギーが一致しなければならない。
このとき注意してほしいのは、気体側から緑色点線の境界線を横切るg気(p,T)曲面と、液体側から緑色点線の境界線を横切るg液(p,T)曲面は緑色点線の部分で互いに交差して反対側に伸びている事です。そして、緑色点線の両側で安定な相はg(p,T)曲面が下側に位置する相です。
このように、交線において二つのg(p,T)曲面が交わって交差する場合は一次の相転移と言われます。また、単に交わるのではなくて、接触するようにして交差する場合を二次の相転移と言います。
このとき他の物理量は、飽和蒸気圧曲線の真上の部分で、気体側から伸びる状態量曲面と液体側から伸びる状態量曲面は互いに交差することなくすれ違いで反対側の領域にのびていることに注意してください。上に示した図では全て飽和蒸気圧曲線の上で反対側に伸びる部分は断ち切られていますが、元々はファン・デル・ワールスの状態方程式曲面と同じように伸びており、同じ(p,T)座標の上に二枚の曲面が存在する。このことがクラウジウス=クラペイロンの式の証明に用いられている微少変分の意味の理解を難しくする。その当たりを次節で解りやすく説明する。
(3)クラウジウス=クラペイロンの式
飽和蒸気圧曲線付近のギブスの自由エネルギーg、エントロピーs、体積vの関数曲面は下図のようになる。[拡大版]
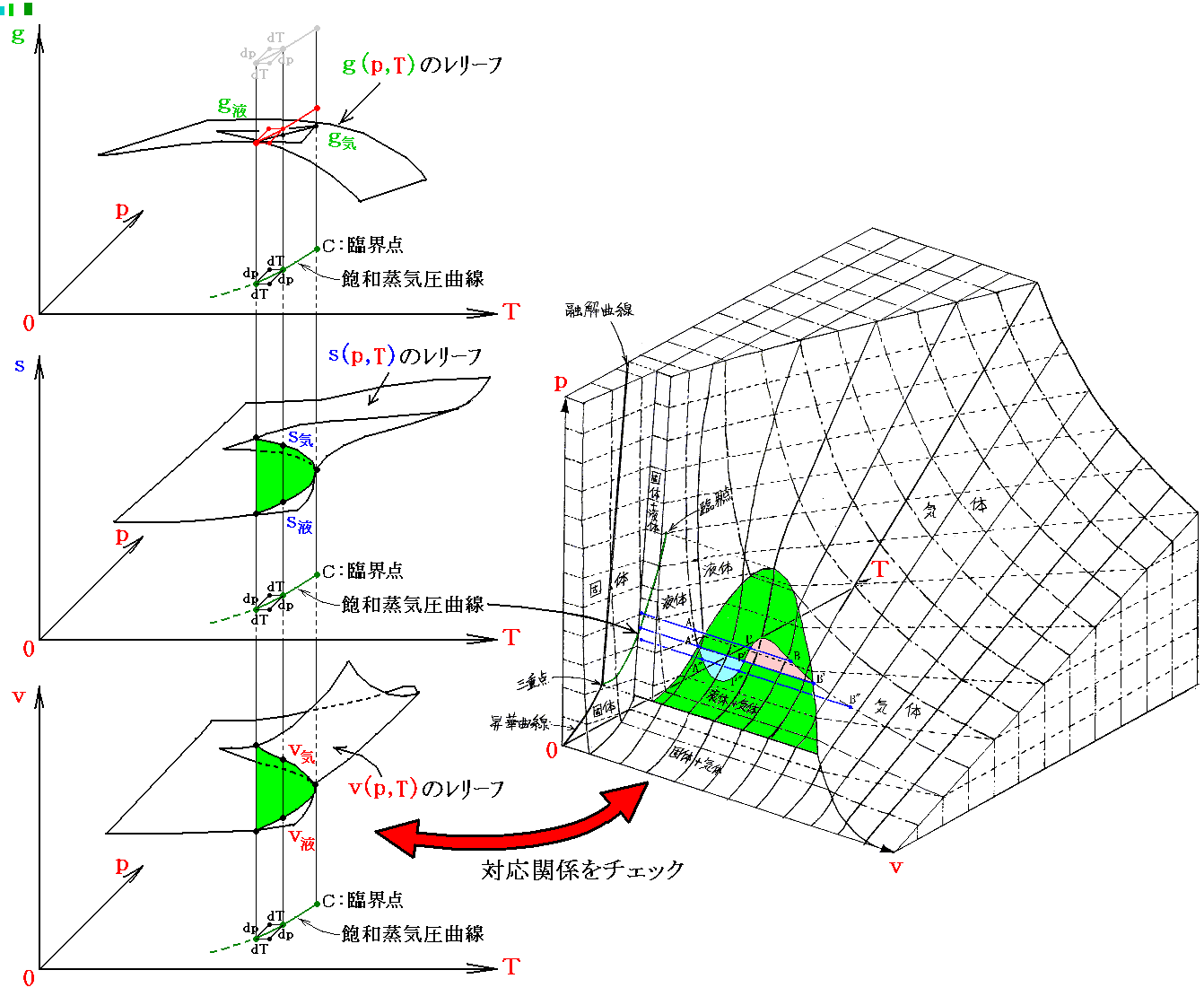
このとき、熱力学関係式
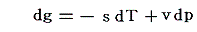
は図中の2枚の関数曲面g気(p,T)とg液(p,T)のいずれに対しても成り立ちます。つまり(p,T)→(p+dp,T+dT)だけ変化したときの変分dgに対して
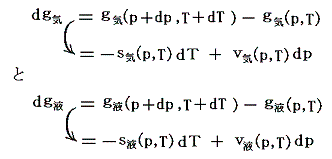
が成り立つ。
このとき dg の定義式で sdT の項と vdp の項の符号が互いに逆であることに注意してください。そのためs曲面とv曲面で飽和蒸気圧曲線上に存在する気相面と液相面とのギャップが互いに打ち消されてg曲面では連続的に繋がる(正確には交差している)事になるのです。このことは上図左側の三枚の曲面図を比較されれば諒解できます。
[補足説明0]
飽和蒸気圧曲線に沿った気相と液相のギブズの自由エネルギーの変化量は互いに等しい》
ここで(dp,dT)の変分を飽和蒸気圧曲線に沿った方向とすると、それはg気(p,T)曲面とg液(p,T)曲面が交差して一致している方向[3(1)[補足説明0]を参照]だから、当然その方向に沿った変分dg気(p,T)とdg液(p,T)も等しいはずである。そのため

が得られる。これがクラウジウス=クラペイロンの式です。
この証明はなかなか解りにくいが、この証明法こそ、W.Gibbsが彼の熱力学第二論文(1873年)の中で熱力学状態方程式曲面の幾何学的性質から証明した独創的証明法です。
これは“ギブズの自由エネルギー”導入の威力を存分に示すものですが、その事については別稿「熱力学関数(状態方程式曲面)の性質」4.(2)をご覧下さい。
[補足説明1]
クラウジウス=クラペイロンの式は、クラウジウス(Clausius)が熱力学的に厳密に証明した。
(Clausius, R. (1850), “Ueber die bewegende Kraft der Wa¨rme und die Gesetze, welche sich daraus fu¨r die Wa¨rmelehre selbst ableiten lassen”, [On the motive power of heat and the laws which can be deduced therefrom regarding the theory of heat]. Annalen der Physik (in German). 155 (4): 500~524.)
上記論文の日本語訳を別稿「Clausiusの熱力学第1論文」で引用しています。その中の3.(4)を御覧下さい。その別稿の3.(2)1.[補足説明1]に記していますように、そこの導き方は熱力学第二法則より直接求める根源的な導き方でして、上記で説明しているギブズの自由エネルギーを介して求める今日的な導き方よりも解りやすいです。
しかし、最初(1834年)に導いたのはクラペイロン(Clapeyron)です。
(Clapeyron, M. C. (1834).“Memoire sur la puissance motrice de la chaleur”,
Journal de lEcole polytechnique(in French). 23: 153~190)
クラペイロンは液体が蒸発する液体-気体の相変化にカルノーサイクルを適用して導いた。その方法はおよそ次の様なものです。[広重徹著「物理学史Ⅰ」倍風館P199~201などを参照]
下図のように、1molのp-v状態図に於いて、その両端を断熱過程でつないだ温度がごくわずか異なる二つの気体・液体共存領域(緑色着色部)を考える。そして、その周りを回るカルノーサイクルを考える。
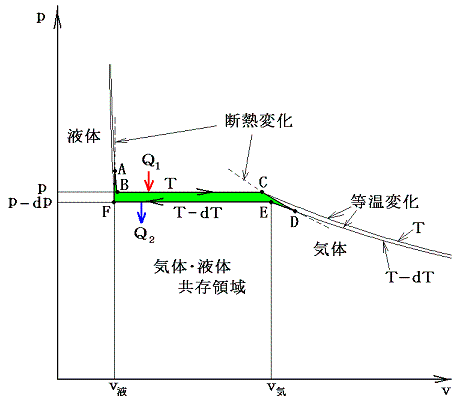
A点に於ける1モルの液体に温度Tの下で熱量Q1を加えて等温的にA→B→Cをへて気体(C点)にする。次に断熱膨張により点Dまで膨張させる。その後、温度T-dTの下でD→E→Fの等温変化により熱Q2を外界に放出しながら液体(F点)に戻す。そしてF点からは断熱圧縮して最初のA点に戻るとする。
このとき、外界に対してなされた仕事(緑色領域の面積)wは熱力学第一法則によりw=Q1-Q2となる。全ての過程は準静的可逆過程で行われるのでカルノーの原理(熱力学第二法則)が成り立ち、その効率は絶対温度のみの関数となる。
このとき、サイクルの両端A→BとD→Eの等温過程に於ける熱の出入りは微少ゆえにq転に比較して無視でき
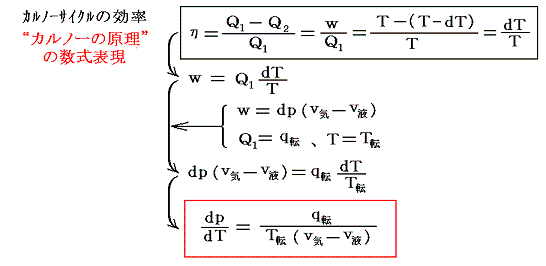
となり、同様な式が得られる。
クラペイロンがこの式を求めた1834年は、カルノーがカルノーサイクルの論文を発表した1824年よりも後ですが、クラウジウスがカルノーサイクルの本質を解明する1850年よりも前であること、さらにファン・デル・ワールスがその状態方程式を発表する1873年よりも遙か前である事に注意して下さい。
クラペイロンはカルノーサイクルの本質を理解していたわけではありませんが、カルノーサイクルの本質の内の、熱機関の効率がその機関が働く高熱源と低熱源の温度差のみに依存するという所だけを用いて求めています。
(4)飽和蒸気圧曲線の求め方
実際の“飽和蒸気圧曲線”はクラウジウス=クラペイロンの式を、各転移点(p,T)における転移熱q転と(v気-v液)を用いて積分すれば得られる。
このとき、q転 は(p,T)の関数です。しかし、近似的にq転 は圧力・温度によらずほぼ一定とおける場合が多い。
問題なのは(v気-v液)が圧力pと温度Tの両方の関数であることです。一般にv気≫v液 だから v気-v液≒v気 として良いだろう。さらに蒸気を理想気体として扱う近似が許されるならば v気=RT/p と表現できる。
これらの近似を用いると

となる。
この積分関数 p(T) が p-T座標上の“飽和蒸気圧曲線”を表す式です。ここで、積分定数 p0 は温度 T0 における飽和蒸気圧 p(T0) の事です。実際 T=T0 を上式に代入すると p(T0)=p0 となる。
このとき以下のように定数を置き直しても良い。
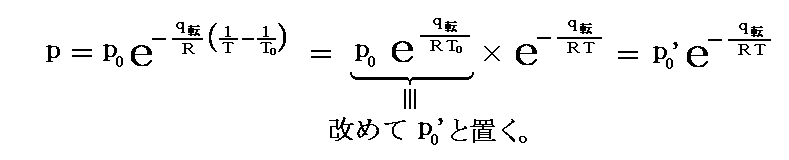
この形の定数p0’はT=T0のときのp(T0)の値ではないが、T=T0の時のpからp0’を決定する事ができます。実際、以下の例ではこの形の式を用いて論じています。ただしそこでは、p0’を改めてp0と書き直しています。
いずれにしても、飽和蒸気圧曲線は絶対温度の上昇に対してほぼ指数関数的に増加することになる。
このとき、様々な温度に於ける飽和蒸気圧を測定して、logepを縦軸に1/Tを横軸にしてプロットすると直線のグラフ
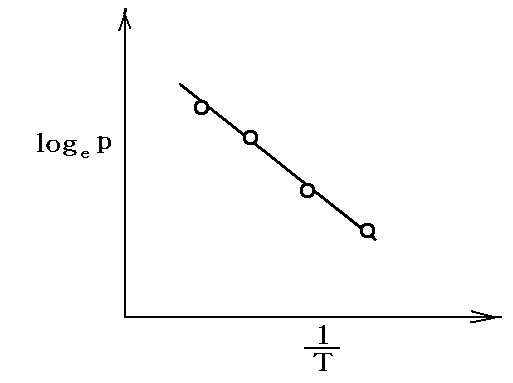
が得られる。その傾き-q転/Rより、転移熱q転が求められる。ただし、これはq転が温度に依らない近似が適応できる場合に言えることです。
例1.水(H2O)
ちなみに水の25℃における“蒸発熱”(気化熱)は q転=4.4×104J/mol 、気体定数は R=8.314J/K・mol であり、水の“臨界点”の温度は374℃(647K)で圧力は218.3気圧(2.21×107Pa=22.1MPa=221bar)です。“臨界点”の値を用いてp0を定めると
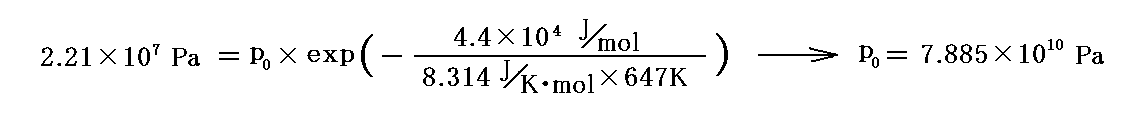
となる。このp0を用いて前記のグラフを描いて見ると
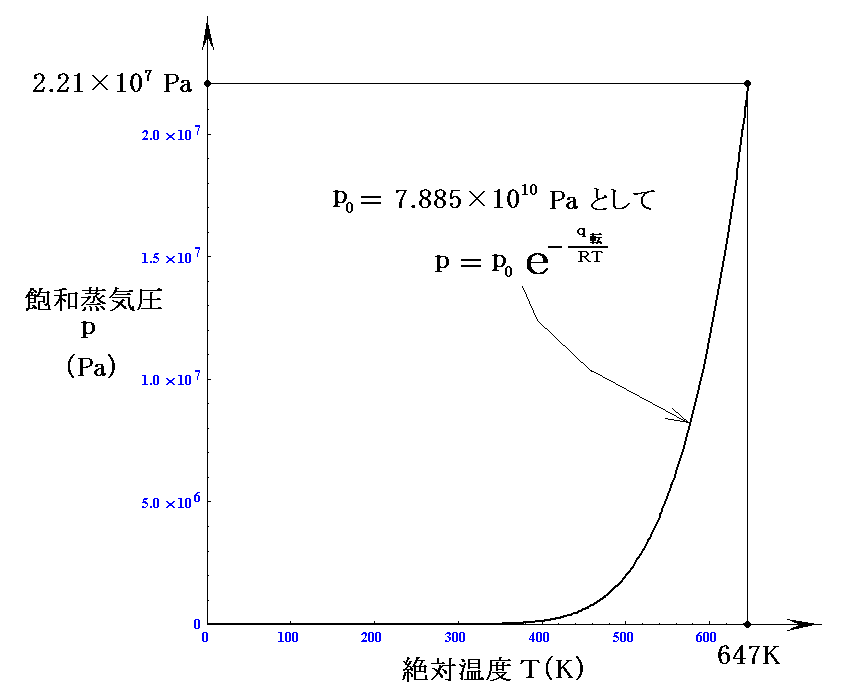
となる。
100℃前後の様子を見るには、100℃(373K)で飽和蒸気圧1.0気圧(1.013×105Pa)のデータから求まるp0
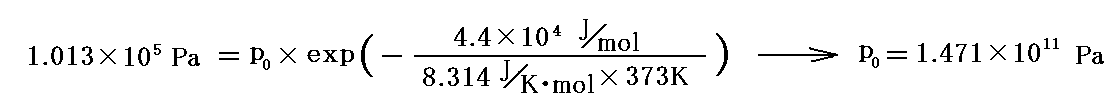
を用いる。これは前記の値と少し違うがオーダー的にはだいたい同じになる。
この値を用いて、横軸を摂氏温度t(℃)とした、グラフを描くと
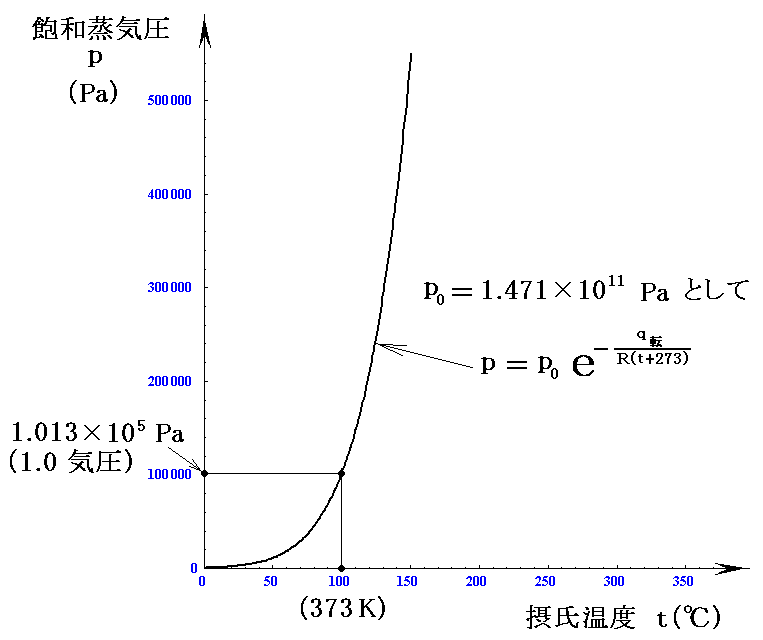
となる。これらのグラフは4.(1)で示したものに近いカーブとなる。
[補足説明1]
実際のq転 は温度と共に減少し、臨界温度ではゼロとなる。下図は水の“転移熱”(蒸発熱)の温度による変化を表しています。
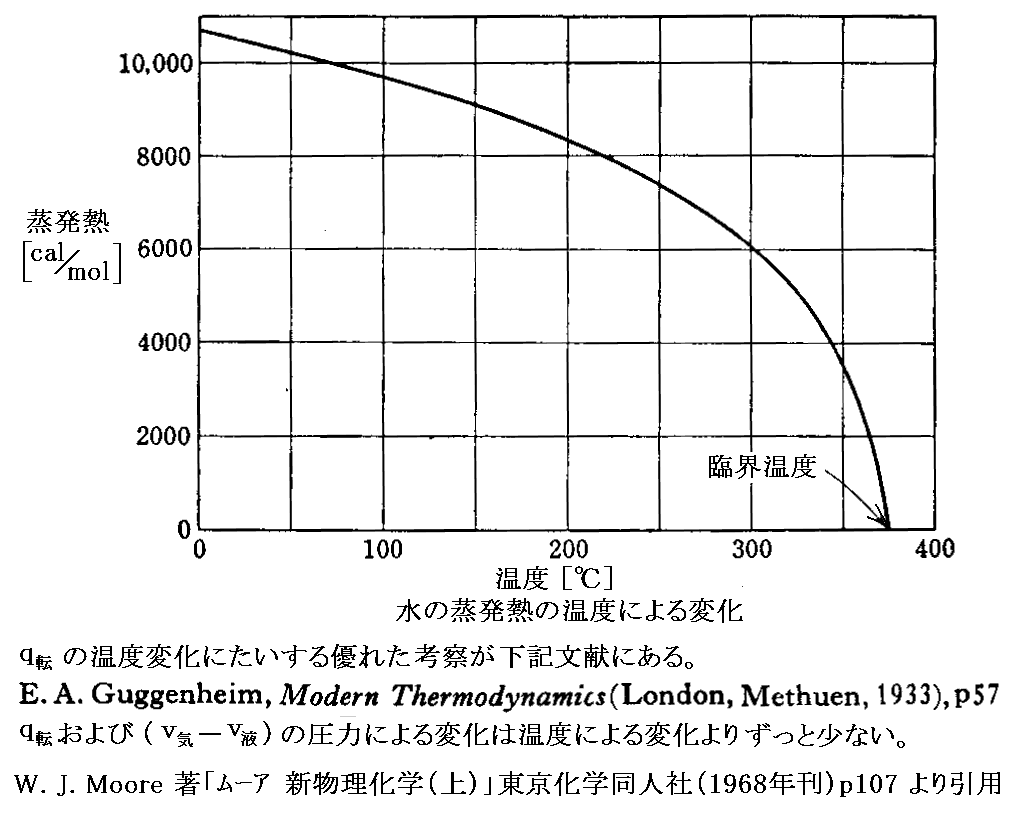
“転移熱”q転 が温度と共に減少し、臨界温度ではゼロとなるのはある意味当然です。なぜなら3.(2)2.で説明した様に、臨界点に近づくと液体と気体の違いはほとんど無くなり、臨界点では気体状態と液体状態は一致します。ならばその二つの状態の転移に熱量の移動が必要無いのは明らかです。
そのため臨界温度までを描いた最初のグラフはかなり修正を要する。実際に火力発電所を設計するときには実測にもとずく正確なデータが必要です。
例2.鉄(Fe)
鉄の蒸発熱はq転=3.40×105J/molです。また、その沸点[つまり蒸気圧が1気圧(1.013×105Pa)となる温度]は3134K(2861℃)です。沸点に於ける値からp0を求めて蒸気圧曲線のグラフを描いてみる。
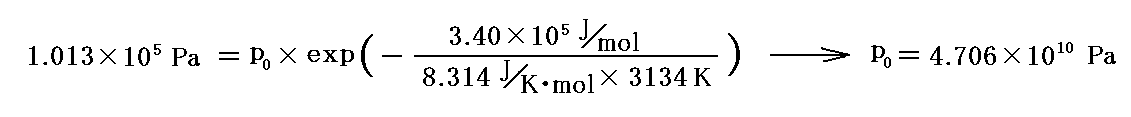
だから
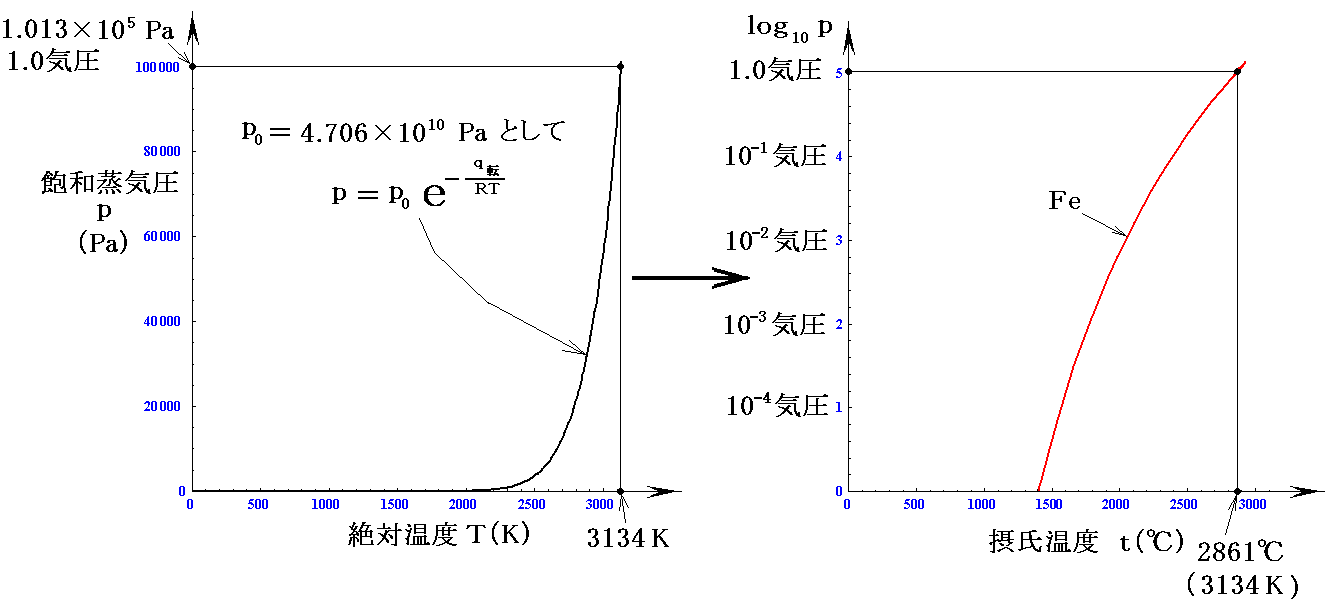
となる。上右グラフは上左グラフを、縦軸log10p、横軸摂氏温度t℃で、プロットし直したものです。
ちなみに、様々な金属の飽和蒸気圧曲線は下図の様になる。
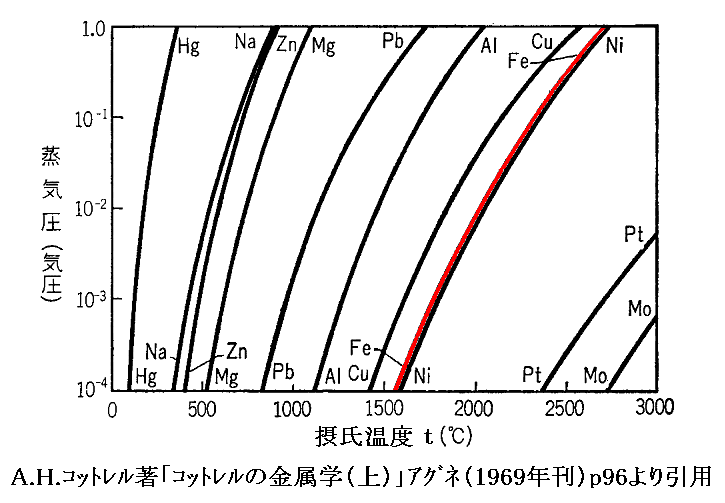
蒸発熱は上図の右側の金属ほど大きくなります。
上図に於いて、常温における水銀の蒸気圧がきわめて低いことに注意。これが初期の真空ポンプの作動媒体として水銀が利用できた理由です。
また、この図はアルミニウム蒸気を金属表面に蒸着させて鏡面を作るとき必要な知見を与えてくれます。
さらに、鉄は融点よりも1000℃以上加熱しても、蒸気圧は1気圧を超えることはない。これが鉄の高炉精錬に於いて蒸発損失を心配する必要がない理由です。
[補足説明2]
本節の最初に述べた飽和蒸気圧曲線に沿った積分の両辺を T と p でやるのではなくて T と (dp/dt)dt で実施すると実用温度計の温度目盛り t を絶対温度 T に結びつける関係式 T(t) が得られます。
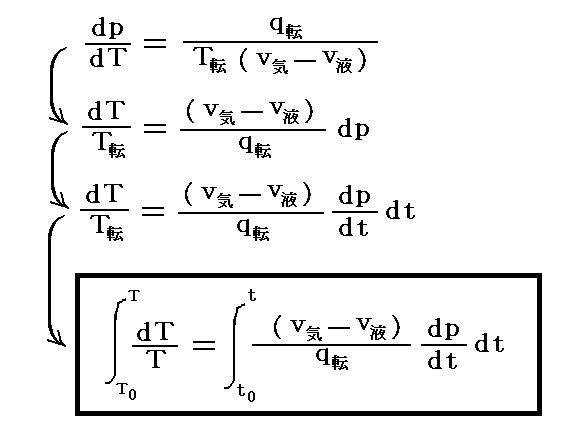
(∂p/∂t)は転移温度 t における飽和蒸気圧曲線の実用温度tに付いての傾きであり、積分は飽和蒸気圧曲線に沿って実用温度t0からtまで行うと、そのときの温度差(t-t0)が絶対温度で(T-T0)に相当するということです。
つまり、実用温度で測った各転移温度 t に於ける“転移熱”q転と“相変化に伴う体積変化”(v気-v液)と“実用温度tの変化に対する圧力変化(∂p/∂t)”の実測値を用いることにより、その実用温度 t が絶対温度 T で何度に相当するかが決定できるのです。
詳しくは別稿「絶対温度とは何か」7.(3)、または参考文献2.§177を御覧下さい。
[補足説明3]
ファン・デル・ワールス状態方程式の様に物質の状態方程式が解っていて、あらかじめ二つの関数曲面g気(p,T)とg液(p,T)が求まっている場合には、その二つの関数曲面の交線として求めることもできます。
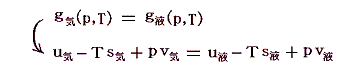
その当たりの詳細が参考文献1.§16.Aや参考文献2.§178で説明されています。その内容をここで紹介しても良いのですが、ここでは別稿「絶対温度とは何か(積分因子とは何か)」の5.(2)3.と5.(3)2.で説明した二つの数式例を、二つの曲面g気(p,T)とg液(p,T)に対応させて説明します。そちらの方が完全微分方程式と積分因子の関係がより明瞭に解ると思います。
曲面g気(p,T)として、上記別稿の5.(2)3.の式を利用します。そこの完全微分方程式 (2xy+6x)dx+(x2-1)dy=0 に於いてxをp、yをTと考えると(2xy+6x)がv気(p,T)に、(x2-1)が-s気(p,T)に相当します。そして、この完全微分方程式の解 φ(x,y)=x2y+3x2-y がg気(p,T)に相当すると考えます。
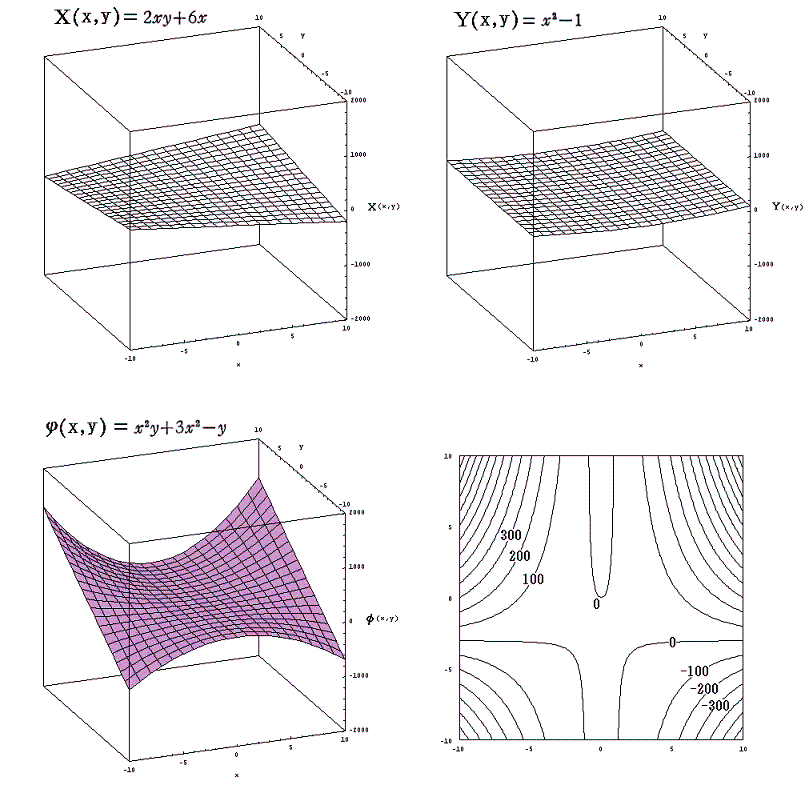
一方、別稿5.(3)2.の (2x+2xy2)dx+(2x2y)dy=0 において同じくxをp、yをTと考えると(2x+2xy2)がv液(p,T)に、(2x2y)が-s液(p,T)に相当します。この完全微分方程式の解 ψ(x,y)=x2+x2y2 がg液(p,T)に相当するとします。
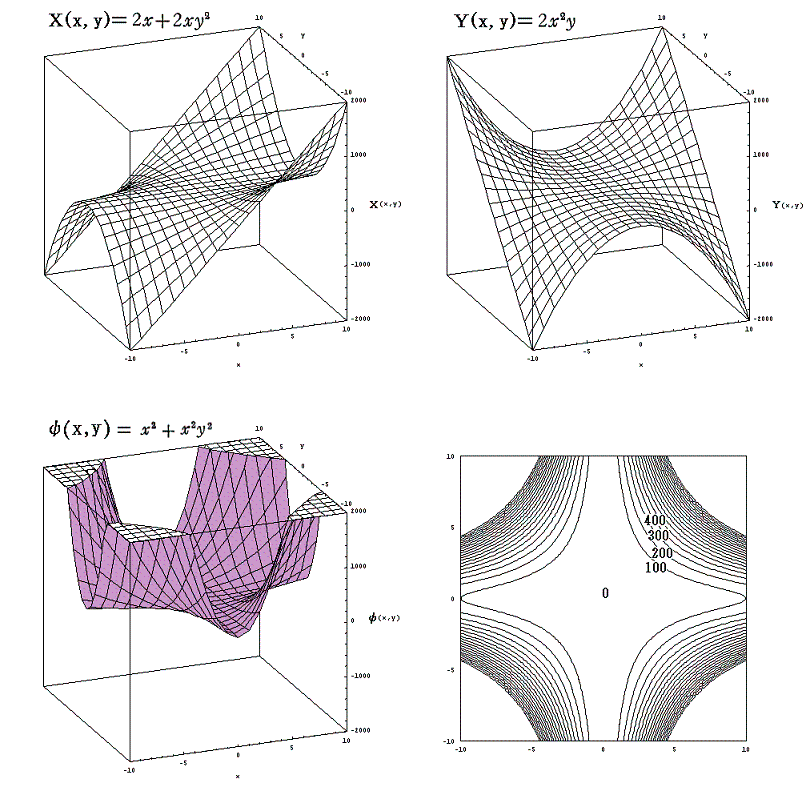
g気(p,T)とg液(p,T)は全く別の2枚の関数曲面ですが、その2枚曲面が交差する曲線をxy平面に射影した曲線が“飽和蒸気圧曲線”です。つまり
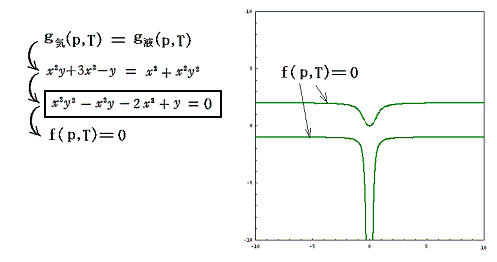
の解が求めるべき飽和蒸気圧曲線 f(x,y)=0 に相当するわけです。
そのとき、もちろん“変分”についての“完全微分方程式”を解いても同じ結論が得られます。
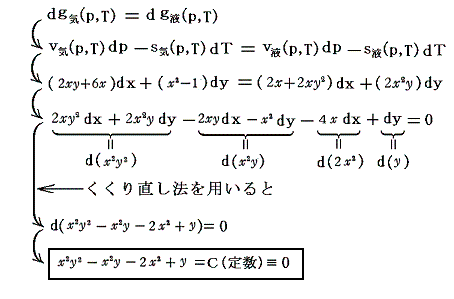
(5)数値例(プランク「熱力学」より)
例として100℃、1気圧の下に於ける水の気化熱をクラウジウス=クラペイロンの式から計算してみよう。

となるので、
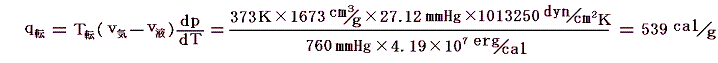
となる。これはHenningによる実際の測定値538.7cal/gときわめて良く一致している。
次式から明らかなように、気化熱の一部は水の内部エネルギーの増加に、他の部分は外部への仕事に費やされる。
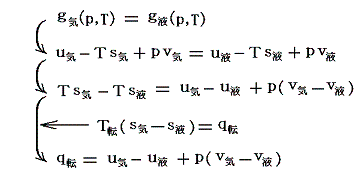
気化熱の中で外部への仕事に費やされる割合は
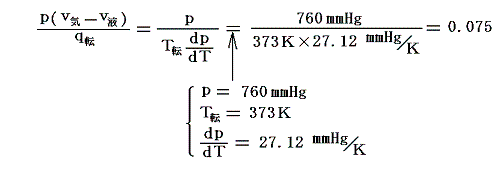
となる。つまり、気化熱の僅か7.5%程度が外部仕事に費やされるだけで、残りの大部分は内部エネルギーの増大に費やされる。
(6)融解曲線、昇華曲線についてのクラウジウス=クラペイロンの式
飽和蒸気圧曲線(気化過程)と同様に、融解曲線(融解過程)や昇華曲線(昇華過程)に対してもクラウジウス=クラペイロンの式が成り立つ。そのとき、融解するとき膨張する物質に対しては圧力が昇るにつれて融解点の温度が昇る。
ところが、水の場合0℃に於いてv固>v液のため逆の現象が起こるので特に興味深い。0℃における1gの氷の融解熱はq転=80cal/g=80cal/g×4.19J/cal=335.2J/gだから

を用いると
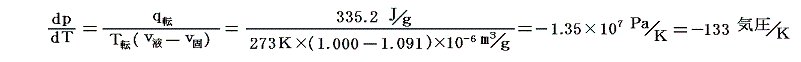
となる。負の値に成るのは、水の場合0℃に於いてv固>v液のためです。これは氷に圧力を加えると融点(凝固点)が低下する事を意味し、融点を1℃下げるのに約130気圧の圧力が必要である。これはW.Thomson(Kelvin)によって最初に確かめられた。
[補足説明1]
歴史的な話をすると、1849年に W.Thomson は下記の矛盾に気がついた。水が凍るときには膨張するので、仕事をさせることができる。ところが水を凍らせるには熱を奪い取らねばらならい。熱の移動無しには仕事はあり得ないと言うのがカルノーの理論であるが、この場合には温度は常に0℃で、温度効果無しに熱が移動し、仕事が得られる事になり、カルノーの理論に矛盾するというのである。
この矛盾は、彼の兄 James Thomson により解決の方策が示された。J.Thomsonは、4.(3)[補足説明]で説明したクラペイロンと同様に氷-水の相平衡にカルノーサイクルを適用[参考文献4.付録8参照]して圧力と氷点の関係を導いて、圧力をかけると水の凝固点の降下が起こることを予測した。そして凝固点の降下が起これば、上記の矛盾は解決できる事を示した。
下図は上右図の固体・液体共存領域に図示しているサイクルを示しています。
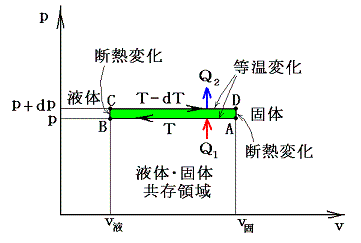
つまり、圧力が高い方の経路が温度が低くて、低温の熱浴に熱を捨てる側になるから矛盾が解消できるのです。
W.Thomson は兄の指針に従って1850年の実験により、加圧すると氷りの凝固点が確かに降下することを確かめた。こうして W.Thomson(Kelvin) はカルノーの理論をますます信頼するようになり、熱力学の完成に近づいていったのです。
ここは、広重徹著「物理学史Ⅰ」倍風館p210 や、山本義隆「熱学思想の史的展開」第27章Ⅵ なども参照されたし。
ここは興味深い所なので、ポール・セン著「宇宙を解く唯一の科学 熱力学」河出書房新社(2021年刊)p55~59を引用。



[補足説明2]
もう一つ補足すると、熱力学は、氷と水の体積では氷の方が大きいということと熱力学第二法則が矛盾しないためには圧力が増大すれば凝固点が下がらなければならないという事を教えてくれます。しかし、何故水より氷りの方が体積が大きくなるのかということに関しては何も教えてくれません。これは熱力学の守備範囲外の事柄です。
5.ジュール=トムソン効果
ファン・デル・ワールスが状態方程式を作り上げたときには熱力学の理論体系は完成していたので、その後の研究に於いて熱力学の知識を存分に利用することができた。第二法則(エントロピー原理)を彼の方程式に適応することにより、ジュール=トムソン効果の温度変化が逆転する境界線を求めることができる。以下で順番に説明する。
(1)熱力学的準備
これは別項「絶対温度とは何か」7.(2)と全く同じですからそこを参照されてお読みください。ただし、ここでの議論は全て「別稿7.(4)まとめ」で説明したやり方に従っています。熱力学第二法則より
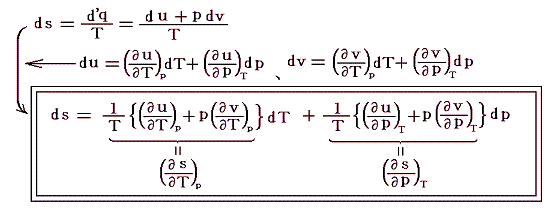
ここでsは状態量ですから、dsが完全微分であることの条件式から
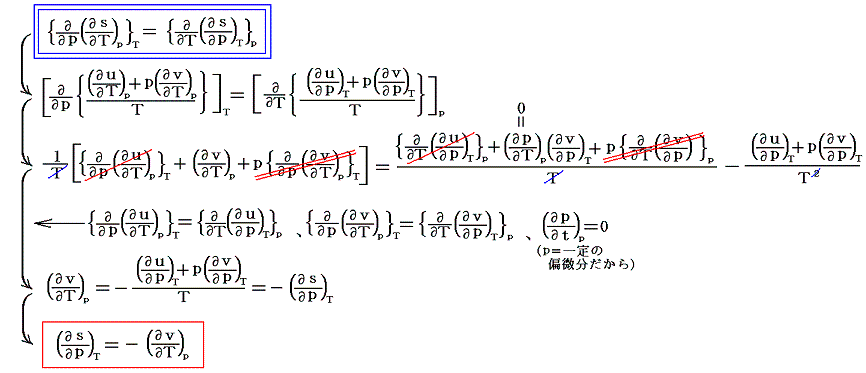
がいえる。
普通これはギブスの自由エネルギー g=u+pv-Ts の微分 dg=-sdT+vdp が完全微分である条件から求められるもので、Maxwellの関係式の一つです。これはもともとエントロピーsの導入とそれが状態量である事に由来するので、ここではあえて泥臭くエントロピーを用いて導いた。
一方、熱力学第一法則(エネルギー保存則)から
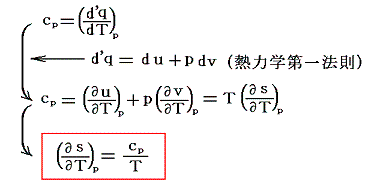
がいえる。
ここで求めた二つの関係式は、どのような物体に対しても一般的に成り立つ普遍的な関係式です。
(2)ジュール=トムソン効果
任意の単位質量の実在気体を、熱の授受無し(q’=0)に、v2-v1の体積膨張をさせる(ジュール=トムソン過程)と、熱力学第一法則(エネルギー保存則)より
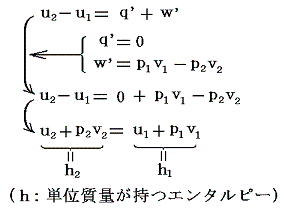
となる。
すなわち、ジュール=トムソン過程はエンタルピーh=一定の過程です。
ここで細孔栓(膨張弁)の両側の圧力差を極めて小さくして気体を流し、両側の状態量の差をΔを付けて表すと

となる。これがJoule=Thomson過程に於いて圧力差Δpで細孔栓(膨張弁)を押し出される気体に起こる温度変化ΔTを表す式です。これは理想気体、実在気体を含めたあらゆる気体に対して一般的に成り立つ式です。もちろん、理想気体の場合には(∂v/∂T)p=R/p=v/TですからΔT=0となります。ちなみに(ΔT/Δp)hをジュール=トムソン係数と言います。
この最終的な関係式にはもはやエントロピーは含まれていないことに注意して下さい。
[補足説明1]
例として実在気体がファン・デル・ワールスの状態方程式で表される場合についてジュール=トムソン係数を計算しみる。1モルの実在気体に付いては
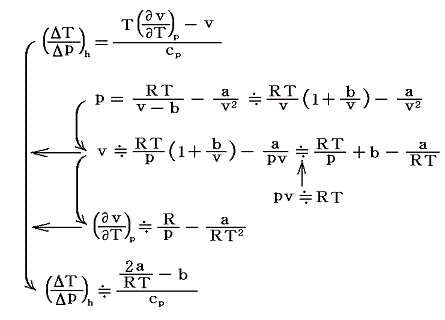
となる。
理想気体のときにはa=b=0であるから、この値はゼロとなり温度変化は無い。つまりジュール=トムソン効果は、実在気体の理想気体からのずれによる効果であることを示している。
そのため、この実在気体の膨張率により実用温度tを定めているのであれば、この実在気体のいろいろな温度tに於けるジュール=トムソン係数を測定することによって、この実在気体温度計が指し示す温度tが現実には存在しない理想気体の膨張率で定義した温度(すなわち絶対温度T)で何度になるかが測定できるのです。
その具体的な手順は別稿「絶対温度とは何か(積分因子とは何か)」7.(2)で説明しておりますので御覧下さい。
[補足説明2]
ジュール=トムソン過程は不可逆過程です。そのため、この変化に伴いエントロピーは常に増大します。なぜなら
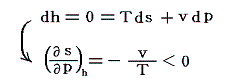
となり、圧力減小(dp<0)に伴いエントロピーは常に増大するからです。
この式の幾何学的な意味を別稿「絶対温度とは何か」5.(2)3.の数式例で説明する。例えば、そこの完全微分方程式 (2xy+6)dx+(x2-1)dy=0 の解 f(x)=x2y+3x2-y がhを意味し、(2xy+6)がv、(x2-1)がT、dxがdp、dyがdsと考えれば、(∂s/∂p)hはf(x)の等高線図のxy平面における傾きを意味します。それは等高線ベクトル(dx,dy)の方向であり、ベクトル場(2xy+6,x2-1)に直行した方向です。今の場合はその傾きが常に負になると言うことです。
1モルの気体の膨張前と、膨張後の状態は不可逆過程で推移した変化ですが、それぞれの状態について状態量hは定義でき、しかもその推移に伴って変化するsやpの関数として、その変分は完全微分の条件を満たしている。
これはエンタルピーhを導入する基になったエントロピーsが、別稿6.(4)1.や4.で注意したように、一つの系の二つの状態間の推移が準静的可逆過程で行われたのか、不可逆過程で行われたのかに関わりなく、それぞれの状態の状態量として定める事ができることに由来します。このエントロピーsの完全微分性こそ積分因子である絶対温度Tを導入することによって得られた最大の成果だったのですから。
[補足説明3]
真空の容器に気体を膨張させるゲーリュサック=ジュールの実験があります。これも断熱の不可逆過程ですが、ジュール=トムソン過程とは異なります。ゲーリュサック=ジュール過程は真空中への膨張ですから、気体は外部に対して仕事をしません。そのため内部エネルギーは不変に保たれます。理想気体の場合にはポテンシャルエネルギーは存在しませんから、膨張しても温度は変化しません。ところが実在気体の場合は内部エネルギー(運動エネルギー+ポテンシャルエネルギー)は一定でもポテンシャルエネルギーが付随するために広がり方が変わると温度は変わります。なぜそうなるかは熱力学からは説明できず統計力学を用いないといけませんが、とにかくそうなります。
ジュール=トムソン過程では細孔栓の左右で圧力と体積が変わります。理想気体の場合はp2v2=p1v1(温度不変の場合)ですから外界に対して仕事はなされず内部エネルギーは保存されます。また気体にポテンシャルエネルギーは付随していませんので、この過程で膨張しても温度は変化しません。つまり細孔栓の中で真空中への膨張と同じような現象が実現されているわけです。しかし実在気体では、一般にp2v2とp1v1は等しくありません。そのため(p2v2-p1v1)だけの仕事が外界に対してなされるため、断熱過程にもかかわらず気体の内部エネルギーは変化します。さらにポテンシャルエネルギーを持っていますのでその意味でも、この過程により温度が変化します。エンタルピーhは一定でも内部エネルギーuは実在気体では変化することに注意して下さい。
(3)ジュール=トムソン係数の逆転曲線
前項の結論を2.(1)で説明した定圧膨張係数(体積膨張率)αで表すと
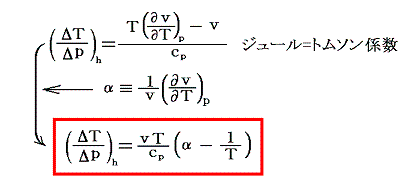
となる。膨張係数αは温度を上げたときの膨張を表す係数だから熱膨張係数と言う場合もある。
いずれにしても、ジュール=トムソン係数(ΔT/Δp)hは、α>(1/T)かα<(1/T)に応じて正になったり負になったりすることを意味する。つまり気体が膨張(Δp<0)する場合に冷却(ΔT<0)や加熱(ΔT>0)がおこる。
ところで実在気体(ファン・デル・ワールス気体)の熱膨張係数αはその状態方程式から求めることができた。そのため2.(1)の結論を用いればジュール=トムソン効果が逆転する境界の曲線(逆転曲線)を求めることができる。逆転曲線が満たすべき式は

であるが、ファン・デル・ワールス気体においてはv>bのみが意味を持つので
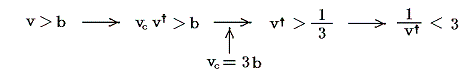
となり、上式の-符号の解のみが選択される。
すなわち
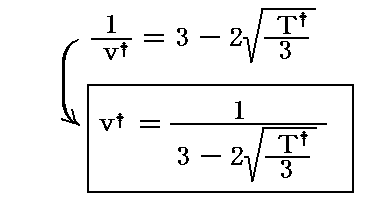
が(v†,T†)面上でジュール=トムソン効果が逆転する境界の曲線(逆転曲線)のグラフを示す関数です。
しかし、変数が(v†,T†)では利用に不便なのでファン・デル・ワールスの状態方程式を用いて変数を(p†,T†)に変換する。
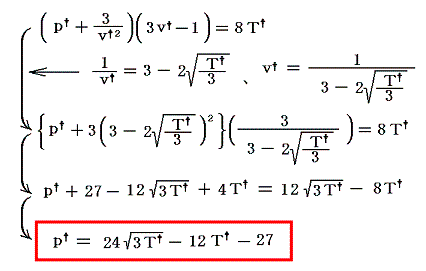
式から明らかなようにT†=3のとき極大値p†=9となる。またp†=0とおいて上式を解くとT†=3/4 or 27/4 の二つの解が得られるので、逆転曲線はその二点でT†軸と交わる下図の様な曲線となることが解る。
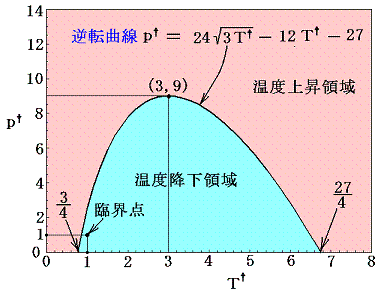
この関係式は任意のファン・デル・ワールス気体について普遍的に成り立つ。
例えば空気では室温で450気圧まで温度降下領域(こちらのN2の図あるいはこちらの空気の図を参照)であるのに対して、水素では室温で常に温度上昇領域となる。高圧に圧縮された水素が傷のできたパイプから漏れ出して自然発火する事故は、この性質が烈しく現れた不幸な例である。水素は33.2×6.7-273=-50℃以下になって初めて温度降下領域が存在し、もっとも効果的に冷却ができる温度は33.2×3-273=-173℃程度の低温域である。
ただし、何度も強調したようにファン・デル・ワールス状態方程式はあくまで近似的な式なので現実の気体の逆転曲線とは完全に一致しない。例えば水素H2の場合、理論曲線とのずれは下図のようになる。
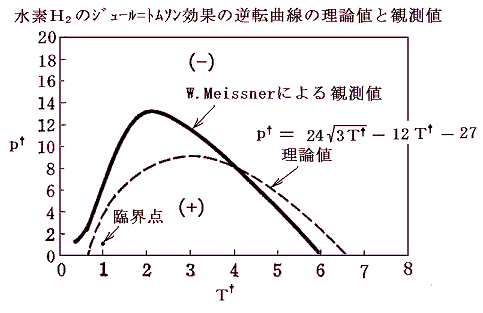
完全には一致しないが、かなり良く再現することがわかる。そのため、初期の水素やヘリウムの液化装置の開発にとってきわめて重要な情報を提供した。
水素のジュール=トムソン効果による温度降下領域を初めて明らかにしたのはファン・デル・ワールスです。デュワーは水素の液化の際、その成果を利用することができた。
また、カマリング・オネスは100℃~-216℃におけるヘリウムの振る舞いから係数a、bを求め、それから臨界点と上記の逆転曲線を求めて、ヘリウムの膨張のさいジュール=トムソン過程によって冷却効果を得るためには、最初の膨張開始温度が15K程度、膨張開始圧力が20気圧程度以下でなければならないことを知ったのです。
オネスは1910年に「ファン・デル・ワールスの仕事は魔法の棒の様に実験を導いた。そしてライデンの低温研究所は彼の理論の影響の下に発展したのである。」と書いているそうです。
[別稿「冷凍・低温技術の歴史」1873年、「冷凍・低温技術の歴史」1908年、「ファン・デル・ワールスのノーベル賞講演」参照]
[補足説明1]
臨界点やジュール=トムソン効果の逆転領域からかけ離れた高温領域のp、v、Tの振る舞いから求めた係数aとbによって、はるかに低い温度における臨界点や、ジュール=トムソン効果の逆転領域が予測できると言うことは驚くべき事です。
それは、とりもなおさずファン・デル・ワールスの状態方程式が、全てのp、v、T領域に於いて、1.(2)~(3)で述べた単純な二つの効果、[排除体積]と[分子間引力]でうまく説明できることを意味している。はるか低温の臨界点領域やジュール=トムソン効果の逆転領域に於いても単純にその二つの効果で状態方程式が説明できるから予測できるのです。
その様に予測できると言うことこそ、上記の仮説が正しい事を示しており、原子や分子の実在性やそれらの持つ性質の実態を明示している。その意味に於いてこの状態方程式の果たした役割は偉大です。
(4)ジュール=トムソン過程による冷却効果
前節の逆転曲線の意味をもう少し説明する。
上流側の温度と圧力がそれぞれT1とp1に固定された流体(したがってエントロピーhを一定に固定した流体)を細孔栓に強制的に流し、下流側の温度T2と圧力p2を測定する。そのとき色々な種類の細孔栓を用いて実験を繰り返すと、下流側のT2とp2として色々な組み合わせの値が得られる。それを圧力に対して温度をプロットすると、T-p線図上にh=一定の曲線が得られる[下左図]。
上流側入り口の圧力と温度を様々に変えて同様な実験を繰り返すと、一つの物質に対して、幾つかのh=一定の曲線を含むT-p線図が得られる[下右図]。
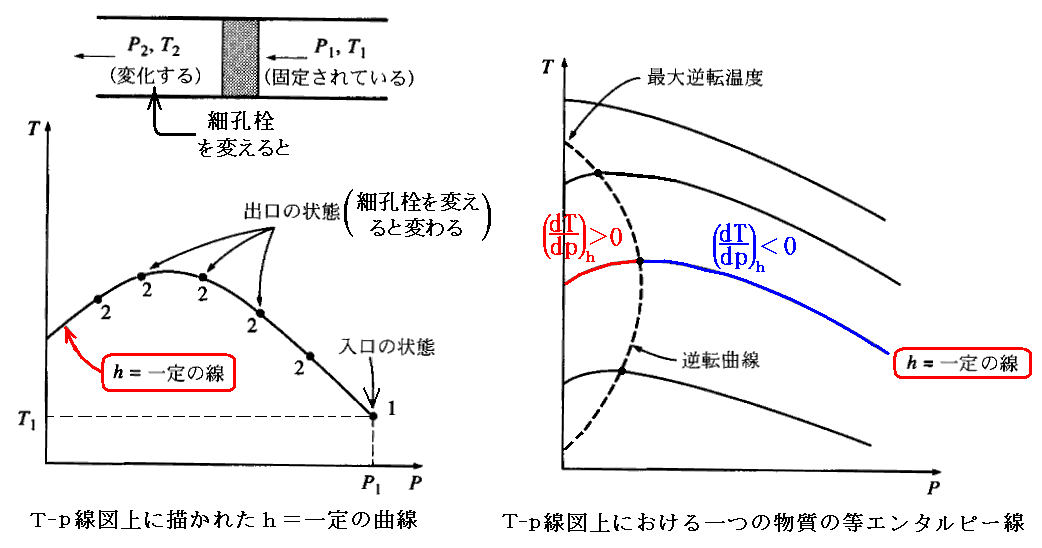
T-p線図上の等エンタルピー線の幾つかは勾配が零、すなわちジュール=トムソン係数が零になる点を通過する。これらの点を結ぶ線が前節で求めた“逆転曲線”です。逆転曲線と等エントタルピー線が交差する点の温度は“逆転温度”と呼ばれる。またp=0の線(縦軸)とこの逆転曲線の上側の線が交わる点の温度は“最大逆転温度”と呼ばれる。
窒素N2とヘリウム4Heの場合を以下に示す。
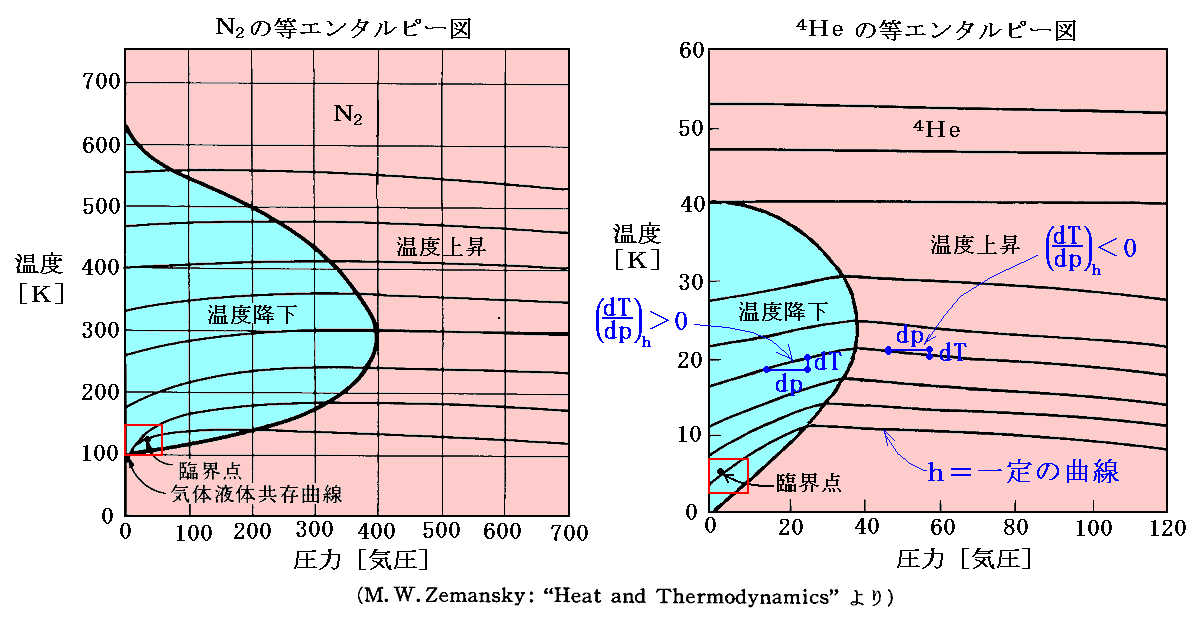
上図の赤四角□で囲った“飽和蒸気圧曲線”付近の(∂T/∂p)hを縦軸にしたレリーフ図を次に示す。気体がCO2の場合ですが、“逆転温度曲線”[(∂T/∂p)h=0の曲線]は右下の隅に僅かですがのぞいています。
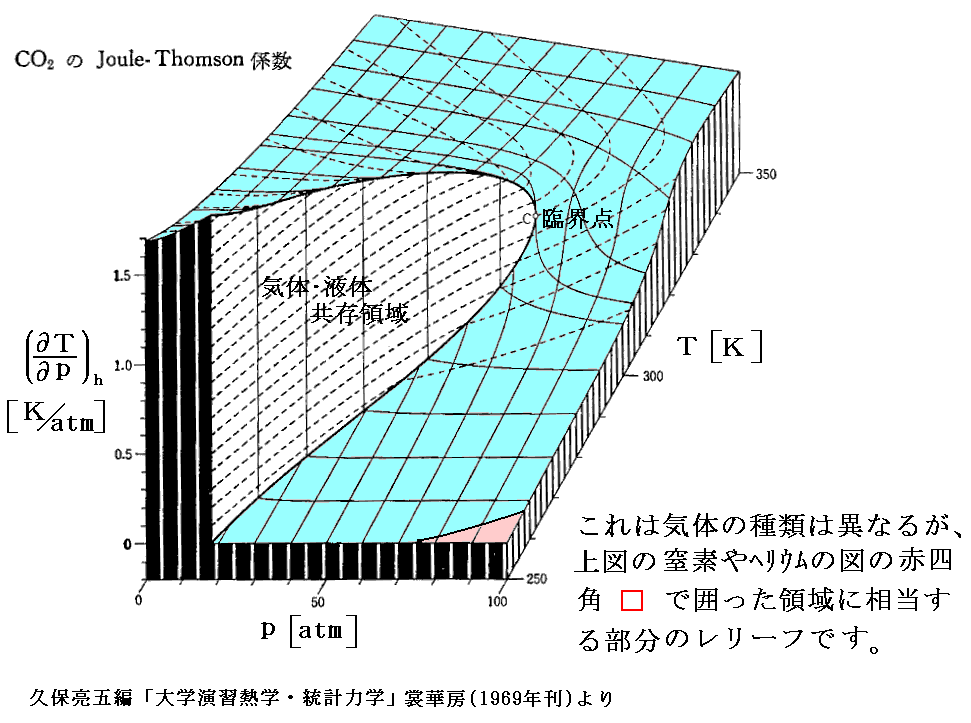
下図は4.(2)でその描き方を説明した h-p-T の三次元レリーフ図です。図中の エンタルピーh=一定 の曲線で (∂T/∂p)h=0 となる点(赤点)を繋いだ線が“ジュール=トムソン係数”の“逆転温度曲線”[(∂T/∂p)h=0の曲線]です。
気体が“空気”の場合を示していますが、先に述べた N2 の場合とほぼ同様の曲線になります。
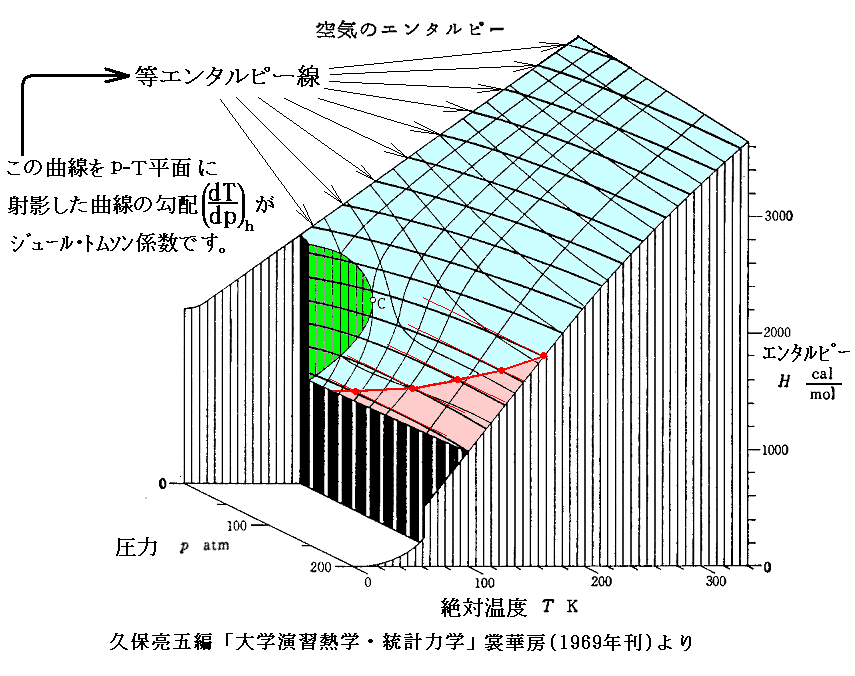
ジュール=トムソン過程を使って冷却をする場合の“温度降下量”は、前記の式を膨張開始圧力から最終的な圧力までエンタルピーhが一定の経路に沿って線積分すればよい。つまり
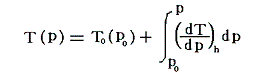
で求まる。
ここで温度 T0 は予備冷却のための液体に何を選ぶかによって決まる。例えば空気の液化には冷水の温度、水素の液化には液体窒素の沸点という風に。また膨張後の圧力
p は大抵大気圧とする場合が多い。そのため普通任意に選べるのは膨張開始圧力 p0 の値のみである。
積分値の意味から考えて p0 を上記の逆転曲線上の値に取った場合に最も低温が得られることは明らかです。その積分値は膨張開始圧力における温度と等エンタルピー線で結ばれる最終圧力における温度の差に相当する。
例えば水素の場合、W.Meissnerの実測値から見積もると、もっとも望ましい予備冷却温度はT0=64Kである。これは液体窒素を低圧で沸騰すれば得られる。そのとき実測された逆転曲線からこの温度に対応する一番望ましい膨張開始圧力を読み取るとp0=160気圧となる。
先ほどの図から解るように、ヘリウムの液化には予備冷却温度としてT0=14K、膨張開始圧力としてp0=29気圧が使われる。この14Kは液体水素を低圧で沸騰させる(Kamerlingh-Onnes)か、または最近ではヘリウムガスを準静的断熱膨張させて(KapitzaまたMeissner)冷やすことにより得られる。
[補足説明1]
ここで、重要な注意をします。
読者の中には、5.(2)で導いたジュール=トムソン係数を表す式
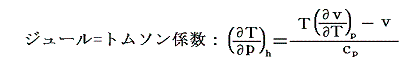
を用いれば、圧力変化に伴う温度降下量(ジュール=トムソン係数の値そのもの)も理論的に導けるのではないかと思われる方がおられるかもしれません。
しかし、残念ながら2.(3)で注意したように定積比熱cpの温度依存性を熱力学理論から求めることはできないので、ジュール=トムソン効果の量的な予測は熱力学理論の適応範囲外の事柄です。上に述べた境界線が求まるだけです。もちろん、他の実験的方法でcpのおよその値が求まれば、この式からその大きさを見積もることは可能です。
このとき逆に考えて、(∂v/∂T)pはp-v-Tの状態方程式から求めることができるのだから、この式を実在気体の[定圧比熱cp(p,T)]の値を[ジュール=トムソン効果の実測値]と[気体の状態方程式の実測値]から求めるのに用いればよい。実際、これは熱力学理論からは求めることができない実在気体の定圧比熱cp(p,T)を測定する有力な方法です。
[補足説明2]
分子間力の働かない理想気体では、真空中に噴出させても温度は変化しない。それは真空の部屋に気体分子が拡散・侵入するとき外部に対して仕事をしないので、そのままの運動エネルギーを保ったままになるからです。その真空の部屋の壁は固定されているので、その部屋の壁と衝突しても完全弾性衝突のために、以後も運動エネルギーの変化は生じない。
ところが、分子間力のある実在気体を、高密度に圧縮して分子間力の働く近距離中に存在する状態[下図のBの領域]から真空の部屋に吹き出し膨張させるとお互いの分子間引力を振り切るための仕事がなされることになる。つまり粒子間距離を大きくした場合、粒子どうしの引力に逆らう仕事をしなければならない。そのため運動エネルギーは減少することになる。これは温度の減少を意味する。これが、高圧に圧縮・冷却した実在気体を絞り弁から低圧の部屋に噴出させると温度が低下するジュール=トムソン効果です。
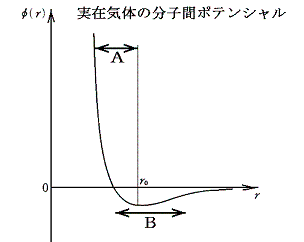
しかし、ここで注意しなければならいことがある。吹き出す前のガスの温度と圧力が高いときには、分子の運動エネルギーが大きいことと密度が高くて衝突の頻度が大きいために、相互に斥力の領域[上図のAの領域]に入り込んでいる時間が長くなる。そのため、吹き出しによって平均距離を大きくしたとき平均のポテンシャルエネルギーが下がり、ガスの温度はむしろ上昇する。
そのため温度が下がるためには始めの状態の温度と密度(圧力)がある範囲以下でなければならなかったのです。
[補足説明3]
5.章で説明した“ジュール=トムソン過程”に於ける“逆転曲線”と同じ様な事情で定まるのが、3.(3)で説明した定温の元での“ボイルの法則”に関係する“Boyle曲線”です。
この曲線の関数形とその意味については別ページで説明していますので、今一度そこの記述を復習してみて下さい。
(5)準静的断熱膨張過程とジュール=トムソン過程
実在気体が準静的断熱膨張したときの圧力変化に伴う温度変化を求めてみる。この過程は断熱過程でしかも準静的可逆過程だからエントロピーが一定の過程です。まず第二法則(エントロピー原理)の変数をsとpに変換する。
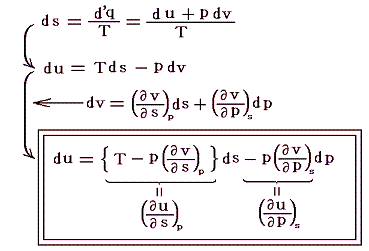
ここで、duが完全微分である条件より
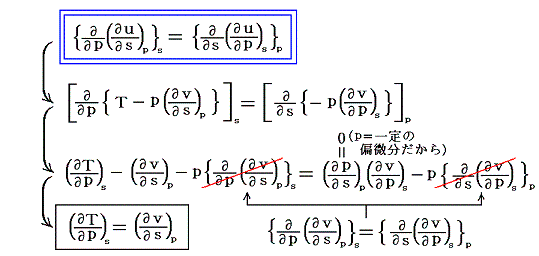
が得られる。
これは普通はエンタルピー h=u+pv の変分 dh=Tds+vdp が完全微分である条件より導かれるもので、Maxwellの関係式の一つです。
この左辺は断熱温度係数といわれるものであるが、右辺を変形してゆくと
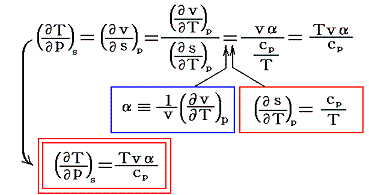
となる。ここでT、v、cpは正であり、定圧体積膨張係数αも普通は常に正と考えて良いので、右辺は常に>0である。つまり準静的断熱膨張で圧力を減小させると温度は常に低下することを示している。
[補足説明1]
上式は2.(4)で求めた関数曲面s(T,p)について数学的に常に成り立つ関係式[これは別稿の3.(2)4.で理想気体の状態方程式曲面の場合についてすでに説明した]に、5.(1)で求めたMaxwellの関係式を適用しても求まる。
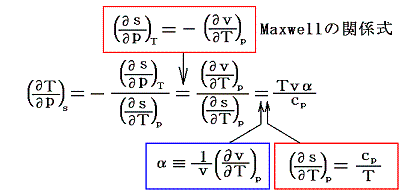
一方、5.(3)で求めたようにジュール=トムソン過程における温度変化は
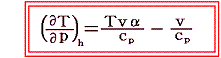
であった。つまり右辺の第二項が余分に付け加わっている。そのため同じ圧力減小であっても準静的断熱膨張過程よりもその差分
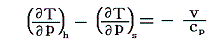
だけ常に温度低下量は少なくなる。また、この項があるため、ジュール=トムソン過程では、負になる(つまり圧力が下がったとき温度が上がる)領域が存在する。
このことから解るように、気体の温度を低下させる目的(例えば液化のために)には、全ての気体がどの圧力領域においても冷却を起こし、さらに温度低下が一層大きい準静的断熱膨張過程の方が、ジュール=トムソン過程よりも優れている。
しかしながら技術的にはジュール=トムソン過程の方が遙かに簡単に実現できる。
6.参考文献
このHPの内容は下記の文献に全面的に依存しています。図や表もそれらから引用しました。感謝!
- アーノルド・ゾンマーフェルト著「理論物理学講座Ⅴ 熱力学および統計力学」講談社(1969年刊)
van der Waals の状態方程式とジュール=トムソン効果、クラウジウス=クラペイロンの式に関する部分は、この本を主に参照しています。これはかなり難しい教科書ですが、ゾンマーフェルトの説明の仕方や言い回しの端々に、熱力学や統計力学が作り上げられていった時代の状況・雰囲気を伺うことができる。まさにその時代を生きた人だからこそ可能な説明ですが、そのあたりの事情を書き残してくれた先人の教科書で今日に伝わっているものは少ない。日本語で読めるものは、わずかにMax.PlanckとArnold.Sommerfeldの教科書をあげることができるのみです。
- マックス・プランク著、芝亀吉訳「熱力学」岩波書店(1941年刊)
クラウジウス=クラペイロンの式に関係した数値例を幾つか引用しました。それと§177が興味深い。
- 久保亮五編「大学演習 熱学・統計力学」裳華房(1969年刊)
具体的な数学計算式は、この本がとても詳しい。ファン・デル・ワールス気体について、幾つか参照しました。とくに第4章の問[B][31]の解答とそこに載っている図は重要です。
- エミリオ・セグレ 著「古典物理学を創った人々」みすず書房(1992年刊)
この本は何度か紹介しましたが、付録8、14を含めて、このHPのテーマに関係する部分も面白い。ただし訳者も注意されているように、付録8のエントロピーdsの完全微分条件からクラウジウス=クラペイロンの式を導く方法は正しくありません。飽和蒸気圧曲線の近傍に於いて液体側からその飽和蒸気圧曲線に近づく
s液(p,T) 曲面と、気体側から飽和蒸気圧曲線に近づく s気(p,T) 曲面が、蒸気圧曲線の所で連続的に繋がっている訳ではありませんので、その位置における完全微分条件を、そこでの議論のように用いるのは正しくありません。その当たりは4.(3)で説明していますので、そこを御覧下さい。
- 谷崎義衛著「化学の話シリーズ4 気体の話」培風館(1983年刊)
高校生向きでとても解りやすい。幾つかの図と説明を利用させてもらいました。
- 中村誠太郎、小沼通二編「ノーベル賞講演 物理学 第2巻」講談社(1979年刊)
ヨハネス ディデリク ファン デル ワールス ノーベル賞講演(1910年12月12日)
参考文献追記(2021年9月)
- ポール・セン著「宇宙を解く唯一の科学 熱力学」河出書房新社(2021年刊)
この中のp55~59を引用。